Skip to main content
SpringerLink
Log in

Synchronization of uncertain constrained hyperchaotic systems and chaos-based secure communications via a novel decomposed nonlinear stochastic estimator

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

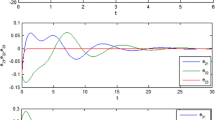
In this paper, a secure chaotic scheme for communications in noisy public channel is proposed. This scheme is based on the concept of carrier encryption in addition to the typical data encryption techniques. At the transmitter end, the unified chaotic system with adaptive parameter and a hyperchaotic Rössler system with uncertain parameters are coupled, constrained and used as a new hyperchaotic system which generates waveforms that are different from those of any known chaotic oscillator. After modulating one of the outputs of the system with the encrypted data signal, the outputs of the system are encrypted using a set of pre-defined encryption rules and transmitted to the receiving end through a noisy public communications channel. At the receiving end, the received outputs are decrypted and the transmitted data are retrieved by reconstructing the constrained hyperchaotic signals using the novel discrete-time iterative decomposed uncertain constrained extended Kalman filter (IDUCEKF). The proposed state estimator, besides being used to handle the estimation problem of uncertain constrained nonlinear dynamical systems, reduces the required processing time and gives good numerical performance. Simulation results are firstly presented to illustrate the applicability of the IDUCEKF in synchronizing the states of the constrained hyperchaotic system. Then, the proposed secure communication scheme is applied to transmit images, and the quality of the transmission process is assessed. The obtained results show the effectiveness of the proposed approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Satish, K., Jayakar, T., Tobin, C., Kadhavi, K., Murali, K.: Chaos based spread spectrum image steganography. IEEE Trans. Consum. Electron. 50, 587–590 (2004)

    Article  Google Scholar 

  2. Fallahi, K., Raoufi, R., Khoshhin, H.: An application of Chen system for secure chaotic communication based on extended Kalman filter and multi-shift cipher algorithm. Nonlinear Sci. Numer. Simul. 13, 763–781 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  3. Heidari Bateni, G., Mc Gillem, C.D.: A chaotic direct sequence spread spectrum communication system. IEEE Trans. Commun. 42, 1524–1527 (1994)

    Article  Google Scholar 

  4. Kolumban, G., Kennedy, M.P., Chua, L.O.: The role of synchronization in digital communications using chaos—part I: fundamentals of digital communications. IEEE Trans. Circuits Syst. I 44, 927–936 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  5. Kolumban, G., Kennedy, M.P., Chua, L.O.: The role of synchronization in digital communications using chaos—part II: chaotic modulation and chaotic synchronization. IEEE Trans. Circuits Syst. I 45, 1129–1140 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  6. Kolumban, G., Kennedy, M.P., Chua, L.O.: The role of synchronization in digital communications using chaos—part III: performance bounds for correlation receivers. IEEE Trans. Circuits Syst. I 47, 1673–1683 (2000)

    Article  MATH  Google Scholar 

  7. Pecora, L.M., Carroll, T.L., Johnson, G.A., Mar, D.J.: Fundamentals of synchronization in chaotic systems, concepts, and applications. Chaos 7, 520–542 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  8. Murali, K.: Digital signal transmission with cascaded heterogeneous chaotic systems. Phys. Rev. E 63, 016217–23 (2001)

    Article  Google Scholar 

  9. Calitoiu, D., Oommen, B.J., Nussbaum, D.: Desynchronizing a chaotic pattern recognition neural network to model inaccurate perception. IEEE Trans. Syst. Man Cybern. B 37, 692–704 (2007)

    Article  Google Scholar 

  10. Ruan, H., Zhai, T., Yaz, E.E.: A chaotic secure chaotic communication scheme with extended Kalman filter based parameter estimation. Proc. IEEE Conf. Control Appl. 1, 404–408 (2003)

    Google Scholar 

  11. Leung, H., Zhu, Z., Ding, Z.: An aperiodic phenomenon of the extended Kalman filter in filtering noisy chaotic signals. IEEE Trans. Signal Process. 48, 1807–1810 (2000)

    Article  Google Scholar 

  12. Li, S.Y., Ge, Z.M.: Fuzzy modelling and synchronization of two totally different chaotic systems via novel fuzzy mode. IEEE Trans. Syst. Man Cybern. B 41, 1015–1026 (2011)

    Article  MathSciNet  Google Scholar 

  13. Zhang, H., Ma, T., Huang, G.-B., Wang, Z.: Robust global exponential synchronization of uncertain chaotic delayed neural network via dual-stage impulsive control. IEEE Trans. Syst. Man Cybern. B 40, 831–844 (2010)

    Article  Google Scholar 

  14. Ahn, C.K.: Takagi–Sugeno fuzzy receding horizon H\(\infty \) chaotic synchronization and its application to the Lorenz system. Nonlinear Anal. Hybrid Syst. 9, 1–8 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  15. Shi, X., Wang, Z.: Robust chaos synchronization of four-dimensional energy resource system via adaptive feedback control. Nonlinear Dyn. 60, 631–637 (2010)

    Article  MATH  Google Scholar 

  16. Lu, J.A., Wu, X.Q., Lu, J.H.: Synchronization of a unified chaotic system and the application in secure communication. Phys. Lett. A 305, 365–370 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  17. Chen, H.H., Sheu, G.J., Lin, Y.L., Chen, C.S.: Chaos synchronization between two different chaotic systems via nonlinear feedback control. Nonlinear Anal. Theory Methods Appl. 70, 4393–4401 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  18. Wang, X., Song, J.: Synchronization of the unified chaotic system. Nonlinear Anal. Theory Methods Appl. 69, 3409–3416 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  19. Lin, J.S., Yan, J.J.: Adaptive synchronization for two identical generalized Lorenz chaotic systems via a single controller. Nonlinear Anal. Real World Appl. 10, 1151–1159 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  20. Njah, A.N.: Tracking control and synchronization of the new hyperchaotic Liu system via backstepping techniques. Nonlinear Dyn. 61(1–2), 1–9 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  21. Xiang-Jun, W., Jing-Sen, L., Guan-Rong, C.: Chaos synchronization of Rikitake chaotic attractor using the passive control technique. Nonlinear Dyn. 53(1–2), 45–53 (2008)

    Article  MathSciNet  Google Scholar 

  22. Ablay, G.: Sliding mode control of uncertain unified chaotic systems. Nonlinear Anal. Hybrid Syst. 3, 531–535 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  23. Smaoui, N., Karouma, A., Zribi, M.: Secure communication based on the synchronization of the hyperchaotic Chen and the unified chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 16, 3279–3293 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  24. Mata-Machuca, J.L., Martínez-Guerra, R., Aguilar-López, R., Aguilar-Ibañez, C.: A chaotic system in synchronization and secure communications. Commun. Nonlinear. Sci. Numer. Simul. 17, 1706–1713 (2012)

    Article  MathSciNet  Google Scholar 

  25. Wang, H., Han, Z.Z., Zhang, W., Xie, Q.Y.: Synchronization of unified chaotic systems with uncertain parameters based on the CLF. Nonlinear Anal. Real World Appl. 10, 715–722 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  26. Wang, H., Han, Z.Z., Xie, Q.Y., Zhang, W.: Finite-time synchronization of uncertain chaotic systems based on CLF. Nonlinear Anal. Real World Appl. 10, 2842–2849 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  27. Nosrati, K., Azemi, A., Pariz, N., Shokouhi-R, A.: Chaotic synchronization of Lorenz system using Unscented Kalman Filter. Proc. Chin. Control Decis. Conf. 1, 848–853 (2011)

    Google Scholar 

  28. Chen, S.H., Yang, Q., Wang, C.P.: Impulsive control and synchronization of unified chaotic system. Chaos Solitons Fract. 20, 153–160 (2004)

    MathSciNet  MATH  Google Scholar 

  29. Yang, X., Yang, Z., Nie, X.: Exponential synchronization of discontinuous chaotic systems via delayed impulsive control and its application to secure communication. Commun. Nonlinear Sci. Numer. Simul. 19, 1529–1543 (2014)

  30. Zhu, Z., Leung, H.: Adaptive blind equalization for chaotic communication systems using extended Kalman filter. IEEE Trans. Circuits Syst. I(48), 979–987 (2001)

    Google Scholar 

  31. Zhu, F.: Observer based synchronization of uncertain chaotic system and its application to secure communications. Chaos Solitons Fract. 40, 2384–2391 (2009)

    Article  MATH  Google Scholar 

  32. Yang, J., Zhu, F.: Synchronization for chaotic systems and chaos-based secure communications via both reduced-order and step-by-step sliding mode observers. Commun. Nonlinear Sci. Numer. Simul. 18, 926–937 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  33. Chen, M., Zhou, D., Shang, Y.: A sliding mode observer based secure communication scheme. Chaos Solitons Fract. 25, 573–578 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  34. Short, K.M.: Unmasking a modulated chaotic communication scheme. Int. J. Bifurc. Chaos 6, 367–375 (1996)

    Article  MATH  Google Scholar 

  35. Perez, G., Cerdeira, H.A.: Extracting messages masked by chaos. Phys. Rev. Lett. 74, 1970–1973 (1995)

    Article  Google Scholar 

  36. Tlelo-Cuautle, E., Carbajal-Gomez, V.H., Obeso-Rodelo, P.J., Rangel-Magdaleno, J.J., Núñez-Pérez, J.C.: FPGA realization of a chaotic communication system applied to image processing. Nonlinear Dyn. (2015). doi:10.1007/s11071-015-2284-x

    MathSciNet  Google Scholar 

  37. Tlelo-Cuautle, E., Rangel-Magdaleno, J.J., Pano-Azucena, A.D., Obeso-Rodelo, P.J., Nunez-Perez, J.C.: FPGA realization of multi-scroll chaotic oscillators. Commun. Nonlinear Sci. Numer. Simul. 27(1), 66–80 (2015)

    Article  MathSciNet  Google Scholar 

  38. García-Martínez, M., Campos-Cantón, E.: Pseudo-random bit generator based on multi-modal maps. Nonlinear Dyn. (2015). doi:10.1007/s11071-015-2303-y

    MathSciNet  Google Scholar 

  39. De la Fraga, L.G., Tlelo-Cuautle, E.: Optimizing the maximum Lyapunov exponent and phase space portraits in multi-scroll chaotic oscillators. Nonlinear Dyn. 76(2), 1503–1515 (2014)

    Article  Google Scholar 

  40. Hassan, M.F.: Optimal Kalman filter for large scale systems using the partitioning approach. IEEE Trans. Syst. Man Cyber. 6, 714–720 (1976)

    Article  MATH  Google Scholar 

  41. Hassan, M.F., Salut, G., Singh, M.G., Titli, A.: A decentralized computational algorithm for the global Kalman filter. IEEE Trans. Automat. Control 23, 262–268 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  42. Mahmoud, M.S., Hassan, M.F., Darwish, M.G.: Large-Scale Control Systems: Theories and Techniques. Marcel Dekker Inc., New York (1985)

    MATH  Google Scholar 

  43. Hassan, M.F.: A Decomposed Estimator for Constrained Uncertain Stochastic Nonlinear Systems (submitted for publication) (2015)

  44. Zhou, Q., Shi, P., Liu, H., Xu, S.: Neural-network-based decentralized adaptive output-feedback control for large-scale stochastic nonlinear systems. IEEE Trans. Syst. Man Cyber. B 42, 1608–1619 (2012)

    Article  Google Scholar 

  45. Liu, S., Zhang, J., Jiang, Z.: Decentralized adaptive output-feedback stabilization for large-scale stochastic nonlinear systems. Automatica 43, 238–251 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  46. Mahmoud, M.S.: Decentralized Control and Filtering in Interconnected Dynamical Systems. CRC Press, Boca Raton (2011)

    MATH  Google Scholar 

  47. Wang, X.Y., Wu, X.J.: Tracking control and synchronization of four-dimensional hyperchaotic Rössler system. Chaos 16, 033121 (2006)

    Article  MATH  Google Scholar 

  48. Meditch, J.S.: Stochastic Optimal Linear Estimation and Control. McGraw-Hill, New York (1965)

    MATH  Google Scholar 

  49. Reif, K., Gunther, S., Yaz, E., Unbehauen, R.: Stochastic stability of the discrete-time extended Kalman filter. IEEE Trans. Automat. Control 44, 714–728 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  50. Hassan, M.F., Alrifai, M.T., Soliman, H.M., Kourah, M.A.: Observer-based controller for constrained uncertain stochastic nonlinear discrete-time systems. Int. J. Robust Nonlinear Control (2015). doi:10.1002/rnc.3396

  51. Luenberger, D.: Optimization by Vector Space Methods. Wiley, New York (1969)

  52. Hassan, M.F.: Iterated constrained state estimator for nonlinear discrete-time systems with uncertain parameters. Int. J. Innov. Comput. Inf. Control 8, 6141–6160 (2012)

    Google Scholar 

  53. Sandri, M.: Numerical calculation of Lyapunov exponents. Math. J. 6, 78–84 (1996)

    Google Scholar 

  54. Eckmann, J.P., Ruelle, D.: Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 57, 617–656 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  55. Holte, J.M.: Discrete Gronwall lemma and applications, MAA-NCS Meeting at the University of North Dakota 24 (2009). http://homepages.gac.edu/~holte/publications/GronwallLemma.pdf

Download references

Acknowledgments

This research was supported by Kuwait University under research Grant No. EE 02/14.

Author information

Authors and Affiliations

  1. Electrical Engineering Department, College of Engineering, Kuwait University, P.O. Box 5969, 13060, Safat, Kuwait

    Mohamed F. Hassan

Authors
  1. Mohamed F. Hassan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohamed F. Hassan.

Appendices

Appendix 1

Proof of Lemma 4.1

For the ith subsystem, by linearizing the system dynamics around \(\hat{\varvec{x}}({\varvec{k}}| {\varvec{k}})\) and \(\bar{\varvec{b}}\) while neglecting higher-order terms, we get:

$$\begin{aligned}&{\varvec{f}}_{\varvec{i}} ({\varvec{x}}({\varvec{k}}),{\varvec{b}}({\varvec{k}}))\cong {\varvec{f}}_{\varvec{i}} (\hat{\varvec{x}}({\varvec{k}}| {\varvec{k}}),\bar{\varvec{b}})+{\hat{\varvec{F}}}_{\varvec{i}}^{\prime } ({\varvec{k}})({\varvec{x}}({\varvec{k}})\nonumber \\&\quad -\,\hat{\varvec{x}}({\varvec{k}}| {\varvec{k}}))+{\hat{{{\varvec{E}}}}}_{\varvec{i}}^{\prime } ({\varvec{k}})({\varvec{b}}({\varvec{k}})-\bar{\varvec{b}}) \end{aligned}$$
(83)

where \({\hat{\varvec{F}}}_{\varvec{i}}^{\prime } \), \({\hat{\varvec{E}}}_{\varvec{i}}^{\prime } \) are as defined by (18).

Substituting (83) into the ith subsystem model (14), we get:

$$\begin{aligned}&{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)\cong {\varvec{f}}_{\varvec{i}} (\hat{\varvec{x}}({\varvec{k}}| {\varvec{k}}),\bar{\varvec{b}})+{\hat{\varvec{F}}}_{\varvec{i}}^{\prime } ({\varvec{k}})({\varvec{x}}({\varvec{k}})-\hat{\varvec{x}}({\varvec{k}}| {\varvec{k}}))\nonumber \\&\quad +\,{\hat{\varvec{E}}}_{\varvec{i}}^{\prime } ({\varvec{k}})({\varvec{b}}({\varvec{k}})-\bar{\varvec{b}})+{\varvec{w}}_{\varvec{i}} ({\varvec{k}}) \end{aligned}$$
(84)

The conditional expectation of (84) given the measurements up to the kth instant of time is given by:

$$\begin{aligned}&\hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})\nonumber \\&\quad \cong \,{\varvec{E}}\Big \{ \Big [ {\varvec{f}}_{\varvec{i}} (\hat{\varvec{x}}({\varvec{k}}| {\varvec{k}}),\bar{\varvec{b}})+{\hat{\varvec{F}}}_{\varvec{i}}^{\prime } ({\varvec{k}})({\varvec{x}}({\varvec{k}})-\hat{\varvec{x}}({\varvec{k}}| {\varvec{k}}))\nonumber \\&\qquad +\,{\hat{\varvec{E}}}_{\varvec{i}}^{\prime } ({\varvec{k}})({\varvec{b}}({\varvec{k}})-\bar{\varvec{b}})+{\varvec{w}}_{\varvec{i}} ({\varvec{k}}) \Big ] \Big |{\varvec{Y}}^{{\varvec{k}}} \Big \} \end{aligned}$$
(85)

where \({\varvec{Y}}^{{\varvec{k}}}=[{\varvec{y}}^{{\varvec{T}}}(1) {\varvec{y}}^{{\varvec{T}}}(2) \cdots {\varvec{y}}^{{\varvec{T}}}({\varvec{k}})]\)

Since \(\hat{\varvec{x}}({\varvec{k}}| {\varvec{k}})\cong {\varvec{E}}\left\{ {{{\varvec{x}}({\varvec{k}})} |{\varvec{Y}}^{{\varvec{k}}}} \right\} \), the variables \({\varvec{Y}}^{{\varvec{k}}}\), \({\varvec{w}}_{\varvec{i}} ({\varvec{k}})\) and \({\varvec{b}}({\varvec{k}})\) are independent, \({\varvec{E}}\left\{ {{\varvec{w}}_{\varvec{i}} ({\varvec{k}})} \right\} =0\) and \({\varvec{E}}\left\{ {{\varvec{b}}({\varvec{k}})} \right\} =\bar{\varvec{b}}\), then the predicted estimate \(\hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})\) takes the form:

$$\begin{aligned} \hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})\cong {\varvec{f}}_{\varvec{i}} (\hat{\varvec{x}}({\varvec{k}}| {\varvec{k}}),\bar{\varvec{b}}) \end{aligned}$$
(86)

let \({\tilde{\varvec{x}}}({\varvec{k}}| {\varvec{k}})={\varvec{x}}({\varvec{k}})-\hat{\varvec{x}}({\varvec{k}}| {\varvec{k}})\), \({\tilde{\varvec{x}}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})={\varvec{x}}_{\varvec{i}} ({\varvec{k}})-\hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})\), and \(\tilde{{\varvec{b}}}({\varvec{k}})={\varvec{b}}({\varvec{k}})-\bar{\varvec{b}}\), then using (84) and (86), we get:

$$\begin{aligned} {\tilde{\varvec{x}}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})\cong {\hat{\varvec{F}}}_{\varvec{i}}^{\prime } ({\varvec{k}}){\tilde{\varvec{x}}}({\varvec{k}}| {\varvec{k}})+{\hat{\varvec{E}}}_{\varvec{i}}^{\prime } ({\varvec{k}})\tilde{\varvec{b}}({\varvec{k}})+{\varvec{w}}_{\varvec{i}} ({\varvec{k}})\nonumber \\ \end{aligned}$$
(87)

The covariance matrix of the prediction error of the ith subsystem is defined by:

$$\begin{aligned} {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} } ({\varvec{k}}+1| {\varvec{k}})={\varvec{E}}\left\{ {{\tilde{\varvec{x}}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}}) {\tilde{\varvec{x}}}^{{\varvec{T}}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})} \right\} \end{aligned}$$
(88)

Substituting from (87) into (88) and with the use of model properties (13) (i.e., \({\varvec{w}}({\varvec{k}})\), and \(\tilde{\varvec{b}}({\varvec{k}})\) are independent, \({\varvec{x}}_{\varvec{i}} ({\varvec{k}})\) is independent of \({\varvec{w}}({\varvec{k}})\) and \({\varvec{b}}({\varvec{k}})\), and \({\varvec{E}}\left\{ {\tilde{\varvec{b}}({\varvec{k}})} \right\} ={\varvec{E}}\left\{ {{\varvec{b}}({\varvec{k}})-\bar{\varvec{b}}} \right\} =0)\), one gets after simple mathematical manipulations:

$$\begin{aligned}&{\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} }^0 ({\varvec{k}}+1| {\varvec{k}} +1)={\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} } ({\varvec{k}}+1| {\varvec{k}})\nonumber \\&\quad \cong \,{\hat{\varvec{F}}}_{\varvec{i}}^{\prime } ({\varvec{k}}) {\varvec{P}}_{{\varvec{k}}| {\varvec{k}}} {\hat{\varvec{F}}}_{\varvec{i}}^{{\prime }\varvec{T}} ({\varvec{k}})\nonumber \\&\qquad +\,{\hat{\varvec{E}}}_{\varvec{i}}^{\prime } ({\varvec{k}}) {\varvec{\varGamma }} ({\varvec{k}}){\hat{\varvec{E}}}_{\varvec{i}}^{{\prime }{\varvec{T}}} ({\varvec{k}})+{\varvec{Q}}_{{\varvec{ii}}} ({\varvec{k}}) \end{aligned}$$
(89)

The cross-covariance matrix of the prediction error of the ith and the jth subsystems is defined by:

$$\begin{aligned} {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}} } ({\varvec{k}}+1| {\varvec{k}})={\varvec{E}}\left\{ {{\tilde{\varvec{x}}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}}) {\tilde{\varvec{x}}}^{{\varvec{T}}}_{\varvec{j}} ({\varvec{k}}+1| {\varvec{k}})} \right\} \end{aligned}$$
(90)

With the assumptions of the model properties and the independency of the noise subvectors \({\varvec{w}}_{\varvec{i}} ({\varvec{k}})\) and \({\varvec{w}}_{\varvec{j}} ({\varvec{k}})\), it is easy to show that

$$\begin{aligned}&{\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}}}^0 ({\varvec{k}}+1| {\varvec{k}} +1)={\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}} } ({\varvec{k}}+1| {\varvec{k}})\nonumber \\&\quad \cong \,{\hat{\varvec{F}}}_{\varvec{i}}^{\prime } ({\varvec{k}}) {\varvec{P}}_{{\varvec{k}}| {\varvec{k}}} {\hat{\varvec{F}}}_{\varvec{i}}^{{\prime }{\varvec{T}}} ({\varvec{k}})+{\hat{\varvec{E}}}_{\varvec{i}}^{\prime } ({\varvec{k}}) {\varvec{\varGamma }} ({\varvec{k}}){\hat{\varvec{E}}}_{\varvec{i}}^{{\prime }{\varvec{T}}} ({\varvec{k}}) \end{aligned}$$
(91)

Equation (86) gives the predicted estimate of \({\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)\) denoted by \(\hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})\) for \(i\in \{1,2,{\ldots },N\}\), Eq. (89) gives the covariance matrices of the prediction estimation error of \({\varvec{x}}_{\varvec{i}} ({\varvec{k}})\), whereas Eq. (91) gives the cross-covariance matrices of the estimation errors of \({\varvec{x}}_{\varvec{i}} ({\varvec{k}})\) and \({\varvec{x}}_{\varvec{j}} ({\varvec{k}}) \quad \forall \; i,j \in \left\{ {i+1, 2, \ldots ,N} \right\} \).

Now, assume that we received the measurement vector \({\varvec{y}}({\varvec{k}}+1)\) at the \((k+1)\)th sampling instant. By decomposing \({\varvec{y}}({\varvec{k}}+1)\in {\varvec{R}}^{{\varvec{m}}}\) into M subvectors \({\varvec{y}}_{\varvec{r}} ({\varvec{k}}+1)\in {\varvec{R}}^{{\varvec{m}}_{\varvec{r}}}\) where \(r\in \{1,2,\ldots , M\}\) and \(\sum _{r=1}^M {m_r =m} \), then the predicted estimates of the state subvectors \(\hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})\) for \(i\in \{1,2,\ldots , N\}\) will be updated successively using the measurement subvectors \({\varvec{y}}_{\varvec{r}} ({\varvec{k}}+1)\) for \(r\in \{1,2,\ldots , M\}\). Therefore, we have

$$\begin{aligned}&\hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1})\nonumber \\&\quad \cong {\varvec{E}}\Big \{ {{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)} | {\varvec{Y}}^{{\varvec{k}}}, {\varvec{y}}_1 ({\varvec{k}}+1),\nonumber \\&\qquad {\varvec{y}}_2 ({\varvec{k}}+1),\ldots , {\varvec{y}}_{\varvec{M}} ({\varvec{k}}+1) \Big \} \end{aligned}$$
(92)

where

$$\begin{aligned} {\varvec{y}}_{\varvec{r}} ({\varvec{k}}\!+\!1)\!=\!{\varvec{h}}_{\varvec{r}} ({\varvec{x}}({\varvec{k}}\!+\!1),{\varvec{c}}({\varvec{k}}\!+\!1))\!+\!{\varvec{v}}_{\varvec{r}} ({\varvec{k}}\!+\!1) \end{aligned}$$
(93)

Using the multiple projection approach [41, 42], we have:

$$\begin{aligned}&\hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1})\nonumber \\&\quad \cong {\varvec{E}}\left\{ {{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)} | {\varvec{Y}}^{{\varvec{k}}}, {\tilde{\varvec{y}}}_1 ({\varvec{k}}+1| {\varvec{k}}), \right. \nonumber \\&\qquad \quad {\tilde{\varvec{y}}}^{1}_2 ({\varvec{k}}+1| {{\varvec{k}}+1}), {\tilde{\varvec{y}}}^{2}_3 ({\varvec{k}}+1| {{\varvec{k}}+1}),\nonumber \\&\qquad \qquad \left. \ldots ,{\tilde{\varvec{y}}}_{\varvec{M}}^{{\varvec{M}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1}) \right\} \nonumber \\&\quad \cong {\varvec{E}}\left\{ {{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)} | {\varvec{Y}}^{{\varvec{k}}} \right\} \nonumber \\&\qquad +\,{\varvec{E}}\left\{ {{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)} | {\tilde{\varvec{y}}}_1 ({\varvec{k}}+1| {\varvec{k}}) \right\} \nonumber \\&\qquad +\,\sum \limits _{{\varvec{r}}=2}^{{\varvec{M}}} {\varvec{E}}\left\{ {{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)} | {\tilde{\varvec{y}}}_{\varvec{r}}^{{\varvec{r}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1}) \right\} \nonumber \\&\quad \cong {\varvec{E}}\left\{ {{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)} | {\varvec{Y}}^{{\varvec{k}}} \right\} \nonumber \\&\qquad +\,\sum \limits _{{\varvec{r}}=1}^{\varvec{M}} {\varvec{E}}\left\{ {{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)} | {\tilde{\varvec{y}}}_{\varvec{r}}^{{\varvec{r}}-1} ({\varvec{k}}+1|{{\varvec{k}}+1}) \right\} \end{aligned}$$
(94)

where for \(r=1\) we have:

$$\begin{aligned} {\tilde{\varvec{y}}}^{0}_1 ({\varvec{k}}+1| {{\varvec{k}}+1})= & {} {\tilde{\varvec{y}}}_1 ({\varvec{k}}+1| {\varvec{k}})\nonumber \\\cong & {} {\varvec{y}}_1 ({\varvec{k}}+1)-\hat{{{\varvec{y}}}}_1 ({\varvec{k}}+1| {\varvec{k}}) \nonumber \\ \hat{{{\varvec{y}}}}^{0}_1 ({\varvec{k}}+1| {{\varvec{k}}+1})= & {} \hat{{{\varvec{y}}}}_1 ({\varvec{k}}+1| {\varvec{k}}) \nonumber \\\cong & {} \hat{\varvec{h}}_1 (\hat{\varvec{x}}({\varvec{k}}+1| {\varvec{k}}),\bar{\varvec{c}}) \end{aligned}$$
(95)

and for \(r \in \{2, 3, \ldots ,M\}\), we have:

$$\begin{aligned}&{\tilde{\varvec{y}}}_{\varvec{r}}^{{\varvec{r}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1})={\varvec{y}}_{\varvec{r}} ({\varvec{k}}+1)-\hat{\varvec{y}}_{\varvec{r}}^{{\varvec{r}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1}) \nonumber \\&\hat{\varvec{y}}_{\varvec{r}}^{{\varvec{r}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1})\cong \hat{\varvec{h}}_{\varvec{r}} (\hat{\varvec{x}}^{{\varvec{r}}-1}({\varvec{k}}+1| {{\varvec{k}}+1}),\bar{\varvec{c}}) \end{aligned}$$
(96)

Using the first submeasurement vector \({\varvec{y}}_1({\varvec{k}}+1)\), the approximated filtered estimate \(\hat{\varvec{x}}^{1}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1})\) for \(i\in \{1,2,\ldots , N\}\) is such that:

$$\begin{aligned}&\hat{\varvec{x}}^{1}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1})\nonumber \\&\quad \cong {\varvec{E}}\left\{ {{{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)} | {\varvec{Y}}^{{\varvec{k}}}} \right\} +{\varvec{E}}\left\{ {{{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)} | {\tilde{\varvec{y}}}_1 ({\varvec{k}}+1| {\varvec{k}})} \right\} \nonumber \\&\quad \cong \hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})+{\varvec{P}}_{{\varvec{x}}_{\varvec{i}} {\tilde{\varvec{y}}}_1} ({\varvec{k}}+1| {\varvec{k}})\nonumber \\&\qquad \times \,{\varvec{P}}^{-1}_{{\tilde{\varvec{y}}}_1 {\tilde{\varvec{y}}}_1} ({\varvec{k}}+1| {\varvec{k}}){\tilde{\varvec{y}}}_1 ({\varvec{k}}+1| {\varvec{k}}) \\&\quad \cong \hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})+{\varvec{K}}_{1{\varvec{i}}}^1 ({\varvec{k}}+1) {\tilde{\varvec{y}}}_1 ({\varvec{k}}+1| {\varvec{k}}) \nonumber \\&\quad \cong \hat{\varvec{x}}^{0}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1})+ {\varvec{K}}_{1{\varvec{i}}}^1 ({\varvec{k}}+1){\tilde{\varvec{y}}}^{0}_1 ({\varvec{k}}+1| {{\varvec{k}}+1})\nonumber \end{aligned}$$
(97)

where

$$\begin{aligned}&{\tilde{\varvec{y}}}_1 ({\varvec{k}}+1| {\varvec{k}})={\varvec{h}}_1 ({\varvec{x}}({\varvec{k}}+1),{\varvec{c}}({\varvec{k}}+1))\nonumber \\&\quad +\,{\varvec{v}}_1 ({\varvec{k}}+1)-\hat{\varvec{h}}_{ 1} (\hat{\varvec{x}}({\varvec{k}}+1| {\varvec{k}}),\bar{\varvec{c}})\end{aligned}$$
(98)
$$\begin{aligned}&{\varvec{K}}_{1{\varvec{i}}}^1 ({\varvec{k}}+1)\cong {\varvec{P}}_{{\varvec{x}}_{\varvec{i}} {\tilde{\varvec{y}}}_1} ({\varvec{k}}+1| {\varvec{k}}){\varvec{P}}^{-1}_{{\tilde{\varvec{y}}}_1{\tilde{\varvec{y}}}_1} ({\varvec{k}}+1| {\varvec{k}}) \end{aligned}$$
(99)

Since \({\varvec{x}}({\varvec{k}}+1)=\hat{\varvec{x}}({\varvec{k}}+1| {\varvec{k}})+{\tilde{\varvec{x}}}({\varvec{k}}+1| {\varvec{k}})\) and \({\varvec{c}}({\varvec{k}}+1)=\bar{\varvec{c}}+\tilde{{\varvec{c}}}({\varvec{k}}+1)\), and assuming that \({\varvec{x}}({\varvec{k}}+1)\) is close to \(\hat{\varvec{x}}({\varvec{k}}+1| {\varvec{k}})\) and \({\varvec{c}}({\varvec{k}}+1)\) is close to \(\bar{\varvec{c}}\) such that \({\varvec{h}}_1 ({\varvec{x}}({\varvec{k}}+1),{\varvec{c}}({\varvec{k}}+1))\) can be replaced by its first-order approximation, i.e., we assume \({\varvec{h}}_1 ({\varvec{x}}({\varvec{k}}+1),{\varvec{c}}({\varvec{k}}+1))\) is affine on a neighborhood of \({\varvec{x}}({\varvec{k}}+1),\hat{\varvec{x}}({\varvec{k}}+1| {\varvec{k}})\) and \({\varvec{c}}({\varvec{k}}+1), \bar{\varvec{c}}\). Then, we have:

$$\begin{aligned}&{\varvec{h}}_1 ({\varvec{x}}({\varvec{k}}+1),{\varvec{c}}({\varvec{k}}+1))\cong \hat{\varvec{h}}_1 (\hat{\varvec{x}}({\varvec{k}}+1| {\varvec{k}}),\bar{\varvec{c}})\nonumber \\&\quad +\,\hat{\varvec{H}}_1 ({\varvec{k}}+1){\tilde{\varvec{x}}}({\varvec{k}}+1| {\varvec{k}})+\hat{\varvec{D}}_1 ({\varvec{k}}+1)\tilde{{\varvec{c}}}({\varvec{k}}+1)\nonumber \\ \end{aligned}$$
(100)

where \(\hat{\varvec{H}}_1 ({\varvec{k}}+1)=\hat{\varvec{H}}^{0}_1 ({\varvec{k}}+1), \hat{\varvec{D}}_1 ({\varvec{k}}+1)=\hat{\varvec{D}}_1^0 ({\varvec{k}}+1)\) are defined by (26) for \(r=1\).

Substituting from (100) into (98) while using (95), we get:

$$\begin{aligned}&{\tilde{\varvec{y}}}^{0}_1 ({\varvec{k}}+1| {{\varvec{k}}+1})={\tilde{\varvec{y}}}_1 ({\varvec{k}}+1| {\varvec{k}})\nonumber \\&\quad \cong \hat{\varvec{H}}_1 ({\varvec{k}}+1){\tilde{\varvec{x}}}({\varvec{k}}+1| {\varvec{k}})+\hat{\varvec{D}}_1 ({\varvec{k}}+1)\tilde{{\varvec{c}}}({\varvec{k}}+1)\nonumber \\&\quad +\,{\varvec{v}}_1 ({\varvec{k}}+1) \end{aligned}$$
(101)

The cross-covariance matrix \({\varvec{P}}_{{\varvec{x}}_{\varvec{i}} {\tilde{\varvec{y}}}_1} ({\varvec{k}}+1| {\varvec{k}})\) is defined by:

$$\begin{aligned}&{\varvec{P}}_{{\varvec{x}}_{\varvec{i}} {\tilde{\varvec{y}}}_1} ({\varvec{k}}+1| {\varvec{k}})={\varvec{E}}\left\{ {{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1) {\tilde{\varvec{y}}}^{{\varvec{T}}}_1 ({\varvec{k}}+1| {\varvec{k}})} \right\} \nonumber \\&\quad = {\varvec{E}}\left\{ {\left( {\hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})+{\tilde{\varvec{x}}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})} \right) {\tilde{\varvec{y}}}^{{\varvec{T}}}_1 ({\varvec{k}}+1| {\varvec{k}})} \right\} \end{aligned}$$

From the Gaussian conditional estimator [48], since \({\varvec{E}}\left\{ {\hat{\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}}) {\tilde{\varvec{y}}}^{{\varvec{T}}}_1 ({\varvec{k}}+1| {\varvec{k}})} \right\} \cong 0\), then we have:

$$\begin{aligned}&{\varvec{P}}_{{\varvec{x}}_{\varvec{i}} {\tilde{\varvec{y}}}_1} ({\varvec{k}}+1| {\varvec{k}})\cong {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{y}}}_1 } ({\varvec{k}}+1| {\varvec{k}}) \\&\quad \cong {\varvec{E}}\left\{ {\tilde{\varvec{x}}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})\left( \hat{\varvec{H}}_1 ({\varvec{k}}+1){\tilde{\varvec{x}}}({\varvec{k}}+1| {\varvec{k}})\right. \right. \nonumber \\&\qquad \left. \left. +\,\hat{\varvec{D}}_1 ({\varvec{k}}+1)\tilde{{\varvec{c}}}({\varvec{k}}+1)+{\varvec{v}}_1 ({\varvec{k}}+1) \right) ^{{\varvec{T}}} \right\} \end{aligned}$$

Since \({\varvec{E}}\left\{ {\tilde{{\varvec{c}}}({\varvec{k}}+1)} \right\} =0\), \({\varvec{E}}\left\{ {{\varvec{v}}_1 ({\varvec{k}}+1)} \right\} =0\) and \({\tilde{\varvec{x}}}({\varvec{k}}+1| {\varvec{k}})\) is independent of both \(\tilde{{\varvec{c}}}({\varvec{k}}+1)\) and \({\varvec{v}}_1 ({\varvec{k}}+1)\), we get:

$$\begin{aligned} {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{y}}}_1 } ({\varvec{k}}+1| {\varvec{k}})={\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}} ({\varvec{k}}+1| {\varvec{k}})\hat{\varvec{H}}^{\varvec{T}}_1 ({\varvec{k}}+1) \end{aligned}$$
(102)

Using (101) and recalling that \({\tilde{\varvec{x}}}({\varvec{k}}+1| {\varvec{k}})\), \(\tilde{{\varvec{c}}}({\varvec{k}}+1)\), and \({\varvec{v}}_1 ({\varvec{k}}+1)\) are mutually independent, we get:

$$\begin{aligned}&{\varvec{P}}_{{\tilde{\varvec{y}}}_1 {\tilde{\varvec{y}}}_1} ({\varvec{k}}\!+\!1| {\varvec{k}})\!=\!\hat{\varvec{H}}_1 ({\varvec{k}}\!+\!1){\varvec{P}}({\varvec{k}}\!+\!1| {\varvec{k}})\hat{\varvec{H}}^{\varvec{T}}_1 ({\varvec{k}}\!+\!1)\nonumber \\&\quad +\,\hat{\varvec{D}}_1 ({\varvec{k}}+1){\varvec{U}}({\varvec{k}}+1)\hat{\varvec{D}}^{{\varvec{T}}}_1 ({\varvec{k}}+1)+{\varvec{R}}_{11} ({\varvec{k}}+1)\nonumber \\ \end{aligned}$$
(103)

where \({\varvec{U}}({\varvec{k}}+1)\) is the covariance matrix of the output model parameter \({\varvec{c}}({\varvec{k}}+1)\) and \({\varvec{R}}_{11} ({\varvec{k}}+1)\) is the covariance matrix of the output noise subvector \({\varvec{v}}_1 ({\varvec{k}}+1)\).

Therefore, substituting from (102) and (103) into (99) while using (22), the gain matrix \({\varvec{K}}_{1{\varvec{i}}}^1 ({\varvec{k}}+1)\) is given by:

$$\begin{aligned} {\varvec{K}}_{1{\varvec{i}},{\varvec{k}}+1}^1= & {} {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}} ({\varvec{k}}+1| {\varvec{k}})\hat{\varvec{H}}^{\varvec{T}}_1 ({\varvec{k}}+1)\nonumber \\&\times \,\Big [ {\hat{\varvec{H}}_1 ({\varvec{k}}+1){\varvec{P}}({\varvec{k}}+1| {\varvec{k}})\hat{\varvec{H}}^{\varvec{T}}_1 ({\varvec{k}}+1)} \nonumber \\&+\,\hat{\varvec{D}}_1 ({\varvec{k}}+1){\varvec{U}}({\varvec{k}}+1)\hat{\varvec{D}}^{{\varvec{T}}}_1 ({\varvec{k}}+1)\nonumber \\&+\,{\varvec{R}}_{11} ({\varvec{k}}+1) \Big ]^{-1} \nonumber \\= & {} {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}}^0 ({\varvec{k}}+1| {\varvec{k}} +1)\hat{\varvec{H}}^{\varvec{T}}_1 ({\varvec{k}}+1)\nonumber \\&\times \,\Big [ \hat{\varvec{H}}_1 ({\varvec{k}}+1){\varvec{P}}({\varvec{k}}+1| {\varvec{k}})\hat{\varvec{H}}^{\varvec{T}}_1 ({\varvec{k}}+1) \nonumber \\&+\,\hat{\varvec{D}}_1 ({\varvec{k}}+1){\varvec{U}}({\varvec{k}}+1)\hat{\varvec{D}}^{{\varvec{T}}}_1 ({\varvec{k}}+1)\nonumber \\&+\,{\varvec{R}}_{11} ({\varvec{k}}+1) \Big ]^{-1} \end{aligned}$$
(104)

The covariance matrix of the estimation error of the filtered estimate \(\hat{\varvec{x}}^{1}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1})\) denoted by \({\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} }^1 ({\varvec{k}}+1| {{\varvec{k}}+1})\) is given by:

$$\begin{aligned}&{\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} }^1 ({\varvec{k}}+1| {{\varvec{k}}+1})\nonumber \\&\quad ={\varvec{E}}\left\{ {{\tilde{\varvec{x}}}^{1}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1}){\tilde{\varvec{x}}}^{1^{{\varvec{T}}}}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1})} \right\} \end{aligned}$$
(105)

where the error \({\tilde{\varvec{x}}}^{1}_i ({\varvec{k}}+1| {{\varvec{k}}+1})\) is defined as:

$$\begin{aligned}&{\tilde{\varvec{x}}}^{1}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1})\nonumber \\&\quad ={\varvec{x}}_{\varvec{i}} ({\varvec{k}}+1)-\hat{\varvec{x}}^{1}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1}) \nonumber \\&\quad ={\tilde{\varvec{x}}}_{\varvec{i}} ({\varvec{k}}+1| {\varvec{k}})-{\varvec{K}}_{1{\varvec{i}}}^1 ({\varvec{k}}+1) {\tilde{\varvec{y}}}_1 ({\varvec{k}}+1| {\varvec{k}}) \end{aligned}$$
(106)

Substituting from (106) into (105) while using (99) and after simple mathematical manipulation, it is easy to get:

$$\begin{aligned}&{\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} }^1 ({\varvec{k}}+1| {{\varvec{k}}+1})\cong {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} } ({\varvec{k}}+1| {\varvec{k}})-{\varvec{K}}_{1{\varvec{i}}}^1 ({\varvec{k}}+1)\nonumber \\&\quad \hat{\varvec{H}}_1 ({\varvec{k}}+1){\varvec{P}}_{{\tilde{\varvec{x}}}{\tilde{\varvec{x}}}_{\varvec{i}}} ({\varvec{k}}+1| {\varvec{k}}) \nonumber \\&{\varvec{Or}}\,{\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} }^1 ({\varvec{k}}\!+\!1| {{\varvec{k}}\!+\!1})\!\cong \!{\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} }^0 ({\varvec{k}}\!+\!1| {{\varvec{k}}\!+\!1})\!-\!{\varvec{K}}_{1{\varvec{i}}}^1 ({\varvec{k}}\!+\!1)\nonumber \\&\quad \hat{\varvec{H}}_1 ({\varvec{k}}+1){\varvec{P}}_{{\tilde{\varvec{x}}}{\tilde{\varvec{x}}}_{\varvec{i}} }^0 ({\varvec{k}}+1| {{\varvec{k}}+1}) \end{aligned}$$
(107)

The cross-covariance matrix of the error of the filtered estimates \(\hat{\varvec{x}}^{1}_{\varvec{i}} ({\varvec{k}}\!+\!1| {{\varvec{k}}+1})\) and \(\hat{\varvec{x}}^{1}_{\varvec{j}} ({\varvec{k}}+1| {{\varvec{k}}+1})\) denoted by \({\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}} }^1 ({\varvec{k}}+1| {{\varvec{k}}+1})\) is given by:

$$\begin{aligned} {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}} }^1 ({\varvec{k}}+1| {{\varvec{k}}+1})={\varvec{E}}\!\left\{ {{\tilde{\varvec{x}}}^{1}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1}){\tilde{\varvec{x}}}^{1^{{\varvec{T}}}}_{\varvec{j}} ({\varvec{k}}+1| {{\varvec{k}}+1})} \!\right\} \end{aligned}$$

where \({\tilde{\varvec{x}}}^{1}_i ({\varvec{k}}+1| {{\varvec{k}}+1})\) is defined by (106) and \({\tilde{\varvec{x}}}^{1}_{\varvec{j}} ({\varvec{k}}+1| {{\varvec{k}}+1})\) is given by:

$$\begin{aligned}&{\tilde{\varvec{x}}}^{1}_{\varvec{j}} ({\varvec{k}}+1| {{\varvec{k}}+1})\nonumber \\&\quad \cong {\varvec{x}}_{\varvec{j}} ({\varvec{k}}+1)-\hat{\varvec{x}}^{1}_{\varvec{j}} ({\varvec{k}}+1| {{\varvec{k}}+1}) \nonumber \\&\quad \cong {\tilde{\varvec{x}}}_{\varvec{j}} ({\varvec{k}}+1| {\varvec{k}})-{\varvec{K}}_{1{\varvec{j}}}^1 ({\varvec{k}}+1) {\tilde{\varvec{y}}}_1 ({\varvec{k}}+1| {\varvec{k}}) \end{aligned}$$
(108)

Again, using (106) and (108), it is easy to show that the cross-covariance matrices for \(j\in \{i+1,\ldots ,N\} \,\, {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}}}^1 ({\varvec{k}}+1| {{\varvec{k}}+1})\) are such that:

$$\begin{aligned} {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}} }^1 ({\varvec{k}}\!+\!1| {{\varvec{k}}\!+\!1})\cong & {} {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}} } ({\varvec{k}}\!+\!1| {\varvec{k}})-{\varvec{K}}_{1{\varvec{i}}}^1 ({\varvec{k}}\!+\!1)\nonumber \\&\hat{\varvec{H}}_1 ({\varvec{k}}\!+\!1){\varvec{P}}_{{\tilde{\varvec{x}}}{\tilde{\varvec{x}}}_{\varvec{j}} } ({\varvec{k}}\!+\!1| {\varvec{k}}) \nonumber \\ {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}} }^1 ({\varvec{k}}\!+\!1| {{\varvec{k}}\!+\!1})\!\cong & {} \! {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}} }^0 ({\varvec{k}}\!+\!1| {{\varvec{k}}\!+\!1})\!-\!{\varvec{K}}_{1{\varvec{i}}}^1 ({\varvec{k}}\!+\!1)\nonumber \\&\hat{\varvec{H}}_1 ({\varvec{k}}\!+\!1){\varvec{P}}_{{\tilde{\varvec{x}}}{\tilde{\varvec{x}}}_{\varvec{j}} }^0 ({\varvec{k}}\!+\!1| {{\varvec{k}}\!+\!1})\nonumber \\ \end{aligned}$$
(109)

Following the same procedure, it can be shown that the filtered estimate \(\hat{\varvec{x}}^{{\varvec{r}}}_{\varvec{i}} ({\varvec{k}}+1| {{\varvec{k}}+1})\) corresponding to the measurements \({\varvec{Y}}^{{\varvec{k}}}, {\varvec{y}}_1 ({\varvec{k}}+1), {\varvec{y}}_2 ({\varvec{k}}+1),\ldots , {\varvec{y}}_{\varvec{r}} ({\varvec{k}}+1)\), its covariance matrix \({\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} }^{\varvec{r}} ({\varvec{k}}+1| {{\varvec{k}}+1})\), and the cross-covariance matrices \({\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}} }^{\varvec{r}} ({\varvec{k}}+1| {{\varvec{k}}+1})\) are given by:

$$\begin{aligned} \hat{\varvec{x}}^{{\varvec{r}}}_{\varvec{i}} ({\varvec{k}}\!+\!1| {{\varvec{k}}\!+\!1})\!= & {} \!\hat{\varvec{x}}_{\varvec{i}}^{{\varvec{r}}\!-\!1} ({\varvec{k}}\!+\!1| {{\varvec{k}}\!+\!1})\\&+\,{\varvec{K}}_{1{\varvec{i}}}^{\varvec{r}} ({\varvec{k}}+1){\tilde{\varvec{y}}}_{\varvec{r}}^{{\varvec{r}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1})\nonumber \end{aligned}$$
(110)

where

$$\begin{aligned}&{\varvec{K}}_{1{\varvec{i}}}^{\varvec{r}} ({\varvec{k}}+1)\cong {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}}^{{\varvec{r}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1})\hat{\varvec{H}}_{\varvec{r}}^{{\varvec{r}}-1^{{\varvec{T}}}} ({\varvec{k}}+1)\nonumber \\&\quad \times \, \Big [ {\hat{\varvec{H}}_{\varvec{r}}^{{\varvec{r}}-1} ({\varvec{k}}+1){\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}}^{{\varvec{r}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1})\hat{\varvec{H}}_{\varvec{r}}^{{\varvec{r}}-1^{{\varvec{T}}}} ({\varvec{k}}+1)} \nonumber \\&\quad +\,\hat{\varvec{D}}_{\varvec{r}}^{{\varvec{r}}-1} ({\varvec{k}}+1){\varvec{U}}({\varvec{k}}+1)\hat{\varvec{D}}_{\varvec{r}}^{{\varvec{r}}-1^{{\varvec{T}}}} ({\varvec{k}}+1)\nonumber \\&\quad +\,{\varvec{R}}_{{\varvec{rr}}} ({\varvec{k}}+1) \Big ]^{-1} \end{aligned}$$
(111)
$$\begin{aligned}&{\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {{\tilde{\varvec{x}}}_{\varvec{i}}}}^{\varvec{r}} ({\varvec{k}}+1| {{\varvec{k}}+1})\cong {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} }^{{\varvec{r}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1})\nonumber \\&\quad -\,{\varvec{K}}_{1{\varvec{i}}}^{\varvec{r}} ({\varvec{k}}+1)\hat{\varvec{H}}_{\varvec{r}}^{{\varvec{r}}-1} ({\varvec{k}}+1){\varvec{P}}_{{\tilde{\varvec{x}}}\, {\tilde{\varvec{x}}}_{\varvec{i}} }^{{\varvec{r}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1}) \end{aligned}$$
(112)
$$\begin{aligned}&{\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}} }^{\varvec{r}} ({\varvec{k}}+1| {{\varvec{k}}+1})\cong {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{j}} }^{{\varvec{r}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1})\nonumber \\&\quad -\,{\varvec{K}}_{1{\varvec{i}}}^{\varvec{r}} ({\varvec{k}}+1)\hat{\varvec{H}}_{\varvec{r}}^{{\varvec{r}}-1} ({\varvec{k}}+1){\varvec{P}}_{{\tilde{\varvec{x}}}\, {\tilde{\varvec{x}}}_{\varvec{j}} }^{{\varvec{r}}-1} ({\varvec{k}}+1| {{\varvec{k}}+1}) \end{aligned}$$
(113)
$$\begin{aligned}&{\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} }^1 ({\varvec{k}}+1| {{\varvec{k}}+1})\cong {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} } ({\varvec{k}}+1| {\varvec{k}})\nonumber \\&\quad -\,{\varvec{K}}_{1{\varvec{i}}}^1 ({\varvec{k}}+1)\hat{\varvec{H}}_1 ({\varvec{k}}+1){\varvec{P}}_{{\tilde{\varvec{x}}}\, {\tilde{\varvec{x}}}_{\varvec{i}} } ({\varvec{k}}+1| {\varvec{k}})\nonumber \\&{\varvec{Or}}\,\,{\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} }^1 ({\varvec{k}}+1| {{\varvec{k}}+1})\cong {\varvec{P}}_{{\tilde{\varvec{x}}}_{\varvec{i}} {\tilde{\varvec{x}}}_{\varvec{i}} }^0 ({\varvec{k}}+1| {{\varvec{k}}+1})\nonumber \\&\quad -\,{\varvec{K}}_{1{\varvec{i}}}^1 ({\varvec{k}}+1)\hat{\varvec{H}}_1 ({\varvec{k}}+1){\varvec{P}}_{{\tilde{\varvec{x}}}\, {\tilde{\varvec{x}}}_{\varvec{i}} }^0 ({\varvec{k}}+1| {{\varvec{k}}+1}) \end{aligned}$$
(114)

\(\square \)

Appendix 2

Proof of Theorem 6.1

  1. 1a.

    Equation (67) can be written in the following alternative form:

    $$\begin{aligned} {\varvec{Z}}({\varvec{k}}+1)={\varvec{\varPhi }}_{{\varvec{ss}}}^{{\varvec{k}}+1} {\varvec{Z}}(0) \end{aligned}$$

    Then, the norm of the expected value of the above equation is given by:

    $$\begin{aligned} \bar{{\bar{{{\varvec{Z}}}}}}({\varvec{k}}+1)\le \Vert {{\varvec{\varPhi }} _{{\varvec{ss}}}^{{\varvec{k}}+1} } \Vert \bar{{\bar{{{\varvec{Z}}}}}}(0) \end{aligned}$$
    (115)

    Since for all the solution of (67) \(\bar{{\bar{{{\varvec{Z}}}}}}({\varvec{k}}+1)\) remains bounded as \({{k}}\rightarrow \infty \), then there exists a constant \({{c}}_1\) such that for \({{k}}+1\ge 0\):

    $$\begin{aligned} \Vert {{\varvec{\varPhi }} _{{\varvec{ss}}}^{{\varvec{k}}+1} } \Vert \le {\varvec{c}}_1 \end{aligned}$$
    (116)

    Equation (68) can be written in the form:

    $$\begin{aligned} {\varvec{Z}}({\varvec{k}}\!+\!\!1)\!=\!{\varvec{\varPhi }}_{{\varvec{ss}}}^{{\varvec{k}}+1} {\varvec{Z}}(0)\!+\!\!\sum \limits _{{\varvec{j}}=1}^{{\varvec{k}}-1} {{\varvec{\varPhi }}_{{\varvec{ss}}}^{{\varvec{k}}-{\varvec{j}}} {\varvec{\varPsi }} ({\varvec{j}}\!+\!1,{\varvec{j}}){\varvec{Z}}({\varvec{j}})} \end{aligned}$$

    Taking the norm of the expected value of this equation while using (70), we have:

    $$\begin{aligned}&\bar{{\bar{{{\varvec{Z}}}}}}_ ({\varvec{k}}+1)\le \Vert {{\varvec{\varPhi }}_{{\varvec{ss}}}^{{\varvec{k}}+1} } \Vert \bar{{\bar{{{\varvec{Z}}}}}}(0)\nonumber \\&\quad +\,\sum \limits _{{\varvec{j}}=0}^{{\varvec{k}}-1} {\Vert {{\varvec{\varPhi }}_{{\varvec{ss}}}^{{\varvec{k}}-{\varvec{j}}} } \Vert } \sqrt{{\varvec{\varTheta }}^{{\varvec{T}}}{\varvec{\varTheta }}}\le {\varvec{c}}_1 \bar{{\bar{{{\varvec{Z}}}}}}(0)\nonumber \\&\quad +\,\sum \limits _{{\varvec{j}}=0}^{{\varvec{k}}-1} {{\varvec{c}}_1 } {\varvec{\lambda }} ({\varvec{j}})\bar{{\bar{{{\varvec{Z}}}}}}({\varvec{j}}) \end{aligned}$$
    (117)

    Let \(g(j)=c_1 \lambda (j)\),

    $$\begin{aligned} \therefore \,\,\bar{{\bar{{{\varvec{Z}}}}}}({\varvec{k}}+1)\le {\varvec{c}}_1 \bar{{\bar{{{\varvec{Z}}}}}}(0)+\sum \limits _{{\varvec{j}}=0}^{{\varvec{k}}-1} {{\varvec{g}}({\varvec{j}})} \bar{{\bar{{{\varvec{Z}}}}}}({\varvec{j}}) \end{aligned}$$

    From the special Gronwall lemma [55], we have:

    $$\begin{aligned} \bar{{\bar{{{\varvec{Z}}}}}}({\varvec{k}}+1)\le & {} {\varvec{c}}_1 \bar{{\bar{{{\varvec{Z}}}}}}(0)\prod _{{\varvec{j}}=0}^{{\varvec{k}}-1} (1+{\varvec{g}}({\varvec{j}}))\nonumber \\\le & {} {\varvec{c}}_1 \bar{{\bar{{{\varvec{Z}}}}}}(0)\exp \left( \sum \limits _{{\varvec{j}}=0}^{{\varvec{k}}-1} {{\varvec{g}}({\varvec{j}})} \right) \end{aligned}$$
    (118)

    By the hypothesis (69), there exists a constant \(c_2\) such that \(\sum \limits _{k=0}^\infty {\lambda (k)} \le c_2 \). Therefore, we have:

    $$\begin{aligned} \bar{{\bar{{{\varvec{Z}}}}}}({\varvec{k}}+1)\le {\varvec{c}}_1 \bar{{\bar{{{\varvec{Z}}}}}}(0)\exp ({\varvec{c}}_1 {\varvec{c}}_2 ) \end{aligned}$$
    (119)

    which shows that the expected value of the norm of the homogeneous system is bounded. Since \({\varvec{E}}\{{\varvec{w}}({\varvec{k}})\}={\varvec{E}}\{\tilde{\varvec{b}}({\varvec{k}})\}={\varvec{E}}\{ \tilde{{\varvec{c}}}({\varvec{k}}+1)\}={\varvec{E}}\{{\varvec{v}}({\varvec{k}}+1)\}=0\), then \({\varvec{E}}\{{\varvec{\mu }} ({\varvec{k}})\}=0\) in (64) or (66). Therefore, the norm of the expected value of (66) as given by (117) is bounded according to (119).

  2. 1b.

    Since the expected value of the constrained equilibrium \({\varvec{x}}_{{\varvec{ss}}} \)is detectable, and the pair \(\left( {\hat{{\varvec{F}}}^{\prime }\!({\varvec{k}}), \hat{\varvec{H}}({\varvec{k}}+1)} \right) \) is detectable for the entire domain \({\varvec{\varOmega }}\) except for a finite number of points, then the matrix \({\varvec{\varPhi }}_{{\varvec{ss}}}\) is stable. Therefore, the origin is the zero equilibrium of the expected value of the estimation error. As a result, there exist \(0\le {\varvec{\delta }}({\varvec{k}}+1) <1\) such that \(\Vert {{\varvec{\varPhi }} _{{\varvec{ss}}}^{{\varvec{k}}+1} } \Vert <[{\varvec{\delta }} ({\varvec{k}}+1)]^{{\varvec{k}}+1}\) for \({{k}}+1\ge {{K}}\).

    In this case, i.e., \(k+1\ge K\), and from the Gronwall lemma while using (69), the inequality (117) takes the form:

    $$\begin{aligned} \bar{{\bar{{{\varvec{Z}}}}}}({\varvec{k}}+1)\le & {} \left\| {{\varvec{\varPhi }}_{{\varvec{ss}}}^{{\varvec{k}}+1} } \right\| \bar{{\bar{{{\varvec{Z}}}}}}(0)+\sum \limits _{{\varvec{j}}=0}^{{\varvec{k}}-1} {\left\| {{\varvec{\varPhi }}_{ss}^{k-j} } \right\| } \sqrt{{\varvec{\varTheta }} ^{{\varvec{T}}}{\varvec{\varTheta }} }\nonumber \\\le & {} {\varvec{c}}_1 \bar{{\bar{{{\varvec{Z}}}}}}(0)+\sum \limits _{{\varvec{j}}=0}^{{\varvec{k}}-1} {{\varvec{c}}_1 } {\varvec{\lambda }} ({\varvec{j}})\bar{{\bar{{{\varvec{Z}}}}}}({\varvec{j}})\nonumber \\ \bar{{\bar{{{\varvec{Z}}}}}}({\varvec{k}}+1)\le & {} \left\| {{\varvec{\varPhi }}_{{\varvec{ss}}}^{{\varvec{k}}+1} } \right\| \bar{{\bar{{{\varvec{Z}}}}}}(0)+\sum \limits _{{\varvec{j}}=0}^{{\varvec{k}}-1} {{\varvec{g}}({\varvec{j}})} \bar{{\bar{{{\varvec{Z}}}}}}(j)\nonumber \\ \bar{{\bar{{{\varvec{Z}}}}}}({\varvec{k}}+1)\le & {} \left\| {{\varvec{\varPhi }}_{{\varvec{ss}}}^{{\varvec{k}}+1} } \right\| \bar{{\bar{{{\varvec{Z}}}}}}(0)\prod _{{\varvec{j}}=0}^{{\varvec{k}}-1} {(1+{\varvec{g}}({\varvec{j}})) } \nonumber \\\le & {} \left\| {{\varvec{\varPhi }}_{{\varvec{ss}}}^{{\varvec{k}}+1} } \right\| \bar{{\bar{{{\varvec{Z}}}}}}(0)\exp \left( \sum \limits _{{\varvec{j}}=0}^{\varvec{k}} {{\varvec{g}}({\varvec{j}})} \right) \nonumber \\ \bar{{\bar{{{\varvec{Z}}}}}}({\varvec{k}}+1)\le & {} [{\varvec{\delta }} ({\varvec{k}}+1)]^{{\varvec{k}}+1}\bar{{\bar{{{\varvec{Z}}}}}}(0)\exp ({\varvec{c}}_1 {\varvec{c}}_2 )\nonumber \\\le & {} \bar{{{\varvec{\delta }}}}^{{\varvec{k}}+1}\bar{{\bar{{{\varvec{Z}}}}}}(0)\exp ({\varvec{c}}_1 {\varvec{c}}_2 ) \end{aligned}$$
    (120)

    where \(\bar{{{\varvec{\delta }} }}=\sup \{{\varvec{\delta }} ({\varvec{j}}), {\varvec{j}}\in ({\varvec{K}},{\varvec{K}}+1,\ldots ,\infty )\}\) and \(0\le \bar{{{{\varvec{\delta }}}}}<1\)

    Since \(\mathop {\lim }\limits _{{\varvec{k}}\rightarrow \infty } \bar{{{\varvec{\delta }} }}^{{\varvec{k}}+1}=0 \), then \( \mathop {\lim }\limits _{{\varvec{k}}\rightarrow \infty } \bar{{\bar{{{\varvec{Z}}}}}}({\varvec{k}}+1)=0\). Therefore, the norm of the expected value of the estimation error is locally exponentially stable.

  3. 2.

    Equation (71) can be written as:

    $$\begin{aligned} {\varvec{Z}}({\varvec{k}}+1)= & {} {\varvec{\varPhi }}_{{\varvec{ss}}}^{{\varvec{k}}+1} {\varvec{Z}}(0)+\sum \limits _{{\varvec{j}}=0}^{{\varvec{k}}-1} {\varvec{\varPhi }}_{{\varvec{ss}}}^{{\varvec{k}}-{\varvec{j}}}\nonumber \\&\times \, \left[ {{\varvec{\varPsi }} ({\varvec{j}}+1,{\varvec{j}}){\varvec{Z}}({\varvec{j}})+{\varvec{\mu }} ({\varvec{j}})} \right] \end{aligned}$$
    (121)

    Using (72), (73) and (116), the expected value of the norm of (121) is given by:

    $$\begin{aligned}&\left\| {{\varvec{Z}}({\varvec{k}}+1)} \right\| _{{\varvec{av}}} \le {\varvec{c}}_1 \left\| {{\varvec{Z}}(0)} \right\| _{{\varvec{av}}}\nonumber \\&\quad +\,\sum \limits _{{\varvec{j}}=0}^{{\varvec{k}}-1} {{\varvec{c}}_1 } \left\{ {{\varvec{\lambda }} ({\varvec{j}})+{\varvec{\varepsilon }} ({\varvec{j}})} \right\} \left\| {{\varvec{Z}}({\varvec{j}})} \right\| _{{\varvec{av}}} \end{aligned}$$
    (122)

    Let \(g^{\prime } (j)=c_1 \left\{ {\lambda (j)+\varepsilon (j)} \right\} \),

    $$\begin{aligned}&\therefore \,\!\left\| {{\varvec{Z}}({\varvec{k}}\!+\!1)} \right\| _{{\varvec{av}}} \!\le \!{\varvec{c}}_1 \left\| {{\varvec{Z}}(0)} \right\| _{{\varvec{av}}}\nonumber \\&\quad +\sum \limits _{{\varvec{j}}\!=\!0}^{{\varvec{k}}-1} {{\varvec{g}}^{\prime } ({\varvec{j}})} \left\| {{\varvec{Z}}({\varvec{j}})} \right\| _{{\varvec{av}}} \end{aligned}$$
    (123)

    Using Gronwall lemma, we have:

    $$\begin{aligned} \left\| {{\varvec{Z}}({\varvec{k}}+1)} \right\| _{{\varvec{av}}}\le & {} {\varvec{c}}_1 \left\| {{\varvec{Z}}(0)} \right\| _{{\varvec{av}}} \prod _{{\varvec{j}}=0}^{{\varvec{k}}-1} (1+{\varvec{g}}^{\prime } ({\varvec{j}}))\nonumber \\\le & {} {\varvec{c}}_1 \left\| {{\varvec{Z}}(0)} \right\| _{{\varvec{av}}} \exp \left( \sum \limits _{{\varvec{j}}=0}^{{\varvec{k}}-1} {{\varvec{g}}^{\prime } ({\varvec{j}})} \right) \nonumber \\ \end{aligned}$$
    (124)

    By the hypothesis (72), there exists a constant \(c_3\) such that \(\sum \limits _{k=0}^\infty {\left\{ {\lambda (k)+\varepsilon (k)} \right\} } \le c_3 \). Hence, (124) is such that:

    $$\begin{aligned} \left\| {{\varvec{Z}}({\varvec{k}}+1)} \right\| _{{\varvec{av}}} \le {\varvec{c}}_1 \left\| {{\varvec{Z}}(0)} \right\| _{{\varvec{av}}} \exp ({\varvec{c}}_1 {\varvec{c}}_3 ) \end{aligned}$$
    (125)

    which proves the boundedness of the expected value of the norm of the non-homogeneous system and hence the root-mean-square of the estimation error.\(\square \)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hassan, M.F. Synchronization of uncertain constrained hyperchaotic systems and chaos-based secure communications via a novel decomposed nonlinear stochastic estimator. Nonlinear Dyn 83, 2183–2211 (2016). https://doi.org/10.1007/s11071-015-2474-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2474-6

Keywords

Search

Navigation