1 Introduction

When predicting landslides, it is important to understand the past landslide cases and prepare for similar case scenarios. By gathering information on frequently occurring slope disaster cases, researchers have determined that landslide behaviors change according to different conditions, including geological and topographical features, rainfall characteristics, and landslide progression (Mahr 1977; Chigira 2020). However, no system has been proposed in which these various conditions can be discussed in a unified manner. In contrast, remote sensing technology is evolving, and the surface profile obtained through light-induced direction and ranging (LiDAR) is numerical information with a history of topographic features and deformations (Demurtas et al. 2021). However, the interpretation by geomorphological and geological experts alone is not versatile enough, and a wide area cannot be determined at a time, leading to oversight. Hence, in this study, we aimed to determine the shared similar topographic features from LiDAR before the landslide.

The topographic feature related to slope failures is gravity deformation. This means continuous deformation of the bedrock occurs near the surface as well as in deep underground. Gravity deformation has been reported in the past in glacial landforms, such as zagging and double mountain ridges, in the Alps (Zischinsky 1966). Dramis and Sorriso-Valvo (1994) and Agliardi et al. (2001) have reported deep-seated gravitational slope deformations (DSGSDs), and they defined large masses as those in which gravitational deformation is caused by small displacements with or without a slip surface. Chigira et al. (2003) showed that the 1999 Tsaoling landslide was not a reactivation of an old landslide but it had already moved slightly before the 1999 event, providing precursor evidence. Crosta et al. (2006) numerically predicted that the upper slopes of large landslides are unstable and the potential instability factors, such as landslide sliding and mobility, in the Italian Pre-Alps. While the close relationship between topographic features and DSGSDs is being clarified, a large-scale rockslide-debris avalanche that occurred in 2006 in southern Leyte in Philippines has attracted attention as a large-scale collapse. Evans et al. (2007) pointed out that the avalanche was related to the Philippine Fault and that non-brittle deformation of the surface rock was observed as a result of slope movement. Guthrie et al. (2009) reported that the rockslide-debris avalanche was caused by not only heavy rainfall and a simultaneous earthquake, but also the result of progressive rupture and structural weakening. In the Kii Peninsula, which is the target area of this study, landslides have been frequently observed in recent disasters. Regarding Typhoon Talas in 2011, approximately a few million m3 of massive landmass moved in rapidly. DSGSDs were determined to be their precursors in most of the landslides (Chigira et al. 2013). Hiraishi and Chigira (2009) and Tsou et al. (2017) noted that large-scale knickpoint formation and gentle slopes influence DSGSD formation. Additionally, knickpoints form during rapid downward erosion. DSGSDs and landslides were categorized into two groups—those entirely within the paleo-surface and those across knickpoints—with 75% of the 2011 landslides being associated with the inner slopes of the valley, two to three times more than those that are entirely within the paleo-surface. Thus, the landslide has some shared topographic features due to DSGSDs. Hence, to predict potential landslide locations, it is necessary to understand DSGSD formation and determine their progression manner.

For making landslide predictions by focusing on topographical features, such as DSGSDs, landslide inventory maps (LIMs) and landslide susceptibility maps (LSMs) (Can et al. 2019) can be used. LIMs portray the extent of landslide phenomena, which helps investigate the distribution, types, pattern, recurrence, and statistics of slope failures. The development of relative and quantitative LIMs was made practical by using high-precision LiDAR (McKean and Roering 2004). High-resolution satellite images and photographs taken by unmanned aerial vehicles (UAVs), including terrestrial and UAV-mounted LiDAR (light detection and ranging) data, have become available in recent years (Ghorbanzadeh et al. 2019a). These data can easily be arranged chronologically, and the geographic data of the same location at different times can be used for analysis. Moreover, LIM is more sophisticated, as it facilitates data sharing owing to the advent of Landslide4Sense (Benchmark Data and Deep Learning Models for Landslide Detection). Landslide4Sense automatically detects landslides based on large multi-source satellite images that are collected from around the world. In particular, a benchmark dataset is provided and the results of an online accuracy evaluation are reported using the advanced landslide detection method (Ghorbanzadeh et al 2022).

LSMs help predict the spatial distribution and identify and classify potentially landscape-prone areas (Guzzetti et al 1999). As most of the geographic data are complex, it can be difficult to analyze such data at large scales, and consequently, some data may be inadvertently overlooked. Machine learning has been a method for complementing multivariate analyses and has been used in LIMs and LSMs using gridded data. LSM-based prediction of landslide areas was conducted by Lee (2004) usingthe sigmoid function. Dahal et al. (2008) used weights-of-evidence modeling conducted using eight elements to predict landslides. Conversely, Chen et al. (2018) reported creating an LSM using an entropy model and support vector machine (SVM). Park and Kim (2019) also reported that the LSM created using the random forest (RF) model performed well and had a prediction rate of 0.851. Merghadi et al (2020) showed that the model used ensemble learning to report that the number of adjustments required before learning is low and highly versatile.

In deep learning analyses, considering that the environmental factors about landslide susceptibility are non-correlated or have nonlinear correlations, 27 environmental factors were analyzed using a fully connected spare auto-encoder for landslide susceptibility prediction (LSP) (Huang et al. 2020). Liu and Wu (2016) indicated that the Deep Auto-encoder network model method outperforms ANN and SVM in terms of precision, recall, and accuracy by evaluating the remote sensing images downloaded from Google Earth.

Images have also been used in analyses that use a convolutional neural network (CNN) instead of gridded data. Many images, as well as the engineer’s perspective, were used as datasets (Wang et al. 2019, 2021). Ghorbanzadeh et al. (2021) achieved an accuracy rating of almost 90% by testing the potential of CNN for slope collapse detection using Sentinel-2 multispectral imagery. Additionally, CNN2D has the ability to outperform traditional methods such as CNN1 and SVM owing to its high prediction rate and generalizability (Youssef et al. 2022). Deep learning algorithms can prevent local optimization and eliminate the need to adjust model parameters based on autonomous processes (Carrio et al. 2017). Meanwhile, attempts have been made to search for the optimal model for the network structure of CNNs using automatically constructed high-performing architectures. This method proposes new structures that can be viewed without human coordination (Real et al. 2020). The results of this method not only reduce and streamline the human design burden, but also indicate the possibility of finding machine learning algorithms that do not use neural networks. These approaches have been used in a variety of fields, in some cases, with better results than human experts (Suganuma et al. 2020).

This study aimed to improve the overall performance of the CNN2D-based model, which has been studied well in landslide susceptibility modeling (LSM), as an automatically constructed model and to systematically compare it with conventional CNN models. Furthermore, this is the first study that focusses on pre-disaster DEM images. We also compared the effectiveness of these self-search models in detail. Specifically, we evaluated the models in a test domain using a set of indicators such as receiver operating characteristic (ROC) and accuracy. We believe that the results of this study can aid researchers and local decision makers in spatial information and erosion control in reducing the local landslide risk.

2 Geological setting and its disaster status

2.1 Outline of the rainstorm hazard

Typhoon Talas (also known as Typhoon #12 in Japan) made landfall and crossed western Japan during September 2, 2011 to September 5, 2011, and brought over 2,000 mm of precipitation to the Kii Mountains. According to Chigira et al. (2013), over 50 DLs occurred because of the typhoon. These DLs occurred when the total precipitation reached 600–1200 mm. However, regions that received over 1200 mm of precipitation did not experience landslides. Matsushi et al. (2012) examined the rainfall and catastrophic landslides and found that DLs occurred when the accumulated rainfall reached over 600 mm within a brief period (48–72 h).

2.2 Geological setting

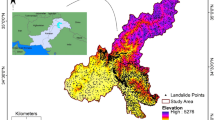
Mount Hakkeiga-take (elevation: 1915 m) is the highest peak in the Kii Mountains, as shown in Fig. 1, which are of similar elevations and form the ridge. The elevation of the study area ranges from 220 to 1915 m. A paleo-surface is in the southern and western parts of the Kumano-gawa basin. The study area comprises the Shimanto Belt on the western part of the Kii Peninsula. The Gobo-Hagi tectonic line bisects the belt; the northern part comprises a Cretaceous accretionary tectonic complex, whereas the southern part of the belt contains a Paleogene accretionary tectonic complex (Kimura 1986). The upper Totsugawa River catchment, which is the focus of this study, is located in the northern belt and contains the Hidakagawa Group that comprises five formations that trend ENE–WSW: (from north to south) the Hanazono, Yukawa, Miyama, Ryujin, and Nyunokawa formations (Hara and Hisada 2007). The Hidakagawa Group is predominantly underlain by the Cretaceous to lower Paleozoic Shimanto accretionary complex with minor amounts of Miocene granite and sedimentary rocks. The complex comprises foliated mudstone, sandstone, acid tuff, chert, and greenstones (Kumon et al. 1988; Hashimoto and Kimura 1999). Following the surveys conducted after the disaster, studies on the micro-topography and geology related to the DLs were conducted. At Akatani and Nagatono where a barrier lake formed, DLs occurred along thrust faults with dominant mudstone layers (Arai and Chigira 2019). Hiraishi and Chigira (2009) geographically analyzed the upstream section of the Nakahara-gawa River in the catchment and found that in the Kii Mountains, the knick line at lower elevations that formed because of downward erosion was a crucial element that caused the landslides and collapses. In regions where many collapses occurred, knick lines (as predispositions to DLs) were observed near the unit boundary within the Miyama formations of the Hidaka Group in the Shimanto Belt on slopes dipping N to NW.

Fig. 1
figure 1

Study area and catchment of the Totsugawa River (upside) landslide data. Red dots indicate deep-seated landslides by Typhoon Talas in 2011

Full size image

3 Materials and methodology

This current study explains the datasets and sources used for machine learning in landslide susceptibility mapping. Four main phases were used in this study. These include various data sources used to generate LSMs and extract landslide influence factors, the application of modeling techniques to generate LSMs, and a validation phase to test model accuracy and performance (Fig. 2). The following sections briefly describe these phases.

Fig. 2
figure 2

Schematic diagram of overall data sources, datasets, and model construction and process

Full size image

3.1 Data setting

We conducted this study via supervised learning because we knew the regions in which landslides occurred when Typhoon Talas made landfall. The learning data were used by turning the pre-slide images of the landslide locations. Airborne laser surveys of the catchment before and after the disaster were conducted by the Kii Mountain Area Sabo Office of the Kinki Regional Development Bureau of the Ministry of Land, Infrastructure, Transport, and Tourism. The measurements were taken before the disaster in July 2009 and after the disaster from December 2011 to February 2012. The measurements were acquired as 1-m mesh DEM using an airborne laser scanner. Thirty-eight locations were identified as having landslides that amounted to over 1000 m2 of collapsed area (Erosion Control and Disaster Prevention Division, Prefectural Land Management Department, Nara Prefecture, 2012) (Fig. 3; the red dots). The data are presented in Online Resource 1. The pre-slide topographic features in the landslide areas included minor scarps, flanks, terminal cliffs, gullies, and irregular undulations (Kikuchi et al. 2019). These features indicate gravitational deformation, which can cause landslides (Fig. 4). The data of these topological features are effective in aiding the prediction of landslides. However, there were areas within the study area without landslides in 2011 that were identified as having DSGSD. These non-slides indicate that, although these regions did not collapse, they had been the geographical features of common characteristics for landslide occurred (Fig. 5). Sixty-three regions fitting these characteristics were identified and extracted (Online Resource 2). We categorized them into a total of three categories of learning data. The locations where a landslide occurred during the 2011 event were designated as “y0: Landslide”. Next, “y1: DSGSD” was not observed with landslide in 2011, but it had the topographic features of DSGSD. Finally, the landforms not included in y0 and y1 were designated as “y2: landforms not related to landslide”. This categorization is based on the study of Tsou et al. (2017).

Fig. 3
figure 3

Geologic map showing the landslide location of Totsugawa River (upside)

Full size image
Fig. 4
figure 4

© NAKANIHON AIR Co.,Ltd. All rights reserved

Images of four of the 38 locations applied to the collapse study (y0). a, d, g, j Pre-landslide slope map, b, e, h, k post-landslide slope map images, c, f, i, l post-landslide oblique aerial photographs, Copyright

Full size image
Fig. 5
figure 5

Images of three of the 63 locations applied to the terrain study (y1) without landslide but had DSGSD: a, c, e slope maps with DSGSD (b, d, f) are orthoimages of aerial photographs

Full size image

3.2 Preparation of image data

The learning data were not created from human-interpreted features of the topographic features to eliminate oversights and individual differences. Instead, the influencing factors with objective features were created from multiple types of image analysis. Working with images of various types simultaneously requires consideration of the effects of different scales. Additionally, the influence of the time of data acquisition on the results must also be considered. Therefore, we used a method that can be created from a 1-m mesh DEM owing to its simplicity and availability. Eight types of influence factors were used: slope angle, eigenvalue ratio, curvature, overground openness, underground openness, topographic wetness index (TWI), wavelet, and elevation. The area subjected to image analysis was approximately twice the range of the slide area. Image analysis methods are explained briefly below (Table 1 and Fig. 6).

Table 1 Eight types of influence factors and data sources
Full size table
Fig. 6
figure 6

Landslide influence factors included in landslide susceptibility modeling (a) slope (b) eigenvalue ratio (c) curvature (d) Underground openness (e) Overground openness (f) TWI (g) wavelet, and (h) elevation

Full size image

The slope angle (slope) is the geomorphic quantity that indicates the gradient in relation to the horizontal plane of each DEM mesh (Burrough et al. 2015). The eigenvalue ratio is an index that indicates ground surface disturbances. The three-dimensional disturbances near the ground surface of the study area were defined by Woodcock (1977) and Woodcock and Naylor (1983) as the differences relative to the surrounding ground surface. McKean and Roering (2004) found that the eigenvalue ratio expresses the roughness of a surface and suggested that it can be an index to estimate landslide activity. In locations where active ground surface activity occurs, the ground surface becomes roughness and the value decreases (Kasai et al. 2009). The average curvature is an index of the unevenness of the terrain (Nishida et al. 1997) and is defined by connecting the shortest distance between the two points on a curve. The calculation consideration range was calculated in a range of 10 m (10 pixels) from the target point on each side. Values close to zero indicate nearly flat surfaces. Profile curvature, which is the vertical plane parallel to the slope direction of downslope flows, also affects erosion and deposition (He et al. 2012; Kannan et al. 2013). Overground openness is the average of the maximum values of the zenith angle that can be seen in the sky from eight directions within a distance of 50 m from the point of interest. Similarly, underground openness is an average of the eight directions based on the maximum values of the nadir angle in which the underground can be seen. (Yokoyama et al. 1999). The TWI (Beven and Kirkby 1979) is based on geological conditions and shows the watershed and water storage amounts. This indicates the total area of the catchment and the valleys, which become the pathway for the water to flow and store upstream of each point of interest. For the wavelet analysis diagram (wavelet), we conducted an analysis using a two-dimensional continuous wavelet transform (Booth et al. 2009). This technique is effective for emphasizing unevenness of the ground surface.

As shown in Fig. 7, the eight influence factor percentages describe the characteristics of landslides and DSGSD. Chigira et al. (2013) noted that the presence of small cliffs and irregular undulations in the landslide indicate an imminent landslide. Seventy one percent of landslides occurred with slopes of 33–42°, and 68% of DSGSD occurred with 36–41° (Fig. 7a, b). Landslides were found to occur on gentler slopes than DSGSD. Fifty eight percent of the landslides occurred with mean eigenvalue ratios ranging from 4.8 to 5.4, and 67% of DSGSD occurred in the same range. (Fig. 7c, d). The roughness indicated the distribution of active landslides between 3 and 6 eigenvalue ratios, consistent with that reported by Kasai et al. (2009). Ninety percent of the landslides occurred in areas with curvature of − 4.0 and 4.0, but 89% of the DSGSDs were distributed between curvatures of 0 and 2.0. (Fig. 7e, f). Landslides are more common in convex terrain than DSGSD. Seventy percent of the landslides occurred in areas with underground openness between 79 and 85, while 79% of the DSGSD were distributed between 79 and 81. (Fig. 7g, h). Landslides were more common in ridge topography than DSGSD. Seventy-one percent of the landslides occurred in areas between the overground openness of 81 and 85, while 73% of the DSGSD were distributed between that of 79 and 82 (Fig. 7g, h). Landslides were found to be more common in valleys than DSGSD. Sixty-seven percent of the landslides occurred with TWI between 0.3 and 1.0, whereas 73% of the DSGSDs were distributed between 0.4 and 0.7. The average TWI of the landslides was 0.57 and DSGSD was 0.46. (Fig. 7k, l). Landslides have a wider catchment area than DSGSD. The mean wavelets are 0.41 for landslides and 0.45 for DSGSD (Fig. 7m, n). 78% of DSGSDs were between 0.3 and 0.6, while landslides had no peak. The mean elevation was 791 for landslide and 757 for DSGSD (Fig. 7o, p). Both had large standard deviations. In the case of landslides, however, 26% were concentrated in the 750–800 m elevation range.

Fig. 7
figure 7

Percent frequency of the influence factors that describe the characteristics of landslides and DSGSD. a, c, e, g, i, k, m, o Percent frequency of pre-landslide, slope, Eigenvalue ratio, curvature, underground openness, overground openness, TWI, wavelet, and elevation, in that order. b, d, f, h, j, l, n, p Percent frequency of DSGSD locations, consisting of slope, Eigenvalue ratio, curvature, underground openness, overground openness, TWI, wavelet, and elevation, in that order

Full size image

These trends indicate that landslide is more gently sloping than DSGSD, resulting in a convex ridge and valley topography. In TWI, the catchment area is clearly wider in landslide than in DSGSD. The concentration at a specific elevation of 750–800 m may be due to the concentration of landslides around the transition line, as described by Tsou et al. (2017).

3.3 Creation of tiles for learning data

The learning data was created by dividing the influence factor image into squares (Fig. 2). These image files are called tiles—we cut the influence factor images from the pre-landslide into 50 × 50-pixel images (in.jpg format) starting from the NW corner. 50 pixels equal 50 m, which means 50 × 50 pixels are equal to 2500 m2. The reason for the choice of the 50-pixel square is that the smallest area of the landslide occurred case includes 1500 m2. Additionally, the DSGSD corresponds to an ultra-micro-topography according to Suzuki (1997), and its scale is 10–100 m. Therefore, the 50 × 50 m tile contains the minimum area for deciphering the micro-topography. Each tile was replicated with a version rotated 90° and another that was mirrored. Creating the rotated images meant we would lose information related to slide direction. The landslides and collapses in this region occurred on north-facing slopes. However, rather than the directional features, it was necessary to learn more about the gravitational deformation features of mountainous bodies, and we increased the learning data by implementing those rotations. Furthermore, the y0 data was expected to have less area than that of the y1 data. Therefore, we also created offset data with 25-pixel shifts in both x- and y-axes to increase the number of tiles.

These tiles were allocated randomly for training and verification purposes, as shown in Table 2. The total number of landslide (y0) tiles eventually became 20,212 images. The tiles of the 63 locations labeled DSGSD (y1) and the outside landslide (y2) were processed in the same manner. There were 3846 and 12,927 images, respectively, resulting in using a combined total of 36,985 images for the training process.

Table 2 Number of data (tiles) used for training and validation
Full size table

3.4 Modeling algorithms

Deep learning techniques were used in the current study. The mentioned models are explained in the following sections.

3.4.1 Deep learning models

Deep learning is an analytical method that uses a neural network, which is a multi-layer structure modeled after the neural circuits of the human brain. Machine learning has been used to create LSM since 2000s, as described in the previous section. The applications of the machine learning-based models on local areas include a case study by Van Dao et al. (2020) using 217 sites in northern Vietnam and a case study using 157 landslide inventories in Malaysia (Al-Najjar and Pradhan 2021). In addition, Wei et al (2022) used inventory data for 203 landslides that covered an area of 18,000 km2 and reported the effectiveness of using the data over a wide area.

We conducted an analysis using a CNN, which is highly effective for image recognition. A CNN is a machine learning method that contains multiple convolutional layers within the structure of the neural network, which convolve and generate the feature values for each layer and pooling layers that compress these values. The convolutional layer of the CNN has a good perception of the local characteristics of the image and can sense the relationship between the pixel of interest and the surrounding pixels (Simonyan 2014).

Image recognition has been used extensively in previous studies. However, identifying images of gravitational deformation in mountainous terrain is a complex and difficult process. The range of collapsed areas is a topographic element that leaves various DSGSD evidence at each juncture, and all are different. Slight differences in the ground surfaces with a complex history may not be discernible in a single image. Therefore, in this study, we used influence factor images that shared the same coordinates. We gave the images multiple perspectives as modal information (see Figs. 6 and 7), called the multi-modal method (Ngiam et al. 2011; Srivastava and Salakhutdinov 2012). This model was used for feature extraction and pre-training in deep neural networks and to obtain common and high-level feature representations from different modal information by connecting the hidden layers of two networks or by sharing latent variables (Baltrušaitis et al. 2019). Several authors have demonstrated that CNN models provide high detection accuracy for landslide-prone areas (Ding et al. 2016; Yu et al. 2017; Fang et al. 2020). A comparison of two CNN architectures, a 1D CNN structure (CNN-1D) and a 2D CNN structure (CNN-2D), shows that the CNN-2D model is the best model for landslide susceptibility mapping (Youssef et al. 2022). In this study, we used a 2D CNN structure (CNN-2D) architecture based on the abovementioned previous studies; CNN-2D has been used for landslide detection in several studies (Wang et al. 2019; Ma et al. 2021).

3.4.2 Model creation

Model construction comprised a learning phase and a testing phase. The hold-out method was used for the learning phase and comprised training and validation. In the training stage, 70% of the tiles were used with the creation of weighted parameters to construct the model, referring to the model construction method proposed by Kohavi (1995). Next, in the validation stage, the remaining 30% of the tiles were used for verification of each parameter and layer structures were constructed by simulating whether the tiles were judged correctly. The model created was called a “trained model.”

The network structure was searched for the best model using an automatically constructed high-performing architecture. Automatically constructed methods show new structures that can be seen without human coordination (Real et al. 2020). The results of this study point to the possibility of finding machine learning algorithms that not only reduce and streamline the burden of human design but also do not use neural networks. A neural network console (Sony Corporation, Tokyo, Japan) was used in this study. In this application, model construction and parameter adjustment were automatically performed using graphical user interfaces (GUIs). This search method used network features and Bayesian optimization with Gaussian process (Wu et al. 2019), which can search for a better network faster than random search (Suganuma et al. 2020). The initial model was LeNet (LeCun et al. 1989), which demonstrated high character recognition rate.

3.4.3 Influence factors’ effectiveness, model validation, and comparison

The tests that could help determine the effectiveness of the influence factors is the multicollinearity method. Parameter independence is assessed using the variance inflation factor (VIF) (Roy et al. 2019). This method identifies variables with high collinearity that need to be filtered out of the models. It is also important to evaluate the correlation between different parameters that are indicative of a landslide. The variance inflation factor (VIF) is an indicator of the degree of multicollinearity; the VIF is a value calculated for each explanatory variable and was obtained. In this paper, the multicollinearity test was performed using the variance inflation factors (VIFs) and tolerance (T), calculated using Eqs. 1 and 2.

$${\text{VIF }} = { 1}/{\text{T}}$$
(1)
$$T = 1 - R_{j}^{2}$$
(2)

T and \(R_{j}^{2}\) are the tolerance and coefficient of determination of each parameter’s regression, respectively. The criterion for multicollinearity is VIF > 10 or T < 0.10. Predictors with such values are judged to have multicollinearity among the explanatory variables (Wooldridge 2015). VIF = 10 when VIF > 10 translates into a correlation coefficient of about 0.95, meaning that the association between the two variables is very strong. Previous studies have reported that predictors with VIF > 5 or T < 0.10 may also contribute to multicollinearity (Rahman et al. 2019; Youssef et al. 2022).

The trained model was summarized using a confusion matrix. A confusion matrix summarizes the results of multi-class classifications (Eqs. (3) and (4)) and is a measure of machine learning model performance. Four standard metrics were used to evaluate the performance. These metrics were calculated based on three numbers measured during the test: (1) true positives (TPs, correct detections), (2) false negatives (FNs, incorrect targets), (3) false positives (FPs, incorrect detections), and (4) true negatives (TNs, correct detections). Recall expresses the proportion of each explanatory variable detected. In the best case, recall is equal to 1, so the CNN detected all category labels (y'0, y'1, and y'2) in the test set. Precision describes the percentage of category labels correctly detected and classified.

$${\text{Recall}} = \frac{{{\text{TP}}}}{{{\text{TP}} + {\text{FN}}}} \left( {{\text{True}}\;{\text{Positive}}\;{\text{Ratio}}} \right), \frac{{{\text{FP}}}}{{{\text{FP}} + {\text{TN}}}}\left( {{\text{False}}\;{\text{Positive}}\;{\text{Ratio}}} \right)$$
(3)
$${\text{Accuracy}} = \frac{{{\text{TP}} + {\text{TN}}}}{{{\text{TP}} + {\text{FP}} + {\text{FN}} + {\text{TN}}}}$$
(4)

To predict and test the performance of the prediction of LSMs in this study, we used the receiver operating characteristic (ROC) curve and area under the curve (AUC) (Bradley 1997). This method is one of the most common techniques to determine the quality and accuracy of CNN models (Jaafari et al. 2018). The performance of the model can be calculated by plotting the TPR (true positive ratio) on the Y-axis and the FPR (false positive ratio) on the X-axis. An acceptable model must have an AUC value between 0.5 (lower accuracy) and 1 (high accuracy).

4 Results

4.1 Multicollinearity test and correlation results

To ensure that the parameters used in the study are truly independent (not highly correlated), we performed statistical collinearity test and found that there was no collinearity between the independent variables (see Table 3). The maximum value for VIF was 3.40 for curvature, which is below the VIF threshold (= 5), and the minimum value for tolerance is 0.29 for curvature, which is above the tolerance threshold (= 0.1). Accordingly, all eight landslide influencing factors were included in the analysis.

Table 3 Multicollinearity results of landslide influence factors
Full size table

4.2 Model validation

The results of the automatically constructed model structure are presented in Table 4 and Fig. 8. Structural search was performed on 80 different models based on LeNet. The best value of AUC was 0.965 (Model-77), while the initial model had AUC = 0.911. The best value of accuracy was 0.887 (Model-78, see Table 4), while the initial model had an accuracy of 0.807. The ROC–AUC method was used to determine the predictive performance of the models. The optimal model was Model-78, with AUC = 0.960 and accuracy = 0.887. Guzzetti et al. (2005) classified the AUC values into categories to give meaning to the evaluation values, with an AUC of 0.75 to 0.8 indicating an acceptable model, an AUC of 0.8 to 0.9 indicating a good landslide susceptibility model, and an AUC of 0.9 or higher 0.9 or higher indicating a good model. As shown in Fig. 9, the result of the optimal model we applied has an AUC value of 0.960, which can be said to be a good and high-performance model (Merghadi et al. 2020).

Table 4 Correct answer rate from optimal model (Model-78)
Full size table
Fig. 8
figure 8

ROC curves for LSMS by automatically constructing for the model structures

Full size image
Fig. 9
figure 9

Change in accuracy and AUC values using automatically construct for the model structure

Full size image

Four typical models after training and validation are shown in Fig. 10. The initial models are faithful reproductions of LeNet (a), Model-37 (b) is the simplest model with only one convolutional layer, and Model-47 (c) consists of eight convolutional layers. The optimal model (d; Model-78) has eight convolutional layers, which have both increased accuracy and AUC compared to model-47. The optimal model was a further evolution of model-47, and the duplication data in two data was more efficient by concatenating with different treatments. A part of convolutions uses DepthwiseConv, which improve accuracy and reduce computational complexity. The activation functions used were SeLU, which is similar to ReLU, and Swish, along with tanh, which is the extended version of the sigmoid function (Ramachandran et al. 2017). As shown in Table 4, the recall for each explanatory variable item (y'0, y'1, y'2) was 97.2%.

Fig. 10
figure 10

Architecture of the applied (a) LeNet, Model-1 (b) Model-37 (c) Model-48 and (d) Model-78 in this study

Full size image

4.3 Landslide susceptibility models (LSMs)

In the current study, models trained with the two initial and optimal models were then evaluated using a test dataset (see Fig. 2; 3 × 2 km2, 60,000 tiles). Landslide susceptibility indices were calculated for each pixel in the study area using each model; these indices were then exported into the QGIS 3.24 software. Subsequently, the indices were converted into LSMs and areas were classified into five classes (very low, low, medium, high, and very high) (Fig. 11) using Natural Breaks Classification (Jenks), which is a common and popular approach (Jenks and Caspall 1971; Nicu 2018). Four representative models showed that learning data (y0, y1) was efficiently selected according to the automatically constructed model. This was the same trend for y'1 and y'2. The distribution of each class for the 80 models is shown in Fig. 12. The four representative models (models 1, 37, 48, and 78) accounted for 18.5%, 23.6%, 13.2%, and 6.7% of the high and very high sensitivity zones, 10.1%, 14.4%, 4.5%, and 2.5% of the medium sensitivity zone, and 71.4%, 62.0%, 82.3%, and 90.8% of the low and very low sensitivity zones, respectively. As a result, the proportion of very high, high, moderate, and low classes was small and stable due to the increase in Accuracy and AUC by the automatically constructed mode.

Fig. 11
figure 11

Landslide susceptibility maps using models 1, 37, 48, and 78

Full size image
Fig. 12
figure 12

Landslide susceptibility class percentages and accuracy eighty models of testing area

Full size image

5 Discussion

Landslides are complex natural phenomena with topography, geology, and rainfall conditions, and can recur under conditions similar to past landslides (Dagdelenler et al. 2016). Landslide susceptibility studies are critical in these areas because they provide local hazard maps and constitute the most basic approach (Roccati et al. 2021). Creating accurate LSMs that can be used to identify landslide-prone areas is the ultimate goal of research in this field (Mandal et al. 2021). Since large-scale deep failures show signs of DSGSD, it is expected that highly accurate DEMs can be used (Chigira et al 2013). In this study, a deep learning algorithm was applied to build an accurate model focusing on landslide-susceptible but more collapse-prone terrain by introducing high accuracy DEM data prior to collapse.

To construct an accurate landslide susceptibility model, it is essential to select an appropriate influencing factor. As a result, a model with high prediction accuracy can be constructed. there are many types of influencing factors, and they vary according to regional characteristics. However, there are no rules for the selection of the influencing factor (Park and Kim 2019; Youssef et al. 2022). Therefore, in this study, we selected the topographic information that can be obtained from one type of DEM information to be the most appropriate to reduce scale effects between data. In this study, eight influence factors were selected to evaluate landslide susceptibility. The validity of this information was verified by applying the VIF, a multicollinearity test to identify relationships among the influence factors that may affect the accuracy of the overall model. The results indicate that there is no multicollinearity among the selected factors. Therefore, all factors could be employed for model building. The properties of the influencing factor follow the assumption that landslides used in the study occurred in areas with slope angles of 26°–46°. This is a broader value than DSGSD, indicating that it has undulations on slopes. Ninety percent of the curvatures were undulating in the − 4 to 4 zone, 70% had an underground openness of 79–85 and 71% had an overground openness of 81–85. The average TWI of the landslides was 0.57 and DSGSD was 0.46. These four items showed mean values different from DSGSD. This trend indicates that the landslide is at a higher elevation near the ridge, with a gentle slope, but no valley or gullies developed, and surface water infiltrated into the subsurface. Thus, frequent rainfall, combined with the topographic conditions, would increase the risk of landslides in the study area.

In this study, an automatically construct high-performing CNN architectures was utilized to find a better model of landslide susceptibility in the southern part of the Kii Peninsula in Japan by comparing it with a deep learning model with multiple structures. LSM validation and comparison were performed using AUC and accuracy of ROC curves to determine the predictive power of the selected model for the study. The validation dataset (landslide: 38, DSGSD: 63 locations, 30% of the total area of 101 locations) was used to validate the models. The comparative analysis showed that the optimized model achieved more satisfactory and significant performance than the initial model (LeNet) or the complex model with eight convolutional layers. The optimal model (accuracy: 88.7%) was found to outperform the initial model (predicted value: 80.7%) by 8.0%. These results were confirmed by the high performance of the optimal model (AUC = 96.0%).

Previous studies have showed that CNN models are considered a promising method for better prediction results in landslide modeling (Fang et al. 2020). Youssef et al. (2022) noted that CNN models are considered a good tool for landslide modeling owing to their significant results and high prediction rates for landslide prediction with spatial information. The performance of deep learning algorithms (CNN) depends on the design of the model, including the structure of the training data, the size of the input data, and the characteristics of the different layers (Ghorbanzadeh et al. 2019b). They concluded that CNN models perform better than traditional machine learning algorithms such as ANN, RF, and SVM in landslide susceptibility studies (Mandal et al. 2021). These results are consistent with our results where the AUC of the optimal model for automatically constructed high-performing CNN architecture is 96.0%. The reason why the accuracy of the optimal model was only 88.7% can be explained by the following reasons: Because the mesh cut is square, not all of the collapse area consists of landslide and DSGSD. The learning data is objectively selected, and it is considered that topographic features that do not relate to the landslide and DSGSD were mixed in the collapse area during the selection process.

The spatial distribution of landslide-prone areas is the primary target of landslide susceptibility models. In this study, it was found that the landslide susceptibility map reflects the actual situation. However, in the study area, the combination of multiple geomorphic features, such as the knick line and terminal cliff, is noted to have an influence on collapse (Chigira et al. 2013). The results of this study are limited by the fact that only one tile is used to determine the extent of collapse, and it is not possible to cover all topographic features, so it is not possible to look at a wider area than 50 m. Therefore, the “y’0; areas with topography similar to that of the 2011 deep-seated landslides,” are shown in Fig. 13 as an analytical diagram averaged over the surrounding five tiles (250 m in diameter). The reason for the 250 m diameter is to cover an average area of 40,865m2 for the 38 landslide sites. As shown Fig. 13, the results for the distribution of the different susceptibility classes showed that these models have similar spatial patterns, with very low and low susceptibility distributed in areas with gentle slope less than 25° and steep slope and very high and high susceptibility zones distributed near gentle slopes above the knick line. This trend is consistent with the claim by Tsou et al. (2017) that deep-sheeted landslides occurred mainly on the gentle slopes of the transition line. The five study sites indicated in the red box are ID35 and ID37, and the continuity of these landforms from the ridge to the riverbed is one indicator of this trend. On the other hand, the “very high and high susceptibility zones” are mostly above a certain elevation and close to the ridge. As shown in Fig. 13, the very high and high susceptibility zones were in 9 paleo surface areas and 12 incised inner gorges. This trend is consistent with Tsou et al. (2017) finding that the percentage of incised inner gorges, landslide, is 20–30% larger than DSGSD, demonstrating that the automatically constructed high-performing CNN architectures in our results are effective.

Fig. 13
figure 13

Distribution of analytical diagram averaged over the surrounding five tiles (250 m in diameter) based landslide susceptibility map of the 2011 events

Full size image

6 Conclusions

In this study, we evaluated 80 different models using the automatically constructed high-performing CNN architectures for landslide detection. We demonstrated the effectiveness of these algorithms in landslide detection using pre-collapse DEM data. We trained and tested the algorithms on a selected set of 38 collapsed sites and 63 non-collapsed sites but recognizable DSGSD from the 2011 Kii Peninsula rainstorm in southwest Japan based on a combined dataset of eight different landslide influence factors from the DEM data.

To the best of our knowledge, no study has yet examined the self-search capability of CNN algorithms for landslide annotation (evaluation) using pre-collapse images. CNN models should be designed through trial and error depending on the type of model to be solved and the amount of data, and it is desirable to find a configuration that can achieve high accuracy. The results showed high performance with the optimal being the OPTIMAL model with 8 convolutional layers with AUC = 0.960 and accuracy = 0.887. Compared to the initial model, an 8% improvement in accuracy and a 5% improvement in AUC were achieved.

Three explanatory variables y0, y1, and y2 were prepared for training and testing the algorithm. The locations where a landslide occurred during the 2011 event were designated as “y0: landslide”. Next, “y1: DSGSD” is non-slide, but it had topographic features of DSGSD. Finally, the landforms not included in y0 and y1 were designated as “y2: landforms not related to landslide”. The results showed that the explanatory variables y0 and y1 do not overlap and retain a high degree of accuracy. Furthermore, the landslide susceptibility map is consistent with the trends in the distribution of gentle slopes and knick lines unique to the study area, and can be used as a powerful method for future landslide prediction.

In future, along with more examples of different regional characteristics, Fang et al. (2020) noted that integrating CNNs with other traditional and hybrid statistical methods in landslide susceptibility modeling can produce better results than using CNN algorithms alone. Moreover, it is expected that integrating and combining CNNs with other statistical models will produce LSMs that are more accurate than CNN-only models. For instance, DInSAR could be selected or approaches that use time series data, such as multiple LiDAR data, could be considered to improve detection results.