Earthquake response of embankment resting on liquefiable soil with different mitigation models

Abstract

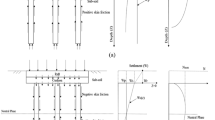
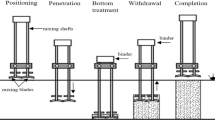
Three different liquefaction mitigation techniques for an earthen embankment resting on saturated loose cohesionless soil have been compared in the present study as densification of foundation soil, stone column mitigation, and hybrid pile-stone column mitigation. Numerical modelling has been done using finite element modelling assuming plane strain condition. Liquefaction behaviour of the foundation soil has been modelled using the effective stress-based elasto-plastic UBC3D-PLM model. All the three mitigation models along with the benchmark model have been analysed under 25 different real ground motions. The maximum embankment crest settlement has been occurred in the Imperial Valley (1979) ground motion having the maximum Arias Intensity. The maximum crest settlement and the maximum excess pore pressure ratio in the mitigation zone below embankment toe found to be increasing with Arias Intensity of ground motions. In case of mitigation using densification of region below the embankment toe, the mitigated zone away from the toe towards the free field liquefies. The stone column mitigation reduces the excess pore pressure more efficiently beneath the embankment toe region than other two mitigation techniques. The hybrid mitigation with a combination of gravel drainage and pile found to be more effective to reduce the excess pore pressure as well as the shear-induced and post-shaking settlement due to the rapid dissipation of excess pore pressure of the foundation soil.

Appendix: Constitutive behaviour of UBC3D-PLM model

A nonlinear, elastic behaviour based on isotropic law was integrated into the UBC3D-PLM model. This law is characterised in terms of the elastic bulk modulus (K) and the elastic shear modulus (G), which are described using the following equations:

$$K = \,k_{B}^{*e} p_{{{\text{ref}}}} \left( {\frac{{p^{^{\prime}} }}{{p_{{{\text{ref}}}} }}} \right)^{{{\text{me}}}} ,\quad G = \,k_{G}^{*e} p_{{{\text{ref}}}} \left( {\frac{{p^{^{\prime}} }}{{p_{{{\text{ref}}}} }}} \right)^{{{\text{ne}}}}$$

(6)

Model considers primary and secondary yield surfaces based on mobilised angle of friction ϕ_mob. The primary yield surface becomes operational when ϕ_mob equals ϕ_p. The secondary yield surface is based on ϕ_mob and simplified kinematic-hardening rule. The Mohr–Coulomb yield function has been used to represent both the yield surfaces which is defined in Eq. (7).

$$f_{m} = \frac{{\sigma_{\max } - \sigma_{\min } }}{2} - \left( {\frac{{\sigma_{\max } + \sigma_{\min } }}{2} + c\,\,\cot (\varphi_{p} )} \right)\,\sin (\varphi_{{{\text{mob}}}} )$$

(7)

In this model, plastic hardening based on the strain hardening principle is utilised (Hardening Soil model). Due to the mobilisation of the shear strength, the hardening rule controls the amount of plastic strain ($\sin \,\,\varphi_{{{\text{mob}}}}$). Equation (8) provides the definition of the anisotropic hardening rule used for the secondary yield surface.

$$K_{{G,{\text{secondary}}}}^{p} = K_{G}^{p} (4 + 0.5\;n_{{{\text{rev}}}} )\,{\text{hard}}\,{\text{fac}}_{{{\text{hard}}}}$$

(8)

$${\text{hard}}\, = \,\min \,(1;\,\max (0.5,\,\;0.1\,\,N_{1,60} )$$

(9)

where, ${\text{hard}}$ parameter used for correcting the densification rule for loose condition, ${\text{fac}}_{{{\text{hard}}}}$ is an input parameter used for adjusting the densification rule and $n_{{{\text{rev}}}}$ is the number of reversal of shear stress from loading to unloading and vice versa.

Formulation of stiffness degradation, which occurs due to the deconstruction of the soil skeleton occurs during dilation, is given in Eqs. (10) and Eq. (11). $\varepsilon_{{{\text{dil}}}}$ is the accumulated plastic deviatoric strain, and E_dil is limited by the parameter $f_{{{\text{Epost}}}}$.

$$K_{{G,\,\,{\text{post-liquefaction}}}}^{*\,p} = K_{G}^{*\,p} \,E_{{{\text{dil}}}}$$

(10)

$$E_{{{\text{dil}}}} = \max (e^{{ - 110\varepsilon_{{{\text{dil}}}} }} \,;\,{\text{fac}}_{{{\text{post}}}} )$$

(11)

The equivalent volumetric strain of the fluid must complement the volumetric strain created in the soil skeleton for there to be volumetric compatibility under undrained conditions. Using Poisson’s ratio of 0.495 (Petalas and Galavi 2013), undrained soil bulk modulus is calculated as follows:

$$K_{u} = \frac{{2G^{e} (1 + \nu_{u} )}}{{3(1 - 2\nu_{u} )}}$$

(12)

Similarly, the drained bulk modulus K_d is calculated using the drained Poisson’s ratio.

$$\nu^{{\prime}} = {{\left( {3K^{e} - 2G^{e} } \right)} \mathord{\left/ {\vphantom {{\left( {3K^{e} - 2G^{e} } \right)} {\left( {6K^{e} + 2G^{e} } \right)}}} \right. \kern-0pt} {\left( {6K^{e} + 2G^{e} } \right)}}$$

(13)