1 Introduction

Under the context of global climate change, the severity of drought increases, which induces a lot of environmental, economic, and social damages, such as, grain yields reduction, economic losses, and higher health risks (Wilhite 2000; Dai 2011; Trenberth et al. 2014). Agricultural drought is closely related to (but not defined as) the soil moisture deficit or the crop water stress over a period (Martínez-Fernández et al. 2015). The agricultural drought impacts are being aggravated by the rise in water demand and the variability in precipitation/temperature as a result of climate change (Mishra and Singh 2010; Leng and Hall 2019). Besides, human activities, for example, the large-scale agricultural practice, increase the vulnerability to droughts worldwide(Wang et al. 2016b). Therefore, accurately agricultural drought monitoring is of high importance to provide a basis for enacting effective measures to prevent potential disasters(Zhao et al. 2017).

Maracchi (2000) considered it was critical to select an appropriate index for assessing and monitoring agricultural drought, analyzing its spatial–temporal characteristics, and determining drought assistance. Given the close association with the below-normal soil moisture (Martínez-Fernández et al. 2015), most of the agricultural drought indices are derived from soil moisture deficiency (Palmer 1965, 1968), such as the crop moisture index (CMI) (Palmer 1968), crop drought index (CDI) (Brunini et al. 2005), crop water stress index (CWSI) (Jackson et al. 1981). These indices can be calculated based on the combination of ground-observed or simulated hydro-meteorological variables (e.g., precipitation, temperature, evaporation, and soil moisture). Recently, benefiting from the development of hydrological models, which can well describe the influences of topography, soil, and landcover on surface water fluxes, the way to obtain these hydro-meteorological variables has been significantly expanded (Li et al. 2016). For example, agricultural drought over the USA was measured by monthly mean soil moisture anomaly percentiles, which were obtained from the North American Land Data Assimilation System (NLDAS) Variable Infiltration Capacity (VIC) and Noah models (Mo 2008). The soil moisture deficit index (SMDI) and evapotranspiration deficit index (ETDI) were developed based on SWAT simulated soil moisture and evapotranspiration (Narasimhan and Srinivasan 2005). Leng et al. (2015a, b) obtained a standardized soil moisture index (SSWI) used VIC model forced by five global circulation models (GCMs) under the RCP8.5 emission scenarios to assess the climate change on agricultural drought.

However, in these previous studies, agricultural drought is generally considered as a natural phenomenon, in the absence of the impact of human activities like irrigation and reservoir regulation(Van Loon et al. 2016; Wan et al. 2017). Irrigation is widely used to mitigate natural moisture deficiency and thus has been an essential part of agricultural practices coping with drought. Therefore, the agricultural drought in irrigated areas is not only associated with precipitation and soil moisture but also regulated by the amount of available water supply for irrigation. In particular, the impact of irrigation is significant in southern China due to the highly developed agricultural water supply facilities (ICOLD 2003). Some previous studies focus on incorporating the process of human activities into the agricultural drought monitoring. For example, Li et al. (2016) developed a new agricultural drought index derived from the simulated soil moisture, which was based on the Variable Infiltration Capacity (VIC) model coupled with an irrigation scheme and a reservoir module. Sun et al. (2015) presented a methodology for agricultural drought assessment under the different irrigational levels supported by run theory, copula functions, and a crop growth model Leng et al. (2015a). investigated the effects of irrigation on global water resources by performing Community Land Model 4.0 (CLM4) and highlighted the need to account for irrigation in assessing regional climate impacts. However, these studies above added parameterized irrigation strategy into a model, requiring additional parameters and local agricultural practices information, which increased the difficulty of model construction. Therefore, skillful and parameter-independent agricultural drought monitoring method is still a challenge. To overcome this limitation, we construct a new agriculture drought index based on the evaluation of whether the local water resources can meet the irrigation water demand during the growth of the crop. The new index eliminates the need for additional irrigation strategy module and is easier to implement in most regions.

To this end, this study aims to develop a new index, irrigation water deficit index (IWDI), based on the estimation of irrigation water demand and supply. Compared with other agricultural drought indices, the primary advantage of IWDI is taking irrigation and water demand of crop growth into consideration, and avoiding the complexity of building irrigation modules. Historical drought analysis is conducted based on the Soil Moisture Anomaly Percentage Index (SMAPI) to verify the performance of the new index. Besides, we use the above new method to quantitatively assess drought conditions over space and time for the study area. The proposed method and index can provide a better understanding of agricultural drought and a more valuable evaluation for decision-makers or stakeholders.

2 Methodology

The proposed index, irrigation water deficit index (IWDI), is calculated based on the estimation of irrigation water demand obtained from the improved FAO-56 crop water model and available water supply derived from the Variable Infiltration Capacity (VIC) model.

2.1 Irrigation water deficit index

The irrigation water deficit index is designed to evaluate the agricultural drought further. Its calculation scheme is shown on Fig. 1. Firstly, the net irrigation water demand is calculated though an improved FAO-56 crop water model (see Sect. 2.2 for details). Secondly, the daily surface water supply is obtained from the simulated results of the Variable Infiltration Capacity (VIC) model (Liang et al. 1994, 1996), and two efficiency factors are employed to estimate the proportion of total water supply used for irrigation (see Sect. 2.3 for more details). Thirdly, the comparison between daily net irrigation water demand and irrigation water supply was made to identify drought occurrence. If the water supply is less than irrigation demand, the drought might occur, and the corresponding period will be regarded as a drought period. The daily irrigate on water deficit will be calculated through the difference between irrigation water demand and water supply for the current time step. Then, the cumulative irrigation water deficit (i.e., CIWD) is obtained. In contrast, if the water supply is more than irrigation water demand, the corresponding period will be regarded as a no-drought period, and CIWD will be considered as zero.

Fig. 1
figure 1

Scheme of the IWDI calculation

Full size image

The cumulative irrigation water deficit may vary with different regions because of the different climate, crops, and irrigation schedules. In other words, it is a regional-dependent variable and cannot be applied as an agricultural drought index for different regions. Therefore, the maximum value of cumulative irrigation water demand (i.e., MCIR) of all drought periods for a designated area is introduced to eliminate the regional disparity. Finally, the irrigation water deficit index (i.e., IWDI) as a new agricultural drought index is calculated as the CIWD value divided by the MCIR value.

$$IWDI{ = }\frac{CIWD}{{MCIR}} \times 100\%$$

It is noted that the improved FAO-56 model and the VIC model are both based on grid cells, so the grid-based variables can be used to calculate the spatial pattern of the IWDI value for the selected basin.

2.2 Irrigation water demand calculation

The net irrigation water demand is calculated though an improved FAO-56 crop water model (Dodds et al. 2005). This improved model was developed by the Food and Agricultural Organization. It provided a comprehensive description of the widely accepted Penman–Monteith method for estimating reference evapotranspiration (Penman 1948; Monteith 1965; Allen et al. 1998) and the FAO Penman–Monteith equation is as follows:

$$ET_{o} = \frac{{0.408\Delta \left( {R_{n} - G} \right) + \gamma \frac{900}{{T + 27U_{2} }}U_{2} \left( {e_{s} - e_{a} } \right)}}{{\Delta + \gamma \left( {1 + 0.34U_{2} } \right)}}$$

where \(ET_{o}\) represents the potential evaporation of a well-watered crop (mm day−1); \(R_{n}\) is the net radiation at the crop surface (MJ/m2day); \(G\) is the soil heat flux density (MJ/m2day); \(T\) is the air temperature at 2 m height (0C); \(U_{2}\) is the wind speed at 2 m height above the ground (m/s); \(e_{s}\) is the saturation vapor pressure (kPa); \(e_{a}\) is the actual vapor pressure; \(\Delta\) is the slope of the vapor pressure curve (kPa/0C) and \(\gamma\) is the psychrometric constant (kPa/0C).

To taking the characteristics of different crops into account, the crop coefficient (\(K_{c}\)) is used to modify the \(ET_{0}\) into \(ET_{{{\text{crop}}}}\) and listed as:

$$ET_{{{\text{crop}}}} = K_{c} \cdot ET_{0}$$

\(K_{c}\) here is determined by crop characteristics and the stage of crop growth.

The effective precipitation and irrigation water are the primary sources to meet the crop water demand, so the irrigation water demand is calculated by the difference between crop evapotranspiration (\(ET_{{{\text{crop}}}}\)) and effective precipitation. Tigkas et al. (2019) provided several empirical methods to estimate the effective precipitation, which mainly refers to the rainwater infiltrated into the soil and evaporated into the air by crops. In this study, the infiltration process was simulated by the VIC model, and the equation of the effective precipitation is given below:

$$P_{eff} = PREP - Q_{d} - Q_{b}$$

where \(P_{eff}\) is the effective precipitation (mm), \(PREP\) is the precipitation reaching the soil surface (mm), \(Q_{d}\) is the direct surface runoff simulated by the VIC model (mm), \(Q_{b}\) is the baseflow simulated by the VIC model (mm).

Then, the net irrigation water demand can be calculated as follows:

$$Irr_{net} = ET_{{{\text{crop}}}} - P_{eff}$$

where \(Irr_{net}\) is the net irrigation water demand if the selected unit (mm). The temporal distribution of irrigation water demand is obtained by the meteorological data and Kc value of the reference crop. Given that the farmland spatial pattern affects the spatial distribution of irrigation water demand, a farmland area fraction (\({f}_{a}\)) is adopted to describe the spatial heterogeneity of the irrigation water demand and modify the net irrigation water demand.

$$Irr = Irr_{net} \cdot f_{a}$$

where \(Irr\) is the irrigation water demand of the selected spatial unit (mm), \(f_{a}\) is the fraction of the farmland area to the total spatial unit area.

2.3 Available irrigation water supply calculation

The daily surface water supply is obtained based on the VIC model, which is a widely used distributed hydrological model to assess water resources, land–atmosphere interactions, and hydrological responses(Gao et al. 2009; Li et al. 2016; Wang et al. 2016a; Shi et al. 2018; Zhu et al. 2018). The principal characters of the VIC model are the representation of multiple land cover types, spatial heterogeneity of soil properties, soil water movement, and surface flow. Among them, surface flow considering both infiltration excess flow and saturation excess flow in the upper soil layer, and baseflow in the lowest soil layer. Due to its finer performance of the hydrological process and streamflow simulation, the latest version of VIC, which partitions the subsurface into three layers (VIC-3L), is selected in this study to estimate the spatial water resources distribution of the study area. Liang et al. (1996) described the detailed information of the formulation of the VIC model.

The gridded streamflow obtained from the calibrated VIC model can be regarded as the water stored in the river channel, which is used to support the local industry, agricultural, and domestic water supply(Shi et al. 2018). Also, two coefficients, water resources utilization coefficient (the proportion of water consumption for human activities and total water resources) and agricultural water proportional coefficient (the proportion of agricultural water consumption and water consumption for human activities) are introduced to estimate the amount of water supply for irrigation.

$$W_{irri} = Q_{s} \cdot f_{1} \cdot f_{2}$$

where \(W_{irri}\) is the available water supply for irrigation(mm/day), \(Q_{s}\) is the simulated surface runoff provided by the VIC model (mm/day), \(f_{1}\) is the water resources utilization coefficient, \(f_{2}\) is the agricultural water proportional coefficient.

The above two coefficients could refer to the annual statistical report published by the local Statistics Bureau or the “water resources report” published by the local water resources management department.

2.4 Soil moisture anomaly percentage index

The traditional agricultural drought indicator, Soil Moisture Anomaly Percentage Index (SMAPI) (Bergman et al. 1988), which was proven to be capable of measuring the severity of agricultural droughts, was calculated to make a comparison with IWDI to verify the performance of the IWDI. The SMAPI equation is:

$${\text{SMAPI}} = \frac{{\theta - \overline{\theta }}}{{\overline{\theta }}} \times 100\%$$

where \(\theta\) and \(\overline{\theta }\) represent the current value of soil moisture and multi-year average in the same time series. In this study, \(\theta\) and \(\overline{\theta }\) were obtained from the simulated soil moisture of the VIC-3L model. SMAPI of 0–100 mm depth (the topsoil layer) and SMAPI of 0–1600 mm depth (the top two soil layers) are used to represent the soil moisture condition.

Besides, the Normalized Difference Vegetation Index (NDVI) (Jiang et al. 2017) was also introduced to make a comparison with the new index IWDI, exploring the response of IWDI to vegetation dynamic.

3 Study area and data

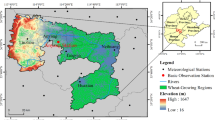
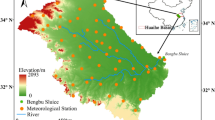
The study area is the upstream of the Zi River basin (i.e., UZRB), which is a part of the Yangtze River basin. It is located around Shaoyang city, Hunan Province, southern China (see Fig. 2). Longhui station, the streamflow station on the outlet of the river basin, controls a drainage area of 5547 km2. Farmland accounts for 35% of the total basin area, covering most of the flat land of the UZRB. The region is dominated by agriculture, and the main crop is double-cropping rice. In this study, the crop coefficient (Kc) value for rice in Asia provided by Doorenbos and Pruitt (1977) is referred and then modified by the irrigation schedule of Hunan Province. According to the “Hunan statistical yearbook,” the water consumption accounted for 19.3% of the total local water resources, and the agricultural water consumption accounted for 69.8% of the full water resources utilization of the UZRB (CSY 2008). Thus, the water resources utilization coefficient (\(f_{1}\)) and agricultural water proportional coefficient (\(f_{2}\)) was determined as 0.193 and 0.698, relatively. The UZRB was divided into 249 grids (0.05° spatial resolution), and the irrigation water demand and supply are both calculated based on the grid cells.

Fig. 2
figure 2

Study area map and its streamflow stations

Full size image

The data collected for the VIC model included meteorological data, geospatial data, and hydrological data. The VIC model was driven by a set of daily meteorological forcing data. The precipitation, maximum, and minimum air temperature, and wind speed were obtained from the China Meteorological Assimilation Driving Datasets for the SWAT model (CMADS) (Meng et al. 2018). The total periods are from 2008.1.1 to 2016.21.31. The spatial resolution of the CMADS dataset is 0.25° and then interpolated into 0.05°grids through an inverse distance weighted (IDW) method. The CMADS meteorological data were also used to calculate the daily ET0 of each grid, which is essential for the estimation of irrigation water demand. The geospatial data include elevation data, soil, and land cover data. The 90 m digital elevation data were obtained from the shuttle radar topography mission digital elevation model (https://srtm.csi.cgiar.org/); The soil data were collected from the Harmonized World Soil Database (HWSD) (https://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/harmonized-world-soil-database-v12/en/), and the land cover map was provided by the University of Maryland’s 1 km Global Land Cover Production (Hansen et al. 2000). All these geospatial maps were resampled to a 0.05° grid. Hydrological data, which includes the historical streamflow series of two stations (Huangqiao and Longhui) from 2008 to 2016, were collected from the Hydrological Bureau of Hunan Province, China and employed to calibrated the VIC model. Besides, the Terra Moderate Resolution Imaging Spectroradiometer (MODIS) Vegetation Indices (MOD13Q1) product provided the monthly NDVI data over the UZRB, with a resolution of 0.05°(Wardlow et al. 2018).

4 Results

4.1 Model calibration

Figure 3 shows the comparison of the simulated and observed monthly streamflow of the two hydrological stations in the UZRB. The determination coefficient (R2), Nash–Sutcliffe coefficient of efficiency (NSE), and Percent Bias (PBIAS) are employed as model performance metrics. According to the performance ratings suggested by Moriasi et al. (2007), the model performance at a monthly scale can be considered satisfactory when NSE > 0.5 and PBIAS <  ± 25%. The R2 and NSE values for the two stations both greater than 0.75 and the PBIAS values lower than 10%, suggesting that the model can simulate reasonably the runoff for the control stations of the UZRB. Once the model was calibrated, the surface runoff series for the research period could be extracted from the VIC model for each grid.

Fig. 3
figure 3

Monthly calibration result for the two hydrological stations: (a) Longhui (b) Huangqiao

Full size image

4.2 Performance of the IWDI in drought monitoring

Figure 4 compares the daily time series of the SMAPI and the IWDI from 2008 to 2016. The IWDI and SMAPI (0–100 mm) showed a dramatic fluctuation between dry and wet periods, while the SMAPI (0–1600 mm) exhibited a lower frequency of change and a longer drought duration.

Fig. 4
figure 4

Comparison of the daily time series of SMAPI(1–100 mm), SMAPI (0–600 mm) against IWDI during 2008–2016 (averaged over the UZRB)

Full size image

According to the definition of the SMAPI and IWDI, the period in which the SMAPI value lower than zero or the IWDI value higher than zero can be recognized as a drought period. The drought periods identified by IWDI are consistent with the drought identified by SMAPI (0–100 mm). For example, the drought period between 2009.8 and 2010.3 was a continuous drought event according to SMAPI (0–1600 mm), while the IWDI and SMAPI (0–100 mm) divided the 2009.8–2010.3 drought period into several short drought events. The possible reason is that the variation of IWDI and SMAPI (0–100 mm) is influenced mainly by present precipitation, while the change of SMAPI (0–1600 mm) depends on long-term moisture conditions. These indicated the keen sensitivity of IWDI in monitoring short-term agricultural drought.

In addition to the drought events duration, the drought severity identified by IWDI and SMAPI had a significant difference. The drought events of 2008.10 and 2013.8 (emphasized with a dotted oval) described by SMAPI showed a similar severity (about -28%). However, the severity of the two events exhibited by IWDI varied notably, which was 39% and 68% relatively. The different results of drought severity may lead to a separate evaluation of drought level. According to the drought disaster statistics of Hunan provided by Hydrological Bureau of Hunan Province, the grain yield losses due to drought disasters in 2008 and 2013 were 900 million kg and 3.34 billion kg. Although the agricultural drought condition in Hunan Province cannot entirely represent the drought condition in the UZRB, the drought records of Hunan indicated a much more drought severity in 2013 than in 2008 over Hunan, which is consistent with IWDI value. That confirmed the accurate drought severity estimation capability of IWDI.

Figure 5 shows the intra-annual variation of monthly average SMAPI, irrigation water demand, irrigation water supply, and IWDI. The intra-annual variation of the irrigation water demand was consistent with the sowing and growth of double-cropping rice in Hunan Province. Generally, the early-season rice is sown in mid-April and harvested in late July, and the late-season rice is planted in early August and harvested in late October. The irrigation water demand was higher from April to October, while the water supply was insufficient to meet the water demand from July to October. Hence, high IWDI values were found from July to October due to the contradiction between water supply and demand.

Fig. 5
figure 5

Intra-annual variation of monthly average: a SMAPI (1–100 mm), SMAPI (0–1600 mm) b irrigation water demand, irrigation water supply, and IWDI averaged over the UZRB

Full size image

There is a big difference between the relatively dry months indicated by SAMPI and IWDI. According to SMAPI, the dry season of the UZRB was autumn (September, October, and November) and winter (December, January, and February). However, the IWDI variation revealed that the summer-autumn period (from July to October) was a dry season. Given that winter is not the season for rice planting, the IWDI did not regard winter as a dry period, although the water supply is relatively low. Overall, the results demonstrated that IWDI considered the growth process of crop and eliminated the impact of invalid soil moisture drought, leading to a more accurate intra-annual agricultural drought evaluation.

4.3 Drought level identification based on the IWDI

The relative and cumulative frequency of IWDI and SMAPI over the UZRB were calculated (Fig. 6). Generally, the frequency distribution of IWDI behaved similarly to SMAPI. Miner difference lay in the tails of the distribution curves (IWDI > 40 and SMAPI < − 0) of the two indices. For extreme drought conditions, the frequency of IWDI was much higher than that of SMAPI.

Fig. 6
figure 6

Frequency distribution of a IWDI and b SMAPI (0–100 mm) values and critical points of different drought levels

Full size image

We understand that the level of drought can be categorized on different quantile values, and quantifying drought levels is of considerable significance to guide the government and farmers to deal with drought. The drought classification based on the SMAPI was conducted in the previous study (Wu et al. 2011), and it was used to classify the drought level in the UZRB (Table 1). Assuming that the drought defined by SMAPI and IWDI has the same frequency distribution, we can find the classification method based on IWDI according to the frequency and critical points of SMAPI. Therefore, the quantile–quantile transformation was used to define the critical points of IWDI for classifying drought levels based on the new index (Table 2). Hence, the drought levels decided by the two indices share the same frequency distribution, which keeping the drought classifications stable and comparable.

Table 1 Drought level classifications based on the SMAPI
Full size table
Table 2 Drought level classifications based on the IWDI
Full size table

4.4 The spatial pattern of the drought frequency based on IWDI

We analyzed the spatial patterns of drought frequency based on the proposed IWDI index to further investigate the drought distribution in the UZRB (Fig. 7). The frequency was calculated as the number of days during drought periods. Four drought levels were considered in the frequency assessment using the classification proposed in 4.2. It is apparent that the spatial frequency distributions for moderate, severe, and extreme drought were quite similar, with a high drought incidence in the southeast and central part of the UZRB and lower in the northwestern part. The high-frequency area of the slight drought was more extensive than that of the other three levels. The spatial distribution of annual precipitation (Fig. 8a) can explain the decreasing tendency of drought frequency from southeast to northwest.

Fig. 7
figure 7

Spatial patterns of drought occurrence frequency of different drought levels based on IWDI: a Slight drought, b Moderate drought, c Severe drought, d Extreme drought

Full size image
Fig. 8
figure 8

Spatial patterns of a annual precipitation and b proportion of the irrigated area

Full size image

Furthermore, the high-frequency zone was restricted by the irrigated area, resulting in that some grids in the southern UZRB with less precipitation but show a low drought frequency. The spatial pattern of the proportion of the irrigated area is presented in Fig. 8b, which was consistent with the distribution of the high-frequency zone of slight droughts. For moderate, severe, and extreme drought, their drought frequencies were high for the grids with more than 50% of irrigated area, and the drought frequency of the grids with less irrigated area depended on precipitation. We can conclude that, with the assessment of the IWDI index, the spatial pattern of drought occurrence frequency is roughly decided by precipitation and modified by the irrigated area. For the drought level from slight to extreme, the decisive role of precipitation is increasing while the impact of irrigated area is weakening.

4.5 Influencing factors of IWDI

To further investigating the possible influencing factors of the new index, correlation analysis was conducted. Five crucial hydrological variables (i.e., precipitation, soil moisture, runoff, actual evapotranspiration, and potential evapotranspiration) were obtained from the VIC model, and their correlation coefficient with IWDI and SMAPI was calculated. The boxplots of correlation coefficients between IWDI and SMAPI against the five hydrological variables are given in Fig. 9. As expected, the IWDI shows a negative correlation with precipitation, soil moisture, and runoff and a positive correlation with actual and potential evapotranspiration, which is precisely the opposite of SMAPI’s results.

Fig. 9
figure 9

The boxplots of correlation coefficients between a IWDI b SMAPI against five hydrological variables. Each box shows the minimum, maximum, median, 25% quantile, 75% quantile, and mean values of correlation coefficients

Full size image

It is worth noting the IWDI performed a higher correlation with precipitation, runoff, and potential evapotranspiration (absolute value of correlation coefficients above 0.5), which implied IWDI had a great relationship with these three variables. Compared with SMAPI, the actual and potential evapotranspiration had a more significant impact on IWDI, while the soil moisture influenced IWDI less. Overall, the water balance variables, water input (precipitation), and output (runoff and evapotranspiration) highly affect IWDI, which implies that the new index is more inclined to reflect comprehensive moisture conditions.

4.6 IWDI performance in the reconstruction of historical agricultural drought events

We understand the drought event in 2013.7–8 is the most severe and the most representative event during the research period, so a specific investigation about the 2013 drought was conducted. According to the historical records, the 2013 southern drought in China caused a direct economic loss of 26.82 billion yuan and affected 8.021 million hectares of crops. Seven provinces were influenced by this drought event and among them, Hunan was the most affected province. Considering the similarity between SMAPI (0–100 mm) and IWDI on temporal variation, SMAPI (0–100 mm) in the 2013 drought event was illustrated together with IWDI (Fig. 10). To investigate the capability of IWDI of detecting vegetation dynamic, NDVI in July and August was also provided (Fig. 11). The higher NDVI indicates a better growth condition of vegetation and vice versa.

Fig. 10
figure 10

Spatial maps of the drought event of 2013.7–8, described by a SMAPI (1-100 mm), b IWDI

Full size image
Fig. 11
figure 11

Monthly spatial maps of the drought event of 2013.7–8 described by NDVI

Full size image

From Fig. 10a, it can be seen the spatial pattern of the 2013 drought propagation indicated by SMAPI. The slight drought first appeared in the southeastern and southern parts of the UZRB in early July. Then, the drought continued and occurred in July to August across the most area of the UZRB except southwest woodland. The SMAPI showed a transparent process of drought, which started in the south and spread throughout the basin. The longevity of the soil moisture drought in critical agricultural months can lead to massive crop losses this year. However, SMAPI failed to distinguish the more severe drought condition in the farmland area with more water demand.

The general northwestward tendency of the drought was captured by IWDI as well (Fig. 10b), but the drought propagation indicated by SMAPI lagged behind that indicated by IWDI. Moreover, the drought area indicated by IWDI was limited to the central plains and did not extend to the surrounding mountain area. The drought condition for the central grids considered as the significant crop-growing areas was emphasized, with the highest drought level. An extensive drought in the central plain on 10 August hinted at the severity of this drought event.

It is seen that IWDI accurately captured the severe drought signal indicated by NDVI, especially in the central grids with the more concentrated farmland cover ( Fig. 11). That was inconsistent with the result of SMAPI, which hardly reflected the vegetation growth anomaly. The findings suggest the capacity of IWDI to monitoring the combination of vegetation growth dynamics and soil moisture.

5 Discussion

5.1 Enlightenment for index construction

This study proposed a new agricultural drought index taking the irrigation water demand and water supply availability into account. As we know, there are already many drought indices over the world; however, none of them is universal reliable for different regions, especially different drought types (Cheng et al. 2020). Therefore, suitable drought indices are still needed for drought monitoring and assessment (Cheng et al. 2018). The results obtained by the new index reveal the superiority of the proposed index compared with the traditional indices based on a single hydrological variable. We were aware of the following enlightenment about agricultural index construction from the research.

Traditional agricultural drought indices are mostly designed to observe a lack of water in the soil. Without considering the underlying surface and crop conditions, traditional agricultural drought indices cannot accurately reflect the impact of water shortage on crops, nor do they consider the aggravation or mitigation effects of human factors (such as irrigation) on drought. Therefore, a comprehensive agricultural drought assessment requires accurate information about the spatial distribution and growth processes of crops. Thus, drought events that have no negative impact on crop growth will be ignored, so that accurate agricultural drought assessment will be obtained, which can directly determine the yield reduction due to drought.

Besides, in the Anthropocene, agricultural drought has both natural and human drivers (Van Loon et al. 2016). The traditional way views drought as a natural phenomenon and regarded human-caused water shortage as a separate process, which is not always useful for drought monitoring and management. We need to understand how human activities modify the agricultural drought processes positively and negatively. Answering the question requires new statistical and modeling tools to analyze qualitative and quantitative datasets on water use, land and water management, and agricultural practices.

5.2 Limitations

Applying the proposed method and index for identifying agricultural drought events, we also need to be fully aware of the following limitations, which are mainly related to two aspects.

Firstly, the net irrigation water demand was used for this study, but the gross irrigation water demand would be more appropriate for this regard. Leng et al. (2016) considered differentiating the irrigation method is important for estimating irrigation water use efficiency, which further determines the gross irrigation water demand. For example, drip irrigation is the most efficient followed by sprinkler and flood irrigation. The choice of different irrigation methods would lead to substantial differences in the gross irrigation demand, even though the net irrigation demand is the same because they differ largely in the irrigation water use efficiency. Therefore, it is helpful to adopt gross irrigation water demand which considering specific irrigation methods for accurate agricultural drought assessment. However, in this study, limited by data availability, we did not highlight the impacts of irrigation methods on irrigation water demand. In the future study, different scenarios with the combination of different irrigation methods will be considered in agricultural drought index construction.

Secondly, the natural streamflow simulated by a hydrological model was used as the water supply in this study. In reality, however, water supply depends on various social-economic factors such as dams, reservoirs, and prices. Water availability is a complex, multifaceted issue and cannot be viewed as a solely natural variable. A comprehensive estimation of the available water resources requires hydrological models or land-surface models that consider the impact of human activities (e.g., reservoir operation, groundwater extraction, and water transfer) and social factors. He et al. (2017) analyzed the contribution of human water management to hydrological drought over California using the PCR-GLOBWB model and found that including management in the modeling framework results in more accurate discharge representation. In the future study, the development of hydrological models or land-surface models considering water management and the socioeconomic process will lead to a more adaptable drought assessment and broaden the definition of drought to include water shortage caused by human processes.

6 Conclusions

Based on the irrigation water deficit during the growth process of crops, a new agricultural drought index, IWDI, was proposed to address the one-sidedness of traditional drought indicators. The improved FAO-56 model and the VIC model was used to estimate the irrigation water demand and supply over the designated river basin. The performance of the new index was assessed over the UZRB, whose landcover is dominated by farmland. The analysis reveals the accuracy and application of the index, which shows the capacity to identify agricultural drought severity and to monitor farmland-based drought spatial patterns.

The main results and conclusions are summarized below.

  1. 1.

    The proposed index can provide a reliable estimate for the agricultural drought condition at the daily scale over the UZRB. The analyses indicated that the IWDI was able to represent the spatial and temporal changes for the historical agricultural drought events during 2008–2016. The proposed index incorporated the growth process of crop and spatial distribution of farmland, showing an excellent performance in combining the dynamic of soil moisture and vegetation growth.

  2. 2.

    The main influence factors of the IWDI are precipitation, runoff, and potential evapotranspiration, which are significantly correlated with IWDI. The IWDI tends to reflect a comprehensive moisture condition with a water balance process.

  3. 3.

    The spatial pattern of drought occurrence frequency was roughly decided by precipitation and modified by irrigated areas. For the drought level from slight to extreme, the decisive role of precipitation is increasing, while the impact of irrigated area distribution is weakening.

  4. 4.

    Compared with SMAPI, the IWDI shows a better performance in quantifying agricultural drought levels, especially for stressing drought conditions in an agricultural concentration area. The IWDI considers the growth process of crop and eliminates the impact of invalid soil moisture drought of non-growing seasons, resulting in a more instructive drought assessment.