Dissipativity of Stochastic Competitive Neural Networks with Multiple Time Delays

Abstract

The $(Q,R,S)-\gamma -$dissipative of stochastic competitive neural networks (SCNNs) with leakage delays and discrete delay is studied. Firstly, Lyapunov–Krasovskii functional is constructed, which studies the relationship between various types of time delays. Secondly, by using integral inequality technique, the linear matrix inequality (LMI) criterion of $(Q,R,S)-\gamma -$dissipative in the mean square sense of SCNNs is obtained. Furthermore, the obtained LMI criterion is extended to the passivity in the mean square sense, stability in the mean square sense, $(Q,R,S)-\gamma -$dissipative and passivity. Finally, the effectiveness of the obtained results are verified by numerical simulation.

1 Introduction

In industrial production applications, the research of various equipment systems has established many different types of models through mathematical modeling, such as neural network model and [1,2,3]. It is well known that neural networks have great value in practical applications, such as associative memory, pattern recognition, image processing and so on. Competitive neural networks (CNNs) are a small branch of neural networks, which are named after competitive relationship between cells. Unlike neural networks with only a kind of state variable, CNNs have two kinds of state variables. Short-term memory (STM) describes fast neuronal activity and long-term memory (LTM) describes slow unsupervised synaptic modification. Correspondingly, CNNs have two types of time scales. One reflects the rapid change of state, and the other reflects the slow change of unsupervised synaptic modification. CNNs are a kind of neural network model that not only exchange information between the corresponding two synapses, but also exchange information within cell layers. Because the CNNs contain this special way of informational transmission, it is great significance to study. Some interesting results on CNNs, such as [4,5,6,7].

In practical applications, disturbances are inevitable due to stochastic factors outside the system, such as various noises. For decades, there had been many research results on stochastic factors, such as [8,9,10,11,12,13,14,15,16,17,18]. In order to truly and accurately describe the actual problems and processes, it is more practical and valuable to consider the perturbation of these stochastic factors in CNNs. For example, [4] studied the synchronization of CNNs with noise intensity functions. The exponential synchronization of switched SCNNs with both interval time-varying delays and distributed delays was studied in [5]. Ali et al. [6] investigated the stability of stochastic fractional-order CNNs with leakage delay.

In the actual operation of the system, time delay is inevitable. Therefore, it is very important to consider the factor of time delay in system modeling. Because leakage delay exists negative feedback term of system. In the proof, the negative feedback term of system cannot be squared. The term coupled with the negative feedback term needs to be scaled or summed, so that get the square form of the negative feedback term. Hence, it is difficult to deal with the leakage delay term. The system with leakage delay term had attracted numerous scholars to study. There had been many research results (for example, [16, 19,20,21,22,23,24]) that reflected the importance of leakage delays. Such as [16] investigated the uniform stability in mean square of stochastic fractional-order memristor fuzzy BAM neural networks with leakage delay terms. Li and Rakkiyappan [20] improved the sufficient conditions for the stability of a class of neutral delay BAM neural networks with leakage delays on the basis of [19]. Li and Cao [21] and Wang et al. [22] studied the stability of neural networks with leakage delay terms. Therefore, it is of great significance and value to study SCNNs with leakage delays.

The concept of dissipativity is an important physical property of the dynamic model, which is closely related to the Lyapunov stability theory. The dissipative theory analyzes the input and output of the system from the perspective of energy. Therefore, the dissipativity of the system had received extensive attention [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. $(Q,S,R)-\gamma -$dissipative means that energy consumed inside the system is less than energy provided externally, so that energy of the system can be maximized. As a special case of generalized dissipativity of the system, strictly $(Q,S,R)-\gamma -$dissipative of the system had attracted attention of many scholars, such as [27] and [39] investigated the problem of $(Q,S,R)-\gamma -$dissipative for a class of Markovian jump neural networks with time-varying delay. Feng et al. [33] studied the delay-dependent $(Q,S,R)-\gamma -$dissipative for continuous time singular systems with time-delay. Wu et al. [35] studied the robust $(Q,S,R)-\gamma -$dissipative analysis for uncertain neural networks with time-varying delay. In [38] and [40], the $(Q,S,R)-\gamma -$dissipative of static neural networks with interval time-varying delay is investigated. However, up to now, there is little research on the dissipativity of SCNNs with multiple time delays. In order to overcome this requirement, the main contribution of this paper is to fill this gap. In this article, we try to obtain the $(Q,S,R)-\gamma -$dissipative criterion of the SCNNs with multiple time delays and leakage delays. This is the motivation of our paper.

The contributions and highlights of this paper are as follows:

• (1) The stochastic terms of CNNs are added to both STM and LTM.

• (2) The relationship between leakage delays and discrete delay is explored.

• (3) The $(Q,R,S)-\gamma -$dissipative in the mean square sense of SNNs criterion is obtained by using integral inequality, and the criterion is given in the form of LMI.

• (4) The obtained LMI criterion is extended to the passivity in the mean square sense, stability in the mean square sense, $(Q,R,S)-\gamma -$dissipative and passivity of the corresponding system.

The rest of this paper is organized as follows. Some Notations, Definitions, Lemmas are introduced in Sect. 2. The $(Q,R,S)-\gamma -$dissipative, passivity and stability in the mean square sense of SCNNs with multiple time delays is investigated in Sect. 3. Typical numerical examples are presented in Sect. 4. The conclusion is finally drawn in Sect. 5.

1.1 Notations

$\mathbb {R}^n,\mathbb {R}^{n\times n}$ denote the Euclidean n-space and $n\times n$ real matrix, respectively. $A>0 (<0)\in \mathbb {R}^{n\times n}$ denote that A is positive definite ( negative definite ) matrix. $A^{T},A^{-1}$ denote the transpose and the inverse of matrix A, respectively. $E\{\cdot \}$ represents mathematical expectation. $*$ denote the corresponding symmetric element. $({\bar{\Omega }},\mathscr {F},\mathscr {P})$ is a complete probability space with a filtration $\{\mathscr {F}_t\}_{t\ge 0}$ satisfying the usual conditions (i.e., the filtration contanins all P-null sets and is right continuous). $C^{2,1}(\mathbb {R}^n \times \mathbb {R}^+, \mathbb {R}^+)$ is the family of all nonnegative functions on $\mathbb {R}^n \times \mathbb {R}^+$. $\mathscr {L}$ is an operator. $\Re ^i_{jk}$ indicates the element at the position of row j and column k of matrix $\Re _i$.

2 Preliminaries and Problem Description

Consider the following CNNs with multiple time delays:

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned} STM:\epsilon \dot{x}_i(t)=&-a_ix_i(t-\sigma )+\sum ^n_{j=1}D_{ij}f_j(x_j(t))+\sum ^n_{j=1}E_{ij}f_j(x_j(t-\tau ))\\&+b_iy_i(t)+U_i(t),\\ LTM:\dot{y}_i(t)=&-c_iy_i(t-\delta )+\sum ^n_{j=1}{\xi }^2_jf_i(x_i(t)),\\ z_i(t)=&f_i(x_i(t)), \end{aligned} \right. \end{aligned} \end{aligned}$$

(1)

where $i=1,2,\cdots ,n$ represents the number of neurons. $x_i(t)$ denotes the current activation level of neurons i at time t, $y_i(t)$ denotes the synaptic effect, $z_i(t)$ denotes the output of the i-th neuron at time t, $a_i>0$ denotes the time constant of the i-th neuron, $c_i>0$ is a one-time scaling constant, $D_{ij}, E_{ij}$ denote the connection strength of the i and j cells at time t and the discrete delay connection weight, respectively. ${\xi }_j$ is a constant external stimulus, $\sigma ,\delta$ are leakage delays, $\tau$ is a discrete delay. $U_i(t)$ is an external input, $f_i(x_i(t))$ is the activation function of neurons, $b_i>0$ is the external stimulus intensity, $\epsilon >0$ is a time scale.

Without loss of generality, let $\epsilon =1,\sum _{j=1}^n{\xi }^2_j=1$. The vector form of the above model is

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned} STM:\dot{x}(t)=&-Ax(t-\sigma )+Df(x(t))+Ef(x(t-\tau ))\\&+By(t)+U(t),\\ LTM:\dot{y}(t)=&-Cy(t-\delta )+f(x(t)),\\ z(t)=&f(x(t)), \end{aligned} \right. \end{aligned} \end{aligned}$$

(2)

where $A=\textrm{diag}\{a_1,\dots ,a_n\},B=\textrm{diag}\{b_1,\dots ,b_n\}, C=\textrm{diag}\{c_1,\dots ,c_n\},D=(D_{ij})_{n\times n}, E=(E_{ij})_{n\times n},U(t)=(U_1(t),\dots ,U_n(t))^T$. When the noise intensity function only exists in the STM, the following model is obtained

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned} STM:d{x}(t)=&[-Ax(t-\sigma )+Df(x(t))+Ef(x(t-\tau ))+By(t)+U(t)]dt\\&+k_1(t,x(t),x(t-\tau ),x(t-\sigma ),y(t))d\omega (t) ,\\ LTM:d{y}(t)=&[-Cy(t-\delta )+f(x(t))]dt,\\ z(t)=&f(x(t)). \end{aligned} \right. \end{aligned} \end{aligned}$$

(3)

When the noise intensity functions exist in the STM and LTM, the following vector form of SCNNs is obtained

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned} STM:d{x}(t)=&[-Ax(t-\sigma )+Df(x(t))+Ef(x(t-\tau ))+By(t)+U(t)]dt\\&+k_1(t,x(t),x(t-\tau ),x(t-\sigma ),y(t))d\omega (t),\\ LTM:d{y}(t)=&[-Cy(t-\delta )+f(x(t))]dt+k_2(t,x(t),y(t-\delta ))d\omega (t),\\ z(t)=&f(x(t)). \end{aligned} \right. \end{aligned} \end{aligned}$$

(4)

Let $k_1(t)=k_1(t,x(t),x(t-\tau ),x(t-\sigma ),y(t)), k_2(t)=k_2(t,x(t),y(t-\delta ))$. Where $k_1(t),k_2(t)$ are the noise intensity function, $\omega (t)$ is a Wiener process defined in probability space $({\bar{\Omega }},\mathscr {F},\mathscr {P})$, and satisfies $E\{d\omega _i^2(t)\}=1$ and $E\{d\omega _i(t)\}=0$.

Remark 1

This paper is different from other articles (such as [8,9,10,11,12,13,14,15,16]). In these articles, the SCNNs only add the noise intensity term to the STM, and the LTM are not added. The model discussed in this paper, not only add stochastic disturbance to STM, but also add stochastic disturbance to LTM. This makes the application of our results more extensive.

Remark 2

When leakage delays $\sigma ,\delta$ are ignored, then (2) will degenerate into the model studied in [7]. Therefore, the model in this paper is more general.

Assumption 1

[18] For any $x,y\in \mathbb {R}$, if there exist constants $l_i^-,l_i^+$, the following inequality holds

$$\begin{aligned} l_i^{-}\le \frac{f_i(x)-f_i(y)}{x-y} \le l_i^{+},i=1,2,\cdots ,n. \end{aligned}$$

Let $L^{-}=\textrm{diag}\{l^{-}_1,\cdots ,l^{-}_n\},L^{+}=\textrm{diag}\{l^{+}_1,\cdots ,l^{+}_n\},$ $W^{+}=\textrm{diag}\{l_1^*,\cdots ,l_n^*\}$. where $l_i^*=\max \{|l^{+}_i|,|l^{-}_i|\}$.

Based on Assumption 1, the system (2) has equilibrium point. Referring to the analyse method of [44], the system (4) can be discussed its dissipativity under zero initial condition.

Assumption 2

[18] Noise intensity function $k_i(t,x(t),y(t)):[0,+\infty ]\times \mathbb {R}^n\times \mathbb {R}^n\rightarrow \mathbb {R}$ is locally Lipschitz continuous and $k_i(0,0,0)=0$. In addition, there exist nonnegative matrices $W_i(i=1,\cdots ,6)$, such that

$k_1(t)=W_1x(t)+W_2x(t-\tau )+W_3x(t-\sigma )+W_4y(t)$,

$k_2(t)=W_5y(t-\delta )+W_6x(t)$.

In order to make the later proof description more concise, the following symbols are introduced

$$\begin{aligned} J_1(t)=&-Ax(t-\sigma )+Df(x(t))+Ef(x(t-\tau ))+By(t)+U(t),\\ J_2(t)=&k_1(t),\\ J_3(t)=&-Cy(t-\delta )+f(x(t)),\\ J_4(t)=&k_2(t), \end{aligned}$$

then (4) is equivalent to

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned} STM:d{x}(t)=&J_1(t)dt+J_2(t)d\omega (t),\\ LTM:d{y}(t)=&J_3(t)dt+J_4(t)d\omega (t),\\ z(t)=&f(x(t)). \end{aligned} \right. \end{aligned} \end{aligned}$$

The initial condition of model (4) is

$$\begin{aligned} x(t)=\varphi (s),y(t)=\psi (s), \end{aligned}$$

where $s\in (min\{-\sigma ,-\tau ,-\delta \},0)$,$\varphi (s),\psi (s)\in \mathbb {C}[(min\{-\sigma ,-\tau ,-\delta \},0), {\mathbb {R}^n}]$.

Remark 3

In [4, 6, 8, 15], the noise intensity function satisfied $k_1^T(t)k_1(t)\le x^T(t)W_1x(t)+y^T(t)W_2y(t),W_1,W_2>0$. In [10] and [12], the noise intensity function satisfied $k_1^T(t)k_1(t)\le x^T(t)W_1^TW_1x(t)+y^T(t)W_2^TW_2y(t)$,where $W_1,W_2$ were nonnegative matrices. The noise intensity function satisfies $k_1^T(t)k_1(t)= x^T(t)W_1^TW_1x(t)+x^T(t-\tau )W_2^TW_2x(t-\tau )+x^T(t-\sigma )W_3^TW_3x(t-\sigma )+y^T(t)W_4^TW_4y(t)$ in this paper, this makes the results more applicable.

Definition 1

The system (4) is strictly $(Q,S,R)-\gamma -$dissipative in the mean square sense. If exists $\gamma >0$, the following inequality holds under the zero initial condition:

$$\begin{aligned} E\left\{ \int _0^{t_f}G(U(t),z(t))dt\right\} \ge \gamma E\left\{ \int _0^{t_f}U^T(t)U(t)dt\right\} ,\forall t_f>0. \end{aligned}$$

where G(U(t), z(t)) with $G(0,0)=0$ is a defined energy supply rate function of the system, and satisfies $G(U(t),z(t))=z^T(t)Qz(t)+2z^T(t)SU(t)+U^T(t)RU(t)$, where Q, S and R are real matrices with $Q^T=Q$, and $R^T=R$.

Definition 2

The system (2) is strictly $(Q,S,R)-\gamma$-dissipative. If exist $\gamma >0$, the following inequality holds under the zero initial condition:

$$\begin{aligned} \int _0^{t_f}G(U(t),z(t))dt\ge \gamma \int _0^{t_f}U^T(t)U(t)dt,\forall t_f>0. \end{aligned}$$

Remark 4

In Definition 1 and Definition 2, if $Q=0,S=I,R=2\gamma I$, then the above definition becomes passive in the mean square sense and passive of system, respectively. When the noise intensity function is ignored, then Definition 1 and Definition 2 are equivalent.

Lemma 1

(${\hat{\textrm{I}}{\textrm{to}}}$ formula) [45] Consider an n-dimensional stochastic differential equation

$$\begin{aligned} dx(t)=f(t)dt+g(t)dw(t), \end{aligned}$$

where x(t) is the n-dimensional ${\hat{{\textrm{I}}}{\textrm{to}}}$ process on $t\ge 0.$ Let $V(x(t),t)\in C^{2,1}(\mathbb {R}^n\times \mathbb {R}^+,\mathbb {R}^+)$, then V(x(t), t) is a real-valued ${\hat{{\textrm{I}}}{\textrm{to}}}$ with its stochastic differential given by

$$\begin{aligned} dV(x(t),t)= \mathscr {L}V(x(t),t)dt+V_{x}(x(t),t)g(t)dw(t), \end{aligned}$$

where $\mathscr {L}V(x(t),t)= V_{t}(x(t),t)+V_{x}(x(t),t)f(t)+\frac{1}{2}trace(g^{T}(t)V_{xx}(x(t),t)g(t)).$

Lemma 2

[46]. If $P\in \mathbb {R}^{n\times n}>0$, scalar function $d=d(t)>0$, and vector-valued function $z(\cdot )$, such that the following integration is well defined, then

$$\begin{aligned} -d\int ^t_{t-d}\dot{z}^T(s)P\dot{z}(s)ds\le -\left( \begin{array}{cc} z(t)\\ z(t-d) \end{array}\right) ^T\left( \begin{array}{cc} P&{}-P\\ *&{}P \end{array}\right) \left( \begin{array}{cc} z(t)\\ z(t-d) \end{array}\right) . \end{aligned}$$

3 Main Results

For convenience, the formulas that need to be used later are presented in advance.

$$\begin{aligned} \begin{array}{lll} \eta (t)=col\{x(t),y(t),x(t-\sigma ),y(t-\sigma ),x(t-\tau ),y(t-\tau ),x(t-\delta ),y(t-\delta ),\\ ~~~~~~~~~~f(x(t)),f(x(t-\tau )),U(t)\},\\ e_i=(0_{n\times (i-1)n}\quad I_n\quad 0_{n\times (11-i)n}), i=1,2,\dots ,11,\\ \Pi _1=(e_1^TW_1+e_2^TW_4+e_3^TW_3+e_5^TW_2,e_1^TW_6+e_8^TW_5)P,\\ \Pi _2=(e_2^TB-e_3^TA+e_9^TD+e_{10}^TE+e_{11}^T,-e_8^TC+e_9^T)\Omega ,\\ \Omega =\sigma ^2G_1+\tau ^2G_2+\delta ^2G_3. \end{array} \end{aligned}$$

Theorem 1

Under Assumptions 1-2, system (4) is strictly $(Q,S,R)-\gamma -$dissipative in the mean square sense. If there exist positive diagonal matrices $P\in \mathbb {R}^{2n\times 2n},R_i(i=1,\dots ,6)\in \mathbb {R}^{2n\times 2n},G_i(i=1,2,3)\in \mathbb {R}^{2n\times 2n},Q_i(i=1,\dots ,3)\in \mathbb {R}^{2n\times 2n}$, $H_i(i=1,2)\in \mathbb {R}^{n\times n}$ and $\Lambda _1\in \mathbb {R}^{n\times n}$, such that

$$\begin{aligned} \left( \begin{array}{ccc} \Phi &{}\Pi _1&{}\Pi _2\\ *&{}-P&{}0\\ *&{}*&{}-\Omega \end{array} \right) <0 \end{aligned}$$

(5)

holds, where $\Phi$ is a 11- dimensional symmetric block matrix. The elements at the corresponding position of $\Phi$ are

and the rest are 0.

Proof

The following Lyapunov functional is constructed as $V(t)=\sum _{i=1}^{5}V_i(t)$, where

$$\begin{aligned} V_1(t)&=\left( \begin{array}{cc} x(t)\\ y(t) \end{array}\right) ^TP\left( \begin{array}{cc} x(t)\\ y(t) \end{array}\right) ,\\ V_2(t)&=\int _{t-\sigma }^t\left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ^TR_1\left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ds+\int _{t-\tau }^t\left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ^TR_2\left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ds\\ {}&+\int _{t-\delta }^t\left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ^TR_3\left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ds,\\ V_3(t)&=\sigma \int _{-\sigma }^0\int _{t+\theta }^t \left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ^TG_1\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) dsd\theta \\&+\tau \int _{-\tau }^0\int _{t+\theta }^t\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ^TG_2\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) dsd\theta \\ {}&+\delta \int _{-\delta }^0\int _{t+\theta }^t\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ^TG_3\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) dsd\theta ,\\ V_4(t)&=2\sum _{i=1}^n\int _0^{x_i(t)}[h_{1i}(f_i(s)-l^-_is)+h_{2i}(l^+_is-f_i(s))]ds,\\ V_5(t)&=(\sigma -\tau )\int _{t-\sigma }^{t-\tau } \left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ^TQ_1\left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ds\\&+(\delta -\sigma )\int _{t-\delta }^{t-\sigma } \left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ^TQ_2\left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ds\\&+(\tau -\delta )\int _{t-\tau }^{t-\delta } \left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ^TQ_3\left( \begin{array}{cc} x(s)\\ y(s) \end{array} \right) ds. \end{aligned}$$

Let $H_1=\textrm{diag}\{h_{11},\dots ,h_{1n}\},H_2=\textrm{diag}\{h_{21},\dots ,h_{2n}\}$.

According to ${{\hat{\textrm{I}}}}{\textrm{to}}$ differential formula, it follows that

$$\begin{aligned} dV(t)=\mathscr {L}V(t)dt+2\left( \begin{array}{cc} x(t)\\ y(t) \end{array}\right) ^TP\left( \begin{array}{cc} J_2(t)\\ J_4(t) \end{array}\right) d\omega (t), \end{aligned}$$

where $\mathscr {L}V(t)=\mathscr {L}[\sum _{i=1}^{5}V_i(t)]$.

$$\begin{aligned} \mathscr {L}V_1(t)=&2\left( \begin{array}{cc} x(t)\\ y(t) \end{array}\right) ^TP\left( \begin{array}{cc} J_1(t)\\ J_3(t) \end{array}\right) +\left( \begin{array}{cc} J_2(t)\\ J_4(t) \end{array}\right) ^TP\left( \begin{array}{cc} J_2(t)\\ J_4(t) \end{array}\right) \nonumber \\ =&\eta ^T(t)\big (2e_1^TP_{11}Ae_3+2e_1^TP_{11}De_9+2e_1^TP_{11}Ee_{10}+2e_1^TP_{11}Be_2\nonumber \\&+2e_1^TP_{11}e_{11}-2e_2^TP_{22}Ce_8+2e_2^TP_{22}e_9-2e_2^TP_{12}^TAe_3+2e_2^TP_{12}^TDe_9\nonumber \\&+2e_2^TP_{12}^TEe_{10}+2e_2^TB^TP_{12}e_2+2e_2^TP_{12}^Te_{11}-2e_1^TP_{12}Ce_8+2e_1^TP_{12}e_9\nonumber \\&+\Pi _1P\Pi _1^T\big )\eta (t). \end{aligned}$$

(6)

$$\begin{aligned} \mathscr {L}V_2(t)=&\left( \begin{array}{cc} x(t)\\ y(t) \end{array} \right) ^T(R_1+R_2+R_3)\left( \begin{array}{cc} x(t)\\ y(t) \end{array} \right) -\left( \begin{array}{cc} x(t-\sigma )\\ y(t-\sigma ) \end{array} \right) ^TR_1\left( \begin{array}{cc} x(t-\sigma )\\ y(t-\sigma ) \end{array} \right) \nonumber \\&-\left( \begin{array}{cc} x(t-\tau )\\ y(t-\tau ) \end{array} \right) ^TR_2\left( \begin{array}{cc} x(t-\tau )\\ y(t-\tau ) \end{array} \right) -\left( \begin{array}{cc} x(t-\delta )\\ y(t-\delta ) \end{array} \right) ^TR_3\left( \begin{array}{cc} x(t-\delta )\\ y(t-\delta ) \end{array} \right) \nonumber \\ =&\eta ^T(t)\big [\left( \begin{array}{cc} e_1\\ e_2 \end{array} \right) ^T(R_1+R_2+R_3)\left( \begin{array}{cc} e_1\\ e_2 \end{array} \right) -\left( \begin{array}{cc} e_3\\ e_4 \end{array} \right) ^TR_1\left( \begin{array}{cc} e_3\\ e_4 \end{array} \right) \nonumber \\&-\left( \begin{array}{cc} e_5\\ e_6 \end{array} \right) ^TR_2\left( \begin{array}{cc} e_5\\ e_6 \end{array} \right) -\left( \begin{array}{cc} e_7\\ e_8 \end{array} \right) ^TR_3\left( \begin{array}{cc} e_7\\ e_8 \end{array} \right) \big ]\eta (t). \end{aligned}$$

(7)

$$\begin{aligned} \mathscr {L}V_3(t)=&\left( \begin{array}{cc} J_1(t)\\ J_3(t) \end{array} \right) ^T(\sigma ^2G_1+\tau ^2G_2+\delta ^2G_3)\left( \begin{array}{cc} J_1(t)\\ J_3(t) \end{array} \right) \nonumber \\&-\sigma \int _{t-\sigma }^t\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ^TG_1\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ds-\tau \int _{t-\tau }^t\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ^TG_2\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ds\nonumber \\&-\delta \int _{t-\delta }^t\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ^TG_3\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ds. \end{aligned}$$

(8)

Apply Lemma 2 into the above integral terms of $\mathscr {L}V_3(t)$, it follows that

$$\begin{aligned}&-\sigma \int _{t-\sigma }^t\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ^TG_1\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ds-\tau \int _{t-\tau }^t \left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ^TG_2\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ds\nonumber \\ {}&-\delta \int _{t-\delta }^t\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ^TG_3\left( \begin{array}{cc} \dot{x}(s)\\ \dot{y}(s) \end{array} \right) ds\nonumber \\ \le&-\left( \begin{array}{cccc} x(t)\\ y(t)\\ x(t-\sigma )\\ y(t-\sigma ) \end{array} \right) ^T\left( \begin{array}{cc} G_1&{}-G_1\\ *&{}G_1 \end{array} \right) \left( \begin{array}{cccc} x(t)\\ y(t)\\ x(t-\sigma )\\ y(t-\sigma ) \end{array} \right) \nonumber \\&-\left( \begin{array}{cccc} x(t)\\ y(t)\\ x(t-\tau )\\ y(t-\tau ) \end{array} \right) ^T\left( \begin{array}{ccc} G_2&{}-G_2\\ *&{}G_2 \end{array} \right) \left( \begin{array}{cccc} x(t)\\ y(t)\\ x(t-\tau )\\ y(t-\tau ) \end{array} \right) \nonumber \\&-\left( \begin{array}{cccc} x(t)\\ y(t)\\ x(t-\delta )\\ y(t-\delta ) \end{array} \right) ^T\left( \begin{array}{cc} G_3&{}-G_3\\ *&{}G_3 \end{array} \right) \left( \begin{array}{cccc} x(t)\\ y(t)\\ x(t-\delta )\\ y(t-\delta ) \end{array} \right) . \end{aligned}$$

(9)

Substituting (9) into $\mathscr {L}V_3(t)$, it follows that

$$\begin{aligned} \mathscr {L}V_3(t)\le&\eta ^T(t)[\Pi _2(\sigma ^2G_1+\tau ^2G_2+\delta ^2G_3)\Pi _2^T- \left( \begin{array}{cc} e_1\\ e_2 \end{array} \right) ^T(G_1+G_2+G_3)\left( \begin{array}{cc} e_1\\ e_2 \end{array} \right) \nonumber \\&+2\left( \begin{array}{cc} e_1\\ e_2 \end{array} \right) ^TG_1\left( \begin{array}{cc} e_3\\ e_4 \end{array} \right) -\left( \begin{array}{cc} e_3\\ e_4 \end{array} \right) ^TG_1\left( \begin{array}{cc} e_3\\ e_4 \end{array} \right) +2\left( \begin{array}{cc} e_1\\ e_2 \end{array} \right) ^TG_2\left( \begin{array}{cc} e_5\\ e_6 \end{array} \right) \nonumber \\&-\left( \begin{array}{cc} e_5\\ e_6 \end{array} \right) ^TG_2\left( \begin{array}{cc} e_5\\ e_6 \end{array} \right) +2\left( \begin{array}{cc} e_1\\ e_2 \end{array} \right) ^TG_3\left( \begin{array}{cc} e_7\\ e_8 \end{array} \right) \nonumber \\&-\left( \begin{array}{cc} e_7\\ e_8 \end{array} \right) ^TG_3\left( \begin{array}{cc} e_7\\ e_8 \end{array} \right) ]\eta (t). \end{aligned}$$

(10)

$$\begin{aligned} \mathscr {L}V_4(t)=&2(f^T(x(t)-x^T(t)L^-)H_1J_1(t)+2(x^T(t)L^+-f^T(x(t)))H_2J_1(t)\nonumber \\ =&\eta ^T(t)[2e_3^T(AH_2-AH_1)e_9+e_9^T(2H_1D-2H_2D)e_9+2e_9^T(H_1E\nonumber \\&-H_2E)e_{10}+2e_2^T(BH_1-BH_2)e_9+2e_9^T(H_1-H_2)e_{17}\nonumber \\&+2e_1^T(L^-H_1A-L^+H_2A)e_3+2e_1^T(L^+H_2D-L^-H_1D)e_9\nonumber \\&+2e_1^T(L^+H_2E-L^-H_1E)e_{10}+2e_1^T(L^+H_2B-L^-H_1B)e_2\nonumber \\&+2e_1^T(L^+H_2-L^-H_1)e_{11}]\eta (t). \end{aligned}$$

(11)

$$\begin{aligned} \mathscr {L}V_5(t) =&\left( \begin{array}{cc} x(t-\tau )\\ y(t-\tau ) \end{array} \right) ^T[(\sigma -\tau )Q_1-(\tau -\delta )Q_3]\left( \begin{array}{cc} x(t-\tau )\\ y(t-\tau ) \end{array} \right) \nonumber \\&+\left( \begin{array}{cc} x(t-\sigma )\\ y(t-\sigma ) \end{array} \right) ^T[(\delta -\sigma )Q_2-(\sigma -\tau )Q_1]\left( \begin{array}{cc} x(t-\sigma )\\ y(t-\sigma ) \end{array} \right) \nonumber \\&+\left( \begin{array}{cc} x(t-\delta )\\ y(t-\delta ) \end{array} \right) ^T[(\tau -\delta )Q_3-(\delta -\sigma )Q_2]\left( \begin{array}{cc} x(t-\delta )\\ y(t-\delta ) \end{array} \right) \nonumber \\ =&\eta ^T(t)\bigg \{\left( \begin{array}{cc} e_5\\ e_6 \end{array} \right) ^T[(\sigma -\tau )Q_1-(\tau -\delta )Q_3]\left( \begin{array}{cc} e_5\\ e_6 \end{array} \right) \nonumber \\&+\left( \begin{array}{cc} e_3\\ e_4 \end{array} \right) ^T[(\delta -\sigma )Q_2-(\sigma -\tau )Q_1]\left( \begin{array}{cc} e_3\\ e_4 \end{array} \right) \nonumber \\&+\left( \begin{array}{cc} e_7\\ e_8 \end{array} \right) ^T[(\tau -\delta )Q_3-(\delta -\sigma )Q_2]\left( \begin{array}{cc} e_7\\ e_8 \end{array} \right) \bigg \}\eta (t). \end{aligned}$$

(12)

In addition, from the previous Assumption 1, for any positive diagonal matrix $\Lambda _1$, the following inequality always hold

$$\begin{aligned} x^T(t-\tau )W^+\Lambda _1 W^+x(t-\tau )-f^T(x(t-\tau ))\Lambda _1 f(x(t-\tau ))\ge 0. \end{aligned}$$

(13)

The following inequality can be obtained by combining formulas (6-8),(10)-(13)

$$\begin{aligned} \mathscr {L}V(t,x(t),y(t))\le \eta ^T(t)(\Phi -\Upsilon +\Pi _1P\Pi _1^T+\Pi _2\Omega \Pi _2^T)\eta (t), \end{aligned}$$

where $\Upsilon =-e^T_9Qe_9-sym\{e^T_9Se_{11}\}-e^T_{11}(R-rI)e_{11}$, that is

$$\begin{aligned} \eta ^T(t)\Upsilon \eta (t)=&-f^T(x(t))Qf(x(t))-f^T(x(t))SU(t)-U^T(t)S^Tf(x(t))\\&-U^T(t)(R-\gamma I)U(t). \end{aligned}$$

In summary, the follow inequality can be obtained

$$\begin{aligned} dV(t,x(t),y(t))\le&\eta ^T(t)(\Phi -\Upsilon +\Pi _1P\Pi _1^T+\Pi _2\Omega \Pi _2^T)\eta (t)\\&+2\left( \begin{array}{cc} x(t)\\ y(t) \end{array}\right) ^TP\left( \begin{array}{cc} J_2(t)\\ J_4(t) \end{array}\right) d\omega (t), \end{aligned}$$

that is

$$\begin{aligned}&dV(t,x(t),y(t))-f^T(x(t))Qf(x(t))-2f^T(x(t))SU(t)-U^T(t)RU(t)\\&+\gamma U^T(t)U(t)\\ \le&\eta ^T(t)[\Phi +\Pi _1P\Pi _1^T+\Pi _2\Omega \Pi _2^T]\eta (t)+2\left( \begin{array}{cc} x(t)\\ y(t) \end{array}\right) ^TP\left( \begin{array}{cc} J_2(t)\\ J_4(t) \end{array}\right) d\omega (t). \end{aligned}$$

Applying Schur complement and (5), it follows that $\Phi +\Pi _1P\Pi _1^T+\Pi _2\Omega \Pi _2^T<0$ holds. Hence, the following inequalities can be obtained

$$\begin{aligned}&dV(t,x(t),y(t))-f^T(x(t))Qf(x(t))-2f^T(x(t))SU(t)-U^T(t)RU(t)\\&+\gamma U^T(t)U(t)\\ \le&2\left( \begin{array}{cc} x(t)\\ y(t) \end{array}\right) ^TP\left( \begin{array}{cc} J_2(t)\\ J_4(t) \end{array}\right) d\omega (t). \end{aligned}$$

Taking mathematical expectations on both sides of the above inequality, it follows that

$$\begin{aligned}&E\{dV(t,x(t),y(t))+\gamma U^T(t)U(t)\}\\ \le&E\{f^T(x(t))Qf(x(t))+2f^T(x(t))SU(t)+U^T(t)RU(t)\}\\&+E\left\{ 2\left( \begin{array}{cc} x(t)\\ y(t) \end{array}\right) ^TP\left( \begin{array}{cc} J_2(t)\\ J_4(t) \end{array}\right) d\omega (t)\right\} \\ =&E\{f^T(x(t))Qf(x(t))+2f^T(x(t))SU(t)+U^T(t)RU(t)\}\\ =&E\{z^T(t)Qz(t)+2z^T(t)SU(t)+U^T(t)RU(t)\}. \end{aligned}$$

Integrating on both sides of the above inequality for 0 to $t_f(t_f>0)$, the following inequality holds.

$$\begin{aligned}&E\{V(t_f,x(t_f),y(t_f))-V(0,x(0),y(0))+\gamma \int _0^{t_f} U^T(t)U(t)dt\}\\ \le&E\{\int _0^{t_f}(z^T(t)Qz(t)+2z^T(t)SU(t)+U^T(t)RU(t))dt\}, \end{aligned}$$

That is

$$\begin{aligned} E\{\gamma \int _0^{t_f} U^T(t)U(t)dt\}\le E\{\int _0^{t_f}(z^T(t)Qz(t)+2z^T(t)SU(t)+U^T(t)RU(t))dt\}. \end{aligned}$$

It can be seen from Definition 1 that the system (4) is $(Q,S,R)-\gamma -$dissipative in the mean square sense. This completes the proof. $\square$

Remark 5

The key to construct Lyapunov functional is to take the state variables, time delay and active function of system as the basis, and ensure that the change rate of this function approaches zero through analysis, so that obtain the stability of system. Compared with [22], the Lyapunov functional in this paper introduces $V_5(t)$. We can observe the Lyapunov functional was independent with the information between leakage delays $\sigma ,\delta$ and discrete delay $\tau$ in [22]. However, the introduction of $V_5(t)$ reflects the relationship between leakage delays $\sigma ,\delta$ and discrete delay $\tau$, indicates that Theorem 1 depends not only on leakage delays $\sigma ,\delta$ and discrete delay $\tau$, but also on $\sigma -\tau ,\delta -\sigma ,\tau -\delta$. It can be seen that conservatism of Theorem 1 can be reduced by adding $V_5(t)$ into V(t).

Remark 6

In [5], authors used inequality $\pm 2a^Tb\le a^TP^{-1}a+b^TPb (a,b\in \mathbb {R}^n,P>0)$ to scale the integral term with delay and delay bound. In [8, 10, 12, 15, 20, 22], the authors used the Jensen ’s inequality to scale the integral term with delay and delay bound. In this paper, Lemma 2 is used to deal with the integral term, which makes the conclusion less conservative.

Remark 7

In [19], authors studied the leakage delay, discrete delay and neutral delay, but did not study the relationship between delays, nor did they study the addition of stochastic terms. In this paper, the relationship between the leakage delays and the discrete delay is studied. In [22], the synchronization of BAM memristive neural network with time-varying leakage delay and discrete time-delay was studied. Lyapunov functional only introduced the relation term between the upper bounds of two delays of the same type, but did not introduce the relation term between different types of delays. In this paper, Lyapunov functional not only introduces the relationship between the same type of delays, but also introduces the relationship between different types of delays for research.

Corollary 1

Under Assumptions 1-2, system (4) is passive in the mean square sense. If there exist positive diagonal matrices $P\in \mathbb {R}^{2n\times 2n},R_i(i=1,\dots ,6)\in \mathbb {R}^{2n\times 2n},G_i(i=1,2,3)\in \mathbb {R}^{2n\times 2n},Q_i(i=1,2,3)\in \mathbb {R}^{2n\times 2n}$, $H_i(i=1,2)\in \mathbb {R}^{n\times n}$ and $\Lambda _1\in \mathbb {R}^{n\times n}$, such that

$$\begin{aligned} \left( \begin{array}{ccc} \Phi ^1&{}\Pi _1&{}\Pi _2\\ *&{}-P&{}0\\ *&{}*&{}-\Omega \end{array} \right) <0 \end{aligned}$$

holds, where $\Phi ^1$ is a 11- dimensional symmetric block matrix. The elements at the corresponding position of $\Phi ^1$ are $\Phi _{99}^1=H_1D+D^TH_1-H_2D-D^TH_2$, $\Phi _{9,11}^1=H_1-H_2-I$, $\Phi _{11,11}^1=-\gamma I$, and the rest of positions are the same as $\Phi$ of Theorem 1.

Corollary 2

If external input U(t) is ignored in system (4). Under Assumptions 1-2, the corresponding system is stability in the mean square sense. If there exist positive diagonal matrices $P\in \mathbb {R}^{2n\times 2n},R_i(i=1,\dots ,6)\in \mathbb {R}^{2n\times 2n},G_i(i=1,2,3)\in \mathbb {R}^{2n\times 2n},Q_i(i=1,2,3)\in \mathbb {R}^{2n\times 2n}$, $H_i(i=1,2)\in \mathbb {R}^{n\times n}$ and $\Lambda _1\in \mathbb {R}^{n\times n}$, such that

$$\begin{aligned} \left( \begin{array}{ccc} \Phi ^2&{}\Pi _1&{}\Pi _2\\ *&{}-P&{}0\\ *&{}*&{}-\Omega \end{array} \right) <0 \end{aligned}$$

holds, where $\Phi ^2$ is a 10- dimensional symmetric block matrix. The elements at the corresponding position of $\Phi ^2$ are the same as the 1–10 row 1–10 column element of $\Phi ^1$.

The dissipativity and passivity of deterministic systems (2) are discussed below. Similar to the derivation of Theorem 1, we can get the following conclusion.

Theorem 2

Under Assumption 1, system (2) is strictly $(Q,S,R)-\gamma -$dissipative. If there exist positive diagonal matrices $P\in \mathbb {R}^{2n\times 2n},R_i(i=1,\dots ,6)\in \mathbb {R}^{2n\times 2n},G_i(i=1,2,3)\in \mathbb {R}^{2n\times 2n},Q_i(i=1,2,3)\in \mathbb {R}^{2n\times 2n}$, $H_i(i=1,2)\in \mathbb {R}^{n\times n}$ and $\Lambda _1\in \mathbb {R}^{n\times n}$, such that

$$\begin{aligned} \left( \begin{array}{cc} \Phi &{}\Pi _2\\ *&{}-\Omega \end{array} \right) <0 \end{aligned}$$

holds.

Proof

. The proof process is similar to Theorem 1, where $dV(t,x(t),y(t))=\mathscr {L}V(t,x(t),y(t))dt$, $\frac{1}{2}trace(g^T(t)V_{xx}g(t))=0$. $\square$

Corollary 3

Under Assumption 1, system (2) is passive. If there exist positive diagonal matrices $P\in \mathbb {R}^{2n\times 2n},R_i(i=1,\dots ,6)\in \mathbb {R}^{2n\times 2n},G_i(i=1,2,3)\in \mathbb {R}^{2n\times 2n},Q_i(i=1,2,3)\in \mathbb {R}^{2n\times 2n}$, $H_i(i=1,2)\in \mathbb {R}^{n\times n}$ and $\Lambda _1\in \mathbb {R}^{n\times n}$, such that $\left( \begin{array}{cc} \Phi ^3&{}\Pi _2\\ *&{}-\Omega \end{array} \right) <0$ holds. $\Phi ^3$ is a 11 - dimensional symmetric block matrix. The elements at the corresponding position of $\Phi ^3$ are $\Phi ^3_{99}=H_1D+D^TH_1-H_2D-D^TH_2$, $\Phi ^3_{9,11}=H_1-H_2-I$, $\Phi ^3_{11,11}=-\gamma I$, and the rest of positions are the same as $\Phi$ of Theorem 1.

4 Examples of Numerical Simulation

Consider CNNs (2), SCNNs (3) and SCNNs (4) with $n=2$, where the parameters are chosen as:

$A=\left( \begin{array}{cc} 2.46&{}0\\ 0&{}1.81 \end{array} \right)$, $B=\left( \begin{array}{cc} 0.95&{}0\\ 0&{}0.91 \end{array} \right)$, $C=\left( \begin{array}{cc} 2.9&{}0\\ 0&{}1.69 \end{array} \right)$,

$D=\left( \begin{array}{cc} -0.42&{}0.77\\ -0.58&{}-0.74 \end{array} \right)$, $E=\left( \begin{array}{cc} 0.4&{}0.81\\ -0.19&{}-0.57 \end{array} \right)$, $W_i =\left( \begin{array}{cc} 0.1&{}0\\ &{}0.1 \end{array} \right)$,

where $i=1,\cdots ,5$, $U(t)=col\{sin(t),cos(t)\}$, $f(x(t))=\frac{1}{2}(tanh(x(t))+x(t))$. Then $l^+=1,l^-=0.5$. $(2,-2,1,-1)$ is the initial condition.

Example 1

According to the relationship between leakage delays $\sigma ,\delta$ and discrete delay $\tau$, it is divided into six situations in Theorem 1. In different cases, the influence of the relationship between the time delays on the $(Q,S,R)-\gamma -$dissipative of the system is explored.

Case 1: $\sigma \le \tau \le \delta$, choose $\sigma =0.19,\tau =0.31,\delta =0.33$.

By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, the feasible solutions can be obtained. The feasible solutions are with the last four digits from the LMI toolbox, which will make the paper lengthy, so they are omitted two decimal places in this example.

$$\begin{aligned} \begin{array}{lll} P_{11}=\left( \begin{array}{cccc} 0.83 &{} -0.41\\ -0.41 &{} 0.93 \end{array} \right) , &{}P_{22}=\left( \begin{array}{cccc} 0.12 &{} -0.01\\ -0.01 &{} 0.16 \end{array} \right) , &{}R^1_{11}=\left( \begin{array}{cc} 0.81 &{} -0.19\\ -0.19 &{} 0.64 \end{array} \right) \\ R^1_{22}=\left( \begin{array}{cc} 0.27 &{} 0.07\\ 0.07 &{} 0.64 \end{array} \right) , &{}R^2_{11}=\left( \begin{array}{cc} 0.85 &{} -0.16\\ -0.16 &{} 0.53 \end{array} \right) , &{}R^2_{22}=\left( \begin{array}{cc} 0.20 &{} 0.05\\ 0.05 &{} 0.51 \end{array} \right) ,\\ R^3_{11}=\left( \begin{array}{cc} 0.39 &{} -0.07\\ -0.07 &{} 0.27 \end{array} \right) , &{}R^3_{22}=\left( \begin{array}{cc} 0.24 &{} 0.04\\ 0.04 &{} 0.52 \end{array} \right) , &{}G^1_{11}=\left( \begin{array}{cc} 8.55 &{} -0.80\\ -0.80 &{} 7.52 \end{array} \right) ,\\ G^1_{22}=\left( \begin{array}{cc} 2.57 &{} -0.43\\ -0.43 &{} 6.02 \end{array} \right) , &{}G^2_{11}=\left( \begin{array}{cc} 0.35 &{} -0.01\\ -0.01 &{} 0.26 \end{array} \right) , &{}G^2_{22}=\left( \begin{array}{cc} 0.17 &{} 0.03\\ 0.03 &{} 0.61 \end{array} \right) ,\\ G^3_{11}=\left( \begin{array}{cc} 0.23 &{} -0.01\\ -0.01 &{} 0.18 \end{array} \right) , &{}G^3_{22}=\left( \begin{array}{cc} 1.18 &{} -0.04\\ -0.04 &{} 2.16 \end{array} \right) , &{}Q^1_{11}=\left( \begin{array}{cc} 22.65 &{} 0.68\\ 0.68 &{} 10.48 \end{array} \right) ,\\ Q^1_{22}=\left( \begin{array}{cc} 4.45 &{} 0.28\\ 0.28 &{} 9.64 \end{array} \right) , &{}Q^2_{11}=\left( \begin{array}{cc} 4.05 &{} -0.48\\ -0.48 &{} 2.63 \end{array} \right) , &{}Q^2_{22}=\left( \begin{array}{cc} 9.02 &{} -1.59\\ -1.59 &{} 10.27 \end{array} \right) ,\\ Q^3_{11}=\left( \begin{array}{cc} 11.79 &{} -0.86\\ -0.86 &{} 10.46 \end{array} \right) , &{}Q^3_{22}=\left( \begin{array}{cc} 28.40 &{} -1.92\\ -1.92 &{} 18.76 \end{array} \right) , &{}H_1=\left( \begin{array}{cc} 1.61&{}0\\ 0&{}2.27 \end{array} \right) , \end{array} \end{aligned}$$

$H_2=\textrm{diag}\{1.13,1.11\}$, $\Lambda _1=\textrm{diag}\{3.27,1.53\}$, $\gamma =0.1004$. By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, it follows that $\gamma =0.0961$ when the relationship between time delays is not considered.

Case 2: $\sigma \le \delta \le \tau$, choose $\sigma =0.13,\tau =0.79,\delta =0.52$.

By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, the feasible solutions can be obtained

$$\begin{aligned} \begin{array}{lll} P_{11}=\left( \begin{array}{cccc} 1.94 &{} -0.51\\ -0.51 &{} 1.34 \end{array} \right) , &{}P_{22}=\left( \begin{array}{cccc} 0.12 &{} 0.01\\ 0.01 &{} 0.26 \end{array} \right) , &{}R^1_{11}=\left( \begin{array}{cc} 1.96 &{} -0.19\\ -0.19 &{} 1.55 \end{array} \right) ,\\ R^1_{22}=\left( \begin{array}{cc} 0.83 &{} 0.10\\ 0.10 &{} 1.31 \end{array} \right) , &{}R^2_{11}=\left( \begin{array}{cc} 1.71 &{} -0.14\\ -0.14 &{} 1.20 \end{array} \right) , &{}R^2_{22}=\left( \begin{array}{cc} 0.55 &{} 0.07\\ 0.07 &{} 1.00 \end{array} \right) ,\\ R^3_{11}=\left( \begin{array}{cc} 1.69 &{} -0.14\\ -0.14 &{} 1.28 \end{array} \right) , &{}R^3_{22}=\left( \begin{array}{cc} 0.92 &{} 0.12\\ 0.12 &{} 1.46 \end{array} \right) , &{}G^1_{11}=\left( \begin{array}{cc} 23.63 &{} -1.30\\ -1.30 &{} 19.54 \end{array} \right) ,\\ G^1_{22}=\left( \begin{array}{cc} 16.25 &{} 0.05\\ 0.05 &{} 20.93 \end{array} \right) , &{}G^2_{11}=\left( \begin{array}{cc} 0.10 &{} -0.01\\ -0.01 &{} 0.06 \end{array} \right) , &{}G^2_{22}=\left( \begin{array}{cc} 0.04 &{} 0.01\\ 0.01 &{} 0.11 \end{array} \right) ,\\ G^3_{11}=\left( \begin{array}{cc} 0.24 &{} -0.02\\ -0.02 &{} 0.16 \end{array} \right) , &{}G^3_{22}=\left( \begin{array}{cc} 0.13 &{} 0.05\\ 0.05 &{} 0.51 \end{array} \right) , &{}Q^1_{11}=\left( \begin{array}{cc} 6.92 &{} -0.11\\ -0.11 &{} 4.53 \end{array} \right) ,\\ Q^1_{22}=\left( \begin{array}{cc} 2.00 &{} 0.20\\ 0.20 &{} 3.92 \end{array} \right) , &{}Q^2_{11}=\left( \begin{array}{cc} 7.83 &{} -0.10\\ -0.10 &{} 6.70 \end{array} \right) , &{}Q^2_{22}=\left( \begin{array}{cc} 20.33 &{} -0.50\\ -0.50 &{} 15.89 \end{array} \right) ,\\ Q^3_{11}=\left( \begin{array}{cc} 10.72 &{} -0.02\\ -0.02 &{} 9.13 \end{array} \right) , &{}Q^3_{22}=\left( \begin{array}{cc} 3.41 &{} 0.22\\ 0.22 &{} 5.45 \end{array} \right) , &{}H_1=\left( \begin{array}{cc} 3.60&{}0\\ 0&{}3.23 \end{array} \right) , \end{array} \end{aligned}$$

$H_2=\textrm{diag}\{2.67,1.65\}$, $\Lambda _1=\textrm{diag}\{7.13,4.88\}$, $\gamma =0.2375$. By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, it follows that $\gamma =0.1449$ when the relationship between time delays is not considered.

Case 3: $\tau \le \sigma \le \delta$, choose $\sigma =0.46,\tau =0.11,\delta =0.54$.

By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, the feasible solutions can be obtained

$$\begin{aligned} \begin{array}{lll} P_{11}=\left( \begin{array}{cc} 0.60 &{} -0.01\\ -0.01 &{} 0.86 \end{array} \right) , &{}P_{22}=\left( \begin{array}{cc} 0.20 &{} 0.02\\ 0.02 &{} 0.42 \end{array} \right) , &{}R^1_{11}=\left( \begin{array}{cc} 2.82 &{} -0.34\\ -0.34 &{} 2.52 \end{array} \right) ,\\ R^1_{22}=\left( \begin{array}{cc} 1.06 &{} 0.09\\ 0.09 &{} 1.67 \end{array} \right) , &{}R^2_{11}=\left( \begin{array}{cc} 2.04 &{} -0.12\\ -0.12 &{} 1.96 \end{array} \right) , &{}R^2_{22}=\left( \begin{array}{cc} 1.26 &{} 0.11\\ 0.11 &{} 1.87 \end{array} \right) ,\\ R^3_{11}=\left( \begin{array}{cc} 1.29 &{} -0.07\\ -0.07 &{} 1.28 \end{array} \right) , &{}R^3_{22}=\left( \begin{array}{cc} 1.37 &{} 0.10\\ 0.10 &{} 1.92 \end{array} \right) , &{}G^1_{11}=\left( \begin{array}{cc} 0.33 &{} -0.07\\ -0.07 &{} 0.26 \end{array} \right) ,\\ G^1_{22}=\left( \begin{array}{cc} 0.18 &{} 0.04\\ 0.04 &{} 0.58 \end{array} \right) , &{}G^2_{11}=\left( \begin{array}{cc} 28.78 &{} -2.19\\ -2.19 &{} 25.29 \end{array} \right) , &{}G^2_{22}=\left( \begin{array}{cc} 22.82 &{} -1.43\\ -1.43 &{} 27.42 \end{array} \right) ,\\ G^3_{11}=\left( \begin{array}{cc} 0.16 &{} -0.02\\ -0.02 &{} 0.16 \end{array} \right) , &{}G^3_{22}=\left( \begin{array}{cc} 0.16 &{} 0.04\\ 0.04 &{} 0.57 \end{array} \right) , &{}Q^1_{11}=\left( \begin{array}{cc} 32.09 &{} -4.92\\ -4.92 &{} 25.69 \end{array} \right) ,\\ Q^1_{22}=\left( \begin{array}{cc} 7.66 &{} 0.11\\ 0.11 &{} 9.92 \end{array} \right) , &{}Q^2_{11}=\left( \begin{array}{cc} 8.88 &{} 0.02\\ 0.02 &{} 9.13 \end{array} \right) , &{}Q^2_{22}=\left( \begin{array}{cc} 16.06 &{} -0.18\\ -0.18 &{} 13.83 \end{array} \right) ,\\ Q^3_{11}=\left( \begin{array}{cc} 4.87 &{} -0.15\\ -0.15 &{} 5.03 \end{array} \right) , &{}Q^3_{22}=\left( \begin{array}{cc} 18.60 &{} -0.83\\ -0.83 &{} 13.82 \end{array} \right) , &{}H_1=\left( \begin{array}{cc} 1.59&{}0\\ 0&{}2.53 \end{array} \right) , \end{array} \end{aligned}$$

$H_2=\textrm{diag}\{0.89,1.19\}$, $\Lambda _1=\textrm{diag}\{6.80,5.79\}$, $\gamma =0.2049$. By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, it follows that $\gamma =0.1920$ when the relationship between time delays is not considered.

Case 4: $\tau \le \delta \le \sigma$, choose $\sigma =0.5,\tau =0.15,\delta =0.35$.

By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, the feasible solutions can be obtained

$$\begin{aligned} \begin{array}{lll} P_{11}=\left( \begin{array}{cc} 0.28 &{} -0.02\\ -0.02 &{} 0.55 \end{array} \right) , &{}P_{22}=\left( \begin{array}{cc} 0.09 &{} 0.02\\ 0.02 &{} 0.27 \end{array} \right) , &{}R^1_{11}=\left( \begin{array}{cc} 1.08 &{} -0.19\\ -0.19 &{} 0.95 \end{array} \right) ,\\ R^1_{22}=\left( \begin{array}{cc} 0.29 &{} 0.06\\ 0.06 &{} 0.86 \end{array} \right) , &{}R^2_{11}=\left( \begin{array}{cc} 1.05 &{} -0.12\\ -0.12 &{} 0.95 \end{array} \right) , &{}R^2_{22}=\left( \begin{array}{cc} 0.47 &{} 0.09\\ 0.09 &{} 1.14 \end{array} \right) ,\\ R^3_{11}=\left( \begin{array}{cc} 0.96 &{} -0.13\\ -0.13 &{} 0.87 \end{array} \right) , &{}R^3_{22}=\left( \begin{array}{cc} 0.50 &{} 0.08\\ 0.08 &{} 1.17 \end{array} \right) , &{}G^1_{11}=\left( \begin{array}{cc} 0.12 &{} -0.02\\ -0.02 &{} 0.09 \end{array} \right) ,\\ G^1_{22}=\left( \begin{array}{cc} 0.06 &{} 0.01\\ 0.01 &{} 0.21 \end{array} \right) , &{}G^2_{11}=\left( \begin{array}{cc} 15.99 &{} -2.51\\ -2.51 &{} 13.63 \end{array} \right) , &{}G^2_{22}=\left( \begin{array}{cc} 9.50 &{} -1.08\\ -1.08 &{} 14.45 \end{array} \right) ,\\ G^3_{11}=\left( \begin{array}{cc} 0.24 &{} -0.03\\ -0.03 &{} 0.22 \end{array} \right) , &{}G^3_{22}=\left( \begin{array}{cc} 0.70 &{} 0.05\\ 0.05 &{} 2.30 \end{array} \right) , &{}Q^1_{11}=\left( \begin{array}{cc} 17.14 &{} -5.51\\ -5.51 &{} 14.51 \end{array} \right) ,\\ Q^1_{22}=\left( \begin{array}{cc} 1.82 &{} 0.28\\ 0.28 &{} 6.06 \end{array} \right) , &{}Q^2_{11}=\left( \begin{array}{cc} 19.65 &{} -2.03\\ -2.03 &{} 18.53 \end{array} \right) , &{}Q^2_{22}=\left( \begin{array}{cc} 3.41 &{} 0.53\\ 0.53 &{} 8.87 \end{array} \right) ,\\ Q^3_{11}=\left( \begin{array}{cc} 11.73 &{} -0.91\\ -0.91 &{} 11.35 \end{array} \right) , &{}Q^3_{22}=\left( \begin{array}{cc} 25.87 &{} -3.24\\ -3.24 &{} 16.91 \end{array} \right) , &{}H_1=\left( \begin{array}{cc} 0.94&{}0\\ 0&{}1.90 \end{array} \right) , \end{array} \end{aligned}$$

$H_2=\textrm{diag}\{0.39,0.75\}$, $\Lambda _1=\textrm{diag}\{4.22,3.08\}$, $\gamma =0.1204$. By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, it follows that $\gamma =0.0799$ when the relationship between time delays is not considered.

Case 5: $\delta \le \sigma \le \tau$, choose $\sigma =0.52,\tau =0.84,\delta =0.13$.

By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, the feasible solutions can be obtained

$$\begin{aligned} \begin{array}{lll} P_{11}=\left( \begin{array}{cc} 0.42 &{} -0.02\\ -0.02 &{} 0.69 \end{array} \right) , &{}P_{22}=\left( \begin{array}{cc} 0.76 &{} -0.02\\ -0.02 &{} 0.73 \end{array} \right) , &{}R^1_{11}=\left( \begin{array}{cc} 1.69 &{} -0.19\\ -0.19 &{} 1.62 \end{array} \right) ,\\ R^1_{22}=\left( \begin{array}{cc} 1.29 &{} 0.01\\ 0.01 &{} 1.37 \end{array} \right) , &{}R^2_{11}=\left( \begin{array}{cc} 1.12 &{} -0.07\\ -0.07 &{} 1.06 \end{array} \right) , &{}R^2_{22}=\left( \begin{array}{cc} 1.09 &{} 0.01\\ 0.01 &{} 1.18 \end{array} \right) ,\\ R^3_{11}=\left( \begin{array}{cc} 1.26 &{} -0.08\\ -0.08 &{} 1.24 \end{array} \right) , &{}R^3_{22}=\left( \begin{array}{cc} 1.23 &{} 0.01\\ 0.01 &{} 1.36 \end{array} \right) , &{}G^1_{11}=\left( \begin{array}{cc} 0.23 &{} -0.05\\ -0.05 &{} 0.21 \end{array} \right) ,\\ G^1_{22}=\left( \begin{array}{cc} 0.36 &{} -0.00\\ -0.00 &{} 0.88 \end{array} \right) , &{}G^2_{11}=\left( \begin{array}{cc} 0.06 &{} -0.01\\ -0.01 &{} 0.07 \end{array} \right) , &{}G^2_{22}=\left( \begin{array}{cc} 0.13 &{} -0.00\\ -0.00 &{} 0.27 \end{array} \right) ,\\ G^3_{11}=\left( \begin{array}{cc} 18.10 &{} -1.50\\ -1.50 &{} 16.60 \end{array} \right) , &{}G^3_{22}=\left( \begin{array}{cc} 15.89 &{} -1.71\\ -1.71 &{} 17.38 \end{array} \right) , &{}Q^1_{11}=\left( \begin{array}{cc} 4.53 &{} 0.09\\ 0.09 &{} 4.36 \end{array} \right) ,\\ Q^1_{22}=\left( \begin{array}{cc} 5.91 &{} 0.00\\ 0.00 &{} 6.14 \end{array} \right) , &{}Q^2_{11}=\left( \begin{array}{cc} 22.76 &{} -3.04\\ -3.04 &{} 20.26 \end{array} \right) , &{}Q^2_{22}=\left( \begin{array}{cc} 9.00 &{} -0.03\\ -0.03 &{} 8.24 \end{array} \right) ,\\ Q^3_{11}=\left( \begin{array}{cc} 5.12 &{} -0.03\\ -0.03 &{} 4.47 \end{array} \right) , &{}Q^3_{22}=\left( \begin{array}{cc} 4.97 &{} -0.01\\ -0.01 &{} 4.86 \end{array} \right) , &{}H_1=\left( \begin{array}{cc} 1.22&{}0\\ 0&{}2.11 \end{array} \right) , \end{array} \end{aligned}$$

$H_2=\textrm{diag}\{0.59,0.91\}$, $\Lambda _1=\textrm{diag}\{4.97,4.22\}$, $\gamma =0.1878$. By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, it follows that $\gamma =0.1050$ when the relationship between time delays is not considered.

Case 6: $\delta \le \tau \le \sigma$, choose $\sigma =0.3,\tau =0.2,\delta =0.1$.

By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, the feasible solutions can be obtained

$$\begin{aligned} \begin{array}{lll} P_{11}=\left( \begin{array}{cc} 0.96 &{} -0.10\\ -0.10 &{} 1.16 \end{array} \right) , &{}P_{22}=\left( \begin{array}{cc} 0.80 &{} 0.08\\ 0.08 &{} 1.00 \end{array} \right) , &{}R^1_{11}=\left( \begin{array}{cc} 3.48 &{} -0.40\\ -0.40 &{} 3.23 \end{array} \right) ,\\ R^1_{22}=\left( \begin{array}{cc} 2.76 &{} 0.16\\ 0.16 &{} 3.08 \end{array} \right) , &{}R^2_{11}=\left( \begin{array}{cc} 4.38 &{} -0.13\\ -0.13 &{} 3.95 \end{array} \right) , &{}R^2_{22}=\left( \begin{array}{cc} 3.09 &{} 0.17\\ 0.17 &{} 3.37 \end{array} \right) ,\\ R^3_{11}=\left( \begin{array}{cc} 2.19 &{} -0.14\\ -0.14 &{} 2.19 \end{array} \right) , &{}R^3_{22}=\left( \begin{array}{cc} 2.66 &{} 0.14\\ 0.14 &{} 3.07 \end{array} \right) , &{}G^1_{11}=\left( \begin{array}{cc} 2.15 &{} -0.76\\ -0.76 &{} 1.45 \end{array} \right) ,\\ G^1_{22}=\left( \begin{array}{cc} 1.48 &{} 0.13\\ 0.13 &{} 3.19 \end{array} \right) , &{}G^2_{11}=\left( \begin{array}{cc} 3.26 &{} -0.26\\ -0.26 &{} 3.36 \end{array} \right) , &{}G^2_{22}=\left( \begin{array}{cc} 4.00 &{} 0.17\\ 0.17 &{} 7.26 \end{array} \right) ,\\ G^3_{11}=\left( \begin{array}{cc} 25.55 &{} 0.30\\ 0.30 &{} 24.42 \end{array} \right) , &{}G^3_{22}=\left( \begin{array}{cc} 26.32 &{} -2.42\\ -2.42 &{} 23.91 \end{array} \right) , &{}Q^1_{11}=\left( \begin{array}{cc} 15.76 &{} -0.72\\ -0.72 &{} 15.80 \end{array} \right) ,\\ Q^1_{22}=\left( \begin{array}{cc} 16.31 &{} 0.08\\ 0.08 &{} 16.64 \end{array} \right) , &{}Q^2_{11}=\left( \begin{array}{cc} 42.94 &{} -2.33\\ -2.33 &{} 35.64 \end{array} \right) , &{}Q^2_{22}=\left( \begin{array}{cc} 18.32&{} 0.13\\ 0.13 &{} 17.46 \end{array} \right) ,\\ Q^3_{11}=\left( \begin{array}{cc} 29.48 &{} 1.72\\ 1.72 &{} 27.52 \end{array} \right) , &{}Q^3_{22}=\left( \begin{array}{cc} 19.27 &{} -0.03\\ -0.03 &{} 18.36 \end{array} \right) , &{}H_1=\left( \begin{array}{cc} 2.43&{}0\\ 0&{}3.23 \end{array} \right) , \end{array} \end{aligned}$$

$H_2=\textrm{diag}\{1.44,1.64\}$, $\Lambda _1=\textrm{diag}\{ 7.37,6.57\}$, $\gamma =0.1883$. By using MATLAB LMI toolbox and solving the LMIs in Theorem 1, it follows that $\gamma =0.1538$ when the relationship between time delays is not considered.

Fig. 1

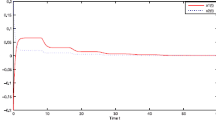
The time response of (4) in case 1 $(\sigma<\tau <\delta )$

Fig. 2

The time response of (4) in case 2 $(\sigma<\delta <\tau )$

Fig. 3

The time response of (4) in case 3 $(\tau<\sigma <\delta )$

Fig. 4

The time response of (4) in case 4 $(\tau<\delta <\sigma )$

Fig. 5

The time response of (4) in case 5 $(\delta<\sigma <\tau )$

Fig. 6

The time response of (4) in case 6 $(\delta<\tau <\sigma )$

To sum up, the following table can be obtained, which shows the influence of adding time-delay relation term to Lyapunov functional on the maximum value $\gamma$ of the system.

Table 1 Dissipativity performance $\gamma$ in Theorem 1 with/without six relationships between time delays

Therefore, the SCNNs (4) is $(Q,S,R)-\gamma -$dissipative in the mean square sense. Figures 1, 2, 3, 4, 5, and 6 are the trajectory diagrams of the solution trajectory of the SCNNs (4). Figures 1, 2, 3, 4, 5, and 6 show that the $(Q,S,R)-\gamma -$dissipative guarantees the stability of the system to a certain extent, which verifies the effectiveness of six cases of Theorem 1. From the above six situations of Table 1, it can be seen that the dissipativity rate $\gamma$ of the system decreases when the time-delay relation term is removed. Therefore, it is better to study the $(Q,S,R)-\gamma -$dissipative in the mean square sense of the system(4) by adding the time-delay relation term.

Table 2 Dissipativity performance $\gamma$ in Theorem 1 when $\tau =\delta$

Table 3 Dissipativity performance $\gamma$ in Theorem 1 when $\sigma =\delta$

Table 4 Dissipativity performance $\gamma$ in Theorem 1 when $\sigma =\tau$

Fig. 7

Dissipativity performance $\gamma$ of various types of time delays

On the whole, Tables 2, 3, and 4 and Fig. 7 show that $\gamma$ decreases with the increase of time delays $\sigma ,\tau ,\delta$, which shows that time delays have a certain influence on the system $(Q,S,R)-\gamma -$dissipative. It can be seen that the leakage delays have certain influence on the system (4). "-" indicates that LMI has no feasible solution.

Put six kinds of size relations with different time delays into the conclusion of Theorem 1, it can be seen from the image that the peak value of the state of the system will be affected by the different size of the time delays. Therefore, it has certain value for practical application.

Example 2

For the first case of Theorem 1, explore the impact of stochastic terms on the system, that is, compare the effects of (2), (3) and (4). $(0,-0.5,0,0.3)$ is the initial condition.

Figures 8, 9 and  1 reveal the state trajectory of the (2),(3) and (4), respectively. Figures 10 and 11 show that the $(Q,S,R)-\gamma -$dissipative guarantee the stability of the system to a certain extent, which verifies the effectiveness of the frist case of Theorem 1. Figures 10 and 11 are the phase diagrams of (2) and (4), (3)and (4), respectively. From the phase diagram of (4)($x_1,x_2,y_1,y_2$), the phase diagram of (2)($x_1^k,x_2^k,y_1^k,y_2^k$) and (3)($x_1^{k1},x_2^{k1},y_1^{k1},y_2^{k1}$), it can be seen from the figures that the stochastic term have an effect on the state trajectory of the system. However, under certain conditions, the $(Q,S,R)-\gamma -$dissipative of the considered system is not affected.

Fig. 8

The time response of (2) in $\sigma<\tau <\delta$

Fig. 9

The time response of (3) in $\sigma<\tau <\delta$

Fig. 10

The phase diagrams in coordinate system (2) and (4) in $\sigma<\tau <\delta$

Fig. 11

The phase diagrams in coordinate system (3) and (4) in $\sigma<\tau <\delta$

Remark 8

From the comparison between Figs. 1,  7 and  8, it can be seen that the stability of the system itself is not affected by the stochastic term, and the existence of the stochastic term affects the dissipativity rate of the system and the bound of the solution of the system.

5 Conclusions

The $(Q,S,R)-\gamma -$dissipative of SCNNs with multiple time delays is investigated. By applying the inequality technique, two sufficient conditions for the $(Q,S,R)-\gamma -$dissipative of SCNNs and the corresponding CNNs with multiple time delays are given. Both theorems are related to the relationship of time delays. Furthermore, the obtained LMI criterion is extended to the passivity and stability in the mean square sense, $(Q,R,S)-\gamma -$dissipative and passivity of the corresponding CNNs. Finally, according to the relationship between time delays, it is divided into six situations. The influence of time delays on the system dissipativity is explored, and the influence of stochastic terms on the system is compared. And both theorems apply to complex and quaternion domains as well.