1 Introduction

Machine learning has progressed dramatically over the past two decades, from laboratory curiosity to a practical technology in widespread commercial use [1]. A prominent aspect of machine learning is the ability to deal with large amounts of unorganized information problems by learning models from labeled data in domain, so sufficiently available labeled data is the basis for reliable results from machine learning models. Currently, machine learning has been widely used in computer vision [2], intrusion detection [3], speech emotion recognition [4, 5], natural language processing [6] and text classification [7].

At present, in order to obtain better accuracy and reliability, the existing traditional machine learning models usually need to meet two basic assumptions: there are enough available data samples in training data set; the training and test data come from the same feature space and distribution [8]. However, in practical applications, training and test data usually come from different fields, and it is difficult to ensure that the data distribution is consistent. In addition, labeled data is scarce in some areas. When the distribution changes, the machine learning algorithm needs to re-collect and re-label training data. In many real-world applications, the cost of re-collecting training data and reconstructing model is very expensive, or even impossible [9]. In this case, transfer learning between learning task domains is desirable, the motivation is that people can use the previously learned knowledge to better solve new problems, and the purpose is to use the label information of another related domain (source domain) for building the model of target domain [10,11,12,13,14]. Unlike traditional machine learning algorithms, them assume that training and test data have the same distribution, transfer learning can use knowledge from different distributions of data. In view of the advantages of transfer learning, a lot of research on it has been launched [15,16,17,18].

On the other hand, the smooth implementation of transfer learning usually requires source and target domains to directly share the original data, which cannot be met in some cases, especially when it involves some confidential or sensitive data. So, the protection of data privacy in transfer learning is becoming an important issue that people pay attention to. The research on privacy protection in transfer learning is very rare. The most recent related work is the differential privacy hypothesis transfer learning method for logistic regression proposed by Wang et al. [19], which uses the public unlabeled source data set to measure the relationship between source and target domain with the hypothesis trained on source domain to improve the learning of target hypothesis. Other related researches focus on variants of transfer learning, such as iterative differential privacy multi-task learning [20], distributed training data aggregation that considers covariate shift (covariate shift) [21], these works either did not consider the distribution differences between data sources, or did not consider the conditional distribution of data.

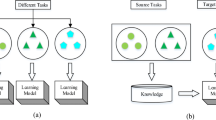
Recently, a class of machine learning methods that use information in group probabilities to train classifier provides an effective way to protect data privacy, this is a type of semi-supervised learning method between supervised learning and unsupervised learning [21,22,23,24]. As shown in Fig. 1, for a set of training data without class labels, if you only know the probability of belonging to a certain class label in each data group, that is, the group probability, then use the group probability information to obtain a classifier that can effectively label the data. A typical application related to group probability is in political election events, where the number of voters in a constituency is known. In order to protect the privacy of each voter, only the number of candidates votes will be provided, and the specific ballot information for each voter is unknown. It can be seen that the group probability information provides an effective means for protecting the privacy of data.

Fig. 1
figure 1

Leaning from group probability

Full size image

In view of the advantages of group probability to protect the privacy of training data in data classification, using group probability to solve the privacy protection problem in transfer learning has attracted the attention of researchers [25, 26]. The existing algorithms only consider the knowledge in a source domain to target learning task, and the marginal probability difference. However, there is more than one source domain related to target domain. Therefore, it is natural that many transfer learning algorithms related to multiple source domains are proposed [27,28,29]. The multi-source transfer method extracts knowledge from data sets of two or more source domains for the learning task of target domain. Compared with the transfer learning method that only uses one source domain, it can increase the chance that transferring relevant knowledge from source domains to target domain and improve learning result. Today, transfer learning has been applied to COVID-19 recognition [30], law article prediction [31], the classification of histological images of colorectal cancer [32], human action recognition [33], cross-domain recommendations [34] and EEG signal analysis [35].

In this paper, we utilize the group probability and multi-source transfer learning theory, in the case of the application scenarios that the target domain has only group probability data with only a small amount of unlabeled data, and multiple source domains contain large amount of labeled data in each source domain, a new multi-source selection transfer learning algorithm with privacy-preserving (MultiSTLP) is proposed. The idea of MultiSTLP algorithm is to use the knowledge of group probability in target domain and the knowledge of labeled data in multiple source domains into the framework of support vector machine structure risk minimization, by constructing the similar distance term between target and each source domains. During the process, considering the marginal and conditional probability differences the knowledge of the representative dataset which is selected form source domains is transferred into target domain, and then the optimizable objective function is constructed. The theoretical proof of the objective function shows that the solution process is a quadratic programming problem with optimal solution. In the algorithm, the group probability protects the privacy of the target data, and the representative dataset of sources domain helps to reduce the size of training samples and improve the efficiency of algorithm training.

Compared with the previous works, the contributions of this paper are:

  1. (1)

    A new multi-source selection transfer learning algorithm with privacy-preserving MultiSTLP is proposed, which utilizes samples of the representative dataset that is selected from multiple sources and unlabeled group probability samples in target domain. MultiSTLP not only improves training efficiency, but also protects data privacy. The objective function of MultiSTLP can be transformed into a traditional standard quadratic programming problem and proved to have global optimal values through rigorous mathematical proof.

  2. (2)

    By reducing the marginal and conditional probability differences, the knowledge of each source domain with similarity to target domain are transferred to the greatest extent, which effectively solves the negative transfer and improves the effect of algorithm. In addition, the representative dataset in source domains can make full use of high-quality samples, reducing the number of training samples and speeding up the algorithm training process.

  3. (3)

    Extensive experiments have been carried out on real datasets, the experimental results show that the result of MultiSTLP is better than the state-of-art algorithms or at least comparable to them.

The rest of the paper is organized as follows. In Sect. 2, the related works of selective transfer learning support vector machine and group probability are briefly reviewed. The MultiSTLP is proposed in Sect. 3. In Sect. 4, we verify the effectiveness of MultiSTLP on four real-world datasets, and the experimental results are analyzed. The last section summarizes the conclusions of this paper and researches in the future.

2 Brief Review of Related Works

We briefly introduce the selective transfer learning support vector machine and group probabilities in this section. In the group probability introduction, we focus on the IC technology and the IC-SVM algorithm.

First of all, we start with the variable definitions of terminologies. For clarity, Table 1 lists the frequently used notations.

Table 1 Notations and descriptions
Full size table

2.1 Selective Transfer Learning Support Vector Machine

For SVM, a lot of training samples is a prerequisite for achieving better training results. This not only requires a lot of manpower to label, but also a lot of time is consumed in the training phase, so the training efficiency of SVM is not satisfactory. In order to improve the efficiency of SVM training, a method of using training samples near the largest hyperplane to train SVM approximate the extreme point support vector machine (AESVM) was proposed in [36]. AESVM no longer needs all training samples to train the learning model. The training sample size can be greatly reduced, so that the training cost of the learning model is reduced.

On this basis, Li et al. [10] proposed a selective transfer learning support vector machine algorithm (STL-SVM), which uses AESVM to select representative dataset from source domain. STL-SVM first utilizes an improved maximum mean discrepancy (MMD) to calculate the weight vector of the importance of the sample in source domain relative to target domain; then AESVM method is applied to select a representative dataset and the weight of samples; finally, combined with the support vector to construct an objective function with the ability the transfer learning.

Given a source domain \({D_S}\) containing n sample data, \({D_S} = \{ (x_1^S,y_1^S),(x_2^S,y_2^S), \ldots ,(x_n^S,y_n^S)\}\), \({X_S} = \{ x_1^S,x_2^S,\ldots ,x_n^S\} \), \({Y_S} = \{ y_1^S,y_2^S,\ldots ,y_n^S\} \), \({Y_S} \in \{ 1 - 1\} \). Similarly, for a target domain \({D_T} = \{ (x_1^T,y_1^T),(x_2^T,y_2^T),\ldots ,(x_m^T,y_m^T)\} \) with m samples, \({X_T} = \{ x_1^T,x_2^T,\ldots ,x_m^T\} \). The objective function of STL-SVM is shown in Eq. (1):

$$\begin{aligned} \left\{ \begin{array}{l} \mathop {\min }\limits _{{w_t},{b_t}} \frac{1}{2}||{w_t}|{|^2} + {C_t}\sum _{i = n + 1}^{n + m} {\xi _i^t} + \frac{1}{2}||{w_s}|{|^2} + \frac{{{C_s}}}{n}\sum _{i = 1}^n {{\beta _i}\xi _i^s} \\ \quad + \frac{\lambda }{2}||{w_t} - {w_s}|{|^2}\\ s.t.\;y_{_i}^s(w_s^T\phi (x_{_i}^s) + {b_s}) \ge 1 - \xi _i^s\\ y_{_i}^t(w_t^T\phi (x_{_i}^t) + {b_t}-{\widetilde{w}}_t^T\phi (x_{_i}^t)-{\widetilde{b}}_t)\ge 0\\ \xi _i^s \ge 0,\quad i = 1,2\ldots n \end{array} \right. \end{aligned}$$
(1)

In Eq. (1), \({w_t}\) and \({b_t}\) represent the parameters in target domain, \({w_s}\) and \({b_s}\) represent the parameters in source domain, these parameters include knowledge in domains; \({\widetilde{w}}_t^T\) and \({\widetilde{b}}_t^T\) represent the knowledge obtained by SVM training only on dataset in target domain; \(\phi ( \cdot )\) is non-linear mapping function; \(\xi _i^t\) (\(\xi _i^t \ge 0\)) and \(\xi _i^s\) (\(\xi _i^s \ge 0\)) are the slack variables in target and source domains, respectively; n is the number of samples in source domain, \(n'\) is the number of samples in representative dataset calculated by AESVM; m is the number of samples in target domain; \({\beta _i} \in [{\beta _1},{\beta _2},\ldots ,{\beta _M}]\) represents the weight value corresponding to each sample in representative data set; \({C_t}\) (\({C_t} \ge 0\)) and \({C_s}\) (\({C_s} \ge 0\)) are the degree of penalty error of the regularization coefficient in target and source domain, respectively; T represents the transposition of the matrix; \(f({x_i}) = {\widetilde{w}}_t^T\phi (x_{_i}^t)+{\widetilde{b}}_t\) is the decision function of SVM classifier in target domain.

Solve the Eq. (1) to obtain the model parameters and, substitute them into the decision function Eq. (2) of STL-SVM:

$$\begin{aligned} f(x) = w_t^T\phi (x) + {b_t} \end{aligned}$$
(2)

On the one hand, STL-SVM reduces the size of training samples in source domain through AESVM and accelerates the learning progress; on the other hand, it uses MMD and objective function construction principles to effectively solve the negative transfer problem that is easy to occur in transfer learning. Therefore, STL-SVM completes the knowledge transfer by effectively fusing the knowledge of the source and target domains, so as to obtain a better classification effect. Experiments on artificial and real datasets show the effectiveness of STL-SVM. Compared with previous research work on transfer learning algorithms, the STL-SVM algorithm can better solve the negative transfer situation and the long training time of the classifier due to too many training samples in source domain. However, the problem with STL-SVM is that it only considers the marginal probability between domains and does not discuss the conditional probability; it only uses the knowledge in one source domain, when there are multiple source domains related to the target domain that will cause a waste of data resources. In addition, it does not have the ability to protect privacy of target data.

2.2 Group Probabilities

Given a dataset \({\mathbf {X}} = \{ {x_i},i = 1,\ldots ,N\} \), \({x_i}\) is \(i\)-th sample, N represents the number of samples, and the class label of samples is unknown. The group probability is defined as follows:

Assuming that the dataset \({\mathbf {X}}\) is divided into \(K\) groups, \({G_k} = \{ {X_{i,k}},i = 1,\ldots ,{N_k},k = 1\ldots ,K\} \), \({N_k}\) represents the total number of samples in each group, and the group probability of each group \({G_k}\) is known as \({p_k}\), which represents the probability that the sample is positive class in the group. In each group, we know the probability that the sample is a positive class, however the class label of each sample is unknown. \({p_k}\) is called the group probability of dataset \({\mathbf {X}}\), which can effectively protect the privacy of dataset \({\mathbf {X}}\).

For the purpose of solving the difficulty of applying the traditional classification model directly to group probability, IC-SVM [22] first labels the group-probability data based on platt model of the inverse calibration technique (IC), then uses these labeled data to train the SVM. IC-SVM utilizes the sigmod function as an estimated SVM posterior probability output method:

$$\begin{aligned} p(y = 1|x) = 1/(1 + \exp ( - Af(x) + B)) \end{aligned}$$
(3)

In Eq. (3), the parameters A and B are obtained by the minimum cross entropy, x is the sample feature vector, y is a class label, \(p(y = 1|x)\) indicates the probability that the sample is positive. Setting \(\mathrm{A}=1\) and \(\mathrm{B}=0\), the Eq. (3) can be converted into the following Eq. (4):

$$\begin{aligned} p = \sigma (y) = \frac{1}{{1 + \exp ( - y)}} \end{aligned}$$
(4)

Further deformation is as follows:

$$\begin{aligned} y = {\sigma ^{ - 1}}(p) = - \log \left( \frac{1}{p} - 1\right) \end{aligned}$$
(5)

In practice, it is difficult to obtain the class label of each sample, so the average values of the class label estimated in each group is approximated as the predicted value of sample, as in Eq. (6):

$$\begin{aligned} \forall i:\frac{1}{{|{G_i}|}}\sum \limits _{j \in {G_i}} {({w^T}{x_j} + b)}={\widetilde{y}}_i \end{aligned}$$
(6)

In Eq. (6), \(|{G_i}|\) is number of group \({G_i}\), \(w\) and \(b\) are the parameters in classification hyperplane of SVM, which sets up a bridge between the group probability information and SVM. The optimization problem of the IC combined with the SVM theory can be expressed as follows:

$$\begin{aligned}&\mathop {\min }\limits _{w,b} \frac{1}{2}||w|{|^2} + C\sum \limits _{i = 1}^K {({\xi _i} + \xi _i^*)} \nonumber \\&s.t.\;\forall _i^K:\frac{1}{{|{G_i}|}}\sum \limits _{j \in {G_i}} {({w^T}{x_j} + b)} \ge {\widetilde{y}}_i - {\varepsilon _i} - {\xi _i},\nonumber \\&\forall _i^K:\frac{1}{{|{G_i}|}}\sum \limits _{j \in {G_i}} {({w^T}{x_j} + b)} \le {\widetilde{y}}_i + {\varepsilon _i} + \xi _i^*,\nonumber \\&{\xi _i} \ge 0,\xi _i^* \ge 0 \end{aligned}$$
(7)

In Eq. (7), K denotes the number of group, \({\varepsilon _i}\) is defined minimum required precision of the estimate. Equation (7) uses SVM classifier to conveniently process group probability information, which also provides theoretical support for the proposed multi-source transfer learning algorithm.

3 Implementation of MultiSTLP

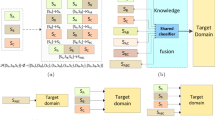
This section describes the multi-source transfer algorithm with group probability in detail. The algorithm framework is shown in Fig. 2. As shown in Fig. 2, the input information of MultiSTLP framework consists of two parts: label samples in target domains which contains unlabeled samples with only group probability information. For convenience, we only consider the binary classification problem (Fig. 3).

\(M\) source domains are defined as: \({D_S} = \{ {D_{{S_i}}} = (x_j^{{S_i}},y_j^{{S_i}})_{j = 1}^{{n_{{S_i}}}},i = 1,\ldots ,M\} \), \(x_j^{{S_i}}\) denotes \(j\)-th sample of \({S_i}\)-th source domain, the corresponding class label is \(y_j^{{S_i}}\), \({n_{{S_i}}}'\) is the number of samples in source domain, \({P_{{S_i}}}\)means joint distribution. Analogously, target domain is \({D_T} = {({x_i})_{i = 1,..,d}}\), \(d\) is the number of group and joint distribution is \({P_T}\). As a class label, \({p_k}= |\{ i \in {G_k},{y_i} = 1\} |/|{G_k}|\) equals to \(P(Y = 1|{G_k})\) that is estimating probability of class label. \({P_{{S_i}}}({x^{{S_i}}})\) and \({P_T}({x^t})\), \({P_{{S_i}}}({y^{{S_i}}}|{x^{{S_i}}})\) and \({P_T}({y^t}|{x^t})\) are the marginal probability and conditional probability of source and target domains, respectively. Normally, \({P_{{S_i}}}({x^{{S_i}}}) \ne {P_T}({x^t})\) and \({P_{{S_i}}}({y^{{S_i}}}|{x^{{S_i}}}) \ne {P_T}({y^t}|{x^t})\). MultiSTLP not only considers the differences between source and target domains, but also transferability of source domain by simultaneously reducing the differences between the marginal and conditional probabilities.

Fig. 2
figure 2

Framework of MultiSTLP

Full size image
Fig. 3
figure 3

Flowchart of MultiSTLP

Full size image

3.1 Select Representative Data Set and Adapt the Probability of Partial Difference

Refer to reference [10], using the AESVM method to calculate the representative data set in source domain \({D_{{S_i}}}\) and its corresponding weight vector \(\beta _j^{{S_i}} \in [\beta _1^{{S_i}},\beta _2^{{S_i}},\ldots ,\beta _{{n_{{S_i}}}}^{{S_i}}]\), the number of samples in representative data set is.

In order to effectively transfer knowledge from source domain that is similar to target domain, this paper adapts both marginal and conditional probability differences. we use MMD to calculate the weights of samples in source domain \({S_i}\) on the marginal probability difference.

$$\begin{aligned} \begin{array}{l} \displaystyle \mathop {\min }\limits _{{\alpha ^{{S_i}}}} \left\| \frac{1}{{{n_{{S_i}}}}}\sum \limits _{j = 1}^{{n_{{S_i}}}} {v_i^{{S_i}}\phi (x_j^{{S_i}}) - } \frac{1}{d}\sum \limits _{j = 1}^d {\phi (x_j^t)} \right\| _H^2\\ s.t.\;v_j^{{S_i}} \ge 0\\ i = 1,\ldots ,m,\\ j = 1,\ldots ,{n_{{S_i}}} \end{array} \end{aligned}$$
(8)

\(\phi (x)\) denotes that feature is mapped to a regenerative kernel Hilbert space \(H\), \({n_{{S_i}}}\) is the number of the representative data set in source domain \({S_i}\), the number of group in target domain is \(d\), \({n_{{S_i}}}\) is also the dimension of \({v^{{S_i}}}\). The minimization problem of Eq. (8) is a standard quadratic programming problem and can be solved using many existing solvers. When constructing the objective function MultiSTLP, by using samples in each source domain we add the corresponding weights as in Eq. (9).

$$\begin{aligned} v_j^{{S_i}} = v_j^{{S_i}} \cdot x_j^{{S_i}} \cdot \beta _j^{{S_i}} \end{aligned}$$
(9)

In Eq. (9), \({v^{{S_i}}}\) represents the sample vector after weighting samples of source domain \({S_i}\). For the convenience of subsequent calculations, set \({x^{{S_i}}} = {v^{{S_i}}}\), that is, the samples of source domain are weighted with \({v^{{S_i}}}\).

On the basis of the above calculation of marginal probability difference, calculate \({\gamma ^{{S_i}}}\) of source domain \({D_{{S_i}}}\), which reflects similarity between source and target domains. First, we learn the classifier \({h^{{S_i}}}:x \rightarrow y\), this ensures that the classifier learned on source domain with similar marginal probability distributions. Then, using \({h^{{S_i}}}\) predicts unlabeled samples in target domain. \({H^S} = [{h^{{S_1}}},\ldots ,{h^{{S_M}}}]\) denotes \(M\) classifiers, \({\gamma ^S} = {[{\gamma ^{{S_1}}},\ldots ,{\gamma ^{{S_M}}}]^T}\) is corresponding weight vector. Therefore, the goal of Eq. (10) is to find the optimal weight by minimizing the difference in prediction labels between two neighboring points in target domain.

$$\begin{aligned} \mathop {\min }\limits _{\gamma :\gamma 'e = 1,\gamma \ge 0} \sum \limits _{i,j = 1}^d {{{(H_i^S{\gamma ^S} - H_j^S{\gamma ^S})}^2}} {W_{ij}} \end{aligned}$$
(10)

\(H_i^S\) is the predicting result of \(i\)-th sample using \({H^S}\) \({W_{ij}}\) is a similarity parameter between two data samples of target domain. Equation (10) can be rewritten as the form of Eq. (11):

$$\begin{aligned} \mathop {\min }\limits _{\varphi :\gamma 'e = 1,\gamma \ge 0} \sum \limits _{i,j = 1}^d {{{({\gamma ^S})}^T}{{({H^S})}^T}L{H^S}} {\gamma ^S} \end{aligned}$$
(11)

In Eq. (11), \(L = D - W\) is the graph Laplacian associated with the data of target domain, \(W\) is the similarity matrix, \(D\) is the diagonal matrix given by \({D_{ii}} = \sum \nolimits _{j = 1}^M {{W_{ij}}} \). The minimization problem of Eq. (11) is also a standard quadratic programming problem, which can be calculated using many existing solvers.

3.2 Construction of Object Function

On the basis of 3.1, we combine the structural risk minimization theory and the similarity distance minimization to construct the objective function of MultiSTLP as follows:

$$\begin{aligned}&\mathop {\min }\limits _{{f_t}{f_s} \in {H_k}} \frac{1}{{2M}}\sum \limits _{i = 1}^M {||{f_{{s_i}}}|{|^2}} + \frac{1}{M}\sum \limits _{i = 1}^M {{C_{{s_i}}}\sum \limits _{j = 1}^{{n_{{S_i}}}} {{l_{{s_i}}}({f_{{s_i}}},{y_j})} } + \frac{1}{2}||{f_t}|{|^2}\nonumber \\&\quad + {C_t}\sum \limits _{i = 1}^d {{l_t}({f_t},{y_i})} + \lambda \frac{1}{{2M}}\sum \limits _{i = 1}^M {d({f_t},{f_{{s_i}}})} \end{aligned}$$
(12)

\({f_s}\) is decision function vector of \(M\) source domains, \({f_t}\) is decision function in target domain. \(||{f_{{s_i}}}|{|^2}\) and \(||{f_t}|{|^2}\) are the structure risk terms controlling the complexity of the classifier in the source domain and the target domain, respectively. \(||f||^2\) indicates L2-norm. \({C_{{s_i}}}\) and \({C_t}\) are the regularization coefficients in source domain \({S_i}\) and target domain. \(l()\) is convex non-negative loss function. \(d()\) is used to quantify the diversity between source and target domains. \(\lambda \) is the trade-off parameter.

Equation (12) consists of three items, the first term \((\frac{1}{{2M}}\sum _{i = 1}^M {||{f_{{s_i}}}|{|^2}} +\) \(\frac{1}{M}\sum _{i = 1}^M {C_{{s_i}}} \sum _{j = 1}^{{n_{{S_i}}}} {{l_{{s_i}}}({f_{{s_i}}},{y_j})} )\) refers to the knowledge learning from source domains. The second term \((\frac{1}{2}||{f_t}|{|^2} + {C_t}\sum _{i = 1}^d {{l_t}({f_t},{y_i})} )\) denotes the knowledge learning from target domain. The third term \((\lambda \frac{1}{{2M}}\sum _{i = 1}^M {d({f_t},{f_{{s_i}}})} )\) is that guarantees good generalization performance by minimizing the differences between each source and target domains.

In further, \(\frac{\lambda }{{2M}}\sum _{i = 1}^M {||{{\mathbf {w}}_t} - {\gamma ^{{S_i}}}{{\mathbf {w}}_{{s_i}}}|{|^2}} \) is utilized to quantify the diversity between domains. So, Eq. (12) can be rewritten into Eq. (13).

$$\begin{aligned}&\mathop {\min }\limits _{{w_t},{b_t},{w_s},{b_s}} \frac{1}{2}||{{\mathbf {w}}_t}|{|^2} + {C_t}\sum \limits _{i = 1}^d {{l_t}({\mathbf {w}}_t^T\varphi ({\mathbf {x}}) + {b_t},{y_i})} \nonumber \\&\quad + \frac{1}{M}\sum \limits _{i = 1}^M {||{w_{{s_i}}}|{|^2}} + \frac{1}{M}\sum \limits _{i = 1}^M {{C_{{s_i}}}\sum \limits _{j = 1}^{{n_{{S_i}}}} {{l_{{s_i}}}({\mathbf {w}}_{{s_i}}^T\varphi ({\mathbf {x}}) + {b_{{s_i}}},{y_j})} } \nonumber \\&\quad + \frac{\lambda }{{2M}}\sum \limits _{i = 1}^M {||{w_t} - {\gamma ^{{S_i}}}{w_{{s_i}}}|{|^2}} \end{aligned}$$
(13)

In Eq. (13), we chose two different hinge loss functions in source and target domains: \({l_s}(f({x_i}),{y_i}) = \max \{ 0,1 - {y_i}f({x_i})\} \) and \({l_t}(f({x_i}),{y_i}) = \max \{ 0,|f({x_i}) - {\widetilde{y}}_i| - \varepsilon \} \). Therefore, Eq. (13) can be formulated as an optimization problem:

$$\begin{aligned}&\mathop {\min }\limits _{{w_t},{b_t},{w_s},{b_s}} \frac{1}{2}||{{\mathbf {w}}_t}|{|^2} + {C_t}\sum \limits _{i = 1 + \sum \limits _j^M {{n_{{S_j}}}} }^{\sum \limits _j^M {{n_{{S_j}}}} + d} {({\xi _i} + } \xi _i^*)\nonumber \\&\quad + \frac{1}{{2M}}\sum \limits _{i = 1}^M {||{{\mathbf {w}}_{{s_\mathrm{{i}}}}}|{|^2}} + \frac{1}{{2M}}\sum \limits _{i = 1}^M {{C_{{s_i}}}\sum \limits _{j = 1}^{{n_{{S_i}}}} {\xi _j^{{s_i}}} } \nonumber \\&\quad +\frac{\lambda }{{2M}}\sum \limits _{i = 1}^M {||{{\mathbf {w}}_t} - {\gamma ^{{S_i}}}{{\mathbf {w}}_{{s_i}}}|{|^2}} \nonumber \\&s.t.\nonumber \\&y_j^{{S_i}}({\mathbf {w}}_{{s_i}}^T\varphi ({\mathbf {x}}_j^{{\mathrm{{S}}_i}}) + {b_{{s_i}}}) \ge 1 - \xi _j^{{s_i}},j = 1,\ldots ,{n_{{S_i}}}{S_i} = 1,\ldots ,M\nonumber \\&\forall _{i = 1}^d:\frac{1}{{|{G_i}|}}\sum \limits _{j \in {G_i}} {({\mathbf {w}}_t^T\varphi ({{\mathbf {x}}_j}) + {b_t})} ) \ge {\widetilde{y}}_i - {\varepsilon _i} - {\xi _i},\nonumber \\&\forall _{i = 1}^d:\frac{1}{{|{G_i}|}}\sum \limits _{j \in {G_i}} {({\mathbf {w}}_t^T\varphi ({{\mathbf {x}}_j}) + {b_t})} ) \le {\widetilde{y}}_i + {\varepsilon _i} + \xi _i^* \end{aligned}$$
(14)

In Eq. (14), \(\xi _j^{{s_i}}\), \({\xi _i}\) and \(\xi _i^*\) are slack variables; the first constraint guarantees that each source domain is classified as accurately as possible; the second and three constraints control estimating class probability of \({G_i}\) in target domain to approximate \({p_i}\). \({\varepsilon _i}\) is the estimated minimum precision of \({\widetilde{y}}_i\) that satisfies the following function:

$$\begin{aligned} {p_i} - \varepsilon \le \frac{1}{{1 + \exp ( - {\widetilde{y}}_i )}} \le {p_i} + \varepsilon \end{aligned}$$
(15)

According to [22], \({\varepsilon _i}\) is set to be \({\varepsilon _i} = \frac{\tau }{{{p_i}(1 - {p_i})}}\), \({p_i}\) is the group probability \(P(Y = 1|{G_k})\), \(\varepsilon \) is a very small positive constant.

3.3 Theorems Related to the Objective Function

Theorem 1

The dual problem of Eq. (14) is a QP problem as shown in Eq. (16).

$$\begin{aligned}&\mathop {\min }\limits _\beta \frac{1}{2}{\beta ^T} {\widetilde{{\mathbf {K}}}} \beta + {\widetilde{{\mathbf {e}}}}^T\beta \nonumber \\&s.t.\;{\mathrm{{f}}^T}\beta = 0\nonumber \\&\beta = {[{\alpha ^{{s_1}}},{\alpha ^{{s_2}}},\ldots ,{\alpha ^{{s_M}}},\alpha ,{\alpha ^*}]^\mathrm{{T}}},\nonumber \\&0 \le \beta \le \left[ \underbrace{{C_{{s_1}}},\ldots ,{C_{{s_1}}}}_{{n_{{S_1}}}}, \ldots ,\underbrace{{C_{{s_M}}},\ldots ,{C_{{s_M}}}}_{{n_{{S_{_M}}}}},\underbrace{{C_t},\ldots ,{C_t}}_d,\underbrace{{C_t},\ldots ,{C_t}}_d\right] ,\nonumber \\&{{\mathbf {f}}^\mathrm{{T}}} = \left[ y_1^{{S_1}},\ldots ,y_{{n_{{S_1}}}}^{{S_1}}, \ldots ,y_1^{{S_M}},\ldots ,y_{{n_{{S_M}}}}^{{S_M}},\underbrace{1,\ldots ,1}_d,\underbrace{ - 1,\ldots , - 1}_d\right] ,\nonumber \\&{\widetilde{{\mathbf {e}}}} = \left[ \underbrace{0,\ldots ,0}_{{n_{{S_1}}}}, \ldots ,\underbrace{0,\ldots ,0}_{{n_{{S_{_M}}}}},\varepsilon - {\widetilde{y}} ,\varepsilon +{\widetilde{y}} \right] \nonumber \\&{\widetilde{{\mathbf {K}}}} ={\left[ \begin{array}{l} \frac{{M + \lambda }}{{1 + 2\lambda M}}{{\mathbf {K}}_{{s_1}}}{,_{{s_1}}} + \frac{\lambda }{M},\ldots ,\frac{{M + \lambda }}{{1\mathrm{{ + }}2\lambda M}}{{\mathbf {K}}_{{s_1}}}{,_{{s_M}}} + \frac{\lambda }{M},\frac{\lambda }{{1 + 2\lambda M}}{{\mathbf {K}}_{{s_1}}}_{,t}, - \frac{\lambda }{{1 + 2\lambda M}}{{\mathbf {K}}_{{s_1}}}_{,t}\\ \ldots \\ \frac{{M + \lambda }}{{1 + 2\lambda M}}{{\mathbf {K}}_{{s_M}}}{,_{{s_1}}} + \frac{\lambda }{M},\ldots ,\frac{{M + \lambda }}{{1\mathrm{{ + }}2\lambda M}}{{\mathbf {K}}_{{s_M}}}{,_{{s_M}}} + \frac{\lambda }{M},\frac{\lambda }{{1 + 2\lambda M}}{{\mathbf {K}}_{{s_M}}}_{,t}, - \frac{\lambda }{{1 + 2\lambda M}}{{\mathbf {K}}_{{s_M}}}_{,t}\\ \frac{\lambda }{{1 + 2\lambda M}}{\mathbf {K}}_{{s_1},t}^T,\ldots ,\frac{\lambda }{{1 + 2\lambda M}}{\mathbf {K}}_{{s_M},t}^T,\frac{{M + \lambda }}{{1 + 2\lambda M}}{{\mathbf {K}}_{t,t}} - \frac{\lambda }{{1 + 2\lambda M}}{{\mathbf {K}}_t}_{,t}\\ - \frac{\lambda }{{1 + 2\lambda M}}{\mathbf {K}}_{{s_1},t}^T,\ldots , - \frac{\lambda }{{1 + 2\lambda M}}{\mathbf {K}}_{{s_M},t}^T, - \frac{{M + \lambda }}{{1 + 2\lambda M}}{{\mathbf {K}}_{t,t}},\frac{{M + \lambda }}{{1 + 2\lambda M}}{{\mathbf {K}}_{t,t}} \end{array} \right] _{\left( \sum \limits _{i \in M} {{n_{{S_i}}}} + 2d\right) \times \left( \sum \limits _{i \in M} {{n_{{S_i}}}} + 2d\right) }}\nonumber \\&{{\mathbf {K}}_{{s_i},{s_i}}} = {(y_j^{{S_i}}y_q^{{S_i}}k(x_j^{{S_i}}x_q^{{S_i}}))_{j,q = 1,2,\ldots ,{n_{{S_i}}}}}\nonumber \\&{{\mathbf {K}}_{{s_i}}}_{,t} = {\left( \frac{{{\widetilde{y}} _j^{{S_i}}}}{{|{G_k}|}}\sum \nolimits _{q \in {G_k}} {k({{\mathbf {x}}_j},{{\mathbf {x}}_q})} \right) _{j = 1,..,{n_{{S_i}}},q = 1,\ldots ,d}},\nonumber \\&{{\mathbf {K}}_{t,t}} = {\left( \frac{1}{{|{G_i}||{G_j}|}}\sum \nolimits _{i' \in {G_i}} {\sum \nolimits _{j' = {G_j}} {k({{\mathbf {x}}_{i'}},{{\mathbf {x}}_{j'}})} } \right) _{i,j = 1,\ldots ,d}}. \end{aligned}$$
(16)

The proof of Theorem 1 can be seen in “Appendix 1”.

Theorem 2

The quadratic form of the optimization problem of Eq. (16) is a standard convex quadratic programming problem.

The proof of Theorem 1 can be seen in “Appendix 2”.

It is clear from the above results that the optimization problem in Eq. (16) for training can be transformed into a convex QP problem and can be directly solved by the traditional SVM solutions. Simultaneously, Eq. (16) is a convex quadratic programming problem, the KKT condition is also a sufficient condition, and thus the obtained solution is the optimal solution.

According to the results obtained by Eq. (16), the results of the optimal solution are as follows:

$$\begin{aligned} {\mathbf {w}}_t^*&= \frac{{\lambda M}}{{1 + 2\lambda M}}\sum \limits _{i = 1}^M {\sum \limits _{j = 1}^{{n_{{S_i}}}} {\widetilde{\alpha } _j^{{s_i}}{\gamma ^{{S_i}}}y_j^{{S_i}}\varphi (x_j^{{S_i}})} }\nonumber \\&\quad + \frac{{M + \lambda }}{{1 + 2\lambda M}}\sum \limits _{i = 1 + \sum \limits _{j = 1}^M {{n_{{S_j}}}} }^{\sum \limits _{j = 1}^M {{n_{{S_j}}}} + d} {\frac{{{\widetilde{\alpha }_i} - \widetilde{\alpha } _i^*}}{{|{G_i}|}}\sum \limits _{j \in {G_i}} {\varphi ({x_j})} } \end{aligned}$$
(17)
$$\begin{aligned} b_t^*&= {y_i} - \frac{{\lambda M}}{{1 + 2\lambda M}}\sum \limits _{i' = 1}^M {{\gamma ^{{S_{i'}}}}\sum \limits _{j = 1}^{{n_{{S_i}}}} {\frac{{\widetilde{\alpha } _j^{{s_j}}{y_j}}}{{|{G_i}|}}\sum \limits _{q \in {G_i}} {k({x_j},{x_q})} } } \nonumber \\&\quad - \frac{{\lambda + M}}{{1 + 2\lambda M}}\sum \limits _{i' = 1}^M {{\gamma ^{{S_{i'}}}}\sum \limits _{j = 1 + \sum \limits _{l \in M} {{n_{{S_{_l}}}}} }^{\sum \limits _{l \in M} {{n_{{S_{_l}}}} + d} } {\frac{{\widetilde{\alpha }_j - \widetilde{\alpha }_j^* }}{{|{G_j}||{G_i}|}}\sum \limits _{j' \in {G_j}} {\sum \limits _{q \in {G_i}} {k({x_{j'}},{x_q})} } } } \end{aligned}$$
(18)

Finally, the decision function of MultiSTLP is expressed as follows:

$$\begin{aligned} f(x) = {{\mathbf {w}}_t}\varphi (x) + {b_t} \end{aligned}$$
(19)

As we can see from Eqs. (17) and (18), the results contain both information of \(M\) source and target domains: such as \({\mathbf {w}}_t^*\), \(\frac{{\lambda M}}{{1 + 2\lambda M}}\sum _{i = 1}^M {\sum _{j = 1}^{{n_{{S_i}}}} {\widetilde{\alpha } _j^{{s_i}}{\gamma ^{{S_i}}}y_j^{{S_i}}\varphi (x_j^{{S_i}})} } \) is the knowledge that is learned from source domains, otherwise the knowledge from target domain is \(\frac{{M + \lambda }}{{1 + 2\lambda M}}\sum _{i = 1 + \sum _{j = 1}^M {{n_{{S_j}}}} }^{\sum _{j = 1}^M {{n_{{S_j}}}} + d} {\frac{{{\widetilde{\alpha }_i} - \widetilde{\alpha } _i^*}}{{|{G_i}|}}\sum \limits _{j \in {G_i}} {\varphi ({x_j})} } \).

3.4 Training MultiSTLP

According to Sects. 3.1–3.3, the training process of MultiSTLP is now summarized and described in Table 2.

Table 2 MultiSTLP algorithm training
Full size table

4 Experimental Results

In this section, for the purpose of testing the generalization performance of MultiSTLP algorithm, we compare MultiSTLP with the benchmark algorithms on four real-world datasets 20-Newsgroups, TRECVID video detection, sentiment analysis, and Email spam. In the experiments, without loss of generality, we only consider the binary classification problem.

4.1 Experimental Environment and Evaluation Criteria

For the fairness of experiments, a 5-fold cross-validation strategy is selected, and we repeat the strategy twice as the final comparison results. In the experiments, we will run 10 times, the average value of classification accuracy, recall, precision, training time with their standard deviations are recorded. The representation of classification accuracy is as follows:

$$\begin{aligned} {\textit{Accuracy}} = \frac{{|\{ x|{x_t} \in {D_t} \cap f({x_i}) = {y_t}\} |}}{{|\{ x|{x_t} \in {D_t}\} |}} \end{aligned}$$

\({D_t}\) represents datasets in the target domain, \({y_t}\) is true tag category, \(f({x_t})\) is the result of classifying \({x_t}\) using the learned classifier.

The recall is expressed as follows:

$$\begin{aligned} {{\mathrm{Re}}} {\textit{call}} = \frac{{{\textit{TP}}}}{{{\textit{TP}} + {\textit{FN}}}} \end{aligned}$$

The precision is:

$$\begin{aligned} \Pr {\textit{ecision}} = \frac{{{\textit{TP}}}}{{{\textit{TP}} + {\textit{FP}}}} \end{aligned}$$

TP represents the number of positive class samples that are accurately classified as positive classes by the classifier; FP is the number of negative class samples that are incorrectly classified as positive classes; and FN is the number that indicates that the positive class samples are incorrectly classified as negative classes.

For each algorithm, a Gaussian kernel function is selected in the form \(k({x_i},{x_j}) = \exp ( - ||{x_i} - {x_j}||)/2{\sigma ^2}\). The parameters \({C_t}\), \({C_s}\) and \(\lambda \) of the proposed MultiSTLP are determined by searching the grid \(\{ {10^{-4}}{10^{ - 3}}{10^{ - 2}},{10^{ - 1}},10,\) \({10^1},{10^2},{10^3},{10^4}\} \). For baseline algorithms, the default parameter settings in their literatures are adopted in our experiments. The hardware setting of all experiments are as follows: Intel Core (TM), 3.6 GHz, 8 GB, Windows 10 operating system.

The following state-of-the-art baseline algorithms are selected as the comparison algorithms for MultiSTLP.

  1. (1)

    TrGNB [25] integrates the transfer learning and group probability information into naive Bayesian framework, the knowledge transfer is completed in the process of solving the naive Bayes by using the maximum posterior probability method. Compared with TrGNB, the advantages of our model are as follows: the marginal and conditional probability between source and target domains are considered; the knowledge in more than one source domains is transferred.

  2. (2)

    IC-SVM [22] is based on the framework of traditional SVM classifier, combined with Inverse Calibration technology (IC) to construct an optimization function of classifier for class labels, which have no the ability of privacy protection and transfer knowledge compared with MultiSTLP.

  3. (3)

    ARTL [17] learns the adaptive classifier by simultaneously optimizing the structural risk function, the joint distribution matching between domains and the manifold consistency behind the marginal distribution. The differences from the proposed method is that only one source domain can be used.

  4. (4)

    STL-SVM [10] compared with the proposed method, which have no the ability of privacy protection and transfer knowledge of multi-source.

  5. (5)

    TSVM-GP [26] integrates transfer term and group probability information into a support vector machine (SVM) to improve the classification accuracy. This method considers only a single source domain and marginal probability compared to the proposed method.

  6. (6)

    SVM [35] is traditional support vector model, which has no ability to learn across domains.

4.2 Datasets

20-Newsgroups [8], TRECVID 2005 [24], Sentiment analysis [20], and Email spam [21] are commonly used in transfer learning applications, so all experiments in this paper are performed on these datasets.

  1. (1)

    20-Newsgroups

The 20-Newsgroups dataset are divided into 4 top categories: comp, rec, sci and talk, which contains about 20,000 documents, and each top category can also be divided into four sub-categories with detailed information as shown in Table 3. According to the construction of task group in [8, 17], two top categories are randomly selected from top categories, one of which is positive class and the other is negative class. Each task group is specifically: comp vs rec, comp vs sci, comp vs talk, rec vs sci, rec vs talk, and sci vs talk.

Table 3 The statistics of 20-Newsgroups
Full size table
  1. (2)

    TRECVID 2005

TRCVID 2005 contains approximately 86 h of video programs and consists of 74,523 video shots. Each shot is represented by a video frame as a keyframe, and each keyframe is depicted by a 273-dimensional feature vector. All shots are manually labeled with 39 semantic categories. These semantics cover a variety of types, including outdoor scenes, indoor scenes, news types, and generally common objects. TRCVID video are from CNN_ENG, NBC_ENG, MSNBC_ENG, CCTV_CHN, NTDTV_CHN and LBC_ARB 6 channels, 13 news programs. Each channel represents a domain, except LBC containing 3 news programs, the other channels contain 2 news programs. The source domains datasets are selected from 3 English channels and 2 Chinese channels, and the target domain dataset is selected from the Arabic dataset.

  1. (3)

    Sentiment analysis

The sentiment analysis dataset contains four different comments of Amazon products: books, DVDs, electronics, and kitchen, which represent four domains Books (B), DVDs (D), Electronics (E), and Kitchen (K). Each comment contains product name, comment title, date, location, and comment content. We will evaluate the product with a rating of 3 stars (0–5 stars) or more as a positive example, a product with a rating of less 3 stars as a negative example, and discard if a fuzzy evaluation is found. In the every domain, there are 2000 labeled instances, and about 4000 unlabeled instances, where the number of positive and negative instances is substantially the same. The dataset details are shown in Table 4.

Table 4 The statistics of sentiment analysis dataset
Full size table
  1. (4)

    Email spam Email spam dataset was released by ECML/PKDD 2006,see Table 5 for details. It contains a set of 4000 publicly available labeled emails (U4) as well as three email sets \(({\textit{each}}\; {\textit{has}}\; 2500\; {\textit{emails}})\) annotated by three different users \((U1,U2\; {\textit{and}}\; U3)\). Therefore, the data distributions of the three user-annotated email sets and the publicly available email set are different from each other, in which one half of the emails are non-spam and the other half are spam. Since the spam and non-spam in four email subsets have been differentiated, their distributions are relevant but different.

Table 5 The statistics of spam dataset
Full size table

4.3 Analysis of Experimental Results

In this section, the experimental results of MultiSTLP and six benchmark algorithms on real datasets are analyzed and compared.

TRECVID 2005 dataset We utilize two Chinese channels CCTV_CHN\(\left( CC\right) \), three English channels CNN_ENG\(\left( CN\right) \), NBC_ENG\(\left( NB\right) \), MSNBC_ENG\(\left( MS\right) \) and NTDTV_CHN\(\left( NT\right) \) as the source domains, and LBC_ARB\(\left( L\right) \) as the target domain. The details are shown in Table 6. The four transfer learning methods in the benchmarks can only use one source domain, so in the experiment, one of these source domains is randomly selected as the training dataset, and the MultiSTLP algorithm uses the datasets in all source domains simultaneously.

Table 6 Description of source and target domains on TRECVID dataset
Full size table

20-Newsgroups dataset: in the experiment, we constructed 3 source domains and one target domain. The details are shown in Table 7. For the four single source domain transfer learning algorithms TrGNB, ARTL, STL-SVM and TSVM-GP randomly select one of the source domains for training, and MultiSTLP can simultaneously use the datasets of the three source domains for training.

Table 7 Description of source and target domains on 20-Newsgroups dataset
Full size table

Sentiment analysis dataset: in this dataset, we use Books, DVDs, and Electronics to construct three source domains, and Kitchen as the target domain. The details of source and target domains are shown in Table 8.

Table 8 Description of source and target domains on Sentiment analysis datase
Full size table

Email Spam dataset: for the MultiSTLP algorithm, three personal email datasets are used as three source domains, and the public email dataset is used as target domain; the other four single source domain transfer learning algorithms randomly select one of the three personal email. The detailed information is shown in Table 9.

Table 9 Description of source and target domains on email spam dataset
Full size table
Table 10 Comparison of average classification accuracy with standard deviation on real-world four transfer datasets
Full size table
Table 11 Comparison of average recall with standard deviation on four real-world transfer datasets
Full size table
Table 12 Comparison of average precision with standard deviation on four real-world transfer datasets
Full size table
Table 13 Comparison of average training time (s) with standard deviation on four real-world transfer datasets
Full size table

Tables 10, 11, 12 and 13 show the average classification accuracies, average recall and average precision with their standard deviations of all the benchmarking classifiers on different transfer learning tasks. From these results, we can draw the following conclusions:

  1. (1)

    In terms of the average classification accuracy, it can be seen from Table 10 that the transfer learning algorithms TrGNB, ARTL, STL-SVM, TSVM-GP and MultiSTLP have better classification results than the non-transfer learning algorithms SVM and IC-SVM. This is because only a small amount of data set with probability information in target domain is not enough to train a reliable learning model, and the transfer learning algorithms can use the knowledge in a large amount of labeled data in source domain to assist target domain to create classification task, so the trained model is better.

In addition, in the transfer learning algorithms TrGNB, ARTL, STL-SVM and TSVM-GP only transfer the knowledge in one source domain, and only consider the marginal probability difference between data between domains, without considering the conditional probability difference. On the one hand, this resulted in insufficient knowledge to be transferred. On the other hand, the large difference between the transferred knowledge and the data in target domain resulted in a negative transfer phenomenon, which harmed the learning effect.

The MultiSTLP algorithm proposed in this paper makes up for the above problems. It not only transfers the knowledge of multiple source domain, but also adapts the marginal probability and conditional probability, and the classification effect is also better. Therefore, the average accuracy of the MultiSTLP algorithm proposed in this article on the four data sets 20-Newsgroups, TRECVID 2005, sentiment analysis and email spam is better than the comparison algorithms, which are 92.45%, 91.16%, 89.25% and 95.05%, respectively.

  1. (2)

    The average recall in Table 11 show that MultiSTLP has certain advantages compared with non-transfer learning algorithms (SVM, IC-SVM) and single source transfer learning algorithms (TrGNB, ARTL, STL-SVM and TSVM-GP) on all transfer learning tasks.

  2. (3)

    The average precision in Table 12, it is can be seen that MultiSTLP is better than benchmark algorithms. On the four data sets 20-Newsgroups, TRECVID 2005, sentiment analysis and email spam, the average precisions are 84.15%, 84.34%, 73.65% and 92.97%, respectively.

  3. (4)

    In terms of training time shown in Table 13, it can also be seen that MultiSTLP has obvious advantage over transfer learning algorithms TrGNB, ARTL, STL-SVM and TSVM-GP in training time, because of selecting representative data set from source domain. IC-SVM needs less training time than other six classifiers in our experiments. This is because its training data only contains the group probabilities constructed from the 5% randomly selected unlabeled target data which is much less than the size of the training data for the other classifiers. Even though, SVM is effective in training time, its classification accuracy is not prominent on transfer learning problems.

In summary, through the comparative analysis of experimental results, we can see that the algorithm proposed in this paper is effective and efficient. It also shows the rationality and effectiveness of the proposed algorithm.

Finally, to test the differences between MultiSTLP and benchmark algorithms with similar classification results, the Wilcoxon signed rank test is applied to these methods. According to the contents of Table 10, the average classification accuracy of all algorithms is shown.

In Table 10, we can see the average classification accuracy of all algorithms on real datasets. The results of the Wilcoxon test on real-world datasets 20-Newsgroups, TRECVID 2005, Sentiment analysis and Email spam are discussed below.

20-Newsgroups: the classification accuracy of MultiSTLP is only 0.97% higher than TrGNB; therefore, when using MultiSTLP and TrGNB to classify three cross-domain tasks, each task is repeated 10 times, the values of \({W^ + }\) and \({W^ - }\) are \(+143\) and \(-24\), respectively. For the bilateral test of \(\alpha = 0.05\), when \(\mathrm{n} = 30\), by querying the distribution table of the Wilcoxon signed rank test, \({T^{0.025}}= 137\). Because of \({W^ + } > {T^{0.025}}\), \({H_0}\) was accepted: there was no significant difference in the classification results between the two methods.

TRECVID 2005: the classification accuracy of MultiSTLP increases 0.89% by comparison with TSVM-GP; therefore, when using MultiSTLP and TSVM-GP to classify 5 cross-domain tasks, each task is repeated 10 times, the values of \({W^ + }\) and \({W^ - }\) are \(+576\) and \(-89\), respectively. For the bilateral test of \(\alpha = 0.05\), when \(\mathrm{n} = 50\), by querying the distribution table of the Wilcoxon signed rank test, \({T^{0.025}} = 434\). Because of \({W^ + } > {T^{0.025}}\), \({H_0}\) was accepted: there was no significant difference in the classification results between the two methods.

Sentiment analysis The classification accuracy of MultiSTLP is only 0.95% higher than STL-SVM; therefore, when using MultiSTLP and STL-SVM to classify three cross-domain tasks, each task is repeated 10 times, the values of \({W^ + }\) and \({W^ - }\) are \(+169\) and \(-29\), respectively. For the bilateral test of \(\alpha = 0.05\), when \(\mathrm{n} = 30\), by querying the distribution table of the Wilcoxon signed rank test, \({T^{0.025}} = 137\). Because of \({W^ + } > {T^{0.025}}\), \({H_0}\) was accepted: there was no significant difference in the classification results between the two methods.

Email spam: compared with TrGNB and ARTL, the classification accuracy of MultiSTLP increases 0.83 and 0.36%. When MultiSTLP, TrGNB and ARTL are used to classify three cross-domain tasks, each task was repeated 10 times. For MultiSTLP and TrGNB, the values of \({W^ + }\) and \({W^ - }\) are \(+159\) and \(-47\), respectively. For the bilateral test of \(\alpha = 0.05\), when \(\mathrm{n} = 30\), by querying the distribution table of the Wilcoxon signed rank test, \({T^{0.025}}= 137\). Because of \({W^ + } > {T^{0.025}}\), \({H_0}\) was accepted: there was no significant difference in the classification results between the two methods. Similarly, for MultiSTLP and TrGNB, the values of \({W^ + }\) and \({W^ - }\) are 182 and \(-26\), \({W^ + } > {T^{0.025}}\), \({H_0}\) is accepted: there is no significant difference in the classification results of the two methods.

4.4 Parameter Sensitivity Analysis

In TrGNB, ARTL and TSVM-GP, they performed sensitivity analysis of parameters with large influence on performance of algorithm: TrGNB analyzed the difference parameter between source and target domains; MMD regularization parameter and manifold regularization parameter were analyzed to determine the influence of parameters on classification performance for ARTL; TSVM-GP analyzed the regularization coefficient of source domain, the regularization coefficient of source of target domains, and the trade-off term. Like them, we analyze the sensitivity of three parameters: regularization coefficient of target domain \({C_t}\), regularization coefficient of source domain \({C_t}\) and trade-off coefficient \(\lambda \) in objective function of MultiSTLP, which illustrates their influence on the classification performance in this section. For each parameter, we fix the other two parameters at the optimal values determined by cross-validation, and then observe the effect of parameter with different values on the classification result. The experimental results are shown in Figs. 4, 5 and 6.

Fig. 4
figure 4

Sensitivity of parameter \({C_t}\) for MultiSTLP

Full size image
Fig. 5
figure 5

Sensitivity of parameter \({C_s}\) for MultiSTLP

Full size image
Fig. 6
figure 6

Sensitivity of parameter \(\lambda \) for MultiSTLP

Full size image

From the results of Figs. 4, 5 and 6, the following conclusions can be drawn:

  1. (1)

    From Figs. 4 and 5, MultiSTLP is considerably sensitive to regularization parameters \({C_s}\)and \({C_t}\) with a wide range. This denotes that it is critical to determine the value of parameter by some effective strategies.

  2. (2)

    In Fig. 6, we can see that shows that MultiSTLP is sensitive to \(\lambda \). When \(\lambda \) approaches 1, MultiSTLP achieves the best classification performance. As \(\lambda \) is too small, the distribution difference between source and target domains is ignored, so the classification performance will be poor. When it is too large, the distribution difference between source and target domains will theoretically be larger, but this will also reduce the knowledge of source domains that can be transferred to target domain, and the classification performance is also poor.

5 Conclusion

Aiming at the current hot data privacy protection problem in machine learning, we propose a MultiSTLP by combining group probability information with transfer learning. MultiSTLP first uses AESVM to select representative dataset in each source domain; secondly, based on minimizing the marginal probability difference calculate the weight of samples of representative dataset; then, according to conditional probability difference calculates the weight of source domains; finally, the group probability knowledge in the target domain and the weighted knowledge of representative dataset from multiple source domains are combined into the support vector machine structure risk minimization framework, the objective function of MultiSTLP is proposed and proved theoretically. MultiSTLP not only improves training efficiency and result, but also protects data privacy. The effectiveness of the classifier obtained by training MultiSTLP is demonstrated on experiments utilizing four real-world datasets 20-Newsgroups, TRECVID 2005, Sentiment analysis and Email spam. Although the experimental results show that the MultiSTLP algorithm has advantages over the benchmark algorithms, it is still a problem worthy of further study in terms of training efficiency and domain similarity.