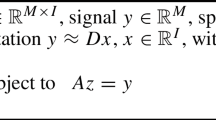Skip to main content
SpringerLink
Log in

Subspace Clustering with Block Diagonal Sparse Representation

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

Structured representation is of remarkable significance in subspace clustering. However, most of the existing subspace clustering algorithms resort to single-structured representation, which may fail to fully capture the essential characteristics of data. To address this issue, a novel multi-structured representation subspace clustering algorithm called block diagonal sparse representation (BDSR) is proposed in this paper. It takes both sparse and block diagonal structured representations into account to obtain the desired affinity matrix. The unified framework is established by integrating the block diagonal prior into the original sparse subspace clustering framework and the resulting optimization problem is iteratively solved by the inexact augmented Lagrange multipliers (IALM). Extensive experiments on both synthetic and real-world datasets well demonstrate the effectiveness and efficiency of the proposed algorithm against the state-of-the-art algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

  1. http://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php.

  2. http://vision.ucsd.edu/~leekc/ExtYaleDatabase/ExtYaleB.html.

  3. http://www.vision.jhu.edu/data/hopkins155/.

References

  1. Lance P, Ehtesham H, Huan L (2004) Subspace clustering for high dimensional data: a review. ACM SIGKDD Explor Newslett 6(1):90–105

    Article  Google Scholar 

  2. Zhenyue Z, Keke Z (2012) Low-rank matrix approximation with manifold regularization. IEEE Trans Patt Anal Mach Intell 35(7):1717–1729

  3. Liansheng Z, Haoyuan G, Zhouchen L, Yi M, Xin Z, Nenghai Y (2012) Non-negative low rank and sparse graph for semi-supervised learning. In: Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), pp 2328–2335

  4. Mahdi A, Patel Vishal M (2018) Multimodal sparse and low-rank subspace clustering. Inform Fusion 39:168–177

    Article  Google Scholar 

  5. Wencheng Z, Jiwen L, Jie Z (2019) Structured general and specific multi-view subspace clustering. Patt Recogn 93:392–403

    Article  Google Scholar 

  6. John W, Yang Allen Y, Arvind G, Shankar SS, Yi M (2008) Robust face recognition via sparse representation. IEEE Trans Patt Anal Mach Intell 31(2):210–227

    Google Scholar 

  7. Chunjie Z, Jing L, Qi T, Changsheng X, Hanqing L, Songde M (2011) Image classification by non-negative sparse coding, low-rank and sparse decomposition. In: Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), pp 1673–1680

  8. Ori B, Michael E (2008) Compression of facial images using the K-SVD algorithm. J Vis Commun Image Represent 19(4):270–282

  9. Przemysław S, Śmieja M, Krzysztof M (2015) Subspaces clustering approach to lossy image compression. In: International conference on computer information systems and industrial management applications (CISIM), pp 571–579

  10. Derin BS, Martin L, Rafael M, Katsaggelos Aggelos K (2012) Sparse Bayesian methods for low-rank matrix estimation. IEEE Trans Sig Process 60(8):3964–3977

    Article  MathSciNet  Google Scholar 

  11. Jing Z, Yue S, Peiguang J, Jing L, Yuting S (2019) A structure-transfer-driven temporal subspace clustering for video summarization. Multimedia Tools Appl 78(17):24123–24145

    Article  Google Scholar 

  12. René V (2011) Subspace clustering. IEEE Sig Process Mag 28(2):52–68

    Article  Google Scholar 

  13. Elhamifar E, René V (2009) Sparse subspace clustering. In: Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), pp 2790–2797

  14. Elhamifar E, Vidal R (2013) Sparse subspace clustering: algorithm, theory, and applications. IEEE Trans Patt Anal Mach Intell 35(11):2765–2781

    Article  Google Scholar 

  15. Liu G, Zhouchen L, Yong Y (2010) Robust subspace segmentation by low-rank representation. In: Proceedings of the international conference on machine learning (ICML), pp 663–670

  16. Guangcan L, Zhouchen L, Shuicheng Yan J, Sun Yong Yu, Yi M (2013) Robust recovery of subspace structures by low-rank representation. IEEE Trans Patt Anal Mach Intell 35(1):171–184

    Article  Google Scholar 

  17. Canyi L, Jiashi F, Zhouchen L, Mei T, Shuicheng Y (2019) Subspace clustering by block diagonal representation. IEEE Trans Patt Anal Mach Intell 41(2):487–501

    Article  Google Scholar 

  18. Patel Vishal M, René V (2014) Kernel sparse subspace clustering. In: Proceedings of the IEEE international conference on image processing (ICIP), pp 2849–2853,

  19. Jun Yu, Yong R, Dacheng T (2014) Click prediction for web image reranking using multimodal sparse coding. IEEE Trans Image Process 23(5):2019–2032

    Article  MathSciNet  Google Scholar 

  20. Jun Yu, Dacheng T, Meng W, Yong R (2014) Learning to rank using user clicks and visual features for image retrieval. IEEE Trans Cybern 45(4):767–779

    Google Scholar 

  21. Wanjun C, Erhu Z, Zhuomin Z (2016) A Laplacian structured representation model in subspace clustering for enhanced motion segmentation. Neurocomputing 208:174–182

    Article  Google Scholar 

  22. Jun W, Daming S, Dansong C, Yongqiang Z, Junbin G (2016) LRSR: low-rank-sparse representation for subspace clustering. Neurocomputing 214:1026–1037

    Article  Google Scholar 

  23. He W, Chen Jim X, Weihua Z (2017) Low-rank representation with graph regularization for subspace clustering. Soft Comput 21(6):1569–1581

    Article  Google Scholar 

  24. Guang LC, Chong Y, René V (2017) Structured sparse subspace clustering: a joint affinity learning and subspace clustering framework. IEEE Trans Image Process 26(6):2988–3001

    Article  MathSciNet  Google Scholar 

  25. Shiqiang D, Yide M, Yurun M (2017) Graph regularized compact low rank representation for subspace clustering. Knowled Based Syst 118:56–69

    Article  Google Scholar 

  26. Lai W, Xiaofeng W, Aihua W, Rigui Z, Changming Z (2018) Robust subspace segmentation by self-representation constrained low-rank representation. Neural Process Lett 48(3):1671–1691

    Article  Google Scholar 

  27. Yanxi C, Gen L, Yuantao G (2018) Active orthogonal matching pursuit for sparse subspace clustering. IEEE Sig Process Lett 25(2):164–168

    Article  Google Scholar 

  28. Chaoqun H, Jun Yu, Jian Z, Xiongnan J, Kyong-Ho L (2018) Multimodal face-pose estimation with multitask manifold deep learning. IEEE Trans Indus Inform 15(7):3952–3961

    Google Scholar 

  29. Jun Yu, Min T, Hongyuan Z, Dacheng T, Yong R (2019) Hierarchical deep click feature prediction for fine-grained image recognition. IEEE Trans Patt Anal Mach Intell

  30. Liu G, Shuicheng Y (2011) Latent low-rank representation for subspace segmentation and feature extraction. In: Proceedings of the IEEE international conference on computer vision (ICCV), pp 1615–1622

  31. Canyi L, Hai M, Zhongqiu Z, Lin Z, Deshuang H, Shuicheng Y (2012) Robust and efficient subspace segmentation via least squares regression. In: Proceedings of the European conference on computer vision (ECCV), pp 347–360

  32. Patel Vishal M, Nguyen Hien V, René V (2013) Latent space sparse subspace clustering. In: Proceedings of the IEEE international conference on computer vision (ICCV), pp 225–232

  33. Jie C, Hua M, Yongsheng S, Zhang Y (2017) Subspace clustering using a symmetric low-rank representation. Knowled Based Syst 127:46–57

    Article  Google Scholar 

  34. Huazhu C, Weiwei W, Xiangchu F, Ruiqiang H (2018) Discriminative and coherent subspace clustering. Neurocomputing 284:177–186

    Article  Google Scholar 

  35. Xian F, Zhixin T, Feiyang S, Jialiang Y (2019) Robust subspace clustering via symmetry constrained latent low rank representation with converted nuclear norm. Neurocomputing 340:211–221

    Article  Google Scholar 

  36. Lu C, Jiashi F, Zhouchen L, Shuicheng Y (2013) Correlation adaptive subspace segmentation by trace lasso. In: Proceedings of the IEEE international conference on computer vision (ICCV), pp 1345–1352

  37. Wang YX, Xu H, Leng C (2013) Provable subspace clustering: when LRR meets SSC. In: Proceedings of the conference on neural information processing systems (NeurIPS), pp 64–72

  38. Xingyu X, Xianglin G, Guangcan L, Jun W (2017) Implicit block diagonal low-rank representation. IEEE Trans Image Process 27(1):477–489

    MathSciNet  MATH  Google Scholar 

  39. Zhouchen L, Minming C, Yi M (2009) The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. Technical Report UILU-ENG-09-2215

  40. Zhi H, Lin L, Suhong Z, Yi S (2016) Learning group-based sparse and low-rank representation for hyperspectral image classification. Patt Recogn 60:1041–1056

    Article  Google Scholar 

  41. Jianbo S, Malik J (2000) Normalized cuts and image segmentation. IEEE Trans Patt Anal Mach Intell 22(8):888–905

    Article  Google Scholar 

  42. Feng J, Zhouchen L, Huan X, Shuicheng Y (2014) Robust subspace segmentation with block-diagonal prior. In: Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), pp 3818–3825

  43. Nene Samer A, Nayar Shree K, Hiroshi M (1996) Columbia object image library (COIL-20). Technical Report CUCS-005-96

  44. Georghiades Athinodoros S, Belhumeur Peter N, Kriegman David J (2001) From few to many: illumination cone models for face recognition under variable lighting and pose. IEEE Trans Patt Anal Mach Intell 23(6):643–660

    Article  Google Scholar 

  45. Chih LK, Jeffrey H, Kriegman David J (2005) Acquiring linear subspaces for face recognition under variable lighting. IEEE Trans Patt Anal Mach Intell 27(5):684–698

    Article  Google Scholar 

  46. van der Maaten L, Geoffrey H (2008) Visualizing data using t-SNE. J Mach Learn Res 9:2579–2605

  47. Tron R, René V (2007) A benchmark for the comparison of 3-D motion segmentation algorithms. In: Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), pp 1–8

  48. Karl P (1901) On lines and planes of closest fit to systems of points in space. Philos Mag 2(11):559–572

    Article  Google Scholar 

  49. Harold H (1933) Analysis of a complex of statistical variables into principal components. J Educ Psychol 24(6):417–441

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to gratefully acknowledge the editors and the anonymous reviewers for their valuable comments. This research is supported in part by the National Natural Science Foundation of China under Grant 61973173.

Author information

Authors and Affiliations

  1. College of Computer Science, Nankai University, Tianjin, 300350, China

    Xian Fang, Zhengxin Li & Xiuli Shao

  2. Tianjin Key Laboratory of Network and Data Security Technology, Tianjin, 300350, China

    Xian Fang, Zhengxin Li & Xiuli Shao

  3. MIT Laboratory for Financial Engineering, Cambridge, MA, 02139, USA

    Ruixun Zhang

Authors
  1. Xian Fang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ruixun Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhengxin Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiuli Shao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiuli Shao.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The proof of Theorem 2 is given as follows.

Proof

For simplicity, Eq. (12) can be rewritten as

$$\begin{aligned}&\hat{\varvec{Z}}^{(t+1)}=\mathop {{{\,\mathrm{argmin}\,}}}_{\varvec{Z}} \frac{1}{2}\Vert \varvec{Z}-\varpi _1 \Vert _F^2 \nonumber \\&\quad \quad \mathrm{s.t.} \ \varvec{Z} \ge 0 \end{aligned}$$
(25)

Then, we have

$$\begin{aligned}&\frac{1}{2}\Vert \hat{\varvec{Z}}^{(t)}-\varpi _1 \Vert _F^2 = \frac{1}{2}\Vert \hat{\varvec{Z}}^{(t)}-\hat{\varvec{Z}}^{(t+1)}+\hat{\varvec{Z}}^{(t+1)}-\varpi _1 \Vert _F^2\nonumber \\&\quad \quad \ \ge \frac{1}{2}\Vert \hat{\varvec{Z}}^{(t)}-\hat{\varvec{Z}}^{(t+1)} \Vert _F^2 + \frac{1}{2}\Vert \hat{\varvec{Z}}^{(t+1)}-\varpi _1 \Vert _F^2 \end{aligned}$$
(26)

Hence, we can obtain

$$\begin{aligned}&\mathcal {F}(\varvec{Z}^{(t+1)}, \varvec{B}^{(t+1)}, \varvec{P}^{(t+1)}, \varvec{Q}^{(t+1)}) \le \mathcal {F}(\varvec{Z}^{(t)}, \varvec{B}^{(t+1)}, \varvec{P}^{(t+1)}, \varvec{Q}^{(t+1)}) \nonumber \\&\quad \quad \ - \frac{1}{2}\Vert \hat{\varvec{Z}}^{(t)}-\hat{\varvec{Z}}^{(t+1)} \Vert _F^2 \end{aligned}$$
(27)

From Eq. (15), we can directly obtain

$$\begin{aligned}&\mathcal {F}(\varvec{Z}^{(t)}, \varvec{B}^{(t+1)}, \varvec{P}^{(t+1)}, \varvec{Q}^{(t+1)}) + \mathcal {G}(\varvec{B}^{(t+1)}) \nonumber \\&\quad \quad \le \mathcal {F}(\varvec{Z}^{(t)}, \varvec{B}^{(t)}, \varvec{P}^{(t+1)}, \varvec{Q}^{(t+1)}) + \mathcal {G}(\varvec{B}^{(t)}) \end{aligned}$$
(28)

For simplicity, Eq. (17) can be rewritten as

$$\begin{aligned} \varvec{P}=\mathop {{{\,\mathrm{argmin}\,}}}_{\varvec{P}} \Vert \varvec{P} \Vert _F^2 + \mu \Vert \varvec{P}-\varpi _2 \Vert _F^2 \end{aligned}$$
(29)

Then, we have

$$\begin{aligned}&\Vert \varvec{P}^{(t+1)} \Vert _F^2 + \mu \Vert \varvec{P}^{(t+1)}-\varpi _2 \Vert _F^2 \le \Vert \varvec{P}^{(t)} \Vert _F^2 + \mu \Vert \varvec{P}^{(t)}-\varpi _2 \Vert _F^2 \nonumber \\&\quad \quad - ((1+\mu ))\Vert \varvec{P}^{(t)}-\varvec{P}^{(t+1)} \Vert _F^2 \end{aligned}$$
(30)

Hence, we can obtain

$$\begin{aligned}&\mathcal {F}(\varvec{Z}^{(t)}, \varvec{B}^{(t)}, \varvec{P}^{(t+1)}, \varvec{Q}^{(t+1)}) \le \mathcal {F}(\varvec{Z}^{(t)}, \varvec{B}^{(t)}, \varvec{P}^{(t)}, \varvec{Q}^{(t+1)}) \nonumber \\&\quad \quad - (1+\mu )\Vert \varvec{P}^{(t)}-\varvec{P}^{(t+1)} \Vert _F^2 \end{aligned}$$
(31)

For simplicity, Eq. (19) can be rewritten as

$$\begin{aligned} \varvec{Q}=\mathop {{{\,\mathrm{argmin}\,}}}_{\varvec{Q}} \Vert \varvec{Q} \Vert _1 + \frac{\mu }{2\lambda _1}\Vert \varvec{Q}-\varpi _3 \Vert _F^2 \end{aligned}$$
(32)

Then, we have

$$\begin{aligned}&\Vert \varvec{Q}^{(t+1)} \Vert _F^2 + \frac{\mu }{2\lambda _1}\Vert \varvec{Q}^{(t+1)}-\varpi _3 \Vert _F^2 \le \Vert \varvec{Q}^{(t)} \Vert _F^2 + \frac{\mu }{2\lambda _1}\Vert \varvec{Q}^{(t)}-\varpi _3 \Vert _F^2 \nonumber \\&\quad \quad - ((1+\frac{\mu }{2\lambda _1}))\Vert \varvec{Q}^{(t)}-\varvec{Q}^{(t+1)} \Vert _F^2 \end{aligned}$$
(33)

Hence, we can obtain

$$\begin{aligned}&\mathcal {F}(\varvec{Z}^{(t)}, \varvec{B}^{(t)}, \varvec{P}^{(t)}, \varvec{Q}^{(t+1)}) \le \mathcal {F}(\varvec{Z}^{(t)}, \varvec{B}^{(t)}, \varvec{P}^{(t)}, \varvec{Q}^{(t)}) \nonumber \\&\quad \quad - (1+\frac{\mu }{2\lambda _1})\Vert \varvec{Q}^{(t)}-\varvec{Q}^{(t+1)} \Vert _F^2 \end{aligned}$$
(34)

Combining Eq. (27), Eq. (28), Eq. (31) and Eq. (34), we can gain

$$\begin{aligned}&\mathcal {F}(\varvec{Z}^{(t+1)}, \varvec{B}^{(t+1)}, \varvec{P}^{(t+1)}, \varvec{Q}^{(t+1)}) + \mathcal {G}(\varvec{B}^{(t+1)}) \le \nonumber \\&\quad \quad \mathcal {F}(\varvec{Z}^{(t)}, \varvec{B}^{(t)}, \varvec{P}^{(t)}, \varvec{Q}^{(t)}) + \mathcal {G}(\varvec{B}^{(t)}) - \frac{1}{2}\Vert \hat{\varvec{Z}}^{(t)}-\hat{\varvec{Z}}^{(t+1)} \Vert _F^2 \nonumber \\&\quad \quad - (1+\mu )\Vert \varvec{P}^{(t)}-\varvec{P}^{(t+1)} \Vert _F^2 - (1+\frac{\mu }{2\lambda _1})\Vert \varvec{Q}^{(t)}-\varvec{Q}^{(t+1)} \Vert _F^2 \end{aligned}$$
(35)

\(\square \)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fang, X., Zhang, R., Li, Z. et al. Subspace Clustering with Block Diagonal Sparse Representation. Neural Process Lett 53, 4293–4312 (2021). https://doi.org/10.1007/s11063-021-10597-5

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-021-10597-5

Keywords

Search

Navigation