Introduction

Surficial and deep earth materials normally consist of several classes with different characteristics. Tectonic, lithological and alteration units, soil types, vegetation classes, plant species, and land uses are examples of such classes. Spatial maps of these classes and their associated uncertainties are vital components in the current strategies for managing projects such as mineral exploration, animal and human health, environmental and ecological planning, efficient management of water resources, geohazard risk assessment, agriculture, and sustainable food production. Class prediction and spatial uncertainty modeling using multivariate spatial data are a common challenge for geoscience modelers. Mechanisms behind geological systems can be explained partly by geochemical data and methods (Buccianti and Grunsky 2014; Grunsky et al. 2014; Tolosana-Delgado and van den Boogaart 2014; Harris and Grunsky 2015; Tolosana-Delgado and McKinley 2016; Caritat et al. 2017). Spatial or spatiotemporal geoscientific entities such as climate zones, ecosystems, landforms, and surface and subsurface geology are related to geochemistry derived from surface and near-surface materials (Drew et al. 2010; Grunsky et al. 2013; McKinley 2015; Grunsky et al. 2017; McKinley et al. 2018). Over the last decade, geochemical surveys at different scales (e.g., regional, national, transnational, and continent scales) have become widely available. These geochemical surveys normally constitute “big data” of high dimensionality making the statistical and spatial analyses challenging (Grunsky 2010). Most geological processes leave some sort of footprint that can be explored by advanced geochemical data analysis. These footprints are complex multivariate statistical and/or spatial patterns hidden deep in the geochemical compositional space. Advanced statistical and/or spatial compositional data analysis should be implemented to explore these patterns. Geochemical data are inherently compositional in nature, presenting several challenges for spatial predictive models (Pawlowsky-Glahn and Olea 2004; Tolosana-Delgado 2006; Tolosana-Delgado and van den Boogaart 2013; van den Boogaart and Tolosana-Delgado 2013; Pawlowsky-Glahn and Egozcue 2016). Compositional data are multivariate, nonnegative values that represent the abundance of some parts of a whole. In such data, the constant sum constraint forces at least one covariance to be negative and induces spurious statistical and spatial correlations and patterns. Furthermore, these data carry just relative information (Aitchison 1986) and interpretations are necessarily multivariate, dependent on all components. To transform compositional data into an unbounded space and to increase mathematical tractability, different log-ratio transformations (Aitchison 1986; Pawlowsky-Glahn and Olea 2004; Tolosana-Delgado 2006) can be applied prior to using standard (geo)statistical techniques. A geochemical survey normally produces thousands of samples and dozens of variables (log-ratios) and as such is practically impossible to effectively visualize and interpret without the assistance of computers and statistical tools. In addition, the underlying geological processes most of the time are obscure and difficult to understand. In such situations, machine learning algorithms (MLAs) have been shown to perform well in the prediction of classes from spatially dispersed data and discovering the underlying geological processes (Kanevski et al. 2009; Harris and Grunsky 2015). However, MLAs are typically not spatially predictive algorithms, which means that they do not consider the multivariate spatial relationships between features. As a result, the probability maps generated via MLAs cannot be accepted as a model of spatial uncertainty. In a geostatistical treatment, spatial relationships are taken into account via means such as second-order ((cross-)variograms) and/or higher-order statistics (training images). To address this limitation of MLAs, an alternative solution is proposed in this study based on the combined use of advanced multivariate geostatistical simulation and MLAs.

The proposed spatial compositional predictive model is twofold: first, spatial simulation of geochemical compositions at unsampled locations and second class prediction for each simulated map via a trained random forest (RF) algorithm (Breiman 2001). Other spatial (Tolosana-Delgado et al. 2015) or nonspatial (Kuhn and Johnson 2013) predictive models can also be implemented, but RF is utilized in this study for its ease of implementation, robustness against over-fitting, ability to handle many types of predictors (sparse, skewed, continuous, categorical, etc.) without the need to preprocess them, ability to handle missing data and to select the most relevant features (Kuhn and Johnson 2013). Once the spatial compositional vectors have been simulated in the study area, MLAs (RF in this study) can be implemented to predict the probability of occurrence of classes conditional to each realization of the compositional random function. To simulate the compositional random function at unsampled locations, the input geochemical compositions are transformed to real space via an isometric log-ratio (ilr, Egozcue et al. 2003) transformation. To avoid violating the assumption of multivariate multi-Gaussianity of geostatistical simulation techniques (Chilès and Delfiner 2012), log-ratios are transformed to multivariate normal space via a flow anamorphosis (FA) algorithm (Mueller et al. 2017; van den Boogaart et al. 2017). The turning bands (TB) algorithm (Emery and Lantuéjoul 2006; Emery 2008) is used to simulate the orthogonal factors at unsampled locations. Finally, the simulated results are back-transformed to the original space to provide several simulated spatial maps of geochemical compositions. Based on the true classes for the input set, a random forest algorithm is trained using the generated features. The ability of RF to rank the features based on their contribution to the predictive model aids the discovery of underlying geological processes. The trained RF is used to predict the probabilities of classes at unsampled locations using the simulated compositions. Minimum, expected, and maximum probability scenarios are defined for each class from simulated probabilities.

The objectives of this research are to introduce a new method to account for spatial uncertainty on classifiers based on a combination of geostatistical simulation and machine learning classification algorithms. The most probable geological classes are predicted out of geochemical survey data using the new model of spatial uncertainty. Finally, a compositional feature selection is introduced and implemented for geological process discovery studies.

The proposed approach is illustrated through two case studies. In the first one, surface regolith geochemistry data are used to predict the major crustal blocks of the Australian continent. Discovering superficial peat deposits in Northern Ireland from regional-scale soil geochemical data is the aim of the second case study.

The organization of this paper is as follows: “Compositional Data Analysis” section discusses the analysis of compositional data. Flow anamorphosis as a powerful technique for transforming input data to multivariate normal space is discussed in “Flow Anamorphosis” section. “Random Forest Algorithm and Feature Selection” section presents the random forest predictive model and the recursive feature elimination with resampling technique. Steps of the proposed method for modeling spatial uncertainty are presented in “Spatial Modeling of Geological Classes” section. “Major Crustal Blocks Prediction Using Surface Regolith Geochemistry” and “Post-glacial Deposits Exploration for Environmental Monitoring” sections present the implementation of the method and results and discussion for the two case studies. Finally, some conclusions and the final thoughts are presented in “Conclusions” section.

Methodology

Compositional Data Analysis

Compositions are multivariate data whose components represent the relative contribution of some parts forming a whole. Typically, these nonnegative components are measured on the same scale (proportions, percentages, ppm, or ppb) and are constrained by a constant sum property. Regionalized compositions are consequently defined as follows:

$$ \vec{Z}\left( u \right) = \left[ {z_{1} \left( u \right),z_{2} \left( u \right), \ldots ,z_{D} \left( u \right)} \right]; \quad \left\{ {\begin{array}{*{20}l} { z_{i} \left( u \right) \ge 0;\quad i = 1,2, \ldots , D,\quad u \in A} \hfill \\ {\mathop \sum \limits_{i = 1}^{D} z_{i} \left( u \right) = m} \hfill \\ \end{array} ,} \right. $$
(1)

where \( z_{i} \left( u \right) \) represents the \( i \)th component measured at location \( u \) within the study area \( \varvec{A} \) and \( m \) is the constant sum. Geochemical data are a typical example of compositional data. It is often the case that the data analyzed do not add to the constant \( m \), in which case an additional variable can be introduced, often called filler or rest, to ensure that the constant sum constraint is satisfied. Compositional data carry by definition relative information (Aitchison 1986), and the constant sum constraint is known to induce the problems of spurious statistical and spatial correlations (Aitchison 1982; Pawlowsky-Glahn and Olea 2004). Constraints of positivity and constant sum and the spurious correlations can be appropriately addressed by implementing log-ratio transformations, for instance, making (geo)statistical treatment more amenable (Aitchison 1986; van den Boogaart and Tolosana-Delgado 2013; Pawlowsky-Glahn et al. 2015; Pawlowsky-Glahn and Egozcue 2016). Several families of log-ratio transformations exist in the literature. The pairwise log-ratio (pwlr), additive log-ratio (alr), and centered log-ratio (clr) transformations were introduced by Aitchison (1986), and the isometric log-ratio (ilr) transformation was proposed by Egozcue et al. (2003). The pairwise log-ratios are readily interpretable and are defined as follows:

$$ {\text{pwlr}}\left( {\vec{Z}\left( u \right)} \right) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & {\ln \left( {\frac{{z_{1} \left( u \right)}}{{z_{2} \left( u \right)}}} \right)} \\ {\ln \left( {\frac{{z_{2} \left( u \right)}}{{z_{1} \left( u \right)}}} \right)} & 0 \\ \end{array} } & {\begin{array}{*{20}c} \cdots & {\ln \left( {\frac{{z_{1} \left( u \right)}}{{z_{D} \left( u \right)}}} \right)} \\ \ldots & {\ln \left( {\frac{{z_{2} \left( u \right)}}{{z_{D} \left( u \right)}}} \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ {\ln \left( {\frac{{z_{D} \left( u \right)}}{{z_{1} \left( u \right)}}} \right)} & {\ln \left( {\frac{{z_{D} \left( u \right)}}{{z_{2} \left( u \right)}}} \right)} \\ \end{array} } & {\begin{array}{*{20}c} \ddots & {} \\ {} & 0 \\ \end{array} } \\ \end{array} } \right] = \left[ {\xi_{ij} \left( u \right)} \right], $$
(2)

where \( i \), \( j \in \left\{ {1,2, \ldots , D} \right\} \). The centered log-ratios present the logarithms of ratios of each component to the geometric mean of all components. They are obtained via the following formula:

$$ {\text{clr}}\left( {\vec{Z}\left( u \right)} \right) = \ln \left( {\frac{{\vec{Z}\left( u \right)}}{{\sqrt[D]{{\mathop \prod \nolimits_{i = 1}^{D} z_{i} \left( u \right)}}}}} \right). $$
(3)

Finally, the isometric log-ratio transformation is defined as follows:

$$ {\text{ilr}}\left( {\vec{Z}\left( u \right)} \right) = V \cdot {\text{clr}}\left( {\vec{Z}\left( u \right)} \right), $$
(4)

where \( V \) is a \( \left( {D - 1} \right) \times D \) matrix whose columns are pairwise orthogonal vectors, each sums to zero. Each matrix \( V \) satisfying these conditions gives rise to an ilr transformation.

All the aforementioned log-ratio transformations are log-contrasts, that is: linear combinations of the components in log-scale with coefficients summing to zero:

$$ \xi_{ } \left( u \right) = \mathop \sum \limits_{i = 1}^{D} \alpha_{i} { \ln }\left( {z_{i} \left( u \right)} \right);\quad \mathop \sum \limits_{i = 1}^{D} \alpha_{i} = 0 ; \quad \alpha_{i} \in {\mathbb{R}} $$
(5)

Complex log-contrasts can be defined to discover hidden underlying geological processes and classes. Many log-contrasts can be defined, and the most appropriate ones depend on the aim of the analysis undertaken (Pawlowsky-Glahn and Buccianti 2011; McKinley et al. 2016).

Flow Anamorphosis

As discussed in the preceding section, compositional data do not have a unique, canonical representation and several log-ratio transformations are available. Invariance of the simulated results under the choice of log-ratio transform is thus highly desirable. This property is known as affine equivariance. Log-ratios are not commonly multivariate normal, so they have to be combined with a normal score transform prior to using geostatistical simulation techniques in order to not violate the assumption of multi-Gaussianity of most of these simulation algorithms (Chilès and Delfiner 2012; Mueller et al. 2014). Conventional normal score transformations based on quantile matching are neither affine equivariant nor do provide multivariate normal transformed scores. The flow anamorphosis is a multivariate form of gaussian anamorphosis which is capable of transforming original multivariate data to multivariate normal space and at the same time is invariant under the choice of log-ratio transform (Mueller et al. 2017; van den Boogaart et al. 2017). FA is applied in this study because of its ability to reproduce complex patterns (e.g., presence of outliers, presence of several populations, nonlinearity, and heteroscedasticity) in the input data, its invariance property under the choice of log-ratio transformation, and its property of generating spatially orthogonal factors that makes geostatistical simulation straightforward. The transformation is controlled by two parameters: \( \sigma_{0} \) and \( \sigma_{1} \) (initial and final spreads of the smoothing kernels of the kernel density estimates) which need to be tuned. The choice of a suitable value for \( \sigma_{0} \) depends on the number of variables, sample size, and complexity of the input data, while \( \sigma_{1} \) controls the ranges of the transformed distributions. The simulated results are subsequently back-transformed to the original space via FA−1.

Random Forest Algorithm and Feature Selection

Tree-based classification models consist of several nested conditions on the predictors that partition the observations into purer subpopulations. Within these partitions, a model is used to predict the class of future observations. Tree-based models are very popular due to their ease of interpretation and implementation, their ability to handle many types of predictors (sparse, skewed, continuous, categorical, etc.) without the need to preprocess them, allow missing data, and conduct feature selection (Kuhn and Johnson 2013). However, single decision trees are prone to instability, which means that slight changes in the input observations can drastically change the structure of the tree and, hence, the subsequent interpretations and predictions. Ensemble methods that combine many simple predictive models (e.g., built from bootstrap samples) into one predictive model have been developed to address this instability and have much better predictive performance (Breiman 1996). The other advantage of the ensemble models is that the predictive performance can be estimated internally, which correlates well with either cross-validation estimates or test set estimates. The left-out observations from each bootstrap sample (called “out-of-bag”) are used to assess the predictive performance of each model in the ensemble. The average of the out-of-bag performance metrics can then be used to measure the overall predictive performance of the entire ensemble. Algorithm 1 shows the processes of a general random forest algorithm (Breiman 2001), a well-known ensemble predictive model.

figure a

For each new observation, each of the \( t \) trees in the forest is used to predict its class and the resulting \( t \) predictions are combined to give the forest prediction. The number of trees in the forest (t) and the number of randomly selected predictors for each split (s) are the most important parameters in the RF algorithm, which need to be tuned. It has been shown that the selection of a large \( t \) will not adversely affect the RF model and does not lead to over-fitting (Breiman 2001); however, it increases the computational burden. Several experiments have shown that the random forest tuning parameter does not have a drastic effect on its accuracy (Kuhn and Johnson 2013). Several approaches have been proposed to quantify the importance of predictors in the RF model such as measuring the improvement in node purities for each predictor at each occurrence of that predictor across the whole forest and aggregating them to determine the overall importance. However, these approaches for measuring the importance of predictors are adversely affected by the correlations between predictors (Strobl et al. 2007).

Due to the high-dimensional characteristic of the log-contrasts\( (\xi) \) calculated from geochemical compositions, determining which subset of them should be included in a predictive model is a critical question. While decision trees are not affected by redundant predictors due to the built-in feature selection, RF shows a moderate degradation in its accuracy due to random selection of predictors for splitting (Kuhn and Johnson 2013). Given the potential negative impact of redundant information (collinearity within log-contrasts), there is a need to find a smaller subset of them by maximizing the predictive performance of the RF algorithm. Feature selection is primarily implemented for removing noninformative or redundant predictors from the model. Multiple predictive models (built from subsets \( s_{i} \) of significant predictors) are evaluated to find the optimal combination of predictors that maximizes model performance. A recursive feature elimination with resampling technique (Guyon et al. 2002; Kuhn and Johnson 2013) is used in this study to select the most informative subset of log-contrasts for the classification purpose. The final predictive model with the highest accuracy is built from this subset of significant predictors (Algorithm 2).

figure b

Spatial Modeling of Geological Classes

To spatially predict geological classes from geochemical composition, the first step is to simulate the compositional random function at unsampled locations. Algorithm 3 shows the procedure of geostatistical simulation of regionalized compositions. In line 1 of this algorithm, any log-ratio transformation can be implemented as long as the selected anamorphosis is affine equivariant. An \( {\text{ilr}} \) transformation (Eq. 4) was used in this study for this purpose. After transforming the log-ratios to multivariate normal space via the FA algorithm, the spatially orthogonal multivariate normal scores are simulated at unsampled locations independently. In this study, a turning bands algorithm will be used for this purpose (Emery and Lantuéjoul 2006; Emery et al. 2016). After generating \( L \) realizations of the compositional random function, the expected spatial map of regionalized compositions is defined as follows:

$$ \vec{Z}^{*} \left( u \right) = C\left[ {\left( {\mathop \prod \limits_{l = 1}^{L} z_{1}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} ,\left( {\mathop \prod \limits_{l = 1}^{L} z_{2}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} , \ldots ,\left( {\mathop \prod \limits_{l = 1}^{L} z_{D}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} } \right], $$
(6)

where \( C \) is the closure operator defined as:

$$ C\left( {\vec{Z}\left( u \right)} \right) = \left[ {\frac{{\left( {\mathop \prod \nolimits_{l = 1}^{L} z_{1}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} }}{{\mathop \sum \nolimits_{d = 1}^{D} \left( {\mathop \prod \nolimits_{l = 1}^{L} z_{d}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} }},\frac{{\left( {\mathop \prod \nolimits_{l = 1}^{L} z_{2}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} }}{{\mathop \sum \nolimits_{d = 1}^{D} \left( {\mathop \prod \nolimits_{l = 1}^{L} z_{d}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} }}, \ldots ,\frac{{\left( {\mathop \prod \nolimits_{l = 1}^{L} z_{D}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} }}{{\mathop \sum \nolimits_{d = 1}^{D} \left( {\mathop \prod \nolimits_{l = 1}^{L} z_{d}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} }}} \right]. $$
(7)

The conditional total compositional variation in the simulated composition at location \( u \) is given by:

$$ {\text{totvar}}_{\text{composition}} \left( {\vec{Z}\left( u \right)} \right) = \frac{1}{2D}\mathop \sum \limits_{i = 1}^{D} \mathop \sum \limits_{j = 1}^{D} {\text{var}}\left( {{ \ln }\frac{{z_{i} \left( u \right)}}{{z_{j} \left( u \right)}}} \right). $$
(8)

The map of the total compositional variations for the simulated compositions can be considered as a means to assess spatial uncertainty of the geochemical compositions. High values of this metric show the most uncertain areas (and vice versa) with respect to the simulated geochemical compositions.

figure c

The second step is to build a predictive model based on the input labeled observations (input geochemical compositions). For such a predictive model, the features consist of log-contrasts\( (\xi) \). To extract relevant compositional information, a combination of the knowledge-driven log-contrasts (based on a geochemical understanding of the processes under consideration) and established mathematical representations (e.g., pwlr and clr) can be used as the input features (McKinley et al. 2016). These features together with the associated classes (e.g., rock types, soil types, mineralized material) are used to train the RF predictive model (Algorithm 1). The significant log-contrasts are recognized and ordered based on their contributions to the predictive model via Algorithm 2. The selected log-contrasts (out of many) and their ranks are very useful for geological process discovery and interpretation. The same selected log-contrasts are calculated from the simulated compositions at unsampled locations. The trained RF is used to predict classes at these locations. For each location \( u \) and for each realization \( l \) of the compositional random function, RF generates a discrete prediction (geological classes \( I^{l} \left( u \right) = k;k = 1, \ldots , K\;{\text{and}}\;l = 1, \ldots ,L \)) and a vector of probabilities \( \vec{p}^{l} \left( u \right) = \left[ {p_{1}^{l} \left( u \right),p_{2}^{l} \left( u \right), \ldots ,p_{K}^{l} \left( u \right)} \right] \). However, the local uncertainty of the discrete predictions is underestimated and should not be used for spatial classification purposes. As an example, consider the information in Table 1, where there are three geological classes \( (k = 1, 2, 3) \) and at location \( u \) a compositional random function has been simulated five times \( (l = 1, \ldots , 5) \). Running a predictive model on these realizations (uncertain inputs) will generate different sets of probabilities. Although the probability of other classes occurring is nonzero for each realization, the final decision for location \( u \) would be class 3 with zero uncertainty, which is not true. This example shows that the spatial uncertainty of geological classes generated by a predictive model might be misleading.

Table 1 Prediction with uncertain inputs
Full size table

As a result, discrete predictions of RF for each realization of geochemical compositions should be ignored and predicted probabilities \( (\vec{p}^{l} \left( u \right) = \left[ {p_{1}^{l} \left( u \right),p_{2}^{l} \left( u \right), \ldots ,p_{K}^{l} \left( u \right)} \right]) \) should be treated as follows: For a location \( u \), the probability of occurrence of a specific class \( k \) varies from \( \hbox{min} (p_{k}^{l} \left( u \right)) \) to \( \hbox{max} (p_{k}^{l} \left( u \right)) \) while the vector of expected probabilities is defined as closure of the vector of geometric means of the probabilities for each class:

$$ \vec{q}\left( u \right) = C\left[ {\left( {\mathop \prod \limits_{l = 1}^{L} p_{1}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} ,\left( {\mathop \prod \limits_{l = 1}^{L} p_{2}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} , \ldots ,\left( {\mathop \prod \limits_{l = 1}^{L} p_{K}^{l} \left( u \right)} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}}} } \right]. $$
(9)

To reach the convergence and generate stable predictions, the number of bootstrap samples in the RF algorithm should be large enough. Having a large number of simple learners (decision trees built from bootstrap samples), there is a chance for all geological classes to occur (although pretty close to zero and negligible in the unlikely situations). However, to avoid multiplying by zero, one way is to replace these zero probabilities by new predictions, using new realizations of the compositional random function until all probabilities of geological classes are nonzero. The expected spatial probability model \( \vec{q}\left( u \right) \) combines the statistical uncertainty (e.g., bootstrapping in the RF model) and the spatial uncertainty \( (L \) realizations of the geostatistical model). For example, in Table 1, the probability of class 1 varies from \( { \hbox{min} }_{l = 1, \ldots ,3} (p_{1}^{l} \left( u \right)) = 0.05 \) to \( \max_{l = 1, \ldots ,3} (p_{1}^{l} \left( u \right)) = 0.15 \) while the expected probability is \( 0.104 \)\( \left( { \vec{q}\left( u \right) = \left[ {0.104, 0.260, 0.636} \right]} \right) \). The most probable class for location \( u \) should be defined from \( \vec{q}\left( u \right) \) which is class 3 in this example. Finally, the conditional total variation in geological classes for a location \( u \) is given by:

$$ {\text{totvar}}_{\text{probability}} \left( u \right) = \frac{1}{2K}\mathop \sum \limits_{i = 1}^{K} \mathop \sum \limits_{j = 1}^{K} {\text{var}}\left( {{ \ln }\frac{{p_{i} \left( u \right)}}{{p_{j} \left( u \right)}}} \right) $$
(10)

High values of this metric show the most uncertain areas (and vice versa) with respect to the predicted geological classes.

Major Crustal Blocks Prediction Using Surface Regolith Geochemistry

Dataset

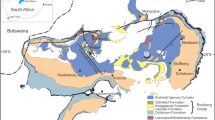
In this first case study, multi-element near-surface geochemical compositions from the National Geochemical Survey of Australia (NGSA) are used to predict the exposed to deeply buried major crustal blocks (MCBs) of the Australian continent. The NGSA is a uniform and internally consistent geochemical database, covering approximately 81% of the continent of Australia (Caritat and Cooper 2011, 2016). The NGSA dataset consists of four subsets based on the sampling depth and grain size. In this study, the focus is on the “total” analysis of the fine-grained fraction (< 75 μm) of the top outlet sediment samples (0–10 cm depth) (for further detail please see Grunsky et al. (2017)). Figure 1a shows the map of the major MCBs over Australia, while the distribution of surface lithology and the geological regions of Australia are shown in Figure 1b. The NGSA sample site locations are shown as black dots on these maps. The MCBs, derived from the major boundaries in the Australian crust as interpreted from geophysical and geological data by Korsch and Doublier (2015, 2016), reflect distinct tectonic domains comprised of early Archean to recent Cenozoic igneous, metamorphic, and sedimentary rock assemblages. The MCBs were numbered in order of decreasing size. Of the 30 MCBs derived from the crustal boundaries, 22 are used in the present analysis as explained in Grunsky et al. (2017). In the present contribution, we introduce and implement a new method for modeling spatial uncertainty of Australian MCBs based on surface regolith geochemistry and for predicting MCBs in areas lacking/between geochemical samples. The most important log-contrasts for distinguishing crustal blocks are introduced and mapped for further geological discovery analysis.

Figure 1
figure 1

Sources: Blake and Kilgour (1998), Caritat and Cooper (2011), Korsch and Doublier (2016), Nakamura and Milligan (2015), Raymond (2012). Modified after Grunsky et al. (2017)

(a) Major crustal blocks of Australia (colored and numbered). The line styles of the MCB boundaries reflect the confidence level in their position/existence (solid thick: high; solid thin: moderate; dashed: low; dot dashed: none). (b) Surface geology and the geological regions of Australia. The NGSA sample site locations are shown as black dots on both maps.

Full size image

Results and Discussion

Input data (1067 compositional samples with 52 variables, 50 elements (Al, As, Au, Ba, Be, Bi, Ca, Ce, Co, Cr, Cs, Cu, Dy, Er, Eu, F, FeT, Ga, Gd, Ge, Hf, Ho, K, La, Lu, Mg, Mn, Na, Nb, Nd, Ni, P, Pb, Pr, Rb, Sc, Se, Si, Sm, Sn, Sr, Tb, Th, Ti, U, V, Y, Yb, Zn, Zr) plus LOI and filler) were transformed to real space via an ilr transformation (Eq. 4). As the ilr-transformed data were not multivariate normal, a transformation to normal space was needed prior to geostatistical simulation. The ilr-transformed scores were transformed to multivariate normal space via flow anamorphosis. Due to the complexity of the data and the number of variables, multivariate normality was not achieved by a single FA. Two successive FA with the same parameters \( (\sigma_{0} = 0.1 \) and \( \sigma_{1} = 1.1) \) were required to achieve multivariate normality. Spatial structural analysis (variography) showed further that the multivariate normal scores are spatially orthogonal, with Tercan’s (1999) \( \bar{\tau } \) and \( \bar{\kappa } \) equal to 0.0954 and 0.9073, respectively, so they could be simulated independently. The scores were simulated independently on a regular grid (25 km × 25 km) via a turning bands algorithm and back-transformed to compositions afterward. In total, 100 realizations of geochemical compositions were generated at unsampled locations. To illustrate the simulated model, the spatial distributions of three major elements (out of 52 jointly simulated variables), Ca, total Fe, and Mg, are depicted in Figure 2. The expected maps were calculated via Eq. 6. Figure 3 shows the map of the conditional total compositional variations for the simulated compositions. This map can be considered as a means of assessing spatial uncertainty of the geochemical compositions. Close to sample locations where direct information is available variation is low, while in areas where no sample was taken, variation is high. Some MCBs generally show higher uncertainty than others, for instance, MCB 06 shows less uncertainty than MCB 01 or southern parts of MCB 04 show higher uncertainty than its northern parts.

Figure 2
figure 2

Input geochemical compositions, two realizations of the geostatistical simulation procedure and expected map for three major components Ca, total Fe, and Mg (warm colors are associated with high values)

Full size image
Figure 3
figure 3

Conditional total compositional variation, a means to assess the spatial uncertainty of the geochemical compositions (warm colors are associated with high uncertainty, and black dots are the location of samples)

Full size image

The RF predictive model was trained based on the input labeled log-ratios. In this case, only pairwise (1326 log-ratios) and centered log-ratios (52 log-ratios) were used as predictors and MCBs as the categorical response variable. Out of 30 MCBs, 8 were not considered due to an insufficient number of sample sites in each of these MCBs (Grunsky et al. 2017). Algorithm 2 was used to select the most informative subset of log-ratios for the classification purpose. The final predictive RF with the highest accuracy was associated with a subset of only 220 log-ratios (Fig. 4). Figure 5 shows the top 30 (out of 220 selected log-ratios) most informative log-ratios for classification of MCBs. To determine the most significant log-ratios for discriminating a crustal block of interest from the remaining blocks, a binary response variable can be defined (e.g., 1 is the block of interest and 0 is all other blocks) and Algorithm 2 can be run again.

Figure 4
figure 4

Recursive feature elimination with resampling to identify the most important subset of log-ratios

Full size image
Figure 5
figure 5

Top 30 most informative log-ratios for classification of all MCBs (the significance of selected log-ratios is decreasing from the top to bottom of the chart)

Full size image

Table 2 shows the top five most important log-ratios (from left to right) for each MCB of interest. For example, for MCB 01 and MCB 02, pwlr(Eu/Na) and pwlr(Th/Ti) are the most significant predictors, respectively. The simulated model for these two log-ratios is depicted in Figure 6. High values (warm colors) of pwlr(Eu/Na) and low values (cool colors) of pwlr(Th/Ti) are associated with MCB 01 and MCB 02, respectively.

Table 2 Top five most important log-ratios (from left to right) associated with each MCB
Full size table
Figure 6
figure 6

Simulated models (two randomly selected realizations) and expected maps for the most significant log-ratios associated with MCBs 01 and 02 (warm colors are associated with high values)

Full size image

The trained RF was used to estimate the probability of occurrence of MCBs at unsampled locations using pwlr and clr of simulated compositions as input predictors. For each location \( u \) of the study area and each MCB \( k \), 100 probabilities were simulated. Maps of minimum, expected (Eq. 9), and maximum estimated probabilities are shown in Figure 7 for MCBs 01–04. Figure 8 shows conditional total variation in simulated MCBs calculated via Eq. 10. Areas close to geochemical samples show lower uncertainty. MCBs 01, 02, and 10 show higher uncertainty than the other MCBs while MCBs 03, 06, 13, and 22 show low uncertainty. Finally, Figure 9 shows the most probable MCBs calculated via the proposed method. The predicted crustal blocks are broadly consistent with the known MCBs (continuous black lines in Fig. 9). Discrepancies may be due to uncertain initial definition of crustal boundaries (e.g., due to ambiguity of geophysical data) or from surficial processes (e.g., chemical weathering and/or physical transport effects) that mask/shift the crustal block geochemical signature (see discussion in Grunsky et al. (2017)). In conclusion, the architecture of the MCBs of Australia can be predicted accurately from geochemical composition of the Australian surface regolith. These results can be used further for managing projects such as mineral exploration, environmental and ecological planning, and efficient usage of water resources.

Figure 7
figure 7

Maps of minimum (first column), expected (middle column), and maximum (last column) probability of occurrence for MCBs 01–04

Full size image
Figure 8
figure 8

Conditional total variation in all simulated MCBs (warm colors show high values)

Full size image
Figure 9
figure 9

Map of most probable MCBs

Full size image

Post-glacial Deposits Exploration for Environmental Monitoring

In this study, regional-scale soil geochemical dataset (obtained as part of the Tellus Project generated by the Geological Survey of Northern Ireland) is analyzed to explore the relationship between soil geochemistry and post-glacial deposits (e.g., surficial peat deposits) for environmental monitoring of this fragile ecosystem. Superficial deposits (e.g., glacial till, post-glacial alluvium, and peat) in this area have been created due to the advance of ice sheets and their meltwaters over the last 100,000 years (Fig. 10). Accurate mapping of peat-covered areas has become important because of the relatively high carbon density of peat and organic-rich soils.

Figure 10
figure 10

Adapted from McKinley et al. (2018)

Post-glacial peat-covered areas.

Full size image

Dataset

The Northern Ireland Tellus Survey (GSNI 2007; Young and Donald 2013) consists of 6862 rural soil samples (X-ray fluorescence (XRF) analyses). Geochemical samples presented in this study were collected at 20 cm depth, with average spatial coverage of one sample site every 2 km2. Each soil sample site was assigned to the post-glacial peat-covered map (Fig. 10), resulting in spatial data for one binary response variable (presence or absence of peat) and 50 continuous geochemical variables (Ag, Al2O3, As, Ba, Bi, Br, CaO, Cd, Ce, Cl, Co, Cr, Cs, Cu, Fe2O3, Ga, Ge, Hf, I, K2O, La, MgO, MnO, Mo, Na2O, Nb, Nd, Ni, P2O5, Pb, Rb, SO3, Sb, Sc, Se, SiO2, Sm, Sn, Sr, Th, TiO2, Tl, U, V, W, Y, Yb, Zn, Zr, and filler which includes Loss on Ignition (LOI)). More information on Tellus Survey field methods and analytical methodology are available in Smyth (2007) and Young and Donald (2013).

Results and Discussion

Input data were transformed to real space via ilr transformation (Eq. 4) and subsequently to multivariate normal space via flow anamorphosis. Two successive FA with the same parameters \( (\sigma_{0} = 0.1 \) and \( \sigma_{1} = 1.1 \)) were required to achieve multivariate normality. The multivariate normal scores were simulated 100 times on a regular grid (1 km × 1 km) independently via the turning bands algorithm and back-transformed to compositions subsequently. Figure 11 shows the map of the conditional total compositional variations (spatial uncertainty of the geochemical compositions) calculated via Eq. 8. Outlines of the peat-covered areas are shown by black polygons. According to this map, geochemical compositions show higher variation close to peat deposits. This may represent random disturbances of the geochemical signal at very small spatial scale due to peat cover.

Figure 11
figure 11

Conditional total compositional variation (warm colors are associated with high values, and black polygons are peat-covered areas)

Full size image

The pairwise log-ratios (1225 log-ratios) and centered log-ratios (50 log-ratios) were used as predictors and peat/non-peat as the binary response variable to train a RF predictive model. The most informative subset of log-ratios for discrimination of peat-covered areas was selected using Algorithm 2. The final predictive RF with the highest accuracy was associated with a subset of only 150 log-ratios (Fig. 12). Figure 13 shows the top 30 most significant log-ratios for discrimination of peat-covered areas. Figure 14 shows the spatial distribution (two randomly selected realizations and the expected map) of the most informative log-ratio, pwlr (Y/filler), where a coincidence between low values (cool colors) of this log-ratio and peat-covered areas is clear. The most informative log-ratios, e.g., pwlr (Y/filler), include the presence of LOI in the filler variable. This supports the previously known association between peat cover and LOI.

Figure 12
figure 12

Recursive feature elimination with resampling to identify the most important subset of log-ratios (Northern Ireland Tellus Survey data)

Full size image
Figure 13
figure 13

Top 30 most informative log-ratios for discrimination of peat-covered areas (the significance of selected log-ratios is decreasing from the top to bottom of the chart)

Full size image
Figure 14
figure 14

Simulated model (two randomly selected realizations) and expected map of the most significant log-ratio (pwlr (Y/filler)) for discrimination of peat-covered areas (warm colors are associated with high values, and black polygons are peat-covered areas)

Full size image

Finally the trained RF was used to predict the probability of occurrence of peat-covered areas at unsampled locations. Maps of minimum, expected (Eq. 9), and maximum estimated probabilities of peat-covered areas are shown in Figure 15 which demonstrate good consistency with the reported peat areas (Fig. 10). Figure 16 shows conditional total variation in predicted peat-covered areas calculated via Eq. 10. Areas close to peat deposits show higher uncertainty. Figure 17 shows the most probable peat-covered areas calculated via the proposed method. Although Figures 15 and 17 show good match with the reported peat-covered areas, inconsistencies may be due to uncertain initial definition of peat-covered areas (Fig. 10) and/or degradation of peat-covered areas since the creation of the superficial deposit classification that masks the peat geochemical signature. Peat-covered areas include upland blanket bog which is more extensive and spatially coherent and lowland ‘raised bogs’ which are smaller more fragile ecosystems. Using the proposed spatial predictive model, the locations of the main upland blanket peat-covered areas have been predicted accurately from geochemical composition of the Northern Ireland Tellus Survey. The association of LOI with peat-covered areas helps to explain the most informative log-ratios, e.g., pwlr (Y/filler). However, the approach has also identified the presence of potentially important marker elements (Y, Ag, and Sn) which may have accumulated in peat which acts as a sink for toxic elements. The results can be used further for managing projects such as environmental and ecological planning. As the underlying geology and spatial distribution of soil types across Northern Ireland are similar to the UK (Jordan et al. 2001) and Northern Europe in general, the proposed techniques in this study can be applied on those areas.

Figure 15
figure 15

Maps of minimum, expected, and maximum probability of occurrence for peat-covered areas

Full size image
Figure 16
figure 16

Conditional total variation in simulated peat-covered areas (warm colors are associated with high values, and black polygons are peat-covered areas)

Full size image
Figure 17
figure 17

Map of the most probable peat-covered areas (shown by red color)

Full size image

Conclusions

This study introduces a novel approach for the spatial modeling of uncertainty and prediction of geological classes using geochemical compositions. The approach is based on the combined use of advanced geostatistical simulation for compositional data (geostatistical simulation using isometric log-ratio transformation and flow anamorphosis) and a random forest predictive model. Due to the high-dimensional characteristics of log-ratios, recursive feature elimination with resampling technique was used to select the most significant log-ratios for the classification purpose. Such a feature selection technique is known to lead to a more stable and accurate predictive model and can be used further as an exploratory data analysis tool for geological process discoveries. The proposed approach was applied on two case studies. In the first case study, the major crustal blocks of the Australian continent were predicted from the surface regolith geochemical compositions while in the second case study the spatial distribution of superficial deposits (peat) was predicted from regional-scale soil geochemical data of Northern Ireland (Tellus Project). The accuracy of the results in these two case studies confirmed the usefulness and applicability of the proposed method.