Introduction 

The remarkable electrical and thermal properties of graphene [1] have drawn a lot of interest to next-generation graphene-based materials since the discovery of exfoliated graphene. According to Balandin et al. [2] and Akaishi et al. [3], these materials are expected to be used in a variety of applications, including thermoelectric devices and semiconducting devices. To create practical applications, it is important to comprehend how these materials bind to water in ambient air hypothesis that graphene is hydrophobic has since been disproved by additional experimental findings. Graphitic surfaces with experimentally established hydrophobicity are partially caused by contamination of the surface by airborne particles [4, 5]. However, later studies revealed that the hydrophilicity of graphene surface has a profound impact on the interactions between graphene and water. For instance, the purest form of monolayer graphene is thought to be hydrophilic, but as the number of layers grows, the graphene becomes more hydrophobic. Because graphene is two-dimensional and hydrophobic [6], it must be put on a substrate for most applications. Graphene is only partially transparent to the wetting characteristics of the underlying substrate as demonstrated in [7]. As a result, graphene’s wetting transparency is compromised when it is applied to superhydrophobic. Changes in the local carrier concentration and work function can significantly alter the wetting characteristics and, consequently, the water adsorption of graphene when only a few layers (i.e., 1–3 LG) are involved. Given that water is the most prevalent dipolar adsorbate in ambient circumstances and that graphene thickness often varies, it is essential to consider how water molecules interact with various thickness domains and how charge transfer is controlled by various substrates.

Significant work has been put into understanding the water-graphene interaction up until this point through theoretical [8] and experimental studies of water on graphitic surfaces. This raises the issue of whether graphene surfaces are naturally hydrophilic or hydrophobic. A surface’s hydrophobicity or hydrophilicity is typically connected with how moist it is. This issue further extends to the development of studies in materials such as solar cells where lower production costs and increases in power conversion efficiency have always been the aims of research on solar cells. Around 90% of silicon is found as crystalline silicon.

The bulk of solar cells is produced via market-based methods, according to [9]. Due to the substantial expense incurred in manufacturing a highly efficient solar panel, the efficiency has achieved up to 22% of the solar panels currently on the market, with still between 14 and 16% in favor. It is imperative to keep in mind that most of the sun’s remaining energy is converted to heat in the solar cell [10], rather than electricity. The power conversion efficiency of the solar cell will suffer because of this rise in temperature, which will also shorten the cell’s lifespan and destroy it. This necessitates controlling the temperature of the solar cells by eliminating excess heat, and this issue has been thoroughly researched. A solar cell’s temperature can be decreased by up to 15 °C with the addition of a passively cooled heat sink, increasing the power production by roughly 7% [11]. One factor preventing heat from traveling between the surfaces of the heat sink and the solar cell is the inter-facial thermal resistance. The two adjacent surfaces’ tiny defects, which cause tiny air gaps between them, are the cause of this. Because air is known to be a rather poor thermal conductor, it would be a great idea to fill these air gaps with a material that has a substantially higher thermal conductivity [12]. This material, or paste, is referred to as a “thermal interface material” (TIM). Most of this research focuses on using top-notch fillers like graphene to improve the thermal conductivity of commercial TIMs that are already on the market.

Graphene is interesting for usage in a range of applications due to its unique properties. The high sensitivity of graphene to the local environment has shown to be both advantageous and detrimental for graphene-based devices like transistors and sensors, because the graphene resistance would alter due to humidity variations. Graphene and graphene oxide have also been demonstrated to be good materials for water desalination, opening the door to the availability of pure water in remote regions [13, 14]. Water interacts with graphene by changing its electrical properties [15]. Graphene is a conductor that can become exceedingly thin, transparent, flexible, and mechanically strong. Its conductivity can be altered over a broad range by either chemical doping or an electric field. The remarkable mobility of graphene is useful in high-frequency electrical applications [16]. Recent technological developments have made it possible to create large graphene sheets. Reference [17] used processes that are almost industrial to produce sheets that are 70 cm wide. Since graphene is a transparent conductor, it can replace the more fragile and expensive indium-tin oxide in technologies like solar cells, touch screens, and light panels (ITO).

The goal of this research is to understand the inter-molecular interactions between water confined in-between graphene sheets, using computational modeling techniques based on both inter-atomic potentials and analytical methods, to further explore the viability of the graphene-water interface materials for use in developing solar cells.

Materials and methods

System modeling and simulation

To elucidate the interaction of graphene with water, Melios et al. [18] reviewed recent theoretical and experimental advances, particularly in modeling of water-graphene interaction and the effects of water on the local and global electronic properties of graphene. The atomistic system that describes the graphene-water interaction was designed using the Lennard–Jones potential and the Coulombic force field, in LAMMPS (large-scale atomic molecular massively parallel simulator) which helps in describing the kinetics at different perturbation levels of the system during the compression process, most importantly without negating its thermodynamic parameters. The MD software used to develop the system is called LAMMPS [19] which is used to model atoms and design mesoscopic systems; it has potentials for solid-state materials (semiconductors) and soft-matter systems (biomolecules and polymers). This software requires parameter files and data files that contain the electronic configuration of the system; the parameter file was developed using MATLAB scripts. The use of other Python libraries was employed to explore the concept of the system; these included DFTB (PYBINDING) [20] and materials project (PYMATGEN) [21].

Molecular dynamics of the system

The molecular dynamics (MD) structure employed in this study closely follows the work of Ranathunga et al. [21]. However, in this study, we carry out MD simulations on water molecules confined between graphene slabs/walls (consisting of 3 layers) above and below. The system consists of approximately 7751 atoms, with run steps of 7000. The TIP4P2005 four-point rigid water model was selected because it extends the transition of the TIP3P model by increasing the sites which are usually mass-less, where the charges associated with the oxygen atoms are placed. This site M is located at a fixed distance part from the HO-H bond angle, which mostly has a bond style of harmonics. This investigation uses the cut-off long-range model and Coulombic solver in order to understand the FFT-based particle–particle meshing, which is crucial in accurately modeling the compression activity.

Simulation details

In this simulation, the PBC (periodic boundary conditions) were applied in the three coordinates and the Verlet algorithm which is a popular algorithm (numerical methods used to integrate the equations of motion) with a time step of 0.1 fs. The Lennard–Jones interactions were then truncated at 8 Å, and the long-range electrostatics were treated with the particle–particle and particle-mesh (PPM) solver with a k-space cut-off of 12 Å. Using a NVE thermostat, the temperature of the system was kept at 300 K, for a fixed number of water molecules. We designed the initial structure for free-energy calculations extracted from equilibrium ensemble created by several iterations of running the MD simulations.

The velocities of the water molecules were estimated at an initial run, at a Boltzmann distribution of 350 K, the system also comprises special bonds, which include angles and dihedrals, which describe the presence of the carbon atoms in the system. The interaction of the carbon and water molecules is initiated by shaking the system using the FIX SHAKE command which applies the bond and angle constraints to the specified special bonds in the simulation. Since the water molecules were confined in between the carbon walls (top and bottom), each simulation was run until more than 85% of the system has undergone relaxation. The corresponding log and output file usually a dump (dummp.lammpstrj) file is generated using some internal system setting commands in the LAMMPS input script. Furthermore, the data from the log file is extracted using a Python script to obtain all specified parameters such as the total energy and kinetic energy into a csv file which can easily be read for further exploratory data analysis using Python to give both analytical and descriptive insight to the system. The dump file which contains the inherent system model is then visualized using OVITO software [22], and a few analyses were made. In order to have a holistic view of this investigation, another software was used to simulate the system; these are PYMATGEN and PYBINDING. PYMATGEN is a python package developed by the materials project, which is an open-source library for materials analysis. It was used to analyze the carbon–water interaction using the phase and Pourbaix diagram to determine the stability of the system. PYBINDING which is a Python library used for numerical tight-binding calculations in solid-state physics is employed to understand the interaction of the system at its fundamental level, from the perspective of the crystal lattice structure and geometry of the graphene walls. The energy parameters were obtained from the simulation, and time-averaged steps are recorded as a function of the z-direction during the simulation at a constant temperature, which has a large influence on the graphene surface. The total interaction of energies between the dynamic confines of the region and the carbon atoms is then computed with time. From the simulation data, the time steps averaged the total energy interactions of the system, which is then used in plotting other systems’ parameters.

Results and discussion

The results obtained from the analysis of the data extracted from the LAMMPS run, using exploratory data analysis methods with Python and the visualization of the structure using the open-source OVITO software [23], to describe the kinematic positioning of atoms in the system and analysis were made using Voronoi and coordination modifiers. Also, outputs from the PYBINDING and PYMATGEN libraries which describe the system both in electronic and analytical scale modeling are presented in this section. The 3D presentation of the simulation results has been recorded in an.avi format movie as a supplemental information file.

OVITO visualization and modification

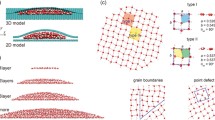
Studying the rate of interacting fixed water molecules confined between two graphene slabs at a constant temperature, it can be observed that the compression process is an ostensible homogeneous nucleation process, which occurs at frequent shifts in the sites of the water molecules. On a subatomic scale, a wide range of behaviors is formed at different extremes of the system. Figure 1 describes the system when it is unperturbed and where the free surface energy of the system exerts a force on the system, which causes the graphene walls to quasi-statically act on the water molecules, therefore causing the graphene surface characteristics to be hydrophobic.

Fig. 1
figure 1

Snapshots of the system configuration, where the non-perturbed water molecules are confined between two graphene walls/sheets with thickness of 1.725 nm and at constant temperature and pressure. The coloring is as follows: oxygen is in red; hydrogen is blue; and the carbon atoms (graphene) are green

Full size image

Figure 2 explains the quasi-static behavior of the system, where the external force is acting on the graphene slab, causing it to exert pressure on the system thus exciting the water molecules to interact with the carbon atoms.

Fig. 2
figure 2

Quasi-static interaction of water molecules at different sites on the graphene surfaces (constrained walls), due to the Van der Waals force present in the system at 41 (ns)

Full size image

Since homogeneous nucleation occurs in the system, the water molecules at different sites can collide with the graphene surface. Figure 3 describes the system fully perturbed, due to the increase in pressure on the system, thus increasing the kinetic energy present in the system, causing the randomness effect at 56 (ns) in the simulation; the ability of the system to return to a relaxation state is dependent on the strong electrostatic force present at the graphene surface. The total energy versus the Van der Waals energy of the system is negligible for mono or 2 layers of graphene, and the water molecules confined do not show much logical and traceable interaction due to the inter-molecular bonds and small size of forces of interaction. Secondly, monolayer graphene is thought to be hydrophilic, but as the number of layers grows, the graphene becomes more hydrophobic.

Fig. 3
figure 3

Summary of the system fully perturbed, where the water molecules start interacting with the carbon atoms, at a denser kinetic ratio, at a simulation time of 56 (ns)

Full size image

The OVITO simulation majorly describes the behavior of the system from its initial to final inter-atomic kinetics and the forces that influence the distance, intra-atomic bonds, and strengths of the system, where the non-bond interactions of C-O are lower in ratio to the C-H bonding at a constant temperature of 300 K, where no additional forces were applied to the water molecules. Figure 4 describes the Voronoi tessellation analysis of the system in 3D, showing the inter-atomic particle correlation pattern and geometry of the system in accordance with the nearest neighbor atoms. In order to further analyze the system and the way its constituent colloidal particles are arranged, the Voronoi analysis modifier in OVITO was used. Describing the system uses the nearest-neighbor particle approaches such as C–C, C-H, H–O, and C-O bonding. It uses geometric and topological features to explain the system’s important structural information about the spatial arrangements of the particles, both at micro and macroscopic levels. The analysis was done at a time step of 7 ns, using an absolute face area threshold of seven and a relative face area threshold of 2%.

Fig. 4
figure 4

Snapshot of the Voronoi tessellation of the system in 3D, showing the interatomic particle correlation and arrangement of the system at 7 ns

Full size image

We calculated the Radial Distribution Function (RDF) of the system to calculate the distance between all particle pairs from the center reference atom (not shown here). It further describes the radius particle function, which takes into consideration the radii of the particles which is independent of the particle sizes. RDF describes the probability of finding any of the particles (O, H, C) at a relative distance to each other, thus describing how water molecules follow the hard sphere model of repulsion; since water molecules experience strong hydrogen bonding and electrostatic interactions, it has a lower coordination number of four in the first sphere and gets peaky for the first coordination at 300 K and 1.8 ATM pressure under the periodic boundary conditions. The atomic arrangements of the constituent elements were calculated and showed that during the interaction there is a total change in the system structure; it is observed that the constituent structures in the system are neither BCC nor FCC nor any other structure in the OVITO database of structures. Graphene is a honeycomb dimensional structure that is closely arranged, with a hexagonal geometry; likewise, water structure is not present thereby classifying both under others. The results for the extracted data from the extracted LAMMPS log file have been analyzed using Python scripts.

LAMMPS data analysis

Using analytical methods to evaluate the data obtained from the LAMMPS parameters, Fig. 5a describes the correlation between the temperature and the increasing time steps of the system from initialization. It shows the relationship between the temperatures of the system at initialization; it is observed that there is a spike at time step 500, where the work done in compressing the water molecules increases the internal energy of the system, hence starts decaying from step 2000 as the thermal energy has been dissipated in the system. Since water molecules reduce the force field by arranging their positive (H’s) and negative (O’s) charges line up in the sites, thus making the compressibility of water low; it then requires a lot of energy to overcome the cohesive forces. Figure 5b describes the steady-state characteristics of the system due to the influence of the total energies contained in the system where the total energy in the system between a steady state through to 5.1 × 106 (kcal/mole), with a rapid increase at 3.9 × 106 (kcal/mole) due to the induced dipoles in the energy function. Since the predominant bond in the system is the hydrogen-bond network since water (H2O) is a complex substance with a variety of unusual properties, it is important to determine its Van der Waals interaction term in the molecular mechanical force field and its correlation with the electrostatic energy term.

Fig. 5
figure 5

a Calculation iteration versus temperature of the system. During the simulation, the time step of 1.0 fs was used for 7000 steps. b Graph of total energy versus the Van der Waals energy of the system due to the inter-molecular bonds and forces of interaction

Full size image

The graphene slabs initiate the pressure and velocity in the system using the shake command in LAMMPS that turns on the energy of the system from its potential to kinetic state as seen in Fig. 6a which describes the transition of the energy in the system before compression from potential to kinetic energy due to the force acting on the slab, since temperature and pressure are core properties of any system. Figure 6b shows the direct linear relationship between the variables; when pressure increases, there is a corresponding increase in temperature as they are directly proportional. Also, one can get a sense of interaction between particles from Fig. 6b as it is giving information about the potential and kinetic energy between graphene and water. The more kinetic energy of particles in interacting with graphene means actually a more intense interaction between particles.

Fig. 6
figure 6

Summary of total energy in the system. a The correlation ratio of the total energy of the system versus the initialized time step process, considering each interaction. Also, the relationship between the potential and kinetic energy induced in the system by the interacting forces. b A plot of temperature vs. pressure of the system, in relation to the energy variation as the system develops through its stepwise process

Full size image

PYMATGEN modeling

It is therefore important to elucidate the stability phases of the multiphase constituent of the system, which is essential for systemic engineering development. The use of computationally driven insight using materials project (PYMATGEN) presents the results in Fig. 7a that describes the convex hull diagram of the system showing the lowest and highest energy states.

Fig. 7
figure 7

a The convex hull diagram shows the lowest and highest set of potential energy states that can be obtained from the system. b The phase diagram shows the stability of the elements against decomposition in the system

Full size image

Figure 7b shows the stable elements contained in the system and their bond formation, which shows the C–C-H2O interaction and found that H2O and CO2, which are stable structures, along the H2, O2, and H-C phases are also present in the convex hull. The black dots represent the stable structures present in the materials project structure database. It is also possible to further use the PYMATGEN tool to predict material structures.

PYBINDING structures

Using computational insights to also understand the surface state of the system, which is formed due to the interaction of the water molecules with the carbon atoms that are found closest to the surface, tight binding was applied to describe the electronic structure of the modeled system. Figure 8a uses tight-binding methods to model a similar system using constituent parameters, the use of a monolayer graphene sheet to describe the surface of the graphene structure before compression. Figure 8b describes the monolayer graphene during compression as it forms bond networks with the hydrogen and oxygen molecules.

Fig. 8
figure 8

a Describes a monolayer graphene structure before compression. b A model of the graphene monolayer structure under compression interacting with water molecules

Full size image

Figure 9 describes the surface characteristics of the modeled system, the water, and the graphene surface before and after the interaction. This figure shows the constituent graphene monolayer structure before compression rendered using the binding technique. The graphene-water interaction under compression and the surface interface interaction of the system has been illustrated in the 2D dimension.

Fig. 9
figure 9

A model of the graphene-water system surface interface

Full size image

In summary, it is important to understand how to investigate molecular interactions that occur in complex systems that have different physical properties, using different tools to compare their intrinsic behavior using specific features. The next section gives a general summary of this investigation.

Conclusions

In summary, this research has performed MD computational simulations to quantify and describe the role of confined water molecules between graphene slabs under compression, using potentials in LAMMPS to develop a well-defined system and to study their unique molecular behavior. The rate of water interaction with the graphene surface was studied using a fixed amount of water and at a constant temperature. The water interaction was linked to properties that were dependent on the interacting surface, compressibility, inter-facial thermal properties, and energy accumulation. During the simulation, the formation of different bonds and interface reactions were investigated. Understanding the prevalent bond in the system, which is the hydrogen bond network, provides insight into the reacting elements of the system and explained the stability and structural arrangement of water as a function of its surface chemistry. It was observed that the graphene surface exhibited a hydrophobic behavior, due to the weak interacting energies, water molecules that encounter the graphene surface tend to form different bonds, which serves as a potential homogeneous nucleation site. When the molecules are large enough, it is then captured by the graphene surface upon collision and assumed a hemispherical shape. Therefore, the repulsive interaction energy regions with the graphene structures indicate a solid/liquid-like interface which is caused by water molecules depleting at hydrophobic interfaces. Also, using computational modeling tools such as PYMATGEN and PYBINDING to describe the similar structure and system configurations at a microscopic level gives valuable insight into the working intermolecular mechanisms that help in developing more efficient materials. Taking all the results of this investigation into account, we can give a more holistic molecular-level insight into water confined under two graphene sheets using MD and computational modeling approach to design and evaluate the kinematics of the system under compression and its microscopic inter-facial characterization. The provided insight into the water and graphene behavior as a function of compressible force can be used to improve the design of solar cells that use graphene materials, for offshore co-location purposes.