1 Introduction

Electrically assisted bicycles are becoming increasingly popular around the world. More than two million electric bikes were sold 2021 in Germany alone. The market share of electric bicycles represented 43% of all bicycles sold that year [1]. A broad positioning in almost all market segments and the obvious advantages of electrical power favors the success of these bicycles. Such advantages involve, for instance, facilitating uphill and long distance rides. A large number of bike variants, in which the arrangement of the additional masses of motor and battery are implemented in different positions, can be found on the market. The influence of the additional weight on the riding characteristics is currently hardly considered during development although the answer to this question plays a decisive role. This applies to the stable and at the same time agile driving style preferred in sports as well as to the mobilization of a physically limited person. To facilitate the transition, the latter, for example, favors a drive characteristic closer to that of a conventional bicycle.

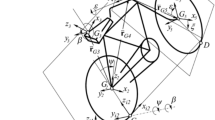
A commonly used model to represent the system behavior of bicycles in a multibody simulation (MBS) is the Carvallo–Whipple (CW) model, see Fig. 1 (left) for a schematic overview. This analytical model is able to represent the complex riding characteristics of a bicycle using four rigid bodies [2–4]. The system consists of a rear frame, a front frame as well as a front and a rear wheel. The degrees of freedom of the system are determined by the roll angle \(\phi \) and the steering angle \(\delta \). For a complete description of the CW model, 25 parameters are required. These define the centers of gravity, masses, and inertia tensors of all four rigid bodies. The system parameters used in this work to describe a bicycle without additional masses correspond to the data on the Gary Fisher bicycle [5]. The rider is also modeled as a rigid body and computed together with the body properties of the frame. The structure and parameterization of the rider model is presented in [6].

Fig. 1
figure 1

Bicycle model consisting of four rigid bodies [7] (left) and the qualitative course of the eigenvalues for the Carvallo–Whipple model (right)

Full size image

The system parameters can be used to set up the equations of motion and calculate its eigenvalues. The characteristic curve of the eigenvalues versus the driving velocity is shown in Fig. 1 (right). Modeling the system according to the CW model results in three eigenvalue progressions, which can be assigned to the characteristic motions, called eigenmodes. The first eigenmode is the “caster mode” and describes a rotational motion of the fork or handlebar. The motion is similar to the fluttering of a shopping-cart roller. The second eigenmode is the “weave mode”, which describes a serpentine ride due to an oscillating rolling and steering motion of the bicycle. The eigenvalues of this mode possess positive real parts for low velocities. From a speed of \(v_{\mathrm{weave}}\), the real parts have a negative sign. Also, with increasing speed, the damping of the weave mode increases. As this behavior plays an important role, the course of the imaginary part is displayed in Fig. 1 (right). The third eigenvalue describes a pure rolling motion of the bicycle without simultaneous change of the steering angle. Because of its similarity to a capsize motion of a ship, it is called “capsize mode”. This mode has a negative real part for low speeds, which changes from \(v_{\mathrm{capsize}}\) on to positive values. The consideration of the eigenvalues allows the subdivision into stable and unstable velocity ranges [7, 8]. An analysis of the driving characteristics of different electric bicycle variants using the eigenbehavior has already been published in [8]. In this investigation, the focus was placed on the beginning and the end of the inherently stable range.

To extend the model, a control system will be used. With this, the system can also be stabilized outside the inherently stable velocity range. The implementation of a driver who influences the system by active steering behavior is presented in [9]. The control system consists of three inner control loops for roll angle stabilization and two outer control loops used for path control, see Fig. 2. The individual control loops are based on visual, vestibular, and proprioceptive sensory perceptions of humans, which are used to detect orientation and position in space. The manipulated variable for controlling the MBS model is the steering torque \(T_{\delta} \). The gain factors within the control loops are determined prior to each simulation run depending on the bicycle parameters and the driving velocity. A more detailed description of the procedure is presented in [9, 10]. This ensures an optimal and comparable closed-loop behavior between different configurations of bicycle and velocity.

Fig. 2
figure 2

Overview of the control system according to [9, 10]

Full size image

First evaluation approaches of driving characteristics of electric bicycles already exist in the scientific literature [8]. This approach examines the influence of the electric drive components and their position on the driving behavior using the eigenvalues of the system. However, in this way only the uncontrolled system behavior is analyzed. In order to expand these investigations, virtual driving tests in open-loop (OL) and closed-loop (CL) test scenarios are presented in this work. In addition, it will be investigated whether the positioning of the drive components plays a decisive role in terms of the overall driving characteristics. The consideration of the driving behavior of an active driver in CL systems allows the analysis of the effects of different arrangement concepts on the driving behavior in more detail. This is reasonable because these investigations go beyond the uncontrolled system behavior. Thus, they are expected to better represent real driving situations. In order to evaluate these experiments, characteristic values are defined. They describe the system behavior in a simple and unambiguous way and allow to conclude about the stability and agility of the different setups of a bicycle. Based on this, the importance of electrical components on the driving behavior is determined. Therefore, the influence of the arrangement of additional masses is compared to the influence of different bicycle types and the rider’s posture.

2 Methodology

The arrangements of additional masses in modern e-bikes can be narrowed down to two positions of the battery and three positions of the motor [8, 11]. The position of the battery is either in the luggage racks, horizontally above the rear wheel or integrated in the down tube (Fig. 3, B1 and B2). The motor designs are defined by one motor in the front wheel hub M1, one motor in the bottom bracket M2, and one motor in the rear wheel hub M3 (Fig. 3). For comparison, the system behavior of a conventional bicycle without additional masses is examined (Fig. 3, C). For all driving tests, the kinematic dimensions are identical.

Fig. 3
figure 3

Sketch of the considered motor and battery positions and the corresponding labels

Full size image

To integrate additional masses into the CW model, the position of the center of gravity, the mass, and the inertia tensor of the respective motor or battery were determined. Representative data based on a market analysis of the dimensions and masses of the battery and motor were taken from [8] for each of the five components shown in Fig. 3. The mass inertia tensor as well as the center of gravity of the components were determined using CAD models with homogeneous density. Depending on the bicycle structure under investigation, the mass, the inertia tensor, and the center of gravity of the corresponding rigid bodies were modified in the CW model of the Gary Fisher bicycle. The integration of rider properties into the rear frame is done analogously.

For the analysis of the dynamic bicycle behavior, a controlled and uncontrolled straight-ahead driving is simulated for each bicycle design. After \(t = 1\text{ s}\), an excitation is applied to the system in the form of a steering torque impulse (STI) \(T_{\delta , \mathrm{{STI}}} \) with a duration of \(\Delta t_{\mathrm{STI}} = 0,2\text{ s}\). The applied torque can be described by a third degree polynomial with a maximum value of \(1\text{ Nm}\). The STI is identical for all performed experiments and can be stabilized by the control system in all performed CL experiments. A relatively low value for the STI was chosen to ensure the latter for all the driving speeds studied. This was done because the rider can only stabilize the bicycle by applying steering torque. Preliminary tests have shown that the system behavior and thus the significance of the investigations are unaffected by the magnitude of the excitation. The target values of the control system in the CL experiments were defined by the roll angle \(\phi _{\mathrm{target}} = 0^{\circ}\) and the lateral acceleration of the front wheel contact point \(\ddot{y}_{\mathrm{FW},\mathrm{target}} = 0 \text{ m}/\text{s}^{2}\). The driving tests are calculated over a period of \(t_{\mathrm{end}} = 40\text{ s}\) and a sample rate of \(1000\text{ Hz}\).

2.1 Driving dynamics characteristics in open-loop scenarios

For the evaluation and interpretation of the driving tests in OL scenarios, the eigenvalues as well as the analysis of virtual driving tests in OL simulations are used. The consideration of the eigenstable velocity range using \(v_{\mathrm{weave}} \) and \(v_{\mathrm{capsize}} \) provides a first insight into the system behavior. Furthermore, a characteristic value is used to evaluate the driving tests. This allows the extension of the evaluation with eigenvalues, as shown in Sect. 3.1. The use of the eigenvalues in combination with the characteristic value provides a simple and clear description of the system behavior and allows to draw conclusions about the driving characteristics. Also, this representation of the eigenbehavior allows comparison to the existing publications [8, 12].

The characteristic value used to evaluate the OL test scenarios is defined as \(K_{\ddot{\phi},\mathrm{OL}}\). It is used in [12] to describe the speed-dependent driving behavior in OL tests for conventional bicycles. \(K_{\ddot{\phi},\mathrm{OL}}\) describes the oscillatory behavior of the bicycle about the longitudinal axis through the magnitude ratio of the first and second extremes of the roll angle acceleration \(\ddot{\phi}_{\mathrm{E1}}\) and \(\ddot{\phi}_{\mathrm{E2}}\), see equation (1). Thus, a value below one represents an increasing oscillation and an unstable system. Values larger than one mark the beginning of the inherently stable velocity range at \(v_{\mathrm{weave}} \). The latter refers to a damped and consequently more stable system behavior according to [12].

$$ K_{\ddot{\phi} , \mathrm{OL}} = | \frac{ \ddot{\phi}_{\mathrm{E1}} }{\ddot{\phi}_{\mathrm{E2}}}| $$
(1)

In OL experiments, the system behavior is analyzed without external control. Hence, the system shows a free oscillation motion after an excitation. Accordingly, the characteristic value \(K_{\ddot{\phi} ,\mathrm{OL}} \) reflects the behavior that corresponds to the eigenvalues and the eigenbehavior of the system. In particular, the damping property of the weave mode is well represented by \(K_{\ddot{\phi} ,\mathrm{OL}} \).

2.2 Driving dynamics characteristics in closed-loop scenarios

The analysis of the driving characteristics in the CL is carried out on the basis of three characteristic values. These characteristic values are used to describe the vibration behavior as well as the steering effort required for stabilization. All characteristic values are aimed at a description of the system behavior that is as simple and unambiguous as possible.

In analogy to the evaluation of the OL tests, the description of the vibration behavior in CL tests is also based on two successive extrema of the roll angle acceleration. However, the superordinate roll angle curve of the bicycle in CL is superimposed with local, high frequency, interventions of the controller. The separation between the superordinate rolling motion of the bicycle \(\phi _{\mathrm{LP}}\) and the local interventions of the controller \(\phi \) can be achieved by means of a low-pass filter, as shown in Fig. 4. Therefore, the ratio of two successive extrema cannot be used to draw unambiguous conclusions about the superordinate course of the rolling motion and thus about the overall oscillation behavior of the bicycle during stabilization by the control loop. This applies to both the course of the angle and the resulting acceleration course.

Fig. 4
figure 4

Controller effects on the roll angle over time. In red the roll angle with local interventions of the controller is shown. The blue curve shows the low-pass filtered roll angle

Full size image

By using the low-pass filtered roll angle \(\phi _{\mathrm{LP}}\) and respectively \(\ddot{\phi}_{\mathrm{LP}}\), the bicycle behavior is described without the influence of local controller interventions. Therefore, with the help of the characteristic value \(K_{\ddot{\phi}, \mathrm{CL}}\), it is possible to make statements about which system is stabilized the fastest after a disturbance by an active driver. High values of the characteristic value are evaluated as positive for the driving dynamics, see equation (2).

$$ K_{\ddot{\phi} , \mathrm{CL}} = | \frac{ \ddot{\phi}_{\mathrm{E7}, \mathrm{LP}} }{\ddot{\phi}_{\mathrm{E8}, \mathrm{LP}}}| $$
(2)

In addition to the consideration of the vibration response through \(K_{\ddot{\phi} , \mathrm{CL}} \), the magnitude of the system response is analyzed using the characteristic value \(K_{\phi _{\mathrm{max}}, \mathrm{CL}} \). The calculation is performed using the magnitude of the maximum roll angle resulting from the STI in the closed-loop simulations, see equation (3). The investigation of the driving characteristics using this characteristic value outside the inherently stable speed range can only be used in CL test scenarios. This is due to the continuous increase of the roll angle in OL tests outside of the inherently stable speed range. With the help of this characteristic value, assumptions can be made about the stability, in the sense of the behavior due to the disturbance torque, along with the agility, in the sense of the performance on corner entry after a steering torque.

$$ K_{\phi _{\mathrm{max}}, \mathrm{CL}} = \mathrm{max}(| \phi |) $$
(3)

In addition to describing the vibration behavior with \(K_{\ddot{\phi} , \mathrm{CL}} \) and \(K_{\phi _{\mathrm{max}}, \mathrm{CL}} \), a third characteristic value is used to determine the steering effort required for stabilization. The characteristic value \(K_{T_{\delta}, \mathrm{CL}}\) is calculated from the amount of control torque accumulated over the simulation time from the control system, see equation (4). Low values of \(K_{T_{\delta}, \mathrm{CL}}\) are evaluated as positive since the bicycle can be stabilized with low effort.

$$ K_{T_{\delta}, \mathrm{CL}} = \int _{0}^{t_{\mathrm{end}}} |T_{\delta}| \,\mathrm{d}t $$
(4)

2.3 Design of experiments

Besides the investigation of the driving characteristics of different electric bicycle combinations, the question arises how relevant these influences are compared to other system properties. To answer this question, the influence of different bicycle types and rider postures on the driving dynamics are determined and compared to the effects of the electric bicycle design. The classification and evaluation is carried out with the aid of Design of Experiments (DOE) [13]. This allows the description of the effects resulting from the positioning of electric drive components on the system in a broader context. Based on this, conclusions are drawn about the importance of these influences on the design of bicycles as done in Sect. 3.3.

In general, statistical DOE is a method for planning and evaluating series of experiments. To apply this method, experiments are conducted with variations of the system parameters with respect to the characteristics. The parameters are called factors, and the characteristics, levels. The experimental design describes the number and type of experiments to be performed. With the help of a full factorial experimental design, the entire parameter space, i.e., all possible combinations of factors and individual levels, are examined. An example is shown in Fig. 5 (left) for three factors, A, B, and C, with two levels (+ and −) each. To evaluate the experiments, one or more responses are considered for each experiment. This is marked as y in Fig. 5 (left). The experimental data can be evaluated with the help of a so called description model, as shown in Fig. 5 (middle). The description model is set up depending on the number of factors and the number of levels. The description model shown in Fig. 5 (middle) is a linear model with four parameters \(\beta _{\mathrm{{i}}}\). The numerical values for the parameter vector \(\mathbf {\beta}\) can be determined with, for example, a least squares approach [13]. The response surface shows the average deviation from the mean value for a certain level, as shown in Fig. 5 (right). The greater the slope of the line in the response surface, the greater the effect of the factor on the response. It can also be seen whether the change between the level of a factor leads to an increase or decrease of the response. In this way, the effects of the individual factors on the system response can be determined [14].

Fig. 5
figure 5

Experimental design (left), approximation function (middle), and the effect diagram (right) [14]

Full size image

The screening tests for the identification of different parameter influences on the driving dynamics are carried out by means of a full factorial test plan. The factors investigated are defined as the rider posture, the type of bicycle, and the positioning of electric drive components (Table 1). The factor describing the electric bicycle design includes the conventional bicycle without additional mass and two designs with vastly different positions of battery and motor. The rider posture from [6], which can be described as upright (Table 1, high), is extended by two additional body positions. First a strongly inclined, sporty position is added as it is common on racing or track bikes (Table 1, low). Second, an ergonomic posture is considered, which is an intermediate position between the one in [6] and the low, athletic position. This reflects a slightly bent forward position on trekking or mountain bikes (Table 1, medium). Based on the data from [6, 15], the centers of gravity and inertia tensors of the additional body postures were determined. The factor of the bicycle describes three different bicycle types. Besides the already used Gary Fischer mountain bike model, a lightweight steel track bicycle (Bianchi Pista) and a heavy, long Dutch city bike (Batavus Browser) are studied (Table 1, Track and City). All model parameters of the bikes were taken from [5]. The positions of electric drive components are adjusted according to the different bicycle kinematics.

Table 1 Factors and levels for the design of the full factorial test plan in terms of the Design of Experiment
Full size table

For each of the individual simulations, carried out in regards to the full factorial test design, the test setup described in Sect. 2 is used. Furthermore, the gain factors of the control are recalculated individually for each simulation according to the procedure described in [9, 10]. The characteristic value \(K_{\ddot{\phi}, \mathrm{CL}}\) is used as the system response. The procedure of statistical design of experiments is applied separately for each speed. The number of used velocities and thus the number of independent DOE is \(n_{\mathrm{DOE}} = 8\). The used description model is a quadratic model, with \(n_{\mathrm{f}} = 3\), shown in equation (5). The parameter vector \(\mathbf {\beta}\) consists of ten entries. The parameters of the description model are obtained using a nonlinear regression function, using least squares estimation. The deviations between the results of the description model and the quality characteristics can therefore be demonstrated for each of the full factorial experimental designs using the Mean Squared Error (MSE). The lower the MSE, the better the significance of the DOE.

$$ y = \beta _{\mathrm{0}} + \sum _{\mathrm{i}=1}^{n_{\mathrm{f}}} \beta _{\mathrm{i}}x_{\mathrm{i}} + \sum _{\mathrm{i}=1}^{n_{ \mathrm{f}}-1} \sum _{\mathrm{j}=\mathrm{i}+1}^{n_{\mathrm{f}}} \beta _{\mathrm{ij}}x_{\mathrm{i}}x_{\mathrm{j}} + \sum _{\mathrm{i}=1}^{n_{ \mathrm{f}}} \beta _{\mathrm{ii}}x_{\mathrm{i}}^{2} $$
(5)

3 Results

In Sect. 3.1 and Sect. 3.2 the results of OL tests and CL tests are described. Here, the effects of motor and battery placement are shown for a given bicycle type and a given rider posture. The influence of motor and battery position on the driving characteristics is shown individually as well as in combination. Finally, in Sect. 3.3, the evaluation of the design of experiment is presented. Here, the influence of the arrangement of additional masses is studied in relation to the influences of different bicycle types and different rider postures.

3.1 Evaluation of the open-loop tests

For the analysis of driving characteristics based on the eigenvalues, the limits of the inherently stable speed range are calculated. These limits are defined by \(v_{\mathrm{weave}} \) and \(v_{\mathrm{capsize}} \). An inherently stable velocity range that occurs as early as possible and also lasts as long as possible is considered generally as positive for the driving characteristics. In Fig. 6, the inherently stable speed ranges for the Gary Fisher bicycle with different setups of motor and battery are shown. The bicycle parameters and driver posture are the same for all variations to isolate the effect of additional masses. It can be seen that the conventional bicycle C as well as the bicycle setup with the motor in the bottom bracket M2 reach the inherently stable speed range first. The combination with the motor in the front M1 hub reaches the inherently stable speed range last. For the bike with the battery in the down tube B2 as well as the setup with the motor in the bottom bracket M2, this range lasts the longest. However, the difference in driving characteristics is not significant, with less than \(5\%\) difference between the eigenvalues of \(v_{\mathrm{weave}} \) as well as \(v_{\mathrm{capsize}} \).

Fig. 6
figure 6

Inherently stable speed range for different arrangements of motor and battery

Full size image

In Fig. 7, the characteristic value \(K_{\ddot{\phi},\mathrm{OL}} \) is plotted versus the driving velocity. \(K_{\ddot{\phi},\mathrm{OL}} \) displays the damping of the bicycle oscillation around the longitudinal axis in OL-tests. This representation of the eigenbehavior allows a more detailed analysis. In addition to reaching the inherently stable speed range at \(K_{\ddot{\phi},\mathrm{OL}} = 1 \), the course of the roll and capsize motion can also be determined. The S-shaped course of the characteristic value shows a characteristic increase with the beginning of the inherently stable speed range. After exceeding \(v_{\mathrm{capsize}} \), the curves flatten significantly. This can be explained by the continuous roll acceleration due to the capsize mode, which leads to a superposition of the stable weave mode and the unstable capsize motion for speeds greater than \(v_{\mathrm{capsize}}\). As \(K_{\ddot{\phi},\mathrm{OL}} \) represents the oscillation damping, the combination of the continuous roll angle acceleration of the capsize mode with the decreasing oscillation of the weave mode leads to a flattening of the curve in Fig. 7.

Fig. 7
figure 7

Characteristic curve of \(K_{\ddot{\phi},\mathrm{OL}} \) for individual components (left) and combinations of battery and motor (right)

Full size image

The bicycle with the motor in the front wheel hub M1 clearly stands out from the courses compared to other bicycles. Below \(v = 6,5\text{ m}/\text{s}\), this bicycle combination has the lowest value for \(K_{\ddot{\phi}, \mathrm{OL}} \). This can be interpreted as a high amplification of the oscillating roll motion for speeds lower than \(v_{\mathrm{weave}}\) or a low damping of the oscillating rolling motion after exceeding \(v_{\mathrm{weave}}\). However, for high speeds, the characteristic value increases to more than twice than some of other bicycles. As a result of the increased mass and inertia at the front axis for the front wheel motor M1, the gyroscopic effect of the front wheel increases for higher driving speeds. This leads to an increased damping of the weave mode and thus to an increase in the stability of the bicycle M1 [16].

The consideration of different bicycle setups with a combination of battery and motor arrangements, shown in Fig. 7 (right), indicates that this combination also leads to a combination of the driving characteristics. In general, the results of the OL tests show only a minor influence of the battery and motor on the position of the inherently stable velocity range, see Fig. 6. Yet, the effects on the vibration behavior can be clearly seen, see Fig. 7. Here, the motor arrangement shows a significantly greater influence on the driving behavior than the position of the battery. Moreover, the obtained results of OL tests are in agreement with [8].

3.2 Evaluation of the closed-loop tests

The evaluation of the CL tests allows an extended analysis of the driving behavior. In contrast to the OL tests, not only the intrinsic behavior but also the system behavior is described taking into account an active driver.

The oscillation course around the longitudinal axis in the CL tests is shown in Fig. 8, displaying the characteristic value \(K_{\ddot{\phi},\mathrm{CL}} \) as a function of the driving speed. All bicycles show a monotonically increasing curve as well as a decaying oscillatory behavior, even in the lower speed range. In accordance with Fig. 7, an increase in the characteristic value can be seen in the beginning of the inherently stable system behavior. However, in the controlled driving tests the course does not flatten out with increasing speed. On the one hand, this can be attributed to the increasing damping of the weave mode. On the other hand, the monotonic capsize motion of the capsize mode is effectively compensated by the control loop. This leads to the conclusion that the capsize mode has only a subordinate role in the stabilization of bicycle systems.

Fig. 8
figure 8

Characteristic curve of \(K_{\ddot{\phi},\mathrm{CL}} \) for individual components (left) and combinations of battery and motor (right)

Full size image

The conventional bicycle C and the bicycle with the motor in the rear hub M3 show the highest increase of the characteristic value \(K_{\ddot{\phi},\mathrm{CL}} \) and thus the fastest decrease of the oscillating rolling motion in CL simulations. In contrast to this, these combinations showed the lowest oscillation decrease in OL tests. This indicates the best controllability in terms of system stabilization. The bicycle with the motor in the front hub M1 shows the lowest vibration decrease across all speeds in the CL tests. In addition, the offset to the values of the other bicycle combinations increases with increasing speed. This can be explained by the gyroscopic torque increasing with higher speed and thus counteracting the steering torque applied by the controller. The controllability in terms of system stabilization is increasingly degraded for the bicycle with the motor in the front wheel hub M1 as speed increases. The consideration of the driving tests with different combinations of motor and battery shows that only the electric bicycles with masses in the rear bicycle area exhibit better controllability than the conventional bicycle C (Fig. 8, right). The riding characteristics with the motor in the bottom bracket M2 are similar to a conventional one, but the control system needs longer to stabilize the motion induced by the external excitation.

Further insight into the vibration behavior is provided by the characteristic value \(K_{\phi _{\mathrm{max}},\mathrm{CL}}\), which represents the largest occurring value of the roll angle for the respective velocity. The curve is plotted as a function of the driving speed, shown in Fig. 9. The curve shows irregular maximum roll angles for speeds below the inherently stable range. With the beginning of the inherently stable velocity range above \(v_{\mathrm{weave}}\), the values of \(K_{\phi _{\mathrm{max}},\mathrm{CL}}\) decrease monotonically. The order of the bicycle setups here is similar to those of \(K_{\ddot{\phi},\mathrm{CL}} \), shown in Fig. 8.

Fig. 9
figure 9

Characteristic curve of \(K_{\phi _{\mathrm{max}},\mathrm{CL}} \) for individual components (left) and combinations of battery and motor (right)

Full size image

The conventional bicycle as well as the bicycle with the motor in the rear wheel hub M3 show a high response to steering torques. On the one hand, high responsiveness can be interpreted as increased agility. On the other hand, high responsiveness leads to more unstable behavior in the presence of external excitations. However, the latter can be compensated more quickly by an active driver due to higher sensitivity. The difference between the maximum roll angle of the bicycle with the motor in the front wheel hub M1 and other simulation results can be explained by the increased inertia in the steering axle due to the additional motor mass. This leads to smaller steering angles as a result of the STI and consequently to smaller maximum roll angles. The study of the driving tests with different combinations of motor and battery shows that the maximum roll angle of each electric bicycle is below the maximum roll angle of a conventional bicycle C due to the presence of a battery.

In Fig. 10 the steering torque of the controller required for stabilization is displayed. The characteristic value \(K_{T_{\delta},\mathrm{CL}} \) is plotted as a function of the driving velocity. \(K_{T_{\delta},\mathrm{CL}} \) shows a monotonically decreasing course with increasing velocity. For speeds below \(v_{\mathrm{weave}} \), a particularly high steering effort for stabilization is observed. This can be explained by the amplification of oscillation as a result of the unstable weave mode in this speed range. \(K_{T_{\delta},\mathrm{CL}} \) shows a dependency on the controllability (\(K_{\ddot{\phi},\mathrm{CL}} \)) and the magnitude of the maximum roll angle (\(K_{\phi _{\mathrm{max}},\mathrm{CL}} \)). In general, all bicycle setups except for the combination with the motor in the front hub M1 show little variation in steering effort. The bicycle with the motor in the front hub M1 has the lowest steering effort for low speeds. This is explained by the low maximum roll angle. In contrast, this bicycle has the highest steering effort for high speeds. This can be attributed to the poor controllability as a consequence of the high gyroscopic torque despite the low maximum roll angle.

Fig. 10
figure 10

Characteristic curve of \(K_{T_{\delta},\mathrm{CL}} \) for individual components (left) and combinations of battery and motor (right)

Full size image

3.3 Evaluation of the design of experiments

The results of the screening tests are presented in the following. After analyzing the influence of additional masses for a given bicycle, the analysis is extended to other system changes. This is done by setting the influence of the motor and battery positioning in relation to changes in the type of bicycle and driver posture. Figure 11 shows the effect of the respective levels of each factor at different speeds on the characteristic value \(K_{\ddot{\phi},\mathrm{CL}}\). In addition to the response surface, the determined MSE for each speed is presented in Fig. 11, right. It can be seen that all deviations of the fit are several orders of magnitude smaller than those of the characteristic value \(K_{\ddot{\phi},\mathrm{CL}}\). Averaged over all experiments performed, the average mean squared error is \(\overline{\mathrm{MSE}} = 3.8 \cdot 10^{-3}\).

Fig. 11
figure 11

Evaluation for the design of experiment for different driving speeds. Bicycle type (left), rider positions (middle), eBike design (right), and the mean squared error for each DOE performed (right)

Full size image

In general, it can be seen that as the speed increases, the influence of different bicycle and eBike designs on the response value \(K_{\ddot{\phi},\mathrm{CL}}\) increases. At high speeds, the driver position is most influential, with a more upright posture resulting in easier system controllability. In the medium speed range, the influence of additional masses on the characteristic value is strongest. As already seen in the preliminary tests, the combination B1 + M3 shows a very similar behavior to the conventional bicycle. On the other hand, the combination B2 + M1 generally leads to lower values of \(K_{\ddot{\phi},\mathrm{CL}}\). This can be attributed to the effects of the motor in the front wheel hub M1. For low speeds, the rider position again shows the highest influence on the riding dynamics. In contrast to high speeds, the upright posture shows the lowest values of \(K_{\ddot{\phi},\mathrm{CL}}\). Although the type of bicycle does not have the highest influence for any speed, it is still not negligible. As seen in Fig. 11 on the left, the mountain bike can be stabilized the slowest by an active rider. In general, the influence of additional masses is significant. Especially at medium speeds, as it is common in everyday use, the positioning of drive components plays a decisive role for the driving dynamics of the bicycle.

4 Conclusion

The analysis of bicycles with electric drive components presented in this paper enables a significant extension of the studies of electric bicycle driving behavior by using closed-loop (CL) simulations. It is shown that the stability behavior determined in open-loop (OL) tests presents a partially opposite behavior in comparison to CL simulations. The analyses of the CL tests with regard to the maximum roll angle and the steering torque required to stabilize the bicycle show that the arrangements with the motor in the rear wheel hub M3 and the positioning of the battery on the rear carrier are most similar to the dynamic properties of a conventional bicycle. This can be used, for example, for the mobilization of physically impaired persons to facilitate a transition from conventional bicycles. The design with the motor in the front wheel hub is particularly interesting. The additional mass in the steering axle and the gyroscopic torque increasing with higher speed lead to a significantly reduced maximum roll angle after an external excitation. However, this configuration makes stabilization by the active driver more difficult. Finally, the influence of the different positioning of the drive components was determined and compared to other system parameters by means of a design of experiment. In relation to the bicycle type and rider position, it was found that the positioning of motor and battery plays an important role, especially for moderate driving speeds. However, for speeds lower than \(v = 6\text{ m}/\text{s}\) and higher than \(v = 9\text{ m}/\text{s}\) the variation of the rider position has the greatest influence on the controllability of the system with respect to all three investigated factors. The knowledge gained could be used to develop user-friendly bicycle setups. These could increase agility for sports use or enable bikes with high stability and controllability at low speeds for everyday use.

In future works, subject tests can validate the simulated results. This could ensure to what extent driving dynamics properties such as controllability are related to subjective driving experience.