Projection continuation for minimal coordinate set formulation and singularity detection of redundantly constrained system dynamics

Abstract

The formulation of (possibly redundantly) constrained system dynamics using coordinate projection onto a subspace locally tangent to the constraint manifold is revisited using the QR factorization of the constraint Jacobian matrix, using column pivoting to identify a suitable subspace, possibly detect any singular configurations that may arise, and extract it. The evolution of the QR factorization is integrated along with that of the constraint Jacobian matrix as the solution evolves, generalizing to redundant constraints a recently proposed true continuation algorithm that tracks the evolution of the subspace of independent coordinates. The resulting subspace does not visibly affect the quality of the solution, as it is merely a recombination of that resulting from the blind application of the QR factorization but avoids the artificial algorithmic irregularities or discontinuities in the generalized velocities that could otherwise result from arbitrary reparameterizations of the coordinate set, and identifies and discriminates any further possible motions that arise at singular configurations. The characteristics of the proposed subspace evolution approach are exemplified by solving simple problems with incremental levels of redundancy and singularity orders.

1 Introduction

Unconstrained mechanical system dynamics problems are formulated as a set of second-order ordinary differential equations (ODE) that depend on a corresponding set of coordinates and their time derivatives. Interactions between parts of the system are often idealized at a purely kinematic level in terms of algebraic relationships between their coordinates, resulting in a system of differential-algebraic equations (DAE). The coordinates of the originally unconstrained problem are no longer independent; the number of independent coordinates reduces to that of the truly independent degrees of freedom of the system. Compliance with the constraints is enforced by suitable generalized constraint reaction forces, usually formulated as Lagrange multipliers, that represent the required internal actions. Possible approaches for the formulation of constrained system dynamics are reviewed in [1, 16].

The system of DAEs that describe the constrained dynamics problem can be solved directly considering the Lagrange multipliers as additional unknowns, resulting in the so-called redundant coordinate set (RCS) formulation. Alternatively, the problem can be manipulated and transformed into the corresponding underlying ODE problem, reducing the set of coordinates to the truly independent (Lagrangian) ones, according to the so-called minimal coordinate set (MCS) approach. Possible approaches are reviewed in [12]. The reduction of the original coordinates into the MCS may be challenging. The nature of the reduced coordinates is local, i.e., no generally valid choice may exist that works for all system configurations [8]. This paper elaborates on a projection continuation formulation originally proposed in [21] and subsequently formalized in [22], extending and generalizing it to the case of redundant constraints and applying it to the detection of singular configurations.

2 Problem description

In this work, we use the MCS approach to formulate the constrained dynamics of a mechanical system, obtaining the coordinate projection matrix from the QR factorization of the constraint Jacobian matrix. An original continuation algorithm, presented in [22], is used to ensure a regular evolution of the coordinate subspace that is tangent to the constraint manifold.

Three main elements of novelty are presented in this work:

• N1: the process of enforcing the orthogonality of the projection matrix resulting from the continuation algorithm with respect to the constraint Jacobian matrix is reformulated as the constrained minimization of a suitable cost function under the orthonormality constraint;

• N2: the QR factorization with column pivoting (QRCP) of the constraint Jacobian matrix is used to analyze problems with redundant constraints; the suitability and advantages of the proposed continuation algorithm become apparent in this case;

• N3: the QRCP of the constraint Jacobian matrix is also used to identify singular configurations of the problem; in this case, the proposed continuation algorithm guarantees the ability to distinguish the continuation of the original configuration from the new motion(s) allowed by the singular configuration.

The paper is organized as follows:

• Sect. 2.1 introduces the constraint dynamics problem;

• Sect. 2.2 briefly presents the MCS approach using coordinate projection;

• Sect. 2.3 discusses the use of QR factorization for optimal subspace selection;

• Sect. 2.4 briefly illustrates the projection continuation proposed in [22];

• Sect. 2.5 handles redundant constraints and discusses singularity detection;

• Sect. 3 presents several application examples that, although simple, are specifically crafted to illustrate the features of the proposed formulation.

Specific details of the formulation are presented in dedicated appendices.

Issues related to the indetermination of the constraint reactions of redundant constraints, in particular concerning implications when the constraints are not ideal, are not discussed, as the proposed continuation algorithm does not change the nature of the formulation in this respect. The interested reader should consult, for example, [18, 20].

2.1 Constrained dynamics problem formulation

A set of $n$ ordinary differential equations (ODE) describes the dynamics of an unconstrained system of $n$ coordinates $\mathbf {x} \in \mathbb{R}^{n}$,

$$\begin{aligned} {\mathbf {M}} \ddot{\mathbf {x}} &= \mathbf {f} \end{aligned}$$

(1)

subjected to a corresponding set of generalized applied forces $\mathbf {f} \in \mathbb{R}^{n}$, energetically conjugated to a virtual perturbation of the coordinates $\delta \mathbf {x}$, where ${\mathbf {M}} \in \mathbb{R}^{n \times n}$ is the symmetric, positive-definite mass matrix.

The problem is constrained by adding $m$ (holonomic, without loss of generality, and ideal for the reasons discussed in the preamble) kinematic constraints in form of a set of algebraic equations

$$\begin{aligned} \mathbf {c}(\mathbf {x}, t) &= \mathbf {0} \end{aligned}$$

(2)

with $\mathbf {c} \in \mathbb{R}^{m}$.

The ODEs of Eq. (1) are modified by addition of the constraint reactions $\mathbf {f}_{c} = - {\mathbf {A}}^{T} {\boldsymbol {\lambda}}$ as follows:

$$\begin{aligned} {\mathbf {M}} \ddot{\mathbf {x}} + {\mathbf {A}}^{T} {\boldsymbol {\lambda}} &= \mathbf {f}, \end{aligned}$$

(3)

where ${\mathbf {A}} = \mathbf {c}_{/\mathbf {x}} \in \mathbb{R}^{m \times n}$ is the partial derivative of the constraint equations $\mathbf {c}$ with respect to the coordinates $\mathbf {x}$, namely the constraint Jacobian matrix, and ${\boldsymbol {\lambda}} \in \mathbb{R}^{m}$ is the array of the corresponding Lagrange multipliers.

The constraint Jacobian matrix is expected to be full-rank when the constraints are independent. It may become rank deficient

• occasionally, when special configurations are reached, or

• structurally, when constraints are redundant.

In the present work, we consider both cases. Constraints are redundant when the constraint Jacobian matrix is not full rank, namely $\operatorname{rank}({\mathbf {A}}) < \min (m, n)$, but a solution that satisfies Eq. (2) exists over continuous portions of the domain of the time $t$.

Specifically, we consider problems with:

• i) $m < n$, with $\operatorname{rank}({\mathbf {A}}) \equiv m$, i.e., independent constraints, and $f = n - m$ degrees of freedom (as in [22]; Sects. 2.4 and 3.2);

• ii) $m \le n$, with $\operatorname{rank}({\mathbf {A}}) < m$, i.e., redundant constraints, and $f = n - \operatorname{rank}({\mathbf {A}})$ degrees of freedom (Sects. 2.5, 3.1, and 3.3);

• iii) $m > n$, with $\operatorname{rank}({\mathbf {A}}) < n$, i.e., redundant constraints, and $f = n - \operatorname{rank}({\mathbf {A}})$ degrees of freedom (Sects. 2.5 and 3.4).

Cases (ii) and (iii) differ essentially because of how the submatrices resulting from the QR factorization are arranged.

2.2 Minimal coordinate set approach

The minimal coordinate set approach consists in defining a suitable subspace ${\mathbf {T}} \in \mathbb{R}^{n \times f}$ of the space spanned by the coordinates $\mathbf {x}$, which is tangent to the constraint manifold, namely ${\mathbf {T}}^{T} {\mathbf {A}}^{T} \equiv {\mathbf {0}} \in \mathbb{R}^{f \times m}$, such that

$$\begin{aligned} \dot{\mathbf {x}} &= {\mathbf {T}} \dot{\mathbf {q}} + {\boldsymbol {\beta}}', \\ \end{aligned}$$

(4a)

$$\begin{aligned} \ddot{\mathbf {x}} &= {\mathbf {T}} \ddot{\mathbf {q}} + {\boldsymbol {\beta}}'', \end{aligned}$$

(4b)

where $\mathbf {q} \in \mathbb{R}^{f}$ are local, truly independent coordinates, with ${\boldsymbol {\beta}}' \in \mathbb{R}^{n}$ and ${\boldsymbol {\beta}}'' \in \mathbb{R}^{n}$ defined accordingly, the former being nonzero only in case of rheonomous constraints, under the assumption that ${\mathbf {T}}^{T} {\boldsymbol {\beta}}' = \mathbf {0}$ and ${\mathbf {T}}^{T} {\boldsymbol {\beta}}'' = \mathbf {0}$, i.e., that the only portion of $\dot{\mathbf {x}}$ and $\ddot{\mathbf {x}}$ spanning the admissible subspace is that related to the time derivatives of the minimal coordinates $\dot{\mathbf {q}}$ and $\ddot{\mathbf {q}}$ such that

$$\mathbf{A}\dot{\mathbf{x}}+{\mathbf{c}}_{/t}=\mathbf{0}\to \mathbf{A}(\mathbf{T}\dot{\mathbf{q}}+{\mathit{\beta }}^{\prime })+{\mathbf{c}}_{/t}=\mathbf{0}\to \mathbf{A}{\mathit{\beta }}^{\prime }=-{\mathbf{c}}_{/t}$$

(5)

as ${\mathbf {A}} {\mathbf {T}} \equiv {\mathbf {0}}$ holds, and analogously

$$\mathbf{A}\ddot{\mathbf{x}}+{\left(\dot{\mathbf{c}}\right)}_{/\mathbf{x}}\dot{\mathbf{x}}+{\left(\dot{\mathbf{c}}\right)}_{/t}=\mathbf{0}\to \mathbf{A}{\mathit{\beta }}^{″}=-{\left(\dot{\mathbf{c}}\right)}_{/\mathbf{x}}\dot{\mathbf{x}}-{\left(\dot{\mathbf{c}}\right)}_{/t}.$$

(6)

Suitable expressions of ${\boldsymbol {\beta}}'$ and ${\boldsymbol {\beta}}''$ are determined later.

The constrained dynamics problem, projected in such a subspace, yields

(7)

The solution is sought by first integrating Eq. (7) to obtain the generalized velocities $\dot{\mathbf {q}}$; then, Eq. (4a) is integrated to obtain an estimate of $\mathbf {x}$, which needs to be subsequently refined by enforcing the constraint at the position level, Eq. (2).

The structural cancellation of the term ${\mathbf {T}}^{T} {\mathbf {A}}^{T}$ in Eq. (7), to eliminate the constraint reactions ${\boldsymbol {\lambda}}$, is at the core of the MCS approach and the essential requirement of the projection matrix ${\mathbf {T}}$.

2.3 QR factorization for optimal minimal coordinate set selection

Among the several approaches proposed in the literature (see, for example, [15]), a robust and general choice for matrix ${\mathbf {T}}$ can be obtained using the QR factorization [3, 7] of the transpose of the constraint Jacobian matrix.

Consider for now the case $m < n$ and $\operatorname{rank}({\mathbf {A}}) \equiv m$; then

$$\begin{aligned} {\mathbf {A}}^{T} &= {\mathbf {Q}} {\mathbf {R}} = \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1} &{\mathbf {Q}}_{2} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} {\mathbf {R}}_{1} \\ {\mathbf {0}} \end{array}\displaystyle \right ] = {\mathbf {Q}}_{1} {\mathbf {R}}_{1}, \end{aligned}$$

(8)

where matrix ${\mathbf {Q}} \in \mathbb{R}^{n \times n}$ is orthonormal and submatrix ${\mathbf {R}}_{1} \in \mathbb{R}^{m \times m}$ is upper triangular. Submatrix ${\mathbf {Q}}_{2} \in \mathbb{R}^{n \times (n - m)}$, although not uniquely determined, is an optimal choice for ${\mathbf {T}}$.

The velocities can then be expressed as

$$\begin{aligned} \dot{\mathbf {x}} &= {\mathbf {Q}}_{2} \dot{\mathbf {q}} + {\mathbf {Q}}_{1} \mathbf {p}' \end{aligned}$$

(9)

with ${\mathbf {Q}}_{1} \mathbf {p}' = {\boldsymbol {\beta}}'$, i.e., by construction only spanning the subspace orthogonal to the constraint manifold, and thus $\mathbf {p}' = - {\mathbf {R}}_{1}^{-T} \mathbf {c}_{/t}$ since, according to Eq. (5) and the orthogonality of submatrix ${\mathbf {Q}}_{1}$, ${\mathbf {A}} {\boldsymbol {\beta}}' = {\mathbf {R}}_{1}^{T} {\mathbf {Q}}_{1}^{T} {\mathbf {Q}}_{1} \mathbf {p}' = {\mathbf {R}}_{1}^{T} \mathbf {p}' = -\mathbf {c}_{/t}$; similarly, the accelerations can be expressed as

$$\begin{aligned} \ddot{\mathbf {x}} &= {\mathbf {Q}}_{2} \ddot{\mathbf {q}} + {\mathbf {Q}}_{1} \mathbf {p}'' \end{aligned}$$

(10)

with ${\mathbf {Q}}_{1} \mathbf {p}'' = {\boldsymbol {\beta}}''$, and thus $\mathbf {p}'' = - {\mathbf {R}}_{1}^{-T} \left [ \left ( \dot{\mathbf {c}} \right ) _{/ \mathbf {x}} \dot{\mathbf {x}} + \left ( \dot{\mathbf {c}} \right ) _{/t} \right ]$ as a consequence of Eq. (6).

According to Eqs. (7) and (9), the problem becomes

$$\begin{aligned} {\mathbf {Q}}_{2}^{T} {\mathbf {M}} {\mathbf {Q}}_{2} \ddot{\mathbf {q}} &= {\mathbf {Q}}_{2}^{T} \left ( \mathbf {f} - {\mathbf {M}} {\boldsymbol{\beta }}'' \right ), \\ \end{aligned}$$

(11a)

$$\begin{aligned} \dot{\mathbf {x}} &= {\mathbf {Q}}_{2} \dot{\mathbf {q}} + {\mathbf {Q}}_{1} \mathbf {p}'. \end{aligned}$$

(11b)

This form, which resembles the one originally devised in 1903 by Maggi [13, 14] and subsequently independently proposed again in 1965 by Kane [11], today is known as Maggi–Kane equations [2].

The integration of Eqs. (11a)–(11b) from time $t_{k}$ to $t_{k+1}$ yields

$$\begin{aligned} \mathbf {x}_{k+1}^{(0)} &= {\mathbf {Q}}_{2_{k}} \mathbf {q}_{k+1} + {\mathbf {Q}}_{1_{k}} \mathbf {p}^{(0)}, \end{aligned}$$

(12)

where the superscript $(\cdot )^{(0)}$ indicates an estimate of the final value, pending verification that it complies with the constraint of Eq. (2). The final value of the unknown $\mathbf {p}$ results from the iterative solution of

$$\begin{aligned} \mathbf {c}(\mathbf {x}_{k+1}, t_{k+1}) &= \mathbf {0}. \end{aligned}$$

(13)

More details can be found in [22].

2.4 Tangent subspace selection and continuation

Submatrices ${\mathbf {Q}}_{1}$ and ${\mathbf {R}}_{1}$ are uniquely determined¹ once matrix ${\mathbf {A}}$ is known. Submatrix ${\mathbf {Q}}_{2}$, instead, is only subjected to matrix ${\mathbf {Q}}$’s general constraint of being orthogonal, namely ${\mathbf {Q}}_{2}^{T} {\mathbf {Q}}_{2} \equiv {\mathbf {I}} \in \mathbb{R}^{(n-m) \times (n-m)}$ and ${\mathbf {Q}}_{2}^{T} {\mathbf {Q}}_{1} \equiv {\mathbf {0}} \in \mathbb{R}^{(n-m) \times m}$, but otherwise undefined.

In fact, the QR factorization produces a “local” representation of the constraint Jacobian matrix; as such, the generalized coordinates associated with the subspace ${\mathbf {T}} = {\mathbf {Q}}_{2}$, which do not have any specific physical meaning, represent a local reparameterization of the subspace of the coordinates that is tangent to the constraint manifold. When the QR factorization is computed at time step $t_{k+1}$, if $n - m > 1$, the columns of the resulting ${\mathbf {Q}}_{2_{k+1}}$ are completely unrelated to those of ${\mathbf {Q}}_{2_{k}}$, their resulting value being solely dictated by the internal intricacies of the QR factorization algorithm. Even for $n - m \equiv 1$, i.e., for single-degree-of-freedom problems, where ${\mathbf {Q}}_{2}$ is a single column, ${\mathbf {Q}}_{2_{k+1}}$ might be directed in a direction that is nearly opposite to that of ${\mathbf {Q}}_{2_{k}}$.

In [21] and [22], a simple and intuitive algorithm was proposed to track the evolution of the subspace spanned by ${\mathbf {Q}}_{2}$. It uses a form of differential “continuation” to preserve the spatial continuity of the generalized coordinates $\mathbf {q}$ by minimizing the amount of deviation of the subspace that is intrinsically required to maintain ${\mathbf {Q}}_{2}$ tangent to the constraint manifold across time steps without altering the quality of the solution. The algorithm is briefly recalled here.

Consider the time derivative of the transpose of the constraint Jacobian matrix in its QR factorized form

$$\begin{aligned} \dot{{\mathbf {A}}}^{T} &= \dot{{\mathbf {Q}}} {\mathbf {R}} + {\mathbf {Q}} \dot{{\mathbf {R}}}. \end{aligned}$$

(14)

The derivative of the QR factorization has been intensively used in so-called “continuous” algorithms for the estimation of Lyapunov characteristic exponents as a means to overcome under- and overflow issues when integrating the evolution of linear, time-dependent problems. An overview of such methods is presented in [6]. Similar concepts, although involving partial differentiation with respect to a set of parameters, have been recently proposed for adjoint sensitivity analysis of multibody problems formulated using the MCS approach [9]. The derivative of matrix ${\mathbf {Q}}$ may be expressed as $\dot{{\mathbf {Q}}} = {\mathbf {Q}} {\boldsymbol {\Omega}}$, where the skew-symmetric nature of matrix ${\boldsymbol {\Omega}} \in \mathbb{R}^{n \times n}$, namely ${\boldsymbol {\Omega}}^{T} = - {\boldsymbol {\Omega}}$, descends from the orthogonality of matrix ${\mathbf {Q}}$:

$$\frac{\mathrm{d}}{\mathrm{d}t}\left({\mathbf{Q}}^T\mathbf{Q}\right)={\dot{\mathbf{Q}}}^T\mathbf{Q}+{\mathbf{Q}}^T\dot{\mathbf{Q}}={\left({\mathbf{Q}}^T\dot{\mathbf{Q}}\right)}^T+{\mathbf{Q}}^T\dot{\mathbf{Q}}=\mathbf{0}\to {\mathbf{Q}}^T\dot{\mathbf{Q}}=\mathbf{\Omega }.$$

(15)

When the problem is integrated numerically, the solution from time step $t_{k}$ to time step $t_{k+1}$ is computed. The QR factorization at time $t_{k}$ yields submatrices ${\mathbf {Q}}_{1_{k}}$ and ${\mathbf {R}}_{1_{k}}$. The generalized velocities at time $t_{k}$ are computed with reference to the subspace spanned by ${\mathbf {Q}}_{2_{k}}$. After computing the solution at the new time step, the Jacobian matrix at time $t_{k+1}$, ${\mathbf {A}}_{k+1}$, is known. As such, through the economy QR factorization of its transpose, submatrices ${\mathbf {Q}}_{1_{k+1}}$ and ${\mathbf {R}}_{1_{k+1}}$ are determined. Instead of using submatrix ${\mathbf {Q}}_{2_{k+1}}$ resulting from the full QR factorization, the proposed continuation algorithm obtains it by integrating Eq. (15). Consider

$$\begin{aligned} {\mathbf {Q}}^{T} \dot{{\mathbf {A}}}^{T} &= {\mathbf {Q}}^{T} \dot{{\mathbf {Q}}} \left [ \textstyle\begin{array}{c} {\mathbf {R}}_{1} \\ {\mathbf {0}} \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{c} \dot{{\mathbf {R}}}_{1} \\ {\mathbf {0}} \end{array}\displaystyle \right ] \end{aligned}$$

(16)

or

$$\begin{aligned} \left [ \textstyle\begin{array}{c} {\mathbf {Q}}_{1}^{T} \\ {\mathbf {Q}}_{2}^{T} \end{array}\displaystyle \right ] \dot{{\mathbf {A}}}^{T} &= \left [ \textstyle\begin{array}{ c@{\quad}c } {\boldsymbol{\Omega }}_{1} &- {\boldsymbol{\Omega }}_{21}^{T} \\ {\boldsymbol{\Omega }}_{21} &{\mathbf {0}} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} {\mathbf {R}}_{1} \\ {\mathbf {0}} \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{c} \dot{{\mathbf {R}}}_{1} \\ {\mathbf {0}} \end{array}\displaystyle \right ] , \end{aligned}$$

(17)

where ${\boldsymbol {\Omega}}_{1} = -{\boldsymbol {\Omega}}_{1}^{T} = {\mathbf {Q}}_{1}^{T} \dot{{\mathbf {Q}}}_{1} \in \mathbb{R}^{m \times m}$, ${\boldsymbol {\Omega}}_{21} = {\mathbf {Q}}_{2}^{T} \dot{{\mathbf {Q}}}_{1} \in \mathbb{R}^{(n-m) \times m}$, and the bottom-right block of matrix ${\boldsymbol {\Omega}}$, corresponding to ${\mathbf {Q}}_{2}^{T} \dot{{\mathbf {Q}}}_{2} \in \mathbb{R}^{(n-m) \times (n-m)}$, uninfluential since it is multiplied by a zero-valued submatrix in ${\mathbf {R}}$, is arbitrarily set to zero. This corresponds to requiring that the subspace ${\mathbf {Q}}_{2}$ is modified as little as possible while transitioning from $t_{k}$ to $t_{k+1}$.

The first block row of Eq. (17), after post-multiplication by ${\mathbf {R}}_{1}^{-1}$, yields

$$\begin{aligned} {\mathbf {Q}}_{1}^{T} \dot{{\mathbf {A}}}^{T} {\mathbf {R}}_{1}^{-1} &= {\boldsymbol {\Omega}}_{1} + \dot{{\mathbf {R}}}_{1} {\mathbf {R}}_{1}^{-1}. \end{aligned}$$

(18)

Matrix $\dot{{\mathbf {R}}}_{1} {\mathbf {R}}_{1}^{-1}$ is the product of two upper triangular matrices, thus it is itself upper-triangular. Matrix ${\boldsymbol {\Omega}}_{1_{L}} = \operatorname{stril}({\boldsymbol {\Omega}}_{1})$, the strictly lower triangular part of matrix ${\boldsymbol {\Omega}}_{1}$, can thus be obtained as

$$\begin{aligned} {\boldsymbol {\Omega}}_{1_{L}} &= \operatorname{stril} \left ( {\mathbf {Q}}_{1}^{T} \dot{{\mathbf {A}}}^{T} {\mathbf {R}}_{1}^{-1} \right ) \end{aligned}$$

(19)

with ${\boldsymbol {\Omega}}_{1} = {\boldsymbol {\Omega}}_{1_{L}} - {\boldsymbol {\Omega}}_{1_{L}}^{T}$. It is worth recalling that ${\mathbf {R}}_{1}$ being an upper-triangular matrix, its inversion merely requires a back-substitution.

The second block row of Eq. (17), after post-multiplication by ${\mathbf {R}}_{1}^{-1}$, yields

$$\begin{aligned} {\boldsymbol {\Omega}}_{21} &= {\mathbf {Q}}_{2}^{T} \dot{{\mathbf {A}}}^{T} {\mathbf {R}}_{1}^{-1}, \end{aligned}$$

(20)

thus completely defining matrix ${\boldsymbol {\Omega}}$.

Submatrix $\dot{{\mathbf {R}}}_{1}$ is irrelevant as the continuation of matrix ${\mathbf {R}}$ is not needed. However, for completeness it can be obtained from the first block row of Eq. (17) as follows:

$$\begin{aligned} \dot{{\mathbf {R}}}_{1} &= {\mathbf {Q}}_{1}^{T} \dot{{\mathbf {A}}}^{T} - {\boldsymbol {\Omega}}_{1} {\mathbf {R}}_{1}. \end{aligned}$$

(21)

The subspace ${\mathbf {Q}}_{2}$ can be integrated starting from an arbitrary value, provided it is orthogonal to the initial value of ${\mathbf {Q}}_{1}$ (the value resulting from Matlab’s implementation of the QR factorization was used in the numerical examples of Sect. 3), taking appropriate measures to guarantee that the resulting matrix ${\mathbf {Q}}$ preserves orthogonality. For example, for ${\boldsymbol {\Omega}}$ constant across a time step of duration $t_{k+1} - t_{k} = h$,

$$\begin{aligned} {\mathbf {Q}}_{k+1} &= {\mathbf {Q}}_{k} \mathrm{e}^{{\boldsymbol {\Omega}} h}. \end{aligned}$$

(22)

Submatrix ${\mathbf {Q}}_{1_{k+1}}$ resulting from the proposed integration should then be discarded because the one resulting from the QR factorization of matrix ${\mathbf {A}}_{k+1}^{T}$ is the most accurate. Submatrix ${\mathbf {Q}}_{2_{k+1}}$ resulting from the proposed integration, instead, represents the natural continuation of ${\mathbf {Q}}_{2_{k}}$; however, it may need to be corrected to guarantee orthogonality with respect to submatrix ${\mathbf {Q}}_{1_{k+1}}$ obtained from the economy QR factorization of ${\mathbf {A}}_{k+1}^{T}$. A suitable reorthogonalization algorithm, of general validity, is proposed in Appendix A. It represents the element of novelty N1.

It is worth recalling that, as anticipated in [22], the proposed tangent subspace selection and continuation algorithm does not alter the quality of the solution. It simply provides a cleaner evolution of the minimal coordinates. However, this does not come at no cost:

• the evolution of matrix ${\mathbf {Q}}$ must be computed according to Eq. (22) at the cost of evaluating an exponential matrix of order $n \times n$, whose computational complexity (CC) depends on the type of approximation and tolerance;

• the reorthogonalization of the evolved submatrix ${\mathbf {Q}}_{2}$ (see Appendix A) requires:

  • the product of an $(n-m) \times n$ matrix by an $n \times (n-m)$ matrix, CC of $O((n-m)^{2} n)$,

  • the square root of the resulting $(n-m) \times (n-m)$ matrix, whose CC again depends on approximation and tolerance,

  • the product of two $(n-m) \times (n-m)$ matrices, CC of $O((n-m)^{3})$, and

  • the product of an $n \times (n-m)$ matrix by an $(n-m) \times (n-m)$ matrix, CC of $O(n (n-m)^{2})$.

No specific CC is added by the QR factorization as it needs to be computed anyway to determine the compliant subspace matrix. The added CC is limited when the number of constraints is comparable to that of the unconstrained coordinates, such that $n-m \ll n$. In those cases, the CC drops to negligible values that scale linearly with the size of the unconstrained problem $n$. As discussed in the next section, one needs to weigh this extra cost with the advantages provided by the proposed formulation in terms of its ability to correctly identify possible motions at singular configurations and, in general, to deal effectively with redundant constraints. When $m \ll n$, as in the case, for example, of problems characterized by flexibility, the MCS approach tends to lose its appeal, as the reduction in problem size tends to become negligible while the CC increases significantly, loosely scaling with $n^{3}$.

2.5 Redundant constraints and singular configurations

To deal with redundant constraints, the projection scheme needs some modifications. They represent the element of novelty N2. Furthermore, the solution process needs some care when considering singular configurations. This is the element of novelty N3.

Redundant constraints occur when their Jacobian matrix is not full-rank, i.e., its rows are not linearly independent. This condition can be structural, in case of overconstraining, or sporadic; in the latter case, a singular configuration has been reached. Notice that a system can be overconstrained and at the same time show sporadic singular configurations.

Without any ambition of thoroughly discussing the topic, this section highlights the required adaptations of the proposed continuation algorithm and the advantages it may offer in such cases.

Rank-deficient constraint Jacobian matrix

Let us consider first the case of matrix ${\mathbf {A}} \in \mathbb{R}^{m \times n}$ not being full-rank, or rank-deficient, although still with $m \le n$. In that case, submatrix ${\mathbf {R}}_{1}$ becomes singular; that is, as many of its diagonal coefficients as the order of rank-deficiency $d$ of matrix ${\mathbf {A}}$ are zero, where the rank-deficiency $d$ of a matrix is the difference between the lesser of its number of rows or columns and its rank, $d = \min (m, n) - \operatorname{rank}({\mathbf {A}})$; in the present case, $d = m - \operatorname{rank}({\mathbf {A}})$.

Consider a QR factorization with column pivoting [4, 10], which yields a transformation

$$\begin{aligned} {\mathbf {A}}^{T} &= {\mathbf {Q}} {\mathbf {R}} {\mathbf {P}}^{T} , \end{aligned}$$

(23)

where ${\mathbf {P}} \in \mathbb{R}^{m \times m}$ is a suitable permutation matrix. It produces a submatrix ${\mathbf {R}}_{1}$ whose diagonal coefficients are sorted in a decreasing order of their norm.² As such, one can effectively evaluate the rank of the constraint Jacobian matrix and thus the presence of any redundant constraints corresponding to the number of diagonal coefficients of submatrix ${\mathbf {R}}_{1}$, starting from the bottom-right corner, that vanish (in practice, fall below a given threshold).

In that case, the three matrices resulting from the factorization can be reorganized as follows:

$$\begin{aligned} {\mathbf {A}}^{T} &= \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1} &{\mathbf {Q}}_{2} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} {\mathbf {R}}_{1} \\ {\mathbf {0}} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} \\ &= \left [ \textstyle\begin{array}{ c@{\quad}c } \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1_{\text{ns}}} &{\mathbf {Q}}_{1_{\text{s}}} \end{array}\displaystyle \right ] &{\mathbf {Q}}_{2} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1_{\text{ns}}} &{\mathbf {R}}_{1_{\text{s}}} \\ \ldots &{\mathbf {0}} \end{array}\displaystyle \right ] \\ {\mathbf {0}} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} \\ &= \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1_{\text{ns}}} &\left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1_{\text{s}}} &{\mathbf {Q}}_{2} \end{array}\displaystyle \right ] \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1_{\text{ns}}} &{\mathbf {R}}_{1_{\text{s}}} \end{array}\displaystyle \right ] \\ {\mathbf {0}} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} \\ &= {\mathbf {Q}}_{1_{\text{ns}}} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1_{\text{ns}}} &{\mathbf {R}}_{1_{\text{s}}} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} \end{aligned}$$

(24)

with ${\mathbf {Q}}_{1_{\text{ns}}} \in \mathbb{R}^{n \times (m - d)}$, ${\mathbf {Q}}_{1_{\text{s}}} \in \mathbb{R}^{n \times d}$, ${\mathbf {R}}_{1_{\text{ns}}} \in \mathbb{R}^{(m - d) \times (m - d)}$, and ${\mathbf {R}}_{1_{\text{s}}} \in \mathbb{R}^{(m - d) \times d}$ (irrelevant for our discussion), where subscripts ‘ns’ and ‘s’ respectively stand for ‘nonsingular’ and ‘singular’, and the subspace that is tangent to the constraint manifold is

$$\begin{aligned} {\mathbf {T}} &= \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1_{\text{s}}} &{\mathbf {Q}}_{2} \end{array}\displaystyle \right ] \end{aligned}$$

(25)

whose size is now ${\mathbf {T}} \in \mathbb{R}^{n \times (n - m + d)}$.

When $m \equiv n$ but the Jacobian matrix of the constraints is rank-deficient, i.e., $\operatorname{rank}({\mathbf {A}}) < n$, submatrix ${\mathbf {Q}}_{2}$ is empty; yet, the rest of the above considerations apply, and the subspace of allowed motion is represented by ${\mathbf {Q}}_{1_{\text{s}}}$ alone. Details on the derivation of the continuation algorithm are reported in Appendix B.

Constraints exceeding the number of coordinates

Similar considerations apply to the case of constraints that exceed the number of coordinates, namely $m > n$, thus being intrinsically redundant. In this case, the column-pivoting QR factorization of ${\mathbf {A}}^{T}$ yields

$$\begin{aligned} {\mathbf {A}}^{T} &= {\mathbf {Q}}_{1} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1} &{\mathbf {R}}_{2} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} \end{aligned}$$

(26)

with ${\mathbf {Q}}_{1} \in \mathbb{R}^{n \times n}$, ${\mathbf {R}}_{1} \in \mathbb{R}^{n \times n}$, and ${\mathbf {R}}_{2} \in \mathbb{R}^{n \times (m - n)}$. If the so-called differential (or instantaneous) mobility $d = n - \operatorname{rank}({\mathbf {A}}) > 0$, $d$ admissible motions remain, and a corresponding number of diagonal elements of submatrix ${\mathbf {R}}_{1}$ are zero, along with the corresponding rows of submatrix ${\mathbf {R}}_{2}$. Thus, the factorization of Eq. (26) can be represented as

$$\begin{aligned} {\mathbf {A}}^{T} &= \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1_{\text{ns}}} &{\mathbf {Q}}_{1_{\text{s}}} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\quad}c } \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1_{\text{ns}}} &{\mathbf {R}}_{1_{\text{s}}} \\ \ldots &{\mathbf {0}} \end{array}\displaystyle \right ] &\left [ \textstyle\begin{array}{c} {\mathbf {R}}_{2_{\text{s}}} \\ {\mathbf {0}} \end{array}\displaystyle \right ] \end{array}\displaystyle \right ] {\mathbf {P}}^{T} \\ &= {\mathbf {Q}}_{1_{\text{ns}}} \left [ \textstyle\begin{array}{ c@{\quad}c@{\quad}c } {\mathbf {R}}_{1_{\text{ns}}} &{\mathbf {R}}_{1_{\text{s}}} & {\mathbf {R}}_{2_{\text{s}}} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} , \end{aligned}$$

(27)

with ${\mathbf {Q}}_{1_{\text{ns}}} \in \mathbb{R}^{n \times (n - d)}$, ${\mathbf {Q}}_{1_{\text{s}}} \in \mathbb{R}^{n \times d}$, ${\mathbf {R}}_{1_{\text{ns}}} \in \mathbb{R}^{(n - d) \times (n - d)}$, ${\mathbf {R}}_{1_{\text{s}}} \in \mathbb{R}^{(n - d) \times d}$, and ${\mathbf {R}}_{2_{\text{s}}} \in \mathbb{R}^{(n - d) \times (m-n)}$. The subspace tangent to the constraint manifold is

$$\begin{aligned} {\mathbf {T}} &= {\mathbf {Q}}_{1_{\text{s}}} \end{aligned}$$

(28)

whose size is now ${\mathbf {T}} \in \mathbb{R}^{n \times d}$. Details on the derivation of the continuation algorithm are reported in Appendix C.

Singular configurations

So far, the discussion presented in this section showed that projection algorithms based on the QR factorization can robustly deal with redundant constraints. Now, we want to discuss how the proposed continuation procedure can help when the number of independent allowed motions changes during the analysis.

A singular configuration occurs when the rank of the constraint Jacobian matrix changes as the system reaches that configuration. When some constraints become redundant, the rank of the constraint Jacobian matrix decreases while the number of allowed independent motions increases, and vice versa.

Let us focus on the case of rank reduction. In this case, the number of allowed motions, and thus potentially of degrees of freedom, suddenly increases. This is highlighted by the fact that some of the bottom-right diagonal elements of submatrix ${\mathbf {R}}_{1}$, resulting from the column-pivoting QR factorization, approach zero. As a consequence, the dimension of the subspace ${\mathbf {T}}$ formed according to Eq. (25) or (28) increases, but the columns that form it, taken from the columns of matrix ${\mathbf {Q}}$, represent an arbitrary combination of the independent directions that characterize that subspace.

However, when the proposed continuation algorithm is used, the portion of the subspace at the singular configuration closest to the original, smaller dimension one that characterized the solution before the topological change of the system can be easily identified as the natural continuation of the original space along with the newly available directions of motion. This can be extremely useful when tracking, for example, the possibility of bifurcations in the solution. The topic is not developed further here, but dedicated examples are presented in Sect. 3.

3 Results

Simple examples are analyzed to illustrate how the proposed method produces a more regular and intuitive choice of the projection subspace during the integration of the solution when constraints are redundant and singular configurations are approached. First, a planar pendulum is analyzed analytically. The subsequent examples are numerically integrated using Matlab’s ode45 explicit Runge–Kutta integration scheme, based on Dormand and Prince’s formula [5].

3.1 Planar pendulum

Single-degree of freedom problems represent a trivial case in the context of the present discussion; in fact, considering the simplest case of redundant constraint single-degree-of-freedom problem, with $m \equiv n$ but $d = m - \operatorname{rank}({\mathbf {A}}) = 1$, the corresponding submatrix ${\mathbf {Q}}_{1_{\text{s}}}$ consists of a single column, which is thus uniquely determined, except for its sign.

What is possibly the simplest single-degree of freedom example, the planar pendulum adapted from that originally presented in [22], is here considered to show how the proposed continuation algorithm, trivially transformed into a case of redundant constraints, avoids the occasional reversing of the sign of ${\mathbf {Q}}_{1_{\text{s}}}$ that occurs when the permuted QR factorization of matrix ${\mathbf {A}}^{T}$ is blindly performed. The solution is obtained analytically.

Consider the equations of motion of a simple point mass pendulum of mass $M$ and length $\ell$ subjected to a uniform gravity field of intensity $g$ along the negative $z$ direction:

$$\begin{aligned} M \ddot{x} + 2 x \lambda _{1} + 2 x \lambda _{2} &= 0, \end{aligned}$$

(29a)

$$\begin{aligned} M \ddot{z} + 2 z \lambda _{1} + 2 z \lambda _{2} + M g &= 0, \end{aligned}$$

(29b)

$$\begin{aligned} x^{2} + z^{2} - \ell ^{2} &= 0, \end{aligned}$$

(29c)

$$\begin{aligned} x^{2} + z^{2} - \ell ^{2} &= 0, \end{aligned}$$

(29d)

where $x$ and $z$ are the horizontal and vertical components of the point mass position, the unconstrained coordinates in the present context, and $\lambda _{1}$ and $\lambda _{2}$ are the Lagrange multipliers associated with the constraints of Eqs. (29c) and (29d). The two constraint equations are identical and represent a trivial case of redundant constraints. The corresponding constraint Jacobian matrix is

$$\begin{aligned} {\mathbf {A}} &= \left [ \textstyle\begin{array}{ c@{\quad}c } 2 x &2 z \\ 2 x &2 z \end{array}\displaystyle \right ] . \end{aligned}$$

(30)

Its rows are identical; thus, its rank is 1. The QR factorization of its transpose can be written as

$$\begin{aligned} {\mathbf {A}}^{T} &= \left [ \textstyle\begin{array}{ c@{\quad}c } 2 x &2 x \\ 2 z &2 z \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{ c@{\ \ }|@{\ \ }c } Q_{11} &Q_{12} \\ Q_{21} &Q_{22} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\ \ }|@{\ \ }c } R_{1_{\text{ns}}} &R_{1_{\text{s}}} \\ \hline 0 &0 \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\quad}c } P_{11} &P_{12} \\ P_{21} &P_{22} \end{array}\displaystyle \right ] ^{T} \\ & = \left [ \textstyle\begin{array}{ c@{\ \ }|@{\ \ }c } -\cos \theta &-\sin \theta \\ \sin \theta &-\cos \theta \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\ \ }|@{\ \ }c } R_{1_{\text{ns}}} &R_{1_{\text{s}}} \\ \hline 0 &0 \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\quad}c } P_{11} &P_{21} \\ P_{12} &P_{22} \end{array}\displaystyle \right ] , \end{aligned}$$

(31)

where matrix ${\mathbf {Q}}$ is orthonormal by construction and defined by the single parameter $\theta$ with

$$\theta =-{tan}^{-1}\left(\frac{z}{x}\right),R_{1_{\text{ns}}}=R_{1_{\text{s}}}=R_1=2\ell ,P_{11}=P_{22}=1,P_{12}=P_{21}=0$$

(32)

as a possible determination of the parameters $\theta$, $R_{1_{\text{ns}}}$, $R_{1_{\text{s}}}$ and of matrix ${\mathbf {P}}$. Submatrices ${\mathbf {Q}}_{1_{\text{ns}}}$ and ${\mathbf {Q}}_{1_{\text{s}}}$ can then be written as

$${\mathbf{Q}}_{1_{\text{ns}}}=\left[\begin{array}{c}x/\ell \\ z/\ell \end{array}\right]{\mathbf{Q}}_{1_{\text{s}}}=\left[\begin{array}{c}-z/\ell \\ x/\ell \end{array}\right].$$

(33)

The velocity and acceleration vectors of the point mass are thus

$$\left\{\begin{array}{c}\dot{x}\\ \dot{z}\end{array}\right\}=\left[\begin{array}{c}-z/\ell \\ x/\ell \end{array}\right]\dot{q}\left\{\begin{array}{c}\ddot{x}\\ \ddot{z}\end{array}\right\}=\left[\begin{array}{c}-z/\ell \\ x/\ell \end{array}\right]\ddot{q}-\left[\begin{array}{c}x/\ell \\ z/\ell \end{array}\right]\frac{{\dot{q}}^2}{\ell }.$$

(34)

The projected equation of motion is

$$\begin{aligned} M \ddot{q} &= - \cfrac{x}{\ell} M g. \end{aligned}$$

(35)

One may observe that redefining $\dot{q} = \ell \dot{\theta}$ the velocity vector can be written as

$$\begin{aligned} \left \{ \textstyle\begin{array}{c} \dot{x} \\ \dot{z} \end{array}\displaystyle \right \} &= - \ell \left [ \textstyle\begin{array}{c} \sin \theta \\ \cos \theta \end{array}\displaystyle \right ] \dot{\theta}, \end{aligned}$$

(36)

which is integrable, yielding

$$\begin{aligned} \left \{ \textstyle\begin{array}{c} x \\ z \end{array}\displaystyle \right \} &= \ell \left [ \textstyle\begin{array}{c} \cos \theta \\ -\sin \theta \end{array}\displaystyle \right ] . \end{aligned}$$

(37)

It is worth recalling that when solving for $\theta$ and $R_{1}$ from Eq. (31), ${\mathbf {A}}^{T} = {\mathbf {Q}} {\mathbf {R}} {\mathbf {P}}^{T}$ yields

$$\begin{aligned} \left [ \textstyle\begin{array}{ c@{\quad}c } 2 x &2 x \\ 2 z &2 z \end{array}\displaystyle \right ] &= \left [ \textstyle\begin{array}{ c@{\quad}c } -R_{1} \cos \theta &-R_{1} \cos \theta \\ R_{1} \sin \theta &R_{1} \sin \theta \end{array}\displaystyle \right ] . \end{aligned}$$

(38)

To extract $R_{1}$, consider the norm of the first column of both sides:

$$4(x^2+y^2)=R_1^2({cos}^2\theta +{sin}^2\theta )\to 4{\ell }^2=R_1^2$$

(39)

or

$$\begin{aligned} R_{1} &= \pm 2 \ell , \end{aligned}$$

(40)

where we arbitrarily chose $R_{1} = + 2 \ell$, but the choice with the negative sign is also legitimate. To extract $\theta$, consider the ratio of the second and first elements of the first column:

$$\frac{2z}{2x}=-\frac{R_{1}sin\theta }{R_{1}cos\theta }\to \theta =-{tan}^{-1}\left(\frac{z}{x}\right)+\frac{\pi }{2}(1-sign(R_1)).$$

(41)

The culprit lies in the fact that in Eq. (31) matrix ${\mathbf {Q}}$ could have been alternatively defined as

$$\begin{aligned} {\mathbf {Q}} &= \left [ \textstyle\begin{array}{ c@{\ \ }|@{\ \ }c } -\cos \theta &\sin \theta \\ \sin \theta &\cos \theta \end{array}\displaystyle \right ] , \end{aligned}$$

(42)

i.e., changing the sign of its second column, submatrix ${\mathbf {Q}}_{1_{\text{s}}}$, at the only cost of no longer representing a rotation matrix (since its determinant would now be −1 instead of $+1$), but without impacting its ability to represent the transpose of the constraint Jacobian matrix as ${\mathbf {Q}} {\mathbf {R}}$, nor that of ${\mathbf {Q}}_{1_{\text{s}}}$ to represent a suitable subspace tangent to the constraint manifold.

If an intermittent change of sign occurs between consecutive QR factorizations, the sign of the derivative of the generalized coordinate $\dot{q}$ also changes, resulting in unnecessary discontinuities, although harmless for what concerns the result in terms of physical variables. Consider $s_{1} = \pm 1$ as the (arbitrary) sign of $R_{1}$ and $s_{2} = \pm 1$ as the (arbitrary, independent from $s_{1}$) sign of submatrix ${\mathbf {Q}}_{1_{\text{s}}}$, such that $s_{1}^{2} = s_{2}^{2} = 1$. The QR factorization of ${\mathbf {A}}^{T}$ then becomes

$$\begin{aligned} \left [ \textstyle\begin{array}{ c@{\quad}c } 2x &2x \\ 2z &2z \end{array}\displaystyle \right ] &= \left [ \textstyle\begin{array}{ c@{\ \ }|@{\ \ }c } -s_{1} \cos \theta &-s_{2} \sin \theta \\ s_{1} \sin \theta &-s_{2} \cos \theta \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\quad}c } s_{1} 2 \ell &s_{1} 2 \ell \\ \hline 0 &0 \end{array}\displaystyle \right ] \end{aligned}$$

(43)

(the pivoting matrix ${\mathbf {P}}$ is omitted since it corresponds to the identity).

Consider its time derivative:

$$\begin{aligned} \left [ \textstyle\begin{array}{ c@{\quad}c } 2\dot{x} &2\dot{x} \\ 2\dot{z} &2\dot{z} \end{array}\displaystyle \right ] &= \dot{\theta} \left [ \textstyle\begin{array}{ c@{\ \ }|@{\ \ }c } s_{1} \sin \theta &-s_{2} \cos \theta \\ s_{1} \cos \theta &s_{2} \sin \theta \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\quad}c } s_{1} 2 \ell &s_{1} 2 \ell \\ \hline 0 &0 \end{array}\displaystyle \right ] = 2 \ell \left [ \textstyle\begin{array}{ c@{\ \ }|@{\ \ }c } \sin \theta &\sin \theta \\ \cos \theta &\cos \theta \end{array}\displaystyle \right ] \dot{\theta}, \end{aligned}$$

(44)

i.e., a matrix whose columns are twice the same expression of Eq. (36).

Consider now the proposed continuation algorithm, whose details are reported in Appendix B; consider first

$$\begin{aligned} {\mathbf {Q}}^{T} \dot{{\mathbf {A}}} {\mathbf {P}} &= {\boldsymbol {\Omega}} {\mathbf {R}} + \dot{{\mathbf {R}}} \end{aligned}$$

(45)

or

$$ \left [ \textstyle\begin{array}{ c@{\quad}c } -s_{1} \cos \theta &s_{1} \sin \theta \\ \hline -s_{2} \sin \theta &-s_{2} \cos \theta \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\quad}c } 2 \dot{x} &2 \dot{x} \\ 2 \dot{z} &2 \dot{z} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{ c@{\quad}c } 0 &-\Omega _{21} \\ \Omega _{21} &0 \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\ \ }|@{\ \ }c } s_{1} 2 \ell &s_{1} 2 \ell \\ \hline 0 &0 \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{ c@{\ \ }|@{\ \ }c } \dot{R}_{1} &\dot{R}_{1} \\ \hline 0 &0 \end{array}\displaystyle \right ] , $$

(46)

where $\Omega _{21}$ and $\dot{R}_{1}$ are the two formal unknowns of this $2 \times 2$ twice-redundant matrix equation. Matrix ${\mathbf {R}}$ in Eq. (45) can no longer be inverted as in the original projection formulation of Eq. (18) since its last row is now zero. However, the problem can be reworked considering the coordinate derivatives of Eq. (36) multiplied by $s_{2}$:

$$\begin{aligned} \left [ \textstyle\begin{array}{ c@{\quad}c } 0 &0 \\ 2 \ell \dot{\theta } &2 \ell \dot{\theta } \end{array}\displaystyle \right ] &= \left [ \textstyle\begin{array}{ c@{\quad}c } 0 &0 \\ s_{1} 2 \ell \Omega _{21} &s_{1} 2 \ell \Omega _{21} \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{ c@{\ \ }|@{\ \ }c } \dot{R}_{1} &\dot{R}_{1} \\ \hline 0 &0 \end{array}\displaystyle \right ] , \end{aligned}$$

(47)

which yields

$$\begin{aligned} \Omega _{21} &= s_{1} \dot{\theta}, \end{aligned}$$

(48)

$$\begin{aligned} \dot{R}_{1} &= 0. \end{aligned}$$

(49)

As a consequence, matrix ${\boldsymbol {\Omega}}$ from Eq. (15) by construction becomes

$$\begin{aligned} {\boldsymbol {\Omega}} &= s_{1} \dot{\theta} \left [ \textstyle\begin{array}{ r@{\quad}r } 0 &-1 \\ 1 &0 \end{array}\displaystyle \right ] \end{aligned}$$

(50)

and the continued integration of matrix ${\mathbf {Q}}$ simply consists in choosing the sign of the new column ${\mathbf {Q}}_{1_{\text{s}}}$ such that it forms the smallest possible angle with the previous one without any indetermination nor arbitrariness in the choice of $s_{2}$ and regardless of the choice of $s_{1}$.

3.2 Double four-bar mechanism

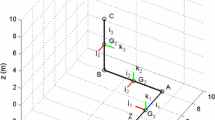
The double 4-bar mechanism sketched in Fig. 1 is a rigid multibody benchmark proposed by IFToMM’s Technical Committee for Multibody Dynamics³ [17] (https://www.iftomm-multibody.org/) and analyzed, for example, in [19].

Fig. 1

Double four-bar mechanism: sketch

It consists of five independent slender bodies of 1 m length, all with a uniformly distributed mass of 1 kg, for a total of 15 degrees of freedom ($n = 15$), and 7 hinges, corresponding to 14 constraints ($m = 14 < n$). The system is subjected to a uniform gravity field of 9.81 m/s². Each body’s kinematics is described through the position of their center of mass $\mathbf {r}_{i} = \{r_{i_{x}}; r_{y_{i}}\}$ at mid-span and their rotation $\theta _{i}$. In the generic configuration, the resulting constraint equations are independent ($\operatorname{rank}({\mathbf {A}}) = 14$, $d = \min (m,n) - \operatorname{rank}({\mathbf {A}}) = 0$), leaving one degree of freedom. When all bodies are aligned horizontally, however, the problem becomes kinematically singular. Figure 2 shows the diagonal elements of matrix ${\mathbf {R}}_{1}$. Two of its diagonal elements vanish at the singular configurations. The rank of the constraint Jacobian matrix reduces to 12, allowing two more motions, illustrated in Fig. 3 for the singular configuration with all bars aligned horizontally on the left. In the figure, $\delta x$, $\delta y$, and $\delta \theta$ respectively indicate the perturbation of each bar’s center of mass position components and rotation as resulting from the columns of matrix ${\mathbf {T}}$. The first motion corresponds to the mechanism’s conventional assembly far from the singular configuration: no horizontal displacement of any bar, identical downward vertical displacement for the bars hinged to the ground, 1, 3, and 5, twice as much vertical displacement for the bars opposed to the ground, 2 and 4, identical and consistent counter-clockwise rotation for bars 1, 3, and 5, and no rotation for bars 2 and 4. The other two allowed motions can be determined from the figure.

Fig. 2

Double four-bar mechanism: the 14 diagonal elements of submatrix ${\mathbf {R}}_{1}$

Fig. 3

Double four-bar mechanism: admissible motions at first singular point

3.3 Modified double four-bar mechanism

The double four-bar mechanism of Sect. 3.2 is modified by turning bars 2 and 4 into a single bar of twice the length and mass, as shown in Fig. 4. There are now four independent bodies, for a total of 12 degrees of freedom ($n = 12$), and six hinges, corresponding to 12 constraints ($m = 12 = n$). However, in the generic configuration, only 11 of the resulting constraint equations are independent ($\operatorname{rank}({\mathbf {A}}) = 11$, $d = \min (m,n) - \operatorname{rank}({\mathbf {A}}) = 1$), leaving one degree of freedom. At any of the singular configurations, the rank of the constraint Jacobian matrix further reduces by one ($\operatorname{rank}({\mathbf {A}}) = 10$, $d = \min (m,n) - \operatorname{rank}({\mathbf {A}}) = 2$), as shown in Fig. 5, introducing a second admissible motion, illustrated in Fig. 6.

Fig. 4

Modified double four-bar mechanism: sketch

Fig. 5

Modified double four-bar mechanism: the 11 diagonal elements of submatrix ${\mathbf {R}}_{1_{\mathrm{ns}}}$

Fig. 6

Modified double four-bar mechanism: admissible motions at first singular point

3.4 Modified triple four-bar mechanism

The modified double four-bar mechanism of Sect. 3.3 is further modified by adding yet another four-bar mechanism, maintaining the top bars connected to form a single rigid body of three times the length and the mass, as shown in Fig. 7. There are now five independent bodies, for a total of 15 degrees of freedom ($n = 15$), and eight hinges, corresponding to 16 constraints ($m = 16 > n$). However, in the generic configuration only 14 of the resulting constraint equations are independent ($\operatorname{rank}({\mathbf {A}}) = 14$, $d = \min (m,n) - \operatorname{rank}({\mathbf {A}}) = 1$), leaving one degree of freedom. At any of the singular configurations, the rank of the constraint Jacobian matrix further reduces by one ($\operatorname{rank}({\mathbf {A}}) = 13$, $d = \min (m,n) - \operatorname{rank}({\mathbf {A}}) = 2$), as shown in Fig. 8, introducing a second admissible motion, illustrated in Fig. 9.

Fig. 7

Modified triple four-bar mechanism: sketch

Fig. 8

Modified triple four-bar mechanism: the 14 diagonal elements of submatrix ${\mathbf {R}}_{1_{\mathrm{ns}}}$

Fig. 9

Modified triple four-bar mechanism: admissible motions at first singular point

Figure 10 shows the three rows of matrix ${\mathbf {T}}$ associated with the motion of bar no. 1 (1–3) as resulting from the traditional QR factorization. As discussed earlier, since the problem has only one degree of freedom, the matrix’s only column is fully determined apart from its sign. The discontinuities that appear in the figure correspond to arbitrary changes of sign dictated by the intricacies of the QR factorization algorithm as it is implemented in Matlab. The zoom on the right also shows that at the first singular point the motion labeled “1^st mov” also shows a discontinuity, along with the single points that represent the other admissible motion at the singularity, labeled “2^nd mov”. Neither the first nor the second admissible motion vectors when crossing the singularity are in continuity with the motion before and after it.

Fig. 10

Modified triple four-bar mechanism: bar 1 components of matrix ${\mathbf {T}}$ column(s), traditional QR factorization

On the contrary, as shown in Fig. 11, the proposed continuation algorithm first of all eliminates the discontinuities in the components of matrix ${\mathbf {T}}$ throughout the simulation, and furthermore makes one of the admissible motion vectors be in continuity with the motion before and after the singularity. The other admissible motion is clearly identified and structurally orthogonal to the first one. It only exists when the mechanism is in the corresponding singular configuration.

Fig. 11

Modified triple four-bar mechanism: bar 1 components of matrix ${\mathbf {T}}$ column(s), QR factorization continuation

3.5 Modified $2\times 2$ four-bar mechanism

In this example, two modified double four-bar mechanisms analogous to that of Sect. 3.3 are connected one another, as shown in Fig. 12, to form a modified $2\times 2$ four-bar mechanism. There are now eight independent bodies, for a total of 24 degrees of freedom ($n = 24$), and 12 hinges, corresponding to 24 constraints ($m = 24 = n$). However, in the generic configuration, only 22 of the resulting constraint equations are independent ($\operatorname{rank}({\mathbf {A}}) = 22$, $d = \min (m,n) - \operatorname{rank}({\mathbf {A}}) = 2$), leaving two degrees of freedom. It is intended to demonstrate the proposed formulation with more than one degree of freedom. Figure 13 shows the trajectories of bars 1 and 5. At any of the singular configurations, the rank of the constraint Jacobian matrix further reduces by one ($\operatorname{rank}( {\mathbf {A}}) = 21$, $d = \min (m,n) - \operatorname{rank}({\mathbf {A}}) = 3$), as shown in Fig. 14 by the vanishing of the smallest diagonal element of submatrix ${\mathbf {R}}_{1_{\mathrm{ns}}}$, introducing a second admissible motion. At $t \approx 0.7\text{ s}$ and $t \approx 1.4\text{ s}$, one diagonal element of submatrix ${\mathbf {R}}_{1_{\mathrm{ns}}}$ vanishes as bar 1 becomes horizontal ($\theta _{1} = 0$ and $\theta _{1} = -\pi$, and $r_{y_{1}} = 0$ in Fig. 13). Similarly, at $t \approx 0.9\text{ s}$ and $t \approx 1.55\text{ s}$, one diagonal element of submatrix ${\mathbf {R}}_{1_{\mathrm{ns}}}$ vanishes as bar 5 becomes horizontal ($\theta _{5} = 0$ and $\theta _{5} = -\pi$, and $r_{y_{5}} = 0$ in Fig. 13).

Fig. 12

Modified $2\times 2$ four-bar mechanism: sketch

Fig. 13

Modified $2\times 2$ four-bar mechanism: trajectories of bars 1 and 5

Fig. 14

Modified $2\times 2$ four-bar mechanism: the 22 diagonal elements of submatrix ${\mathbf {R}}_{1_{\mathrm{ns}}}$

Figure 15 illustrates the time derivatives of the generalized coordinates $\dot{q}_{1}$ and $\dot{q}_{2}$ when the traditional and the continuation formulations are used. As discussed earlier, the traditional formulation results in rather erratic and discontinuous patterns, whereas the proposed continuation gives extremely regular results, although both present essentially identical results in terms of physical coordinates.

Fig. 15

Modified $2\times 2$ four-bar mechanism: generalized velocities

4 Conclusions

This paper presented a continuation algorithm for the redefinition of the subspace of minimal coordinates that is tangent to the constraint manifold. It is based on the full QR factorization of the constraint Jacobian matrix to initialize the subspace through the portion of the space defined by the orthogonal matrix Q that is orthogonal to the constraint Jacobian matrix. The economy QR factorization is then used to exactly factor the subspace in which the constraint Jacobian matrix lies, while the evolution of the tangent subspace is tracked by integrating the time derivative of matrix Q, eventually re-orthogonalizing the result to eliminate possible drift from the integrated tangent subspace. Numerical examples show that the analysis results are unchanged, but the generalized velocities no longer show the discontinuities that occasionally characterize them when the tangent subspace is recomputed without considering its value at the previous time step. The approach is extended to the case of redundant constraints, and its potential usefulness in case of topology changes originating from singular configurations is outlined.

Appendices

Appendix A: Reorthogonalization after continuation

Consider submatrix $\hat{{\mathbf {Q}}}_{2}$ as the one resulting from the complete QR factorization of ${\mathbf {A}}_{k+1}^{T}$ and submatrix $\tilde{{\mathbf {Q}}}_{2}$ as the one resulting from the continuation algorithm.⁴ The subspaces spanned by the two matrices may differ because of accumulated numerical error during the integration of Eqs. (11a)–(11b) for the former and Eq. (15) for the latter, including for the former the correction of the physical coordinates solution to bring it back onto the constraint manifold according to Eq. (13).

The desired matrix ${\mathbf {Q}}_{2}$ must consist of

• i) a recombination of the columns of $\hat{{\mathbf {Q}}}_{2}$ (the “exact” subspace);

• ii) that is as close as possible to $\tilde{{\mathbf {Q}}}_{2}$ (the “continued” subspace).

Requirement (i) is met by constructing ${\mathbf {Q}}_{2}$ as

$$\begin{aligned} {\mathbf {Q}}_{2} &= \hat{{\mathbf {Q}}}_{2} {\mathbf {P}} \end{aligned}$$

(51)

with ${\mathbf {P}} \in \mathbb{R}^{(n-m)\times (n-m)}$ orthonormal, i.e., subjected to the constraint

$$\begin{aligned} {\mathbf {P}} {\mathbf {P}}^{T} &= {\mathbf {I}} \end{aligned}$$

(52)

such that

$$\begin{aligned} \hat{{\mathbf {Q}}}_{1}^{T} {\mathbf {Q}}_{2} &= \hat{{\mathbf {Q}}}_{1}^{T} \hat{{\mathbf {Q}}}_{2} {\mathbf {P}} = {\mathbf {0}} {\mathbf {P}} = {\mathbf {0}}, \end{aligned}$$

(53)

where submatrix $\hat{{\mathbf {Q}}}_{1}$ also results from the QR factorization of matrix ${\mathbf {A}}_{k+1}^{T}$, and

$$\begin{aligned} {\mathbf {Q}}_{2}^{T} {\mathbf {Q}}_{2} &= {\mathbf {P}}^{T} \hat{{\mathbf {Q}}}_{2}^{T} \hat{{\mathbf {Q}}}_{2} {\mathbf {P}} = {\mathbf {P}}^{T} {\mathbf {P}} = {\mathbf {I}}. \end{aligned}$$

(54)

Requirement (ii) is met by determining matrix ${\mathbf {P}}$ subjected to the condition

$$\begin{aligned} \min _{{\mathbf {P}}} \left \| \tilde{{\mathbf {Q}}}_{2}^{T} {\mathbf {Q}}_{2} - {\mathbf {I}} \right \| , \end{aligned}$$

(55)

where $\left \| \cdot \right \|$ indicates a suitable matrix norm to be defined.

1.1 A.1 Constrained minimization

The problem can be recast in the minimization of a cost function $J$ consisting of the trace⁵ of the product of matrix

$$\begin{aligned} {\mathbf {E}} &= \tilde{{\mathbf {Q}}}_{2}^{T} {\mathbf {Q}}_{2} - {\mathbf {I}} = {\mathbf {C}} {\mathbf {P}} - \mathbf {I} \end{aligned}$$

(56)

by its transpose, with

$$\begin{aligned} {\mathbf {C}} &= \tilde{{\mathbf {Q}}}_{2}^{T} \hat{{\mathbf {Q}}}_{2} \end{aligned}$$

(57)

or the square of matrix ${\mathbf {E}}$’s Frobenius norm, i.e., a quadratic form with respect to matrix ${\mathbf {P}}$ subjected to the constraint of Eq. (52). The latter can be imposed by transforming the constrained minimization into an unconstrained one with the addition of the constraint equation to the cost function using the Lagrange multipliers as

$$\begin{aligned} \min _{{\mathbf {P}}, {\boldsymbol {\Lambda}}} J \end{aligned}$$

(58)

with

$$\begin{aligned} J &= \operatorname{tr} \left ( \left ( {\mathbf {C}} {\mathbf {P}} - {\mathbf {I}} \right ) \left ( {\mathbf {C}} {\mathbf {P}} - {\mathbf {I}} \right ) ^{T} \right ) + \operatorname{tr} \left ( \left ( {\mathbf {P}} {\mathbf {P}}^{T} - {\mathbf {I}} \right ) {\boldsymbol{\Lambda }} \right ) , \end{aligned}$$

(59)

where ${\boldsymbol {\Lambda}} \in \mathbb{R}^{(n-m)\times (n-m)}$ is the (symmetric) matrix of the Lagrange multipliers.

A stationary point may be found by setting to zero the partial derivatives of the cost function $J$ with respect to matrices ${\mathbf {P}}$ and ${\boldsymbol {\Lambda}}$. Setting the partial derivative of $J$ with respect to ${\boldsymbol {\Lambda}}$ equal to ${\mathbf {0}}$ yields the constraint equation, Eq. (52). Setting the partial derivative of $J$ with respect to ${\mathbf {P}}$ equal to ${\mathbf {0}}$ yields

$$\begin{aligned} \cfrac{\partial J}{\partial {\mathbf {P}}} &= 2 {\mathbf {C}}^{T} \left ( {\mathbf {C}} {\mathbf {P}} - {\mathbf {I}} \right ) + 2 {\boldsymbol {\Lambda}} {\mathbf {P}} = {\mathbf {0}}, \end{aligned}$$

(60)

i.e.,

$$\begin{aligned} {\mathbf {P}}^{-1} &= {\mathbf {C}}^{-T} \left ( {\mathbf {C}}^{T} {\mathbf {C}} + {\boldsymbol{\Lambda }} \right ) = {\mathbf {P}}^{T} , \end{aligned}$$

(61)

where, owing to its orthonormality, ${\mathbf {P}}^{-1} = {\mathbf {P}}^{T}$ is used. Replacing ${\mathbf {P}}$ from Eq. (61) in the orthonormality constraint of Eq. (52) yields

$$\begin{aligned} {\boldsymbol {\Lambda}} + {\boldsymbol {\Lambda}}^{T} + {\boldsymbol {\Lambda}}^{T} {\mathbf {C}}^{-1} {\mathbf {C}}^{-T} {\boldsymbol {\Lambda}} + {\mathbf {C}}^{T} {\mathbf {C}} - {\mathbf {I}} &= {\mathbf {0}}, \end{aligned}$$

(62)

i.e., a continuous algebraic Riccati equation in ${\boldsymbol {\Lambda}}$, whose solution is used in Eq. (61) to obtain

$$\begin{aligned} {\mathbf {P}} &= \left ( {\mathbf {C}}^{T} {\mathbf {C}} + {\boldsymbol{\Lambda }} \right ) {\mathbf {C}}^{-1} \end{aligned}$$

(63)

and thus the optimal ${\mathbf {Q}}_{2}$ from Eq. (51).

1.2 A.2 Polar decomposition

Alternatively, according to the polar decomposition theorem, the transpose of matrix ${\mathbf {C}}$ can be decomposed in the product of an orthonormal matrix ${\mathbf {U}} \in \mathbb{R}^{(n-m)\times (n-m)}$ and a symmetric, positive (semi)definite matrix ${\mathbf {D}} \in \mathbb{R}^{(n-m)\times (n-m)}$, namely ${\mathbf {C}}^{T} = {\mathbf {U}} {\mathbf {D}}$. The product

$$\begin{aligned} {\mathbf {C}} {\mathbf {C}}^{T} &= {\mathbf {D}}^{T} {\mathbf {U}}^{T} {\mathbf {U}} {\mathbf {D}} = {\mathbf {D}}^{T} {\mathbf {D}} \overset{\mathrm{sym.}}{=} {\mathbf {D}}^{2} \end{aligned}$$

(64)

gives the opportunity to compute

$$\begin{aligned} {\mathbf {D}} &= \left ( {\mathbf {C}} {\mathbf {C}}^{T} \right ) ^{1/2}, \end{aligned}$$

(65)

where operator $(\cdot )^{1/2}$ indicates the matrix square root operation, and thus

$$\begin{aligned} {\mathbf {U}} &= {\mathbf {C}}^{T} {\mathbf {D}}^{-1}. \end{aligned}$$

(66)

Matrix ${\mathbf {U}}$ corresponds to the optimal matrix of Eq. (63).

Proof

We assume for ${\mathbf {P}}$ matrix ${\mathbf {U}}$ from Eq. (66) with a multiplicative perturbation by an arbitrary orthogonal matrix, and show that when replaced in the cost function of Eq. (59), it gives a value that is minimal when ${\mathbf {P}} \equiv {\mathbf {U}}$.

Assume for matrix ${\mathbf {P}}$ a perturbation of matrix ${\mathbf {U}}$, formulated as

$$\begin{aligned} {\mathbf {P}} &= {\mathbf {U}} {\mathbf {W}}, \end{aligned}$$

(67)

where ${\mathbf {W}} \in \mathbb{R}^{(n-m)\times (n-m)}$ is an arbitrary orthonormal matrix, namely ${\mathbf {W}}^{T} {\mathbf {W}} \equiv {\mathbf {I}}$, such that matrix ${\mathbf {P}}$ satisfies Eq. (52), and thus Eq. (51) satisfies requirement (i). The value of the cost function of Eq. (59), having enforced by assumption the satisfaction of the orthonormality constraint for ${\mathbf {P}}$, is

$$\begin{array}{rl}{J}_{\mathbf{W}}& =tr({\mathbf{D}}^2-\mathbf{D}\mathbf{W}-{\mathbf{W}}^T\mathbf{D}+\mathbf{I})\\ & =tr({\mathbf{D}}^2-2\mathbf{D}\mathbf{W}+\mathbf{I})& \mathrm{\text{[since }}tr({\mathbf{M}}^T)=tr(\mathbf{M})\text{].}\end{array}$$

(68)

The variation of the cost function considering the perturbation matrix ${\mathbf {W}}$ is

$$\begin{aligned} J_{{\mathbf {W}}} - J_{{\mathbf {W}}\equiv {\mathbf {I}}} &= \operatorname{tr} \left ( {\mathbf {D}}^{2} - 2 {\mathbf {D}} {\mathbf {W}} + {\mathbf {I}} \right ) - \operatorname{tr} \left ( {\mathbf {D}}^{2} - 2 {\mathbf {D}} + {\mathbf {I}} \right ) \\ &= 2 \operatorname{tr} \left ( {\mathbf {D}} \left ( {\mathbf {I}} - {\mathbf {W}} \right ) \right ) . \end{aligned}$$

(69)

Consider now, without loss of generality, the simplest possible perturbation matrix ${\mathbf {W}}$ consisting of the equivalent of a 2D rotation of the first two directions in the coordinate space, namely

$$\begin{aligned} {\mathbf {W}} &= \left [ \textstyle\begin{array}{ c@{\quad}c@{\quad}c@{\quad}c@{\quad}c } \cos \theta &-\sin \theta &0 &\ldots &0 \\ \sin \theta &\cos \theta &0 &\ldots &0 \\ 0 &0 &1 &\ldots &0 \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ 0 &0 &0 &\ldots &1 \end{array}\displaystyle \right ] . \end{aligned}$$

(70)

The product ${\mathbf {D}} {\mathbf {W}}$ yields

$$ {\mathbf {D}} {\mathbf {W}} = \left [ \textstyle\begin{array}{ c@{\quad}c@{\quad}c@{\quad}c@{\quad}c } D_{11} \cos \theta + D_{12} \sin \theta &&&\ldots & \text{(irrelevant)} \\ &-D_{12} \sin \theta + D_{22} \cos \theta &&\ldots & \\ &&D_{33} &\ldots & \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ \text{(irrelevant)} &&&\ldots &D_{(n-m)(n-m)} \end{array}\displaystyle \right ] , $$

(71)

where the symmetry of matrix ${\mathbf {D}}$ was exploited. Its trace is

(72)

which is smaller than or at most equal to⁶ the trace of ${\mathbf {D}}$ alone for $\theta \equiv 0$, as $\cos \theta \le 1$ $\forall \theta$, yielding

$$\begin{aligned} J_{{\mathbf {W}}} - J_{{\mathbf {W}}\equiv {\mathbf {I}}} &= 2 \operatorname{tr} \left ( {\mathbf {D}} \left ( {\mathbf {I}} - {\mathbf {W}} \right ) \right ) = 2 \left ( D_{11} + D_{22} \right ) \left ( 1 - \cos \theta \right ) \ge 0. \end{aligned}$$

(73)

This is a second-order variation with respect to the perturbation: for $\left | \theta \right | \ll 1$, $\cos \theta \approx 1 - \theta ^{2}/2$, thus

$$\begin{aligned} J_{{\mathbf {W}}} - J_{{\mathbf {W}}\equiv {\mathbf {I}}} \approx \left ( D_{11} + D_{22} \right ) \theta ^{2}, \end{aligned}$$

(74)

i.e., $\theta \equiv 0$ represents a minimum since $D_{ii} \ge 0$.

Since an arbitrary perturbation can be transformed into the proposed one by an appropriate coordinate transformation, this proves the optimality of the proposed alternative formulation. Since the same cost function of the constrained minimization was used, it also proves their equivalence. □

Appendix B: QR continuation when $m \le n$

Consider the QR factorization of the constraint Jacobian matrix in the overconstrained, rank-deficient case, Eq. (26), here reported for clarity:

$$\begin{aligned} {\mathbf {A}}^{T} &= {\mathbf {Q}} {\mathbf {R}} {\mathbf {P}}^{T} = \left [ \textstyle\begin{array}{ c@{\quad}c } \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1_{\mathrm{ns}}} &{\mathbf {Q}}_{1_{\mathrm{s}}} \end{array}\displaystyle \right ] &{\mathbf {Q}}_{2} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1_{\mathrm{ns}}} &{\mathbf {R}}_{1_{\mathrm{s}}} \\ {\mathbf {0}} &{\mathbf {0}} \end{array}\displaystyle \right ] \\ {\mathbf {0}} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} \end{aligned}$$

(75)

with ${\mathbf {A}} \in \mathbb{R}^{m \times n}$, ${\mathbf {Q}} = \in \mathbb{R}^{n \times n}$ (${\mathbf {Q}}^{T} {\mathbf {Q}} \equiv {\mathbf {I}}$), ${\mathbf {Q}}_{1_{\mathrm{ns}}} \in \mathbb{R}^{n \times (m-d)}$, ${\mathbf {Q}}_{1_{\mathrm{s}}} \in \mathbb{R}^{n \times d}$, ${\mathbf {Q}}_{2} \in \mathbb{R}^{n \times (n-m)}$, ${\mathbf {R}} \in \mathbb{R}^{n \times m}$, ${\mathbf {R}}_{1_{\mathrm{ns}}} \in \mathbb{R}^{(m-d) \times (m-d)}$ (upper triangular), ${\mathbf {R}}_{1_{\mathrm{s}}} \in \mathbb{R}^{(m-d) \times d}$, and ${\mathbf {P}} \in \mathbb{R}^{m \times m}$ (${\mathbf {P}}^{T} {\mathbf {P}} \equiv {\mathbf {I}}$). It is assumed that the rank of the constraint Jacobian matrix, ${\mathbf {A}}$, is less than $n$, corresponding to a rank-deficiency index $d = n - \operatorname{rank}({\mathbf {A}}) > 0$, thus allowing a corresponding number of degrees of freedom for the constrained problem.

Reorganize it as

$$\begin{aligned} {\mathbf {A}}^{T} &= \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1_{\mathrm{ns}}} &{\mathbf {T}} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1_{\mathrm{ns}}} &{\mathbf {R}}_{1_{\mathrm{s}}} \end{array}\displaystyle \right ] \\ {\mathbf {0}} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} \end{aligned}$$

(76)

with

$$\begin{aligned} {\mathbf {T}} &= \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1_{\mathrm{s}}} &{\mathbf {Q}}_{2} \end{array}\displaystyle \right ] \end{aligned}$$

(77)

${\mathbf {T}} \in \mathbb{R}^{n \times (n - m + d)}$. The time derivative of matrix ${\mathbf {A}}$ is

$$\begin{aligned} \dot{{\mathbf {A}}}^{T} &= \dot{{\mathbf {Q}}} {\mathbf {R}} {\mathbf {P}}^{T} + {\mathbf {Q}} \dot{{\mathbf {R}}} {\mathbf {P}}^{T} \\ & = \left [ \textstyle\begin{array}{ c@{\quad}c } \dot{{\mathbf {Q}}}_{1_{\mathrm{ns}}} &\dot{{\mathbf {T}}} \end{array}\displaystyle \right ] {\mathbf {R}} {\mathbf {P}}^{T} + {\mathbf {Q}} \left [ \textstyle\begin{array}{c} \left [ \textstyle\begin{array}{ c@{\quad}c } \dot{{\mathbf {R}}}_{1_{\mathrm{ns}}} &\dot{{\mathbf {R}}}_{1_{\mathrm{s}}} \end{array}\displaystyle \right ] \\ {\mathbf {0}} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} \end{aligned}$$

(78)

since $\dot{{\mathbf {P}}} \equiv {\mathbf {0}}$ by definition of pivoting matrix. After pre-multiplication by ${\mathbf {Q}}^{T}$ and post-multiplication by ${\mathbf {P}}$, one obtains

$$\begin{aligned} {\mathbf {Q}}^{T} \dot{{\mathbf {A}}}^{T} {\mathbf {P}} &= {\mathbf {Q}}^{T} \dot{{\mathbf {Q}}} \left [ \textstyle\begin{array}{c} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1_{\mathrm{ns}}} &{\mathbf {R}}_{1_{\mathrm{s}}} \end{array}\displaystyle \right ] \\ {\mathbf {0}} \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{c} \left [ \textstyle\begin{array}{ c@{\quad}c } \dot{{\mathbf {R}}}_{1_{\mathrm{ns}}} &\dot{{\mathbf {R}}}_{1_{\mathrm{s}}} \end{array}\displaystyle \right ] \\ {\mathbf {0}} \end{array}\displaystyle \right ] \end{aligned}$$

(79)

exploiting the orthogonality of both matrices. Define

$$\begin{aligned} {\mathbf {Q}}^{T} \dot{{\mathbf {Q}}} &= {\boldsymbol {\Omega}} = - {\boldsymbol {\Omega}}^{T} \end{aligned}$$

(80)

with ${\boldsymbol {\Omega}} \in \mathbb{R}^{n \times n}$ because of the orthogonality of matrix ${\mathbf {Q}}_{1}$. Replacing the definitions of ${\mathbf {Q}}$ and $\dot{{\mathbf {Q}}}$,

$$\begin{aligned} {\mathbf {Q}}^{T} \dot{{\mathbf {Q}}} &= \left [ \textstyle\begin{array}{c} {\mathbf {Q}}_{1_{\mathrm{ns}}}^{T} \\ {\mathbf {T}} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\quad}c } \dot{{\mathbf {Q}}}_{1_{\mathrm{ns}}} &\dot{{\mathbf {T}}} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1_{\mathrm{ns}}}^{T} \dot{{\mathbf {Q}}}_{1_{\mathrm{ns}}} & {\mathbf {Q}}_{1_{\mathrm{ns}}}^{T} \dot{{\mathbf {T}}} \\ {\mathbf {T}}^{T} \dot{{\mathbf {Q}}}_{1_{\mathrm{ns}}} &{\mathbf {T}}^{T} \dot{{\mathbf {T}}} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{ c@{\quad}c } {\boldsymbol{\Omega }}_{\mathrm{ns}} &- {\boldsymbol{\Omega }}_{\mathrm{s}}^{T} \\ {\boldsymbol{\Omega }}_{\mathrm{s}} &{\mathbf {0}} \end{array}\displaystyle \right ] \end{aligned}$$

(81)

with ${\boldsymbol {\Omega}}_{\mathrm{ns}} \in \mathbb{R}^{(m-d) \times (m-d)}$ (${\boldsymbol {\Omega}}_{\mathrm{ns}}^{T} = -{\boldsymbol {\Omega}}_{\mathrm{ns}}$) and ${\boldsymbol {\Omega}}_{\mathrm{s}} \in \mathbb{R}^{(n-m+d) \times (m-d)}$. The bottom-right block of matrix ${\boldsymbol {\Omega}}$ is arbitrarily set to zero to minimize the re-orientation of the columns of matrix ${\mathbf {Q}}_{2}$ that correspond to the directions of motion allowed by the rank-deficiency of the constrain Jacobian matrix ${\mathbf {A}}$.

Consider Eq. (79):

$$\begin{aligned} {\mathbf {Q}}^{T} \dot{{\mathbf {A}}}^{T} {\mathbf {P}} &= {\boldsymbol {\Omega}} {\mathbf {R}} + \dot{{\mathbf {R}}} = {\mathbf {J}}. \end{aligned}$$

(82)

Explode everything in nonsingular ‘ns’ and singular ‘s’ blocks:

$$\begin{aligned} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {J}}_{11} &{\mathbf {J}}_{12} \\ {\mathbf {J}}_{21} &{\mathbf {J}}_{22} \end{array}\displaystyle \right ] &= \left [ \textstyle\begin{array}{ c@{\quad}c } {\boldsymbol{\Omega }}_{\text{ns}} &- {\boldsymbol{\Omega }}_{\text{s}}^{T} \\ {\boldsymbol{\Omega }}_{\text{s}} &{\mathbf {0}} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1_{\text{ns}}} &{\mathbf {R}}_{1_{\text{s}}} \\ {\mathbf {0}} &{\mathbf {0}} \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{ c@{\quad}c } \dot{{\mathbf {R}}}_{1_{\text{ns}}} &\dot{{\mathbf {R}}}_{1_{\text{s}}} \\ {\mathbf {0}} &{\mathbf {0}} \end{array}\displaystyle \right ] \end{aligned}$$

(83)

with ${\mathbf {J}}_{11} \in \mathbb{R}^{(m-d) \times (m-d)}$, ${\mathbf {J}}_{12} \in \mathbb{R}^{(m-d) \times d}$, ${\mathbf {J}}_{21} \in \mathbb{R}^{d \times (m-d)}$, and ${\mathbf {J}}_{22} \in \mathbb{R}^{d \times d}$. This yields the four equations

$$\begin{aligned} {\mathbf {J}}_{11} &= {\boldsymbol {\Omega}}_{\text{ns}} {\mathbf {R}}_{1_{\text{ns}}} + \dot{{\mathbf {R}}}_{1_{\text{ns}}}, \end{aligned}$$

(84a)

$$\begin{aligned} {\mathbf {J}}_{12} &= {\boldsymbol {\Omega}}_{\text{ns}} {\mathbf {R}}_{1_{\text{s}}} + \dot{{\mathbf {R}}}_{1_{\text{s}}}, \end{aligned}$$

(84b)

$$\begin{aligned} {\mathbf {J}}_{21} &= {\boldsymbol {\Omega}}_{\text{s}} {\mathbf {R}}_{1_{\text{ns}}}, \end{aligned}$$

(84c)

$$\begin{aligned} {\mathbf {J}}_{22} &= {\boldsymbol {\Omega}}_{\text{s}} {\mathbf {R}}_{1_{\text{s}}}. \end{aligned}$$

(84d)

2.1 B.1 Matrix ${\boldsymbol {\Omega}}$

From Eq. (84c):

$$\begin{aligned} {\boldsymbol {\Omega}}_{\text{s}} &= {\mathbf {J}}_{21} {\mathbf {R}}_{1_{\text{ns}}}^{-1}. \end{aligned}$$

(85)

From Eq. (84a):

$$\begin{aligned} {\mathbf {J}}_{11} {\mathbf {R}}_{1_{\text{ns}}}^{-1} &= {\boldsymbol {\Omega}}_{\text{ns}} + \dot{{\mathbf {R}}}_{1_{\text{ns}}} {\mathbf {R}}_{1_{\text{ns}}}^{-1}. \end{aligned}$$

(86)

Consider its strictly lower triangular part

(87)

Then

$$\begin{aligned} {\boldsymbol {\Omega}}_{\text{ns}} &= {\boldsymbol {\Omega}}_{L} - {\boldsymbol {\Omega}}_{L}^{T}. \end{aligned}$$

(88)

Matrix ${\boldsymbol {\Omega}}$ is then used for the continuation of matrix ${\mathbf {Q}}$, and specifically of the subspace ${\mathbf {T}}$ of Eq. (77), as discussed in Sect. 2.4 with reference to matrix ${\mathbf {Q}}$ and subspace ${\mathbf {Q}}_{2}$.

2.2 B.2 Matrix $\dot{{\mathbf {R}}}$

Matrix $\dot{{\mathbf {R}}}$ is irrelevant as the continuation of matrix ${\mathbf {R}}$ is not needed. However, for completeness, it can be obtained by considering again Eq. (84a):

$$\begin{aligned} \dot{{\mathbf {R}}}_{1_{\text{ns}}} &= {\mathbf {J}}_{11} - {\boldsymbol {\Omega}}_{\text{ns}} {\mathbf {R}}_{1_{\text{ns}}}. \end{aligned}$$

(89)

Then, from Eq. (84b):

$$\begin{aligned} \dot{{\mathbf {R}}}_{1_{\text{s}}} &= {\mathbf {J}}_{12} - {\boldsymbol {\Omega}}_{\text{ns}} {\mathbf {R}}_{1_{\text{s}}}. \end{aligned}$$

(90)

Equation (84d) must be intrinsically complied with, owing to the rank-deficiency of the constraint Jacobian matrix. One could use it to verify the consistency of the solution. Otherwise, if $\dot{{\mathbf {R}}}$ is not needed, then one may ignore Eqs. (84b) and (84d).

Appendix C: QR continuation when $m > n$

Consider the QR factorization of the constraint Jacobian matrix in the overconstrained, rank-deficient case, Eq. (26), here reported for clarity:

$$\begin{aligned} {\mathbf {A}}^{T} &= {\mathbf {Q}} {\mathbf {R}} {\mathbf {P}}^{T} = {\mathbf {Q}}_{1} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1} &{\mathbf {R}}_{2} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} \end{aligned}$$

(91)

with ${\mathbf {A}} \in \mathbb{R}^{m \times n}$, ${\mathbf {Q}} = {\mathbf {Q}}_{1} \in \mathbb{R}^{n \times n}$ (${\mathbf {Q}}^{T} {\mathbf {Q}} \equiv {\mathbf {I}}$), ${\mathbf {R}} \in \mathbb{R}^{n \times m}$, ${\mathbf {R}}_{1} \in \mathbb{R}^{n \times n}$ (upper triangular), ${\mathbf {R}}_{2} \in \mathbb{R}^{n \times (m - n)}$, and ${\mathbf {P}} \in \mathbb{R}^{m \times m}$ (${\mathbf {P}}^{T} {\mathbf {P}} \equiv {\mathbf {I}}$). It is assumed that the rank of the constraint Jacobian matrix ${\mathbf {A}}$ is less than $n$, corresponding to a rank-deficiency index $d = n - \operatorname{rank}({\mathbf {A}}) > 0$, thus allowing a corresponding number of degrees of freedom for the constrained problem.

The time derivative of matrix ${\mathbf {A}}$ is

$$\begin{aligned} \dot{{\mathbf {A}}}^{T} &= \dot{{\mathbf {Q}}} {\mathbf {R}} {\mathbf {P}}^{T} + {\mathbf {Q}} \dot{{\mathbf {R}}} {\mathbf {P}}^{T} = \dot{{\mathbf {Q}}}_{1} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1} &{\mathbf {R}}_{2} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} + {\mathbf {Q}}_{1} \left [ \textstyle\begin{array}{ c@{\quad}c } \dot{{\mathbf {R}}}_{1} &\dot{{\mathbf {R}}}_{2} \end{array}\displaystyle \right ] {\mathbf {P}}^{T} \end{aligned}$$

(92)

since $\dot{{\mathbf {P}}} \equiv {\mathbf {0}}$ by the definition of pivoting matrix. After pre-multiplication by ${\mathbf {Q}}_{1}^{T}$ and post-multiplication by ${\mathbf {P}}$, one obtains

$$\begin{aligned} {\mathbf {Q}}_{1}^{T} \dot{{\mathbf {A}}}^{T} {\mathbf {P}} &= {\mathbf {Q}}_{1}^{T} \dot{{\mathbf {Q}}}_{1} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1} &{\mathbf {R}}_{2} \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{ c@{\quad}c } \dot{{\mathbf {R}}}_{1} &\dot{{\mathbf {R}}}_{2} \end{array}\displaystyle \right ] , \end{aligned}$$

(93)

exploiting the orthogonality of both matrices. Define

$$\begin{aligned} {\mathbf {Q}}_{1}^{T} \dot{{\mathbf {Q}}}_{1} &= {\boldsymbol {\Omega}} = - {\boldsymbol {\Omega}}^{T} \end{aligned}$$

(94)

with ${\boldsymbol {\Omega}} \in \mathbb{R}^{n \times n}$ because of the orthogonality of matrix ${\mathbf {Q}}_{1}$ or

$$\begin{aligned} {\mathbf {Q}}_{1}^{T} \dot{{\mathbf {Q}}}_{1} &= \left [ \textstyle\begin{array}{c} {\mathbf {Q}}_{1_{\text{ns}}}^{T} \\ {\mathbf {Q}}_{1_{\text{s}}}^{T} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\quad}c } \dot{{\mathbf {Q}}}_{1_{\text{ns}}} &\dot{{\mathbf {Q}}}_{1_{\text{s}}} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {Q}}_{1_{\text{ns}}}^{T} \dot{{\mathbf {Q}}}_{1_{\text{ns}}} & {\mathbf {Q}}_{1_{\text{ns}}}^{T} \dot{{\mathbf {Q}}}_{1_{\text{s}}} \\ {\mathbf {Q}}_{1_{\text{s}}}^{T} \dot{{\mathbf {Q}}}_{1_{\text{ns}}} & {\mathbf {Q}}_{1_{\text{s}}}^{T} \dot{{\mathbf {Q}}}_{1_{\text{s}}} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{ c@{\quad}c } {\boldsymbol{\Omega }}_{\text{ns}} &- {\boldsymbol{\Omega }}_{\text{s}}^{T} \\ {\boldsymbol{\Omega }}_{\text{s}} &{\mathbf {0}} \end{array}\displaystyle \right ] \end{aligned}$$

(95)

with ${\boldsymbol {\Omega}}_{\text{ns}} \in \mathbb{R}^{(n-d) \times (n-d)}$, ${\boldsymbol {\Omega}}_{\text{s}} \in \mathbb{R}^{d \times (n-d)}$ (${\boldsymbol {\Omega}}_{\text{ns}}^{T} = - {\boldsymbol {\Omega}}_{\text{ns}}$). The bottom-right block of matrix ${\boldsymbol {\Omega}}$ is arbitrarily set to zero to minimize the re-orientation of the columns of matrix ${\mathbf {Q}}_{2}$ that correspond to the directions of motion allowed by the rank-deficiency of the constrain Jacobian matrix ${\mathbf {A}}$.

Consider the first $n$ columns of both sides of Eq. (93):

$$\begin{aligned} \left [ {\mathbf {Q}}_{1}^{T} \dot{{\mathbf {A}}}^{T} {\mathbf {P}} \right ] (:, 1:n) &= {\boldsymbol {\Omega}} {\mathbf {R}}_{1} + \dot{{\mathbf {R}}}_{1} = {\mathbf {J}}. \end{aligned}$$

(96)

Explode everything in nonsingular ‘ns’ and singular ‘s’ blocks:

$$\begin{aligned} \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {J}}_{11} &{\mathbf {J}}_{12} \\ {\mathbf {J}}_{21} &{\mathbf {J}}_{22} \end{array}\displaystyle \right ] &= \left [ \textstyle\begin{array}{ c@{\quad}c } {\boldsymbol{\Omega }}_{\text{ns}} &- {\boldsymbol{\Omega }}_{\text{s}}^{T} \\ {\boldsymbol{\Omega }}_{\text{s}} &{\mathbf {0}} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{ c@{\quad}c } {\mathbf {R}}_{1_{\text{ns}}} &{\mathbf {R}}_{1_{\text{s}}} \\ {\mathbf {0}} &{\mathbf {0}} \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{ c@{\quad}c } \dot{{\mathbf {R}}}_{1_{\text{ns}}} &\dot{{\mathbf {R}}}_{1_{\text{s}}} \\ {\mathbf {0}} &{\mathbf {0}} \end{array}\displaystyle \right ] \end{aligned}$$

(97)

with ${\mathbf {J}}_{11} \in \mathbb{R}^{(n-d) \times (n-d)}$, ${\mathbf {J}}_{12} \in \mathbb{R}^{(n-d) \times d}$, ${\mathbf {J}}_{21} \in \mathbb{R}^{d \times (n-d)}$, ${\mathbf {J}}_{22} \in \mathbb{R}^{d \times d}$, ${\mathbf {R}}_{1_{\text{ns}}} \in \mathbb{R}^{(n-d) \times (n-d)}$ (upper triangular, as its time derivative $\dot{{\mathbf {R}}}_{1_{\text{ns}}}$), and ${\mathbf {R}}_{1_{\text{s}}} \in \mathbb{R}^{(n-d) \times d}$. This yields the four equations:

$$\begin{aligned} {\mathbf {J}}_{11} &= {\boldsymbol {\Omega}}_{\text{ns}} {\mathbf {R}}_{1_{\text{ns}}} + \dot{{\mathbf {R}}}_{1_{\text{ns}}}, \end{aligned}$$

(98a)

$$\begin{aligned} {\mathbf {J}}_{12} &= {\boldsymbol {\Omega}}_{\text{ns}} {\mathbf {R}}_{1_{\text{s}}} + \dot{{\mathbf {R}}}_{1_{\text{s}}}, \end{aligned}$$

(98b)

$$\begin{aligned} {\mathbf {J}}_{21} &= {\boldsymbol {\Omega}}_{\text{s}} {\mathbf {R}}_{1_{\text{ns}}}, \end{aligned}$$

(98c)

$$\begin{aligned} {\mathbf {J}}_{22} &= {\boldsymbol {\Omega}}_{\text{s}} {\mathbf {R}}_{1_{\text{s}}}. \end{aligned}$$

(98d)

3.1 C.1 Matrix ${\boldsymbol {\Omega}}$

From Eq. (98c):

$$\begin{aligned} {\boldsymbol {\Omega}}_{\text{s}} &= {\mathbf {J}}_{21} {\mathbf {R}}_{1_{\text{ns}}}^{-1}. \end{aligned}$$

(99)

From Eq. (98a):

$$\begin{aligned} {\mathbf {J}}_{11} {\mathbf {R}}_{1_{\text{ns}}}^{-1} &= {\boldsymbol {\Omega}}_{\text{ns}} + \dot{{\mathbf {R}}}_{1_{\text{ns}}} {\mathbf {R}}_{1_{\text{ns}}}^{-1}. \end{aligned}$$

(100)

Consider its strictly lower triangular part

(101)

Then

$$\begin{aligned} {\boldsymbol {\Omega}}_{\text{ns}} &= {\boldsymbol {\Omega}}_{L} - {\boldsymbol {\Omega}}_{L}^{T}. \end{aligned}$$

(102)

Matrix ${\boldsymbol {\Omega}}$ is then used for the continuation of matrix ${\mathbf {Q}}_{1}$, and specifically of the subspace ${\mathbf {R}} = {\mathbf {Q}}_{1_{\text{s}}}$, as discussed in Sect. 2.4 with reference to matrix ${\mathbf {Q}}$ and subspace ${\mathbf {Q}}_{2}$.

3.2 C.2 Matrix $\dot{{\mathbf {R}}}$

Matrix $\dot{{\mathbf {R}}}$ is irrelevant because the continuation of matrix ${\mathbf {R}}$ is not needed. However, for completeness, it can be obtained by considering again Eq. (98a):

$$\begin{aligned} \dot{{\mathbf {R}}}_{1_{\text{ns}}} &= {\mathbf {J}}_{11} - {\boldsymbol {\Omega}}_{\text{ns}} {\mathbf {R}}_{1_{\text{ns}}}. \end{aligned}$$

(103)

Then, from Eq. (98b):

$$\begin{aligned} \dot{{\mathbf {R}}}_{1_{\text{s}}} &= {\mathbf {J}}_{12} - {\boldsymbol {\Omega}}_{\text{ns}} {\mathbf {R}}_{1_{\text{s}}}. \end{aligned}$$

(104)

Equation (98d) must be intrinsically complied with, owing to the rank-deficiency of the constraint Jacobian matrix. One could use it to verify the consistency of the solution. Consider now columns $(n+1):m$ of Eq. (93):

$$\begin{aligned} \left [ {\mathbf {Q}}_{1}^{T} \dot{{\mathbf {A}}}^{T} {\mathbf {P}} \right ] (:, n+1:m) &= {\boldsymbol {\Omega}} {\mathbf {R}}_{2} + \dot{{\mathbf {R}}}_{2} = {\mathbf {L}} \end{aligned}$$

(105)

with ${\mathbf {L}} \in \mathbb{R}^{n \times (m - n)}$, which yields

$$\begin{aligned} \dot{{\mathbf {R}}}_{2} &= {\mathbf {L}} - {\boldsymbol {\Omega}} {\mathbf {R}}_{2}. \end{aligned}$$

(106)

Otherwise, if $\dot{{\mathbf {R}}}$ is not needed, then one may ignore Eqs. (98b), (98d), and (105).