Skip to main content
SpringerLink
Log in

Coupling rub-impact dynamics of double translational joints with subsidence for time-varying load in a planar mechanical system

  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

Abstract

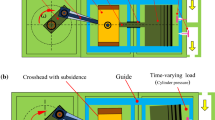
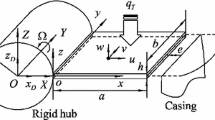
In this paper, a novel dynamic model of coupling translation joints with subsidence for time-varying load in a planar mechanical system is established. One translational joint has four working scenarios, which are free motion, one corner rub-impact, two adjacent corners rub-impact and two opposite corners rub-impact. However, the rub-impact of double coupling translation joints are not a simple superposition of these scenarios, but rather a more complex rub-impact configuration that should be considered in this model. An adaptive fourth-order Runge–Kutta method is utilized to solve the dynamic differential equations. After that, we discuss the dynamic behavior of the rub-impact coupling by taking a triplex member of the crosshead slider, piston rod and piston slider as an example in the reciprocating compressor system. The results show that the double coupling translation joints experience free motion, continuous contact motion and rub-impact motion. The difference is that, in the rub-impact motion, for the crosshead slider there only appears one single corner and two adjacent corners impacting the guide, while the coupling piston slider experiences multiple rub-impact situations including one single corner, two adjacent corners and two opposite corners impacting the guide. Moreover, the results reveal that the subsidence has a significant influence on the rub-impact behavior of the coupling translation joints, and the greater the subsidence, the more severe the vibration response of the slider impacting the guide. Finally, in this rub-impact coupling system, the existence of chaotic behavior is confirmed by the Poincaré section and the largest Lyapunov exponent approaches.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24

Similar content being viewed by others

Abbreviations

\(P\) :

cylinder pressure

\(P_{s}\) :

pressure coefficient

\(\theta _{1}\) :

rotation angle of the crankshaft

\(\theta _{2}\) :

rotation angle of the linkage

\(\theta _{3}\) :

rotation angle of the crosshead slider

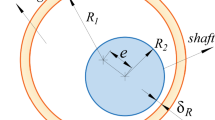
\(\delta _{i}\) :

relative penetration depth for the \(i\)th corner of the slider

\(S_{Ni}\) :

distance between each corner of the slider and the surface of the guide

\(e\) :

width of the guide

\(b_{1}\) :

width of the crosshead slider

\(r_{c}\) :

clearance between the crosshead slider and the upper edge of guide

\(d\) :

subsidence size

\(a_{2}\) :

length of the piston slider

\(b_{2}\) :

width of the piston slider

\(m_{1}\) :

mass of the crankshaft

\(m_{2}\) :

mass of the linkage

\(m_{3}\) :

mass of the crosshead

\(m_{4}\) :

mass of the piston rod

\(m_{5}\) :

mass of the piston

\(l_{1}\) :

length of crankshaft

\(l_{2}\) :

length of linkage

\(l_{3}\) :

distance between the crosshead slider and the piston slider

\(F_{Ni}\) :

normal contact force of each slider corner

\(n\) :

power exponent

\(K\) :

generalized stiffness constant

\(E_{1}\) :

Young’s modulus of the slider

\(E_{2}\) :

Young’s modulus of the guide

\(\dot{\delta }_{i}\) :

relative penetration velocity

\(\dot{\delta }_{i}^{( - )}\) :

initial impact velocity

\(c_{r}\) :

restitution coefficient

\(F_{Ti}\) :

friction force of each slider corner

\(c_{f}\) :

dynamic friction coefficient

\(v_{t}\) :

relative tangential velocity along the direction of the guide

\(c_{d}\) :

dynamic correction coefficient

\(Q_{c}\) :

resultant of normal contact force and friction force

\(\omega _{1}\) :

angular velocity of the crankshaft

\(\omega _{2}\) :

angular velocity of the linkage

\(\omega _{3}\) :

angular velocity of the slider

\(Q_{c,j}\) :

nonconservative generalized force

\(E\) :

kinetic energy

\(V\) :

potential energy

\(M\) :

the external moment acting on the crankshaft

\(E_{1}\) :

kinetic energy of the crankshaft

\(E_{2}\) :

kinetic energy of the linkage

\(E_{3}\) :

kinetic energy of the crosshead slider

\(E_{4}\) :

kinetic energy of the piston rod

\(E_{5}\) :

kinetic energy of the piston slider

\(J_{1}\) :

moment of inertia of the crankshaft around the its centroid

\(J_{2}\) :

moment of inertia of the linkage around the its centroid

\(J_{3}\) :

moment of inertia of the crosshead slider around the its centroid

\(J_{4}\) :

moment of inertia of the piston rod around the crosshead slider’s centroid

\(J_{5}\) :

moment of inertia of the piston slider around the crosshead slider’s centroid

References

  1. Zhang, J., Wang, Q.: Modeling and simulation of a frictional translational joint with a flexible slider and clearance. Multibody Syst. Dyn. 38(4), 367–389 (2016)

    MathSciNet  MATH  Google Scholar 

  2. Flores, P., Ambrosio, J., Claro, J.C.P.: Kinematics and Dynamics of Multibody Systems with Imperfect Joints Models and Case Studies. Lecture Notes in Applied and Computational Mechanics. Springer, Berlin (2008)

    MATH  Google Scholar 

  3. Erkaya, S., Dogan, S., Ulus, S.: Effects of joint clearance on the dynamics of a partly compliant mechanism: numerical and experimental studies. Mech. Mach. Theory 88, 125–140 (2015)

    Google Scholar 

  4. Erkaya, S., Dogan, S.: A comparative analysis of joint clearance effects on articulated and partly compliant mechanisms. Nonlinear Dyn. 81(1–2), 323–341 (2015)

    Google Scholar 

  5. Farahan, S.B., Ghazavi, M.R., Rahmanian, S.: Bifurcation in a planar four-bar mechanism with revolute clearance joint. Nonlinear Dyn. 87(2), 955–973 (2017)

    Google Scholar 

  6. Erkaya, S.: Experimental investigation of flexible connection and clearance joint effects on the vibration responses of mechanisms. Mech. Mach. Theory 121, 515–529 (2018)

    Google Scholar 

  7. Tan, H., Hu, Y., Li, L.: A continuous analysis method of planar rigid-body mechanical systems with two revolute clearance joints. Multibody Syst. Dyn. 40(4), 347–373 (2017)

    MathSciNet  Google Scholar 

  8. Ting, K.-L., Hsu, K.-L., Yu, Z., Wang, J.: Clearance-induced output position uncertainty of planar linkages with revolute and prismatic joints. Mech. Mach. Theory 111, 66–75 (2017)

    Google Scholar 

  9. Salahshoor, E., Ebrahimi, S., Zhang, Y.: Frequency analysis of a typical planar flexible multibody system with joint clearances. Mech. Mach. Theory 126, 429–456 (2018)

    Google Scholar 

  10. Zhong, S., Zhong, J., Zhang, Q., Maia, N.: Quasi-optical coherence vibration tomography technique for damage detection in beam-like structures based on auxiliary mass induced frequency shift. Mech. Syst. Signal Process. 93, 241–254 (2017)

    Google Scholar 

  11. Cui, L., Huang, J., Zhang, F., Chu, F.: HVSRMS localization formula and localization law: localization diagnosis of a ball bearing outer ring fault. Mech. Syst. Signal Process. 120, 608–629 (2019)

    Google Scholar 

  12. Wang, X., Liu, G., Ma, S., Tong, R.: Study on dynamic responses of planar multibody systems with dry revolute clearance joint: numerical and experimental approaches. J. Sound Vib. 438, 116–138 (2019)

    Google Scholar 

  13. Erkaya, S., Dogan, S., Sefkatlioglu, E.: Analysis of the joint clearance effects on a compliant spatial mechanism. Mech. Mach. Theory 104, 255–273 (2016)

    Google Scholar 

  14. Flores, P., Ambrosio, J., Claro, J.C.P., Lankarani, H.M.: Dynamics of multibody systems with spherical clearance joints. J. Comput. Nonlinear Dyn. 1(3), 240–247 (2006)

    MATH  Google Scholar 

  15. Marques, F., Isaac, F., Dourado, N., Souto, A.P., Flores, P., Lankarani, H.M.: A study on the dynamics of spatial mechanisms with frictional spherical clearance joints. J. Comput. Nonlinear Dyn. 12(5), 051013 (2017)

    Google Scholar 

  16. Tian, Q., Zhang, Y., Chen, L., Flores, P.: Dynamics of spatial flexible multibody systems with clearance and lubricated spherical joints. Comput. Struct. 87(13–14), 913–929 (2009)

    Google Scholar 

  17. Tian, Q., Flores, P., Lankarani, H.M.: A comprehensive survey of the analytical, numerical and experimental methodologies for dynamics of multibody mechanical systems with clearance or imperfect joints. Mech. Mach. Theory 122, 1–57 (2018)

    Google Scholar 

  18. Flores, P., Lankarani, H.M.: Dynamic response of multibody systems with multiple clearance joints. J. Comput. Nonlinear Dyn. 7(3), 636–647 (2012)

    Google Scholar 

  19. Flores, P., Ambrosio, J., Claro, J.C.P., Lankarani, H.M.: Translational joints with clearance in rigid multibody systems. J. Comput. Nonlinear Dyn. 3(1), 011007 (2008)

    Google Scholar 

  20. Stoenescu, E.D., Marghitu, D.B.: Dynamic analysis of a planar rigid-link mechanism with rotating slider joint and clearance. J. Sound Vib. 266(2), 394–404 (2003)

    Google Scholar 

  21. Wilson, R.: the dynamics of the slider crank mechanism with clearance in the sliding bearing. Ph.D. thesis, University of Newcastle upon Tyne (1971)

  22. Wilson, R., Fawcett, J.N.: Dynamics of the slider-crank mechanism with clearance in the sliding bearing. Mech. Mach. Theory 9(1), 61–80 (1974)

    Google Scholar 

  23. Farahanchi, F., Shaw, S.W.: Chaotic and periodic dynamics of a slider-crank mechanism with slider clearance. J. Sound Vib. 177(3), 307–324 (1994)

    MATH  Google Scholar 

  24. Flores, P., Leine, R., Glocker, C.: Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach. Multibody Syst. Dyn. 23(2), 165–190 (2010)

    MathSciNet  MATH  Google Scholar 

  25. Flores, P., Leine, R., Glocker, C.: Application of the nonsmooth dynamics approach to model and analysis of the contact-impact events in cam-follower systems. Nonlinear Dyn. 69(4), 2117–2133 (2012)

    MathSciNet  Google Scholar 

  26. Qi, Z., Luo, X., Huang, Z.: Frictional contact analysis of spatial prismatic joints in multibody systems. Multibody Syst. Dyn. 26(4), 441–468 (2011)

    MathSciNet  MATH  Google Scholar 

  27. Qi, Z., Xu, Y., Luo, X., Yao, S.: Recursive formulations for multibody systems with frictional joints based on the interaction between bodies. Multibody Syst. Dyn. 24(2), 133–166 (2010)

    MathSciNet  MATH  Google Scholar 

  28. Zhuang, F., Wang, Q.: Modeling and simulation of the nonsmooth planar rigid multibody systems with frictional translational joints. Multibody Syst. Dyn. 29(4), 403–423 (2013)

    MathSciNet  Google Scholar 

  29. Zhuang, F.-F., Wang, Q.: Modeling and analysis of rigid multibody systems with driving constraints and frictional translation joints. Acta Mech. Sin. 30(3), 437–446 (2014)

    MathSciNet  MATH  Google Scholar 

  30. Cavalieri, F.J., Cardona, A.: Non-smooth model of a frictionless and dry three-dimensional revolute joint with clearance for multibody system dynamics. Mech. Mach. Theory 121, 335–354 (2018)

    Google Scholar 

  31. Wu, L., Marghitu, D.B., Zhao, J.: Nonlinear dynamics response of a planar mechanism with two driving links and prismatic pair clearance. Math. Probl. Eng. 2017, 1–12 (2017)

    Google Scholar 

  32. Xiao, S., Liu, S., Cheng, S., Xue, X., Song, M., Sun, X.: Dynamic analysis of reciprocating compressor with clearance and subsidence. J. Vibroeng. 19(7), 5061–5085 (2017)

    Google Scholar 

  33. Xiao, S., Zhang, H., Liu, S., Jiang, F., Song, M.: Dynamic behavior analysis of reciprocating compressor with subsidence fault considering flexible piston rod. J. Mech. Sci. Technol. 32(9), 4103–4124 (2018)

    Google Scholar 

  34. Xiao, S., Liu, S., Jiang, F., Song, M., Cheng, S.: Nonlinear dynamic response of reciprocating compressor system with rub-impact fault caused by subsidence. J. Vib. Control 25(11), 1737–1751 (2019)

    MathSciNet  Google Scholar 

  35. Hertz, H.: On the Contact of Solids—on the Contact of Rigid Elastic Solids and on Hardness. MacMillan, London (1896)

    Google Scholar 

  36. Lankarani, H.M., Nikravesh, P.E.: A contact force model with hysteresis damping for impact analysis of multibody systems. J. Mech. Des. 112(3), 369–376 (1990)

    Google Scholar 

  37. Lankarani, H.M.: Canonical equations of motion and estimation of parameters in the analysis of impact problems. Ph.D. thesis, University of Arizona (1988)

  38. Bai, Z.F., Zhao, J.J., Chen, J., Zhao, Y.: Design optimization of dual-axis driving mechanism for satellite antenna with two planar revolute clearance joints. Acta Astronaut. 144, 80–89 (2018)

    Google Scholar 

  39. Dubowsky, S.: On predicting the dynamic effects of clearances in planar mechanisms. J. Eng. Ind. 96(1), 317–323 (1974)

    Google Scholar 

  40. Rooney, G.T., Deravi, P.: Coulomb friction in mechanism sliding joints. Mech. Mach. Theory 17(3), 207–211 (1982)

    Google Scholar 

  41. Threlfall, D.C.: The inclusion of Coulomb friction in mechanisms programs with particular reference to DRAM au programme DRAM. Mech. Mach. Theory 13(4), 475–483 (1978)

    Google Scholar 

  42. Ambrósio, J.A.C.: Impact of Rigid and Flexible Multibody Systems: Deformation Description and Contact Models, vol. 103. Springer, Netherlands (2003)

    MATH  Google Scholar 

  43. Song, Z., Yang, X., Huang, H., Li, B.: Dynamic analysis of planar mechanisms with revolute clearance joints based on two evaluation indices. Mech. Based Des. Struct. Mach. 44(3), 231–249 (2016)

    Google Scholar 

  44. Erkaya, S.: Clearance-induced vibration responses of mechanical systems: computational and experimental investigations. J. Braz. Soc. Mech. Sci. Eng. 40(2), 90 (2018)

    Google Scholar 

  45. Chen, Y., Sun, Y., Chen, C.: Dynamic analysis of a planar slider-crank mechanism with clearance for a high speed and heavy load press system. Mech. Mach. Theory 98, 81–100 (2016)

    Google Scholar 

  46. Flores, P., Ambrósio, J., Claro, J.C.P., Lankarani, H.M.: Influence of the contact-impact force model on the dynamic response of multi-body systems. Proc. Inst. Mech. Eng., Proc., Part K, J. Multi-Body Dyn. 220(1), 21–34 (2006)

    Google Scholar 

  47. Ahmed, S., Lankarani, H.M., Pereira, M.F.O.S.: Frictional impact analysis in open-loop multibody mechanical systems. J. Mech. Des. 121(1), 119–127 (1999)

    Google Scholar 

  48. Lankarani, H.M., Pereira, M.F.O.S.: Treatment of impact with friction in planar multibody mechanical systems. Multibody Syst. Dyn. 6(3), 203–227 (2001)

    MATH  Google Scholar 

  49. Varedi, S.M., Daniali, H.M., Dardel, M.: Dynamic synthesis of a planar slider-crank mechanism with clearances. Nonlinear Dyn. 79(2), 1587–1600 (2015)

    Google Scholar 

  50. Chen, J.L., Zhang, L.B., Duan, L.X., Hu, C.: Diagnosis of reciprocating compressor piston-cylinder liner wear fault based on lifting scheme packet. J. China Univ. Pet. 35(1), 130–145 (2011)

    Google Scholar 

  51. Wolf, A., Swift, J.B., Swinney, H.L., Vastano, J.A.: Determining Lyapunov exponents from a time series. Physica D 16, 285–317 (1985)

    MathSciNet  MATH  Google Scholar 

  52. Kapitaniak, T.: Chaotic Oscillations in Mechanical Systems. Manchester University Press, Manchester (1991)

    MATH  Google Scholar 

Download references

Acknowledgements

This work is supported by the Natural Science Foundation of China (Grant Nos. 51575331 and 61603238), Research project for Serving local special project of Ningde Normal University (Grant No. 2018ZX409 and 2019ZX403), Young and Middle-aged Teacher in Fujian Province (Grant No. JT180601) and Young teacher special project of Ningde Normal University (Grant No. 2018Q101). These supports are gratefully acknowledged.

Author information

Authors and Affiliations

  1. School of Mechatronic Engineering and Automation, Shanghai University, Shanghai, 200072, People’s Republic of China

    Shungen Xiao, Shulin Liu, Nie Ang & Hongli Zhang

  2. School of Information, Mechanical and Electrical Engineering, Ningde Normal University, Ningde, 352100, People’s Republic of China

    Shungen Xiao & Mengmeng Song

Authors
  1. Shungen Xiao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shulin Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mengmeng Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Nie Ang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hongli Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shulin Liu.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xiao, S., Liu, S., Song, M. et al. Coupling rub-impact dynamics of double translational joints with subsidence for time-varying load in a planar mechanical system. Multibody Syst Dyn 48, 451–486 (2020). https://doi.org/10.1007/s11044-019-09718-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11044-019-09718-9

Keywords

Search

Navigation