A modified neo-Hookean model for semi-crystalline thermoplastics assessed by relaxation and zero-stress creep tests of recycled polypropylene and polyoxymethylene

Abstract

The mechanical behavior of thermoplastics is strongly rate-dependent, and oftentimes it is difficult to find constitutive models that can accurately describe their behavior in the small to moderate strain regime. In this paper, a hyperelastic network model (modified neo-Hookean) and a set of experiments are presented. The testing consists of monotonic tensile loading as well as stress relaxation and zero stress creep. Two materials were tested, polyoxymethylene (POM) and recycled polypropylene (rPP), representing one more rigid and brittle and one softer and more ductile semi-crystalline polymer. The model contains two main novelties. The first novelty is that the stiffness is allowed to vary with the elastic deformation (in contrast to a standard neo-Hookean model). The second novelty is that the exponent governing viscous relaxation is allowed to vary with the viscous deformation. The basic features of the new model are illustrated, and the model was fitted to the experimental data. The model proved to be able to describe the experimental results well.

1 Introduction

Semi-crystalline polymers are widely used today in a vast array of applications. Accurate modeling of the mechanical response of these materials is therefore of great importance. The mechanical response of these materials is complicated and strongly rate-dependent. During their service life, these materials may be exposed to large deformations, and material models valid for finite strains are therefore needed. The duty life may also include long-time loading that may result in substantial creep and/or stress relaxation.

The present work includes both experimental testing and constitutive modeling. Two materials are considered: recycled polypropylene (rPP) and polyoxymethylene (POM). Both rPP and POM are semi-crystalline thermoplastics. POM is a rigid and brittle copolymer with good hydrolysis resistance. It also has high resistance to thermal and oxidative degradation. It is widely used in different applications from automotive industry to consumer goods as well as reinforcement in airport pavement concrete. In comparison to POM, rPP is a more ductile polymer. The mechanical behavior of POM and rPP has been tested in previous studies. Hartmann (2006) and Kroon and Rubin (2023) investigate the stress-strain behavior of POM at different strain rates and also during cyclic loading. Fischer et al. (2019) also study the tensile properties of POM, and Tscharnuter and Muliana (2013) investigate the mechanical response at small to moderate strains and at elevated temperatures. Shariati et al. (2011) investigate the response of POM under cyclic uniaxial tensile testing and also the fatigue properties. Schrader et al. (2020) and Berer et al. (2014) study the fracture and fatigue properties of POM. Another method to characterize materials is to study scratching and indentation of the surface of materials, and these methods were applied to POM by Pistor and Friedrich (1997). The mechanical properties of rPP have also been addressed in previous studies. The tensile and fracture properties of rPP were studied by Brachet et al. (2008) at different temperatures, and Ladhari et al. (2021) provide a review of the tensile and fracture properties of rPP. Aurrekoetxea et al. (2001) investigate the effects of recycling on both the microstructure and the mechanical properties of polypropylene. In the present study, these two materials were tested in uniaxial tensile tests. The main focus was on stress relaxation and unloading behavior of these two materials.

Many investigations have been devoted to exploring the microstructure in semi-crystalline polymers both in the virgin state and during deformation, see e.g. Katti and Schultz (1982), Galeski et al. (1992), Bartczak et al. (1994), Lin and Argon (1994b), Li et al. (2003), Argon et al. (2005), Addiego et al. (2006). The picture is very complicated. Phenomenological models for the mechanical response are therefore needed. Many constitutive models employ the multiplicative decomposition of the deformation gradient into elastic and inelastic parts (Kröner 1960; Lee 1968; Boyce et al. 1989). Some material models actually try to connect the microstructural processes to the theory of the model, for instance, Parks and Ahzi (1990), Lee et al. (1993), van Dommelen et al. (2003), and Nikolov et al. (2006). Most attempts, however, are more phenomenologically oriented. Some of the attempts that can be mentioned are Duan et al. (2001), Bedoui et al. (2006), Hartmann (2006), Ayoub et al. (2010), Zeng et al. (2010), Polanco-Loria et al. (2010), Balieu et al. (2013), Krairi and Doghri (2014), Abdul-Hameed et al. (2014), Garcia-Gonzalez et al. (2017), and Kroon and Rubin (2023). Most models assume isothermal conditions, but a few models account for temperature changes as well (e.g. Bergström et al. 2003; Nguyen et al. 2008; Maurel-Pantel et al. 2015; Garcia-Gonzalez et al. 2017; Felder et al. 2020; Hao et al. 2022).

The experimental results in the present study are assessed by the use of a new constitutive model for semi-crystalline polymers. The model builds on the well-established framework of the multiplicative decomposition of the deformation gradient into elastic and inelastic parts. The elastic behavior of the model is characterized by a modified neo-Hookean model, where an extra feature allows for a variable initial stiffness of the material. Also, exponents related to the relaxation behavior is allowed to evolve during the deformation of the material.

The paper is organized as follows: Sect. 2 describes the experimental setup. In Sect. 3, the theory and the new constitutive model is presented, and in Sect. 4, a parameter study illustrates the main features of the proposed model. Section 5 provides some details of the numerical implementation of the model. In Sect. 6, the main results of the study are presented, and a discussion and some concluding remarks are provided in Sect. 7.

2 Experiments

Uniaxial tensile tests were performed on two semi-crystalline polymers: polyoxymethylene (POM) and recycled polypropylene (rPP). The specimen layout and parameter extraction were according to ISO527 (2012). The force history was registered during the tests using a load cell. The longitudinal strain in the specimens during the tests was quantified both in terms of the global (linear) strain, i.e., load cell travel divided by the initial distance between the grips in the testing machine, and the local (linear) strain, which was measured using DIC (digital image correlation). In the latter case, a speckle pattern was applied to the specimens, and the tests were video-recorded. Not all tests were analyzed using DIC, though, but a relation between the global strain and the local strain was established based on the DIC analyses. Three types of load histories were considered, from here on referred to as test types 1, 2, and 3.

Test type 1

The monotonic tensile tests were conducted according to (ISO527 2012). Two velocities were used: 50 mm/min and 800 mm/min. The former is common practice and makes it easier to compare to commercial material data. The second was the maximum capacity of the tensile testing machine. This test was done in the following order:

• Monotonic loading until failure.

Test type 2

This test was performed at three different strain levels for stress relaxation, which were decided based on the previous monotonic tensile tests. This test was done in the following order:

• Loading up to given strain level,

• Stress relaxation at constant strain during 20 h,

• Unloading to zero stress,

• Creep under zero stress for 4 h.

Test type 3

This test was performed in the same manner as test type 2 but without the stress relaxation phase. This test was performed with three different maximum/return strain levels. This test was done in the following order:

• Loading up to given strain level,

• Unloading to zero stress,

• Creep under zero stress for 4 h.

3 Theoretical framework

3.1 Kinematics

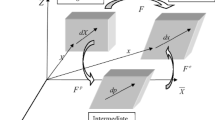
The deformation gradient is given by $\textbf{F}=\partial \textbf{x}/\partial \textbf{X}$, where x and X are the current and the reference position vectors, respectively. The deformation gradient might be divided further into an elastic and a viscous part following the multiplicative decomposition, i.e., $\textbf{F}=\textbf{F}_{\mathrm{e}}\textbf{F}_{\mathrm{v}}$. The volumetric part of the deformation can be written as $J={\mathrm{det}}(\textbf{F})={\mathrm{det}}(\textbf{F}_{\mathrm{e}})\cdot {\mathrm{det}}( \textbf{F}_{\mathrm{v}})$.

The viscous part is assumed to be incompressible. Hence, $J_{\mathrm{v}}={\mathrm{det}}(\textbf{F}_{\mathrm{v}})\equiv 1$, and thereby $J={\mathrm{det}}(\textbf{F}_{\mathrm{e}})=J_{\mathrm{e}}$. The relations between the isochoric parts of the deformation gradient and the finger tensor (b) are as follows:

$$ \textbf{F}=J^{1/3}\bar{\textbf{F}}, \quad \quad \textbf{b}=\textbf{F} \textbf{F}^{T}, \quad \quad \textbf{b}=J^{1/3}\bar{\textbf{F}}(J^{1/3} \bar{\textbf{F}})^{T}=J^{2/3}\bar{\textbf{b}}, $$

(1)

where $\bar{\textbf{b}}$ is a unimodular tensor that models the volume-preserving (distortional, isochoric) part of the deformation. The deviatoric part of the unimodular finger tensor can be written as

$$ \centering \bar{\textbf{b}}'=\bar{\textbf{b}}-\frac{1}{3}\bar{\textbf{b}}: \textbf{I}, $$

(2)

where $\bar{\textbf{b}}:\textbf{I}$ denotes a double contraction of the two second-order tensors $\bar{\textbf{b}}$ and $\textbf{I}$, and $\textbf{I}$ is the second-order unit tensor.

In a similar fashion, the elastic part of the finger tensor is introduced:

$$ \textbf{b}_{\mathrm{e}} = \textbf{F}_{\mathrm{e}}\textbf{F}_{\mathrm{e}}^{\mathrm{T}}, \quad \quad \bar{\textbf{b}}_{\mathrm{e}}=J^{-2/3}\textbf{b}_{\mathrm{e}} \quad \quad \bar{\textbf{b}}'_{\mathrm{e}}=\bar{\textbf{b}}_{\mathrm{e}}-\frac{1}{3} \bar{\textbf{b}}_{\mathrm{e}}:\textbf{I} \quad \quad \bar{I}_{\mathrm{e1}}= \bar{\textbf{b}}_{\mathrm{e}}:\textbf{I}, $$

(3)

where $\bar{I}_{\mathrm{e1}}$ is the first invariant of $\bar{\textbf{b}}_{\mathrm{e}}$. For viscous deformation, the entities

$$ \textbf{b}_{\mathrm{v}} = \textbf{F}_{\mathrm{v}}\textbf{F}_{\mathrm{v}}^{\mathrm{T}}, \quad \quad I_{\mathrm{v1}}=\textbf{b}_{\mathrm{v}}:\textbf{I} $$

(4)

are introduced.

The velocity gradient is given by $\textbf{L}=\dot{\textbf{F}}\textbf{F}^{-1}$. The velocity gradient can be divided into a symmetric part and an anti-symmetric part, referred to as the rate of deformation (d) and spin tensor (w), respectively. Furthermore, the velocity gradient might be split into an elastic and a viscous part:

$$ \begin{aligned} \textbf{L}=\dot{\textbf{F}}\textbf{F}^{-1}=\cdots= \dot{\textbf{F}}_{\mathrm{e}}\textbf{F}_{\mathrm{e}}^{-1}+\textbf{F}_{\mathrm{e}} \tilde{\textbf{L}}_{\mathrm{v}}\textbf{F}_{\mathrm{e}}^{-1}=\textbf{L}_{\mathrm{e}}+ \textbf{L}_{\mathrm{v}}, \end{aligned} $$

(5)

where $\tilde{\textbf{L}}_{\mathrm{v}}=\dot{\textbf{F}}_{\mathrm{v}}\textbf{F}_{\mathrm{v}}^{-1}$ is a velocity gradient defined in the intermediate configuration, and $\tilde{\textbf{d}}_{\mathrm{v}}$ is the symmetric part of $\tilde{\textbf{L}}_{\mathrm{v}}$. The viscous part of the velocity gradient can be divided into a symmetric part and an anti-symmetric part, $\textbf{L}_{\mathrm{v}}=\textbf{d}_{\mathrm{v}}+\textbf{w}_{\mathrm{v}}$.

3.2 Constitutive behavior

The constitutive model is based on the Helmholtz free energy. In this model, the deviatoric part of the elastic deformation is accounted for by the first invariant $\bar{I}_{\mathrm{e1}}$, and the volumetric part is represented by the Jacobian $J$. The model is related to the neo-Hookean model, but with a nonlinearity due to a strain-dependent shear modulus:

$$ \psi _{\mathrm{M}}=\frac{1}{2}\left (\mu _{\mathrm{i}}\left (\bar{I}_{\mathrm{e1}}-3 \right )+\beta _{\mathrm{e}}(\mu _{\mathrm{f}}-\mu _{\mathrm{i}})\ln \left [{\mathrm{cosh}} \left (\frac{\bar{I}_{\mathrm{e1}}-3}{\beta _{\mathrm{e}}}\right )\right ] \right )+\frac{\kappa}{2}(J-1)^{2}. $$

(6)

Above, $\psi _{\mathrm{M}}$ denotes the strain energy of a single Maxwell branch. Later this will be generalized to a model with several branches. Furthermore, $\mu _{\mathrm{i}}$ and $\mu _{\mathrm{f}}$ are the initial and final shear moduli, respectively, $\beta _{\mathrm{e}}$ is a reference strain, and $\kappa$ is the bulk modulus. Internal dissipation must be nonnegative, requiring that

$$ J \boldsymbol{\sigma} : \textbf{d}-\dot{\psi}_{\mathrm{M}}\ge 0, $$

(7)

where $\boldsymbol{\sigma}$ is the Cauchy stress, and the second term can be written as follows:

$$ \dot{\psi}_{\mathrm{M}}(\bar{I}_{e1},J)=\cdots= \left [\mu _{\mathrm{eff}}(\bar{I}_{ \mathrm{e1}})\bar{\textbf{b}}'_{\mathrm{e}}+\kappa J(J-1)\textbf{I}\right ]: \textbf{d}-\mu _{\mathrm{eff}}(\bar{I}_{\mathrm{e1}})(\textbf{F}_{\mathrm{e}} \tilde{\textbf{d}}_{\mathrm{v}}\textbf{F}_{\mathrm{e}}^{\mathrm{T}}):\textbf{I}, $$

(8)

where

$$ \mu _{\mathrm{eff}}(\bar{I}_{\mathrm{e1}})=\mu _{\mathrm{i}}+(\mu _{\mathrm{f}}-\mu _{ \mathrm{i}}){\mathrm{tanh}}\left (\frac{\bar{I}_{\mathrm{e1}}-3}{\beta _{\mathrm{e}}} \right ). $$

(9)

The effective shear modulus $\mu _{\mathrm{eff}}$ is based on the current elastic deformation, quantified by $\bar{I}_{\mathrm{e1}}$. Equation (7) can thereby be rewritten as

$$ \left [J\boldsymbol{\sigma}-\mu _{\mathrm{eff}}(\bar{I}_{\mathrm{e1}}) \bar{\textbf{b}}'_{\mathrm{e}}-\kappa J(J-1)\textbf{I}\right ]:\textbf{d}+ \mu _{\mathrm{eff}}(\bar{I}_{\mathrm{e1}})(\textbf{F}_{\mathrm{e}}\tilde{\textbf{d}}_{ \mathrm{v}}\textbf{F}_{\mathrm{e}}^{\mathrm{T}}):\textbf{I}\ge 0. $$

(10)

Based on the result above, the Cauchy stress is defined as

$$ \boldsymbol{\sigma}=\frac{\mu _{\mathrm{eff}}(\bar{I}_{\mathrm{e1}})}{J} \bar{\textbf{b}}'_{e}+\kappa (J-1)\textbf{I}. $$

(11)

For the viscous deformation, it is assumed that $\textbf{L}_{\mathrm{v}}$ is symmetric, i.e., $\textbf{w}_{\mathrm{v}}\equiv \mathbf{{0}}$. The evolution of the viscous deformation is then modeled as

$$ \textbf{d}_{\mathrm{v}}=\dot{\gamma}\textbf{N}, $$

(12)

where $\dot{\gamma}$ governs the rate of viscous deformations and

$$ \textbf{N}=\frac{\boldsymbol{\sigma}'}{\tau}, $$

(13)

where $\boldsymbol{\sigma}'$ is the deviatoric stress tensor, and $\tau =(\boldsymbol{\sigma}':\boldsymbol{\sigma}')^{1/2}$ is the Frobenius norm. The assumptions above result in an evolution law for $\textbf{F}_{\mathrm{v}}$ in the form

$$ \dot{\textbf{F}}_{\mathrm{v}}=\dot{\gamma}\textbf{F}_{\mathrm{e}}^{-1}\textbf{N} \textbf{F}. $$

(14)

The flow rate $\dot{\gamma}$ is given by

$$ \dot{\gamma}=\dot{\gamma}_{0}\left (\frac{\tau}{\hat{\tau}+aR(p)} \right )^{m_{\mathrm{eff}}}, $$

(15)

where $\dot{\gamma}_{0}$ is an arbitrary reference rate (set to 1/s) included for dimensional consistency. The ramp function is defined as $R(x)=(x+|x|)/2$, $p=-(\boldsymbol{\sigma}:\textbf{I})/3$ is the hydrostatic pressure, and $a$, $\hat{\tau}$, and $m_{\mathrm{eff}}$ are material parameters and functions. The exponent $m_{\mathrm{eff}}$ is a strain-dependent parameter and is defined as

$$ m_{\mathrm{eff}}=m_{\mathrm{i}}+(m_{\mathrm{f}}-m_{\mathrm{i}}){\mathrm{tanh}}\left ( \frac{I_{\mathrm{v1}}-3}{\beta _{\mathrm{v}}}\right ), $$

(16)

where $\beta _{\mathrm{v}}$ is a reference strain, and $m_{\mathrm{i}}$ and $m_{\mathrm{f}}$ are the initial and the final values of $m_{\mathrm{eff}}$, respectively.

Returning to (7) above, it is concluded that the internal dissipation takes the form

$$ J\boldsymbol{\sigma}:\textbf{d}-\dot{\psi}_{\mathrm{M}}=\cdots = \frac{\mu _{\mathrm{eff}}^{2}\dot{\gamma}}{\tau}\bar{\textbf{b}}'_{\mathrm{e}}: \bar{\textbf{b}}'_{\mathrm{e}}\ge 0, $$

(17)

which is always nonnegative. It can also be shown that the choice of $\dot{\textbf{F}}_{\mathrm{v}}$ above ensures that the unimodularity of $\textbf{F}_{\mathrm{v}}$ is preserved in the sense that

$$ \dot{\overline{{\mathrm{det}}\textbf{F}_{\mathrm{v}}}}={\mathrm{det}}\textbf{F}_{\mathrm{v}} \cdot (\textbf{F}_{\mathrm{v}}^{-1}:\dot{\textbf{F}}_{\mathrm{v}})=\cdots = \dot{\gamma}\textbf{N}:\textbf{I}=0, $$

(18)

since $\textbf{N}$ is a deviatoric tensor.

The description so far is essentially valid for a simple Maxwell element. For the material considered here, relaxation is assumed to take place at different time scales. The description above is therefore expanded to a generalized Maxwell model with three branches:

$$ \psi =\sum _{\alpha =A}^{C}\frac{1}{2}\left \{\mu _{\mathrm{i},\mathrm{\alpha}} \left (\bar{I}_{\mathrm{e1},\mathrm{\alpha}}-3\right )+ \beta _{\mathrm{e},\mathrm{\alpha}}(\mu _{ \mathrm{f},\mathrm{\alpha}}-\mu _{\mathrm{i},\mathrm{\alpha}}) \ln \left [{\mathrm{cosh}}\left ( \frac{\bar{I}_{\mathrm{e1},\mathrm{\alpha}}-3}{\beta _{\mathrm{e},\mathrm{\alpha}}}\right )\right ]\right \}+\frac{\kappa}{2}(J-1)^{2}. $$

(19)

An extra index’$\alpha$’ is added to the description, denoting the individual branches. Branch A is taken to be perfectly elastic, i.e., $\textbf{F}_{{\mathrm{v}},A}\equiv \textbf{I}$. The total Cauchy stress is a summation of the stress in the three branches:

$$ \boldsymbol{\sigma}=\sum _{\alpha =A}^{C}\frac{1}{J}\left [\mu _{{ \mathrm{i}},\alpha}+(\mu _{{\mathrm{f}},\alpha}-\mu _{{\mathrm{i}},\alpha}){\mathrm{tanh}} \left (\frac{\bar{I}_{{\mathrm{e1}},\alpha}-3}{\beta _{{\mathrm{e}},\alpha}} \right )\right ]\bar{\textbf{b}}'_{{\mathrm{e}},\alpha}+\kappa (J-1) \textbf{I}. $$

(20)

Also, each branch has its own set of state variables and evolution equations, according to the description above.

When comparing the model to experiments, the first Piola–Kirchhoff stress $\textbf{P}=J\boldsymbol{\sigma}\textbf{F}^{-\mathrm{T}}$ and the linear strain $\boldsymbol{\varepsilon}=\textbf{U}-\textbf{I}$ are also utilized, where $\textbf{U}$ is the right stretch tensor associated with $\textbf{F}$.

4 Parameter study

4.1 Influence of model parameters

The springs in the proposed model are modeled by a modified neo-Hookean model, where the distortional and volumetric stiffness are governed by the shear modulus and the bulk modulus. The nonlinearly elastic part is controlled through the parameters $\mu _{\mathrm{i}}$, $\mu _{\mathrm{f}}$, and $\beta _{\mathrm{e}}$. The two values $\mu _{\mathrm{i}}$ and $\mu _{\mathrm{f}}$ are the two limit values that the stiffness can vary between. The parameter $\beta _{\mathrm{e}}$ is the strain that defines when the transition between $\mu _{\mathrm{i}}$ and $\mu _{\mathrm{f}}$ occurs, see Fig. 1.

Fig. 1

Variation of $\mu _{\mathrm{eff}}$ for $\mu _{\mathrm{i}}=200$ MPa, $\mu _{\mathrm{f}}=100$ MPa, and $\beta _{\mathrm{e}}=0.2$

The dampers are modeled as power-law damper, each depending on five parameters: $\hat{\tau}$, $a$, $m_{\mathrm{i}}$, $m_{\mathrm{f}}$, and $\beta _{\mathrm{v}}$. (The reference flow rate $\dot{\gamma}_{0}$ is set to 1/s.) The parameter $\hat{\tau}$ is the activator stress of the dampers at the reference flow $\dot{\gamma}_{0}$, see Fig. 2. The parameter $a$ controls the influence of compression. Due to the ramp function, this will only be active for negative hydrostatic stress states (compression). This paper does not include the effects of compression, and this factor is set to zero. The exponent $m_{\mathrm{eff}}$ governs the velocity dependency, see Fig. 2, where the influence of changes in a constant $m_{\mathrm{eff}}=m$ is shown.

Fig. 2

Influence of $m_{\mathrm{eff}}=m=5$, 10, and 100 (Color figure online)

4.2 Convexity of strain energy and material stability

To ensure the existence of solutions to boundary value problems and to avoid numerical problems associated with negative material stiffness, it is desirable that the strain energy function is convex. The volumetric term in (6) is convex, but the deviatoric term in (6) is not necessarily convex. The primary problem is that if $\mu _{\mathrm{f}}$ is too low in relation to $\mu _{\mathrm{i}}$, the strain energy becomes nonconvex.

The formal requirement for convexity can be stated as

$$ \psi \left (\xi \textbf{F}_{1} + (1-\xi )\textbf{F}_{2}\right ) \le \xi \psi (\textbf{F}_{1}) + (1-\xi )\psi (\textbf{F}_{2}), $$

(21)

where $\xi \in [0,1]$, and $\textbf{F}_{1}$ and $\textbf{F}_{2}$ are two different deformation gradients (cf. Ball 1977; Hartmann and Neff 2003). The formal definition of convexity is simple in principle, but to show that a particular strain energy function is convex for all possible deformations is not necessarily straightforward. Here, we investigate three shear-dominated load cases—uniaxial tension, biaxial tension, and simple shear—where it is possible to identify a range for $\mu _{\mathrm{f}}$ that guarantees convexity of the strain energy. This will also guarantee that the stiffness tensor remains positive definite, i.e., negative material stiffness is avoided.

In the following, it is assumed that the material behaves elastically and that it responds incompressibly. In the cases of uniaxial tension, biaxial tension, and simple shear, the respective deformation gradients take the forms

$$ \textbf{F}_{\mathrm{ut}} = \left [ \textstyle\begin{array}{ccc} \lambda & 0 & 0 \\ 0 & 1/\sqrt{\lambda} & 0 \\ 0 & 0 & 1/\sqrt{\lambda}\end{array}\displaystyle \right ], \quad \textbf{F}_{\mathrm{bt}} = \left [ \textstyle\begin{array}{ccc} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & 1/\lambda ^{2} \end{array}\displaystyle \right ], \quad \textbf{F}_{\mathrm{ss}} = \left [ \textstyle\begin{array}{ccc} 1 & \gamma & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\displaystyle \right ], $$

(22)

i.e., for uniaxial and biaxial tension, the deformation is parameterized by the stretch $\lambda$, and simple shear is parameterized by the shear $\gamma$. These three load cases are investigated numerically for the deformation ranges $\lambda \in [0.7,1.3]$ and $\gamma \in [0,0.3]$ and for the parameter space $\mu _{\mathrm{f}}/\mu _{\mathrm{i}}\in [0,1]$, $\beta _{\mathrm{e}}\in [0.001,0.1]$. This should cover the deformation and parameter space of practical interest. Thus, for each combination of $\mu _{\mathrm{f}}/\mu _{\mathrm{i}}$ and $\beta _{\mathrm{e}}$, (21) is evaluated numerically for $\lambda \in [0.7,1.3]$ and $\gamma \in [0,0.3]$. These variables are discretized so that $\lambda ^{n}$ and $\lambda ^{n+1}$ and $\gamma ^{n}$ and $\gamma ^{n+1}$ denote consecutive values of these two variables, respectively, where $\lambda ^{n+1}-\lambda ^{n}=\gamma ^{n+1}-\gamma ^{n}=0.01$. For the deformation ranges of interest, (21) is evaluated, where $\textbf{F}_{1}$ and $\textbf{F}_{2}$ are evaluated using $\lambda ^{n}$ (or $\gamma ^{n}$) and $\lambda ^{n+1}$ (or $\gamma ^{n+1}$), and $\xi =0.5$ is applied. In this way, it can be established numerically what combinations of $\mu _{\mathrm{f}}/\mu _{\mathrm{i}}$ and $\beta _{\mathrm{e}}$ give a nonconvex strain energy in the deformation range of practical interest. It turns out that the regions of convexity/nonconvexity are about the same for all three load cases, and as long as $\mu _{\mathrm{f}}/\mu _{\mathrm{i}}\ge 0.4$, the strain energy remains convex for all three load cases and for all values of $\beta _{\mathrm{e}}$ investigated.

If each branch of the strain energy is to be convex, $\mu _{\mathrm{f}}/\mu _{\mathrm{i}}$ must be set to a value that is greater or equal to 0.4 in each branch. In the end, however, it is the total response of the model that should be convex, i.e., the total response of the three branches. For this reason, it can still be acceptable to let one of the branches have a stiffness ratio $\mu _{\mathrm{f}}/\mu _{\mathrm{i}}$ that is below 0.4, as long as the total response is convex.

5 Numerical implementation

5.1 Uniaxial tensile test

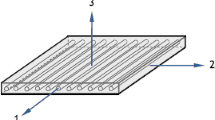
Different forms of uniaxial tensile loading are simulated. Thereby the deformation gradients and stress tensor can be simplified to diagonal tensors. The existence of a Cartesian coordinate system, with basis vectors $\mathbf{e}_{1}$, $\mathbf{e}_{2}$, and $\mathbf{e}_{3}$, is assumed. The load is applied in the 1-direction. The 2- and 3-directions are traction-free and respond equally due to isotropy. The deformation gradient is then expressed as

$$ \textbf{F} = \begin{bmatrix} \lambda _{1} & 0 & 0 \\ 0 & \lambda _{2} & 0 \\ 0 & 0 & \lambda _{2} \end{bmatrix} , $$

(23)

and the decomposition $\textbf{F}=\textbf{F}_{\mathrm{e}}\textbf{F}_{\mathrm{v}}$ yields

$$ \begin{bmatrix} \lambda _{1} & 0 & 0 \\ 0 & \lambda _{2} & 0 \\ 0 & 0 & \lambda _{2} \end{bmatrix} = \begin{bmatrix} \lambda _{\mathrm{e1}} & 0 & 0 \\ 0 & \lambda _{\mathrm{e2}} & 0 \\ 0 & 0 & \lambda _{\mathrm{e2}} \end{bmatrix} \begin{bmatrix} \lambda _{\mathrm{v}} & 0 & 0 \\ 0 & \lambda _{\mathrm{v}}^{-1/2} & 0 \\ 0 & 0 & \lambda _{\mathrm{v}}^{-1/2} \end{bmatrix} , $$

(24)

where isotropy has been assumed and ${\mathrm{det}}\textbf{F}_{\mathrm{v}}=1$ has been enforced. Hence, $\lambda _{1}$ is prescribed, and $\sigma _{11}$ is the main outcome of the analysis. The evolution law for $\textbf{F}_{\mathrm{v}}$ in (14) yields

$$ \dot{\lambda}_{\mathrm{v}} = \dot{\gamma}\lambda _{\mathrm{v}}N_{11}, $$

(25)

where each branch in the total viscoelastic model has its own $\lambda _{\mathrm{v}}$.

Time $t$ is discretized with a time increment $\Delta t$, yielding a set of discrete values $t=t_{0}, t_{1}, \ldots, t_{n}, \ldots$, and $(\bullet )^{n}$ denotes the value of entity $(\bullet )$ at time $t_{n}$. The problem is solved using an implicit numerical scheme. For each time step, the variables $\lambda _{2}^{n}$, $\lambda _{\mathrm{v},\mathrm{B}}^{n}$, and $\lambda _{\mathrm{v},\mathrm{C}}^{n}$ are determined by requiring that the lateral stress $\sigma _{22}$ vanishes and that the (implicitly) discretized evolution equations for the two viscosity variables are fulfilled.

5.2 Optimization

The material parameters were optimized using several methods, regarding optimization algorithms, sampling, and error estimation. The optimization scheme has been set up using two different commercially available software. The different methods used are briefly explained below. Independently of software used, each test consists of two curve matching operations: engineering stress vs strain and engineering stress vs time. The tensile tests have been given a higher weight factor.

LS-OPT

LS-OPT uses a sequential metamodel with domain reduction (SRSM). The optimum is found by minimizing the area between the experimental curves and the model prediction. One advantage of using this method is that the optimization process is no longer dependent on the distribution of data points. This is especially helpful in the case of test types 2 and 3, where the time is a continuously increasing variable, while both stress and strain will shift direction as well as be stationary. That is, due to the three dimensions, an advanced point distribution need to be used to avoid point clusters, thereby introducing an indirect weight function by itself if conventional error methods are to be used.

MCalibration

In contrast to LS-OPT this software uses a series of optimization search algorithms, such as random search, Levenberg–Marquardt, Nelder–Mead, and NEWUOA, which it will loop through during the fitting process. The optimum is found by minimizing the mean absolute difference (MAD). However, to be able to get equal weights for the different load cases a normalization of the MAD was made (NMAD). This method will in contrast to the area reduction method be point-dependent as it will compare the values of the used data points. The definition of the NMAD function that is minimized is

$$ NMAD= \frac{\langle |\sigma _{Model}-\sigma _{Exp}|\rangle}{\langle |\sigma _{Exp}|\rangle}, $$

(26)

where $\langle ...\rangle$ is the arithmetic mean.

6 Results

6.1 Preliminaries

A Cartesian coordinate system with basis vectors $\mathbf{e}_{1}$, $\mathbf{e}_{2}$, and $\mathbf{e}_{3}$ is again assumed. In the experiments, loading is imposed in the 1-direction, the 2-direction is the in-plane lateral direction, and the 3-direction is the thickness (out-of-plane) direction.

When comparing the experimental results to the model response, it is desirable to use the local strain in the middle of the test specimen rather than the global strain based on machine displacement. The relation between the local strain and the global strain was investigated using DIC. Figure 3 (a) and (b) shows the relation between local longitudinal linear strain $\varepsilon _{11}$ and the global longitudinal linear strain $E_{11}$ (based on grip separation in the machine) during deformation of the POM and rPP materials. When comparing the experiments to the model responses, deformations are confined to the strain regimes $\varepsilon _{11},E_{11}\in [0,0.075]$ and $\varepsilon _{11},E_{11}\in [0,0.05]$ for POM and rPP, respectively. As can be seen from Fig. 3, the local strain does not correspond exactly to the global strain, but in the subsequent presentation, $\varepsilon _{11}\approx E_{11}$ is assumed.

Fig. 3

Relation between local and global strain for a) POM and b) rPP

Poisson’s ratio was measured through DIC. In the simulations, the bulk modulus $\kappa$ is taken to be a function of the shear modulus and Poisson’s ratio according to

$$ \kappa =\frac{2}{3}\frac{\mu _{\mathrm{tot}}(1+\nu )}{(1-2\nu )} $$

(27)

with $\mu _{\mathrm{tot}}=\mu _{\mathrm{i},\mathrm{A}}+\mu _{\mathrm{i},\mathrm{B}}+\mu _{\mathrm{i},\mathrm{C}}$. Hence, in the optimization of the model, $\kappa$ depended on $\mu _{\mathrm{tot}}$ according to (27) and was therefore not an independent variable.

Data from DIC for Poisson’s ratio measurement are illustrated in Fig. 4. Figure 4(a) shows the evolution of the lateral strain vs. the longitudinal strain during a tensile test. As can be seen, this relation is not a straight line. The variation of $-\varepsilon _{22}/\varepsilon _{11}$ is shown in Figs. 4(b) and (c). Following the standard ISO527 (2012), Poisson’s ratio should be evaluated for $\varepsilon _{11}=0.0025$. Hence, the estimates from DIC of Poisson’s ratios were $\nu =$0.40 and 0.42 for POM and rPP, respectively.

Fig. 4

Data for measurement of Poisson’s ratio for rPP: a) Strain relation, b) Variation of strain ratio, c) Close-up of strain ratio

6.2 Experimental results: test type 1

The tests of type 1 consist of uniaxial tensile tests with monotonic loading. The results from these tests are shown in Fig. 5 for both POM and rPP. The loading rate was 800 mm/min, and five tests were performed for each material. Up to the point of yielding, the dispersion in the results is very small for both materials. For POM, the dispersion is small even after yielding, but the failure strain varies significantly between different specimens. For rPP, there is some dispersion in the yield stress, about 2–3%, but the variation in failure strain is significant.

Fig. 5

Uniaxial tensile tests with monotonic loading at 800 mm/min. Dots indicate common strain levels for tests 2 and 3; strain levels marked with triangles are unique for test type 2; squares indicate strain levels unique for test type 3. a) POM and b) rPP

Both of the materials show a decreasing stress at strains beyond yielding, but it is emphasized that the stress shown is the nominal stress. In the strain regimes of practical interest for the two materials, no visible necking was observed in the test specimens. Instead, the strain was evenly distributed in the test area of the specimens. At large strains (far beyond the regime of practical interest), the rPP specimens showed an extended type of necking with a gradual thinning of the specimen when moving from the ends of the specimen towards the center of it. So even in that case, no distinct necking was observed.

Based on the monotonic response, a number of stress/strain levels are chosen for each material for the stress relaxation and unloading tests, see Fig. 5.

6.3 Experimental results: test types 2 and 3 for rPP

Results from test types 2 and 3 are shown in Figs. 6 and 7 for rPP. Figure 6(a) shows the stress-strain response for test type 2. The material is loaded up to three target strain levels. After that the material experiences stress relaxation at constant strain for 20 h, which is followed by unloading and creep at zero stress for 4 h. Figure 6(b) shows the strain history during the four last hours of creep at zero stress. All of the strain levels are reached before 0.5 s, and both for the highest as well as for the mid-level it can be seen that the stress starts to drop more or less immediately. The stress then drops exponentially for another 5 hours where is starts to follow a more linear path for the next 15 hours. In Fig. 8(a) and (b), the stress relaxation during test 2 is demonstrated both in the regular time domain but also in the logarithmic time space. The stress curves in Fig. 8(a) have been normalized by the maximum stress for each strain level. The maximum stress $P_{\mathrm{max}}$ for the strain levels 0.35$\%$, 1.07$\%$, and 2.82$\%$ was 5.3 MPa, 13.0 MPa, and 21.1 MPa, respectively. As shown in Fig. 8(a) the relative stress relaxation increases with the applied strain.

Fig. 6

Results from test type 2 for rPP: a) Stress-strain response and b) Normalized strain history during unloading and zero stress creep (Color figure online)

Fig. 7

Results from test type 3 for rPP: a) Stress-strain response and b) Normalized strain history during unloading and zero stress creep (Color figure online)

Fig. 8

Stress relaxation for rPP a) Normalized stress drop. b) Logarithmic time scale (Color figure online)

Figure 7 shows the results for test type 3 for rPP. Figure 7(a) shows the loading-unloading path for three maximum strain levels, and Fig. 7(b) shows the strain history during the 4 h of creep at zero stress. It is clear from Fig. 7(b) that since the material was directly unloaded after reaching the given max strain level, the strain does not change very much after unloading.

6.4 Model calibration for rPP

When comparing the proposed model to the experimental data, all of the data is used, i.e., the results from test types 1, 2, and 3. rPP is first considered. The model proposed in the present work is fitted to the experimental data, but as a reference, the commonly used ‘Parallel Rheological Framework’ (PRF) model (Bergström 2012; Hibbitt, Karlsson and Sorensen 2016) is also fitted to the same experimental data. The main purpose of using the PRF model as a reference is that it is widely used and it is available in many commercial finite element software. All models explored went through the same parameter optimization scheme to give them the best possible fit. In the PRF model, three parallel networks are used, where each network consists of a standard neo-Hookean spring ($\mu _{\mathrm{f}}=\mu _{\mathrm{i}}$) and constant exponents in the evolution of viscosity ($m_{\mathrm{f}}=m_{\mathrm{i}}$). It has been shown in Melly et al. (2021) that for moderate strains, the neo-Hookean and Yeoh models behave equally. Because of its simplicity, a neo-Hookean spring rather than a Yeoh spring (which is most common in practice when using the PRF model) is used here.

Figure 9 shows the outcome when the PRF model with a standard neo-Hookean spring is fitted to the experimental data. The data consists of test 1 (monotonic stress-strain data performed at two different strain rates), as well as tests 2 and 3. Figure 9(a) shows the stress-strain response and Fig. 9(b) shows stress relaxation. The stress relaxation data are well represented by the model, but the stress-strain model response does not capture the experimental data. During the fitting procedure it was obvious that a trade-off had to be made between fitting the stress-strain data and fitting the stress relaxation data. Hence, a model with just the standard neo-Hookean spring does not seem to be able to describe the experimental data at hand. Hence, there seems to be a need for a more advanced model.

Fig. 9

Result when fitting a standard PRF model to the rPP data: a) Stress-strain relations, b) Stress relaxation and zero stress creep

The model proposed here is then applied to the experimental data. But as a start, an attempt with a version of the new model with only two legs active instead of three is made. That is, the model consists of one elastic branch and one viscoelastic branch. In Fig. 10, this 2-leg version is fitted to the same experimental data as before. The stress relaxation in Fig. 10(b) is rather well captured also in this case. The stress-strain response in Fig. 10(a) is better than the calibration with the neo-Hookean spring in Fig. 9(a), but there are still significant deviations compared to the experiments.

Fig. 10

Result when fitting a 2-leg version of the new model to the rPP data: a) Stress-strain relations, b) Stress relaxation and zero stress creep

The full 3-leg version of the new model is then applied to the data, and in Fig. 11, the calibration of the full version of the present model is demonstrated. Two versions of the new model are applied: one version where $\mu _{\mathrm{f}}$ in each branch is free to take on any value and one version where $\mu _{\mathrm{f}}\ge 0.4\mu _{\mathrm{i}}$ is enforced. This requirement forces each term in the strain energy function to be convex. As can be seen from Fig. 11(a), the stress-strain response of both versions of the model agrees fairly well with the experimental data. However, for the highest loading curve in the stress relaxation data, there is a discrepancy between model and experiments. The predicted stress-strain response during zero-stress creep shows a spurious wave-like behavior. Hence, the viscous part of the model is not fully able to capture the zero-stress creep process.

Fig. 11

Result when fitting the new model to the rPP data: a) Stress-strain relations, b) Stress relaxation and zero stress creep (Color figure online)

The model parameters used in Fig. 11 are listed in Table 1. The two model parameters $\mu _{\mathrm{eff}}$ and $m_{\mathrm{eff}}$ evolve during the simulations, and the evolution of these two parameters during the tests is illustrated in Fig. 12. The evolution of the effective shear modulus is shown in the upper three graphs, and the evolution of the two effective exponents in the two viscoelastic branches of the model is shown in the lower two graphs. Results are shown for the model with no restriction on $\mu _{\mathrm{f}}$. The stiffness of the elastic branch (A) varies greatly with the deformation, as can be seen in the upper left graph. The same conclusion holds for branch B. On the other hand, the stiffness of branch C does not vary at all with the deformation in the different tests and simulations. The exponent in branch B is also virtually constant and independent of deformation, as seen in the lower left graph. On the other hand, the exponent in branch C shows a dramatic variation during the simulations.

Fig. 12

Evolution of $\mu _{\mathrm{eff}}$ and $m_{\mathrm{eff}}$ for rPP during different tests (Color figure online)

Table 1 Material parameters for rPP

6.5 Experimental results and model calibration for POM

Figure 13 demonstrates the outcome when the proposed model is fitted to the experimental data for POM. Again, the model is calibrated by use of results from test types 1, 2, and 3.

Fig. 13

Result when fitting the new model to the POM data: a) Stress-strain relations, b) Stress relaxation and zero stress creep (Color figure online)

Similar results are seen in the POM as for the rPP, i.e., the same type of trade-off between results in the stress-strain domain and the stress relaxation behavior. However, this more brittle material actually shows a bit different response, especially for the recovery phase. Nevertheless, the fit is still rather good, as can be seen in Fig. 13. Just as for rPP, two versions of the model are fitted: one version where $\mu _{\mathrm{f}}$ is allowed to take on any value, and one version where the convexity bound is applied to $\mu _{\mathrm{f}}$. The model with the convexity bound overestimates the stress at high strains somewhat, as can be seen from Fig. 13(a), whereas the unbounded version of the model provides a very nice fit, in terms of both the stress-strain response in Fig. 13(a) and the stress relaxation response in Fig. 13(b).

For the model parameters shown in Table 2, the response is a bit different compared to rPP, as can be seen when comparing Fig. 14 and Fig. 12. Here, the damper in leg C is not as active as the spring is.

Fig. 14

Evolution of $\mu _{\mathrm{eff}}$ and $m_{\mathrm{eff}}$ for POM during different tests (Color figure online)

Table 2 Material parameters for POM

7 Discussion and concluding remarks

The present study contains an experimental study focusing primarily on the stress relaxation and creep behavior in uniaxial tension of rPP and POM. A new constitutive model suitable for modeling these materials at moderate strain levels was also proposed.

The materials under study here are strongly rate- and history-dependent. For this reason, it is not straightforward to compare the present experimental results to other studies, where other loading rates and other load histories may have been used. However, at large, the experimental findings here seem to be consistent with previous studies. For instance, the stiffness and yield stress of POM obtained here seem to agree reasonably well with the results in Kroon and Rubin (2023) and Fischer et al. (2019). Also, the stiffness and yield stress of rPP seem to agree fairly well with the findings in Brachet et al. (2008).

The proposed model builds on the well-established concept of the multiplicative decomposition of the deformation gradient into elastic and inelastic parts. There is a vast array of models that are based on this concept. The present model has some similarities with a model proposed by Bergström (2012). The main difference is that Bergström (2012) uses an evolution law for the stiffness. Also, instead of using the neo-Hookean model as the starting point, Bergström (2012) uses a model based on Langevin statistics, which takes the finite extensibility of polymer chains into account.

The fitting of the model to the experimental data implies optimization of a nonlinear problem with a large number of parameters. It is a complicated task, and there is no guarantee that the global solution to the problem is found. When fitting the model to the experiments, it was obvious that a trade-off had to be made between fitting the stress-strain data and fitting the stress relaxation data. It was also observed, that in one of the optimized parameter sets for rPP, for instance, $\mu _{\mathrm{f}}$ was virtually equal to $\mu _{\mathrm{i}}$. This is an indication that the optimization procedure is not fully able to explore the entire solution space or that the proposed model has more degrees of freedom than what is necessary for the particular polymer grade. To explore as much of the solution space as possible, optimization attempts with different initial values of parameters were made. This had no strong influence on the final estimates.

Semi-crystalline materials have a complicated microstructure, but they basically consist of two phases: the crystalline and the amorphous phase. It has been argued (Bergström et al. 2002; Bergström and Bischoff 2010; Lin and Argon 1994a) that the behavior of the viscoelastic legs in the model (if a network model is used) can be connected to the response of the two different phases. This is an interesting and attractive idea, but for highly phenomenological models like the present one it seems to be difficult to draw any certain conclusions about the different phases based on the behavior of the two viscoelastic branches in the model.

As discussed earlier, convexity of the strain energy might be an issue with the present model. Above, it was concluded that if each branch in the model fulfills $\mu _{\mathrm{f}}>0.4\mu _{\mathrm{i}}$, then the whole model is guaranteed to be convex. However, the model as a whole can still be convex even if one of the branches is not. When fitting the model to the experimental data, it was clear that the convexity constraint made it slightly more difficult to fit the data, as could be seen in Figs. 11 and 13. It was verified that the optimized models that were obtained from the model calibrations with no restrictions on $\mu _{\mathrm{f}}$ were indeed convex. One example that might have seemed to be nonconvex was the monotonic response of POM at the lower loading rate in Fig. 13(a). The stress response for this case does in fact start to drop at high strains, but this is because of stress relaxation and not because of elastic nonconvexity.

In future work, the present model will be implemented into a finite element context, and hence a 3D numerical implementation must be developed. There are several frameworks available for implementing elasto-plasticity based on the multiplicative decomposition of the deformation gradient. The present formulation does not include any yield criterion, and hence there is no consistency condition to be taken into account. The numerical implementation to be developed will essentially follow along the lines of the procedures proposed by Simo and Ortiz (1985), Simo (1988), Simo and Miehe (1992), and Weber and Anand (1990).

In summary, two sets of experiments have been performed on two semi-crystalline polymers, i.e., rPP and POM. The testing focused mainly on the stress relaxation behavior and creep at zero stress, but the monotonic response was also explored. The data were compared to a new constitutive model, i.e., a network model with three viscoplastic branches, where the initial stiffness depends on the elastic deformation. The model enabled a reasonably good fit to all the experimental results. The application of the new model to the experimental data should be seen as a proof of concept, and further studies where the model is applied to more complicated, multi-axial problems are needed.