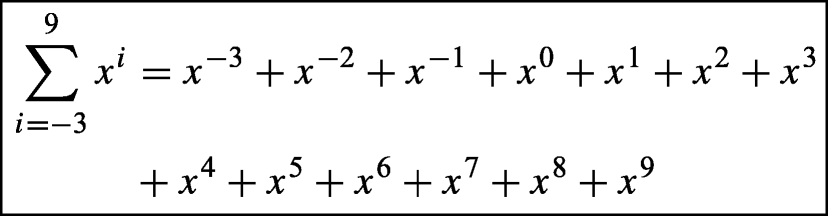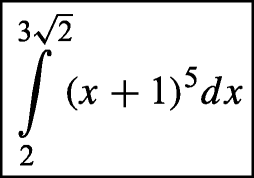1 Introduction

1.1 Motivation

A proper and effective Human-Computer Interaction (HCI) model is an essential and challenging issue in the design of modern computer based systems, especially those intended for e-learning [21, 23], mobile devices [45] or support for people with special needs [26, 33, 35, 42], including elderly ones [34]. The research in this area takes into account many different users’ needs, and main conclusions point out the need to increase flexibility and adaptivity of user experience [6].

These challenges are especially important in the field of computer interaction with visually impaired people [14], who are unable to use the common graphical user interface and require specialized assistance [9, 12], such as adaptable screen content presentation, screen readers [31], touchscreen systems [7] or specialized Braille languages interfaces [15, 16]. One of the key difficulties in this area is establishing technique for proper input and output of mathematical content, such as formulae or equations [25, 27]. The nature of the mathematical notation obstructs semantic reception of the equations and hence often becomes a significant barrier for visually impaired people, who then need the assistance of peer readers or an automated speech system. Unfortunately, most of the present alternative input methods for mathematics do not provide versatile help in editing complex equations.

1.2 Problem of verbalizing mathematics and available solutions

Mathematical notation is based on a variety of symbols, graphs and diagrams, usually describing abstract objects that are impossible to present linearly without extensive usage of parenthesis. This non-linearity becomes the main challenge in designing an accurate tool for automatic translation of mathematical notation. Moreover, the verbalization of math notation requires keeping the accuracy while the brevity of the message increases in order to make it still understandable for the audience. Another important issue in machine translation of mathematics is the rigidity of translation rules that are typically used regardless the context, language or particular subject. The issues which concern grammar and templates for processing of the mathematical notation are elaborated in [43] and [24].

Different approaches have been used for automatic conversion to/from spoken form of mathematical notation. One possible solution for the system to read (or write) mathematics in an understandable and proper way is to equip it with a tool for machine translation from mathematical symbolic notation to spoken language [13] and the speech synthesis [18] which often needs additional efforts for non-English national languages [36]. Most of the existing TTS systems intended for mathematics are focused on particular type of input (like LATE X or MathML) and use a set of pre-defined translation rules in the translation process. Such rigid approach may lead to superfluous translations, which are not natural and comprehensible for the audience. Exemplary systems of this type include AudioMath [20], a tool applying rigid verbalization rules stored in databases, Math Speak & Write [40], a solution integrating Lisp with MS Windows Speech API, some assistive solutions for the visually impaired, like TalkMaths [3, 48], a system for dictating mathematical contents or MathSpeak [30], a tool for LATE X automatic translation.

Other approaches include for example math OCR for recognition of graphically presented expressions followed by an analysis of their 2D structure to linearize the presentation for further processing [29], or a LATE X package for converting LATE X commands into their natural language counterparts [1].

It should be emphasized that majority of the existing solutions support only English language, including the commercial tools like MathPlayer plugin for MS Office or MathTalk. Due to grammar and semantics these solutions cannot be directly used for other national languages. There are dedicated tools proposed for some national languages, like Slovak [10], Portuguese [20], Chinese [46] or Thai [50]. Moreover, most of the presented systems are developed and tested on relatively simple examples and do not support more complex expressions (see also [2, 4, 5]). Some of them require manual pre-editing of the alternative content by the specialized operator [1, 28]. There is a lack of a flexible solution, which would enable switching the languages of translation, setting the mathematical context and editing translation rules.

In the view of the above introduction, the aim of the work presented within this paper was to develop a math-to-speech system, which allows for adapting the translation rules to individual user’s needs. The proposed solution extends the basic math-to-speech system [8], which was originally developed for translation of mathematical expressions into Polish and was based on hard-coded set of translation rules. Multiple tests run on the system revealed the need to develop a solution, which would offer flexibility in rule setting. The system has been re-designed and extended by the universal scripting language, providing a unique possibility to edit, correct or alter the machine translation algorithm by the final user. The implementation details and the unit-testing results of the proposed system are presented in the subsequent sections. In addition, the obtained values of standard measures for translation quality evaluation are provided as a reference for the performance quality of the system. Also, the conclusions from questionnaires filled by the users performing typical tasks with the use of introduced scripting tools are discussed.

2 Material and methods

2.1 The core math-to-speech system

The basic math-to-speech system described in [8] performs machine translation with the use of hard-coded rules. It verbalizes mathematical expressions defined in various formats: web math notation (MathML), LATE X and EQED (introduced in the included visual equation editor) to linear textual form of natural spoken language in Polish. As Text-To-Speech (TTS) engines are built-in into common computer operating systems or available at low cost, the main problem is the proper linear composition of the meaning of mathematical expressions. The resulting translation should be suitable for speaking and understandable without ambiguity, and should take into account the personal preferences of the user (e.g. the permissible level of simplification, dialect or context).

In the basic math-to-speech system the following types of inputs have been implemented both in the standard/full (SM) and the optimized/simplified (OM) mode: quotients, powers, roots, brackets, indices, integrals, sums, products and limits. The two modes SM and OM were introduced in order to adjust the produced translation to particular user’s requirements. In SM the system produces the full linear translation based on the set of strict translation rules, which sometimes may sound superfluous especially in the case of relatively simple and short expressions. This excess is reduced in the OM, which implements a number of simplified contextual translation rules at the expense of translation explicitness. Detailed presentation of the system performance in Polish interface is given in [8]. The system integrates a math notation visualizing engine, interactive equation editor desktop application and a set of basic hard-coded translation rules. It allowed to distinguish and fine-tune the rule sets for different areas of mathematics, however the process was time consuming due to the complexity of testing procedure and the need of subsequent recompilation. The rule sets were determined for Polish language only.

2.2 Scripting capabilities in the math-to-speech translation

Hard-coding of the basic math-to-speech system made it easier to implement and interact with internal data structures containing mathematical notation. However, every modification of the translation system involved the need for recompile the application. This way the math-to-speech interface was adaptable only within the borders of implemented rules.

Introducing scripting language for the translation process opens up new opportunities, such as dynamic exchange of rules, additions of novel dialects and national versions. After the re-implementation of the existing rules we were able to add some valuable factors to the math-to-speech engine. First, the English version of the translation was added. Exemplary translations obtained for the formula

$$ \sum\limits_{i=1}^{n^{2}} \left( \frac{1}{2} + \sqrt[n]{\sqrt{i}} \right)^{3} $$

in both modes of English version (standard SM and optimized OM) are presented below:

SM::

summation from i equals 1 to n squared of open parenthesis fraction: numerator: 1, denominator: 2, end of fraction plus root of degree n of square root of i , end of root, , end of root, closed parenthesis cubed end of summation

OM::

summation from i equals 1 to n squared of open parenthesis 1 half plus nth root of square root of i , end of root, , end of root, closed parenthesis cubed end of summation

Secondly, we added a universal set of test equations with their translations and provided fast and convenient way of test automation for the math-to-speech process. In the end we provided the possibility to extend the translation engine with new, user-defined rule sets, which interact with GUI of equation editor and can be chosen by the user on-the-fly.

This way we have extended the adaptivity and adaptation functions of the math-to-speech system. These extensions were tested by several users – mathematicians without special knowledge in script programming. The results of the surveys seem promising, as all the respondents were satisfied with the efficiency of proposed solution. In this case the HCI is both complex enough to provide wide and comprehensive solutions, and easy to learn and implement on the other hand.

3 Theory and implementation

There are many popular scripting languages, as for example Visual Basic, PHP, PascalScript, Javascript, Python and Lua. The chosen solution for our project was Lua: easy to learn with notation close to Pascal, with small footprint, well designed to interact with other languages and having enough ready libraries to develop even complex applications. Lua language was indeed developed with software automation in mind. It is also widely used in production environments, which ensures stability and maturity of the project. The best known implementations of Lua are gaming platforms: Corona SDK, Moai SDK or LÖVE SDK. Lua in also widely used in science projects, especially as a tool for definition of complex, rule-based systems designed to process natural language [38] and for general software automation, for example in LuaTE X project [41].

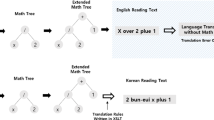
Inside the core of the equation editor developed by our team and used in all experiments (“Equation wizard”), the mathematical notation is stored as a tree of objects. Therefore, the translation process is a top-down traversal of this internal data structure, verbalizing the expression recursively. We decided to leave the traversal in the main application and call specialized Lua functions to translate particular elements of mathematical notations. This way we did not need to rewrite big parts of the engine and could keep the Lua functions short and easy to learn or modify. Moreover, the multiplatform software development tools used for ”Equation wizard” project (i.e. RAD Studio from Embarcadero), give the opportunity to port the core engine and create user experience for popular mobile operating systems without significant effort [44]. The scheme in the Fig. 1 shows these two levels of the translation process. In the second phase a set of additional subsequent text replacements is performed, allowing simple substitution of names for Greek letters and other basic symbols.

Fig. 1
figure 1

The flowchart for the translation of the mathematical notation into speech. Two translation phases: recursive (the traversal of the internal object tree, and replacements (dictionary conversion) performed by scripting engine (dashed box)

Full size image

The translation algorithm operates recursively whenever a nested part is found in the translated expression. Nevertheless, the overall execution time remains linear with respect to the total number of atomic symbols to be translated. Some additional processing is required only when the parser has to back propagate to the previous symbol, however this results in only one additional operation to be performed and has no remarkable influence on the overall complexity of the translation algorithm. The system is designed to be an efficient interactive tool – the processing time of a relatively long formula is of no significance in terms of user experience as the operation is real-time for a typical PC with Windows 10. However, designed for interaction, the solution in current form is rather not scalable to process big data sets – for these kind of applications hard-coded rules ensure better efficiency of the translation algorithms.

3.1 Details of the Lua scripting implementation

The syntax of Lua language is similar to Pascal with some exceptions: 1. there are no typed variables, 2. every code block is determined by end keyword (there is no begin keyword). Lua deals with long unicode character strings very well, so it is suitable for our goals.

Several Lua functions with fixed names were introduced for each of the translation rule sets. Every translation rule set is stored in a separate external text file, easy to edit. The rule set defined in a single Lua file is intended to be used for translation in the particular national language, mathematical dialect or verbalization approach (like standard/optimized modes).

User can define additional help functions, which can be used to solve particular translation problems. Fix-named functions share the following signature:

TEname_of_element(indH, indL, Body, Prev)

where name_of_element can be for example root, int, brackets etc. The translated descriptions of high and low index, main part of the sub-expression (the body), and previous element should be passed into respective parameters.

In every case, name_of_element is an equivalent of the internal object in the ”Equation wizard” editor core, representing particular mathematical symbol with its context. It means, that for example power should have sub-expression in superscript (exponent), but integral should have upper and lower bounds. The elements which are not obligatory can be passed to translation functions as empty strings.

Therefore, the indH and indL parameters have the context dependant meaning, for example indH is used to describe numerator in fractions, root degree, exponent or upper bound of the definite integral. Similary, indL is used to denote lower index, denominator in fractions or lower bound of the definite integral (sum, product, limit etc.)

Providing verbalized value of the previous element (prev parameter) allows to assure the contextual interpretation of the appropriate parts of the expression. For example it is used in the TEfrac function to determine if the conjunction ”and” should be placed before the actual verbalization of the fraction (see Listing 1). This way we receive the correct ”two and fraction...” for ”\( 2\frac {a}{b}\)”.

Listing 1
figure c

“Prev” parameter usage in the beginning of the Lua translation function for fractions

Full size image

Common signature of translation functions simplifies the interface between the core tree-alike data structure used by ”Equation wizard” editor and Lua interpreter. It is realized through the single internal function:

function LuaInvoke(L: lua_State; fname, indH, indL, Body, Prev: ↩ String): String;

which calls Lua function named fname with the following parameters. Parameter fname should certainly correspond with the name of the function to call from Lua source file (rule set), i.e. TEname_of_element. The two next parameters and their contextual usage was discussed above.

The most seldom used parameter is Prev, so the extra wrapper function fills it with default empty string:

function LuaSpeak(fname, indH, indL, Body: String; Prev : String ↩ = ”):String;

Wrapper function LuaSpeak initializes Lua interpreter, passes Lua source code (rule set) with translation definitions according to chosen context and national language and calls LuaInvoke in the end. As a result we receive the translation actually performed with the use of Lua functions (describing translation rules), defined in the external files. As these files are simple text-files with source code in Lua, they are easy to edit, change, correct and extend, without the need to recompile the whole editor application. The GUI of ”Equation wizard” editor scans for the translation rule set files automatically, so there is no need for re-run of the editor after editing the Lua part. This way our solution offers the convenient way to add national languages, dialects or user-preferred versions.

The mutual relations between the modules of the solution developed during our experiments is shown in Fig. 1. The main translation loop traverses recursively the internal tree-alike data structure stored in the ”Equation wizard” editor core calling EqSpeak function. Math-to-speech translation of every particular symbol or subexpression requires a call to the appropriate Lua function. This translation procedure can be described alternatively by the simplified pseudocode from Algorithm 1.

figure d

Additionally, every file with source code for the translation rule set may contain special functions providing automatic tests of any number of equations. This way we help to build stable solutions and avoid regression errors while editing functions with definitions of translation rules.

3.2 Examples of the math-to-speech translation Lua functions

The Listing 2 presents an example of the translation function for roots. This particular example is designed for Polish optimized version i.e. version taking into account context and the level of complication. The implementation differentiates between square roots and roots of given degree.

Listing 2
figure e

Lua translation function for root symbols (Polish optimized version)

Full size image

English translation for the same element takes into account roots of degree 2, 3 and the other, as well as empty degree (which traditionally refers to square root – see Listing 3). These two very simple examples illustrate the elastic approach for the translation resulting in possibilities to build adaptive versions of the math-to-speech system.

Listing 3
figure f

Lua translation function for root symbols (English optimized version)

Full size image

Much more complex Lua functions describe for example translations for superscripts or brackets. They deal with length of the sub-expressions and check if parts of equations are integer numbers or operators.

3.3 User interface for the translation module in the host application

User experience for the functionality described above is provided through the interactive dialog window, which contains a list of available translations with their descriptions. The short names used in listbox, as well as longer informative commentaries are loaded dynamically from the Lua source with the use of predefined functions TEGetName and TEGetDescription (Fig. 2).

Fig. 2
figure 2

Graphical user interface for the translation module. The main ”Equation wizard” window in the background

Full size image

Keeping many versions of translation rule sets can be very helpful, especially to provide exact compatibility with the national or regional regulations and de-facto standards. As one of the most obvious usages of the math-to-speech interfaces is the extended support for visually impaired people, it is worth to note how easy it becomes to develop rules for phonetic alphabet speak-out of one letter variables (i.e. ”alpha” for ”a”, ”bravo” for ”b”, ”charlie” for ”c”, etc. [19])

3.4 Automated tests of the math-to-speech algorithms

Software automation with the use of Lua scripting language helped also to develop a set of tests. Manually triggered by the user, they check every translation function against pattern equations and their reference spoken versions. The tests do not take into account whitespaces, which do not matter for verbal effects in the TTS engines. This kind of testing helps to avoid simple regression errors while the translation engine rule sets are edited, so it is an equivalent of unit-tests in common programming languages.

The corpus of the test functions checks all the elements and subexpression types, which can appear in the equations understandable by the developed system. There are many simple and relatively short examples in the set, as well as a few larger examples, checking nested parts of equations.

Some exemplary English optimized translations for roots are presented in the Table 1. Every test equation is assigned to its description in the internal ”Equation wizard” (EQED) notation and reference translation.

Table 1 Exemplary mathematical expressions used for automatic translation testing
Full size table

The interaction between main application GUI and Lua test code is provided by the special call-back function TEtest. This function responds to the following commands:

  1. 1.

    GETREF with the index of test in the parameter: returns EQED notation for the test equation,

  2. 2.

    GETSPEECH with the index of test in the parameter: returns reference verbal translation according to the chosen translation rule set (i.e. given Lua file),

  3. 3.

    CHECK with the index of test in the first parameter, verbal translation to compare in the second parameter and possibly a flag NOPUNCTATION in the third parameter: returns boolean value for passed or failed test.

The source data for tests is stored in two-dimensional Lua table. Thanks to Lua special syntax, it is possible to embed raw multi-line text data into the source code easily. So, the EQED descriptions can be directly copied from editor to the test suite.

The test corpus for optimized English includes several dozens of equations. The simplest samples in the set contain just a few symbols. They are used for testing particular rules in the translation system. On the other hand, the most complex expressions contain over 50 mathematical symbols and they are suitable to test nested subexpressions. The sample output log from this test suite is shown by the Listing 4.

Listing 4
figure g

A sample from automatic test log of translation from structural math notation to spoken English

Full size image

4 Results and discussion

4.1 System transcriptions vs human perception

In order to verify the established translation rules, a spoken outcome of few sample formulae has been compared with human perception abilities. A group of 41 engineering students has been asked to write down the original mathematical formulae, basing on the spoken transcriptions produced by our system. The students took the tests in smaller groups of 6, 8 and 27 and they heard the translation only once. There were seven tasks (formulae) to be performed in the test (instead of transcriptions we give only the symbolic formulae):

  1. (a)

    \(\sqrt [n]{\frac {a^{4}}{2}}\),

  2. (b)

    \( \left (\frac {2}{x}\right )^{5}\),

  3. (c)

    \(\int f(x+5) dx\),

  4. (d)

    \(\sqrt {\frac {2}{5} +1}\),

  5. (e)

    \( a_{2n+1}^{3} = b_{2n}^{3n-4}\),

  6. (f)

    (a + b + c)2 − (a − b − c)2 = 4(ab + ac),

  7. (g)

    \(\left [\frac {\sqrt [4]{3x^{2}-5}}{(x-y)^{x+y}} \right ]\).

All answers were then collected and analyzed in terms of possible dissimilarities with the symbolic formulae. A majority (nearly 83%) of the answers were absolutely correct, i.e. the formulae written by respondents were exactly those entered to the math-to-speech system. The worst results were observed for the formula (e), which was successfully recovered only by a half of students. The mistakes were usually made with lower and upper indices, which refer strongly to the visual form of the formula and therefore are hard to process linearly by human brain. Also, in a total number of 15 answers the mistakes related to bracket placing was observed. On the other hand, formula (f) was correctly recovered by all students, and the general success rate of 82,9% can be considered satisfactory. Table 2 presents the detailed results for all seven formulae.

Table 2 Accuracy of recovery of the original formulae by students
Full size table

The survey has proved the usability of the proposed system for educational purposes. Of course, the perception of people with visual impairment may be different, hence an additional test of our system for these people is planned.

4.2 Word metrics for translation quality evaluation

In order to evaluate the quality of the output from the math-to-speech engine, one should decide on metrics for measuring the distance form the model transcript of the given expression to the respective output produced by the system. In our study we used two standard metrics independently: WER (Word Error Rate) and BLEU (BiLingual Evaluation Understudy). WER is the metric based on the implementation of Levenshtein distance at the words level. It is defined as:

$$ WER = \frac{S+D+I}{N} $$

where S – the number of substitutions, D – the number of deletions, I – the number of insertions and N – the number of words in the reference. By definition, smaller WER indicates better similarity (the reference and candidate strings are closer).

BLEU is the contemporary standard and widely used metric for evaluation of machine translation systems [49] that allows to consider more than one reference translation. Although BLEU is mostly used for analysis of statistical translation systems, it can be also implemented in assessment of rule-based translations [17]. In the included examples, the standard BLEU values are given. The are calculated as

$$ BLEU = BP \cdot \sqrt[4]{ \prod\limits_{n=1}^{4} P_{n}} $$

where Pn denotes the precision of n-grams (tuples of n words), defined as

$$ P_{n} = \min (\max (\text{\# n-grams in reference file), \# n-grams in candidate file}) , $$

BP – Brevity Penalty, defined as

$$ BP = \left\{ { 1\quad\quad for \quad c>r \atop e^{1-\frac{r}{c}}\quad for\quad c\leq r} \right., $$

c – number of words in candidate string, r – the number of words in reference string. Standard BLEU is a number between 0 and 1 and the higher BLEU value is, the more the compared strings are similar. For details of the BLEU metric calculations we refer the reader to [32].

4.3 Quality evaluation for different translation modes

A few examples demonstrating the effectiveness of equation reader run with two versions of modified Lua scripts: Standard English (SM) and Optimized English (OM) are listed below. The respective WER and BLEU metrics for the quality of translation performed in each case in comparison to the assumed natural language transcription(s) of the exemplary formulae (referred to as Spoken English) were calculated in each case.

The assumed verbalization are based on own elaboration and literature sources, including fundamental book [11], as well as some academic reports [19, 22, 37] and textbooks [47].

The following examples present the capabilities of the verbalization algorithm and may be used as reference for comparison with other solutions. The results are classified into basic categories of mathematical expressions implemented in our system: fractions, powers, roots, summation/products, subscripts and special symbols. In the end some miscellaneous formulae containing expressions of various categories are given.

  1. 1.

    Fractions:Footnote 1

    figure h

    • Reference: fraction: numerator: n minus 1, denominator: n plus 1, end of fraction plus 1 and a half plus 5 and 23 thirds minus 8 quarters minus 2 over 1 plus 71 over 5 plus 2n over 3m

    • OM: fraction: numerator: n minus 1, denominator: n plus 1, end of fraction plus 1 and 1 half plus 5 and 23 thirds minus 8 quarters minus 2 over 1 plus 71 over 5 plus 2n over 3m; BLEU = 0.937, WER = 0.0238

    • SM: fraction: numerator: n minus 1, denominator: n plus 1, end of fraction plus 1 and fraction: numerator: 1, denominator: 2, end of fraction plus 5 and fraction: numerator: 23, denominator: 3, end of fraction minus fraction: numerator: 8, denominator: 4, end of fraction minus fraction: numerator: 2, denominator: 1, end of fraction plus fraction: numerator: 71, denominator: 5, end of fraction plus fraction: numerator: 2n, denominator: 3m, end of fraction; BLEU = 0.2133, WER = 1.6667

  2. 2.

    Powers:

    figure i

    • Reference:2 to the power of: i, plus 2 to the power of: i plus 1 end of exponent, plus 2 to the nth plus 2 to the power of: 3 squared

    • OM: 2 to the power of: i end of exponent, plus 2 to the power of: i plus 1 end of exponent, plus 2 to the nth plus 2 to the power of: 3 squared end of exponent,; BLEU = 0.8132, WER = 0.1667

    • SM: 2 to the power of exponent i end of exponent plus 2 to the power of exponent i plus 1 end of exponent plus 2 to the power of exponent n end of exponent plus 2 to the power of exponent 3 squared end of exponent ; BLEU = 0.4354, WER = 0.4722

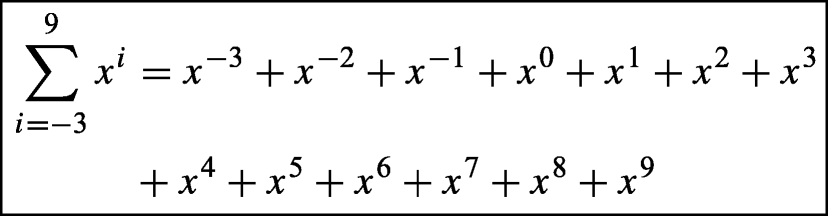
    • Reference: summation from i equals minus 3 to 9 of x to the power of i equals x to the power of minus third, plus x to the power of minus second, plus x to the power of minus first, plus x to the zeroth, plus x to the first, plus x squared plus x cubed plus x to the fourth, plus x to the fifth, plus x to the sixth, plus x to the seventh, plus x to the eighth, plus x to the ninth

    • OM: summation from i equals minus 3 to 9 of x to the power of: i end of exponent, end of summation equals x to the power of minus third, plus x to the power of minus second, plus x to the power of minus first, plus x to the zeroth, plus x to the first, plus x squared plus x cubed plus x to the fourth, plus x to the fifth, plus x to the sixth, plus x to the seventh, plus x to the eighth, plus x to the ninth, ; BLEU = 0.8987, WER = 0.0842;

    • SM: summation from i equals minus 3 to 9 of x to the power of exponent i end of exponent end of summation equals x to the power of exponent minus 3 end of exponent plus x to the power of exponent minus 2 end of exponent plus x to the power of exponent minus 1 end of exponent plus x to the power of exponent 0 end of exponent plus x to the power of exponent 1 end of exponent plus x squared plus x cubed plus x to the power of exponent 4 end of exponent plus x to the power of exponent 5 end of exponent plus x to the power of exponent 6 end of exponent plus x to the power of exponent 7 end of exponent plus x to the power of exponent 8 end of exponent plus x to the power of exponent 9 end of exponent; BLEU = 0.3324, WER = 0.8316;

  3. 3.

    Roots:

    figure k

    • Spoken 1: square root of x plus cube root of x minus 1, plus 4th root of 2 over 5 plus 9th root of 2 plus root of degree 123 of 7x plus 1, plus root of degree n plus 1 of n minus 1

    • Spoken 2: square root of x plus cube root of the quantity: x minus 1, plus 4th root of 2 over 5 plus 9th root of 2 plus root of degree 123 of the quantity: 7x plus 1, plus root of degree n plus 1 of the quantity n minus 1

    • OM: square root of x , end of root, plus cube root of x minus 1 , end of root, plus 4th root of 2 over 5 , end of root, plus 9th root of 2 , end of root, plus root of degree 123 of 7x plus 1 , end of root, plus root of degree n plus 1 of n minus 1 , end of root, ; BLEU = 0.5248, WER1 = 0.6; WER2 = 0.6604;

    • SM: square root of x , end of root, plus cube root of x minus 1 , end of root, plus root of degree 4 of fraction: numerator: 2, denominator: 5, end of fraction , end of root, plus root of degree 9 of 2 , end of root, plus root of degree 123 of 7x plus 1 , end of root, plus root of degree n plus 1 of n minus 1 , end of root,; BLEU = 0.36, WER1 = 1.0222, WER2 = 1.0189;

  4. 4.

    Subscripts, special characters and summation:

    • Reference 1: summation from k equals 1 to N of z sub k, dot z bar sub k, equals summation from k equals 1 to N of open parenthesis a sub k, plus b sub k, dot i closed parenthesis dot open parenthesis a sub k, minus b sub k, dot i closed parenthesis equals summation from k equals 0 to N minus 1 of open parenthesis a sub k plus 1, squared plus b sub k plus 1, squared closed parenthesis

    • Reference 2: summation from k equals 1 to N of product of z sub k and z bar sub k, equals summation from k equals 1 to N of open parenthesis a sub k, plus b sub k, dot i closed parenthesis dot open parenthesis a sub k, minus b sub k, dot i closed parenthesis equals summation from k equals 0 to N minus 1 of open parenthesis a sub k plus 1, squared plus b sub k plus 1, squared closed parenthesis

    • OM: summation from k equals 1 to N of z sub k, cdot z with bar sub k, end of summation equals summation from k equals 1 to N of open parenthesis a sub k, plus b sub k, cdot i closed parenthesis cdot open parenthesis a sub k, minus b sub k, cdot i closed parenthesis end of summation equals summation from k equals 0 to N minus 1 of open parenthesis a sub k plus 1, squared plus b sub k plus 1, squared closed parenthesis end of summation ; BLEU = 0.7514, WER1 = 0.1591, WER2 = 0.191;

    • SM: summation from k equals 1 to N of z sub k, cdot z with bar sub k, end of summation equals summation from k equals 1 to N of open parenthesis a sub k, plus b sub k, cdot i closed parenthesis cdot open parenthesis a sub k, minus b sub k, cdot i closed parenthesis end of summation equals summation from k equals 0 to N minus 1 of open parenthesis a subscript: k plus 1 end of subscript, squared plus b subscript: k plus 1 end of subscript, squared closed parenthesis end of summation ; BLEU = 0.6095, WER1 = 0.2727, WER2 = 0.3034;

    figure m

    • Reference: det A equals summation over sigma in S sub n, of minus 1 to the power of: sgn of sigma end of exponent, product from i equals 1 to n of A sub i, sigma of i

    • OM: det A equals summation over sigma in S sub n, of open parenthesis minus 1 closed parenthesis to the power of: sgn open parenthesis sigma closed parenthesis end of exponent, product from i equals 1 to n of A sub i, sigma of i, end of product end of summation; BLEU = 0.6246, WER = 0.3659;

    • SM: det A equals summation over sigma in S sub n, of open parenthesis minus 1 closed parenthesis to the power of exponent sgn open parenthesis sigma closed parenthesis end of exponent product from i equals 1 to n of A subscript: i, sigma of i end of subscript, end of product end of summation; BLEU = 0.466, WER = 0.5366 ;

  5. 5.

    Miscellaneous:

    figure n

    • Reference 1: f of x equals one over 3x times sine of 2x

    • Reference 2: f of x equals the product of one over 3x and sine of 2x

    • OM: f of x equals one over 3x cdot sine of 2x; BLEU = 0.7017, WER1 = 0.0909, WER2 = 0.2857 ;

    • SM: f of x equals fraction: numerator: 1, denominator: 3x, end of fraction cdot sine of 2x; BLEU = 0.1751, WER1 = 1.1818, WER2 = 0.9286 ;

    figure o

    • Reference 1: n-2 factorial equals n factorial over n dot n-1

    • Reference 2: n-2 factorial equals n factorial over n times n-1

    • Reference 3: open parenthesis n-2 closed parenthesis factorial equals n factorial over n times open parenthesis n-1 closed parenthesis

    • OM: open parenthesis n minus 2 closed parenthesis factorial equals fraction: numerator: n factorial , denominator: n cdot open parenthesis n minus 1 closed parenthesis, end of fraction; BLEU = 0.1246, WER1 = 2.8889, WER2 = 2.8889, WER3 = 1.1765

    • SM: open parenthesis n minus 2 closed parenthesis factorial equals fraction: numerator: n factorial , denominator: n cdot open parenthesis n minus 1 closed parenthesis, end of fraction; BLEU = 0.1246, WER1 = 2.8889, WER2 = 2.8889, WER3 = 1.1765

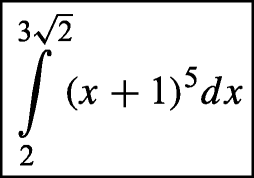
    figure p

    • Reference 1: integral from 2 to 4 cube roots of 2 of open parenthesis x plus 1 closed parenthesis to the fifth, dx

    • Reference 2: integral from 2 to 4 cube roots of 2 of the quantity x plus 1, to the fifth, dx

    • OM: integral from 2 to 4 cube root of 2 , end of root, of open parenthesis x plus 1 closed parenthesis to the fifth, dx; BLEU = 0.6544, WER1 = 0.2727, WER2 = 0.4762 ;

    • SM: integral from 2 to 4 cube root of 2 , end of root, of open parenthesis x plus 1 closed parenthesis to the power of exponent 5 end of exponent dx; BLEU = 0.4575, WER1 = 0.5909, WER2 = 0.8095;

Both metrics used for the algorithm evaluation prove that the Optimized Mode produced translations, which are much more consistent with the natural language when comparing to standard mode. The drawback of both natural language and OM is however, that it may cause confusion if not pronounced properly, i.e. with proper intonation indicating pauses. The main difficulty is the composition of the meaning of mathematical expression in a linear form, suitable to be spoken by TTS and understandable without ambiguity. To overcome this difficulty in the proposed translation rule set the commas were implemented as separators for the TTS system to properly indicate pauses. This solution worked well with the use of MSSpeech TTS engine built in Windows operating system, so we have tested it thoroughly with the voice ”MS Paulina Desktop”, which is available for free. The quality of sound was near to human and we did not experience any problems with understanding of individual words or intonation. In contrary, an open-source solution producing artificial speech called eSpeak was much less understandable even during the basic experiments [8].

It is worth to note, that mathematical notation has some special characteristics that make it sensitive to even small differences in translation algorithms. Most of all, the syntactical meaning of the expression strongly depends on single and sometimes very small symbols [39]. This sometimes happens in the other natural languages, but for proper verbalization of formal maths equations it seems to be essential. On the other hand, there are examples of translations which differ significantly due to the semantic interpretation done by the human reference reader. We are also aware of some abbreviations and possible ambiguities in the reference equations, which make them useful for the common e-learning purposes, but not for visually impaired audience. In general, resolving ambiguities in processing of mathematical notation is the challenging task and key issue to avoid computational overload [43]. Therefore, we should strive for very high overall results of quality factors in the math-to-speech field.

In Table 3 all obtained (best) translation quality characteristics are presented collectively. Clearly the OM shows better performance in resembling the natural spoken references than the SM Mode, both at average and in each of the particular examples. On the other hand, some rules used in SM mode (although commonly leading to the longer output) auto-protect against misunderstandings and ambiguities. Therefore it is not clear, which mode would better fit particular audience. Our system gives the choice at this point, helping to adapt the verbalization process to user’s level of the experience.

Table 3 Translation quality measures in different modes
Full size table

4.4 User experience evaluation for common script editing tasks

To evaluate expansion possibilities of the developed translation system, we have conducted the survey about it among maths teachers. The participants had four tasks to solve, from the very basic one, to the more significant modifications of the translation function. Solutions of these tasks were representative to common needs in the area of the translation of the mathematical notation into the speech. Knowledge about their quantitative (duration) and qualitative (difficulty) characteristics would certainly help to develop better and more efficient human-computer interaction in the field of the math-to-speech verbalization.

The tasks were as follows:

  1. 1.

    add root with explicit index equal 2 to the condition for the shortened version of root description in Polish,

  2. 2.

    add ordinals for two-digit exponents in Polish,

  3. 3.

    add information about definite integrals when both bounds are not empty,

  4. 4.

    add information about the end of integral for inner expressions with spoken transcription longer than 50 characters (normally math-to-speech system do not indicate end of integral, as it ends up with a symbol dx or its equivalent).

The solution of the first task required just one additional condition, i.e. “or (trim(indH)==‘2’)” in appropriate translation function. To solve second task one should extend the helper function IntToSpeech and change the condition limits in the translation function. Third task required inserting two extra conditionals to if statement, so it was similar to the first one. In the last task the solution involved additional if statement with more complex condition than before, as well as modification of the result value.

Carefully conducted, all four tasks were not very difficult for participants, as all the teachers had at least a basic knowledge of programming. With the help of Lua syntax documentation they were able to extend existing translation functions or introduce additional conditions for the size and contents of the input data.

There were seven participants in our tests, everyone holding a university degree in mathematics or related disciplines. All of the respondents performed all the tasks, although three needed some help from the test moderator during experiment. The main test was preceded by some training conducted to ensure that participants understand the naming structure for Lua functions and the basics of the language itself.

The respondents rated the difficulty of all the tasks in a five point Likert scale: 1 – Very easy, 2 – Easy, 3 – Neutral, 4 – Difficult, 5 – Very difficult. In average, all tasks were rated as easy or neutral. The execution time of tasks correspond to the difficulty ratings, as illustrated in the Figs. 3 and 4.

Fig. 3
figure 3

The difficulty of typical translation tasks (average users scores)

Full size image
Fig. 4
figure 4

The average time needed to solve typical translation tasks

Full size image

Our experiment proved that introduction of scripting language affects the efficiency of translation in the positive way. The operator is able to modify, extend or correct the translation algorithm in a reasonable time. Moreover, it is possible to develop completely new translations for different national languages or mathematical dialects, all without the need to recompile the main application. We did not observe any significant problems in the usage of Lua language, as its syntax is simple and similar to Pascal, widely used in the education area.

5 Conclusions

The Lua scripts have proved to be very efficient in adapting our math-to-speech verbalizing system to various needs. The script code is quite intuitive, and makes the scripts easily editable to most users with mathematical background. The survey proved that the users are able to operate successfully with designed framework and are satisfied with the results.

Also, we introduced complex set of equations, covering all the details supported in the ”Equation wizard” engine as a unit-test for the translation. This way we can ensure the quality of verbalization during changes in the script sources and avoid regression errors, which is extremely important from the engineering point of view.

The efficiency of the math-to-speech translation was evaluated with the use of standard metrics. It is worth noting that the analyzed equations were not trivial and contained nested sub-expressions, special Greek symbols and other diacritical marks as accents. The results of the evaluation of the reference translations based on English literature sources are quite promising, therefore we can hope for as good results of further studies involving native speakers. Moreover, the obtained results can be the solid base for the development of speech recognition systems complementary to math-to-speech interfaces.

Contrary to the various existing math-to-speech solutions based on the predefined hard-coded translation rules, our system offers a unique and novel possibility of adjusting the translation rules by the user. Our main contribution is the design of solution that allows to manually adjust the output translations to particular language and to follow the domain specific requirements (fields of mathematics, physics, etc.). This way the developed system becomes a versatile tool for various e-learning and assistive applications.

Declarations of interest: none.