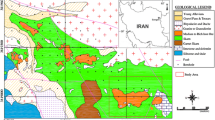
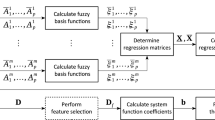
The effectiveness of boundary integral equation and grid-free methods for radial grids, as well as solutions of classical and nonclassical modeling and recovery problems for geological fields are analyzed. It is shown that, as opposed to the methods employing a variational technique and radial basis neural networks, hybrid algorithms (fuzzy neural networks, genetic algorithms, and Kalman filter) for solving identification and recovery problems are more stable with respect to noise and give positive results even with conflicting data and significant measurement noise.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. M. Pashayev, R. A. Sadykhov, F. T. Ildyz, and Kh. T. Karabork, “Reconstruction of the parameters of geofields,” Izmer. Tekhn., No. 12, 3–9 (2005).
A. M. Pashayev, R. A. Sadykhov, F. G. Ramazanov, and F. S. Nazirli, “Reconstructing the parameters of geofields taking measurement noise into account. Part I. Techniques for smoothing, filtration, and regularization,” Izmer. Tekhn., No. 8, 3–11 (2010).
A. M. Pashayev, R. A. Sadykhov, F. G. Ramazanov, and F. S. Nazirli, “Reconstructing the parameters of geofields taking measurement noise into account. Part II. Techniques for identification, regularization, and soft computing,” Izmer. Tekhn., No. 10, 6–14 (2010).
V. F. D’yachenko, “The free point method for problems of continuous media,” Comp. Meth. Appl. Mech. Eng., 2, 265–277 (1973).
S. Mukherjee and Yu. Mukherjee, Boundary Methods: Elements, Contours, and Nodes, Taylor & Francis, New York (2005).
R. A. Sadykhov, Mathematical Models and Efficient Algorithms for Solving Optimization Problems in Automatic Control Systems for Oil Production: Doctoral Thesis in Tech. Sci., Moscow (1995).
M. P. Galanin and S. B. Savinkov, Numerical Analysis Techniques for Mathematical Models, MGTU im. Baumana (2010).
A. Pashayev, D. Askerov, R. Sadigov, and A. Samedov, “Numerical modeling of gas turbine cooled blades,” Aviation. Vilnius, IX, No. 3, 9–18 (2005).
A. A. Samarskii and P. N. Babishevich, Numerical Methods for Solving Inverse Problems in Mathematical Physics, Editorial URSS, Moscow (2004).
A. N. Vasil’ev and D. A. Tarkov, Neural Network Modeling. Principles. Algorithms. Applications, IPU. St. Petersburg (2009).
T. Rutkovskaya, M. Pilinskii, and L. Rutkovskii, Neural Networks, Genetic Algorithms, and Fuzzy Systems, Goryachaya Liniya-Telekom, Moscow (2008).
G. R. Liu and Y. T. Gu, An Introduction of Mesh-Free Methods and Their Programming, Springer, New York (2005).
V. V. Meshcheryakov, Problems in Statistics and Regression Analysis with Matlab, Dialog-MIFI, Moscow (2009).
R. A. Aliev, A. E. Tserkovnyi, and G. A. Mamedova, Production Control with Fuzzy Initial Data, Energoatomizdat, Moscow (1991).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Izmeritel’naya Tekhnika, No. 2, pp. 7–14, February, 2017.
Rights and permissions
About this article
Cite this article
Pashayev, A.M., Sadykhov, R.A. & Habibullayev, S.B. Modeling, Reproduction, and Mapping of Geofields with and Without Measurement Noise. Part 3. Integral Equation, Radial Grid, and Soft Computing Methods. Meas Tech 60, 109–120 (2017). https://doi.org/10.1007/s11018-017-1159-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11018-017-1159-6