1 Introduction

For decades, the mechanics of deep penetration has been extensively studied due to its wide-ranging applications in engineering and medicine. The focus lies in investigating the behaviour of a foreign object, as it deeply penetrates a soft target material. Penetration inevitably involves laceration of the material and/or expansion of existing flaws in the material itself. Typically, the penetrating object is a rigid tool, but also flexible needles are explored in the literature (e.g. see [1,2,3,4,5,6,7,8]). The mechanics of puncturing is relevant in several applications in medical procedures, both manual and automated, such as injections [9], blood testing [10], biopsies [11], and design of advanced surgical instruments [12]. Additionally, deep penetration plays a crucial role in essential natural processes within living organisms where tissue penetration is vital. To gain a better understanding of the mechanical aspects of puncture with respect to material properties, extensive experimentation, numerical and theoretical analyses have been conducted, both on solid blocks of materials [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] and on thin membranes [28,29,30,31,32,33,34,35,36,37,38].

However, one aspect that has received relatively little attention is the role of friction in this process, and a comprehensive exploration of this phenomenon is lacking in the current scientific literature. Most of the existing theoretical models rely on the assumption of frictionless contact, resulting in a penetration force that remains independent of the needle’s depth within the material. This contradicts experimental findings, which indicate a linear increase in force with depth during puncture experiments. The force increment can be attributed to the effects of friction and adhesion between the needle and the solid, and it should be accurately quantified to provide a detailed description of the phenomenon. For this purpose, through numerical simulations, Fregonese and Bacca [39] established a correlation between the force-displacement slope and various material properties and geometrical features such as rigidity, toughness, radius of the penetrator, and interfacial strength.

In this paper, an experimental campaign is carried out on the quasi-static penetration of a rigid needle into a soft solid containing a coaxial cylindrical cavity. Depending on the misfit between needle diameter and cavity dimension, and considering the axisymmetric hyperelastic solution of an expanding circular hole, the parameters describing the interface bond between needle and material can experimentally be quantified. Such parameters are then used to interpret the experimental load–displacement curves of needle penetration into a bulk solid, involving the mechanism of laceration of the material. To this end, a theoretical model describing the needle penetration due to mode I cracking is presented.

2 Energy balance during the deep penetration of a needle

The mechanics of an object piercing a target solid can be characterised by two different stages: an initial stage of indentation and a subsequent stage of penetration. In the former, the tip of the indenter is in contact with the target bulk solid, which accumulates strain energy while the indentation progresses. The indentation stage terminates when an energetically favourable mechanism of laceration takes place in the target solid [22]. According to Shergold and Fleck [40], for soft materials either mode-II crack ring or mode-I planar cracks develop for flat-bottomed punch and sharp-tipped punch, respectively. The latter mechanism features the development of a crack linearly increasing its depth with the penetration depth of the indenter.

In the present paper, a rigid sharp-tipped punch (needle) of radius R is assumed to penetrate a large soft solid along a direction normal to the surface of the solid. The puncturing process which takes place in the material can be described using an energy-based formulation. Neglecting inelastic phenomena in the bulk of the material, the increment of external work generated by the puncturing force is consumed by the elastic strain energy, the work of fracture and the frictional dissipation. The general incremental form of the energy balance is

$$\begin{aligned} \textrm{d}{U_\textrm{ext}} = \textrm{d}{U_\textrm{s}} + \textrm{d}{U_\textrm{G}} + \textrm{d}{U_\textrm{f}}\,, \end{aligned}$$
(1)

where \(\textrm{d}{U_\textrm{ext}}\) is the external work input, \(\textrm{d}{U_\textrm{s}}\) is the strain energy variation in the solid, \(\textrm{d}{U_\textrm{G}}\) is the energy spent to advance the crack, and \(\textrm{d}{U_\textrm{f}}\) is the energy dissipated due to friction at the needle-solid interface. A force F is exerted on the needle in order to penetrate a small amount \(\textrm{d}{D}\), so that \(\textrm{d}{U_\textrm{ext}}=F\textrm{d}{D}\).

3 Mechanism of needle penetration by mode I cracking

3.1 Linear elastic fracture mechanics formulation

This section briefly summarises a theoretical model (details of the solution to this problem are provided in Terzano et al. [41] and Spagnoli et al. [42]) that explores the steady-state penetration of a needle employing the principles of linear elastic fracture mechanics (LEFM). The model considers the plane strain problem related to a cross section of the target solid normal to the penetration direction. Accordingly, the mode I crack, featuring a crack plane of dimensions \(2a \times D\), is opened by the action of the needle (Fig. 1). The target solid is constituted by a bulk material, i.e. containing no flaws or cavities (\(b=0\) according to the nomenclature of Fig. 3 below).

Fig. 1
figure 1

Sketch depicting the mode-I crack mechanism during the continuous penetration of a rigid circular needle into a target bulk solid. The enlarged view reveals the crack’s shape and its contact area with the needle. The dimensions provided in the drawings refer to the initial, undeformed state; such dimensions are not to scale and are shown in this form for the sake of graphical clarity

Full size image

Such an action imposes prescribed opening displacements to the crack faces where the needle is in contact with the target material. The resulting stress intensity factor (SIF), K, is illustrated in Fig. 2 as a function of the normalised needle radius R/a. Also, the position of the point of separation at the needle-solid interface \(a_1\) is shown against the R/a ratio. The SIF is normalised with respect to \(K_\textrm{R}\), namely the stress intensity factor related to the needle filling the entire crack (\(R/a=1\)). This is defined as

$$\begin{aligned} K_\textrm{R}= \frac{E^*}{2}\sqrt{\pi R}\,. \end{aligned}$$
(2)

where \(E^* = E/\left( 1-\nu ^2\right)\). Figure 2 can be employed to determine the critical condition of crack propagation, for a given radius of the needle and fracture toughness \(K_\textrm{c}\) of the target material (based on Irwin’s relation of LEFM \(K_c = \sqrt{E^* G_c}\), where \(G_c=\) fracture energy). According to the LEFM model, the planar crack of semi-length a forms so that \(K=K_\textrm{c}\) at the crack tips. The critical value of the relative radius R/a as well as the critical value of the contact relative semi-length \(a_1/a\) are therefore obtained from Fig. 2 by posing \(K=K_\textrm{c}\).

Fig. 2
figure 2

LEFM model of puncturing: normalised SIF and contact length against normalised relative radius of the penetrating needle

Full size image

3.2 Contact pressure and frictional characteristics

When the needle penetrates for a depth D, strain energy accumulates in the target material due to its deformation induced by the contact pressure at the needle-solid interface. As a first estimation, we assume a uniform contact pressure equal to \(q=E^*/2\) acting on a contact length \(2a_1\). Such a contact pressure corresponds to the traction applied to the crack face which produces a maximum crack opening displacement equal to the needle radius R [43]. Alternatively, the contact pressure can be calculated by considering an Hertzian contact between the needle and the solid. The assumption of uniform contact pressure is appropriate when \(a_1/a \rightarrow 1\) [41, 42].

In the presence of friction and adhesion, by considering the actual surface of the needle-solid interface in the deformed configuration, the work done by the frictional forces required to push the needle by a depth \(\textrm{d}{D}\) is

$$\begin{aligned} \begin{aligned} \textrm{d}{U_\textrm{f}}&=(c+\xi q)2\pi a_1DdD \\&=(c+\xi q)\left( \frac{a_1}{a}\right) \left( \frac{a}{R}\right) 2\pi RD dD, \end{aligned} \end{aligned}$$
(3)

where c is the adhesion shear stress, \(\xi\) is the Coulomb friction coefficient and q is the contact pressure between the solid and the lateral surface of the needle. In Eq. 3, the normalised lengths \(a_1/a\) and R/a are deliberately introduced to highlight the dependence of \(\textrm{d}U_\textrm{f}\) on the material toughness (see Fig. 2). The adhesion contribution c accounts for the sliding resistance in the absence of a contact pressure (\(q = 0\)). The derivative of \(U_f\) in Eq. 3 with respect to D yields the frictional force

$$\begin{aligned} F_f=\frac{\textrm{d}U_\textrm{f}}{\textrm{d}D} = (c+\xi q)\left( \frac{a_1}{a}\right) \left( \frac{a}{R}\right) 2\pi RD \end{aligned}$$
(4)

Equation  4 shows that the penetration force increases linearly with D, as it will be observed in experiments reported below. Hence, with the assumption of a constant contact pressure between the needle and the target material, it is possible to obtain the expression of the slope of the force-displacement curve (the other contributions related to strain energy and fracture energy are independent on D)

$$\begin{aligned} \frac{{d}F}{\textrm{d}D} = \pi \left( \frac{a_1}{a}\right) \left( \frac{a}{R}\right) R (2 c + \xi E^*). \end{aligned}$$
(5)

4 Mechanism of needle penetration by cavity expansion

In order to investigate the frictional interaction between the needle and the solid during the puncturing process, we decide to introduce a priori a cylindrical cavity of dimensions (2b × H) into the target solid (Fig. 3).

Fig. 3
figure 3

Sketch of the puncturing mechanism for evaluating the frictional characteristics during the penetration of a rigid circular needle into a target solid containing a cylindrical cavity of radius b (with \(R \ge b\))

Full size image

This approach enables us to evaluate the adhesion shear stress by employing a needle with the same radius as that of the cavity (\(R = b\)), while larger needles (\(R > b\)) are utilised to estimate the Coulomb friction coefficient. By taking \(R=b\), the first two components of the right hand side of Eq. 1 disappear and the external work is only balanced by the frictional contribution, therefore

$$\begin{aligned} \textrm{d}{U_\textrm{ext}} = \textrm{d}{U_\textrm{f}}\ \end{aligned}$$
(6)

In the case of \(R>b\), the incremental energy balance experiences the additional contribution of the strain energy, that is

$$\begin{aligned} \textrm{d}{U_\textrm{ext}} = \textrm{d}{U_\textrm{s}}+\textrm{d}{U_\textrm{f}}\ \end{aligned}$$
(7)

where \(\textrm{d}{U_\textrm{s}}\) is independent on the penetration depth D as demonstrated in the next section.

The frictional energy \(\textrm{d}{U_\textrm{f}}\) takes the following form

$$\begin{aligned} \textrm{d}{U_\textrm{f}} =(c+\xi q)2\pi RD dD, \end{aligned}$$
(8)

where the contact pressure q is given by the radial Cauchy stress derived in the next section.

4.1 Hyperelastic model for cavity expansion

In this section, we determine the stress and strain field in an infinite solid containing a circular cylindrical cavity enlarged from an initial radius b to a final radius R. We consider a slice of an hyperelastic large solid undergoing a perforation with a cylindrical needle. The slice is taken normal to the penetration direction of the needle, so that we can study a large plate of unit thickness under plane strain condition containing a cylindrical hole, expanded by the rigid circular cross section of the needle (see Fig. 4).

The problem is treated as an axisymmetric one so that the plate has an external radius \(R_e \rightarrow \infty\). A cylindrical coordinate system \(r \theta z\) is adopted in the deformed configuration so that \(R \le r\). The radial coordinate in the reference configuration is s, with \(b \le s\). Note that \(\left( R-b\right)\) is the imposed radial displacement on the internal cavity inducing its expansion.

Fig. 4
figure 4

Deformation of a cylindrical annulus of the solid of unit height from a radius s to a radius r, due to the expansion of a cavity from a radius b to a radius R: a undeformed configuration, b deformed configuration

Full size image

Assuming isochoric deformations under plane strain condition of the material, the principal stretches are (\(J=\lambda _r \lambda _\theta \lambda _z =1\))

$$\begin{aligned} \lambda _r = \frac{s}{r}, \quad \lambda _\theta = \lambda _r^{-1} = \frac{r}{s}, \quad \lambda _z = 1 \end{aligned}$$
(9)

Note that \(\lambda _r\) is the independent stretch during the axisymmetric deformation.

Let us take an Ogden potential [44] with \(\alpha =2\) (Neo-Hookean material)

$$\begin{aligned} \Psi = \frac{\mu }{2}\left( {\lambda _r^2 + \lambda _\theta ^2 + \lambda _z^2 - 3} \right) - p\left( {J - 1} \right) \end{aligned}$$
(10)

where p is the hydrostatic pressure. The Neo-Hookean model is widely used to characterise the nonlinear stress–strain behaviour of materials undergoing large deformations. This model relies solely on a single constant, the initial shear modulus \(\mu\), being incompressibility assumed.

By derivation we obtain the principal Cauchy stresses (\(\sigma _a=\sigma _r,\sigma _\theta ,\sigma _z\)) from

$$\begin{aligned} {\sigma _a} = {J^{ - 1}}{\lambda _a}\frac{{\partial \Psi }}{{\partial {\lambda _a}}} = \mu \lambda _a^2 - p \end{aligned}$$
(11)

that are

$$\begin{aligned} {\sigma _r} = \mu {\lambda ^2} - p,\quad {\sigma _\theta } = \mu {\lambda ^{ - 2}} - p,\quad {\sigma _z} = \mu - p \end{aligned}$$
(12)

where \(\lambda =\lambda _r\).

Now, by exploiting the isochoric condition \(r^2-R^2=s^2-b^2\), one can express the radial stretch as

$$\begin{aligned} \lambda =\sqrt{\frac{b^2}{r^2}-\frac{R^2}{r^2}+1} \end{aligned}$$
(13)

Then the equilibrium in the deformed configuration of a half elementary annulus of internal radius r and of thickness dr yields

$$\begin{aligned} r\frac{{d{\sigma _r}}}{{dr}} + {\sigma _r} = {\sigma _\theta } \end{aligned}$$
(14)

By plugging into (14) the expressions of the principal stresses (12), since the first derivative of the function \(\lambda (r)\) is

$$\begin{aligned} \frac{d\lambda }{dr}=\frac{R^2-b^2}{r^2 \sqrt{b^2+r^2-R^2}}, \end{aligned}$$
(15)

we obtain the following equation of the hydrostatic pressure p

$$\begin{aligned} \begin{aligned} \frac{dp}{dr}=&2 \mu \frac{R^2-b^2}{r^2 \sqrt{b^2+r^2-R^2}} \sqrt{\frac{b^2}{r^2}-\frac{R^2}{r^2}+1} +\\&+\mu \left( \frac{r}{R^2-b^2-r^2}-\frac{R^2}{r^3}+\frac{b^2}{r^3}+\frac{1}{r} \right) \end{aligned} \end{aligned}$$
(16)

By integrating Eq. (16) we finally get

$$\begin{aligned} \begin{aligned} \frac{p(r)}{\mu }=&\frac{\left( b^2 - R^2\right) }{2 r^2}+\\&+\frac{1}{2} \left( \log (r^2)-\log (b^2 + r^2-R^2)\right) +C\\ \end{aligned} \end{aligned}$$
(17)

where the integration constant C can be obtained by imposing the equilibrium boundary condition of \(\sigma _r=0\) at \(r=R_e\). A graphical representation of the radial stress \(\sigma _r\) (see Eqs. 12 and 17) is given in Fig. 5, for different needle diameters. Figure 5 offers a view of the radial true stress as a function of the radial coordinate in the deformed configuration, for different values of R/b ratio. Such plot could be useful to have an insight of the stress state in the target material, as well as of the contact pressure at the needle-solid interface.

Fig. 5
figure 5

Normalised radial stress \(\sigma _r\) against normalised radial coordinate, for increasing needle radius R with respect to the cavity radius b

Full size image

The total strain energy stored in the solid slice of unit thickness (with \(R_e \rightarrow \infty\)) due to a cavity expansion from radius b to R is obtained by

$$\begin{aligned} \frac{{d{U_s}}}{{dD}}=2\pi \int _{R}^{\infty } \Psi r \,dr \ \end{aligned}$$
(18)

which results in

$$\begin{aligned} \frac{{d{U_s}}}{{dD}}=\pi \mu R^2\ \left( \frac{b^2}{R^2}\ -1 \right) \ \log \left( \frac{b}{R} \right) \end{aligned}$$
(19)

Note that the quantity in Eq. 19 corresponds to the constant force \(F_e\) required to expand the cavity during needle penetration.

5 Experiments and discussion

In order to verify the theoretical findings presented in the previous sections, a series of experiments have been carried out.

Cylindrical samples have been manufactured with a commercial silicone, Elite Double 32 (ED32) by Zhermack Dental. This silicone is a Polyvinyl Siloxane (PVS) elastomer, widely employed for model duplication in the dentistry field. An FDM 3D printed cylindrical specimen made of Acrylonitrile Butadiene Styrene (ABS) has been used as a mould for the silicone.

The preparation protocol of a representative silicone sample is summarised in Fig. 6a. The mechanical parameters of such a silicone are taken from Montanari et al. [14]. In particular, assuming the silicone to be incompressible, \(E^*\) = \(4 \mu\) = 1.215 MPa and \(G_\textrm{c}\) = 1.162 N/mm. All the puncturing experiments have been performed on a cylindrical sample with radius \(R_e\) equal to 45 mm and height H equal to 45 mm. The specimens contain a central cilyndrical cavity with radius equal to \(b=0.55 \, \text {mm}\) and height H, see Fig. 3. A sharp-tipped steel punch (tip opening angle \(\alpha\) equal to 30 deg) with circular cross-section having different diameters (\(2R=3.95, 4.97, 5.98, 7.91\) \(\text {mm}\)) is inserted under displacement-control into the target material at a constant speed of 1 mm/min (Fig. 6d). All the mechanical tests are performed by using a universal testing machine Galdabini Quasar 2.5, equipped with a 3 kN load cell, with computer control and data acquiring system, at a room temperature of \(20\,^{\circ }\hbox {C}\), 24 h after the preparation of the specimens. Pictures during the experiments are taken by means of a Basler acA5472-17uc USB 3.0 camera (Fig. 6c).

Fig. 6
figure 6

Manufacturing procedure of the silicone specimens (a), dimension of the cavity (b), experimental setup (c), view of the needles used in the experiments (d)

Full size image

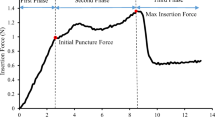
Results of the puncturing experiments related to specimens containing a cavity are illustrated in Fig. 7a. Here, the force-displacement curves obtained during the puncturing tests are shown separately for each needle diameter. From the analysis of the results, it turns out that such curves can be divided in two different regions: the first one governed by the hyperelastic deformation of the cavity expanding in the solid while the second one, corresponding to the linear region, in which friction between the needle and the solid is the only mechanism involved. The cavity expansion force \(F_\textrm{e}\) is identified as the force at the onset of the linear behaviour. Figure 7b shows pictures of a puncturing test using a needle with diamater \(2R = 4.97\) mm, at different applied displacements.

Fig. 7
figure 7

Force-displacement curves resulting from the puncturing experiments on samples with a cylindrical cavity, for different needle diameters (a) and pictures of a puncturing test at different needle depths (see chart on top right in a) (b)

Full size image

Moreover, Fig. 8 shows the results of puncturing experiments, taken from Montanari et al. [14], on bulk silicone samples (with no cavity, \(b=0\)) using different diameters (\(2R=1.28, 1.50, 2.15, 2.72\) \(\text {mm}\)). From these curves it is possible to define the penetration force \(F_\textrm{p}\) as the point at which steady-state penetration begins, occurring after material rupture and subsequent relaxation.

Fig. 8
figure 8

Force-displacement curves resulting from the puncturing experiments on bulk specimens (\(b=0\)), for different needle diameters. Load–displacement slope in the post-fracture region is highlighted by a dashed red line

Full size image

In order to evaluate both friction and adhesion between the needle and the solid, we performed an experiment on the sample with the cavity but employing a needle with diameter 2R equal to 1.1 mm (the same as the cavity 2b). The resulting force-displacement curve is presented in 9a. From the slope of the curve dived by \(2 \pi R\) (see Eq. 8 with \(q=0\) and its second order derivative with respect to D), it is possible to estimate \(c = 40\) kPa.

On the other hand, from the slopes of the linear region of the experimental curves presented in Fig. 7a, it is possible to estimate the friction coefficient \(\xi\). In particular, by inverting the second derivative with respect to D of \(U_f\) in Eq. 8,

$$\begin{aligned} \xi = \frac{1}{q}\left( \frac{dF/dD}{2 \pi R}-c\right) \end{aligned}$$
(20)

where \(q=\sigma _r(r=R)\) (see Eqs. 12 and 17), it is possible to estimate an average Coulomb friction coefficient equal to \(\xi = 0.37\) (see Fig. 9b).

Fig. 9
figure 9

Force-displacement curve and linear fitting (dashed red line) resulting from the friction test (cavity with \(b=R\)) (a), friction coefficients (experimental data, average and standard deviation) evaluated for the different needle diameters (cavity with \(R>b\)) (b)

Full size image

Figure 10 shows the experimentally obtained hole expansion forces \(F_e\) in the voided specimens with cavity (\(b<R\)) and force slope dF/dD in the bulk specimens without cavity (\(b=0\)), respectively, for the various needle diameters. In addition, the theoretical results are also reported, where the expansion force is calculated according to Eq. 19 and the force slope according to Eq. 5 with \(a_1/a \approx 1\) and \(R/a \approx 1\) for the material under consideration. The results turn out to be quite satisfactory, since an overall average 15% error is obtained.

Fig. 10
figure 10

Theoretical and experimental results of the cavity expansion force \(F_e\) in the specimens with cavity (\(b<R\)) (a) and force slope dF/dD in the specimens without cavity (\(b=0\)) (b), against the needle diameter

Full size image

6 Conclusion

This work delves into the interplay of friction and adhesion at the interface between the needle and solid material during quasi-static puncture experiments. In particular, we introduce a novel experimental approach for assessing the frictional characteristics of a rigid needle as it penetrates a soft material.

Several experiments are carried out by inserting a rigid sharp-tipped punch with circular cross section of radius R in silicone specimens containing an initial cylindrical cavity of radius \(b \le R\). The results in terms of penetration force-displacement curves, together with the theoretical findings related to the hole expansion in an hyperelastic solid, are employed to determine the relevant friction parameters at the needle-solid interface: the adhesive shear stress c and the Coulomb friction coefficient \(\xi\). Such parameters allow the estimation of the load–displacement slope dF/dD in the steady state needle penetration into a bulk solid. Furthermore, the investigation explores the mechanism of cavity expansion, offering initial insights into the behaviour of flawed soft solids during needle penetration. The comparison between the theoretical and experimental outcomes, in terms of force slopes dF/dD and cavity expansion forces \(F_e\), is quite good, as it yields an overall average error of about 15%. The competing mechanism of needle penetration due to mode I cracking is also discussed on the basis of a simple theoretical model based on linear elastic fracture mechanics.

This work might serve as a valuable tool for predicting the needle-tissue mechanical interaction in biomedical applications, such as robot-assisted surgical procedures.