An extended 2D Gao beam model

Abstract

This work derives and simulates a two-dimensional extension of the nonlinear Gao beam, by adding the cross-sectional shear variable, similarly to the extension of the usual Bernoulli–Euler beam into the Timoshenko beam. The model allows for oscillatory motion about a buckled state, as well as adds vertical shear of the cross sections, thus reflecting better nonlinear thick beams. The static model is derived from the principle of virtual elastic energy, and is in the form of a highly nonlinear coupled system for the beams transverse vibrations and the motion of the cross sections. The model allows for general distributive transversal and longitudinal loads and a compressive horizontal load acting on its edges. The model is simulated numerically, using the dynamic version for better insight into the steady solutions. The terms that distinguish our numerical solutions from the solutions of the Gao beam, described in the literature, are highlighted. The numerical scheme and its characteristic finite element matrices allow us to obtain simulation results that demonstrate the type of vibrations of our extended and modified beam, and also the differences between these solutions and those of the Gao beam model.

1 Introduction

We derive, study and simulate a model for large displacement and small plane strain deformations of a moderately thick nonlinear beam subjected to general distributive transversal and longitudinal loads and a compressive horizontal load acting on its edges. The model is in the form of a coupled system of three nonlinear differential equations, and is derived from virtual potential energy considerations. The beam allows for buckling, similarly to the usual Gao beam, and includes the deflection of the cross sections, similarly to the Timoshenko beam, thus including the advantages of both.

Mathematical models of beams, structures in which one dimension is substantially larger than the other two, were studied extensively over the decades, starting with the linear Bernoulli-Euler model for a beam. Recently, they have been modified in the literature for non-standard applications and expanded with additional nonlinear terms, to achieve a more accurate representation of real beams in appropriate settings. This work extends this trend and by adding the shear of the cross sections, allows for a better description of the motion of moderately thick beams. Indeed, we show that in our model, removing the thickness part reduces it to the nonlinear Gao beam [1], which supports oscillations about a buckled equilibrium state, and by removing the nonlinear parts, it reduces to the linear Timoshenko beam, see e.g., [2].

There exists an extensive literature about the Timoshenko beam, see e.g., [2,3,4] and the references therein. Currently, there is a rapidly growing scientific literature about the Gao beam, see, e.g., [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. These publications deal with the modeling, mathematical analysis and computer simulations of the various aspects of the Gao beam model. The basic mathematical analysis of the model, including establishing the existence of the solutions, and also a study of contact problems, can be found in [20]. The dynamic contact of a Gao beam with an elastic or rigid foundation was described in [12]. The case of vibrations of a Gao beam with restricted movement between two rigid or elastic obstacles was studied in [7], while the analysis of two coupled Gao beams connected via a joint with a gap can be found in [11]. Vibration characteristics of one-dimensional structures in contact with a Gao beam were conducted in [10], which includes the model, existence of weak solutions, and computer simulations. Furthermore, an interesting problem analyzing the growth of a crack in a Gao beam was studied and simulated in [9]. For models regarding contact, one can refer to [21] and the numerous references provided therein. Furthermore, recently in [13], a model for the vibrations of a viscoelastic Gao beam in contact with a deformable random foundation and subject to stochastic inputs, was presented and analyzed. The body force was represented by a stochastic integral incorporating Brownian motion, while the gap between the beam and the foundation was treated as a stochastic process. The existence and uniqueness of strong solutions to the model were established.

The Bernoulli-Euler linear beam model has been extended in [22] by incorporating a nonlinear term that accounts for the influence of axial force. In [6] two new dynamical beam models in finite deformations were presented dealing with the nonlinear vibrations of thicker beams subjected to arbitrary external loads. The total potentials of these beam models were non-convex, with a double-well structure, which was used in post-buckling analysis and also frictional contact problems. The analytical and numerical solutions of the model were applied to a structure subjected to a moving inertial load [14, 15], representing a wheel moving on a rail. It has been shown that an inertial load significantly altered the dynamic response of the system and that omitting the nonlinear term in the differential equation led to incorrect qualitative and quantitative solutions. The Gao beam has been studied in numerous works by Machalová, Netuká et al. In [17] the static contact problem for a large deformed beam with an elastic obstacle was formulated, analyzed, and numerically simulated. By employing a decomposition method, the nonlinear variational inequality was reformulated as a min-max problem of a saddle point of a Lagrangian [16]. Then, using a mixed finite element method with independent discretization and interpolations for the foundation and beam elements, the continuous-space nonlinear contact problem was transformed into a nonlinear mixed complementarity problem. In [18] the authors considered either pure bending or a unilateral contact with an elastic foundation, where the normal compliance condition was employed. Under additional assumptions on the data, higher regularity of solution was proved. It enabled to transform the problem into a control variational problem. Finally, [19] deals with the identification of coefficients in the nonlinear Gao beam model which can act as the control variables.

The main novelty in this work is that it combines and extends both the Timoshenko and the Gao beam models. In this way, we obtain a 2D model that may vibrate about a buckled state, and allows for the rotation of the cross sections, which generates additional planar strain. Moreover, the model allows taking into account longitudinal body loads, and allows for more complex boundary conditions. We construct the static model in Sect. 2, based on the principle of virtual energy. To depict the properties of the model, we construct in Sect. 3 a dynamic finite element scheme for the solution of the model. Then, in Sect. 4 we show numerical simulations of a dynamic case to better visualize the properties of the system under investigation, treating the dynamic problem as a sequence of static steps. The vibrations about buckled states can be seen clearly. Section 5 concludes the paper with some unresolved interesting issues, to be investigated in the future.

2 Mathematical model

This section constructs a model of a moderately thick, two-dimensional (2D), Gao beam. It is based on elastic energy considerations and neglects some second order terms. We show, as was noted in the Introduction, that the linear terms correspond to the well-known Timoshenko beam, and in the 1D approximation, it reduces to the Gao beam.

Fig. 1

The beam; w – vertical displacement of the central axis, u – longitudinal displacement, $\theta$ – shear or rotational angle of the cross section; $q_v$ – vertical body force, $q_h$ – horizontal body force, $p_0, p_L$ – compressive end tractions

Fig. 2

The shear deformation $\theta$ and the derivative $w_{,x}$

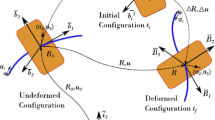
We consider relatively large displacements and small planar strain deformations of a moderately thick beam, which is subjected to applied transversal and horizontal loads, $q_v, q_h$, respectively and a loads $p_0, p_L$ applied to the ends. The beam, of length L and thickness 2h (with a unit depth), has as a reference configuration $\Omega =\{(x,y): 0\le x\le L, -h\le y\le h\}$. The left end of the beam’s central axis is placed at the center of the coordinate system. The setting is depicted in Fig. 1, with the cross-section detail in Fig. 2. As in the 1D Gao beam, to cause buckling, the horizontal loads $p_0$ and $p_L$ are applied at the ends $(x=0,L)$, respectively. These must be sufficiently large if one is interested in buckling. As we show below, when the applied horizontal load vanishes, $q_h(x)=0$, the horizontal stress is constant and we must take into account the equal and opposite reaction at $x=0$ from the support, i.e., for applied load $p_L=p$ at $x=L$, we must set $p_0=-p$. When $q_h(x)\ne 0$, the compatibility condition is more complicated and is given in (2.15).

We introduce the notation u(x), w(x) and $\theta (x)$ for the longitudinal displacement, vertical displacement and the shear or rotational angle of the cross sections, respectively, as functions of $0\le x\le L$. The vector of horizontal and vertical displacements of the beam is assumed to be

$$\begin{aligned} \textbf{u}(x,y)= \left[ \begin{array}{c} u-y\theta \\w \end{array} \right] . \end{aligned}$$

(2.1)

We note that w, u and $\theta$ depend only on x, while the displacement vector $\textbf{u}$ depends also on y.

We take into account the shear strain explicitly, hence $w_{,x}\ne \theta$, where here and below, for the sake of simplicity, we denote the x-derivative of a function g(x) by $g_{,x}=\frac{\partial g}{\partial x}$. We use the comma to distinguish from directional index.

Since we use large displacements, we use the full Lagrangian of finite strain, as a function of the displacement gradient tensor, is given by

$$\begin{aligned} \textbf{E}=\frac{1}{2}\left[ \nabla \textbf{u}+(\nabla \textbf{u})^\textsf{T}+(\nabla \textbf{u})^\textsf{T}\nabla \textbf{u}\right] . \end{aligned}$$

(2.2)

Using (2.1), the strain tensor $\textbf{E}$ can be written in matrix form as

$$\begin{aligned} \textbf{E}\!=\! \left[ \! \begin{array}{cc} u_{,x}-y\theta _{,x}+\frac{1}{2}\left( u_{,x}-y\theta _{,x}\right) ^2+\frac{1}{2}(w_{,x})^2 &{} \frac{1}{2}(w_{,x}-\theta )-\frac{1}{2}(u_{,x}-y\theta _{,x})\theta \\ \frac{1}{2}(w_{,x}-\theta )-\frac{1}{2}(u_{,x}-y\theta _{,x})\theta &{} \frac{1}{2}\theta ^2 \end{array} \!\right] . \end{aligned}$$

(2.3)

We assume that the longitudinal displacements u are much smaller than the lateral displacements w. Therefore, the relationship $u\sim w_{,x}$ holds, where $\sim$ means the same order of magnitude. This assumption leads to the second-order terms which we retain or neglect. Using the engineering strain notation, we obtain,

$$\begin{aligned} \left[ \begin{array}{c} \varepsilon _x\\ \varepsilon _y\\ \gamma \end{array} \right] = \left[ \begin{array}{c} E_{11}\\ E_{22}\\ 2E_{12} \end{array} \right] = \left[ \begin{array}{c} u_{,x}-y\theta _{,x}+\frac{1}{2}(w_{,x})^2\\ \frac{1}{2}\theta ^2\\ w_{,x}-\theta \end{array} \right] . \end{aligned}$$

(2.4)

We assume, using linear elasticity, that the constitutive equations have linear stress–strain relationship. In the case of the small strain, which is the case here, the plane stress is given by

$$\begin{aligned} \sigma _x=\frac{E}{1-\nu ^2}(\varepsilon _x+\nu \varepsilon _y),\ \ \ \ \sigma _y=\frac{E}{1-\nu ^2}(\varepsilon _y+\nu \varepsilon _x),\ \ \ \ \tau =G\gamma , \end{aligned}$$

(2.5)

where E is the elastic Young modulus, $\nu$ is the Poisson ratio and G is the shear modulus, $G=E/2/(1+\nu ).$

The elastic strain energy of the beam is given by

$$\begin{aligned} \begin{aligned} \Pi&=\frac{1}{2}\int _0^L\int _{-h}^h \left( \sigma _x\varepsilon _x+\sigma _y\varepsilon _y+\tau \gamma \right) \text{ d }y\text{ d }x-2h\\&\int _0^Lq_v(x)w\text{ d }x - 2h\int _0^Lq_h(x)u\text{ d }x\\&+\int _{-h}^h p_0(y)u \text{ d }y|_{x=0} -\int _{-h}^h p_L(y)u \text{ d }y|_{x=L}\\&=\frac{1}{2}\int _0^L\int _{-h}^h\left[ \frac{E}{1-\nu ^2} \left( \varepsilon _x^2+\varepsilon _y^2+2\nu \varepsilon _x\varepsilon _y\right) +G\gamma ^2\right] \text{ d }y\text{ d }x-2h\\&\int _0^Lq_v(x)w\text{ d }x \\&\hspace{24.0pt}- 2h\int _0^Lq_h(x)u\text{ d }x +\int _{-h}^h p_0(y)u \text{ d }y|_{x=0} \\&- \int _{-h}^h p_L(y)u \text{ d }y|_{x=L}. \end{aligned} \end{aligned}$$

(2.6)

Here, $q_v(x)$ and $q_h(x)$ are distributed loads acting on the beam vertically and horizontally, respectively, $p_0$ and $p_L(y)$ are the horizontal tractions acting at $x=0, L$, respectively. For the sake of simplicity, we assume that the loads $q_v$ and $q_h$ are independent of y. However, it is straightforward to assume that $q_v(x,y)$ and $q_h(x,y)$, i.e., depend on y too.

According to (2.4) and (2.5) the first variation of $\Pi$ with respect to u, w and $\theta$, is given by

$$\begin{aligned} \begin{aligned} \delta \Pi =&\int _0^L\int _{-h}^h\left[ \sigma _x\left( \delta u_{,x}-y\delta \theta _{,x}+w_{,x}\delta w_{,x}\right) +\sigma _y\theta \delta \theta \right. \\&\left. +\tau \left( \delta w_{,x}-\delta \theta \right) \right] \text{ d }y\,\text{ d }x\\&-2h\int _0^Lq_v(x)\delta w\text{ d }x - 2h\int _0^Lq_h(x)\delta u\text{ d }x \\&+ \int _{-h}^h p_0(y)\delta u \text{ d }y|_{x=0,L} \\&-\int _{-h}^h p_L(y)\delta u \text{ d }y|_{x=L}. \end{aligned} \end{aligned}$$

(2.7)

Using integration by parts, we obtain

$$\begin{aligned} \begin{aligned} \delta \Pi&=\left. \int _{-h}^h\sigma _x\,\delta u\,\text{ d }y\right| _{x=0,L}\\&-\int _0^L\int _{-h}^h\sigma _{x,x}\,\delta u\,\text{ d }y\,\text{ d }x-\left. \int _{-h}^h\sigma _x y\,\delta \theta \,\text{ d }y\right| _{x=0,L}\\&+\int _0^L\int _{-h}^h\sigma _{x,x}y\,\delta \theta \,\text{ d }y\,\text{ d }x+\left. \int _{-h}^h\sigma _x w_{,x}\,\delta w\,\text{ d }y\right| _{x=0,L}\\&-\int _0^L\int _{-h}^h(\sigma _{x,x}w_{,x}+\sigma _x w_{,xx})\, \delta w\,\text{ d }y\,\text{ d }x\\&+\int _0^L\int _{-h}^h\sigma _y\theta \,\delta \theta \,\text{ d }y\,\text{ d }x\\&+\left. \int _{-h}^h\tau \,\delta w\,\text{ d }y\right| _{x=0,L}\\&-\int _0^L\int _{-h}^h\tau _{,x}\,\delta w\,\text{ d }y\,\text{ d }x-\int _0^L\int _{-h}^h\tau \,\delta \theta \,\text{ d }y\,\text{ d }x\\&-2h\int _0^Lq_v(x)\,\delta w\,\text{ d }x -2h \int _0^Lq_h(x)\,\delta u\,\text{ d }x\\&+\int _{-h}^h p_0(y)\,\delta u\,\text{ d }y|_{x=0} \\&- \int _{-h}^hp_L(y)\,\delta u\,\text{ d }y|_{x=L}=0. \end{aligned} \end{aligned}$$

(2.8)

Next, we note that the variational displacements $\delta u$, $\delta w$ and $\delta \theta$ are independent and arbitrary. Since to minimize the energy we must have $\delta \Pi =0$, therefore, the corresponding terms in the variations must vanish separately. Separating the terms with $\delta u$, $\delta w$ and $\delta \theta$, we find that equation (2.8) is satisfied if and only if the following equalities hold,

$$\begin{aligned} \int _{-h}^h\sigma _{x,x}\text{ d }y=-2h q_h, \end{aligned}$$

(2.9)

$$\begin{aligned} \int _{-h}^h(\sigma _{x,x}w_{,x}+\sigma _x w_{,xx}+\tau _{,x})\text{ d }y+2hq_v=0, \end{aligned}$$

(2.10)

$$\begin{aligned} \int _{-h}^h(\sigma _{x,x}y+\sigma _y\theta -\tau )\,\text{ d }y=0. \end{aligned}$$

(2.11)

These expressions lead to the model equations. We note that if we assume that $q_v=q_v(x,y)$ and $q_h=q_h(x,y)$, so that both depend also on y, then we need to replace $2hq_h$ with $\int _{-h}^hq_h(x,y)\text{ d }y$ and $2hq_v$ with $\int _{-h}^hq_v(x,y)\text{ d }y$ in the expressions above and everywhere below.

Furthermore, the boundary variational terms in (2.8) yield the boundary conditions

$$\begin{aligned} \int _{-h}^h\left. (\sigma _x + p_0)\delta u\text{ d }y\right| _{x=0}=0,\quad \int _{-h}^h\left. (\sigma _x- p_L)\delta u\text{ d }y\right| _{x=L}=0, \end{aligned}$$

(2.12)

$$\begin{aligned} \int _{-h}^h\left. (\sigma _xw_{,x}+\tau )\,\delta w\,\text{ d }y\right| _{x=0,L}=0, \end{aligned}$$

(2.13)

$$\begin{aligned} \int _{-h}^h\left. y\sigma _x\delta \theta \,\text{ d }y\right| _{x=0,L}=0. \end{aligned}$$

(2.14)

These lead to the following boundary conditions for the model, however, we first obtain a compatibility condition on the horizontal forces. It follows from (2.12) that at the ends

$$\begin{aligned} \sigma _x(0) =- \int _{-h}^h p_0\text{ d }y=-\hat{p}_0,\quad \sigma _x(L)=\int _{-h}^h p_L\text{ d }y =\hat{p}_L. \end{aligned}$$

Then, (2.9) yields upon integration over $0\le s \le x$,

$$\begin{aligned} \sigma _x(x)=\sigma _x(0)+2h\int _0^x q_h(s)\text{ d }s =-\hat{p}_0+2h\int _0^x q_h(s)\text{ d }s. \end{aligned}$$

Therefore, we obtain the horizontal loads compatibility condition

$$\begin{aligned} \sigma _x(0) +\sigma _x(L)=\hat{p}_0+\hat{p}_L= 2h\int _0^L q_h(s)\text{ d }s. \end{aligned}$$

(2.15)

In particular, when the horizontal traction vanishes ($q_h=0$), we obtain

$$\begin{aligned} \hat{p}_L= -\hat{p}_0, \end{aligned}$$

(2.16)

so the reaction of the support acting at $x=0$ has to balance the applied load acting at the right end, to prevent the beam from moving horizontally as a rigid body.

Explicitly, the force compatibility condition imposes the following compatibility conditions on the boundary conditions,

$$\begin{aligned} u_{,x}(0)+\frac{1}{2} (w_{,x})^2(0)+\frac{\nu }{2} \theta ^2(0) = \frac{1-\nu ^2}{E}\hat{p}_0 = -\frac{1-\nu ^2}{E}\hat{p}_L \end{aligned}$$

$$\begin{aligned} +\frac{(1-\nu ^2)2h}{E}\int _0^L q_h(s)\text{ d }s, \end{aligned}$$

(2.17)

and

$$\begin{aligned} u_{,x}(L)+\frac{1}{2} (w_{,x})^2(L)+\frac{\nu }{2} \theta ^2(L) =\frac{1-\nu ^2}{E}\hat{p}_L, \end{aligned}$$

(2.18)

where $\hat{p}_L$ is the total traction acting horizontally at $x=L$.

We note that the horizontal boundary conditions at the ends are coupled, and need to be carefully assigned.

It follows from (2.13), (2.5) and algebraic manipulations that at both ends ($x=0,L$),

$$\begin{aligned}{} & {} \left( \frac{2\hat{p}_0}{1-\nu }+1\right) w_{,x}(0)+\theta (0)=0,\nonumber \\{} & {} \quad \left( \frac{2\hat{p}_L}{1-\nu }+1\right) w_{,x}(L)+\theta (L)=0. \end{aligned}$$

(2.19)

Finally, (2.14) and the expression for $\sigma _x$ yield $-\frac{2}{3}h^3\theta _{,x}=0,$ hence

$$\begin{aligned} \theta _{,x}(0)=\theta _{,x}(L)=0. \end{aligned}$$

(2.20)

We now show that the system equations yields an expression for u in terms of w and $\theta$, thus decoupling the system for w and $\theta$ from the equation for u. To that end, we substitute (2.4) and (2.5) into (2.9)-(2.11), and assuming that all the integrands are continuous, obtain

$$\begin{aligned} u_{,xx}+w_{,x}w_{,xx}+\nu \theta \theta _{,x}=\left( u_{,x}+\frac{1}{2} (w_{,x})^2+\frac{\nu }{2} \theta \right) _{,x}=-\widetilde{q}_h. \end{aligned}$$

(2.21)

Here, to simplify some of the equations, we let

$$\begin{aligned}{} & {} \widetilde{q}_h=\frac{2(1-\nu ^2)h}{E}q_h,\qquad \widetilde{q}_v=\frac{1-\nu }{E}q_v,\nonumber \\{} & {} \qquad \widetilde{p}_L=\frac{(1-\nu ^2)}{E}{\hat{p}}_L. \end{aligned}$$

(2.22)

Integration over x, using (2.17) and some manipulations, we obtain

$$\begin{aligned} u_{,x}(x)+\frac{1}{2} (w_{,x})^2(x)+ \frac{\nu }{2} \theta ^2(x)= \int _x^L\widetilde{q}_h(s)\text{ d }s - \widetilde{p}_L. \end{aligned}$$

(2.23)

Next, it follows from (2.10) and (2.5), after y integration, rearranging and using (2.22), that

$$\begin{aligned}{} & {} u_{,xx}w_{,x}+\frac{3}{2} (w_{,x})^2 w_{,xx}+ \nu \theta \theta _{,x}w_{,x}+ u_{,x}w_{,xx}\nonumber \\{} & {} +\frac{\nu }{2} \theta ^2 w_{,xx} +\frac{(1-\nu )}{2}(w_{,xx}-\theta _{,x})=-\widetilde{q}_v. \end{aligned}$$

(2.24)

Then, (2.11) and (2.5) imply that

$$\begin{aligned} \frac{2h^2}{3}\theta _{,xx}-\nu \theta ^3-2\nu u_{,x}\theta -\nu (w_{,x})^2\theta +(1-\nu )(w_{,x}-\theta )=0. \end{aligned}$$

(2.25)

The model equations are now (2.21), (2.24) and (2.25).

Next, to decouple (2.24) and (2.25) from u, we use (2.21)and (2.23) in the form

$$\begin{aligned} u_{,xx}=-w_{,x}w_{,xx}-\nu \theta \theta _{,x}-\widetilde{q}_h. \end{aligned}$$

Also, for the sake of simplicity, we let

$$\begin{aligned} Q_{hL}(x)=\int _x^L\widetilde{q}_h(s)\text{ d }s - \widetilde{p}_L. \end{aligned}$$

(2.26)

Then, straightforward manipulations, using the expressions above, yield the highly nonlinear system for w and $\theta$. To complete the system we must consider the boundary conditions. It follows from (2.20) that $\theta {,x}(0)=\theta {,x}(L)=0$. Next, (2.19) implies that once $w_{,x}(0)=w_{x}^0$ and $w_{,x}(L)=w_{x}^L$ are prescribed, the values of $\theta (0)$ and $\theta (L)$ are given, once $\hat{p}_0$ and $\hat{p}_L$ are prescribed. Indeed,

$$\begin{aligned} \theta (0)=-\frac{2\hat{p}_0+1-\nu }{1-\nu }w_{x}^0,\qquad \theta (L)=-\frac{2\hat{p}_L+1-\nu }{1-\nu }w_{x}^L. \end{aligned}$$

(2.27)

Finally, the same conclusion follows from (2.17) and (2.18), once $w_{,x}(0)=w_{x}^0$ and $w_{,x}(L)=w_{x}^L$ are prescribed and $\hat{p}_0$ and $\hat{p}_L$ are given, then

$$\begin{aligned} u_{,x}(0)=-\frac{1}{2} (w_{x}^0)^2-\frac{1}{2} \theta ^2(0)+\frac{(1-\nu ^2)}{E}\hat{p}_0, \end{aligned}$$

$$\begin{aligned} u_{,x}(L)=-\frac{1}{2} (w_{x}^L)^2-\frac{1}{2} \theta ^2(L)+\frac{(1-\nu ^2)}{E}\hat{p}_L. \end{aligned}$$

(2.28)

To complete the boundary conditions, we may prescribe $u(0)=u^0$.

We summarize our findings in the following Static Model.

Model 2.1

Given the vertical body force $q_v$, the longitudinal force $q_h$ and the traction $\hat{p}_L$, find the three functions $(w(x), u(x), \theta (x))$, for $0\le x\le L,$ such that

$$\begin{aligned} 2Q_{hL}w_{,xx}+(1-\nu )(w_{,xx}-\theta _{,x})-2\widetilde{q}_hw_{,x}=-2\widetilde{q}_v, \end{aligned}$$

(2.29)

$$\begin{aligned} \frac{2h^3}{3}\theta _{,xx}-2\nu Q_{hL}\theta - \nu (1-\nu )\theta ^3 +(1-\nu )(w_{,x}-\theta )=0. \end{aligned}$$

(2.30)

Together with the boundary conditions

$$\begin{aligned} \theta _{,x}(0)=\theta _{,x}(L)=0, \end{aligned}$$

(2.31)

$$\begin{aligned} \sigma _{x}(L)=\hat{p}_L, \end{aligned}$$

(2.32)

$$\begin{aligned} w_{,x}(0)=w_{x}^0,\qquad w_{,x}(L)=w_{x}^L, \end{aligned}$$

(2.33)

$$\begin{aligned} u(0)=u^0. \end{aligned}$$

(2.34)

Then, u is obtained by the integration of (2.23),

$$\begin{aligned}{} & {} u(x)=u^0-\frac{1}{2} \int _0^x \left( (w_{,x}(s))^2-\nu \theta ^2(s)\right) \text{ d }s \nonumber \\{} & {} + \int _x^L\widetilde{q}_h(s)\text{ d }s - \widetilde{p}_L. \end{aligned}$$

(2.35)

This nonlinear system of coupled ordinary differential equations describes static large displacements of a moderately thick beam.

We note that although the loads and tractions that act on the system may be functions of the y-coordinate, the loads in the model depend only on x, and the y-dependence is ‘integrated out.’ Nevertheless, the displacement vector $\textbf{u}=(u-y\theta , w)^T$ depends linearly on y.

The existence of solutions, the model’s well-posedness and the mathematical analysis of this system are open questions, yet. Generally, such systems do no have closed form solutions, and to gain insight into the model solutions we describe its numerical simulations below.

3 Numerical model

As noted above, generally, Model 2.1 does not have closed form or analytical solutions. It is even difficult to solve semi-analytically. For this reason, we obtain approximate numerical solutions in which all the characteristic properties of the mathematical model are visible. Due to the better presentation of the properties and easier interpretation of the phenomena, the inertial forces $\textbf{M}$ were added to the numerical model and the simulations were performed in the dynamic formulation as a transient problem. Then the steady or static solutions were obtained as limits of large time. It should be noted here that we treat this dynamic problem as a sequence of static problems which, under the influence of dissipative forces, tend towards a static solution in the limit of large time. However, before reaching the limit and reducing the velocity to zero, an oscillatory motion takes place about the static equilibrium position, which is a solution of the model.

The domain of the beam is partitioned into spatial finite elements, and the interval of a finite element is defined by

$$\begin{aligned} \Omega =\{x:\,0\le x\le b\}. \end{aligned}$$

(3.1)

A linear interpolation $\textbf{N}$ of the nodal values of the finite element is applied independently to the transverse displacements w and the rotations $\theta$.

$$\begin{aligned} w(x)=\textbf{N}{} \textbf{w}, \qquad \theta (x)=\textbf{N}\varvec{\theta }, \end{aligned}$$

(3.2)

where

$$\begin{aligned} \textbf{N}= \left[ \begin{array}{cc} 1-\frac{x}{b}&\frac{x}{b} \end{array} \right] , \qquad \textbf{w}^\textsf{T}= \left[ \begin{array}{cc} w_1&w_2 \end{array} \right] , \qquad \varvec{\theta }^\textsf{T}= \left[ \begin{array}{cc} \theta _1&\theta _2 \end{array} \right] . \end{aligned}$$

The virtual displacement $w^*$ and the angle of rotation $\theta ^*$, are given by

$$\begin{aligned} w^*=\left( \textbf{N}^*\,\textbf{w}^*\right) ^\textsf{T}, \ \ \ \ \ \theta ^*=\left( \textbf{N}^*\,\varvec{\theta }^*\right) ^\textsf{T}, \end{aligned}$$

(3.3)

where

$$\begin{aligned} w^*=0\ \ \text{ and }\ \ \ \theta ^*=0,\ \ \ \text{ for }\ \ x=0,b. \end{aligned}$$

(3.4)

The discrete weak forms of equations (2.29) and (2.30) are

$$\begin{aligned} \Pi _w^*=\int _\Omega w^*\left\{ 2Q_{hL}w_{,xx}+(1-\nu )(w_{,xx}-\theta _{,x})-2\widetilde{q}_hw_{,x}+2\widetilde{q}_v\right\} \text{ d }\Omega , \end{aligned}$$

(3.5)

$$\begin{aligned} \Pi _\theta ^*=\int _\Omega \theta ^*\left\{ \frac{2h^3}{3}\,\theta _{,xx}-2\nu Q_{hL}\theta -\nu (1-\nu )\theta ^3+(1-\nu )(w_{,x}-\theta )\right\} \text{ d }\Omega . \end{aligned}$$

(3.6)

After integration by parts in (3.5) and (3.6), the stationarity condition yields a pair of equations

$$\begin{aligned} \begin{aligned} \int _\Omega&\left\{ -2Q_{hL}(\textbf{N}_{,x}^*)^\textsf{T}{} \textbf{N}_{,x}{} \textbf{w}-(1-\nu )\left[ (\textbf{N}_{,x}^*)^\textsf{T}{} \textbf{N}_{,x}{} \textbf{w}+(\textbf{N}^*)^\textsf{T}{} \textbf{N}_{,x}\varvec{\theta }\right] \right. \\&\left. -2\widetilde{q}_h(\textbf{N}^*)^\textsf{T}{} \textbf{N}_{,x}\textbf{w}+2\widetilde{q}_v(\textbf{N}^*)^\textsf{T}\right\} \text{ d }\Omega =0, \end{aligned} \end{aligned}$$

(3.7)

and

$$\begin{aligned} \begin{aligned} \int _\Omega&\left\{ -\frac{2h^3}{3}\,(\textbf{N}_{,x}^*)^\textsf{T}\textbf{N}_{,x}\varvec{\theta }-2\nu Q_{hL}\,(\textbf{N}^*)^\textsf{T}\textbf{N}\varvec{\theta }-\nu (1-\nu )\,(\textbf{N}^*)^\textsf{T}(\textbf{N}\varvec{\theta })^2\textbf{N}\varvec{\theta }\right. \\&\left. +(1-\nu )\left[ (\textbf{N}^*)^\textsf{T}{} \textbf{N}_{,x}{} \textbf{w}-(\textbf{N}^*)^\textsf{T}\textbf{N}\varvec{\theta }\right] \right\} \text{ d }\Omega . \end{aligned} \end{aligned}$$

(3.8)

The stiffness matrix $\textbf{K}$ of the finite beam element is then a sum of five components

$$\begin{aligned} \textbf{K}=\textbf{K}_s+\textbf{K}_b+\textbf{K}_p+\textbf{K}_n+\textbf{K}_{qh}. \end{aligned}$$

(3.9)

Nodal degrees of freedom are organized in the sequence

$$\begin{aligned} \textbf{Q}=\left[ \begin{array}{cccc} w_1&\theta _1&w_2&\theta _2 \end{array} \right] ^\textsf{T} . \end{aligned}$$

The matrices in (3.9) are as follows

$$\begin{aligned} \textbf{K}_s=(1-\nu ) \left[ \begin{array}{cccc} 1/b &{} -1/2 &{} -1/b &{} 1/2\\ 1/2 &{} b/3 &{} -1/2 &{} b/6\\ -1/b &{} -1/2 &{} 1/b &{} 1/2\\ 1/2 &{} b/6 &{} -1/2 &{} b/3 \end{array} \right] , \end{aligned}$$

$$\begin{aligned} \textbf{K}_b=\frac{2h^3}{3} \left[ \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 1/b &{} 0 &{} -1/b\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} -1/b &{} 0 &{} 1/b \end{array} \right] , \end{aligned}$$

$$\begin{aligned} \textbf{K}_p=Q_{hL} \left[ \begin{array}{cccc} 2/b &{} 0 &{} -2/b &{} 0\\ 0 &{} \nu b/3 &{} 0 &{} \nu b/6\\ -2/b &{} 0 &{} 2/b &{} 0\\ 0 &{} \nu b/6 &{} 0 &{} \nu b/3 \end{array} \right] , \end{aligned}$$

$$\begin{aligned} \textbf{K}_n=\frac{\nu (1-\nu )b}{60} \left[ \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 12\theta _L^2+6\theta _L\theta _R+2\theta _R^2 &{} 0 &{} 3\theta _L^2+4\theta _L\theta _R+3\theta _R^2\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 3\theta _L^2+4\theta _L\theta _R+3\theta _R^2 &{} 0 &{} 2\theta _L^2+10\theta _L\theta _R+12\theta _R^2 \end{array} \right] , \end{aligned}$$

where $\theta _L$ and $\theta _R$ are the angles $\theta$ at the left and right node of the finite element.

Finally,

$$\begin{aligned} \textbf{K}_{qh}=\widetilde{q}_h \left[ \begin{array}{cccc} -1 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ -1 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right] , \qquad \textbf{F}=\widetilde{q}_vb \left[ \begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array} \right] . \end{aligned}$$

The matrix $\textbf{K}_s$ contains the shear factors, $\textbf{K}_b$ represents the bending of the element, $\textbf{K}_\lambda$ contains the force p, and $\textbf{K}_n$ includes nonlinear terms in $\theta$.

Moreover, the inertia matrix $\textbf{M}$ of the beam element and the moment of the cross-section are

$$\begin{aligned} \textbf{M}=\rho \frac{b}{6} \left[ \begin{array}{cccc} 4h &{} 0 &{} 2h &{} 0\\ 0 &{} 2I_x &{} 0 &{} I_x\\ 2h &{} 0 &{} 4h &{} 0\\ 0 &{} I_x &{} 0 &{} 2I_x \end{array} \right] ,\qquad I_x=\iint _A y^2\,dA. \end{aligned}$$

These allow us to use the scheme of integration for the equation of motion. The time integration was performed with the scheme described for the space-time finite element method in [23, 24]. Then, the formulas joining two successive velocity vectors are

$$\begin{aligned}{} & {} \left[ \left( \alpha -\frac{1}{2}\alpha ^2\right) \Delta t\,\textbf{K}-\frac{1}{h}{} \textbf{M}\right] {\varvec{ \dot{Q}}}^{t}\nonumber \\{} & {} +\left[ \frac{1}{2}\alpha ^2\Delta t\,\textbf{K}+\frac{1}{h}{} \textbf{M}\right] {\varvec{\dot{Q}}}^{t+\Delta t}+\textbf{K}\textbf{Q}^{t}=\textbf{F}, \end{aligned}$$

(3.10)

is coupled energetically with

$$\begin{aligned} \textbf{Q}^{t+\Delta t}=\textbf{Q}^{t}+ \Delta t \left( \alpha {\varvec{\dot{Q}}^t}+ (1-\alpha ){\varvec{\dot{Q}}^{t+\Delta t}}\right) \ . \end{aligned}$$

(3.11)

This numerical model of vibrating beam (3.10)-(3.11) with matrices (3.9) consists of a nonlinear system of algebraic equations, providing the numerical solution at each time step.

4 Results

Generally, as was noted above, Model 2.1 does not have any closed form, analytical or even semi-analytical solutions. Therefore, we present numerical approximate solutions, in which the main characteristic properties of the mathematical model are preserved and can be clearly seen.

The following data were used in the computations of (2.22):

• beam’s length: L=100 cm,

• beam’s thickness: 2h=8.50 cm,

• cross sectional area: A=68.0 cm$^2$,

• second moment of a cross section: $I_x$=409.4 cm$^4$,

• mass density: $\rho$=7.7 g/cm$^3$,

• Young modulus: E=207 GPa,

• Poisson ratio: $\nu$=0.3,

• volume loads: $q_h$=0, $q_v$=0,

• G=E/2/(1+$\nu$),

• damping coefficient: $c=20$ Ns/m (unless another value is specified),

• $p=\hat{p}_L$: axial traction at $x=L$, positive when compressive.

• Initial conditions: $\dot{w}(x,0)=0$, $w(x,0)=w_0\sin (\pi x/l)$.

Although these quantities can be reduced to dimensionless parameters, we keep them dimensional for the sake of simplicity of the simulations interpretation.

Fig. 3

Deflection in time of the mid-point w(50, t) of the beam for various damping coefficient c, with $p=1$ MN. The buckled steady states are $w=\pm 3.093$ and the vibrations are about two stable equilibrium states

We turn to the simulations results. We start with Fig. 3, which shows the transverse displacements of the beam’s mid-point ($x=50$ cm) over time, with an initial deflection $w_0=0.1$ cm, and compressive force $p=1$ MN. It is found numerically that there are two stable equilibrium positions, namely $w(50)=\pm 3.093$ cm, and the system vibrations, because of the damping, end up about one of them. Indeed, the deflections in the initial phase occur according to three different scenarios. At low damping values ($c=0$ Ns/cm, 0.05 Ns/cm), the motion is oscillatory, crosses both equilibria, and the unsteady $w=0$ state, while gradually damping dissipates the energy and the system ends oscillating about $w=3.093$ cm. With slightly higher damping ($c=0.15$ Ns/cm), the oscillatory motion shifts to negative ranges and the oscillations are about $w=- 3.093$ cm. With even higher damping ($c=1$ Ns/cm, 5 Ns/cm), significant dissipation prevents the mid-point from crossing the zero and very quickly approaches $w=3.093$ cm.

Next, Fig. 4 depicts the amplitudes of the midpoint of the beam over time, as the end traction changed. The contour lines that represent points with the same constant deflection values have been overlaid. The changing frequency bands along the time axis in the lower part of the figure illustrate the vibrations centered at the zero displacement point, which is stable when the value of $p=\hat{p}_L$ is below the buckling point. Indeed, the the zero displacement point is a stable state of static equilibrium, and the vibrations occur about it at a low compressive force $p=\hat{p}_L$, which is below the critical value $p_{cr}$. In the upper part of the figure with a higher force, $p>p_{cr}$, the free vibrations are centered on an equilibrium state with $w\ne 0$. For $p=100$ kN in Fig. 4 the equilibrium state is at the deflection $w=0.34$ cm, and for $p=120$ kN it is at $w=0.46$ cm. At higher values of $p=1000$ kN when higher deflection ranges occur, this fact can be observed in Fig. 3.

Between these two regions, i.e., the lower and upper regions in the Fig.  4, a horizontal line of constant deflection without oscillations, at $w=0.1$ cm, is visible. This occurs at the critical compressive force value of $p_{cr}=65$ kN.

Fig. 4

Deflection, in time, of the mid-point of the beam for various axial forces $\hat{p}_L$; the initial deflection is $w_0=0.1$ cm

Figure 5 also shows the displacements over time at different axial force values, when the initial deflection was five times greater, $w_0=0.5$ cm. We observe here, too, that the lower region of the graph is where oscillations are around the zero displacement point. The amplitudes in this case are small and correspond to the range of the initial displacements $w_0$. The upper part of the graph illustrates vibrations with significantly larger amplitudes, obtained at higher axial force values exceeding the critical force, which in this case is approximately $p_{cr}=494$ kN. Similarly to the previous case, both regions are separated by a line representing the critical force $p_{cr}$ in the absence of vibrations. The slight reduction in amplitudes, particularly noticeable at the upper edges of both maps (Figs. 4 and 5), is due to the application of small damping.

Fig. 5

Deflection, in time, of the mid-point of the beam for various axial forces $\hat{p}_L$; the initial deflection $w_0=0.5$ cm

The problem is highly nonlinear and the initial deflection that is five times greater, depicted in Fig. 5, results in a thirty fold larger vibration amplitudes. Therefore, when using the model to calculate the displacements of real beams, all the necessary data must be entered very precisely. Indeed, since the problem is strongly nonlinear, different data would yield results that may differ significantly from those presented here. The following examples should therefore just reflect the our choice of the data. It is found that the relationship between displacements and the associated deformations is significant, and to better capture the phenomena in a real setting, material nonlinearity as well as other geometric nonlinearities should also be considered. However, this is beyond the scope of the current study.

Fig. 6 shows an important phenomenon, presenting the total energy of the system, which in this case is the sum of potential and kinetic energy over time, for different values of axial force $\hat{p}_L$ and different initial deflections $w_0$, ranging from 0.1 cm to 0.6 cm. It is worth emphasizing, as is depicted in Fig. 7, that the system’s energy depends solely on the square of the initial value $w_0$.

Fig. 6

Total energy for the initial deflections $w_0=0.1,..., 0.6$ cm and forces $\hat{p}_L$: a – $p=10$ kN, b – $p=20$ kN, c – $p=100$ kN, d – $p=200$ kN

Fig. 7

Total energy

Fig. 8 depicts the deflections of the mid-point of the beam over time for zero axial force and an axial force $p=575$ kN. The initial displacement of the mid-point was 0.2 cm. The free vibrations are depicted with zero axial force with the specified initial kinematic conditions. The amplitudes remain constant, while our current Timoshenko-like beam exhibits a slightly longer period in accordance with the theory. Figure 8b compares the two Gao beams based on the Bernoulli-Euler and the Timoshenko theories. The applied damping ensures the small decay of the vibrations. Both curves are illustrative as both models are highly nonlinear and can not be simply compared. Quantitative estimation of the influence of individual material constants, initial conditions, and loading on displacements requires further research, and the results will be presented in future studies.

Fig. 8

Comparison of a thin (Bernoulli-Euler-like) and a thick (Timoshenko-like) models of Gao beam in the case of free vibration with $p=0$ kN, $c=2$ Ns/m (a) and compressed with a force $p=575$ kN, $c=50$ Ns/m (b)

5 Conclusions and future studies

This work presents a unified extension of both the Timoshenko and the Gao beam models. It results in a system of two highly nonlinear equations for the displacements of the central axis of the beam, and the rotation of its cross sections. The steady equations are derived from the principle of minimum or stationarity of the potential energy. To describe the system behavior, we use computer simulations of the related dynamic problems, which exhibit the various types of beam’s behavior, and in particular, vibrations about the buckled states. A FEM algorithm is constructed and implemented for the computer simulations, which indicate the following characteristics of the model.

The total energy of the system does not depend on the axial force $p=p_h$, only on the initial deflection of the beam axis $w_0(x)$.

The responses of vibrating beams based on the Bernoulli-Euler and Timoshenko models are found to be qualitatively similar, however, they differ quantitatively. The new beam model exhibits slightly lower stiffness as compared to the Gao beam.

It is found that there exists a critical force $p_{cr}$, dependent on the initial conditions, at which no vibrations occur, and the problem becomes fully static. The critical value of the force increases with an increase in the initial dynamic deflection $w_0$. There are either one or three equilibrium states. The zero equilibrium state, where vibrations occur around $w=0$ with a small axial force $p<p_{cr}$ is unique, and it is conjectured to be stable and attracting. When $p>p_{cr}$, the zero equilibrium seems to loose its stability and two stable equilibrium states $\pm w_{st}$ appear, around which vibrations occur. The amplitudes of the transverse vibrations are significantly higher for $p > p_{cr}$ as compared with $p < p_{cr}$.

When damping is included, the position of the deformed axis stabilizes into one of the two stable equilibrium positions, which supports our conjecture that these are stable and attracting (asymptotically stable). With an axial force $p>p_{cr}$, vibrations may occur alternately around the equilibrium positions $\pm w_{st}$, switching to the opposite side of the zero axis from the $+w_{st}$ to the $-w_{st}$ state under small perturbations, after several or several dozen cycles.

The equilibrium displacement values depend on the magnitude of the axial force p.

Next, to show the usefulness of the new model, we suggest some future directions to continue this line of study.

The dynamic and quasistatic versions of the model are of interest, both theoretically and in simulations, as was done above for the dynamic case, to depict the wide range of the model solutions. As was noted above, a thorough investigation of the differences between the Bernoulli-Euler-like and the Timoshenko-like Gao beams is of interest. It may provide insight into when using the new model may lead to improved predictions accuracy.

Theoretically, the model system is highly nonlinear and the existence of solutions needs to be established, as well as the model’s analysis. In particular, the conjectures on the stability of the one or three steady states are of practical and well as theoretical importance. Finally, the analysis of the dynamic and quasistatic versions of the model is of interest.