1 Introduction

We study discrete vibrating spring-mass systems composed by chains of one dimensional harmonic oscillators. This kind of systems can be used to approximate the dynamical behavior of continuous systems. Several applications can be seen in [5, 7], regarding vibrations on structures, elastic bands, [24, 31, 34], regarding solid state physics and statistical physics, and [21, 3937 or ], regarding metamaterials, among others; inverse problems were considered in [4, 13, 16, 19, 20, 33]. We assume that the elementary parts of the system are chains of identical oscillators, which will be the building blocks for constructing more complex systems. Each chain is characterized by its physical characteristics: total mass, particle mass, spring constant, damping coefficient, number of oscillators and length. In [6] we considered the problem of determining the eigenvalues and eigenvectors for a chain of harmonic oscillators obtained from the coupling of two homogeneous chains, through a composition process. This composition process is the coupling of the chains through either a gluing mass particle, with a given mass m, or a gluing spring with a given spring constant \(\kappa\). We have shown how to determine, analytically, the solution of the new non-homogeneous system in terms of the eigenvectors and eigenvalues of the composing (homogeneous) chains, which are assumed to be known, or easily determined.

In the present work we extend our previous results to the case of damped linear harmonic oscillators, thus obtaining explicit solutions for coupled damped system in terms of the solutions of the original homogeneous chains which constitute the system. Therefore, we are able to analyze how the system changes its dynamical behavior in terms of the dynamical behavior of the constituting parts. A complete introduction to damped linear systems can be found in [36]. See also [17, 18].

2 Preliminaries

We deal with spring-mass systems, as the one in Fig. 1, composed by particles \(i\in \left\{ 1,\ldots ,n\right\}\) with mass \(m_{i}\) which are connected to its left and right neighbors by two springs (with constants \(\kappa _{i}\) and \(\kappa _{i+1}\)), and two dampers (with constants \(d_i\) and \(d_{i+1}\)). The springs are labeled by the set \(\left\{ 1,\ldots ,n+1\right\}\). The left endpoint of the first spring and damper as well as the right endpoint of the last spring and damper are the boundary conditions of the chain, which are fixed and mean that the chain is isolated. We will use this boundary points to produce different couplings with other chains, in which case they are no longer fixed. The displacement of the oscillator with mass \(m_i\), with respect to its equilibrium position, will be denoted by \(x_{i}\). The length of the spring i is variable and its variation is given by \(x_{i}-x_{i-1}\), except for the spring 1 and spring \(n+1\) which are, respectively, \(x_{1}\) and \(-x_{n}\).

Fig. 1
figure 1

Chain of n coupled one-dimensional damped harmonic oscillators

Full size image

The state of the system is given by \(x_{i}\left( t\right)\) and their time derivatives \(\overset{\cdot }{x_{i}}\left( t\right)\), at each instant t. The force applied at each point is proportional to the displacement with respect to its equilibrium condition, as a consequence of the harmonic condition.

The complete chain can be described by the vector differential equation in matrix coefficients

$$\begin{aligned} M\overset{\cdot \cdot }{x}\left( t\right) +D\overset{\cdot }{x}\left( t\right) +Kx\left( t\right) =0, \end{aligned}$$
(1)

where

$$\begin{aligned}{} & {} x(t)=\left[ x_{1}(t),\ldots ,x_{n}(t)\right] ^{T},\text { }{\dot{x}}(t)=\left[ \dot{ x}_{1}(t),\ldots ,{\dot{x}}_{n}(t)\right] ^{T},\text { }\ddot{x}(t)\\{} & {} =\left[ \ddot{x} _{1}(t),\ldots ,\ddot{x}_{n}(t)\right] ^{T}. \end{aligned}$$

As a consequence of the physical interpretation of the model we are dealing, the mass matrix \(M=\textrm{diag}\left( m_{1},m_{2},\ldots ,m_{n}\right)\) is an invertible diagonal matrix. Therefore, we can write Eq. (1) as

$$\begin{aligned} \overset{\cdot \cdot }{x}\left( t\right) +M^{-1}D\overset{\cdot }{x}\left( t\right) +M^{-1}Kx\left( t\right) =0. \end{aligned}$$
(2)

The viscous damping matrix D is

$$\begin{aligned} D=\left( \begin{array}{ccccccc} d_{1}+d_{2} &{} -d_{2} &{} 0 &{} &{} &{} &{} 0 \\ -d_{2} &{} d_{2}+d_{3} &{} -d_{3} &{} &{} \ddots &{} &{} \\ 0 &{} -d_3 &{} &{} &{} &{} 0 &{} \\ &{} 0 &{} &{} \ddots &{} &{} &{} \\ {} &{} &{} \ddots &{} &{} &{} &{} 0 \\ &{} &{} &{} &{} &{} d_{n-1}+d_{n} &{} -d_{n} \\ 0 &{} &{} &{} &{} 0 &{} -d_{n} &{} d_{n}+d_{n+1} \end{array} \right) \end{aligned}$$

and the stiffness matrix K is

$$\begin{aligned} K=\left( \begin{array}{ccccccc} \kappa _{1}+\kappa _{2} &{} -\kappa _{2} &{} 0 &{} &{} &{} &{} 0 \\ -\kappa _{2} &{} \kappa _{2}+\kappa _{3} &{} -\kappa _{3} &{} &{} \ddots &{} &{} \\ 0 &{} -\kappa _3 &{} &{} &{} &{} 0 &{} \\ &{} 0 &{} &{} \ddots &{} &{} &{} \\ {} &{} &{} \ddots &{} &{} &{} &{} 0 \\ &{} &{} &{} &{} &{} \kappa _{n-1}+\kappa _{n} &{} -\kappa _{n} \\ 0 &{} &{} &{} &{} 0 &{} -\kappa _{n} &{} \kappa _{n}+\kappa _{n+1} \end{array} \right) \end{aligned}$$

which are, as \(d_{i},\ \kappa _{i}>0\), \(i=1,\ldots ,n+1\), positive definite invertible symmetric matrices, see e.g. [1] or [29], and the eigenvalues of both \(M^{-1}D\) and \(M^{-1}K\) are simple, which follows easily as these matrices are tridiagonal, see e.g. [12] or [32].

In the case the system is homogeneous, the mass matrix is a scalar multiple of the identity matrix, that is, \(M=mI\), where m is the mass of each particle, and

$$\begin{aligned} \Lambda =d^{-1}D=\kappa ^{-1}K=\left( \begin{array}{ccccc} 2 &{} -1 &{} &{} &{} \\ -1 &{} 2 &{} -1 &{} &{} \\ &{} -1 &{} \ddots &{} &{} \\ &{} &{} &{} 2 &{} -1 \\ &{} &{} &{} -1 &{} 2 \end{array} \right) , \end{aligned}$$

where d is the damping coefficient and \(\kappa\) is the spring constant. The dimension of the matrices is denoted by \(n>0\) and corresponds to the number of particles. Whenever is convenient, we write \(\Lambda _{n}=\Lambda\), \(D_{n}=D\), \(K_{n}=K\), \(M_{n}=M\), or \(I_{n}=I\)

Homogeneous damped chains are characterized by their physical parameters: mass per particle m, number of particles n, damping coefficient d, spring constant \(\kappa\) and total length \(\ell\). A chain of this type will be designated by \(X_{\left( n,\ell ,m,d,\kappa \right) }\). We call the parameters n, \(\ell\) the extensive parameters of the chain and m, d, \(\kappa\) the intensive parameters. The ratio \(\omega ^{2}=\kappa /m\) is the relevant parameter for dynamical purposes, gives the natural frequency of each oscillator and d is the damping parameter, which controls the energy dissipation of the system. The length \(\ell\) serves as a reference value for initial conditions choice, since the linear system has no preferential scale. If we are considering real systems with an approximation to small oscillations, in order to use the linear model, the estimation for the value \(\ell\), and \(\ell /n\) gives us an approximation of the magnitude of the amplitudes involved. For homogeneous chains we have an internal symmetry

$$\begin{aligned} X_{\left( n,\ell ,m,d,\kappa \right) }\leftrightarrow X_{\left( n,\ell ,am,ad,a\kappa \right) } \end{aligned}$$

for some positive constant a. That is, the solutions are the same for the referred systems. To deal with different chains simultaneously, we use the notation \(X_{i}=X_{\left( n_{i},\ell _{i},m_{i},d_{i},\kappa _{i}\right) }\), \(i\in {\mathbb {N}}\). The composition of two homogeneous chains with distinct intensive parameters

$$\begin{aligned} X_{\left( n_{1},\ell _{1},m_{1},d_{1},\kappa _{1}\right) }\circ X_{\left( n_{2},\ell _{2},m_{2},d_{2},\kappa _{2}\right) }:=X_{\left( n_{1},\ell _{1},m_{1},d_{1},\kappa _{1}\right) \left( n_{2},\ell _{2},m_{2},d_{2},\kappa _{2}\right) }, \end{aligned}$$

gives us a non-homogeneous chain. In this case, the notation must take into account the order of the coupling, that is, \(X_{1}\circ X_{2}:=X_{12}\) which is in general different from \(X_{21}=:X_{2}\circ X_{1}\). The normalization constant \(\omega _{j}=\frac{\kappa _{j}}{m_{j}}\), which depends on the mass particle and the spring constant, is fixed at each block \(j=1,2\).

The idea here is to use our results from previous work, which where obtained for the undamped case, to address the damped case. For the sake of completeness, we recall here the relevant parts.

The eigenvectors and eigenvalues for the homogeneous undamped chain system can be explicitly determined (see the seminal work [12], or [38]) through an iterated map defined recursively by

$$\begin{aligned} g_{0}\left( \lambda \right)= & {} 0,\text { }g_{1}\left( \lambda \right) =1, \\ g_{j+1}\left( \lambda \right)= & {} \left( 2-\lambda \right) g_{j}\left( \lambda \right) -g_{j-1}\left( \lambda \right) ,\text { }j\ge 1. \end{aligned}$$

In fact, the matrix \(\Lambda\) has n distinct positive real eigenvalues given by the solutions of

$$\begin{aligned} g_{n+1}\left( \lambda \right) =0\text {.} \end{aligned}$$

Given \(\lambda \in \textrm{spec}\left( \Lambda \right)\), the eigenvector of \(\Lambda\) with respect to \(\lambda\), is, up to scalar multiplication,

$$\begin{aligned} v_{n}(\lambda )=\left( 1,g_{2}\left( \lambda \right) ,g_{3}\left( \lambda \right) ,\ldots ,g_{j}\left( \lambda \right) ,\ldots ,g_{n}\left( \lambda \right) \right) . \end{aligned}$$
(3)

Therefore, the set \(\left\{ v_{n}(\lambda ):\lambda \in \textrm{spec}\left( \Lambda \right) \right\}\) is a set of n linearly independent vectors. It is then a simple exercise to write the general solution of

$$\begin{aligned} \overset{\cdot \cdot }{x}\left( t\right) =-\omega ^{2}\Lambda x\left( t\right) , \end{aligned}$$

which is

$$\begin{aligned} x\left( t\right) =\sum _{\lambda \in \textrm{spec}\left( \Lambda \right) }\left( c_{\lambda }e^{i\omega \sqrt{\lambda }t}+{\overline{c}}_{\lambda }e^{-i\omega \sqrt{\lambda }t}\right) v_{\lambda }, \end{aligned}$$
(4)

\({\overline{c}}_{\lambda }\) complex conjugate of \(c_{\lambda }\), which can be determined from the initial conditions. In [6] we have seen that the reversed vector

$$\begin{aligned} \left( g_{n}\left( \lambda \right) ,\ldots ,g_{j}\left( \lambda \right) ,\ldots ,g_{2}\left( \lambda \right) ,1\right) , \end{aligned}$$

is the eigenvector associated with \(\lambda\), with a different normalization. Taking this fact into account, we will use the following definitions

$$\begin{aligned} \upsilon _{n}\left( \lambda \right) :=\left( 1,g_{2}\left( \lambda \right) ,g_{3}\left( \lambda \right) ,\ldots ,g_{j}\left( \lambda \right) ,\ldots ,g_{n}\left( \lambda \right) \right) , \\ \upsilon _{n}^{*}\left( \lambda \right) :=\left( g_{n}\left( \lambda \right) ,\ldots ,g_{j}\left( \lambda \right) ,\ldots ,g_{2}\left( \lambda \right) ,1\right) . \end{aligned}$$

On the other hand, this means that \(\upsilon _{n}^{*}\left( \lambda \right) =\pm \upsilon _{n}\left( \lambda \right)\), and \(g_{n}\left( \lambda \right) =\pm 1\). Note that the sequence of polynomials \(g_{n}\left( \lambda \right)\) has a symmetry property regarding increasing and decreasing indexes,

$$\begin{aligned}{} & {} g_{j+1}\left( \lambda \right) =\left( 2-\lambda \right) g_{j}\left( \lambda \right) -g_{j-1}\left( \lambda \right) \Leftrightarrow g_{j-1}\left( \lambda \right) \\{} & {} =\left( 2-\lambda \right) g_{j}\left( \lambda \right) -g_{j+1}\left( \lambda \right) . \end{aligned}$$

The vector \(\upsilon _{n}\left( \lambda \right)\), when \(g_{n+1}\left( \lambda \right) =0\), is an eigenvector of the matrix \(\Lambda\). The vector \(\upsilon _{n}\left( \frac{\lambda }{\omega }\right)\), when \(g_{n+1}\left( \frac{\lambda }{\omega }\right) =0\) is an eigenvector of the matrix \(\omega \Lambda\), therefore is this one which gives the solution of the homogeneous system.

To obtain the solutions of equation (1), with \(D\ne 0\), we must now solve the quadratic eigenvalue problem

$$\begin{aligned} (\lambda ^{2}M+\lambda D+K)u=0, \end{aligned}$$
(5)

that is, find all \(\lambda \in {\mathbb {R}}\) and \(u\in {\mathbb {R}}^{n}\backslash \{0\}\) satisfying the above equation, which we call eigenvalues and associated eigenvectors. We then have 2n solutions \((\lambda _i,u_i)\), \(i=1,\ldots ,2n\), where each \(\lambda _i\) is, in our case, complex with negative real part and \(u_i\) are also complex. Although the method to solve this equations is well known, in general, this task can be difficult. See the references [11, 15, 26] for the theory of matrix polynomials. A complete survey about the quadratic eigenvalue problem, with several applications, can be found in [35]. See also [22, 23, 28, 30].

The solution of equation (1) is given by (see [27], which traces back to [10])

$$\begin{aligned} x(t)=Xe^{Jt}C, \end{aligned}$$
(6)

where \(X\in {\mathbb {C}}_{n\times 2n}\) is a rectangular matrix whose columns are the Jordan chains and \(J=\text {diag}\left( J_{1},\ldots ,J_{s}\right) \in {\mathbb {C}}_{2n\times 2n}\) is the block diagonal matrix of the Jordan blocks associated to the eigenvectors \(\lambda _{1},\ldots ,\lambda _{s}\), and the constant column vector \(C\in {\mathbb {C}}_{2n}\) is determined by the initials conditions. Of course, when the eigenvalues are distinct then J reduces to \(J=\text {diag}\left( \lambda _{1},\ldots ,\lambda _{2n}\right)\) and X is the matrix whose columns are the eigenvectors associated with the eigenvalues \(\lambda _{1},\ldots ,\lambda _{2n}\). A specially interesting case is that when \(DM^{-1}K\) is a symmetric real matrix, it follows that \(DM^{-1}K=KM^{-1}D\) and so the eigenvectors are the same for the undamped case (and all of them are real), as it was established a long time ago, see [3]. This in fact follows from linear algebra, as two matrices share the same eigenvectors if and only if they commute, proved in [2]. Using the eigenvectors of \(M^{-1}K\) we can decouple the equation of motion: If S is the matrix of eigenvectors of the positive definite symmetric matrix \(M^{-1}K\), then

$$\begin{aligned} S^{T}M^{-1}KS= & {} \text {diag}(\lambda _{1},\ldots ,\lambda _{n}) \\ S^{T}M^{-1}DS= & {} \text {diag}(2\zeta _{1}\sqrt{\lambda _{1}},\ldots ,2\zeta _{n} \sqrt{\lambda _{n}}), \end{aligned}$$

where \(\lambda _{i}\) are the square of the natural frequency of the undamped system and \(\zeta _{i}\) are the modal damping ratios, \(i=1,\ldots ,n\). Besides the fact that the eigenvectors are shared between the damped and undamped case, it is clear that the eigenvalues are given by

$$\begin{aligned} -\zeta _i\sqrt{\lambda _i}\pm \sqrt{\lambda _i(\zeta _i^2-1)},\ i=1,\ldots ,n, \end{aligned}$$
(7)

and, as in the homogeneous case the matrix D is a multiple of matrix K, \(D=\frac{d}{\kappa }K\), then

$$\begin{aligned} \zeta _i=\frac{\frac{d}{\kappa }\lambda _i}{2\sqrt{\lambda _i}}=\frac{d\sqrt{ \lambda _i}}{2\kappa } \end{aligned}$$

and so in fact we have

$$\begin{aligned} -\frac{d}{2\kappa }\lambda _i\pm \sqrt{\frac{d^2}{4\kappa ^2}\lambda _i^2- \lambda _i},\ i=1,\ldots ,n. \end{aligned}$$
(8)

We can now summarize the relevant information in the following:

Proposition 1

Let \(n\ge 1\). Given the n distinct positive real solutions \(\lambda _{1},\ldots ,\lambda _{n}\) of

$$\begin{aligned} g_{n+1}\left( \frac{\lambda }{\omega }\right) =0, \end{aligned}$$

the eigenvalues of the matricial equation (5) are given by

$$\begin{aligned} -\frac{d}{2\kappa }\lambda _{i}\pm \sqrt{\frac{d^{2}}{4\kappa ^{2}}\lambda _{i}^{2}-\lambda _{i}},\ i=1,\ldots ,n \end{aligned}$$

and the corresponding eigenvectors, by

$$\begin{aligned} v_{n}\left( \frac{\lambda }{\omega }\right) =\left( 1,g_{2}\left( \frac{ \lambda }{\omega }\right) ,g_{3}\left( \frac{\lambda }{\omega }\right) ,\ldots ,g_{j}\left( \frac{\lambda }{\omega }\right) ,\ldots ,g_{n}\left( \frac{ \lambda }{\omega }\right) \right) . \end{aligned}$$

Therefore, the set \(\left\{ v_{n}\left( \frac{\lambda }{\omega }\right) :\lambda \text { satisfy }g_{n+1}\left( \frac{\lambda }{\omega }\right) =0\right\}\) is a set of n linearly independent vectors.

We are now interested in coupling two damped homogeneous systems with distinct intensive parameters. There are mainly two different ways of doing it, using our results obtained in [6]: one way is by deducing formulas for the damped case using the techniques we developed there (for the undamped case), see Sect. 5 below; the other, which is by far more appealing, is to use our previous results for the undamped case directly for the damped case, using the above facts of decoupling systems of equations when \(DM^{-1}K\) is symmetric, see Sects. 3 and 4 below.

We will use the following notation for the direct sum of vectors:

Let \(x_{1}=\left( x_{1,1},\ldots ,x_{1,n_{1}}\right) \in {\mathbb {R}} ^{n_{1}}\), \(x_{2}=\left( x_{2,1},\ldots ,x_{2,n_{2}}\right) \in {\mathbb {R}} ^{n_{2}}\) and let \(z\in {\mathbb {R}}\). The direct sum

$$\begin{aligned} x_{1}\oplus x_{2}=\left( x_{1,1},\ldots ,x_{1,n_{1}},x_{2,1},\ldots ,x_{2,n_{2}}\right) \in {\mathbb {R}} ^{n_{1}+n_{2}}, \end{aligned}$$

and

$$\begin{aligned} x_{1}\oplus z\oplus x_{2}=\left( x_{1,1},\ldots ,x_{1,n_{1}},z,x_{2,1},\ldots ,x_{2,n_{2}}\right) \in {\mathbb {R}} ^{n_{1}+n_{2}+1}. \end{aligned}$$

3 First case, gluing particle in damped system

Fig. 2
figure 2

Chain of n coupled one-dimensional damped harmonic oscillators with a gluing particle

Full size image

In this case we add an extra particle, of mass m, to join two different homogeneous chains, see Fig. 2. This extra particle is the coupling parameter. The system will then be described by Eq. (1), where now we have as mass matrix

$$\begin{aligned} M=\left( \begin{array}{ccc|c|ccc} &{} &{} &{} 0 &{} 0 &{} \dots &{} 0 \\ &{} m_{1}I_{n_{1}} &{} &{} \vdots &{} \vdots &{} &{} \vdots \\ &{} &{} &{} 0 &{} 0 &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} 0 &{} m &{} 0 &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} 0 &{} 0 &{} &{} &{} \\ \vdots &{} &{} \vdots &{} \vdots &{} &{} m_{2}I_{n_{2}} &{} \\ 0 &{} \dots &{} 0 &{} 0 &{} &{} &{} \end{array} \right) , \end{aligned}$$
(9)

viscous damping matrix D

$$\begin{aligned} D=\left( \begin{array}{ccc|c|ccc} &{} &{} &{} 0 &{} 0 &{} \dots &{} 0 \\ &{} d_{1}\Lambda _{n_{1}} &{} &{} \vdots &{} \vdots &{} &{} \vdots \\ &{} &{} &{} -d_{1} &{} 0 &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} -d_{1} &{} d_{1}+d_{2} &{} -d_{2} &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} 0 &{} -d_{2} &{} &{} &{} \\ \vdots &{} &{} \vdots &{} \vdots &{} &{} d_{2}\Lambda _{n_{2}} &{} \\ 0 &{} \dots &{} 0 &{} 0 &{} &{} &{} \end{array} \right) \end{aligned}$$
(10)

and stiffness matrix K

$$\begin{aligned} K=\left( \begin{array}{ccc|c|ccc} &{} &{} &{} 0 &{} 0 &{} \dots &{} 0 \\ &{} \kappa _{1}\Lambda _{n_{1}} &{} &{} \vdots &{} \vdots &{} &{} \vdots \\ &{} &{} &{} -\kappa _{1} &{} 0 &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} -\kappa _{1} &{} \kappa _{1}+\kappa _{2} &{} -\kappa _{2} &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} 0 &{} -\kappa _{2} &{} &{} &{} \\ \vdots &{} &{} \vdots &{} \vdots &{} &{} \kappa _{2}\Lambda _{n_{2}} &{} \\ 0 &{} \dots &{} 0 &{} 0 &{} &{} &{} \end{array} \right) . \end{aligned}$$
(11)

We have the following results for the corresponding eigenvalues and eigenvectors of the system, for the case \(\frac{d_{1}}{\kappa _{1}}=\frac{ d_{2}}{\kappa _{2}},\)

Corollary 1

Let \(\kappa _{1}\),\(\kappa _{2},m_{1},m_{2},m>0\) and \(d_{1},d_{2}\ge 0\), with

$$\begin{aligned} \frac{d_{1}}{\kappa _{1}}=\frac{d_{2}}{\kappa _{2}}=\alpha \in {\mathbb {R}} _{0}^{+} \end{aligned}$$
(12)

and \(n_{1},n_{2}\ge 1\). The eigenvalues of the system are given by

$$\begin{aligned} \mu _{i}=-\frac{\alpha }{2}\lambda _{i}\pm \sqrt{\frac{\alpha ^{2}}{4} \lambda _{i}^{2}-\lambda _{i}},\ i=1,\ldots ,n_{1}+n_{2}+1, \end{aligned}$$
(13)

where \(\lambda _{1},\ldots ,\lambda _{n_{1}+n_{2}+1}\) are the solutions, positive and distinct, of the equation

$$\begin{aligned} \left. \begin{array}{c} \kappa _{1}g_{n_{1}}\left( \frac{\lambda }{\omega _{1}}\right) g_{n_{2}+1}\left( \frac{\lambda }{\omega _{2}}\right) +\left( m\lambda -\left( \kappa _{1}+\kappa _{2}\right) \right) g_{n_{1}+1}\left( \frac{ \lambda }{\omega _{1}}\right) g_{n_{2}+1}\left( \frac{\lambda }{\omega _{2}} \right) + \\ +\kappa _{2}g_{n_{1}+1}\left( \frac{\lambda }{\omega _{1}}\right) g_{n_{2}}\left( \frac{\lambda }{\omega _{2}}\right) =0. \end{array} \right. \end{aligned}$$

If

$$\begin{aligned} g_{n_{2}+1}\left( \frac{\lambda }{\omega _{2}}\right) \ne 0,\ g_{n_{1}+1}\left( \frac{\lambda }{\omega _{1}}\right) \ne 0 \end{aligned}$$

then the eigenvector \(w\left( \mu \right)\) of the system, for the eigenvalue \(\mu\), is given up to scalar multiplication by

$$\begin{aligned} w\left( \mu \right) =g_{n_{2}+1}\left( \frac{\lambda }{\omega _{2}}\right) \upsilon _{n_{1}}\left( \frac{\lambda }{\omega _{1}}\right) \oplus g_{n_{1}+1}\left( \frac{\lambda }{\omega _{1}}\right) g_{n_{2}+1}\left( \frac{\lambda }{\omega _{2}}\right) \\ \oplus g_{n_{1}+1}\left( \frac{\lambda }{ \omega _{1}}\right) \upsilon _{n_{2}}^{*}\left( \frac{\lambda }{\omega _{2}}\right) . \end{aligned}$$

If

$$\begin{aligned} g_{n_{2}+1}\left( \frac{\lambda }{\omega _{2}}\right) =0,\ g_{n_{1}+1}\left( \frac{\lambda }{\omega _{1}}\right) =0 \end{aligned}$$

then \(w\left( \mu \right)\) is given, up to scalar multiplication, by

$$\begin{aligned} w\left( \mu \right) =-\kappa _{2}g_{n_{2}}\left( \frac{\lambda }{\omega _{2}} \right) \upsilon _{n_{1}}\left( \frac{\lambda }{\omega _{1}}\right) \oplus 0\oplus \kappa _{1}g_{n_{1}}\left( \frac{\lambda }{\omega _{1}}\right) \upsilon _{n_{2}}^{*}\left( \frac{\lambda }{\omega _{2}}\right) . \end{aligned}$$

Proof

The matrix product \(DM^{-1}K\) is a symmetric matrix iff (12 ) holds. In fact,

$$\begin{aligned} DM^{-1}K = \\ {\tiny {\left( \begin{array}{cccc|c|cccc} \! &{}\! &{}\! &{}\! &{}\! 0 &{}\! 0 &{}\! 0 &{}\! \dots &{}\! 0 \\ \! &{}\! &{}\! &{}\! &{}\! \vdots &{}\! \vdots &{}\! \vdots &{}\! &{}\! \vdots \\ \! &{}\! &{}\! &{}\! \frac{\kappa _{1}d_{1}}{m_{1}}\Gamma _{n_{1}} &{}\! \frac{\kappa _{1}d_{1}}{m_{1}} &{}\! 0 &{}\! 0 &{}\! \dots &{}\! 0 \\ \! &{}\! &{}\! &{}\! &{}\! -\frac{2\kappa _{1}d_{1}}{m_{1}}-\frac{\kappa _{1}(d_{1}+d_{2})}{m } &{}\! \frac{\kappa _{1}d_{2}}{m} &{}\! 0 &{}\! \dots &{}\! 0 \\ \hline \! 0 &{}\! \dots &{}\! \frac{\kappa _{1}d_{1}}{m_{1}} &{}\! -\frac{2\kappa _{1}d_{1}}{m_{1}} -\frac{d_{1}(\kappa _{1}+\kappa _{2})}{m} &{}\! \frac{\kappa _{1}d_{1}}{m_{1}}+ \frac{(\kappa _{1}+\kappa _{2})(d_{1}+d_{2})}{m}+\frac{\kappa _{2}d_{2}}{ m_{2}} &{}\! -\frac{(\kappa _{1}+\kappa _{2})d_{2}}{m}-\frac{2\kappa _{2}d_{2}}{ m_{2}} &{}\! \frac{\kappa _{2}d_{2}}{m_{2}} &{}\! \dots &{}\! 0 \\ \hline \! 0 &{}\! \dots &{}\! 0 &{}\! \frac{\kappa _{2}d_{1}}{m} &{}\! -\frac{\kappa _{2}(d_{1}+d_{2}) }{m}-\frac{2\kappa _{2}d_{2}}{m_{2}} &{}\! &{}\! &{}\! &{}\! \\ \! 0 &{}\! \dots &{}\! 0 &{}\! 0 &{}\! \frac{\kappa _{2}d_{2}}{m_{2}} &{}\! \frac{\kappa _{2}d_{2}}{m_{2}}\Omega _{n_{2}} &{}\! &{}\! &{}\! \\ \vdots &{}\! &{}\! \vdots &{}\! \vdots &{}\! \vdots &{}\! &{}\! &{}\! &{}\! \\ \! 0 &{}\! \dots &{}\! 0 &{}\! 0 &{}\! 0 &{}\! &{}\! &{}\! &{}\! \end{array} \right) }} \end{aligned}$$

where \(\Gamma _{n_1}\) is the \(n_1\times n_1\) matrix given by

$$\begin{aligned} \Gamma _{n_1}=\left( \begin{array}{rrrrrrrrr} {\small 5} &{} {\small -4} &{} {\small 1} &{} {\small 0} &{} {\small \dots } &{} {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small 0} \\ {\small -4} &{} {\small 6} &{} {\small -4} &{} {\small 1} &{} {\small \ddots } &{} {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small 0} \\ {\small 1} &{} {\small -4} &{} {\small 6} &{} {\small -4} &{} {\small \ddots } &{} {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small 0} \\ {\small 0} &{} {\small 1} &{} {\small -4} &{} {\small 6} &{} {\small \ddots } &{} {\small \ddots } &{} {\small 0} &{} {\small 0} &{} {\small 0} \\ {\small \vdots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \vdots } \\ {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small \ddots } &{} {\small \ddots } &{} {\small 6} &{} {\small -4} &{} {\small 1} &{} {\small 0} \\ {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small \ddots } &{} {\small \ddots } &{} {\small -4} &{} {\small 6} &{} {\small -4} &{} {\small 1} \\ {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small \ddots } &{} {\small 1} &{} {\small -4} &{} {\small 6} &{} {\small -4} \\ {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small \dots } &{} {\small 0} &{} {\small 1} &{} {\small -4} &{} {\small 6} \end{array} \right) \end{aligned}$$

and \(\Omega _{n_2}\) is the \(n_2\times n_2\) matrix given by

$$\begin{aligned} \Omega _{n_2}=\left( \begin{array}{rrrrrrrrr} {\small 6} &{} {\small -4} &{} {\small 1} &{} {\small 0} &{} {\small \dots } &{} {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small 0} \\ {\small -4} &{} {\small 6} &{} {\small -4} &{} {\small 1} &{} {\small \ddots } &{} {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small 0} \\ {\small 1} &{} {\small -4} &{} {\small 6} &{} {\small -4} &{} {\small \ddots } &{} {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small 0} \\ {\small 0} &{} {\small 1} &{} {\small -4} &{} {\small 6} &{} {\small \ddots } &{} {\small \ddots } &{} {\small 0} &{} {\small 0} &{} {\small 0} \\ {\small \vdots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \ddots } &{} {\small \vdots } \\ {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small \ddots } &{} {\small \ddots } &{} {\small 6} &{} {\small -4} &{} {\small 1} &{} {\small 0} \\ {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small \ddots } &{} {\small \ddots } &{} {\small -4} &{} {\small 6} &{} {\small -4} &{} {\small 1} \\ {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small \ddots } &{} {\small 1} &{} {\small -4} &{} {\small 6} &{} {\small -4} \\ {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small 0} &{} {\small \dots } &{} {\small 0} &{} {\small 1} &{} {\small -4} &{} {\small 5} \end{array} \right) . \end{aligned}$$

In this case, it follows that the eigenvectors must be shared with the undamped case and consequently, as matrices M and K are the same in Theorem 1 of [6], one has the desired result. Furthermore, from (12) we have

$$\begin{aligned} D=\alpha K \end{aligned}$$

and so (13) follows where \(\lambda _{i}\) and their distinctness are given by Theorem 1 and Lemma 1, respectively, of [6]. \(\square\)

Remark 1

In the case where

$$\begin{aligned} \frac{d_{1}}{\kappa _{1}}=\frac{d_{2}}{\kappa _{2}}=\alpha \in {\mathbb {R}} \end{aligned}$$

does not hold, then \(DM^{-1}K\) in not symmetric and then the above result fails. Furthermore, the natural frequency will be different from the natural frequency \(\sqrt{\lambda _{i}}\) of the undamped case, even in the cases of low damped ratio, see e.g. [25].

4 Second case, joining two homogeneous chains by gluing its end-springs and its end-dampers

Fig. 3
figure 3

Joining two chains of coupled one-dimensional damped harmonic oscillators by gluing both its end-springs and end-dampers

Full size image

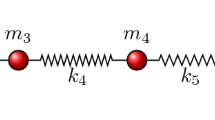
In this case, we join two different homogeneous chains by attaching its corresponding end-springs and end-dampers, see in Fig. 3. This attachment is intended to be done in such a way that the obtained equivalent spring has also a linear behavior, with spring constant \(\kappa\).

The system will now be described by Eq. (1), with mass matrix

$$\begin{aligned} M=\left( \begin{array}{ccc|ccc} &{} &{} &{} 0 &{} \dots &{} 0 \\ &{} m_{1}I_{n_{1}} &{} &{} \vdots &{} &{} \vdots \\ &{} &{} &{} 0 &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} 0 &{} &{} &{} \\ \vdots &{} &{} \vdots &{} &{} m_{2}I_{n_{2}} &{} \\ 0 &{} \dots &{} 0 &{} &{} &{} \end{array} \right) , \end{aligned}$$
(14)

viscous damping matrix

$$\begin{aligned} D=\left( \begin{array}{ccc|c|c|ccc} &{} &{} &{} 0 &{} 0 &{} 0 &{} \dots &{} 0 \\ &{} d_{1}\Lambda _{n_{1}-1} &{} &{} \vdots &{} \vdots &{} \vdots &{} &{} \vdots \\ &{} &{} &{} -d_{1} &{} 0 &{} 0 &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} -d_{1} &{} d_{1}+d &{} -d &{} 0 &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} 0 &{} -d &{} d+d_{2} &{} -d_{2} &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} 0 &{} 0 &{} -d_{2} &{} &{} &{} \\ \vdots &{} &{} \vdots &{} \vdots &{} \vdots &{} &{} d_{2}\Lambda _{n_{2}-1} &{} \\ 0 &{} \dots &{} 0 &{} 0 &{} 0 &{} &{} &{} \end{array} \right) \end{aligned}$$
(15)

and stiffness matrix

$$\begin{aligned} K=\left( \begin{array}{ccc|c|c|ccc} &{} &{} &{} 0 &{} 0 &{} 0 &{} \dots &{} 0 \\ &{} \kappa _{1}\Lambda _{n_{1}-1} &{} &{} \vdots &{} \vdots &{} \vdots &{} &{} \vdots \\ &{} &{} &{} -\kappa _{1} &{} 0 &{} 0 &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} -\kappa _{1} &{} \kappa _{1}+\kappa &{} -\kappa &{} 0 &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} 0 &{} -\kappa &{} \kappa +\kappa _{2} &{} -\kappa _{2} &{} \dots &{} 0 \\ \hline 0 &{} \dots &{} 0 &{} 0 &{} -\kappa _{2} &{} &{} &{} \\ \vdots &{} &{} \vdots &{} \vdots &{} \vdots &{} &{} \kappa _{2}\Lambda _{n_{2}-1} &{} \\ 0 &{} \dots &{} 0 &{} 0 &{} 0 &{} &{} &{} \end{array} \right) . \end{aligned}$$
(16)

We have the following result, for the case \(\frac{d_{1}}{\kappa _{1}}=\frac{ d_{2}}{\kappa _{2}}=\frac{d}{\kappa }\).

Corollary 2

Let \(\kappa _{1}\),\(\kappa _{2},k,m_{1},m_{2}>0\) and \(d_{1},d_{2},d\ge 0\), with

$$\begin{aligned} \frac{d_{1}}{\kappa _{1}}=\frac{d_{2}}{\kappa _{2}}=\frac{d}{\kappa }=\alpha \in {\mathbb {R}}_{0}^{+}, \end{aligned}$$
(17)

and \(n_{1},n_{2}\ge 1\). The eigenvalues of the system are given by

$$\begin{aligned} \mu _{i}=-\frac{\alpha }{2}\lambda _{i}\pm \sqrt{\frac{\alpha ^{2}}{4} \lambda _{i}^{2}-\lambda _{i}},\ i=1,\ldots ,n_{1}+n_{2}, \end{aligned}$$
(18)

where \(\lambda _{1},\ldots ,\lambda _{n_{1}+n_{2}}\) are the solutions, positive and distinct, of the equation

$$\begin{aligned} \left. \begin{array}{c} \kappa ^{2}g_{n_{1}}\left( \frac{\lambda }{\omega _{1}}\right) g_{n_{2}}\left( \frac{\lambda }{\omega _{2}}\right) \\ -\left( \kappa _{2}g_{n_{2}+1}\left( \frac{\lambda }{\omega _{2}}\right) +\left( \kappa -\kappa _{2}\right) g_{n_{2}}\left( \frac{\lambda }{\omega _{2}}\right) \right) \left( \kappa _{1}g_{n_{1}+1}\left( \frac{\lambda }{ \omega _{1}}\right) +\left( \kappa -\kappa _{1}\right) g_{n_{1}}\left( \frac{ \lambda }{\omega _{1}}\right) \right) =0. \end{array} \right. \end{aligned}$$

For each given eigenvalue \(\mu\), the corresponding eigenvector \(w\left( \mu \right)\) of the system is given up to scalar multiplication by

$$\begin{aligned}{} & {} w\left( \mu \right) =\kappa g_{n_{2}}\left( \frac{\lambda }{\omega _{2}} \right) \upsilon _{n_{1}}\left( \frac{\lambda }{\omega _{1}}\right) \oplus \left( \kappa _{1}g_{n_{1}+1}\left( \frac{\lambda }{\omega _{1}}\right) \right. \\{} & {} \left. +\left( \kappa -\kappa _{1}\right) g_{n_{1}}\left( \frac{\lambda }{\omega _{1}}\right) \right) \upsilon _{n_{2}}^{*}\left( \frac{\lambda }{\omega _{2}}\right) . \end{aligned}$$

Proof

The proof is similar to the proof of Corollary 1, just noting that now the matrix product \(DM^{-1}K\) is a symmetric matrix iff (17) holds, where now

$$\begin{aligned} DM^{-1}K = \\ \hspace{-1cm}{\tiny {\left( \begin{array}{cccc|c|c|cccc} \! &{}\! &{}\! &{}\! &{}\! 0 &{}\! 0 &{}\! 0 &{}\! 0 &{}\! \dots &{}\! 0 \\ \! &{}\! &{}\! &{}\! \frac{\kappa _{1}d_{1}}{m_{1}}\Gamma _{n_{1}-1} &{}\! \vdots &{}\! \vdots &{}\! \vdots &{}\! \vdots &{}\! &{}\! \vdots \\ \! &{}\! &{}\! &{}\! &{}\! \frac{\kappa _{1}d_{1}}{m_{1}} &{}\! 0 &{}\! 0 &{}\! 0 &{}\! \dots &{}\! 0 \\ \! &{}\! &{}\! &{}\! &{}\! -\frac{2\kappa _{1}d_{1}+d_{1}(\kappa _{1}+\kappa ) }{m_{1}} &{}\! \frac{\kappa d_{1}}{m_{1}} &{}\! 0 &{}\! 0 &{}\! \dots &{}\! 0 \\ \hline \! 0 &{}\! \dots &{}\! \frac{\kappa _{1}d_{1}}{m_{1}} &{}\! -\frac{2\kappa _{1}d_{1}+\kappa _{1}(d_{1}+d)}{m_{1}} &{}\! \frac{\kappa _{1}d_{1}}{m_{1}}+\frac{ (\kappa _{1}+\kappa )(d_{1}+d)}{m_{1}}+\frac{\kappa d}{m_{2}} &{}\! -\frac{ \kappa (d_{1}+d)}{m_{1}}+\frac{(\kappa +\kappa _{2})d}{m_{2}} &{}\! \frac{\kappa _{2}d}{m_{2}} &{}\! 0 &{}\! \dots &{}\! 0 \\ \hline \! 0 &{}\! \dots &{}\! 0 &{}\! \frac{\kappa _{1}d}{m_{1}} &{}\! -\frac{(\kappa _{1}+\kappa )d}{ m_{1}}+\frac{\kappa (d+d_{2})}{m_{2}} &{}\! \frac{\kappa d}{m_{1}}+\frac{(\kappa +\kappa _{2})(d+d_{2})}{m_{2}} &{}\! -\frac{\kappa _{2}(d+d_{2})+ 2\kappa _{2}d_{2}}{m_{2}} &{}\! \frac{\kappa _{2}d_{2}}{m_{2}} &{}\! \dots &{}\! 0 \\ \hline \! 0 &{}\! \dots &{}\! 0 &{}\! 0 &{}\! \frac{\kappa d_{2}}{m_{2}} &{}\! -\frac{(\kappa +\kappa _{2})d_{2}+2\kappa _{2}d_{2}}{m_{2}} &{}\! &{}\! &{}\! &{}\! \\ \! 0 &{}\! \dots &{}\! 0 &{}\! 0 &{}\! 0 &{}\! \frac{\kappa _{2}d_{2}}{m_{2}} &{}\! &{}\! &{}\! &{}\! \\ \vdots &{}\! &{}\! \vdots &{}\! \vdots &{}\! \vdots &{}\! &{}\! \frac{\kappa _{2}d_{2}}{m_{2}} \Omega _{n_{2}-1} &{}\! &{}\! &{}\! \\ \! 0 &{}\! \dots &{}\! 0 &{}\! 0 &{}\! 0 &{}\! &{}\! &{}\! &{}\! &{}\! \end{array} \right) }} \end{aligned}$$

and using, from [6], Lemma 2 and Theorem 2 in the place of Lemma 1 and Theorem 1, respectively. \(\square\)

Remark 2

In the case where

$$\begin{aligned} \frac{d_{1}}{\kappa _{1}}=\frac{d_{2}}{\kappa _{2}}=\frac{d}{\kappa }=\alpha \in {\mathbb {R}} \end{aligned}$$

does not hold, then \(DM^{-1}K\) is not symmetric and then the above result fails. Furthermore, the natural frequency will be different form the natural frequency \(\sqrt{\lambda _{i}}\) from the undamped case, even if the cases of low damped ratio, as observed in Remark 1.

5 When \(DM^{-1}K\) in not symmetric

The symmetry of \(DM^{-1}K\) indeed simplifies the analysis. However, this property is not true in general, see [35]. In this section we will explore the coupling cases for which \(DM^{-1}K\) in not a symmetric matrix and thus the approach of the previous sections does not apply.

The idea is as follows: taking advantage of the fact that each one of the two systems are homogeneous, the corresponding eigenvalues and eigenvectors are easily determined (see Proposition 2 below). Then, applying similar techniques to those developed by us in previous works, we obtain results for more general cases (see Sects. 5.1 and 5.2 ) than the ones of the antecedent section. This is obtainable, off course, at the expense of more involved computations.

Proposition 2

The eigenvalues of Eq. (5) are given by the solutions of

$$\begin{aligned} f_{n+1}(\lambda )=0, \end{aligned}$$

where

$$\begin{aligned} f_{0}(\lambda )= & {} 0,\ f_{1}(\lambda )=1, \\ f_{j+1}(\lambda )= & {} (\lambda ^{2}m+2\lambda d+2\kappa )f_{j}(\lambda )-(\lambda d+\kappa )^{2}f_{j-1}(\lambda ),\ j\ge 1 \end{aligned}$$

and their corresponding eigenvectors are given by

$$\begin{aligned} v_{n}(\lambda )=\left( 1,\frac{1}{\lambda d+\kappa }f_{2}(\lambda ),\frac{1}{ (\lambda d+\kappa )^{2}}f_{3}(\lambda ),\ldots ,\frac{1}{(\lambda d+\kappa )^{n-1}}f_{n}(\lambda )\right) , \end{aligned}$$

Therefore, the set \(\left\{ v_{n}\left( \lambda \right) :\lambda \text { satisfy }f_{n+1}(\lambda )=0\right\}\) is a set of n linearly independent vectors.

Proof

Consider the n equations, arising from Eq. (5), writing \(u=\left( u_{1},\ldots ,u_{n}\right)\),

$$\begin{aligned} \left\{ \begin{array}{l} u_{2}=\frac{\lambda ^2m+2\lambda d+2\kappa }{\lambda d+k} u_{1}=\frac{1}{ \lambda \kappa +d }f_2(\lambda )u_1 \\ u_{3}=\frac{\lambda ^2m+2\lambda d+2\kappa }{\lambda d+k} u_{2}-u_1=\frac{1}{ (\lambda \kappa +d)^2 }f_3(\lambda )u_1 \\ \cdots \\ u_{j}=\frac{1}{(\lambda \kappa +d)^{j-1} }f_{j}\left( \lambda \right) u_{1} \\ \cdots \\ u_{n}=\frac{1}{(\lambda \kappa +d)^{n-1} }f_{n}\left( \lambda \right) u_{1} \\ \left( \lambda ^2m+2\lambda d+2\kappa \right) u_{n}-(\lambda d+\kappa )u_{n-1}=0\Leftrightarrow \frac{1}{(\lambda d+\kappa )^{n-1}} f_{n+1}(\lambda )u_1=0 \end{array} \right. \end{aligned}$$

The 2n eigenvalues are the solutions of the last equation in the system, \(f_{n+1}\left( \lambda \right) =0\), and the system leads directly to the form of the eigenvector \(v_n(\lambda )\), associated with each conjugated pair of eigenvalues \(\lambda\). Because in the homogeneous case \(DM^{-1}K\) is a symmetric matrix, it follows that both eigenvalues and eigenvectors are the same of Proposition 1, and so \(\left\{ v_n \left( \lambda \right) : \lambda \right\}\) is a set of n linearly independent vectors. \(\square\)

We will now explore the cases of joining two different homogeneous chains. These results will include the results from Corollary 1 and Corollary 2 as particular cases.

5.1 First case, gluing particle in damped system

Here we add an extra particle, of mass m, as a coupling parameter. The system is described by Eq. (1), where M, D and K are given by (9), (10) and (11), respectively. We have the following result.

Theorem 3

The eigenvalues of Eq. (5) are given by the solutions of

$$\begin{aligned} \left. \begin{array}{c} -(\lambda d_{1}+\kappa _{1})^{2}f_{n_{1}}(\lambda )f_{n_{2}+1}(\lambda )-(\lambda d_{2}+\kappa _{2})^{2}f_{n_{2}}(\lambda )f_{n_{1}+1}(\lambda )+ \\ +(\lambda ^{2}m+\lambda (d_{1}+d_{2})+(\kappa _{1}+\kappa _{2}))f_{n_{1}+1}(\lambda )f_{n_{2}+1}(\lambda )=0 \end{array} \right. \end{aligned}$$

and their corresponding eigenvectors are given by

$$\begin{aligned}&w\left( \lambda \right) =\frac{1}{(\lambda d_{2}+\kappa _{2})^{n_{2}}} f_{n_{2}+1}(\lambda )\upsilon _{n_{1}}\left( \lambda \right) \\&\oplus \frac{1}{(\lambda d_{1}+\kappa _{1})^{n_{1}}(\lambda d_{2}+\kappa _{2})^{n_{2}}}f_{n_{1}+1}(\lambda )f_{n_{2}+1}(\lambda )\\&\oplus \frac{1}{ (\lambda d_{1}+\kappa _{1})^{n_{1}}}f_{n_{1}+1}(\lambda )\upsilon _{n_{2}}^{*}\left( \lambda \right) , \end{aligned}$$

where \(f_{n_{1}+1}(\lambda )\ne 0\) and \(f_{n_{2}+1}(\lambda )\ne 0\). Else, if \(f_{n_{1}+1}(\lambda )=0\) and \(f_{n_{2}+1}(\lambda )=0\), then

$$\begin{aligned} w\left( \lambda \right) =\frac{1}{(\lambda d_{2}+\kappa _{2})^{n_{2}-2}} f_{n_{2}}(\lambda )\upsilon _{n_{1}}\left( \lambda \right) \oplus 0\oplus \frac{1}{(\lambda d_{1}+\kappa _{1})^{n_{1}-2}}f_{n_{1}}(\lambda )\upsilon _{n_{2}}^{*}\left( \lambda \right) . \end{aligned}$$

Proof

If we consider now the \(n_{1}+n_{2}+1\) equations, arising from the quadratic eigenvalue equation (5), writing \(u=\left( v_{1},\ldots ,v_{n_{1}},s,u_{1},\ldots ,u_{n_{2}}\right)\), we have

$$\begin{aligned} \left\{ \begin{array}{l} \left( \lambda ^{2}m_{1}+2\lambda d_{1}+2\kappa _{1}\right) v_{1}-(\lambda d_{1}+\kappa _{1})v_{2}=0 \\ -(\lambda d_{1}+\kappa _{1})v_{1}+\left( \lambda ^{2}m_{1}+2\lambda d_{1}+2\kappa _{1}\right) v_{2}-(\lambda d_{1}+\kappa _{1})v_{3}=0 \\ \cdots \\ -(\lambda d_{1}+\kappa _{1})v_{n_{1}-2}+\left( \lambda ^{2}m_{1}+2\lambda d_{1}+2\kappa _{1}\right) v_{n_{1}-1}-(\lambda d_{1}+\kappa _{1})v_{n_{1}}=0 \\ -(\lambda d_{1}+\kappa _{1})v_{n_{1}-1}+\left( \lambda ^{2}m_{1}+2\lambda d_{1}+2\kappa _{1}\right) v_{n_{1}}-(\lambda d_{1}+\kappa _{1})s=0 \\ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ -(\lambda d_{1}+\kappa _{1})v_{n_{1}}+\left( \lambda ^{2}m+\lambda (d_{1}+d_{2})+(\kappa _{1}+\kappa _{2})\right) s-(\lambda d_{2}+\kappa _{2})u_{1}=0 \\ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ -(\lambda d_{2}+\kappa _{2})s+\left( \lambda ^{2}m_{2}+2\lambda d_{2}+2\kappa _{2}\right) u_{1}-(\lambda d_{2}+\kappa _{2})u_{2}=0 \\ -(\lambda d_{2}+\kappa _{2})u_{1}+\left( \lambda ^{2}m_{2}+2\lambda d_{2}+2\kappa _{2}\right) u_{2}-(\lambda d_{2}+\kappa _{2})u_{3}=0 \\ \cdots \\ -(\lambda d_{2}+\kappa _{2})u_{n_{2}-2}+\left( \lambda ^{2}m_{2}+2\lambda d_{2}+2\kappa _{2}\right) u_{n_{2}-1}-(\lambda d_{2}+\kappa _{2})u_{n_{2}}=0 \\ -(\lambda d_{2}+\kappa _{2})u_{n_{2}-1}+\left( \lambda ^{2}m_{2}+2\lambda d_{2}+2\kappa _{2}\right) u_{n_{2}}=0 \end{array} \right. \end{aligned}$$

The first \(n_{1}+1\) equations can be solved through

$$\begin{aligned} \left\{ \begin{array}{l} v_{2}=\frac{\lambda ^{2}m_{1}+2\lambda d_{1}+2\kappa _{1}}{\lambda d_{1}+\kappa _{1}}v_{1}=\frac{1}{\lambda d_{1}+\kappa _{1}}f_{2}(\lambda )v_{1} \\ v_{3}=\frac{\lambda ^{2}m_{1}+2\lambda d_{1}+2\kappa _{1}}{\lambda d_{1}+\kappa _{1}}v_{2}-v_{1}=\frac{1}{(\lambda d_{1}+\kappa _{1})^{2}} f_{3}(\lambda )v_{1} \\ \cdots \\ v_{j}=\frac{1}{(\lambda d_{1}+\kappa _{1})^{j-1}}f_{j}(\lambda )v_{1} \\ \cdots \\ v_{n_{1}}=\frac{1}{(\lambda d_{1}+\kappa _{1})^{n_{1}-1}}f_{n_{1}}(\lambda )v_{1} \\ s=\frac{1}{(\lambda d_{1}+\kappa _{1})^{n_{1}}}f_{n_{1}+1}(\lambda )v_{1} \\ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ -\frac{1}{(\lambda d_{1}+\kappa _{1})^{n_{1}-2}}f_{n_{1}}(\lambda )v_{1}+ \frac{\lambda ^{2}m+\lambda (d_{1}+d_{2})+(\kappa _{1}+\kappa _{2})}{ (\lambda d_{1}+\kappa _{1})^{n_{1}}}f_{n_{1}+1}(\lambda )v_{1}-(\lambda d_{2}+\kappa _{2})u_{1}=0\ (*) \end{array} \right. \end{aligned}$$

Reserving the last equation labeled by \((*)\). Next, we solve the following \(n_{2}\) equations with reversed order, which gives us

$$\begin{aligned} \left\{ \begin{array}{l} u_{n_{2}-1}=\frac{1}{\lambda d_{2}+\kappa _{2}}f_{2}(\lambda )u_{n_{2}} \\ u_{n_{2}-2}=\frac{1}{(\lambda d_{2}+\kappa _{2})^{2}}f_{3}(\lambda )u_{n_{2}} \\ \cdots \\ u_{n_{2}-j}=\frac{1}{(\lambda d_{2}+\kappa _{2})^{j}}f_{j+1}(\lambda )u_{n_{2}} \\ \cdots \\ u_{1}=\frac{1}{(\lambda d_{2}+\kappa _{2})^{n_{2}-1}}f_{n_{2}}(\lambda )u_{n_{2}} \\ s=\frac{1}{(\lambda d_{2}+\kappa _{2})^{n_{2}}}f_{n_{2}+1}(\lambda )u_{n_{2}} \end{array} \right. \end{aligned}$$

In particular, we have

$$\begin{aligned} s=\frac{1}{(\lambda d_{1}+\kappa _{1})^{n_{1}}}f_{n_{1}+1}(\lambda )v_{1}= \frac{1}{(\lambda d_{2}+\kappa _{2})^{n_{2}}}f_{n_{2}+1}(\lambda )u_{n_{2}}. \end{aligned}$$

Note that \(s\ne 0\) is equivalent to the assumption \(f_{n_{1}+1}(\lambda )\ne 0\) and \(f_{n_{2}+1}(\lambda )\ne 0\). From \((*)\), using \(u_{1}= \frac{1}{(\lambda d_{2}+\kappa _{2})^{n_{2}-1}}f_{n_{2}}(\lambda )u_{n_{2}}\) and the previous formula, assuming \(s\ne 0\), we obtain

$$\begin{aligned} \left. \begin{array}{c} -(\lambda d_{1}+\kappa _{1})^{2}f_{n_{1}}(\lambda )f_{n_{2}+1}(\lambda )v_{1}-(\lambda d_{2}+\kappa _{2})^{2}f_{n_{2}}(\lambda )f_{n_{1}+1}(\lambda )v_{1} \\ +(\lambda ^{2}m+\lambda (d_{1}+d_{2})+(\kappa _{1}+\kappa _{2}))f_{n_{1}+1}(\lambda )f_{n_{2}+1}(\lambda )v_{1}=0 \end{array} \right. \end{aligned}$$

whose solutions gives us the eigenvalues, because \(v_{1}\ne 0\).

The eigenvector \(w\left( \lambda \right) =\left( w_{i}\left( \lambda \right) \right) _{i=1,\ldots ,n_{1}+n_{2}+1}\) associated with \(\lambda\), solution of the above equation, choosing the normalizing constants \(v_{1}= \frac{1}{(\lambda d_2+\kappa _2)^{n_2}} f_{n_2+1}(\lambda )\) and \(u_{n_{2}}= \frac{1}{(\lambda d_1+\kappa _1)^{n_1}} f_{n_1+1}(\lambda )\), is given by

$$\begin{aligned} w_{1}\left( \lambda \right)= & {} v_1=\frac{1}{(\lambda d_2+\kappa _2)^{n_2}} f_{n_2+1}(\lambda ) \\ w_{2}\left( \lambda \right)= & {} v_{2}=\frac{1}{(\lambda d_1+\kappa _1)(\lambda d_2+\kappa _2)^{n_2}} f_{n_2+1}(\lambda ) f_2(\lambda ) \\{} & {} \ldots \\ w_{n_{1}}\left( \lambda \right)= & {} v_{n_{1}}=\frac{1}{(\lambda d_1+\kappa _1)^{n_1-1}(\lambda d_2+\kappa _2)^{n_2}} f_{n_2+1}( \lambda )f_{n_1}(\lambda ) \\ w_{n_{1}+1}\left( \lambda \right)= & {} s=\frac{1}{(\lambda d_1+\kappa _1)^{n_1}(\lambda d_2+\kappa _2)^{n_2}} f_{n_2+1}( \lambda )f_{n_1+1}(\lambda ) \\ w_{n_{1}+2}\left( \lambda \right)= & {} u_{1}= \frac{1}{(\lambda d_1+\kappa _1)^{n_1}(\lambda d_2+\kappa _2)^{n_2-1}} f_{n_1+1}(\lambda ) f_{n_2}(\lambda ) \\{} & {} \ldots \\ w_{n_{1}+n_{2}}\left( \lambda \right)= & {} u_{n_{2}-1}=\frac{1}{(\lambda d_1+\kappa _1)^{n_1}(\lambda d_2+\kappa _2)} f_{n_1+1}(\lambda ) f_2(\lambda ) \\ w_{n_{1}+n_{2}+1}\left( \lambda \right)= & {} u_{n_{2}}=\frac{1}{(\lambda d_1+\kappa _1)^{n_1}} f_{n_1+1}(\lambda ). \end{aligned}$$

Therefore the eigenvector can be written as claimed. On the other hand, if \(s = 0\) then \(f_{n_2+1}(\lambda )=0\), \(f_{n_1+1}(\lambda )=0\) and \(f_{n_2}(\lambda ) \ne 0\), \(f_{n_1}(\lambda ) \ne 0\) (otherwise, from Proposition 2, it will follow \(f_n(\lambda )=0\), for each \(n\ge \text {min}\{n_1,n_2\}\)). This means that, from (\(*\)), we now obtain

$$\begin{aligned} u_{n_{2}}=-\frac{(\lambda d_2+\kappa _2)^{n_2-2}}{(\lambda d_1+\kappa _1)^{n_1-2}} \frac{f_{n_1}(\lambda )}{f_{n_2}(\lambda )} v_{1} \end{aligned}$$

and the eigenvector \(w_{\lambda }\), choosing the normalizing constant \(v_{1}=- \frac{1}{(\lambda d_2+\kappa _2)^{n_2-2}}f_{n_2}(\lambda )\) is given by

$$\begin{aligned} w_{1}\left( \lambda \right)= & {} v_1=-\frac{1}{(\lambda d_2+\kappa _2)^{n_2-2}} f_{n_2}(\lambda ) \\ w_{2}\left( \lambda \right)= & {} v_{2}=-\frac{1}{(\lambda d_1+\kappa _1)(\lambda d_2+\kappa _2)^{n_2-2}}f_{n_2}(\lambda ) f_2(\lambda ) \\{} & {} \ldots \\ w_{n_{1}}\left( \lambda \right)= & {} v_{n_{1}}=-\frac{1}{(\lambda d_1+\kappa _1)^{n_1-1}(\lambda d_2+\kappa _2)^{n_2-2}}f_{n_2}(\lambda ) f_{n_1}(\lambda ) \\ w_{n_{1}+1}\left( \lambda \right)= & {} s=0 \\ w_{n_{1}+2}\left( \lambda \right)= & {} u_{1}=-\frac{1}{(\lambda d_1+\kappa _1)^{n_1-2}(\lambda d_2+\kappa _2)^{n_2-1}} f_{n_1}(\lambda ) f_{n_2}(\lambda ) \\{} & {} \ldots \\ w_{n_{1}+n_{2}}\left( \lambda \right)= & {} u_{n_{2}-1}=-\frac{1}{(\lambda d_1+\kappa _1)^{n_1-2}(\lambda d_2+\kappa _2)} f_{n_1}(\lambda ) f_2(\lambda ) \\ w_{n_{1}+n_{2}+1}\left( \lambda \right)= & {} u_{n_{2}}=-\frac{1}{(\lambda d_1+\kappa _1)^{n_1-2}} f_{n_1}(\lambda ). \end{aligned}$$

\(\square\)

5.2 Second case, gluing two end-springs and two end-dampers in damped system

Here we join two different homogeneous chains by gluing its end-springs and end dampers. This coupling, as seen before, is done in such a way that both spring and damper have a linear behavior. The system is now described by equation (1) with M, D and K are given by (14), (15) and (16), respectively. Furthermore, we have:

Theorem 4

The eigenvalues of equation (5) are given by the solutions of

$$\begin{aligned} \left. \begin{array}{ll} &{} -\frac{(\lambda d+\kappa )^{2}}{(\lambda d_{1}+\kappa _{1})^{n_{1}-1}} f_{n_{1}}(\lambda )f_{n_{2}}(\lambda ) \\ {} &{} +\frac{\lambda ^{2}m_{2}+\lambda (d+d_{2})+(\kappa +\kappa _{2})}{(\lambda d_{1}+\kappa _{1})^{n_{1}-1}}f_{n_{2}}(\lambda ) \\ &{} \times \left( (\lambda ^{2}m_{1}+\lambda (d_{1}+d)+(\kappa _{1}+\kappa ))f_{n_{1}}(\lambda )-(\lambda d_{1}+\kappa _{1})^{2}f_{n_{1}-1}(\lambda )\right) \\ {} &{} -f_{n_{2}-1}(\lambda )\frac{(\lambda d_{2}+\kappa _{2})^{2}}{(\lambda d_{1}+\kappa _{1})^{n_{1}-1}} \\ &{}\times \left( (\lambda ^{2}m_{1}+\lambda (d_{1}+d)+(\kappa _{1}+\kappa ))f_{n_{1}}(\lambda )-(\lambda d_{1}+\kappa _{1})^{2}f_{n_{1}-1}(\lambda )\right) =0 \end{array} \right. \end{aligned}$$

and their corresponding eigenvectors are given by

$$\begin{aligned} \small {\left. \begin{array}{c} w\left( \lambda \right) =(\lambda d+\kappa )f_{n_{2}}(\lambda )\upsilon _{n_{1}}\left( \lambda \right) \oplus \\ \oplus \frac{(\lambda d_{2}+\kappa _{2})^{n_{2}-1}}{(\lambda d_{1}+\kappa _{1})^{n_{1}-1}}\left( (\lambda ^{2}m_{1}+\lambda (d_{1}+d)+(\kappa _{1}+\kappa ))f_{n_{1}}(\lambda )-(\lambda d_{1}+\kappa _{1})^{2}f_{n_{1}-1}(\lambda )\right) \upsilon _{n_{2}}^{*}\left( \lambda \right) , \end{array} \right. } \end{aligned}$$

where \(f_{n_{1}}(\lambda )\ne 0\) and \(f_{n_{2}}(\lambda )\ne 0\).

Proof

The \(n_{1}+n_{2}\) equations arising from the quadratic eigenvalue equation (5), writing \(u=\left( v_{1},\ldots ,v_{n_{1}},u_{1},\ldots ,u_{n_{2}}\right)\), are now

$$\begin{aligned} \left\{ \begin{array}{l} \left( \lambda ^{2}m_{1}+2\lambda d_{1}+2\kappa _{1}\right) v_{1}-(\lambda d_{1}+\kappa _{1})v_{2}=0 \\ -(\lambda d_{1}+\kappa _{1})v_{1}+\left( \lambda ^{2}m_{1}+2\lambda d_{1}+2\kappa _{1}\right) v_{2}-(\lambda d_{1}+\kappa _{1})v_{3}=0 \\ \cdots \\ -(\lambda d_{1}+\kappa _{1})v_{n_{1}-2}+\left( \lambda ^{2}m_{1}+2\lambda d_{1}+2\kappa _{1}\right) v_{n_{1}-1}-(\lambda d_{1}+\kappa _{1})v_{n_{1}}=0 \\ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ -(\lambda d_{1}+\kappa _{1})v_{n_{1}-1}+\left( \lambda ^{2}m_{1}+\lambda (d_{1}+d)+(\kappa _{1}+\kappa )\right) v_{n_{1}}-(\lambda d+\kappa )u_{1}=0 \\ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ -(\lambda d+\kappa )v_{n_{1}}+\left( \lambda ^{2}m_{2}+\lambda (d+d_{2})+(\kappa +\kappa _{2})\right) u_{1}-(\lambda d_{2}+\kappa _{2})u_{2}=0 \\ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ -(\lambda d_{2}+\kappa _{2})u_{1}+\left( \lambda ^{2}m_{2}+2\lambda d_{2}+2\kappa _{2}\right) u_{2}-(\lambda d_{2}+\kappa _{2})u_{3}=0 \\ \cdots \\ -(\lambda d_{2}+\kappa _{2})u_{n_{2}-2}+\left( \lambda ^{2}m_{2}+2\lambda d_{2}+2\kappa _{2}\right) u_{n_{2}-1}-(\lambda d_{2}+\kappa _{2})u_{n_{2}}=0 \\ -(\lambda d_{2}+\kappa _{2})u_{n_{2}-1}+\left( \lambda ^{2}m_{2}+2\lambda d_{2}+2\kappa _{2}\right) u_{n_{2}}=0 \end{array} \right. \end{aligned}$$

The first \(n_{1}\) equations can be solved through

$$\begin{aligned} \left\{ \begin{array}{l} v_{2}=\frac{\lambda ^{2}m_{1}+2\lambda d_{1}+2\kappa _{1}}{\lambda d_{1}+\kappa _{1}}v_{1}=\frac{1}{\lambda d_{1}+\kappa _{1}}f_{2}(\lambda )v_{1} \\ v_{3}=\frac{\lambda ^{2}m_{1}+2\lambda d_{1}+2\kappa _{1}}{\lambda d_{1}+\kappa _{1}}v_{2}-v_{1}=\frac{1}{(\lambda d_{1}+\kappa _{1})^{2}} f_{3}(\lambda )v_{1} \\ \cdots \\ v_{j}=\frac{1}{(\lambda d_{1}+\kappa _{1})^{j-1}}f_{j}(\lambda )v_{1} \\ \cdots \\ v_{n_{1}}=\frac{1}{(\lambda d_{1}+\kappa _{1})^{n_{1}-1}}f_{n_{1}}(\lambda )v_{1} \\ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ -\frac{1}{(\lambda d_{1}+\kappa _{1})^{n_{1}-3}}f_{n_{1}-1}(\lambda )v_{1}+ \frac{\lambda ^{2}m_{1}+\lambda (d_{1}+d)+(\kappa _{1}+\kappa )}{(\lambda d_{1}+\kappa _{1})^{n_{1}-1}}f_{n_{1}}(\lambda )v_{1}-(\lambda d+\kappa )u_{1}=0\ (*) \\ \end{array} \right. \end{aligned}$$

Reserving the last equation labeled by \((*)\). Next, we solve the following \(n_{2}\) equations with reversed order, which gives us

$$\begin{aligned} \left\{ \begin{array}{l} u_{n_{2}-1}=\frac{1}{\lambda d_{2}+\kappa _{2}}f_{2}(\lambda )u_{n_{2}} \\ u_{n_{2}-2}=\frac{1}{(\lambda d_{2}+\kappa _{2})^{2}}f_{3}(\lambda )u_{n_{2}} \\ \cdots \\ u_{n_{2}-j}=\frac{1}{(\lambda d_{2}+\kappa _{2})^{j}}f_{j+1}(\lambda )u_{n_{2}} \\ \cdots \\ u_{1}=\frac{1}{(\lambda d_{2}+\kappa _{2})^{n_{2}-1}}f_{n_{2}}(\lambda )u_{n_{2}} \\ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ -(\lambda d+\kappa )v_{n_{1}}+\frac{\lambda ^{2}m_{2}+\lambda (d+d_{2})+(\kappa +\kappa _{2})}{(\lambda d_{2}+\kappa _{2})^{n_{2}-1}} f_{n_{2}}(\lambda )u_{n_{2}}-\frac{1}{(\lambda d_{2}+\kappa _{2})^{n_{2}-3}} f_{n_{2}-1}(\lambda )u_{n_{2}}=0(**) \end{array} \right. \end{aligned}$$

Applying \(u_{1}=\frac{1}{(\lambda d_{2}+\kappa _{2})^{n_{2}-1}} f_{n_{2}}(\lambda )u_{n_{2}}\) in \((*)\), we obtain

$$\begin{aligned} \frac{\lambda d+\kappa }{(\lambda d_{2}+\kappa _{2})^{n_{2}-1}} f_{n_{2}}(\lambda )u_{n_{2}}=\\ \left( \frac{\lambda ^{2}m_{1}+\lambda (d_{1}+d)+(\kappa _{1}+\kappa )}{(\lambda d_{1}+\kappa _{1})^{n_{1}-1}} f_{n_{1}}(\lambda )-\frac{1}{(\lambda d_{1}+\kappa _{1})^{n_{1}-3}} f_{n_{1}-1}(\lambda )\right) v_{1} \end{aligned}$$

and consequently, if \(f_{n_{2}}(\lambda )\ne 0\),

$$\begin{aligned} u_{n_{2}}=\frac{(\lambda d_{2}+\kappa _{2})^{n_{2}-1}}{\lambda d+\kappa } \left( \frac{\frac{\lambda ^{2}m_{1}+\lambda (d_{1}+d)+(\kappa _{1}+\kappa ) }{(\lambda d_{1}+\kappa _{1})^{n_{1}-1}}f_{n_{1}}(\lambda )-\frac{1}{ (\lambda d_{1}+\kappa _{1})^{n_{1}-3}}f_{n_{1}-1}(\lambda )}{ f_{n_{2}}(\lambda )}\right) v_{1} \end{aligned}$$

Now, with this information and with \(v_{n_{1}}=\frac{1}{(\lambda d_{1}+\kappa _{1})^{n_{1}-1}}f_{n_{1}}(\lambda )v_{1}\), from \((**)\) we obtain the desired eigenvalue equation.

The eigenvector \(w\left( \lambda \right) =\left( w_{i}\left( \lambda \right) \right) _{i=1,\ldots ,n_{1}+n_{2}}\) associated with \(\lambda\), solution of the above system of equations, is given by

$$\begin{aligned} w_{1}\left( \lambda \right)= & {} v_1 \\ w_{2}\left( \lambda \right)= & {} v_{2}=\frac{1}{\lambda d_1+\kappa _1} f_2(\lambda )v_{1} \\ w_3(\lambda )= & {} v_3=\frac{1}{(\lambda d_1+\kappa _1)^2} f_3(\lambda )v_{1} \\{} & {} \ldots \\ w_{n_{1}}\left( \lambda \right)= & {} v_{n_{1}}=\frac{1}{(\lambda d_1+\kappa _1)^{n_1-1}} f_{n_1}(\lambda ) v_1 \\ w_{n_{1}+1}\left( \lambda \right)= & {} u_1=\frac{\gamma }{\lambda d+\kappa } v_{1} \\ w_{n_{1}+2}\left( \lambda \right)= & {} u_{2}= \frac{(\lambda d_2+\kappa _2)}{ \lambda d+\kappa }\frac{\gamma }{f_{n_2}(\lambda ) } f_{n_2-1}(\lambda ) v_{1} \\{} & {} \ldots \\ w_{n_{1}+n_{2}}\left( \lambda \right)= & {} u_{n_2}=\frac{(\lambda d_2+\kappa _2)^{n_2-1}}{\lambda d+\kappa }\frac{\gamma }{f_{n_2}(\lambda )} v_{1}. \end{aligned}$$

with \(\gamma =\frac{\lambda ^2m_1+\lambda (d_1+d)+(\kappa _1+\kappa )}{(\lambda d_1+\kappa _1)^{n_1-1}} f_{n_1}(\lambda )- \frac{1}{(\lambda d_1+\kappa _1)^{n_1-3}} f_{n_1-1}(\lambda )\). The form for the solution \(w\left( \lambda \right)\) follows choosing the normalizing constant \(v_{1}= (\lambda d+\kappa ) f_{n_{2}}\left( \lambda \right)\).

On the other hand, if \(f_{n_{2}}\left( \lambda \right) =0\), then from (\(*\)) we have

$$\begin{aligned}{} & {} -\frac{1}{(\lambda d_1+\kappa _1)^{n_1-3}} f_{n_1-1}(\lambda ) v_{1}\\{} & {} +\frac{ \lambda ^2m_1+\lambda (d_1+d)+(\kappa _1+\kappa )}{(\lambda d_1+\kappa _1)^{n_1-1}} f_{n_1}(\lambda ) v_{1}=0 \end{aligned}$$

This means that

$$\begin{aligned} f_{n_1}(\lambda )=\frac{(\lambda d_1+\kappa _1)^{n_1-1}}{(\lambda ^2m_1+\lambda (d_1+d)+(\kappa _1+\kappa ))(\lambda d_1+\kappa _1)^{n_1-3}} f_{n_1-1}(\lambda ) \end{aligned}$$

which is impossible. Therefore \(f_{n_{2}}\left( \lambda \right) \ne 0\). The same reasoning applied now to \((**)\) will give \(f_{n_{1}}\left( \lambda \right) \ne 0\). \(\square\)

5.3 Eigenvalues and eigenvectors: discussion

Although we were able to deduce formulas for the eigenvectors and eigenvalues whenever \(DM^{-1}K\) is not a symmetric matrix, the obtained formulas are much more cumbersome than the ones for the symmetric case, as pointed out before. Another major question that we have to answer, meanwhile, is what we do know about the nature of the eigenvalues and corresponding eigenvectors? Do the set of eigenvectors span the full space? In which cases?

Firstly, notice that after coupling, matrices M, D an K are still symmetric and positive definite thus we always have eigenvalues that are real or appear in complex conjugate pairs, with \(\text {Re}(\lambda )<0\) in both cases. When \(D=0\), the eigenvalues are pure imaginary and appear in conjugate pairs; it is well-known that we have a full set of eigenvectors, see e.g. [1] or [29]. For \(D\ne 0\), different cases must be analyzed. In the case D is “sufficiently large” or, more precisely, when the system is over-damped, we know [8] that all eigenvalues are real non-positive and we have a full set of linear independent eigenvectors (see also [9] and the extremely complete reference [26]). We say that the system (5) is over-damped when M, D, and K are real symmetric, M, D are positive definite and K is positive semi-definite, \(({\overline{x}}^{T}Dx)^{2}-4( {\overline{x}}^{T}Mx)({\overline{x}}^{T}Kx)>0\), \(\forall x\ne 0\).

The systems that lay between this two extreme cases were studied in [14] through the matrix polynomial

$$\begin{aligned} L(\lambda ,\varepsilon )=\lambda ^{2}A+\varepsilon \lambda B+C, \end{aligned}$$
(19)

in which A, B, C are positive definite (as in our work) and \(\varepsilon\) is a non-negative parameter. Notice that when \(\varepsilon =0\) we are in the undamped case and when \(\varepsilon\) is sufficiently large we are in the over-damped case. To be precise, they assumed, without loss of generality, \(A=I\). They proved that the class of systems for which \(\text {det}(L(\lambda ,\varepsilon ))\) that have at least \(2n-1\) distinct eigenvalues \(\forall \varepsilon \ge 0\) is generic in the following sense: if \(Q_{0}\) is the set of all pairs of positive definite matrices (B, C) such that, for every \(\varepsilon \ge 0\), the polynomial \(\text {det}(L(\lambda ,\varepsilon ))\) has at least \(2n-1\) distinct zeros in the complex plane and Q is the set of all pairs (B, C) of positive definite matrices, then \(Q_{0}\) is dense in Q. Furthermore, they proved that in fact for \((B,C)\in Q_{0}\), \(\text {det} (L(\lambda ,\varepsilon ))\) has 2n distinct zeros except for a finite number of \(\varepsilon\)’s, while this finite number belongs to the interval \([n,2n^{2}]\). They also examine in detail those values of \(\varepsilon\) at which the system has less than 2n distinct zeros.