Shear-thickening of dense bidispersed suspensions

Abstract

We study the rheological behaviour of a dense bidispersed suspension varying the relative size of the two dispersed phases. The main outcome of our analysis is that an enhanced flowability (reduced relative viscosity) of the suspension can be achieved by increasing the dispersion ratio of the phases. We explain the observed result by showing that the presence of large particles increases the packing efficiency of the suspension, leading to a reduction of the contribution of the contacts on the overall viscosity of the suspension in the shear-thickening regime, i.e. where the contacts are the dominating component.

1 Introduction

Dense suspensions of rigid, spherical particles immersed in a Newtonian fluid tend to exhibit a lower flowability, acting almost like a rigid solid when subjected to an increasing shear stress. This behaviour, which is well-known in the framework of non-Newtonian fluids, undergoes the name of shear-thickening [2, 16, 34, 35, 45]. Shear-thickening suspensions are becoming increasingly important in industry, with preferential applications in shock absorbers, such as soft-body armours, or into smart fluids with rheological properties that can be tuned by acting on the mechanisms of the stress transmission [10, 28, 38]. The growing relevance of such fluids has stimulated the recent progress made to unravel the mechanisms that dominate the thickening behaviour. In particular, simulations and experiments have shown that, when an increasing stress that exceeds a critical value is applied to a dense suspension, the rhelogical response due to the interacting particles switches from mainly lubricative to chains of frictionally contacting grains that transmit the stress and reduce the flowability of the suspension [14, 19, 27, 42, 46]. Shear thickening has been classified into two regimes, named after the macroscopic behaviour of the dense suspensions: continuous shear thickening (CST), i.e. identifiable as a smooth increase of the viscosity with the shear rate, and discontinuous shear thickening (DST), i.e. an abrupt transition to a solid-like suspension with reduced flowability [5, 6, 14, 33, 42]. The two behaviours have been observed for several kinds of dense suspensions that span from monodisperse to polydisperse in terms of size of the beads [11, 31, 41], and made of Brownian [2, 33] or non-Brownian particles [26, 32, 36, 46].

Considering bidispersed suspensions, several parameters can be used to control the shear-thickening regime. Surely, one of those is the friction coefficient of the particles, that can be tuned to increase or reduce the viscosity in the thickened regime [23, 24, 37, 40]. Among the other parameters, the dispersion ratio and the relative percentage of volume fraction of the two dispersed phases can also be used to modify the shear-thickening behaviour [3, 25, 30, 31]. However, within the literature, there are interpretation of experimental results that look in contrast with the theory of maximally random jammed (MRJ) packings [13, 44] and of the densest binary sphere packings [21, 22]. The latter show that adding particles of different sizes is a more efficient way of packing particles, with an increased MRJ packing, thus suggesting, in the case of flowing suspensions, an increased flowability and a postponement of the onset (critical value of the stress) of the DST when gradually enhancing the total volume fraction of the suspension. This was also observed by [12], who characterized the rheological behaviour of bimodal colloidal suspensions. On the other side, recent experimental studies [30, 31] show that, by adding an increasing volume fraction of large particles, the suspension can be successfully led to a transition from CST to DST, thus resulting in a larger suspension viscosity at a fixed shear rate in the presence of large particles. The authors proposed a geometrical explanation based on an excluded-volume effect to justify the experimental observations: the presence of large particles causes the formation of shells around them (with size linked to the radius of the small ones), mostly composed of aqueous solution since the small beads are hindered of densely packing around a large sphere, resulting in a local decrease of the concentration of the small particles within the volume of the shells. This local decrease of volume fraction is compensated by an increased concentration in other regions of the suspension, due to mass-conservation, that triggers the discontinuous thickening [30, 31].

Fig. 1

Visualization of bidispersed dense suspensions at volume fraction $\phi =0.50$, for different size of the larger particles dispersed (increasing from left to right). The grey colour shows the smaller particles, while the green, red and blue colours show the larger particles for the suspension with dispersion ratio $\lambda =\{1.5,3.0,6.0\}$, respectively. This colour-scheme will be used for referring to the different configurations throughout the whole manuscript

In this work, we reconcile the apparent contradiction between the literature data on the subject by showing that the suspension viscosity reduces when mixing large particles in a suspensions at a fixed total volume fraction and shear rate. As a consequence, we show that a dense bidispersed suspension with large dispersion size exhibits a milder shear thickening regime compared to a suspension having identical volume fraction and a lower dispersion ratio, consistent with the higher efficiency of the MRJ packing shown by the highly bidispersed suspensions [22]. Studies on the effect of the particles sizes were carried out in the past [7,8,9, 39]. These works numerically tackled the effect of bidispersion by varying the dispersion size and the relative volume ratio between the large and small dispersed particles. A decrease in viscosity has been recorded as the suspension moved from monodisperse to bidispersed, with a minimum taking place when the $\phi _2/\phi =0.65$, where $\phi _2$ is the volume fraction of the large dispersed phase and $\phi$ is the volume fraction of the suspension [39]. A further decrease in viscosity has been observed when the dispersion ratio increases, i.e. increasing the size of the larger dispersed phase compared to the smaller one [39]. The suspensions studied in those works, however, contained a relatively small number of particles $n \le 2000$, and no variation of the shear-rate has been included. Here, we extend the previous studies by increasing the number of particles of the suspensions and by introducing the shear-rate dependency, specifically studying the effect of bidispersion on the shear-thickening.

2 Methodology

The problem at hand has been tackled by numerically investigating the effects on the shear-thickening region for three configurations of bidispersed suspensions of frictional particles subjected to a uniform shear-flow, with dispersion size $\lambda =a_2/a_1$ in the range $\{1.5, 3.0, 6.0\}$ ($a_1$ and $a_2$ being the radius of the small and large suspended phase, respectively). The total number of particles is set to $n=2^{16}$, with the number of particles of the two dispersed phases determined by fixing the relative volume between them equal to $V_2/V_1=0.25$; four total volume fractions of the suspension are considered: $\phi =\{0.45,0.50,0.55,0.60\}$. To extend the validity of the results, for the suspension with $\phi =0.60$, we considered three relative volumes of the dispersed phases, such that $\phi _2/\phi =\{0.2, 0.5, 0.8\}$, where $\phi _2$ is the volume fraction of the larger phase. Figure 1 shows a representation of the three dispersion sizes considered, with the larger phase highlighted with a colour-scheme that will be kept through the whole manuscript.

Fig. 2

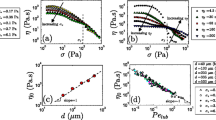
Panel a: Relative viscosity $\eta _r$ as a function of the non-dimensional shear-rate $\dot{\gamma }/\dot{\gamma }_0$. Panel b: First normal stress difference $N_1/(\eta _0 \dot{\gamma })$ as a function of the non-dimensional shear-rate $\dot{\gamma }/\dot{\gamma }_0$. The curve for the case ($\phi =0.60$, $\lambda =1.5$) largely exceeds the limits of the figure, reaching positive values of about $N_1\sim 8000$, and are not shown to maintain the other curves visible. Panel c: Second normal stress difference $-N_2/(\eta _0 \dot{\gamma })$ as a function of the non-dimensional shear-rate $\dot{\gamma }/\dot{\gamma }_0$. Panel d: Pressure $-\Pi /(\eta _0 \dot{\gamma })$ as a function of the non-dimensional shear-rate $\dot{\gamma }/\dot{\gamma }_0$. In all the figures, the curves are obtained for suspensions at volume fraction $\phi =\{0.45,0.50,0.55,0.60\}$, denoted by the triangle, square, star and star hexagon markers, respectively. The shades of green, red and blue represent the different dispersion ratio $\lambda =\{1.5,3.0,6.0\}$, as shown in Fig. 1. The markers and the colours are summarized within the legend shown in the top right of the figure.

The numerical investigation is carried out using a validated and publicly available software, CFF-Ball-0x [36]. CFF-Ball-0x is an in-house software that models a dense, non-Brownian suspension (volume fraction $\phi \ge 0.40$) of quasi-inertialess, neutrally-buoyant, rigid spherical particles in a shear-flow defined by the shear-rate $\dot{\gamma }$. The code tackles the Newton-Euler equations that govern the translational and rotational dynamics of the rigid particles,

$$\begin{aligned} {\left\{ \begin{array}{ll} m_i \dfrac{\textrm{d}\varvec{u}_i}{\textrm{d}t} &{}= \sum \limits _{j=1}^{N_H} \varvec{F}^H_{ij} + \sum \limits _{j=1}^{N_C} \varvec{F}^C_{ij} + \sum \limits _{j=1}^{N_E} \varvec{F}^E_{ij}, \\ \mathbb {I}_i \dfrac{\textrm{d}\varvec{\omega }_i}{\textrm{d}t} + \varvec{\omega }_i \times (\mathbb {I}_i \varvec{\omega }_i) &{}= \sum \limits _{j=1}^{N_H} \varvec{T}^H_{ij} + \sum \limits _{j=1}^{N_C} \varvec{T}^C_{ij} + \sum \limits _{j=1}^{N_E} \varvec{T}^E_{ij}, \\ \end{array}\right. } \end{aligned}$$

(1)

where the subscript i indicates the particle $i\in [1,N]$, being N the number of particles. The right-hand side of System (1) lists the forces and torques resulting from particle-flow and particle-particle interactions with the jth neighbour, and the superscripts H, C and E indicate the nature of contribution, i.e. hydrodynamics, inelastic contacts and electro-chemical effects, respectively. The forces and torques are applied to the centre of mass of the ith particle, with mass $m_i$ and inertia tensor $\mathbb {I}_i$ and cause a variation in the translational and angular velocities of the particles, here denoted by the symbols $\varvec{u}_i$ and $\varvec{\omega }_i$, respectively.

Next, we describe the models implemented for the three contributions listed above. Concerning the hydrodynamics of the system, dense suspensions of rigid particles immersed in a low-Reynolds-number flow experience a Stokes drag and a pair-wise, short-range lubrication force [32], caused by the relative motion of near particles that squeezes the fluid flowing in the narrow gaps between them. The two contributions are implemented as a linear relationship between forces (torques) and velocities (angular velocities) [1, 32], $\varvec{F}^H=-\mathbb {R}(\varvec{u}-\varvec{U}^\infty )$, where $\mathbb {R}$ is a resistance matrix that is obtained by neglecting the far-field effects and considering only the dominant near-field divergent elements coming from the squeeze, shear and pump modes, following the work by Mari et al. [32].

The contact contribution is modelled with the stick-and-slide method [29]. This method mimics the inelastic contacts with spring-dashpot systems that start operating when two spheres overlap. The force can be expressed as $\varvec{F}^C=(k_n\delta + \gamma _n\dot{\delta })\varvec{n} + k_t\xi \varvec{t}$; the spring-dashpot systems are oriented along the normal (centre-to-centre) $\varvec{n}$ and tangential $\varvec{t}$ directions (the latter to model the frictional component of the contacts) and are characterised by the spring and dashpot constants, ($k_n$,$\gamma _n$) and ($k_t$,$\gamma _t=0$), respectively, where the subscript indicate the direction (n normal and t tangential). The values $\delta$ and $\xi$ indicate the normal and tangential displacements of the springs and $\dot{\delta }$ the normal projection of the overlapping velocity. The tangential contribution is subject to the Coulomb’s law, $|\varvec{F}^C_t|\le \mu |\varvec{F}^C_n|$, where $\mu$ is the frictional coefficient. In this work, the friction coefficient is set to $\mu =0.5$ for all the scenarios analysed, as we did in a previous work where we compared our results with experimental data [41].

Fig. 3

Panel a: Relative viscosity $\eta _r$ as a function of the non-dimensional shear-rate $\dot{\gamma }/\dot{\gamma }_0$. Panel b: First normal stress difference $N_1/(\eta _0 \dot{\gamma })$ as a function of the non-dimensional shear-rate $\dot{\gamma }/\dot{\gamma }_0$. The curve for the case ($\phi =0.60$, $\lambda =1.5$) largely exceeds the limits of the figure, reaching positive values of about $N_1\sim 8000$, and are not shown to maintain the other curves visible. Panel c: Second normal stress difference $-N_2/(\eta _0 \dot{\gamma })$ as a function of the non-dimensional shear-rate $\dot{\gamma }/\dot{\gamma }_0$. Panel d: Pressure $-\Pi /(\eta _0 \dot{\gamma })$ as a function of the non-dimensional shear-rate $\dot{\gamma }/\dot{\gamma }_0$. In all the figures, the curves are obtained for suspensions at volume fraction $\phi =0.60$ (hexagon markers) varying the relative volume fractions of the dispersed phases, with $\phi _2/\phi =\{0.2, 0.5, 0.8\}$, from darker colours to lighter ones. The shades of green, red and blue represent the different dispersion ratio $\lambda =\{1.5,3.0,6.0\}$, as shown in Fig. 1. The markers and the colours are summarized within the legend shown in the top right of the Fig.

The last contribution considered in this work are forces that arise from the electrochemical properties of the suspension. These contributions are modelled as a sum of an inter-particle, distance-decaying repulsion force, and an attraction force in van der Waals form [17, 43], $\varvec{F}^E = \varvec{F}^R+\varvec{F}^A$, where the superscripts E, R, A stand for electrochemical, repulsive and attractive, respectively. The force resulting from the repulsive contribution can be written as $\varvec{F}^R=F_0 e^{-h/L_s}\varvec{n}$, where $F_0$ is the magnitude of the force, $L_s$ is the screening length and h is the particle-particle surface distance, while the attractive force can be written as $\varvec{F}^A = A\overline{a}/12(h^2+\varepsilon ^2) \varvec{n}$, where A is the Hamaker constant, $\overline{a}$ is the harmonic mean radius of the two particles involved and $\varepsilon$ is a smoothing term to eliminate the singularity when the two particles touch, i.e. $h=0$.

Several parameters dominate the physics of the suspension described by the system of equations (1). Considering the translational equation of (1) and gathering the dimensional quantities, we can apply the Buckingham’s $\Pi$ theorem and find the set of the non-dimensional groups that can be tuned to outline the desired dynamics of the suspension. In particular, by choosing as independent fundamental quantities the scales that define the hydrodynamics, the three following non-dimensional groups emerge: the Stokes number

$$\begin{aligned} St = \rho _p a_0^2 \dot{\gamma }/\eta _0, \end{aligned}$$

(2)

that arises from the inertial term and compares the time-scale of the particles with the time-scale of the hydrodynamics. In the equation above, $\rho _p$ is the density of the particles (equal to the density of the carrier fluid in the cases we considered), $a_0$ is the typical length scale of the system (the radius of the particles of the smallest phase of the suspension), $\eta _0$ is the viscosity of the carrier fluid and $\dot{\gamma }$ is the shear-rate applied to the suspension. The constraint $St \ll 1$ is applied to enforce the inertialess regime. The second number is the non-dimensional stiffness

$$\begin{aligned} \hat{k}=k_n/(\eta _0 a_0 \dot{\gamma }), \end{aligned}$$

(3)

that weighs the importance of the contacts contributions compared to the hydrodynamic term. In this case, the constraint $\hat{k}\gg 1$ is set to force the particles to be rigid. We considered the normal spring constant $k_n$ as the dominant term of the spring-dashpot systems since we enforce the additional constraints $k_t=2/7k_n$ and $\gamma _n\dot{\gamma }/k_n \ll 1 \sim O(10^{-7})$, where the latter is the relaxation time of the spring-dashpot system. Finally, the last non-dimensional group, i.e. the equivalent shear-rate

$$\begin{aligned} \hat{\dot{\gamma }} = |\varvec{F}^E (d_{ij}=0)|/(\eta _0 a_0^2 \dot{\gamma }) = \dot{\gamma }_0/\dot{\gamma }, \end{aligned}$$

(4)

refers to the time-scale introduced by the electrochemical contribution and is tuned to set a shear-rate dependent rheology on the suspension. Here $d_{ij}$ is the relative surface-surface distance between the particles i and j.

More details can be found in our previous publication [36], together with validations against theory, numerical simulations and experimental measurements. The software can be freely downloaded at the following link https://github.com/marco-rosti/CFF-Ball-0x.

Fig. 4

Contributions to the relative viscosity $\eta _r$ of the contacts (black), hydrodynamics (darker grey) and electrochemical potentials (lighter grey), as a function of the non-dimensional shear-rate $\dot{\gamma }/\dot{\gamma }_0$. The suspensions represented have increasing volume fractions from the top row ($\phi =0.45$) to the bottom row ($\phi =0.60$) and increasing dispersion ratio, $\lambda =\{1.5,3.0,6.0\}$, from left to right. Note that, in the last row, the bars in the left panel are on a different scale compared with the bars in the central and right panels

3 Results

We start the analysis by looking at the rheological properties of the suspensions. Panel a of Fig. 2 shows the flow curve of the suspension, i.e. how the relative viscosity $\eta _r$ of the suspension varies with the applied shear rate $\dot{\gamma }/\dot{\gamma }_0$. The curves are grouped using the markers to distinguish the different volume fractions analyzed (triangles: $\phi =0.45$; squares: $\phi =0.50$; stars: $\phi =0.55$; star hexagons: $\phi =0.60$) and the colours to discriminate the dispersion ratio, in accordance with Fig. 1 (green: $\lambda =1.5$; red: $\lambda =3.0$; blue: $\lambda =6.0$). This is recapped in the legend of Fig. 2. All the curves plotted show a shear-thinning region followed by the a Newtonian plateau at low shear-rates, followed by a region of viscosity increase, i.e. the shear-thickening regime, and a final plateau at high shear rates. We observe that the presence of large particles reduces, at high shear-rates, the relative viscosity of the suspension and weakens its shear-thickening behaviour: thus, we find that a bidispersed suspension with large dispersion ratio exhibit CST where an equivalent suspension (with same volume fraction) of monodispersed particles would have an abrupt change of the rheological properties, e.g. DST. The effect of the dispersion ratio is enhanced for large volume fractions, as getting closer to the jamming. These findings are consistent with those by [12], but different from those by [30, 31]. A possible explanation of this discrepancy has to be traced back to the increase of the total volume fraction of the suspension in the latter [30, 31].

When studying the rheology of a suspension, the two independent normal stress differences must be considered, along with the viscosity. The values obtained by the numerical simulations of these quantities together with the pressure are shown in Fig 2, panels b, c, d, where panel b shows the first normal stress difference $N_1 = \Sigma _{11}-\Sigma _{33}$, panel c the second normal stress difference $N_2 = \Sigma _{22}- \Sigma _{33}$, and panel d the pressure $\Pi = {{\,\textrm{Tr}\,}}{(\Sigma )}/3$; in the definition of the rheological quantities, $\Sigma$ represents the stress-tensor computed by means of the stresslet theory [18]. The three rheological quantities are shown for all the cases studied in this work. Overall, we observe that the first normal stress difference is small and dominated by fluctuations, as already observed by other authors [32, 43]. The second normal stress difference is always negative and its absolute value exhibit a trend similar to the pressure and relative viscosity, consistently to the ones observed in the literature [32]. The effect of the dispersion ratio for these two quantities, closely reflects the behaviour shown by the relative viscosity, with the exception of the first normal stress difference which suddenly changes sign and strongly increases by several orders of magnitude when the suspension undergoes DST.

After that, we picked the most interesting case in terms of rheological properties, i.e. $\phi =0.60$ where $\lambda$ affects DST ($\lambda =1.5$) by weakening it to CST ($\lambda =\{3.0, 6.0\}$), and we analysed the trends of the relative viscosity, normal stress differences and pressure varying the relative volume fraction of the dispersed phase, i.e. $\phi _2/\phi =\{0.2, 0.5, 0.8\}$. As per Fig. 2, panel a of Fig. 3 shows the flow curve of the suspension, i.e. how the relative viscosity $\eta _r$ of the suspension varies with the applied shear rate $\dot{\gamma }/\dot{\gamma }_0$. The curves are grouped using the colours to discriminate the dispersion ratio, in accordance with Fig. 1 (green: $\lambda =1.5$; red: $\lambda =3.0$; blue: $\lambda =6.0$) and the shades of the colours to identify the relative volume fractions analysed, with colours going from light to dark for increasing $\phi _2/\phi$. This is recapped in the legend of Fig. 3 (note that the curves $\phi _2/\phi =\{0.5, 0.8\}$ at $\lambda =1.5$ almost overlap). The curves show, as in Fig. 2, a shear-thinning region followed by the Newtonian plateau at low shear-rates, followed by a region of viscosity increase, i.e. the shear-thickening regime, and a final plateau at high shear rates. The effect of the relative volume fractions controls the relative viscosity, reducing it when the two phases have similar volume fractions and increasing it when the dispersion tends towards the monodispersion. For the cases with $\phi _2/\phi =\{0.2, 0.8\}$, consistently with the previous works [7,8,9, 20, 39], the relative viscosity is higher when there are more smaller particles than larger ones immersed in the suspension. Even in this case, we observe that the relative volume fraction can reduce, at high shear-rates, the relative viscosity of the suspension and weakens its shear-thickening behaviour, especially when $\phi _2=\phi _1$. However, the effect of the relative volume fraction does not have a strong impact as the the relative size of the dispersed phases.

The normal stresses of these suspensions, instead, are shown in Fig. 3, panels b, c, d, where panel b shows the first normal stress difference $N_1 = \Sigma _{11}-\Sigma _{33}$, panel (c) the second normal stress difference $N_2 = \Sigma _{22}- \Sigma _{33}$, and panel (d) the pressure $\Pi = {{\,\textrm{Tr}\,}}{(\Sigma )}/3$, as in Fig. 2; in the definition of the rheological quantities, $\Sigma$ represents the stress-tensor computed by means of the stresslet theory [18]. The three rheological quantities are shown for all the pairs of relative volume fractions $( \phi _1, \phi _2 )$ at $\phi =0.60$ studied in this work. We observe that the first normal stress difference is small and still dominated by fluctuations. Once more, the second normal stress difference is always negative and its absolute value exhibit a trend similar to the pressure and relative viscosity, consistently to the ones observed in the literature [32]. The effect of the relative volume fractions of the two phases reflects the behaviour shown by the relative viscosity, with the exception of the first normal stress, similarly to what has been observed in Fig. 2.

In order to highlight the origin of the reduced relative viscosity of the suspension with increasing dispersion ratio of the particles, we separate the contributions to the total stress accounted by the contacts, hydrodynamics and electrochemical potentials. In particular, Fig. 4 shows the contributions to the relative viscosity for the suspensions at different dispersion ratios. Figure 4 is structured in a $4\times 3$ matrix of panels, where each row of the matrix shows the contributions to the relative viscosity for increasing volume fractions ($\phi$ increases from top to bottom), while each column shows the effect for different dispersion ratios ($\lambda$ increases from left to right). In each panel of the figure, we report the contribution to the total relative viscosity (golden lines) of the contacts (black bars), hydrodynamics (darker grey) and electrochemical potentials (lighter grey), as a function of the shear-rate. Figure 4 reveals that, at low shear rates (left end of each panel), the suspension rheology is dominated by the electrochemical potentials, with a little contribution due to the hydrodynamics and a null contribution of the contacts. On the other hand, at high shear-rates (right end of each panel), the hydrodynamics has a small, almost shear-independent, contribution and the electrochemical potentials play no role, as expected; the contacts dominate the rheology of the suspension at these shear-rates, in agreement with the theory that relates shear-thickening and (frictional) contacts, recently proposed and experimentally proved [14, 27, 32, 33, 42]. Figure 4 shows that, while the hydrodynamics remains constant in the shear-thickening regime and the consequent plateau, the contribution of the contacts drops when increasing the size of the larger phase dispersed. This phenomenon becomes more evident when dealing with larger volume fractions, where DST can be reduced to CST by simply adding larger particles (see the last row of panels of Fig. 4). This provides a quantitative explanation of the behaviour observed in the flow curves of Fig. 2.

Fig. 5

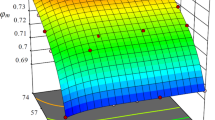
Relative viscosity in the high shear-rate limit, $\eta _{r,\infty }=\eta _r(\dot{\gamma }/\dot{\gamma }_0 \rightarrow \infty )$, as a function of the volume fraction $\phi$. The colour of the curves and the style of the markers reflect the ones used in Fig. 2. The solid lines are obtained from fitting the data available with power-laws $\eta _{r,\infty }=\alpha \left( 1-\phi /\phi _{MRJ}\right) ^{-\beta }$ (as shown in the inset) and the dashed lines correspond to the values of $\phi _{MRJ}$ obtained for the three configurations of suspensions considered. The best fitting parameters are $\left( \phi _{MRJ},\alpha ,\beta \right) _{\lambda =1.5} =\left( 0.6015,2.20,1.79\right)$, $\left( \phi _{MRJ},\alpha ,\beta \right) _{\lambda =3.0} =\left( 0.6125,2.18,1.79\right)$, $\left( \phi _{MRJ},\alpha ,\beta \right) _{\lambda =6.0} =\left( 0.6375,2.28,1.90\right)$

The reduction of contacts we observed for large values of $\lambda$, which is the origin of the lower relative viscosity, can be explained geometrically as a reduced total surface area of the suspension in the case with high dispersion ratios. Indeed, as $\lambda$ grows, the total surface area $A=\pi a_1^2(n_1+n_2\lambda ^2)$ monotonically decreases when the total volume fraction $\phi$ is kept constant (together with the relative volume fractions of the two phases that establish a non-linear dependency of $n_1$ and $n_2$ on $\lambda$). In other terms, for a given volume fraction of the dispersed phases, the area available for contacts among particles is smaller for larger $\lambda$, thus reducing the probability of having contacts between the particles. Note that this is valid only for spheres. This result is confirmed by the coordination number defined as $N_c = 4 \pi \int _0^{\overline{r}/a_0}\! r^2\, g(r)\, N/V \, \textrm{d}r$, where r is the distance from the origin, V is the volume of the computational box, and g(r) is the radial distribution function. Here, $\overline{r}/a_0=20$ is used to take into account the large dispersion ratio. The coordination number is an indicator of the average number of collisions between particles. We computed $N_c$ for all the dispersion ratios of the suspensions at $\phi =60$ shown in Fig. 5 and, to emphasize the results, we normalised $N_c$ by the coordination number of the case with $\lambda =1.5$. Thus, we obtain $N_c=[1,0.859,0.856]$ for $\lambda =[1.5,3.0,6.0]$. As for the relative viscosity and the total surface area A, the coordination number shows a decreasing trend with $\lambda$. More quantitatively, the change of A with $\lambda$ modifies the properties of the packing of the suspension as demonstrated by Hopkins et al. [21, 22]. In particular, it was shown that the increase of the dispersion ratio $\lambda$ enhances the efficiency of the packing, resulting in an increase of $\phi _{MRJ}$. This geometrically constraint affects the rheological properties of the suspension when it approaches the jamming transition, i.e., when the contacts dominate the rheology. In this case, the relative viscosity $\eta _r$ can be expressed as a power law diverging for $\phi \rightarrow \phi _{MRJ}$, i.e., $\eta _r \sim \left( 1-\phi / \phi _{MRJ} \right) ^{-\beta }$ [4, 15, 32]. We show this by considering the relative viscosity in the high shear-rate limit as a function of the volume fraction $\eta _{r,\infty }(\phi ) = \eta _r(\phi ,\dot{\gamma }/\dot{\gamma }_0\rightarrow \infty )$, see Fig. 5, where the plotted curves have been obtained by fitting our numerical data with a power-law of the form $\eta _{r,\infty }= \alpha \left( 1-\phi / \phi _{MRJ}\right) ^{-\beta }$, as shown in the inset of the same figure [32]. Figure 5 proves that $\phi _{MRJ}$ grows with $\lambda$, and thus explains that the differences in the values of the relative viscosity, previously observed at the beginning of this work for the different dispersion ratios Fig. 2, is a direct consequence of the variation of the packing efficiency which determines the infinite shear-rate limit of $\eta _r$ to be achieved after the shear-thickening region.

4 Conclusion

In this work, we studied the rheological behaviour of bidispersed suspensions of non-Brownian spherical particles, and we showed that the presence of a large dispersed phase reduces the shear-thickening behaviour of the suspension. This phenomenon is caused by the more efficient maximally random jammed packing exhibited by the suspensions with large dispersion ratio, that results in a reduction of contacts and thus of their contribution to the relative viscosity of the suspension. We also studied the effect of the relative volume fractions of the dispersed phases and we found that a lower viscosity is achieved when the dispersed phases have similar (identical in our work) volumes, coherently with the results already discussed in the literature. The effect of the latter parameter on the rheological properties of the suspensions, however, is not as important as the bidispersion ratio. The results discussed here are of particular interests as a simple control strategy for the rheology of particle suspensions, especially in their shear-thickening regime, with direct impact on the flowability of the complex material. Indeed, it is possible to force the transition from DST to CST (or vice-versa) by simply substituting a partial volume fraction of a monodispersed suspension, with an equivalent one of large (or small) particles.