1 Introduction

The mechanical behavior of most structures at the nanoscale is typically size dependent due to the influence of long-range inter-atomic forces, and classical approaches of continuum mechanics cannot capture this peculiar characteristic. Therefore, enriched continuum theories have been then introduced to analyze the mechanical response of micro or nano structures, and several models have been developed, such as micro-morphic theory [1], couple stress theory [2], mechanically based nonlocal theory [3, 4], and strain gradient elasticity theory [5,6,7].

Among these theories, nonlocal elasticity theory, firstly introduced by Eringen [8,9,10,11], has been extensively applied to various mechanical problems generally involving structures at the micro and nano scales [12, 13]. In this theory, the stress at some reference point is assumed to be a functional of the strain field at every point in the body, leading to constitutive equations defined in terms of a set of integro-partial differential equations. In this manner, the size-effect feature is captured in the model through an additional material parameter generally referred to as “the nonlocal parameter”. Note that, these integral constitutive equations have been conveniently transformed into an equivalent set of (singular) partial differential equations [11], leading to enhanced simplicity for the numerical treatment of the associated mechanical problems. This has paved the way for the application of Eringen’s nonlocal elasticity theory in a plethora of studies involving the mechanical behavior of several structural systems at the nanoscale, mostly related to nanobeams [12,13,14,15,16,17,18,19,20,21].

However, it should be emphasized that the transformation of the original integral formulation to the differential one represents an approximation, whose validity can be proved for points far from the boundaries [11, 22]. Thus, in the last decade several issues and paradoxical results have been also discussed in the literature related to the proper definition of the boundary conditions in nonlocal structures. For instance, counterintuitive results have arisen for beam-like structures when clamped and free boundary conditions are involved, such as in the case of nonlocal cantilever beams [23,24,25].

Recently, Eringen’s nonlocal elasticity theory has been also used for the analysis on nanoplates. For instance, the seminal contributions in [21, 26] treated both isotropic linear elastic Kirchhoff plates as well as nonlinear plates considering higher-order shear deformation theory. Notably, most of these studies have focused on plates with simple rectangular shape. In this regard, the classical Navier’s or Levy’s approaches have been used in [26,27,28,29,30], while other numerical approaches have been discussed in [31,32,33,34,35,36], to cite a few.

Few other studies have been devoted to the analysis of nonlocal plates of different shapes, with most contributions mainly related to circular shapes [36, 37], where also some exact analytical solutions have been determined [38, 39], while the bending analysis of nonlocal plates with general shapes has been recently discussed in [40] using a boundary element method. Finally, the case of nonlocal polygonal Kirchhoff plates has been analyzed in [22], where a solution of the bending problem has been found considering only simply-supported boundary conditions, and resorting to analogies with the solution of the classical (local) Kirchhoff plate. These results have been then exploited in [41] to compare the response of different plates models at the nano scale.

In conjunction with the preceding conspectus, this paper focuses on the bending response of micro and nanoscale Kirchhoff plate, using Eringen’s nonlocal theory, and considering arbitrary geometries and general boundary conditions. Specifically, the so-called Line Element-less Method (LEM), used in [42,43,44] for classical local plates, is here extended to determine the deflection and bending moments of nonlocal plates subjected to transversal loads. Notably, the proposed procedure only requires the solution of simple line integrals of harmonic polynomials with unknown coefficients, along the boundary parametric equation and, eventually, the solution of a set of linear algebraic equations for these unknown terms. Finally, the LEM is completely element-free, since it does not require any discretization, be it in the domain or in the boundary, and it also differs from other so-called meshfree procedures since the expansion coefficients are not determined by collocation.

It is worth mentioning that, this procedure yields approximate analytical solutions for generally shaped nonlocal plates, and even exact closed-form solutions for some particular geometries and boundary conditions. These aspects clearly represent attractive features of the proposed procedure, especially with respect to other meshfree methods that are of numerical nature only. In this regard, several applications will be discussed, assessing the simplicity and accuracy of the considered approach.

2 Problem definition

Consider a homogeneous, isotropic, linear elastic Kirchhoff plate of arbitrary shape with contour \(\Gamma\), domain \(\Omega\), and uniform thickness h, subjected to a transverse distributed load \(q\left( {x,y} \right)\), and satisfying the Eringen’s nonlocal model [9]. The plate is characterized by the modulus of elasticity E, Poisson’s ratio \(\nu\), and nonlocal parameter \(\lambda = \left( {l\,e_{0} } \right)^{2} \ge 0\), where \(l\) is an internal characteristic length, whereas \(e_{0}\) is the small length scale coefficient. Note that when \(\lambda = 0\) the classical local Kirchhoff plate is obtained.

According to the Eringen’s nonlocal differential formulation, and based on the Kirchhoff thin plate assumptions, the constitutive relations of the nonlocal plate can be expressed in terms of transverse deflection \(w\left( {x,y} \right)\) as

$$ \sigma_{x} - \lambda \left( {\frac{{\partial^{2} \sigma_{x} }}{{\partial x^{2} }} + \frac{{\partial^{2} \sigma_{x} }}{{\partial y^{2} }}} \right) = - \frac{E\,z}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right), $$
(1.a)
$$ \sigma_{y} - \lambda \left( {\frac{{\partial^{2} \sigma_{y} }}{{\partial x^{2} }} + \frac{{\partial^{2} \sigma_{y} }}{{\partial y^{2} }}} \right) = - \frac{E\,z}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right), $$
(1.b)
$$ \tau - \lambda \left( {\frac{{\partial^{2} \tau }}{{\partial x^{2} }} + \frac{{\partial^{2} \tau }}{{\partial y^{2} }}} \right) = - \frac{E\,z}{{1 + \nu }}\frac{{\partial^{2} w}}{\partial x\,\partial y}, $$
(1.c)

where \(\sigma_{x} \left( {x,y} \right)\), \(\sigma_{y} \left( {x,y} \right)\), and \(\tau \left( {x,y} \right)\) denote the normal stresses in the x and y directions and the shear stress, respectively.

In this manner, multiplying Eqs. (1) by the transverse coordinate z, and integrating over the z-direction, the corresponding moment–curvature equations can be obtained as

$$ M_{x} - \lambda \left( {\frac{{\partial^{2} M_{x} }}{{\partial x^{2} }} + \frac{{\partial^{2} M_{x} }}{{\partial y^{2} }}} \right) = - D\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right), $$
(2.a)
$$ M_{y} - \lambda \left( {\frac{{\partial^{2} M_{y} }}{{\partial x^{2} }} + \frac{{\partial^{2} M_{y} }}{{\partial y^{2} }}} \right) = - D\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right), $$
(2.b)
$$ M_{xy} - \lambda \left( {\frac{{\partial^{2} M_{xy} }}{{\partial x^{2} }} + \frac{{\partial^{2} M_{xy} }}{{\partial y^{2} }}} \right) = - D\left( {1 - \nu } \right)\frac{{\partial^{2} w}}{\partial x\,\partial y}, $$
(2.c)

where \(M_{x} \left( {x,y} \right)\) and \(M_{y} \left( {x,y} \right)\) are the bending moments, \(M_{xy} \left( {x,y} \right)\) is the twisting moment, and \(D = {{Eh^{3} } \mathord{\left/ {\vphantom {{Eh^{3} } {12\left( {1 - \nu^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {12\left( {1 - \nu^{2} } \right)}}\) is the flexural rigidity of the plate.

Further, from equilibrium considerations shear forces can be expressed as

$$ V_{x} = \frac{{\partial M_{x} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y}, $$
(3.a)
$$ V_{y} = \frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{y} }}{\partial y}, $$
(3.b)

considering that

$$ \frac{{\partial V_{x} }}{\partial x} + \frac{{\partial V_{y} }}{\partial y} = - q. $$
(4)

Note that, substituting Eqs. (2) and (3) into Eq. (4) yields

$$ \frac{{\partial^{2} M_{x} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy} }}{\partial x\,\partial y} + \frac{{\partial^{2} M_{y} }}{{\partial y^{2} }} = - q, $$
(5)

which represents the relation among moments and transversal load, that does not depend on the nonlocal parameter \(\lambda\).

Further, by substituting Eqs. (2) into (5), yields

$$ D\left( {\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}} \right)\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) = \left[ {q - \lambda \left( {\frac{{\partial^{2} q}}{{\partial x^{2} }} + \frac{{\partial^{2} q}}{{\partial y^{2} }}} \right)} \right], $$
(6)

which is the biharmonic governing differential equation for bending of the Eringen’s nonlocal plate. Introducing the two-dimensional Laplace operator \(\nabla^{2} \left( \cdot \right) = \frac{{\partial^{2} \left( \cdot \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} \left( \cdot \right)}}{{\partial y^{2} }}\), Eq. (6) can be rewritten as

$$ D\,\nabla^{2} \nabla^{2} w\left( {x,y} \right) = \left( {1 - \lambda \nabla^{2} } \right)q\left( {x,y} \right). $$
(7)

Note that, the effect of the nonlocal model appears only at the right-hand-side of Eq. (7), due to the additional term (with respect to classical local model) \(\lambda \nabla^{2} q\left( {x,y} \right)\). Clearly, if a uniform load is considered, this term would be equal to zero, and Eq. (7) would revert to the classical equation of Kirchhoff local plates.

Next, introduce the Marcus’ moment sum \(M\left( {x,y} \right)\), defined as [46, 47]

$$ M\left( {x,y} \right) = \frac{{M_{x} + M_{y} }}{1 + \nu }. $$
(8)

Therefore, summing Eqs. (2.a) and (2.b) yields

$$ D\,\nabla^{2} w\left( {x,y} \right) = - \left( {1 - \lambda \nabla^{2} } \right)M\left( {x,y} \right). $$
(9)

In this manner, applying the Laplace operator to both side of Eq. (9), and using the interchangeability of differentiation, the governing equation Eq. (7) can be rewritten as

$$ \left( {1 - \lambda \nabla^{2} } \right)\nabla^{2} M\left( {x,y} \right) = - \left( {1 - \lambda \nabla^{2} } \right)q\left( {x,y} \right). $$
(10)

Further, by skipping the common operator \(\left( {1 - \lambda \nabla^{2} } \right)\) as in [22, 41], Eq. (10) leads to the following more compact form of the equilibrium equation in terms of Marcus’ moment

$$ \nabla^{2} M\left( {x,y} \right) = - q\left( {x,y} \right), $$
(11)

and, substituting Eq. (11) into Eq. (9), the Marcus’ moment sum can be also explicitly expressed as

$$ M\left( {x,y} \right) = - D\,\nabla^{2} w\left( {x,y} \right) - \lambda \,q\left( {x,y} \right). $$
(12)

Note that, in this manner, the solution of the plate problem Eq. (7) reduces to the integration, in sequence, of the two Poisson differential equations Eqs. (11) and (9), respectively, which is sometimes preferred depending upon the employed method of solution.

2.1 Formulation of boundary conditions

As far as the boundary conditions (BCs) are concerned, denote as n and t the outward unit normal and tangent vector at a point A of a generic curvilinear edge of the contour \(\Gamma\), and let \(\alpha\) be the angle between the normal n and the x axis (see Fig. 1). Thus, the BCs for the curvilinear edge can be assumed as those of the classical local plate as [21]

  1. (i)

    Simply-supported edge

    $$ w\left( {x,y} \right) = 0, $$
    (13.a)
    $$ M_{n} \left( {x,y} \right) = 0, $$
    (13.b)
Fig. 1
figure 1

Plate with arbitrary shape

Full size image

where \(M_{n} \left( {x,y} \right)\) denotes the normal bending moment applied at the edge, and is given as

$$ M_{n} \left( {x,y} \right) = \,n_{x}^{2} \,M_{x} + \,n_{y}^{2} \,M_{y} + 2\,n_{x} \,n_{y} \,M_{xy} , $$
(14)

where \(n_{x}\) and \(n_{y}\) are the components of the unitary vector \({\mathbf{n}}\) along the x and y axes, respectively.

  1. (ii)

    Clamped edge

    $$ w\left( {x,y} \right) = 0, $$
    (15.a)
    $$ \frac{{\partial w\left( {x,y} \right)}}{\partial n} = n_{x} \frac{\partial w}{{\partial x}} + n_{y} \frac{\partial w}{{\partial y}} = 0. $$
    (15.b)
  2. iii.

    Free edge

    $$ M_{n} \left( {x,y} \right) = 0, $$
    (16.a)
    $$ \tilde{V}_{n} = V_{n} + \frac{{\partial M_{nt} }}{\partial s} = 0, $$
    (16.b)

where \(M_{n\,t} \left( {x,y} \right)\) and \(V_{n} \left( {x,y} \right)\) are given as

$$ M_{n\,t} \left( {x,y} \right) = \left( {n_{x}^{2} + n_{y}^{2} } \right)M_{xy} + n_{x} \,n_{y} \left( {M_{y} - M_{x} } \right), $$
(17)

and

$$ V_{n} \left( {x,y} \right) = n_{x} \,V_{x} + n_{y} \,V_{y} . $$
(18)

It is worth mentioning that, the above reported BCs considerably simplify for straight edges [22], as for instance in the case of polygonal plates. In this regard, consider a simply supported rectangular plate, of length \(a\) and width \(b\). The boundary conditions for the four edges are given as [41]

$$ M_{x} = \frac{{\partial^{2} M_{x} }}{{\partial y^{2} }} = 0,\,\,\,\frac{{\partial^{2} w}}{{\partial y^{2} }} = \frac{{\partial^{4} w}}{{\partial y^{4} }} = 0,\,\,\,w = 0, $$
(19.a)

for edges \(x = 0\) and \(x = a\), while

$$ M_{y} = \frac{{\partial^{2} M_{y} }}{{\partial x^{2} }} = 0,\,\,\,\frac{{\partial^{2} w}}{{\partial x^{2} }} = \frac{{\partial^{4} w}}{{\partial x^{4} }} = 0,\,\,\,w = 0, $$
(19.b)

for edges \(y = 0\) and \(y = b\).

Further, taking into account Eqs. (19), Eqs. (2) yields

$$ D\frac{{\partial^{2} w}}{{\partial x^{2} }} = \lambda \frac{{\partial^{2} M_{x} }}{{\partial x^{2} }},\,\,\,{\text{in}}\,x = 0\,\,{\text{and}}\,x = a, $$
(20.a)

and

$$ D\frac{{\partial^{2} w}}{{\partial y^{2} }} = \lambda \frac{{\partial^{2} M_{y} }}{{\partial y^{2} }},\,\,\,{\text{in}}\,y = 0\,\,{\text{and}}\,y = b, $$
(20.b)

which show that the boundary conditions for nonlocal plate bending problems also contain the nonlocal parameter.

Observe that this feature is the basis of the controversy in the literature on the appropriate applications of the BCs for nonlocal plates. Specifically, certain problems and paradoxical results have been increasingly discussed in the literature of nonlocal beams and plates, due to the proper definition and treatment of the associated boundary conditions [24, 29, 30]. This problem arises because normal and shear stresses (and hence bending and twisting moments too) cannot be directly related to the displacement function, as shown in Eqs. (1). Thus, the definition of simply-supported and free edges BCs may be ambiguous, and requires particular attention. Clearly, an exception is represented by the use of all-side clamped edge BCs since, in this case, conditions are required only in terms of displacements, thus avoiding the possible ambiguity related to the constitutive relations in Eqs. (1).

Nevertheless, commonly in the literature the issue related to the proper definition of the BCs has been overcome expressing, under some approximations, the (nonlocal) bending and twisting moments in Eqs. (2) in terms of the classical (local) Kirchhoff model ones. Specifically, recalling that bending and twisting moments in the classical (local) Kirchhoff theory of plates are given as

$$ M_{x}^{\left( K \right)} = - D\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right), $$
(21.a)
$$ M_{y}^{\left( K \right)} = - D\left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right), $$
(21.b)
$$ M_{xy}^{\left( K \right)} = - D\left( {1 - \nu } \right)\frac{{\partial^{2} w}}{\partial x\,\partial y}, $$
(21.c)

then, Eqs. (2) can be equivalently rewritten as

$$ \left( {1 - \lambda \nabla^{2} } \right)M_{x} = M_{x}^{\left( K \right)} , $$
(22.a)
$$ \left( {1 - \lambda \nabla^{2} } \right)M_{y} = M_{y}^{\left( K \right)} , $$
(22.b)
$$ \left( {1 - \lambda \nabla^{2} } \right)M_{xy} = M_{xy}^{\left( K \right)} . $$
(22.c)

In this manner, taking into account Eqs. (21) and (22), bending and twisting moments can be approximately expressed in terms of the classical Kirchhoff’s model ones as [37, 40]

$$ M_{x} = \sum\limits_{j = 0}^{\infty } {\lambda^{j} \,\nabla^{2j} M_{x}^{\left( K \right)} } = - D\sum\limits_{j = 0}^{\infty } {\lambda^{j} \,\nabla^{2j} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)} , $$
(23.a)
$$ M_{y} = \sum\limits_{j = 0}^{\infty } {\lambda^{j} \,\nabla^{2j} M_{y}^{\left( K \right)} } = - D\sum\limits_{j = 0}^{\infty } {\lambda^{j} \,\nabla^{2j} \left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} , $$
(23.b)
$$ M_{xy} = \sum\limits_{j = 0}^{\infty } {\lambda^{j} \,\nabla^{2j} M_{xy}^{\left( K \right)} } = - D\left( {1 - \nu } \right)\sum\limits_{j = 0}^{\infty } {\lambda^{j} \,\nabla^{2j} \left( {\frac{{\partial^{2} w}}{\partial x\,\partial y}} \right)} , $$
(23.c)

where \(\nabla^{2j} \left( \cdot \right) = \underbrace {{\nabla^{2} \nabla^{2} \cdots \nabla^{2} }}_{j - times}\left( \cdot \right)\).

Notably, as it can be observed, Eq. (23) directly relates moments to the deflection function \(w\left( {x,y} \right)\) and, in this manner, also shear forces can be expressed in terms of \(w\left( {x,y} \right)\) using Eqs. (3). Therefore, the previously mentioned difficulty in the definition of the BCs due to the constitutive relations in Eqs. (1) can be circumvented.

2.2 Background on simply-supported polygonal plate

Recently, a solution to the issue pertaining to how appropriately handle simply-supported BCs in polygonal plates has been developed in [22], using an approach based on the Marcus’ moment sum. In this regard, it has been shown that the BCs can equivalently be written as

$$w\left( {x,y} \right) = 0,$$
(24.a)
$$ D\frac{{\partial^{2} w\left( {x,y} \right)}}{{\partial {\mathbf{n}}^{2} }} = - \lambda \,q\left( {x,y} \right). $$
(24.b)

Further, both the moment sum and the deflection functions can be decomposed into their local part and a nonlocal correction term

$$ M\left( {x,y} \right) = M_{l} \left( {x,y} \right) + M_{\lambda } \left( {x,y} \right), $$
(25.a)
$$ w\left( {x,y} \right) = w_{l} \left( {x,y} \right) + w_{\lambda } \left( {x,y} \right). $$
(25.b)

Thus, it has been proved that \(M_{\lambda } = 0\), while the local part is given by the solution of the following equation

$$ \nabla^{2} M_{l} \left( {x,y} \right) = - q\left( {x,y} \right), $$
(26)

assuming as BCs \(M_{l} = 0\) in \(\Gamma\). In this manner, the local part of the deflection function has been derived solving the equation

$$ \nabla^{2} w_{l} \left( {x,y} \right) = - M_{l} \left( {x,y} \right), $$
(27)

assuming as BCs \(w_{l} = 0\) in \(\Gamma\). Finally, the nonlocal correction term in Eq. (25.b) has been given as

$$ w_{\lambda } \left( {x,y} \right) = \frac{\lambda }{D}M_{l} \left( {x,y} \right). $$
(28)

3 Line element-less method for nonlocal plate analysis

In this section LEM approach is introduced for the analysis of nonlocal Kirchhoff plates of general shape, subjected to a transversal load \(q\left( {x,y} \right)\). Specifically, based on the previous studies on the use of the LEM [42,43,44,45, 48,49,50,51,52,53] and considering Eqs. (9) and (11), \(M\left( {x,y} \right)\) and \(w\left( {x,y} \right)\) can be expressed in terms of the so-called harmonic polynomials \(P_{k}\) and \(Q_{k}\), generally defined as

$$ P_{k} \left( {x,y} \right) = {\text{Re}} \left( {x + iy} \right)^{k} , $$
(29.a)
$$ Q_{k} \left( {x,y} \right) = {\text{Im}} \left( {x + iy} \right)^{k} , $$
(29.b)

or, recursively as

$$ P_{k} \left( {x,y} \right) = P_{k - 1} x - Q_{k - 1} y, $$
(30.a)
$$ Q_{k} \left( {x,y} \right) = Q_{k - 1} x - P_{k - 1} y, $$
(30.b)

which are valid for \(k > 0\), and with \(P_{0} = 1\) and \(Q_{0} = 0\).

Further, the derivatives of the harmonic polynomials are

$$ \frac{{\partial P_{k} }}{\partial x} = kP_{k - 1} ;\,\,\frac{{\partial P_{k} }}{\partial y} = - kQ_{k - 1} , $$
(31.a)
$$ \frac{{\partial Q_{k} }}{\partial x} = kQ_{k - 1} ;\,\,\frac{{\partial Q_{k} }}{\partial y} = kP_{k - 1} , $$
(31.b)
$$ \nabla^{2} P_{k} = 0\,;\,\,\,\nabla^{2} Q_{k} = 0\,\,\,\,\forall k. $$
(31.c)

Based on the above relations, a solution of Eq. (11) can be obtained expressing the moment sum function in terms of harmonic polynomials, satisfying the Laplace equation as in Eq. (31.c), plus a particular solution of the Poisson equation Eq. (11), namely \(M_{c} \left( {x,y} \right)\). That is

$$ M\left( {x,y} \right) \cong \sum\limits_{k = 0}^{p} {a_{k} P_{k} \left( {x,y} \right)} + \sum\limits_{k = 1}^{p} {b_{k} Q_{k} \left( {x,y} \right)} + M_{c} \left( {x,y} \right), $$
(32)

where \(a_{k}\) and \(b_{k}\) are \(\left( {2p + 1} \right)\) unknown coefficients to be determined, and \(p\) is the truncation limit of the series expansion.

Note that, as far as the particular solution \(M_{c} \left( {x,y} \right)\) of Eq. (11) is concerned, this can be obtained in closed-form using the approach in [42] (see also “Appendix A” for further details) when the load function \(q\left( {x,y} \right)\) is represented by a homogeneous polynomial of degree N

$$ q\left( {x,y} \right) = \sum\limits_{k = 0}^{N} {A_{k} \,x^{N - k} y^{k} } , $$
(33)

where \(A_{k}\) are known coefficients. For instance, for the typical case of a uniformly distributed load \(q\left( {x,y} \right) = q_{0}\), the following expressions of \(M_{c} \left( {x,y} \right)\) can be easily obtained

$$ M_{c} \left( {x,y} \right) = - \frac{{q_{0} }}{4}\left( {x^{2} + y^{2} } \right), $$
(34)

while solutions for other typical cases are reported in [42]. Observe that, if the function \(q\left( {x,y} \right)\) cannot be directly represented as in Eq. (33), it can be initially approximated by a truncated series of Chebyshev polynomials which can be recast in the form of Eq. (33). Clearly, this yields a quite versatile tool for expressing various shapes of transverse load functions, and even concentrated forces as shown in [42].

As far as the unknown coefficients in Eq. (32) are concerned, the \(\left( {2p + 1} \right)\) values of \(a_{k}\) and \(b_{k}\) can be determined appropriately imposing the specified BCs of the plate. In this context, it is convenient to firstly address the case of polygonal plates with simply-supported edges, while the generalization to arbitrary shaped plates will be presented in the following.

3.1 Simply-supported polygonal plate

Consider a nonlocal plate of polygonal shape with all the edges simply-supported. According to Eq. (13.b) the moment sum function must be zero along the entire contour of the polygonal plate; thus, the following relation holds

$$ M_{n} \left( {x,y} \right) = M\left( {x,y} \right) = 0,\,\,\,\,\,\,in\,\,\Gamma . $$
(35)

Following the approach in [42], the unknown coefficients \(\left( {a_{k} ,\,b_{k} } \right)\) in Eq. (32) can be evaluated applying a minimization procedure on the closed contour path integral of the squared moment sum function

$$ \Psi \left( {a_{k} ,\,b_{k} } \right) = \oint\limits_{\Gamma } {\left[ {M\left( {x,y} \right)} \right]}^{2} d\gamma . $$
(36)

Thus, performing variations of the aforementioned functional with respect to \(\left( {a_{k} ,\,b_{k} } \right)\), yields

$$ \left\{ \begin{gathered} \frac{{\partial \Psi \left( {a_{k} ,\,b_{k} } \right)}}{{\partial a_{k} }} = 0 \hfill \\ \,\frac{{\partial \Psi \left( {a_{k} ,\,b_{k} } \right)}}{{\partial b_{k} }} = 0 \hfill \\ \end{gathered} \right., $$
(37)

which is a linear algebraic system of \(\left( {2p + 1} \right)\) equations in the unknowns \(\left( {a_{k} ,\,b_{k} } \right)\). In this manner, once the coefficients are determined, the moment sum function can be found through Eq. (32).

Next, the deflection function \(w\left( {x,y} \right)\) can be obtained solving Eq. (9). In this regard, following the same approach used for the moment sum function, a solution of Eq. (9) can be sought assuming \(w\left( {x,y} \right)\) as the sum of harmonic polynomials, and a particular solution of the Poisson equation Eq. (9), namely \(w_{c} \left( {x,y} \right)\); that is

$$ w\left( {x,y} \right) \cong \sum\limits_{k = 0}^{m} {c_{k} P_{k} \left( {x,y} \right)} + \sum\limits_{k = 1}^{m} {d_{k} Q_{k} \left( {x,y} \right)} + w_{c} \left( {x,y} \right), $$
(38)

where \(c_{k}\) and \(d_{k}\) are \(\left( {2m + 1} \right)\) unknown coefficients to be determined, and \(m\) is the truncation limit of the series expansion. Again, note that the particular solution \(w_{c} \left( {x,y} \right)\) can be evaluated applying the procedure in “Appendix A”, considering the term at the right-hand side of Eq. (9), namely \(\left[ { - \left( {1 - \lambda \nabla^{2} } \right)M\left( {x,y} \right)} \right]\).

As far as the unknown coefficients in Eq. (38) are concerned, the \(\left( {2m + 1} \right)\) values of \(c_{k}\) and \(d_{k}\) are determined appropriately imposing the BCs. In this regard, considering that for a simply-supported plate Eq. (13.a) holds, the coefficients \(\left( {c_{k} ,\,d_{k} } \right)\) can be found minimising the closed contour path integral of the squared deflection function; that is

$$ \Theta \left( {c_{k} ,\,d_{k} } \right) = \oint\limits_{\Gamma } {\left[ {w\left( {x,y} \right)} \right]}^{2} d\gamma . $$
(39)

Introducing Eq. (38) into Eq. (39), and performing variation with respect to the unknown coefficients leads to an algebraic linear system in terms of the unknowns \(\left( {c_{k} ,\,d_{k} } \right)\), as

$$ \left\{ \begin{gathered} \frac{{\partial \Theta \left( {c_{k} ,\,d_{k} } \right)}}{{\partial c_{k} }} = 0 \hfill \\ \,\frac{{\partial \Theta \left( {c_{k} ,\,d_{k} } \right)}}{{\partial d_{k} }} = 0 \hfill \\ \end{gathered} \right.. $$
(40)

Solution of the set of \(\left( {2m + 1} \right)\) equations yields the sought deflection function of the plate \(w\left( {x,y} \right)\) through Eq. (38).

3.2 General plate analysis

As previously mentioned, the above discussed procedure is strictly valid for polygonal plates with all edges simply-supported. In this case, in fact, both the moment sum and the deflection functions are equal to zero on the contour, and this allows the functionals \(\Psi \left( {a_{k} ,\,b_{k} } \right)\) and \(\Theta \left( {c_{k} ,\,d_{k} } \right)\) to be expressed as in Eqs. (36) and (39), respectively.

Clearly, in the generic case of arbitrarily shaped plates with different BCs, neither \(M\left( {x,y} \right)\) nor \(w\left( {x,y} \right)\) equal zero on the entire contour. Thus, the possibility of the moment sum or the deflection functions not to vanish in \(\Gamma\) needs to be appropriately addressed, for the evaluation of the unknown coefficients.

In this regard, if the plate BCs vary on the contour \(\Gamma\), as shown in Fig. 2, it is feasible to appropriately subdivide \(\Gamma\) in the \(N_{\gamma }\) edges \(\Gamma_{i}\) on which the BCs are kept constant, that is \(\Gamma = \bigcup\nolimits_{i = 1}^{{N_{\gamma } }} {\Gamma_{i} }\). Therefore, the functional in Eq. (36) can be modified as

$$ \tilde{\Psi }\left( {a_{k} ,\,b_{k} } \right) = \sum\limits_{i = 1}^{{N_{\gamma } }} {\int\limits_{{\Gamma_{i} }} {\left[ {M\left( {x,y} \right) - \tilde{M}_{i} \left( {x,y} \right)} \right]^{2} \,d\gamma } } , $$
(41)

where the symbol \(\int\limits_{{\Gamma_{i} }} {\left( \cdot \right)\,d\gamma }\) denotes the classical line integration and \(M\left( {x,y} \right)\) is given in Eq. (32). Further, \(\tilde{M}_{i} \left( {x,y} \right)\) are appropriately introduced additional functions, accounting for the generic plate BCs, where the subscript \(i\) refers to the i-th edge \(\Gamma_{i}\) (see Fig. 2). For consistency, \(\tilde{M}_{i} \left( {x,y} \right)\) can be also expressed in terms of harmonic polynomials as

$$ \tilde{M}_{i} \left( {x,y} \right) \cong \sum\limits_{k = 0}^{{\tilde{p}}} {\tilde{a}_{k}^{\left( i \right)} P_{k} \left( {x,y} \right)} + \sum\limits_{k = 1}^{{\tilde{p}}} {\tilde{b}_{k}^{\left( i \right)} Q_{k} \left( {x,y} \right)} ;\quad i = 1, \ldots ,N_{\gamma } , $$
(42)

in which \(\tilde{a}_{k}^{\left( i \right)}\) and \(\tilde{b}_{k}^{\left( i \right)}\) are unknown coefficients to be determined, while \(\tilde{p}\) is the truncation limit of the series expansion, with \(\tilde{p} < p\) and generally small.

Fig. 2
figure 2

Plate of arbitrary shape with mixed BCs and \(N_{\gamma } = 4\)

Full size image

Notably, since \(\tilde{M}_{i} \left( {x,y} \right)\) is equal to zero only for simply-supported straight edges, the function \(\tilde{M}_{i} \left( {x,y} \right)\) represents the Marcus’ moment sum on the corresponding edge.

Analogously, to allow for the possibility of vertical deflections on the contour, the functional in Eq. (39) can be modified as

$$ \tilde{\Theta }\left( {c_{k} ,\,d_{k} } \right) = \sum\limits_{i = 1}^{{N_{\gamma } }} {\int\limits_{{\Gamma_{i} }} {\left[ {w\left( {x,y} \right) - \tilde{w}_{i} \left( {x,y} \right)} \right]^{2} \,d\gamma } } , $$
(43)

where \(w\left( {x,y} \right)\) is given in Eq. (38) and \(\tilde{w}_{i} \left( {x,y} \right)\) is an additional function, conveniently introduced to take into account the possibility of boundary deflections. Expressing \(\tilde{w}_{i} \left( {x,y} \right)\) in terms of harmonic polynomials, yields

$$ \tilde{w}_{i} \left( {x,y} \right) \cong \sum\limits_{k = 0}^{{\tilde{m}}} {\tilde{c}_{k}^{\left( i \right)} \,P_{k} \left( {x,y} \right)} + \sum\limits_{k = 1}^{{\tilde{m}}} {\tilde{d}_{k}^{\left( i \right)} \,Q_{k} \left( {x,y} \right)} \,;\quad i = 1, \ldots ,N_{\gamma } , $$
(44)

in which \(\tilde{c}_{k}^{\left( i \right)}\) and \(\tilde{d}_{k}^{\left( i \right)}\) are unknown coefficients to be determined, while \(\tilde{m}\) is the chosen truncation limit of the series expansion, with \(\tilde{m} < m\) and generally small.

Note that, the additional functions \(\tilde{w}_{i} \left( {x,y} \right)\) must be considered only for the plate edges \(\Gamma_{i}\) that are allowed to move vertically (such as in a free edge). Therefore, when all the edges are restrained against vertical deflections, \(\tilde{w}_{i} \left( {x,y} \right) = 0\,\,\forall i\), and the functional in Eq. (43) reverts to the more simple one in Eq. (39).

As far as the solution procedure is concerned, a three steps scheme, similar to the one described in Sect. 3.1, can be followed.

The first step is associated with the solution of Eq. (11), which leads to the moment sum function \(M\left( {x,y} \right)\). In this regard, minimising the functional in Eq. (41), that is performing the variation of the functional with respect to the unknown coefficients \(\left( {a_{k} ,\,b_{k} } \right)\), yields a linear system of \(\left( {2p + 1} \right)\) algebraic equations, as

$$ \left\{ \begin{gathered} \frac{{\partial \tilde{\Psi }\left( {a_{k} ,\,b_{k} } \right)}}{{\partial a_{k} }} = 0 \hfill \\ \,\frac{{\partial \tilde{\Psi }\left( {a_{k} ,\,b_{k} } \right)}}{{\partial b_{k} }} = 0 \hfill \\ \end{gathered} \right.. $$
(45)

Note that, solving Eq. (45) leads to the determination of the coefficients \(\left( {a_{k} ,\,b_{k} } \right)\) in terms of the unknowns \(\tilde{a}_{k}^{\left( i \right)}\) and \(\tilde{b}_{k}^{\left( i \right)}\). In this manner, the moment sum function \(M\left( {x,y} \right)\) can be found through Eq. (32) in terms of the coefficients \(\left( {\tilde{a}_{k}^{\left( i \right)} ,\,\tilde{b}_{k}^{\left( i \right)} } \right)\).

The second step is associated with the solution of Eq. (9), which yields the deflection function \(w\left( {x,y} \right)\). In this regard, a particular solution of Eq. (9) \(w_{c} \left( {x,y} \right)\), which is required in Eq. (38), can be evaluated as discussed in “Appendix A”, considering the term at the right-hand side of Eq. (9), namely \(\left[ { - \left( {1 - \lambda \nabla^{2} } \right)M\left( {x,y} \right)} \right]\). Further, the variation of the functional in Eq. (43), with respect to the unknown coefficients \(\left( {c_{k} ,\,d_{k} } \right)\), can be performed as

$$ \left\{ \begin{gathered} \frac{{\partial \tilde{\Theta }\left( {c_{k} ,\,d_{k} } \right)}}{{\partial c_{k} }} = 0 \hfill \\ \,\frac{{\partial \tilde{\Theta }\left( {c_{k} ,\,d_{k} } \right)}}{{\partial d_{k} }} = 0 \hfill \\ \end{gathered} \right., $$
(46)

which is a set of \(\left( {2m + 1} \right)\) linear algebraic equations, whose solution leads to the coefficients \(\left( {c_{k} ,\,d_{k} } \right)\) in terms of the unknowns \(\left( {\tilde{c}_{k}^{\left( i \right)} ,\,\tilde{d}_{k}^{\left( i \right)} } \right)\). Once these coefficients are found, the deflection function \(w\left( {x,y} \right)\) can be evaluated via Eq. (38).

As a final step, the unknown terms \(\left( {\tilde{a}_{k}^{\left( i \right)} ,\,\tilde{b}_{k}^{\left( i \right)} } \right)\) and \(\left( {\tilde{c}_{k}^{\left( i \right)} ,\,\tilde{d}_{k}^{\left( i \right)} } \right)\) are determined appropriately imposing the specified BCs on the edges \(\Gamma_{i}\). Specifically, for the most common cases, considering Eqs. (13), (15), and (16) the following functionals can be defined for each edge \(\Gamma_{i}\):

  1. (i)

    Simply-supported curved edge

    $$ \Xi_{i} \,\left( {\tilde{a}_{k}^{\left( i \right)} ,\,\tilde{b}_{k}^{\left( i \right)} } \right) = \int\limits_{{\Gamma_{i} }} {\left[ {M_{n} \left( {x,y} \right)} \right]^{2} \,d\gamma } . $$
    (47)
  2. (ii)

    Clamped edge

    $$ \Xi_{i} \,\left( {\tilde{a}_{k}^{\left( i \right)} ,\,\tilde{b}_{k}^{\left( i \right)} } \right) = \int\limits_{{\Gamma_{i} }} {\left[ {\frac{{\partial w\left( {x,y} \right)}}{{\partial {\mathbf{n}}}}} \right]^{2} \,d\gamma } . $$
    (48)
  3. (iii)

    Free edge

$$ \Xi_{i} \,\left( {\tilde{a}_{k}^{\left( i \right)} ,\,\tilde{b}_{k}^{\left( i \right)} } \right) = \int\limits_{{\Gamma_{i} }} {\left[ {M_{n} \left( {x,y} \right)} \right]^{2} \,d\gamma } , $$
(49.a)
$$ \Lambda_{i} \left( {\tilde{c}_{k}^{\left( i \right)} ,\,\tilde{d}_{k}^{\left( i \right)} } \right) = \int\limits_{{\Gamma_{i} }} {\left[ {\tilde{V}_{n} \left( {x,y} \right)} \right]^{2} \,d\gamma } . $$
(49.b)

In this context, observe that even more complex BCs, or variations of the BCs on the same edge \(\Gamma_{i}\), may be taken into account in a similar manner [42].

Clearly, minimising the above defined functionals, that is performing the variation with respect to the unknown terms as

$$ \left\{ \begin{gathered} \frac{{\partial \Xi_{i} \left( {\tilde{a}_{k}^{\left( i \right)} ,\,\tilde{b}_{k}^{\left( i \right)} } \right)}}{{\partial \tilde{a}_{k}^{\left( i \right)} }} = 0 \hfill \\ \,\frac{{\partial \Xi_{i} \left( {\tilde{a}_{k}^{\left( i \right)} ,\,\tilde{b}_{k}^{\left( i \right)} } \right)}}{{\partial \tilde{b}_{k}^{\left( i \right)} }} = 0 \hfill \\ \end{gathered} \right.\,,\,\,\,\,i = 1, \ldots ,N_{\gamma } , $$
(50)

and

$$ \left\{ \begin{gathered} \frac{{\partial \Lambda_{i} \left( {\tilde{c}_{k}^{\left( i \right)} ,\,\tilde{d}_{k}^{\left( i \right)} } \right)}}{{\partial \tilde{c}_{k}^{\left( i \right)} }} = 0 \hfill \\ \,\frac{{\partial \Lambda_{i} \left( {\tilde{c}_{k}^{\left( i \right)} ,\,\tilde{d}_{k}^{\left( i \right)} } \right)}}{{\partial \tilde{d}_{k}^{\left( i \right)} }} = 0 \hfill \\ \end{gathered} \right.\,,\,\,\,\,i = 1, \ldots ,N_{\gamma } , $$
(51)

yields a linear system of algebraic equations, that can be easily solved for the sought coefficients \(\left( {\tilde{a}_{k}^{\left( i \right)} ,\,\tilde{b}_{k}^{\left( i \right)} } \right)\) and \(\left( {\tilde{c}_{k}^{\left( i \right)} ,\,\tilde{d}_{k}^{\left( i \right)} } \right)\). In this manner the complete definition of the deflection function \(w\left( {x,y} \right)\) is obtained.

It is worth noting that the entire procedure only requires the evaluation of simple line integrals, and the solution of linear system of algebraic equations, which can be performed in a straightforward manner in any numerical or symbolic program, such as Wolfram Mathematica.

On this base, an attractive characteristic of the proposed approach for nonlocal plate analysis is the possibility of determining in some cases exact closed-form solutions of the problem, as it will be shown in the following. In the other cases, the method yields approximate analytical solutions, and this may be regarded as an additional appealing feature of the proposed procedure with respect to classical FEM and meshless approaches, which are of numerical nature. Further, the method does not require the definition of any mesh, and few terms in the series expansions are generally needed, thus keeping at minimum the computational cost.

4 Applications

In this section, the proposed LEM is applied to several nonlocal plate configurations, considering various shapes and boundary conditions. Specifically, firstly the proposed method is employed for the analysis of different well-known examples, showing the ability of the procedure to yield even exact solutions. In this regard, a triangular simply-supported nonlocal plate, circular simply-supported and clamped nonlocal plates, as well as elliptical clamped nonlocal plates are considered. Further, as approximate analytical solutions, rectangular nonlocal plates with different boundary conditions and load distributions are employed.

As far as the selection of the number of terms in the series expansions is concerned, it is noted that these values strongly depend on the specific problem under consideration. In this regard, in general a higher number of terms might be required in case of complex shapes or BCs, and in case of complex load distributions. Interested readers are also referred to [42] for further insights. Nevertheless, as a rule of thumb, the procedure can be performed for few different values of p and m, until convergence of the deflection function is reached.

Finally, note that in the following applications only simply-supported and clamped boundary conditions are used, due to the aforementioned issues pertaining to the proper definition of the BCs for the Eringen’s nonlocal model. Applications comprising free-edges, or even more complex BCs, can be also carried out using the proposed procedure as shown in [42], provided that functionals in Eq. (49) are represented exploiting the approximate expressions in Eqs. (23).

4.1 Exact solution: triangular plate

Consider the case of an equilateral triangular shaped plate (see Fig. 3a) under a uniformly distributed load \(q\left( {x,y} \right) = q_{0}\) and with simply-supported edges. Applying the previously described procedure, that is solving the linear system in Eq. (40), the obtained non-null series coefficients of the deflection function Eq. (38) are

$$ \begin{gathered} c_{0} = \frac{{\left( {q_{0} \,l^{2} + 4\lambda q_{0} } \right)l^{2} }}{12D};\;c_{2} = \frac{{\left( {l^{2} + 3\lambda } \right)q_{0} \,}}{12D};\;c_{4} = \frac{{q_{0} }}{64D} \hfill \\ d_{3} = \frac{{ - \left( {q_{0} \,l^{2} - 4\lambda q_{0} } \right)}}{48\,l\,D};\;d_{5} = \frac{{q_{0} \,}}{192\,l\,D} \hfill \\ \end{gathered} $$
(52)
Fig. 3
figure 3

Geometrical dimensions: a triangular plate; b circular plate; c elliptical plate

Full size image

Substituting in Eq. (38) yields

$$ w\left( {x,y} \right) = \frac{{q_{0} }}{192\,l\,D}\left( {l - y} \right)\left[ {\left( {2l - y} \right)^{2} - 3x^{2} } \right]\left( {4l^{2} - x^{2} - y^{2} + 16\lambda } \right), $$
(53)

which is the exact solution of the considered problem, recently obtained in [22] following the procedure discussed in Sect. 2.2. Note also that, Eq. (53) yields the classical local solution [54] for \(\left( {\lambda = 0} \right)\), as expected.

4.2 Exact solution: circular plates

Consider next the case of a circular plate (Fig. 3b) of radius \(r\) under a uniformly distributed load \(q_{0}\). The equilibrium equations of axisymmetric bending of circular nanoplates in polar coordinates are [38]

$$ \left[ {\rho Q_{r} \left( \rho \right)} \right]\,^{^{\prime}} = \rho \,q_{0} , $$
(54.a)
$$ \rho Q_{r} \left( \rho \right) = - \left[ {\rho M_{r} \left( \rho \right)} \right]\,^{^{\prime}} + M_{\theta } \left( \rho \right), $$
(54.b)

where \(\rho\) is the radial coordinate, the prime \(\left( ^{\prime} \right)\) denotes \({{d\left( \cdot \right)} \mathord{\left/ {\vphantom {{d\left( \cdot \right)} {d\rho }}} \right. \kern-\nulldelimiterspace} {d\rho }}\), \(M_{r} \left( \rho \right)\) and \(M_{\theta } \left( \rho \right)\) are the radial and circumferential moments, respectively, while \(Q_{r} \left( \rho \right)\) is the transverse shear force. Further, the nonlocal bending moments in terms of deflections are given by

$$ M_{r} - \lambda \left( {M_{r} ^{\prime\prime} + \frac{1}{\rho }M_{r} ^{\prime}} \right) = - D\left( {w^{\prime\prime} + \frac{\nu }{\rho }w^{\prime}} \right), $$
(55.a)
$$ M_{\theta } - \lambda \left( {M_{\theta } ^{\prime\prime} + \frac{1}{\rho }M_{\theta } ^{\prime}} \right) = - D\left( {\nu w^{\prime\prime} + \frac{1}{\rho }w^{\prime}} \right). $$
(55.b)

As stated in [38], Eqs. (54) and (55) may be decoupled for the explicit expression of the bending moments and shear force, leading to

$$ M_{r} = - D\left( {w^{\prime\prime} + \frac{\nu }{\rho }w^{\prime}} \right) + \lambda q_{0} - \frac{\lambda D}{{2\rho^{3} }}\left[ {\rho^{4} \frac{{d^{5} w}}{{d\rho^{5} }} + 6\rho^{3} \frac{{d^{4} w}}{{d\rho^{4} }} + \left( {3 + 2\nu } \right)\rho^{2} \frac{{d^{3} w}}{{d\rho^{3} }} + \left( {1 - 2\nu } \right)\left( {\rho w^{\prime\prime} - w^{\prime}} \right)} \right] $$
(56.a)
$$ \begin{gathered} M_{\theta } = - D\left( {\nu w^{\prime\prime} + \frac{1}{\rho }w^{\prime}} \right) - \frac{D}{2\rho }\left[ {\rho^{3} \frac{{d^{4} w}}{{d\rho^{4} }} + 2\rho^{2} \frac{{d^{3} w}}{{d\rho^{3} }} - \rho w^{\prime\prime} + w^{\prime} - \frac{{q_{0} \rho^{3} }}{D}} \right] - 5\lambda q_{0} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{3\lambda D}{{2\rho^{3} }}\left[ {\rho^{4} \frac{{d^{5} w}}{{d\rho^{5} }} + 6\rho^{3} \frac{{d^{4} w}}{{d\rho^{4} }} + \left( {3 + 2\nu } \right)\rho^{2} \frac{{d^{3} w}}{{d\rho^{3} }} + \left( {1 - 2\nu } \right)\left( {\rho w^{\prime\prime} - w^{\prime}} \right)} \right], \hfill \\ \end{gathered} $$
(56.b)

and

$$ \begin{gathered} Q_{r} = D\left( {\frac{{d^{3} w}}{{d\rho^{3} }} + \frac{1}{\rho }w^{\prime\prime} + \frac{1}{{\rho^{2} }}w^{\prime}} \right) + \frac{{4\lambda q_{0} }}{\rho } \hfill \\ \,\,\,\,\,\,\, - \frac{\lambda D}{{\rho^{4} }}\left[ {\rho^{4} \frac{{d^{5} w}}{{d\rho^{5} }} + 6\rho^{3} \frac{{d^{4} w}}{{d\rho^{4} }} + \left( {3 + 2\nu } \right)\rho^{2} \frac{{d^{3} w}}{{d\rho^{3} }} + \left( {1 - 2\nu } \right)\left( {\rho w^{\prime\prime} - w^{\prime}} \right)} \right]. \hfill \\ \end{gathered} $$
(57)

Note that, moments and shear force equations reduce to those of the classical local plate when the nonlocal parameter \(\lambda\) is set to zero.

Consider now the circular plate to be clamped along the entire contour \(\left( {N_{\gamma } = 1} \right)\), with BCs given in Eq. (15). Using the following transformation of variable

$$ \left\{ \begin{gathered} x = \rho \cos \theta \hfill \\ y = \rho \sin \theta \hfill \\ \end{gathered} \right.,\quad 0 \le \theta \le 2\pi ,\,\,0 \le \rho \le r, $$
(58)

the plate boundary \(\Gamma\) can be defined by the parametric curve, specifying Eq. (58) for \(\rho = r\).

Since the boundary is curvilinear, the additional moment sum function \(\tilde{M}_{1} \left( {x,y} \right) \ne 0\) in Eq. (41) is necessary, while \(\tilde{w}_{1} \left( {x,y} \right)\) in Eq. (43) can be set to zero. In this manner, coefficients \(\left( {a_{k} ,\,b_{k} } \right)\) and \(\left( {c_{k} ,\,d_{k} } \right)\) are found using Eq. (45) and (46), respectively, in terms of the unknowns \(\left( {\tilde{a}_{k}^{\left( 1 \right)} ,\,\tilde{b}_{k}^{\left( 1 \right)} } \right)\). Finally, considering Eq. (47), these remaining coefficients can be obtained solving the linear system of equations in Eq. (50). This yields the exact closed-form solution of the deflection function on the nonlocal plate as

$$ w\left( {x,y} \right) = \frac{{q_{0} \left( {x^{2} + y^{2} - r^{2} } \right)^{2} }}{64\,D\,}, $$
(59)

obtained also in [39] following a different procedure. As it can be seen, this function is independent of the nonlocal parameter \(\lambda\), and it is equal to the solution of the classical local plate. Further, substituting Eq. (59) into Eqs. (56) and (57) gives the moments and shear force as

$$ M_{r} \left( \rho \right) = \frac{{q_{0} }}{16}\left[ {r^{2} \left( {1 + \nu } \right) - \left( {\rho^{2} + 4\lambda } \right)\left( {3 + \nu } \right)} \right], $$
(60.a)
$$ M_{\theta } \left( \rho \right) = \frac{{q_{0} }}{16}\left[ {r^{2} \left( {1 + \nu } \right) - \left( {\rho^{2} + 4\lambda } \right)\left( {1 + 3\nu } \right)} \right], $$
(60.b)
$$ Q_{r} \left( \rho \right) = \frac{{q_{0} }}{2\rho }\left[ {\rho^{2} + \lambda \left( {1 - \nu } \right)} \right], $$
(60.c)

where the dependence on the nonlocal parameter can be observed.

Notably, substituting Eqs. (59) and (60) into the equilibrium equations Eq. (55) and bending moment equations Eq. (56), these differential equations as well as the boundary conditions Eqs. (15) are satisfied. Also, Eqs. (60) reverts to the corresponding expression for the classical local plate for \(\left( {\lambda = 0} \right)\).

In passing, it should be mentioned that Eqs. (59–60) differ from the solution reported in [38], given as

$$ w\left( {x,y} \right) = \frac{{q_{0} \left( {x^{2} + y^{2} - r^{2} } \right)^{2} }}{{8\left( {7 + \nu } \right)\,D\,}}, $$
(61)

which is also independent on the nonlocal parameter, but does not yields the classical local solution, as it should, for \(\left( {\lambda = 0} \right)\).

Next, consider the circular plate simply-supported along the boundary, with BCs given in Eqs. (13). Thus, as in the previous case, \(\tilde{M}_{1} \left( {x,y} \right) \ne 0\) and \(\tilde{w}_{1} \left( {x,y} \right) = 0\). However, particular attention should be paid to appropriately take into account the BCs, due to the previously mentioned issue related to the definition of the BCs for nonlocal plates. Specifically, to allow for \(M_{n} \left( {x,y} \right)\) to be equal to zero, as in Eq. (13.b), the bending and twisting moments need to be expressed in terms of the deflection \(w\left( {x,y} \right)\). In this regard, approximate expressions in Eqs. (23) could be employed for generally shaped plates. However, in this case exact expressions in Eqs. (56.a) are available, and can be used to determine the exact solution of the deflection function.

Specifically, following the previously described procedure, coefficients \(\left( {a_{k} ,\,b_{k} } \right)\) and \(\left( {c_{k} ,\,d_{k} } \right)\) are found using Eq. (45) and (46), respectively, in terms of the unknowns \(\left( {\tilde{a}_{k}^{\left( 1 \right)} ,\,\tilde{b}_{k}^{\left( 1 \right)} } \right)\) in Eq. (42). Clearly, \(w\left( {x,y} \right)\) now depends only on the coefficients \(\left( {\tilde{a}_{k}^{\left( 1 \right)} ,\,\tilde{b}_{k}^{\left( 1 \right)} } \right)\). Finally, taking into account Eqs. (60), the normal bending \(M_{n} \left( {x,y} \right)\) can be determined considering that, for the circular plate, \(M_{n} \left( {x,y} \right) = M_{r} \left( {x,y} \right)\), where \(M_{r} \left( {x,y} \right)\) is obtained combining Eqs. (58) and (60). In this manner, the coefficients \(\left( {\tilde{a}_{k}^{\left( 1 \right)} ,\,\tilde{b}_{k}^{\left( 1 \right)} } \right)\) are found solving the linear system of equations in Eq. (50). Thus, the exact closed-form solution of the deflection function of the nonlocal simply-supported circular plate can be found as

$$ w\left( {x,y} \right) = \frac{{q_{0} \left( {r^{2} - x^{2} - y^{2} } \right)\left[ { - \left( {x^{2} + y^{2} } \right)\left( {1 + \nu } \right) + r^{2} \left( {5 + \nu } \right) + 8\lambda \left( {3 + \nu } \right)} \right]}}{64\,D\,(1 + \nu )}. $$
(62)

As it can be seen, this function corresponds to the solution reported in [39], and it depends on the nonlocal parameter \(\lambda\). Further, substituting Eq. (62) into Eqs. (56) and (57) gives the moments and shear force as

$$ M_{r} \left( \rho \right) = \frac{{q_{0} \left( {3 + \nu } \right)}}{16}\left( {r^{2} - \rho^{2} } \right), $$
(63.a)
$$ M_{\theta } \left( \rho \right) = \frac{{q_{0} }}{16}\left[ {r^{2} \left( {3 + \nu } \right) - \rho \left( {1 + 3\nu } \right) - 8\lambda \left( {\nu - 1} \right)} \right], $$
(63.b)
$$ Q_{r} \left( \rho \right) = \frac{{q_{0} }}{2\rho }\left[ {\rho^{2} + \lambda \left( {1 - \nu } \right)} \right]. $$
(63.c)

Note that, substituting Eqs. (62) and (63) into Eqs. (55) and (56), equilibrium equations, bending moment equations, as well as the boundary conditions Eqs. (13) are satisfied. Also, Eqs. (62–63) reverts to the corresponding expression for the classical local plate for \(\left( {\lambda = 0} \right)\). Again, it should be mentioned that Eq. (62) differs from the solution reported in [38], given as

$$ w\left( {x,y} \right) = \frac{{q_{0} \left( {r^{2} - x^{2} - y^{2} } \right)}}{{8\left( {7 + \nu } \right)D}}\left[ {\frac{5 + \nu }{{1 + \nu }}r^{2} - x^{2} - y^{2} + \frac{{4\left( {7 + \nu } \right)}}{1 + \nu }\lambda } \right], $$
(64)

which does not yield the classical local solution, as it should, for \(\left( {\lambda = 0} \right)\).

It is also worth mentioning that a different solution would have been found if Eqs. (23) had been used instead of Eqs. (56) in the proposed procedure, since as discussed Eqs. (23) are approximate.

4.3 Exact solution: elliptical plate

Consider the case of a clamped elliptical plate (Fig. 3c) of axes \(a\) and \(b\), with BCs specified in Eq. (15), under a uniformly distributed load \(q_{0}\). Using the following transformation of variable

$$ \left\{ \begin{gathered} x = a\rho \cos \theta \hfill \\ y = b\rho \sin \theta \hfill \\ \end{gathered} \right.,\quad 0 \le \theta \le 2\pi ,\,\,0 \le \rho \le 1, $$
(65)

the plate boundary \(\Gamma\) can be defined by the parametric curve specifying Eq. (65) for \(\rho = 1\).

As in the previous case, taking into account the BCs and the plate shape, \(N_{\gamma } = 1\), \(\tilde{M}_{1} \left( {x,y} \right) \ne 0\) and \(\tilde{w}_{1} \left( {x,y} \right) = 0\). Following the previously described procedure, coefficients \(\left( {a_{k} ,\,b_{k} } \right)\) and \(\left( {c_{k} ,\,d_{k} } \right)\) are found using Eq. (45) and (46), respectively, in terms of the unknowns \(\left( {\tilde{a}_{k}^{\left( 1 \right)} ,\,\tilde{b}_{k}^{\left( 1 \right)} } \right)\). Finally, considering Eq. (47), these remaining coefficients can be obtained solving the linear system of equation in Eq. (50). This yields the deflection function as

$$ w\left( {x,y} \right) = \frac{{q_{0} \left[ {b^{2} x^{2} + a^{2} \left( { - b^{2} + y^{2} } \right)} \right]^{2} }}{{8\left( {3a^{4} + 2a^{2} b^{2} + 3b^{4} } \right)D}}. $$
(66)

Note that, since Eq. (66) satisfies Eq. (7) and the boundary conditions, it represents the exact closed-form solution of the elliptical clamped nonlocal plate under a uniform load. As in the analogous case of the circular clamped plate in Eq. (59), Eq. (66) is independent on the nonlocal parameter and correspond to the classical local solution. Note that, to the best of authors’ knowledge, this solution has never been reported in the literature so far.

In addition, approximate expressions of the bending and twisting moments can be obtained from Eq. (66) employing Eqs. (23), leading to

$$ M_{x} \left( {x,y} \right) = 4D\,w_{0} \left[ {M_{x}^{\left( K \right)} \left( {x,y} \right) - \frac{2\lambda }{{a^{4} b^{4} }}\left[ {3b^{4} + 3\nu a^{4} + a^{2} b^{2} \left( {1 + \nu } \right)} \right]} \right], $$
(67.a)
$$ M_{y} \left( {x,y} \right) = 4D\,w_{0} \left[ {M_{y}^{\left( K \right)} \left( {x,y} \right) - \frac{2\lambda }{{a^{4} b^{4} }}\left[ {3a^{4} + 3\nu b^{4} + a^{2} b^{2} \left( {1 + \nu } \right)} \right]} \right], $$
(67.b)
$$ M_{xy} \left( {x,y} \right) = 4D\,w_{0} \frac{{2xy\left( {\nu - 1} \right)}}{{a^{4} b^{4} }}, $$
(67.c)

where \(w_{0}\) is the value of the deflection at the center of the plate, that is \(w_{0} = w\left( {0,0} \right)\). Further, \(M_{x}^{\left( K \right)} \left( {x,y} \right)\) and \(M_{y}^{\left( K \right)} \left( {x,y} \right)\) are the bending moments of the pertinent classical (local) Kirchhoff model, given as [54]

$$ M_{x}^{\left( K \right)} \left( {x,y} \right) = \frac{{4D\,w_{0} }}{{a^{4} b^{4} }}\left[ {\nu a^{4} \left( {b^{2} - 3y^{2} } \right) - 3b^{4} x^{2} + a^{2} b^{2} \left( {b^{2} - y^{2} - \nu x^{2} } \right)} \right], $$
(68.a)
$$ M_{y}^{\left( K \right)} \left( {x,y} \right) = \frac{{4D\,w_{0} }}{{a^{4} b^{4} }}\left[ {a^{4} \left( {b^{2} - 3y^{2} } \right) - 3\nu b^{4} x^{2} + a^{2} b^{2} \left( {\nu b^{2} - x^{2} - \nu y^{2} } \right)} \right]. $$
(68.b)

where the apex \(\left( K \right)\) refers to the classical local Kirchhoff model.

Clearly, values of the normal bending moment \(M_{n} \left( {x,y} \right)\) and twisting moment \(M_{nt} \left( {x,y} \right)\) can be readily found substituting Eqs. (68) into Eqs. (14) and (17), respectively.

4.4 Numerical application: rectangular plate

As a final example, consider the case of a rectangular plate of length \(a\) and width \(b\), with all edges simply-supported (see Fig. 4a). Material properties are \(E = 210\,{\text{GPa}}\) and \(\nu = 0.3\). Further, two different loading distributions are considered, namely a uniformly distributed load \(q_{0}\), and a sinusoidal load given by

$$ q\left( {x,y} \right) = q_{0} \sin \left( {\frac{x}{a}\pi } \right)\sin \left( {\frac{y}{b}\pi } \right), $$
(69)

which can be recast in the form of Eq. (33) expanding in Taylor series Eq. (69) (here 8 terms in \(x\) and \(y\) are used). Note that, for these cases analytical solutions have been previously obtained using Navier’s approach in [26].

Fig. 4
figure 4

Rectangular plates: a simply-supported; b clamped; c two sides clamped and two simply supported

Full size image

Following the procedure in Sect. 3.1, approximate analytical expression of the deflection function can be determined. In this regard, introduce the non-dimensional deflection as

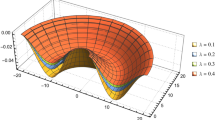
$$ \hat{w}\left( {x,y} \right) = \frac{{w\left( {x,y} \right)D}}{{q_{0} a^{4} }}. $$
(70)

Pertinent profiles are shown in Fig. 5, for several values of the nonlocal parameter \(\lambda\), assuming \(a = b = 10h\) and \(h = 0.5\,\upmu {\text{m}}\). Further, comparison with analytical solution in [26, 41] is also reported. Note that in these examples the number of terms in Eq. (38) has been set to 14 for both the uniform and sinusoidal load distributions.

Fig. 5
figure 5

Profiles of \(\tilde{w}\left( {x,y} \right)\) for \(y = 0\) (simply-supported plate): a uniform load; b sinusoidal load

Full size image

As it can be seen, an excellent agreement is achieved between analytical solution and proposed LEM approach, assessing the accuracy of the considered procedure.

Further, analogous analyses have been performed considering the case of the aforementioned rectangular plate, with all edges clamped (Fig. 4b). In this case, the general procedure in Sect. 3.2 should be followed setting \(N_{\gamma } = 1\), \(\tilde{M}_{1} \left( {x,y} \right) \ne 0\) and \(\tilde{w}_{1} \left( {x,y} \right) = 0\). In this regard, pertinent profiles of the non-dimensional deflection Eq. (70) are shown in Fig. 6 for several values of the nonlocal parameter \(\lambda\), assuming \(a = b = 10h\) and \(h = 0.5\,\upmu {\text{m}}\). Analyses have been carried out using 14 terms in Eq. (38). Further, comparison with pertinent Finite Element (FE) data is also reported. Note that, FE analyses have been performed directly solving Eq. (7) with BCs in Eq. (15), using the PDE numerical solver toolbox in MATLAB environment, and considering as mesh size \({a \mathord{\left/ {\vphantom {a {100}}} \right. \kern-\nulldelimiterspace} {100}}\).

Fig. 6
figure 6

Profiles of \(\hat{w}\left( {x,y} \right)\) for \(y = 0\) (clamped plate): a uniform load; b sinusoidal load

Full size image

As it can be seen, excellent agreement has been achieved between proposed method data and FE results. Notably, the non-dimensional deflection function is independent on the nonlocal parameter for the clamped plate under a uniform load, as for the other plate shapes. This is due to the BCs and the constant load, since the term \(\lambda \nabla^{2} q\left( {x,y} \right)\) in Eq. (7) would be zero. On the other hand, when the sinusoidal load is used, \(\hat{w}\left( {x,y} \right)\) changes with \(\lambda\).

As a final example, consider the case of a rectangular plate, under a uniformly distributed load \(q_{0}\), with two opposite edges clamped and the other two simply-supported (Fig. 4c). In this regard, applying the procedure in Sect. 3.2, the plate boundary is divided into four edges \(\Gamma_{i}\), so that \(N_{\gamma } = 4\). Note that, since the two edges \(\Gamma_{1}\) and \(\Gamma_{2}\) are simply-supported, the corresponding functions \(\tilde{M}_{2} \left( {x,y} \right)\) and \(\tilde{M}_{4} \left( {x,y} \right)\) in Eq. (41) are equal to zero. Thus, only the two functions \(\tilde{M}_{1} \left( {x,y} \right)\) and \(\tilde{M}_{3} \left( {x,y} \right)\) must be considered for the two clamped edges. Further, since no edge can undergo vertical deflections, \(\tilde{w}_{i} \left( {x,y} \right) = 0,\quad i = 1, \ldots ,4\). For this numerical example, properties are taken from [32], that is \(E = 70\,{\text{GPa}}\), \(\nu = 0.35\), and \(a = b = 12h\). Further, 14 coefficients have been used in the expansion in Eq. (38).

In this regard, Fig. 7 shows the maximum non-dimensional deflection for different values of the nonlocal parameter. Specifically, proposed method results vis-à-vis those in [32] are reported. Note however that data in [32] have been obtained applying a FE procedure considering the first-order shear deformation theory of plate, while in this paper the classical Kirchhoff model has been assumed. Thus, the small discrepancies shown in Fig. 7 are due to the different model employed. However, this comparison may give an additional assessment of the correctness of the LEM-based results. In fact, note that a good degree of accuracy is achieved despite the different models employed, further assessing the reliability of the proposed procedure.

Fig. 7
figure 7

Maximum values of \(\hat{w}\left( {x,y} \right)\) for several values of nonlocal parameter

Full size image

5 Concluding remarks

In this paper, the so-called Line Element-Less Method (LEM) has been appropriately extended for determining the static response of micro and nano plates endowed with arbitrary shape. Specifically, the classical Kirchhoff plate model has been assumed, employing the well-known Eringen’s nonlocal elasticity theory to capture small length scale effects. The method is based on an expansion of the deflection function in terms of harmonic polynomials, whose expansion coefficients can be easily found solving a linear system of algebraic equations. Notably, this system is determined by performing variations on appropriately introduced functionals that take into account the plate boundary conditions (BCs). In this regard, the entire procedure proves to be entirely mesh-free, since it only requires the definition of simple line integrals and, unlike classical Finite Element or Boundary Element procedures, any mesh or discretization is avoided. Further, the proposed approach yields approximate analytical solutions for general plate shapes and BCs, which clearly represents an attractive feature of the LEM. Note also that, in this manner exact closed form solutions of the deflection functions of nonlocal plates have been found. In this regard, exact solutions have been determined for the nonlocal triangular simply-supported plate, circular simply-supported and clamped plate, and elliptical clamped plate, the latter representing an additional novel contribution of the paper. Further analyses have been carried out also for rectangular nonlocal plates, to show the applicability of the procedure in case of different loading distributions and mixed BCs. In all these examples, comparisons of LEM based results vis-à-vis pertinent data available in the literature have been reported, assessing the accuracy an reliability of the proposed approach.