A note on non-symmetric flow: surface shrinking in mutually orthogonal directions

Abstract

In this note, we extend the problem treated in (Lok, Math Modelling Anal 24:617–634 (2019)) to the case of permeable surface which is shrinking in mutually orthogonal directions. Both numerical and asymptotic solutions are obtained for two important governing parameters, $\gamma$ the shrinking rate and S characterizing the fluid transfer through the boundary. In this problem, a restriction on S is required for a solution to exist. This contrasts with the problem in (Lok, Math Modelling Anal 24:617–634 (2019)) where no restriction on S is needed. Numerical solutions show that for a fixed value of S, two critical points $\gamma _c$ are observed for $S > 2$. Conversely, two critical points $S_c$ are found for a given value of $\gamma$ when $S > 2$. A discussion on the nonexistence of solution for $S = 2$ is given and asymptotic solutions for S large and $(S-2)$ small are also presented.

1 Introduction

In a previous paper [1] we considered the non-symmetric flow over a moving surface in an otherwise quiescent fluid. We assumed that the surface was stretching in one direction and could be either stretching or shrinking in a direction mutually perpendicular to it. Here consider the same set up but now examine the case not treated in [1] whereby the surface is shrinking in both directions, in effect completing the discussion given in [1]. The basic model for this problem as well as the motivation for studying it is described fully in [1]. Here we take for the surface velocity $(u_w,v_w,w_w)$

$$\begin{aligned} u_w&=-\overline{A}\,x, \quad v_w=-\overline{B}\,y \quad \text{ where } \nonumber \\ \overline{A}&>0, \ \overline{B}\ge 0, \quad w_w=W_0, \end{aligned}$$

(1)

for constants $\overline{A}, \, \overline{B}$ and $W_0$ and put, following [1],

$$\begin{aligned} u&=\overline{A}\,x\,f'(\eta ), \ \ v=\overline{B}\,y\,g'(\eta ), \nonumber \\ w&=-\bigl (\overline{A}\,f(\eta )+\overline{B}\,g(\eta )\bigr )\left( \nu /\overline{A}\,\right) ^{\! 1/2}, \ \nonumber \\ \eta&= z\left( \overline{A}/\nu \right) ^{\! 1/2}. \end{aligned}$$

(2)

This gives

$$\begin{aligned}&f'''+f\,f''-f'^{\,2}+\gamma \,g\,f''=0, \end{aligned}$$

(3)

$$\begin{aligned}&g'''+\gamma \,(g\,g''-g'^{\, 2})+f\,g''=0, \end{aligned}$$

(4)

where primes denote differentiation with respect to $\eta$ and $\gamma =\overline{B}/\overline{A}$, where $\gamma \ge 0$. The boundary conditions are, for this case,

$$\begin{aligned}&f(0)+\gamma \,g(0)=S, \ \ f'(0)=-1, \ \ g'(0)=-1, \nonumber \\&f' \rightarrow 0, \ \ g' \rightarrow 0 \ \text{ as } \ \eta \rightarrow \infty , \end{aligned}$$

(5)

where $\displaystyle S=-\frac{W_0}{\sqrt{\nu \,\overline{A}}}$.

Following directly from [1] and exploiting the symmetry inherent in the problem, we can modify boundary condition (5) to

$$\begin{aligned} f(0)=S, \ \ \ g(0)=0. \end{aligned}$$

(6)

To see why this is possible we assume that $f(0)=a_0, \, g(0)=b_0$ for constants $a_0, b_0$. Boundary condition (5) gives $a_0+\gamma \,b_0=S$. We then put $f=a_0-S+\tilde{f}, \, g=b_0+\tilde{g}$, with Eqs. (3, 4) giving

$$\begin{aligned}&\tilde{f}'''+\tilde{f}\,\tilde{f}''-\tilde{f}'^{\,2}+\gamma \,\tilde{g}\,\tilde{f}'' +(a_0+\gamma \,b_0-S)\,\tilde{f}''=0, \end{aligned}$$

(7)

$$\begin{aligned}&\tilde{g}'''+\gamma \,(\tilde{g}\,\tilde{g}''-\tilde{g}'^{\, 2})+\tilde{f}\,\tilde{g}''+(a_0+\gamma \,b_0-S)\tilde{g}''=0, \end{aligned}$$

(8)

from which we recover Eqs. (3, 4) with $\tilde{f}(0)=S, \, \tilde{g}(0)=0$.

We start by considering the case when $\gamma =0$.

2 Solution when $\gamma =0$

When $\gamma =0$, Eq. (3) has a solution in the form

$$\begin{aligned} f(\eta )=c+\frac{1}{c}\,\text{ e}^{-c\,\eta } \ \ \text{ for } \text{ some } \ c>0. \end{aligned}$$

(9)

The boundary condition on $\eta =0$ then gives

$$\begin{aligned} c+\frac{1}{c}=S \ \ \ \text{ giving } \ \ \ c=\frac{S\pm \sqrt{S^2-4}}{2}. \end{aligned}$$

(10)

Expression (10) requires that $S>0$ to have $c>0$ and further that $S \ge 2$. Since $f''(0)=c$ there are for $S>2$ two solutions with

$$\begin{aligned} f''(0)&=\frac{S+\sqrt{S^2-4}}{2} \ \ \ \text{ and } \nonumber \\ f''(0)&=\frac{S-\sqrt{S^2-4}}{2}. \end{aligned}$$

(11)

Expression (9) gives, from Eq. (4),

$$\begin{aligned} g'&=\frac{1}{(\text{ e}^{1/c^2}-1)}\,\biggl (1-\text{ exp }(\frac{\text{ e}^{-c\,\eta }}{c^2}) \biggr ) \ \ \ \text{ giving } \nonumber \\ g''(0)&=\frac{\text{ e}^{1/c^2}}{c(\text{ e}^{1/c^2}-1)}, \end{aligned}$$

(12)

where c is given in (10).

Previously in [1] there was no restriction on the wall mass transfer parameter S though the corresponding solution for $\gamma =0$ gave only one solution. Here the boundary condition on $f'$ is changed from $f'(0)=1$ in [1] to $f'(0)=-1$. This change puts a restriction on S, namely requiring $S \ge 2$, to have a solution though it does provide two possible solutions. For $S<0$, Eq. (10) gives $c<0$ and so solution (9) no longer holds. We also note in passing that we were unable to find any numerical solutions for $\gamma >0$ with $S<0$ With this in mind we now treat only the case when $S>0$, i.e. only suction through the surface.

3 Numerical solutions

In Fig. 1 we plot $f''(0)$ and $g''(0)$ against $\gamma$ for $S=4.0$, obtained from the numerical solution of Eqs. (3, 4, 5, 6). Expressions (11, 12) give respectively 3.73205 and 0.26795 for $f''(0)$ and 3.86763 and 3.73205 for $g''(0)$ at $\gamma =0$. These two sets of values at $\gamma =0$ give rise to two separate sections for the solution which appear to remain separate in $\gamma >0$. The section of solution associated with the larger value of $f''(0)$ at $\gamma =0$ has a critical point at $\gamma =\gamma _c\simeq 3.3780$ limiting its range of existence to $0\le \gamma \le \gamma _c$. On the lower branch of this section of solutions the values of $f''(0)$ loop back towards $\gamma =0$ with $f''(0)$ approaching a finite value, possibly its original value at $\gamma =0$. The values of $g''(0)$ on the lower branch emerging from the critical point initially appear to be tending towards a finite value at $\gamma =0$. However, at about $\gamma =1$ they diverge rapidly from this, becoming negative and increasingly larger in magnitude, appearing to becoming infinite as $\gamma \rightarrow 0$.

Fig. 1

Plots of (a) $f''(0)$ and (b) $g''(0)$ against $\gamma$ for $S=4.0$ obtained from the numerical solution of Eqs. (3, 4, 5, 6)

Fig. 2

Plot of $f''(0)$ against S for $\gamma =1.0$ obtained from the numerical solution of Eqs. (3, 4, 5, 6). For this value of $\gamma$, $g''(0)=f''(0)$. Asymptotic expressions (20) are shown by broken lines

The section of solution with the smaller value of $f''(0)$ at $\gamma =0$ has a critical point at $\gamma _c\simeq 2.9748$ with $f''(0)$ increasing and $g''(0)$ decreasing on its lower branch. The upper solution branch of this section, as seen in Fig. 1a, terminates at $\gamma \simeq 2.12$. From the outer boundary conditions on $f'$ and $g'$, $f \rightarrow f_\infty$ and $g \rightarrow g_\infty$ through exponentially small terms as $\eta \rightarrow \infty$. For $\eta$ large Eqs. (3, 4) then become approximately

$$\begin{aligned} f'''+(f_\infty +\gamma \,g_\infty )f''=0, \quad \ \ g'''+(f_\infty +\gamma \,g_\infty )g''=0, \end{aligned}$$

(13)

requiring $a_0\equiv (f_\infty +\gamma \,g_\infty )>0$. On the upper branch we find that $g_\infty <0$ and that the solution terminates as $a_0 \rightarrow 0$ at $\gamma \simeq 2.12$.

In Fig. 2 we plot $f''(0)$ against S for $\gamma =1.0$. For this value of $\gamma$, $f=S+g$ so that $g''(0)=f''(0)$. Again we see the existence of two critical points at $S=S_{c,1} \simeq 2.6235$ and $S_{c,2} \simeq 2.8144$ with solutions existing only in $S \ge S_{c,1}$. Two solution branches emerge from the larger critical point $S_{c,2}$, the upper branch proceeds to large S with $f''(0)>0$ and increasing, apparently linearly. The lower branch also proceeds to large S but now has $f''(0)<0$. The upper branch arising at the smaller critical value $S_{c,1}$ again proceeds to large S, parallel with the previous upper solution for larger S. The lower branch terminates at a finite value $S\simeq 2.848$, as seen in Fig. 2, where $(f_\infty +\gamma \,g_\infty )$ goes to zero.

Fig. 3

Plots of (a) $f''(0)$ and (b) $g''(0)$ against S for $\gamma =2.0$ obtained from the numerical solution of Eqs. (3, 4, 5, 6). Asymptotic expressions (20) are shown by broken lines

Fig. 4

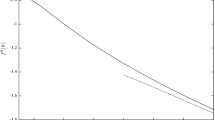
Critical values: plots of $\gamma _c$ against S. Asymptotic expression (34) for $(S-2)$ small is shown by a broken line

We also consider the case when $\gamma =2$, with plots of $f''(0)$ and $g''(0)$ against S being shown in Fig. 3. In this case $f''(0)$ and $g''(0)$ are different as can be seen in the figure. There are again two critical points, now at $S_{c,1} \simeq 3.2547$ and at $S_{c,2} \simeq 3.4805$. Both solution branches emerging from the smaller critical point $S_{c,1}$ continue to large S, both with $f''(0)$ and $g''(0)$ positive. The upper solution branch, as seen in Fig. 3a, emerging from the larger critical point $S_{c,2}$ terminates at finite values of S, $S \simeq 3.893$, where, as noted previously, $(f_\infty +\gamma \,g_\infty )$ goes to zero. On the lower solution branch $g''(0)>0$ and appears to be increasing linearly with S. On this branch $f''(0)$ decreases, becomes negative at $S \simeq 4.775$ and decreases rapidly as S is increased further.

We can calculate the critical points $\gamma _c$ for a given S seen in Figs. 1, 2 and 3 numerically using the approach described in [2, 3], for example. The results are shown in Fig. 4 with a plot of $\gamma _c$ against S. This plot shows two almost parallel curves giving two critical points for a given value of $S>2$ or conversely two critical values $S_c$ of S for a given value of $\gamma$, as seen in the figures. On both curves $\gamma _c$ increases as S is increased. This figure shows the region where solutions can exist in the $\gamma -S$ space and the region where no solutions are possible as indicated on the figure.

3.1 Solution for S large

Expressions (10, 11) give, for S large and $\gamma =0$,

$$\begin{aligned}&c \sim S-S^{-1}+\cdots , \quad \ \text{ giving } \nonumber \\&f''(0) \sim S+\cdots \ \ g''(0) \sim S^{-1}+\cdots , \end{aligned}$$

(14)

on taking the $+$ sign for the upper branch solutions, as seen in Figs. 2 and 3. This leads us to put, on following [1],

$$\begin{aligned} f=S+S^{-1}\,F, \ \ \ g=S^{-1}\,G, \ \ \ Y=S\,\eta , \end{aligned}$$

(15)

with Eqs. (3, 4) becoming

$$\begin{aligned}&F'''+F''+S^{-2}(F\,F''-F'^2+\gamma \,G\,F'')=0, \nonumber \\&G'''+G''+S^{-2}\bigl (\gamma (G\,G''-G'^2)+F\,G''\bigr )=0, \end{aligned}$$

(16)

subject to

$$\begin{aligned} F(0)=0, \ \ F'(0)=-1, \ \ G(0)=0, \ \ G'(0)=-1, \ \ \ F', G' \rightarrow 0 \ \text{ as } \ Y \rightarrow \infty , \end{aligned}$$

(17)

where primes now denote differentiation with respect to Y.

Equations (16) suggest an expansion of the form

$$\begin{aligned} F(Y;S)&=F_0(Y)+S^{-2}\,F_1(Y)+\cdots , \nonumber \\ G(Y;S)&=G_0(Y)+S^{-2}\,G_1(Y)+\cdots , \end{aligned}$$

(18)

where we find $F_0=G_0=\text{ e}^{-Y}-1$ and

$$\begin{aligned} F_1&=-\left( \frac{4+3\,\gamma }{4}\right) +\left( \frac{\gamma +2}{2}\right) \text{ e}^{-Y}+(\gamma +1)\,Y\,\text{ e}^{-Y} \nonumber \\&\qquad +\frac{\gamma }{4}\,\text{ e}^{-2Y},\nonumber \\ G_1&= -\left( \frac{4\,\gamma +3}{4}\right) +\left( \frac{2\,\gamma +1}{2}\right) \text{ e}^{-Y}+(\gamma +1)\,Y\,\text{ e}^{-Y} \nonumber \\&\qquad +\frac{1}{4}\,\text{ e}^{-2Y}, \end{aligned}$$

(19)

from which it follows that

$$\begin{aligned}&f''(0) \sim S-\frac{\gamma +2}{2}\,S^{-1}+\cdots , \nonumber \\&g''(0)\sim S- \frac{2\,\gamma +1}{2}\,S^{-1}\cdots \ \text{ as } \ S \rightarrow \infty . \end{aligned}$$

(20)

Asymptotic expressions (20) hold for the upper solution branch and are shown in Figs. 2 and 3 by broken lines giving very good agreement with the numerically determined values. Here we are concerned only with the upper branch solution as this solution is more physical realizable and, from previous studies of related problems, we expect this to be the temporally stable solution.

This analysis, as in [1], requires $\gamma \ll S^2$ and when $\gamma$ is large, of $O(S^2)$, we put $\gamma =S^2\,\mu$. Equations (3 – 5) become at leading order, on applying the transformation (15),

$$\begin{aligned} F'''+F''+\mu \,G\,F''=0,\ \quad \ G'''+G''+\mu (G\,G''-G'^2)=0, \end{aligned}$$

(21)

still subject to boundary conditions (17). Equation (21) has the solution

$G=-b^{-1}(1-\text{ e}^{-b\,Y})$ for some $b>0$ to be found. Applying this solution in (21) gives

$$\begin{aligned} b^2-b+\mu =0 \ \ \text{ giving } \ \ b=\frac{1\pm \sqrt{1-4\mu }}{2} \ \text{ and } \ G''(0)=b. \end{aligned}$$

(22)

Expression (22) requires $\mu \le 1/4$ giving a critical value of $\mu _c=1/4$ and hence

$$\begin{aligned} \gamma _c \sim \frac{S^2}{4}\cdots \quad \text{ as } \ S \rightarrow \infty . \end{aligned}$$

(23)

In table 1 we compare the values of $\gamma _c$ calculated numerically with those given by expression (23) for representative values of S. We see that there is reasonable agreement between the two sets of results. Further examination of these results by considering the differences between the numerical and asymptotic values shows this difference changes only slightly as S is increased, from approximately 0.62 for $S=4$ to approximately 0.58 for $S=13$. This suggests that the correction to (23) is of O(1), as is also apparent from the asymptotic form of the Eq. (16).

Table 1 A comparison between the numerically determined values of $\gamma _c$ on the upper curve in Fig. 4 and the asymptotic expression (23)

We can then solve equation for F to obtain

$$\begin{aligned} F'&=\frac{1-\text{ exp }\,(\mu \,\text{ e}^{-bY}/b^2)}{\text{ e}^{\mu /b^2}-1} \ \ \text{ giving } \nonumber \\ F''(0)&= \frac{\mu \,\text{ e}^{\mu /b^2}}{b(\text{ e}^{\mu /b^2}-1)}, \end{aligned}$$

(24)

where b is given by (22). From expression (22), $b \rightarrow 1$ and $b \sim \mu$ as $\mu \rightarrow 0$ so that $F''(0) \rightarrow 1$ for both cases and $G''(0) \rightarrow 1$ and $G''(0) \sim \mu$.

3.2 Singularity at $S=2$

Our numerical integrations of Eqs. (3, 4, 6) indicate that there are no solutions in $\gamma >0$ when $S=2$. To investigate this we look for a solution to these equations for small $\gamma$, assuming for the present that $\gamma >0$. An expansion in powers of $\gamma$ is suggested by the equations. However, we find that we cannot solve the equations at $O(\gamma )$ since these have a complimentary function that satisfies homogeneous boundary conditions. To get over this difficulty we modify our expansion to

$$\begin{aligned} f(\eta ;\gamma )&=f_0(\eta )+\gamma ^{1/2}\,f_1(\eta )+\gamma \,f_2(\eta )+\cdots , \nonumber \\ g(\eta ;\gamma )&=g_0(\eta )+\gamma ^{1/2}\,g_1(\eta )+\gamma \,g_2(\eta )+\cdots . \end{aligned}$$

(25)

At leading order we have, from (9 – 12), for $S=2$

$$\begin{aligned} f_0&=1+\text{ e}^{-\eta }, \nonumber \\ g_0'&=\frac{1}{e-1}\,\biggl (1-\text{ e}^{e^{-\eta }}\biggr ). \end{aligned}$$

(26)

The equations at $O(\gamma ^{1/2})$ are homogeneous and have the solution

$$\begin{aligned} f_1&=A_1\bigl ((\eta +2)\,f_0'+f_0\bigr ), \nonumber \\ g_1&=A_1(\eta \,g_0'-g_0), \end{aligned}$$

(27)

satisfying $f_1(0)=f_1'(0)=g_1(0)=g_1'(0)=0$ and the outer boundary condition for some constant $A_1$.

At $O(\gamma )$ we then have

$$\begin{aligned}&f_2''' + f_0\,f_2''-2\,f_0'\,f_2'+f_0''\, f_1 = -g_0\, f_0'' \nonumber \\&\qquad -A_1^2\big [(\bigl (\eta +2)f_0'+f_0\bigr ) \bigl ((\eta +2)f_0'''+3f_0'') \nonumber \\&\qquad -\bigl ((\eta +2)f_0''+2f_0'\bigr )^2\big ], \end{aligned}$$

(28)

$$\begin{aligned}&g_2'''+f_0\,g_2''+f_2\,g_0'' \nonumber \\&\quad =-A_1^2\,\bigl [(\eta \,g_0'''+g_1'') (\eta (g_0'+f_0')-g_0+f_0)-\eta ^2\,g_0''^{\,2})\bigr ], \end{aligned}$$

(29)

subject to

$$\begin{aligned} f_2(0)=f_2'(0)=g_2(0)=g_2'(0)=0, \quad \ f_2', \,g_2' \rightarrow 0 \ \text{ as } \ \eta \rightarrow \infty . \end{aligned}$$

(30)

We construct a solution to Eq. (28) in the form

$$\begin{aligned} f_2=f_a+A_1^2\, f_b, \end{aligned}$$

(31)

where $f_a$ satisfies Eq. (28) with the terms in $A_1^2$ put to zero and $f_b$ with the first term on the right-hand side omitted and with $A_1^2=1$. In both cases, because of the complementary function (27), we can put $f_a''(0)=f_b''(0)=0$. An examination of Eq. (28) shows that $f_i' \rightarrow C_i, \, (i=a,b)$, where $C_i$ is a constant. Numerical integrations give $C_a=0.214097$, $C_b=0.367879$. Hence to satisfy the outer boundary condition we require $C_a+A_1^2\,C_b=0$. This leads to having $A_1^2<0$ and a contradiction. At this point we note that, without the term in $A_1^2$, we would be unable to satisfy the outer boundary conditions.

To resolve this difficulty we now assume that $\gamma <0$ and expand in $(-\gamma )^{1/2}$. The problems at leading order and at $O((-\gamma )^{1/2})$ are the same. At $O(-\gamma )$ it leads to a change of sign for the first term on the right-hand side of Eq. (28) and a consequent change in sign for $C_a$. The outer boundary condition now gives $A_1^2=-C_a/C_b$ and then $A_1\simeq \pm 0.76283$. Hence

$$\begin{aligned}&f''(0) \sim 1 \pm 0.76283\, (-\gamma )^{1/2}+\cdots , \nonumber \\&g''(0) \sim 1.58198( 1 \pm 0.76283\, (-\gamma )^{1/2}+\cdots ) \nonumber \\&\qquad \text{ as } \ \gamma \rightarrow 0, (\gamma <0). \end{aligned}$$

(32)

Expression (32) shows the singular nature of the solution and the critical values as $\gamma \rightarrow 0$ when $S=2$. It also explains why we were unable to find any numerical solutions in $\gamma >0$ for $S=2$. The solution at $O(\gamma ^{-1})$ is not fully defined at this stage as any multiple of the complementary function (27) can be added to (31).

3.3 $(S-2)$ small

To discuss the case when $(S-2)$ is small we again assume that $\gamma >0$ and we modify the above analysis to the case when $(S-2)$ is small by writing $S=2+\lambda \,\gamma$, ($\lambda >0)$. This results in looking for a solution to (28) in the form

$$\begin{aligned} f_2=f_a+A_1^2\, f_b + \lambda \,f_c, \end{aligned}$$

(33)

where $f_c$ satisfies Eq. (28) with the right-hand side put to zero and with $f_c(0)=1$. As before, $f_c'\rightarrow C_c$ as $\eta \rightarrow \infty$ where $C_c=-0.367879$. Satisfying the outer boundary condition gives $C_a+A_1^2\,C_b+\lambda \,C_c=0$, giving $A_1=\pm (\lambda -0.58198)^{1/2}$. This gives a critical value at $\lambda =0.58198$ from which it follows that

$$\begin{aligned} \gamma _c \sim 1.7183\,(S-2)+\cdots \quad \text{ for } \ (S-2) \ll 1, \end{aligned}$$

(34)

or, alternatively

$$\begin{aligned} S_c \sim 2+0.5820\, \gamma +\cdots \quad \text{ as } \ \gamma \rightarrow 0. \end{aligned}$$

(35)

Expression (34) is plotted in Fig. 4 by a broken line and gives a good representation how the upper curve seen in Fig. 4 behaves for $(S-2)$ small. From (33) we have

$$\begin{aligned} f''(0) \sim 1\pm \bigl ((S-2)-0.58198\,\gamma \bigr )^{1/2}+\cdots \ \ \text{ as } \gamma \rightarrow 0. \end{aligned}$$

(36)

The above analysis indicates that for small $\gamma$ there is only one critical point whereas in Figs. 1, 2 and 3 we can see that there are two distinct critical points. We examine this further in Fig. 5 where plot $f''(0)$ and $g''(0)$ against $\gamma$ for a range of S starting with $S=2.05$ on the left, with the smallest critical point, and increasing to $S=2.8$ on the right, with the largest critical point. For this range of S we see that there is just one critical point with, from (36), $f_c''(0) \sim 1$ for the smaller values of $\gamma$. When $S=2.8$ we can see that a second critical point is just starting to emerge.

Fig. 5

Plots of (a) $f''(0)$ and (b) $g''(0)$ against $\gamma$ for $S=2.05, \, 2.1, \, 2.15,\, 2.2,\,2.4,\,2.5,\,2.8$ (from left to right) obtained from the numerical solution of Eqs. (3, 4, 5, 6)

Fig. 6

Plots of (a) $f''(0)$ and (b) $g''(0)$ against $\gamma$ for $S=2.825$, full line, and $S=2.85$, broken line, obtained from the numerical solution of Eqs. (3, 4, 5, 6)

This becomes clearer in Fig. 6 where we plot $f''(0)$ and $g''(0)$ for $S=2.825$, full line and $S=2.85$, broken line. The upper branch solutions start with the values of $f''(0)$ and $g''(0)$ given by upper solution in (11, 12) both decreasing to the critical point at $\gamma _c \sim 1.308$ and $\gamma _c \sim 1.347$ respectively after which $f''(0)$ loops back towards $\gamma =0$, increasing as it approaches the axis. The values of $g''(0)$ on this branch decrease as $\gamma$ is reduced from the critical point. The lower branches start with the values of $f''(0)$ and $g''(0)$ given by lower solution in (11, 12) with $f''(0)$ increasing and $g''(0)$ decreasing as $\gamma$ is increased. There are further critical points appearing on these branches. These additional critical points lead to a loop in the values of $g''(0)$ for $S=2.85$ with the solutions terminating as $f_\infty +\gamma \,g_\infty$ goes to zero. It appears that the two critical points seen for the larger values of $\gamma$ in Figs. 2 and 3 emerge from the lower branch solutions.

4 Conclusions

We have considered the non-symmetric flow over a permeable surface which is shrinking in one direction as well as in the direction perpendicular to it. The problem is reduced to similarity form and involves two dimensionless parameters, $\gamma$ the shrinking rate and S the suction rate. We started by considering the case $\gamma = 0$, noting that the case of shrinking puts a restriction on S to the existence of solutions. Numerical solutions are obtained for representative values of S and $\gamma$, Figs. 1-3. We saw the existence of two critical points $\gamma _c$ of $\gamma$ dependent on S, and also the existence of two critical points $S_c$ of S dependent on $\gamma$. The plot of critical values $\gamma _c$ in Fig. 4 shows two almost parallel curves, increasing as the values of S are increased.

An asymptotic solution for large S is derived for the upper solution branch with expressions for $f''(0)$ and $g''(0)$ being in (20) requiring that $\gamma \ll S^2$. On putting $\gamma =S^2\,\mu$ we find that expression (22) shows the existence of a critical point at $\mu _ c = 0.25$, with two solution branches emerging from this critical point. Investigation on the nonexistence of solution when S = 2 shows that a singularity happens as $\gamma \rightarrow 0$. Results for the case of $(S-2)$ small show much more interesting behaviour. From Figs. 5 and 6, it is found that only one critical point exists for small $\gamma$ but when gradually increasing the values of S, second critical point starts to emerge which lead to double-region structure that can be seen in Figs. 1-3.