Skip to main content
SpringerLink
Log in

Temporal instability characteristics of Rayleigh–Taylor and Kelvin–Helmholtz mechanisms of an inviscid cylindrical interface

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

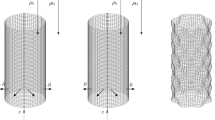
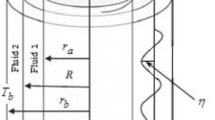
The stability characteristics of an inviscid, incompressible and immiscible cylindrical interface are examined using linear temporal theory. The cylindrical interface is subjected to two instability mechanisms, namely Rayleigh–Taylor (R–T) and Kelvin–Helmholtz (K–H) instabilities. The combined action of R–T and K–H in the presence of surface tension is investigated for a hollow jet in an unbounded liquid medium and reported. The problem includes the motion in an axial direction (K–H mechanism) and the radial direction (R–T mechanism) to destabilize the interface. The instability behavior is described by a few operating parameters, namely, Bond number (Bo), Weber number (We) and Atwood number (A). Here, Bond number is attributed to R–T instability whereas Weber number is attributed to K–H instability. The temporal analysis reveals that the Bond number plays a significant role in determining the dominant growth rate, most unstable axial wavenumber and cut-off axial wavenumber. Furthermore, it is also shown through dimensionless energy budget arguments, even a small amount of energy in the radial motion causes the most unstable wavenumber associated with primary atomization to increase significantly.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Zhou Ye (2017a) Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I Phys Rep 720:1–136

    MathSciNet  MATH  Google Scholar 

  2. Zhou Ye (2017b) Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II Phys Rep 723:1–160

    MathSciNet  MATH  Google Scholar 

  3. Zhou Ye, Clark Timothy T, Clark Daniel S, Gail Glendinning S, Aaron Skinner M, Huntington Channing M, Hurricane Omar A, Dimits Andris M, Remington Bruce A (2019) Turbulent mixing and transition criteria of flows induced by hydrodynamic instabilities. Phys Plasmas 26(8):080901

    Article  Google Scholar 

  4. Lin SP, Reitz RD (1998) Drop and spray formation from a liquid jet. Ann Rev Fluid Mech 30:85–105

    Article  MathSciNet  Google Scholar 

  5. Vadivukkarasan M, Dhivyaraja K, Panchagnula MV (2020) Breakup morphology of expelled respiratory liquid: from the perspective of hydrodynamic instabilities. Phys Fluids 32(9):094101

    Article  Google Scholar 

  6. Villermaux E (2020) Fragmentation versus cohesion. J Fluid Mech 898:P1

    Article  MathSciNet  Google Scholar 

  7. Plesset MS, Prosperetti A (1977) Bubble dynamics and cavitation. Ann Rev Fluid Mech 9(1):145–185

    Article  Google Scholar 

  8. Chandrasekhar S (1961) Hydrodynamic and hydromagnetic stability. Dover Publications, Mineola

    MATH  Google Scholar 

  9. Santangelo PJ, Sojka PE (1995) A holographic investigation of the near-nozzle structure of an effervescent atomizer-produced spray. Atomiz Sprays 5:137–155

    Article  Google Scholar 

  10. Chen F, Xu A, Zhang Y, Zeng Q (2020) Morphological and non-equilibrium analysis of coupled Rayleigh–Taylor–Kelvin–Helmholtz instability. Phys Fluids 32(10):104111

    Article  Google Scholar 

  11. Hoshoudy GA, Awasthi MK (2020) Compressibility effects on the Kelvin–Helmholtz and Rayleigh–Taylor instabilities between two immiscible fluids flowing through a porous medium. Eur Phys J Plus 135(2):169

    Article  Google Scholar 

  12. Wang LF, Xue C, Ye WH, Li YJ (2009) Destabilizing effect of density gradient on the Kelvin–Helmholtz instability. Phys Plasmas 16(11):112104

    Article  Google Scholar 

  13. Wang LF, Ye WH, Li YJ (2010) Combined effect of the density and velocity gradients in the combination of Kelvin–Helmholtz and Rayleigh–Taylor instabilities. Phys Plasmas 17(4):042103

    Article  Google Scholar 

  14. Ye WH, Wang LF, Xue C, Fan ZF, He XT (2011) Competitions between Rayleigh–Taylor instability and Kelvin–Helmholtz instability with continuous density and velocity profiles. Phys Plasmas 18:022704

    Article  Google Scholar 

  15. Krechetnikov R (2009) Rayleigh–Taylor and Richtmyer–Meshkov instabilities of flat and curved interfaces. J Fluid Mech 625:387–410

    Article  MathSciNet  Google Scholar 

  16. Krechetnikov R (2010) Stability of liquid sheet edges. Phys Fluids 22(9):092101

    Article  Google Scholar 

  17. Awasthi MK, Agarwal S (2020) Instability of a radially moving cylindrical surface: a viscous potential flow approach. J Fluids Eng 142(9):094501

    Article  Google Scholar 

  18. Chen XM, Schrock VE, Peterson PF (1997) Rayleigh–Taylor instability of cylindrical jets with radial motion. Nucl Eng Des 177:121–129

    Article  Google Scholar 

  19. Zeng RH, Tao JJ, Sun YB (2020) Three-dimensional viscous Rayleigh–Taylor instability at the cylindrical interface. Phys Rev E 102:023112

    Article  Google Scholar 

  20. Vadivukkarasan M (2020) Transition from absolute to convective instability in a compound jet. Eur J Mech B/Fluids 84:186–192

    Article  MathSciNet  Google Scholar 

  21. Yang HQ (1992) Asymmetric instability of a liquid jet. Phys Fluids 4:681–689

    Article  Google Scholar 

  22. Vadivukkarasan M, Panchagnula MV (2016) Helical modes in combined Rayleigh–Taylor and Kelvin–Helmholtz instability of a cylindrical interface. Int J Spray Comb Dyn 8:219–234

    Article  Google Scholar 

  23. Vadivukkarasan M, Panchagnula MV (2020) Destabilization characteristics of three dimensional Rayleigh–Taylor mechanism on a cylindrical interface. Meccanica 55(1):69–86

    Article  MathSciNet  Google Scholar 

  24. Krechetnikov R (2017) Stability of a growing cylindrical blob. J Fluid Mech 827:R3

    Article  MathSciNet  Google Scholar 

  25. Plesset MS (1954) On the stability of fluid flows with spherical symmetry. J Appl Phys 25:96–98

    Article  MathSciNet  Google Scholar 

  26. Vadivukkarasan M, Panchagnula MV (2017) Combined Rayleigh–Taylor and Kelvin–Helmholtz instabilities on an annular liquid sheet. J Fluid Mech 812:152–177

    Article  MathSciNet  Google Scholar 

  27. Lasheras JC, Villermaux E, Hopfinger EJ (1998) Break-up and atomization of a round water jet by a high-speed annular air jet. J Fluid Mech 357:351–379

    Article  Google Scholar 

  28. Marmottant P, Villermaux E (2004) On spray formation. J Fluid Mech 498:73–111

    Article  Google Scholar 

  29. Rayleigh L (1878) On the instability of jets. Proc Lond Math Soc 10:4–13

    Article  MathSciNet  Google Scholar 

  30. Bremond N, Clanet C, Villermaux E (2007) Atomization of undulating liquid sheets. J Fluid Mech 585:421–456

    Article  MathSciNet  Google Scholar 

  31. Clanet C, Villermaux E (2002) Life of a smooth liquid sheet. J Fluid Mech 462:307–340

    Article  MathSciNet  Google Scholar 

  32. Villermaux E, Clanet C (2002) Life of a flapping liquid sheet. J Fluid Mech 462:341–363

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The work was supported by Department of Science and Technology INSPIRE Faculty Award /Batch-12/2017 (IFA17-ENG220).

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Institute of Technology Puducherry, Karaikal, 609609, India

    M. Vadivukkarasan

Authors
  1. M. Vadivukkarasan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Vadivukkarasan.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vadivukkarasan, M. Temporal instability characteristics of Rayleigh–Taylor and Kelvin–Helmholtz mechanisms of an inviscid cylindrical interface. Meccanica 56, 117–124 (2021). https://doi.org/10.1007/s11012-020-01275-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-020-01275-2

Keywords

Search

Navigation