Analytical estimates of the pull-in voltage for carbon nanotubes considering tip-charge concentration and intermolecular forces

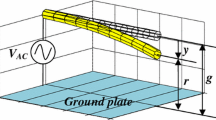
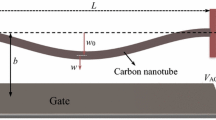
Abstract

Two-side accurate analytical estimates of the pull-in parameters of a carbon nanotube switch clamped at one end under electrostatic actuation are provided by considering the proper expressions of the electrostatic force and van der Waals interactions for a carbon nanotube, as well as the contribution of the charge concentration at the free end. According to the Euler–Bernoulli beam theory, the problem is governed by a fourth-order nonlinear boundary value problem. Two-side estimates on the centreline deflection are derived. Then, very accurate lower and upper bounds to the pull-in voltage and deflection are obtained as function of the geometrical and material parameters. The analytical predictions are found to agree remarkably well with the numerical results provided by the shooting method, thus validating the proposed approach. Finally, a simple closed-form relation is proposed for the minimum feasible gap and maximum realizable length for a freestanding CNT cantilever.

Appendix

The proofs of the two lemmas used in Sect. 3 for obtaining the upper and lower bounds to the CNT deflection are given in the following. These proofs were also given in [16, 17] and are reported here for the sake of convenience.

Lemma A

Let the functionh(x) be continuous up to the third derivative forx ∈ [0, 1] and satisfy the following conditions

$$h\left( 0 \right) = 0,\quad h\left( 1 \right) = 0,\quad h^{\prime } \left( 0 \right) = 0, h^{\prime \prime } \left( 1 \right) = 0,\quad h^{\prime \prime \prime } \left( 1 \right) = 0,$$

(51)

and

$$h^{\text{V}} \left( x \right) \le 0,\quad {\text{for}}\quad x \in \left[ {0, \, 1} \right]$$

(52)

then

$$h\left( x \right) \ge 0,\quad {\text{for}}\quad x \in \left[ {0, \, 1} \right]$$

(53)

Proof

By using the mean value theorem, from continuity and conditions (51)_1,2 it follows that there exists x₁ ∈ [0, 1] such that h′(x₁) = 0. Then, by using conditions (51)_3,4 there exist x₂ ∈ [0, x₁] and x₃ ∈ [x₂, 1] such that h′′(x₂) = 0 and h′′′(x₃) = 0. Since the function h′′′(x) is concave for x ∈ [0, 1] according to (52), it follows that h′′(x) ≤ 0 for x ∈ [x₂, 1] and h′′(x) ≥ 0 for x ∈ [0, x₂]. Therefore, h′(x) ≥ 0 for x ∈ [0, x₁] and h′(x) ≤ 0 for x ∈ [x₁, 1]. Since h(0) = h(1) = 0 according to Eq. (51)_1,2, then it necessarily follows that h(x) ≥ 0 for x ∈ [0, 1], so that condition (53) holds true. □

Lemma B

Let the functiong(x) be continuous up to the third derivative forx ∈ [0, 1] and satisfy the following conditions

$$g\left( 0 \right) = 0,\quad g\left( 1 \right) = 0,\quad g^{{\prime }} \left( 0 \right) = 0,\quad g^{{{\prime \prime }}} \left( 1 \right) = 0.$$

(54)

and

$$g^{\text{IV}} \left( x \right) \ge 0,\quad {\text{for}}\quad x \in \left[ {0, \, 1} \right]$$

(55)

then

$$g\left( x \right) \ge 0,\quad {\text{for}}\quad x \in \left[ {0, \, 1} \right]$$

(56)

Proof

By using the mean value theorem, from conditions (54)_1,2 it follows that there exists x₁ ∈ [0, 1] such that g′(x₁) = 0. Moreover, by using conditions (54)_3,4 there exists x₂ ∈ [0, x₁] such that g′′(x₂) = 0. Condition (55) then implies that g′′(x) is convex. It follows that g′′(x) ≤ 0 for x ∈ [x₂, 1] and g′′(x) ≥ 0 for x ∈ [0, x₂], and thus g′(x) ≥ 0 for x ∈ [0, x₁] and g′(x) ≤ 0 for x ∈ [x₁, 1]. Since g(0) = g(1) = 0 according to conditions (54)_1,2, then it necessarily follows that inequality (56) holds true. □