Elastic indentation of a rough surface by a conical punch

Abstract

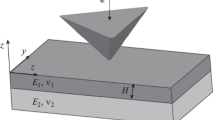
In the contact of a cone with a rough plane the mean pressure in the contact area is constant. In particular, above a critical ratio of the opening angle of the cone with respect to the rms gradient of surface roughness, the mean pressure is the same of that for nominally flat contact, no matter how large is the normal load. We introduce a new variable, namely, the local density of contact area, whose integral over the smooth nominal contact domain gives the real contact area. The results given by the theoretical model agree with the numerical simulations of the same problem presented in the paper.

Appendix

The expression of local contact area density, which in radially symmetrical cases has the form of Eq. (10), can be derived from the procedure of integration in the pressure domain described by Manners and Greenwood [20], obtaining an expression similar to the one presented in the paper, differing only in the choice of a constitutive parameter, i.e., the normalizing pressure.

Let us introduce the following notation:

• $F_P(p)=\text {Prob}(P<p)$, the cumulative distribution function of the smooth pressure distribution;

• $f_P(p)= \frac{d F_P(p)}{d p}$, the corresponding probability density function;

• $V=\frac{1}{4}{E^*}^2{h'_{\text{rms}}}^2$, the variance of the contact pressure needed to close all the gaps between the surfaces. This expression pertains to a 2D isotropic surface $h(x,y)$, where the orthogonal components of the slope $\partial h/\partial x$ and $\partial h/\partial y$ are uncorrelated, and similarly the pressures needed to squeeze flat the surface. While the variance of full contact pressure for a 1D profile is $V=\frac{1}{4}{E^*}^{2}\sigma _{m}^{2}$, where $\sigma _{m}^{2}=m_{2}$ is the variance of profile slopes, for a 2D surface $V=\frac{1}{4}{E^*}^{2}\,2\sigma _{m}^{2}=\frac{1}{2}{E^*}^{ 2}\sigma _{m}^{2}= \frac{1}{2}{E^*}^{2}m_{2}=\frac{1}{4}{E^*}^{ 2}{h'_{\text{rms}}}^{2},$ where $h'_{\text{rms}}$ is the root mean square of the “areal roughness gradient”: $h'_{\text{rms}}=\sqrt{\langle |\nabla h|^2\rangle }=\sqrt{2m_{2}}=\sqrt{ 2\sigma _{m}^{2}}$.

The expression of the contact area ratio given in [20] is

$$ \frac{A}{{A_{{{\text{cone}}}} }} = \int_{0}^{\infty } {f_{P} } (p){\text{erf}}\left( {\frac{p}{{\sqrt {2V} }}} \right){\text{d}}p. $$

(19)

In radial symmetrical cases, when the radial profile of the pressure is monotone, there is a one-to-one correspondence between the pressure $p$ and the radius $r$, so that a change of variable can be made, giving

$$ \begin{aligned} \frac{A}{{A_{{{\text{cone}}}} }} & = \int_{a}^{0} {f_{P} } (p(r)){\text{erf}}\left( {\frac{{p(r)}}{{\sqrt {2V} }}} \right)\frac{{dp}}{{dr}}{\text{d}}r \\ & = \int_{a}^{0} {\frac{{dF_{P} (r)}}{{dr}}} \frac{{dr}}{{dp}}{\text{erf}}\left( {\frac{{p(r)}}{{\sqrt {2V} }}} \right)\frac{{dp}}{{dr}}{\text{d}}r \\ & = \int_{a}^{0} {\frac{{dF_{P} (r)}}{{dr}}} \, {\text{erf}}\left( {\frac{{p(r)}}{{\sqrt {2V} }}} \right){\text{d}}r. \\ \end{aligned} $$

Now, due to radial symmetry, for the conical indenter $F_P(r)=1-r^2/a^2$, so that $\frac{d F_P(r)}{d r}=-\frac{2r}{a^2}$. Transforming further the one-dimensional integral into a surface integral by introducing the azimuth angle $\phi$, we have

$$ \begin{aligned} \frac{A}{{A_{{{\text{cone}}}} }} & = \frac{1}{{\pi a^{2} }}\int_{0}^{{2\pi }} {\int_{0}^{a} r }\, {\text{erf}}\left( {\frac{{p(r)}}{{\sqrt {2V} }}} \right){\text{d}}r{\text{d}}\phi \\ & = \frac{1}{{\pi a^{2} }}\int_{0}^{a} 2 \pi r\, {\text{erf}}\left( {\frac{{p(r)}}{{\sqrt {2V} }}} \right){\text{d}}r. \\ \end{aligned} $$

Comparison between this expression and Eq. (12) gives the local contact area density as:

$$ \gamma (r) = {\text{erf}}\left( {\frac{{p(r)}}{{\sqrt {2V} }}} \right). $$

Our definition of the local contact density (Eq. 10) is slightly different, due to a different choice of the normalizing pressure for the argument of the error function, i.e., $p_{\text{PR}}=2\,p_{\text{rough}}/{\sqrt{\pi }}$ (as proposed by Pastewka and Robbins [5]), instead of $p_{\text{MG}}=\sqrt{2V}$, used by Manners and Greenwood [20].

According to Eq. (2), we have

$$ p_{{{\text{PR}}}} = \frac{2}{{\sqrt \pi }}\frac{{E^{*} h^{\prime}_{{{\text{rms}}}} }}{k} $$

and, by using the expression of $V$ given above:

$$ p_{{{\text{MG}}}} = \frac{{E^{*} h^{\prime}_{{{\text{rms}}}} }}{{\sqrt 2 }}, $$

so that, letting $k=2$, we have $p_{\text{MG}}=\sqrt{\pi /2}\,p_{\text{PR}}.$

As apparent from this discussion, the definition of a local contact density leads to results coincident with those given by the integration in the pressure domain. The validity of this approach does not depend on the normalizing pressure. The choice of a certain normalizing pressure amounts to a constitutive assumption about the response of the rough interface to the value assumed by the normal pressure at a point of the contact domain.

The choice of a normalizing pressure different from the results of Persson’s theory is adopted in order to get the correct linear trend, as numerically observed, in the linear range of the ${{\mathrm{erf}}}$ function. Since the latter covers a quite extensive region (up to contact area fraction almost of 50%), we think it is important to make this modification. However, there is more ground to this correction, since even in the case of large area fractions, there are various authors who have commented that Persson’s solution may underestimate the contact area, and this comes also from a simple asperity model.

It can be shown (Greenwood, personal communication) that Eq. (19) can be evaluated in quadrature as

$$ \frac{A}{{A_{{{\text{cone}}}} }} = 2\int_{0}^{\infty } {\frac{{\sinh q}}{{\cosh ^{3} q}}}\, {\text{erf}}\left( {q\frac{{p_{{m,c}} }}{{\sqrt {2V} }}} \right){\text{d}}q, $$

which can be transformed, after substitution of $p_{\text{MG}}$ with $p_{\text{PR}}$, into the form obtained in the paper, given by Eq. (12).