Abstract
A numerical state-space approach is proposed to examine the natural frequencies and critical buckling limits of marine risers. A large axial tension in the riser model causes numerical limitations. These limitations are overcome by using the modified Gram–Schmidt orthonormalization process as an intermediate step during the numerical integration process with the fourth-order Runge–Kutta scheme. The obtained results are validated against those obtained with other numerical methods, such as the finite-element, Galerkin, and power-series methods, and are found to be in good agreement. The state-space approach is shown to be computationally more efficient than the other methods. Also, we investigate the effect of a high applied tension, a high apparent weight, and higher-order modes on the accuracy of the numerical scheme. We demonstrate that, by applying the orthonormalization process, the stability and convergence of the approach are significantly improved.






Similar content being viewed by others
References
Song L, Fu S, Cao J, Ma L, Wu J (2016) An investigation into the hydrodynamics of a flexible riser undergoing vortex-induced vibration. J Fluids Struct 63:325–350
Mazzilli CE, Rizza F, Dias T (2016) Heave-imposed motion in vertical risers: a reduced-order modelling based on Bessel-like modes. Procedia IUTAM 19:136–143
Dai HL, Abdelkefi A, Wang L (2014) Modeling and nonlinear dynamics of fluid-conveying risers under hybrid excitations. Int J Eng Sci 81:1–14
Clementi F, Demeio L, Mazzilli CEN, Lenci S (2015) Nonlinear vibrations of non-uniform beams by the MTS asymptotic expansion method. Contin Mech Thermodyn 27:703–717
Chen W-L, Zhang Q-Q, Li H, Hu H (2015) An experimental investigation on vortex induced vibration of a flexible inclined cable under a shear flow. J Fluids Struct 54:297–311
Assi GRS, Srinil N, Freire CM, Korkischko I (2014) Experimental investigation of the flow-induced vibration of a curved cylinder in convex and concave configurations. J Fluids Struct 44:52–66
Modarres-Sadeghi Y, Hover FS, Triantafyllou MS (2008) Fatigue calculation of risers using a van der pol wake oscillator model with random parameters. American Society of Mechanical Engineers, New York
Huang T, Dareing DW (1968) Buckling and lateral vibration of drill pipe. J Manuf Sci Eng 90:613–619
Dareing D, Huang T (1976) Natural frequencies of marine drilling risers. J Pet Technol 28:813–818
Paidoussis M (1966) Dynamics of flexible slender cylinders in axial flow Part 1. Theory. J Fluid Mech 26:717–736
Kirk CL, Etok EU, Cooper MT (1979) Dynamic and static analysis of a marine riser. Appl Ocean Res 1:125–135
Kim YC, Triantafyllou MS (1984) The nonlinear dynamics of long, slender cylinders. J Energy Res Technol 106:250–256
Laird WM, Fauconneau G (1966) Upper and lower bounds for the eigenvalues of vibrating beams with linearly varying axial load. DTIC Document
Triantafyllou MS, Triantafyllou GS (1991) The paradox of the hanging string: an explanation using singular perturbations. J Sound Vib 148:343–351
Wu MC, Lou JYK (1991) Effects of rigidity and internal flow on marine riser dynamics. Appl Ocean Res 13:235–244
Chatjigeorgiou IK (2007) Solution of the boundary layer problems for calculating the natural modes of riser-type slender structures. J Offshore Mech Arct Eng 130:011003
Mazzilli CEN, Lenci S, Demeio L (2014) Non-linear free vibrations of tensioned vertical risers. In: Proceedings of 8th European nonlinear dynamics conference—ENOC2014. Viena, Austria
Nayfeh AH (2011) Introduction to perturbation techniques. Wiley, Hoboken
Sparks C (1980) Mechanical behavior of marine risers mode of influence of principal parameters. J Energy Res Technol 102:214–222
Chen Y, Chai YH, Li X, Zhou J (2009) An extraction of the natural frequencies and mode shapes of marine risers by the method of differential transformation. Comput Struct 87:1384–1393
Chen Y, Zhang J, Zhang H, Li X, Zhou J (2015) Re-examination of natural frequencies of marine risers by variational iteration method. Ocean Eng 94:132–139
Huang K, Chen H-C, Chen C-R (2011) Numerical scheme for riser motion calculation during 3-D VIV simulation. J Fluids Struct 27:947–961
Cheng Y, Vandiver JK, Moe G (2002) The linear vibration analysis of marine risers using the WKB-based dynamic stiffness method. J Sound Vib 251:750–760
Moe G, Cheng Y, Vandiver JK (2002) Riser analysis by means of some finite element approaches. In: Proceedings of ETCE/OMAE
Scott MR, Watts HA (1977) Computational solution of linear two-point boundary value problems via orthonormalization. SIAM J Numer Anal 14:40–70
Hadian J, Nayfeh AH (1993) Free vibration and buckling of shear-deformable cross-ply laminated plates using the state-space concept. Comput Struct 48:677–693
Holmes PJ (1977) Bifurcations to divergence and flutter in flow-induced oscillations: a finite dimensional analysis. J Sound Vib 53:471–503
Paidoussis MP (2014) Fluid–structure interactions. Academic Press, Oxford
Aktas Z, Stetter HJ (1977) A classification and survey of numerical methods for boundary value problems in ordinary differential equations. Int J Numer Methods Eng 11:771–796
Fousse L, Hanrot G, Lefèvre V, Pélissier P, Zimmermann P (2007) MPFR: a multiple-precision binary floating-point library with correct rounding. ACM Trans Math Softw 33:13
Comsol (2012) COMSOL multiphysics: version 4.3a, Comsol
Orszag SA (1971) Accurate solution of the Orr–Sommerfeld stability equation. J Fluid Mech 50:689–703
Ascher UM, Mattheij RM, Russell RD (1994) Numerical solution of boundary value problems for ordinary differential equations. Siam, New Delhi
Cheney E, Kincaid D (2012) Numerical mathematics and computing. Cengage Learning, Boston
Alfosail FK, Nayfeh AH, Younis MI (2016) Natural frequencies and mode shapes of statically deformed inclined risers. Int J Non-Linear Mech
Alfosail FK, Nayfeh AH, Younis MI (2017) An analytic solution of the static problem of inclined risers conveying fluid. Meccanica 52(4–5):1175–1187
Meng D, Chen L (2012) Nonlinear free vibrations and vortex-induced vibrations of fluid-conveying steel catenary riser. Appl Ocean Res 34:52–67
Meirovitch L (2001) Fundamentals of vibrations. McGraw-Hill, New York
Schenk O, Gärtner K, Fichtner W, Stricker A (2001) PARDISO: a high-performance serial and parallel sparse linear solver in semiconductor device simulation. Future Gener Comput Syst 18:69–78
Acknowledgements
This research was made possible through the fund and resources of the IT Research Computing at King Abdullah University of Science and Technology (KAUST) in Thuwal, Saudi Arabia. Also, the first author acknowledges the support of Saudi Aramco.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Appendix
Appendix
1.1 Convegence of the methods used to compute the riser eigenvalues
We present convergence of the methods used to compute the first natural frequency presented in Table 2. For higher order modes and higher values of tension, more steps are needed in each method to achieve convergence.
1.1.1 Galerkin method
In the Galerkin method, we use the mode shapes of a straight beam given by the boundary-value problem in [38]. Then, substituting the mode shapes and applying the orthogonality condition on Eq. (7) reduces it to a set of n algebraic equations that need to be solved. The determinant of the matrix containing the coefficient of the algebraic equations gives the characteristic equation of the frequencies. Convergence of the frequency is shown in Fig. 7.
1.1.2 Chebyshev tau method
In this method, the governing Eq. (7) is solved using a spectral decomposition in shifted Chebyshev polynomials [32]. The converged results are shown in Fig. 8.
It was shown in [14] that 320 Chebyshev polynomials are required to achieve convergence for the first natural frequency for tension dominated structures.
1.1.3 Finite element
We use lagrange interpolation with quadratic shape functions in the FE procedure. The mesh is divided into three domains where an adaptive mesh is applied near each end. The solver is a built-in parallel computing algorithm given by the PARDISO solver [39]. A relative tolerance of 10−10 is used to compute the amplitude of the mode shape before the next mesh refining step. Convergence of the eigenvalue is shown in Fig. 9 (see Figs. 7, 8, 9).
Rights and permissions
About this article
Cite this article
Alfosail, F.K., Nayfeh, A.H. & Younis, M.I. A state space approach for the eigenvalue problem of marine risers. Meccanica 53, 747–757 (2018). https://doi.org/10.1007/s11012-017-0769-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-017-0769-z


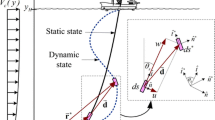
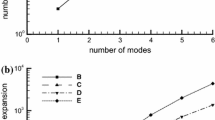


 ’) relative error and (‘
’) relative error and (‘ ’) convergence of
’) convergence of 
 ’) relative error and (‘
’) relative error and (‘ ’) convergence of
’) convergence of 
 ’) relative error and (‘
’) relative error and (‘ ’) convergence of
’) convergence of