An analytic solution of the static problem of inclined risers conveying fluid

Abstract

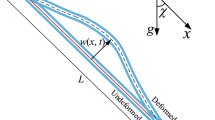
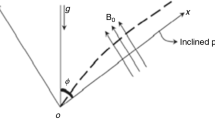
We use the method of matched asymptotic expansion to develop an analytic solution to the static problem of clamped–clamped inclined risers conveying fluid. The inclined riser is modeled as an Euler–Bernoulli beam taking into account its self-weight, mid-plane stretching, an applied axial tension, and the internal fluid velocity. The solution consists of three parts: an outer solution valid away from the two boundaries and two inner solutions valid near the two ends. The three solutions are then matched and combined into a so-called composite expansion. A Newton–Raphson method is used to determine the value of the mid-plane stretching corresponding to each applied tension and internal velocity. The analytic solution is in good agreement with those obtained with other solution methods for large values of applied tensions. Therefore, it can be used to replace other mathematical solution methods that suffer numerical limitations and high computational cost.

Appendix: Simplified eigenvalue problem

The objective of this section is to illustrate how to reduce the eigenvalue problem equation of an inclined riser to an equation of a beam by using a weightless structure assumption. This simplification makes the use of beam mode shapes in the Galerkin approximation more favorable than other sophisticated techniques. The equation of motion of the structure neglecting fluid drag forces is written as

$$\begin{aligned} EI{\frac{{\partial^{4} \hat{y}}}{{\partial \hat{x}^{4} }}} + M\left( {\frac{{\partial^{2} \hat{y}}}{{\partial \hat{t}^{2} }}} \right) + 2m_{f} U_{i} \left( {\frac{{\partial^{2} \hat{y}}}{{\partial \hat{x}\partial \hat{t}}}} \right) + \left( {m_{f} U_{i}^{2} - \left( {T_{e} - W_{e} \sin \left( \theta \right)\left( {L - \hat{x}} \right)} \right) - {\frac{{EA_{p} }}{2L}}\mathop \int \limits_{0}^{L} \left[ {\left( {\frac{{\partial \hat{y}}}{{\partial \hat{x}}}} \right)^{2} } \right]d\hat{x}} \right)\left( {\frac{{\partial^{2} \hat{y}}}{{\partial \hat{x}^{2} }}} \right) \\ - W_{e} \sin \left( \theta \right)\left( {\frac{{\partial \hat{y}}}{{\partial \hat{x}}}} \right) + c\left( {\frac{{\partial \hat{y}}}{{\partial \hat{t}}}} \right) = - W_{e} \cos \left( \theta \right) \\ \end{aligned}$$

(43)

where $M$ denotes the total mass defined as $M = m_{s} + m_{f} + m_{A}$. The subscripts s, f, and A denote the structure, fluid, and added mass, respectively, and c denotes the structural damping. To simplify the analysis, we introduce the following dimensionless variables:

$$\begin{aligned} y = {\frac{{\hat{y}}}{D}};\quad x = {\frac{{\hat{x}}}{L}};\quad t = {\sqrt {\frac{EI}{ML^{4}}}} \hat{t};\quad \bar{\sigma } = {\frac{{W_{e} L^{3} \sin (\theta )}}{EI}};\quad \bar{\eta } = {\frac{{A_{p} D^{2} }}{2I}};\quad \bar{F}_{s} = {\frac{{W_{e} L^{3} \cos (\theta )}}{{EID_{e} }}};\quad \\ \bar{v} = {\frac{{U_{i} {\sqrt {m_{f}}} L}}{\sqrt {EI}}};\quad \bar{T} = {\frac{{T_{e} L^{2} }}{EI}};\quad \beta = {\frac{{m_{f} }}{M}};\quad \bar{c} = {\frac{{cL^{2} }}{\sqrt {MEI}}} \\ \end{aligned}$$

(44)

Then Eq. (43) becomes

$$\frac{{\partial^{4} y}}{{\partial x^{4} }} + \frac{{\partial^{2} y}}{{\partial t^{2} }} + 2{\sqrt {\beta}} \bar{v}\frac{{\partial^{2} y}}{\partial x\partial t} + \left( {\bar{v}^{2} - \left( {\bar{T}_{e} - \bar{\sigma }\left( {1 - x} \right)} \right) - \bar{\eta }\mathop \int \limits_{0}^{L} \left[ {\left( {\frac{\partial y}{\partial x}} \right)^{2} } \right]\partial x} \right)\frac{{\partial^{2} y}}{{\partial x^{2} }} - \bar{\sigma }\frac{\partial y}{\partial x} + \bar{c}\frac{\partial y}{\partial t} = - \bar{F}_{s}$$

(45)

The boundary conditions of the structure are written as

$$y(0) = 0;\quad \left. {\frac{dy}{dx}} \right|_{x = 0} = 0;\quad y(1) = 0;\quad \left. {\frac{dy}{dx}} \right|_{x = 1} = 0$$

(46)

We set $\bar{\sigma } = 0$ to reduce Eq. (45) to the following well-known nonlinear equation of horizontal straight beams:

$$\frac{{\partial^{4} y}}{{\partial x^{4} }} + \frac{{\partial^{2} y}}{{\partial t^{2} }} + 2{\sqrt {\beta}} \bar{v}\frac{{\partial^{2} y}}{\partial x\partial t} + \left( {\bar{v}^{2} - \bar{T}_{e} - \bar{\eta }\mathop \int \limits_{0}^{L} \left[ {\left( {\frac{\partial y}{\partial x}} \right)^{2} } \right]\partial x} \right)\frac{{\partial^{2} y}}{{\partial x^{2} }} + \bar{c}\frac{\partial y}{\partial t} = - \bar{F}_{s}$$

(47)

To obtain the mode shapes, we solve the linear free vibration problem of inclined risers given by Eq. (47) by neglecting the mid-plane stretching, damping, and static force term $\bar{F}_{s}$; that is,

$$\frac{{\partial^{4} y}}{{\partial x^{4} }} + \frac{{\partial^{2} y}}{{\partial t^{2} }} + 2{\sqrt {\beta}} \bar{v}\frac{{\partial^{2} y}}{\partial x\partial t} + \left( {\bar{v}^{2} - \bar{T}_{e} } \right)\frac{{\partial^{2} y}}{{\partial x^{2} }} = 0$$

(48)

with the boundary conditions given by Eq. (46).

We assume a solution of Eq. (48) in the following form:

$$y(x,t) = \phi (x)e^{i\omega t}$$

(49)

Substituting solution (49) into Eq. (48) and assuming that $\phi (x) = e^{isx}$, we obtain the following algebraic equation:

$$s^{4} - \left( {\bar{v}^{2} - \bar{T}_{e} } \right)s^{2} - 2s{\sqrt {\beta}} \bar{v}\omega - \omega^{2} = 0$$

(50)

The roots of Eq. (50) govern the eigenvalues of the mode shapes which can be written after further manipulation as [29, 30]

$$\phi_{j} \left( x \right) = A\;\cosh \left( {s_{1j} x} \right) + B\;\sinh \left( {s_{1j} x} \right) + C\;\cos \left( {s_{2j} x} \right) + D\;\sin \left( {s_{2j} x} \right)$$

(51)

where the $s_{1j}$ and $s_{2j}$ are the real and complex roots of Eq. (50), respectively. The constants $A,B,C,$ and $D$ are obtained by applying the boundary conditions

$$\phi (0) = 0;\quad \left. {\frac{d\phi }{dx}} \right|_{x = 0} = 0;\quad \phi (1) = 0;\quad \left. {\frac{d\phi }{dx}} \right|_{x = 1} = 0$$

(52)

Using the above mode shapes, we seek an approximation to the static defletion governed by Eq. (45) by using the Galerkin approximation in the following form:

$$y(x,t) = \sum\limits_{i = 1}^{n} {\phi {}_{i}(x)} \;u(t)$$

(53)

Substituting Eq. (53) into Eq. (45) yields

$$\sum\limits_{i = 1}^{n} {\frac{{d^{4} \phi {}_{i}}}{{dx^{4} }}} u(t) + \left( {\bar{v}^{2} - \left( {\bar{T}_{e} - \bar{\sigma }\left( {1 - x} \right)} \right) - \bar{\eta }\mathop \int \limits_{0}^{L} \left[ {\left( {\sum\limits_{i = 1}^{n} {\frac{{d\phi {}_{i}}}{dx}} u(t)} \right)^{2} } \right]dx} \right)\left( {\sum\limits_{i = 1}^{n} {\frac{{d^{2} \phi {}_{i}}}{{dx^{2} }}} u(t)} \right) - \bar{\sigma }\sum\limits_{i = 1}^{n} {\frac{{d\phi {}_{i}}}{dx}} u(t) = - \bar{F}_{s}$$

(54)

We multiply Eq. (54) with $\phi {}_{i}(x)$, integrate the outcome, and use the orthogonality of the mode shapes. We note that the result would be a nonlinear system of algebraic equations. For convergence, we use seven terms in the Galerkin approximation [13, 14, 29]. This number of modes provides sufficient accuracy because the participation of the low-frequency mode shapes is larger than that of the high-frequency modes.