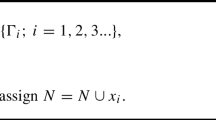Exact Simulation of Poisson-Dirichlet Distribution and Generalised Gamma Process

Abstract

Let $J_1>J_2>\dots$ be the ranked jumps of a gamma process $\tau _{\alpha }$ on the time interval $[0,\alpha ]$, such that $\tau _{\alpha }=\sum _{k=1}^{\infty }J_k$. In this paper, we design an algorithm that samples from the random vector $(J_1, \dots , J_N, \sum _{k=N+1}^{\infty }J_k)$. Our algorithm provides an analog to the well-established inverse Lévy measure (ILM) algorithm by replacing the numerical inversion of exponential integral with an acceptance-rejection step. This research is motivated by the construction of Dirichlet process prior in Bayesian nonparametric statistics. The prior assigns weight to each atom according to a GEM distribution, and the simulation algorithm enables us to sample from the N largest random weights of the prior. Then we extend the simulation algorithm to a generalised gamma process. The simulation problem of inhomogeneous processes will also be considered. Numerical implementations are provided to illustrate the effectiveness of our algorithms.

1 Introduction

Consider a subordinator $\tau _{\alpha ,\sigma }$ with the Lévy-Khintchine representation

$$\begin{aligned} \mathbb {E}(\exp (-\beta \tau _{\alpha ,\sigma })) = \exp \left( -\alpha \int _{0}^{\infty }(1-e^{-\beta w}) w^{-\sigma -1}e^{-w}dw \right) . \end{aligned}$$

When $\alpha >0$ and $\sigma =0$, the subordinator $\tau _{\alpha }:=\tau _{\alpha ,0}$ is a gamma process; while for $\alpha >0$ and $0<\sigma <1$, $\tau _{\alpha ,\sigma }$ is a generalised gamma process. From the basic properties of Poisson random measure (see, for example, Section 2.2 of Kyprianou 2006) we know both processes are pure-jump with infinite activity. Thus, they can be written as $\tau _{\alpha ,\sigma }=\sum _{k=1}^{\infty }J_k$, where $J_1>J_2>\dots >0$ are the ranked jumps of $\tau _{\alpha ,\sigma }$ on the time interval $[0, \alpha ]$. In this paper, we design an acceptance-rejection algorithm that samples from the N largest jumps, $J_1, \dots , J_N$, and the sum of the smaller jumps, $\sum _{k=N+1}^{\infty }J_k$, of the subordinator simultaneously.

This research is motivated by the simulation problem of a Poisson-Dirichlet distribution, which is a random probability measure on the set of decreasing positive sequences with sum 1. The definition is given as follows.

Definition 1

(Poisson-Dirichlet distribution) For $\alpha >0$, suppose that independent random variables $V_i$ are such that $V_i$ has $Beta(1, \alpha )$ distribution. Let

$$\begin{aligned} \tilde{\pi }_1=V_1, \quad \tilde{\pi }_k=V_k\prod _{i=1}^{k-1}(1-V_i), \quad \text {for}\quad k=2, 3, \dots . \end{aligned}$$

Define the Griffiths-Engen-McCloskey distribution with parameter $\alpha$, abbreviated $\text {GEM}(\alpha )$ to be the resultant distribution $(\tilde{\pi }_1, \tilde{\pi }_2, \dots )$. Moreover, define $(\pi _1, \pi _2, \dots )$ to be their sorted values such that $\pi _1>\pi _2>\dots$. Then $(\pi _1, \pi _2, \dots )$ follows the Poisson-Dirichlet distribution with parameter $\alpha$, abbreviated $\text {PD}(\alpha )$.

Results of Perman et al. (1992) show that the sequence $\{ \tilde{\pi }_k \}_{k=1}^{\infty }$ is a size-biased permutation of $\{ \pi _k \}_{k=1}^{\infty }$, i.e., the same sequence presented in a random order $(\pi _{\sigma _1}, \pi _{\sigma _2}, \dots )$, where $\mathbb {P}$$(\sigma _1=i)=\pi _i$, and for k distinct $i_1, \dots , i_k$,

$$\begin{aligned} \mathbb {P}(\sigma _k=i_k \mid \sigma _1=i_1, \dots , \sigma _{k-1}=i_{k-1})=\frac{\pi _{i_k}}{1-(\pi _{i_1}+\dots +\pi _{i_{k-1}})}. \end{aligned}$$

An index i with bigger ‘size’ $\pi _i$ tends to appear earlier in the permutation, hence the name size-biased. On the other hand, we revert to the $\text {PD}(\alpha )$ distribution by sorting the random weights of $\text {GEM}(\alpha )$ in descending order.

The application of $\text {PD}(\alpha )$ distribution appears in many fields, for example, to study the asymptotic distribution of the prime factorization of a randomly drawn integer in number theory, see Donnelly and Grimmett (1993), Tenenbaum (1995), Billingsley (1972) and Vershik (1986); to model the asymptotic distribution of the ranked relative cycle lengths in a random permutation in combinatorics, see Arratia et al. (2003), Aldous (1985), Hansen (1994) and Schmidt and Vershik (1977); to describe the limiting distribution of several sequences of discrete stochastic models of the infinitely-many-neutral-alleles type in population genetics, see Ewens (1990), Watterson (1976) and Kingman (1980); and in particular, to construct the Dirichlet process prior in Bayesian nonparametric statistics, see Ferguson (1973). As we will see in Sect. 2, the construction of Bayesian nonparametric priors also leads us to the simulation problem of a generalised gamma process.

Despite its huge variety of applications, the exact simulation algorithm for $\text {PD}(\alpha )$ is less frequently examined. Wolpert and Ickstadt (1998b) introduced the inverse Lévy measure (ILM) algorithm that samples from the largest jumps of a gamma process and use them to approximate the Ferguson-Klass representation (Ferguson and Klass 1972) of a Poisson-Dirichlet distribution. Zarepour and Labadi (2012) suggested to approximate the distribution of the largest jumps by a gamma density. Due to the difficulty in simulation, these methods ignore the infinite number of smaller jumps of the gamma process in the Ferguson-Klass representation. However, a recent research Dassios et al. (2019) proposed an exact simulation algorithm for the truncated gamma process. The algorithm can be used to sample from the sum of the smaller jumps. In this paper, we will combine these methods together and design an exact simulation algorithm for the N largest components of a Poisson-Dirichlet distribution.

In the meanwhile, a trivial simulation algorithm for $\text {PD}(\alpha )$ is immediately obtained from Definition 1.

Theorem 1

(Trivial algorithm) This algorithm generates an approximation for the N largest components of a $\text {PD}(\alpha )$ distribution.

• 1. Initialise $\alpha$ and N, select a positive integer $m>>N$ (for example $m=10N$).

• 2. For each $i=1, \dots , m$, generate a beta random number $V_i \leftarrow \text {Beta} (1,\alpha )$.

• 3. For each $i=1, \dots , m$, set $\tilde{\pi }_i \leftarrow (1-V_1) \dots (1-V_{i-1})V_i$.

• 4. Sort $\{\tilde{\pi }_i\}_{i=1, \dots , m}$ in descending order and let $\pi _1>\pi _2> \dots >\pi _m$ be the ranked values of $\{\tilde{\pi }_i\}_{i=1, \dots , m}$.

• 5. Truncate the sequence $\{\pi _i\}_{i=1, \dots , m}$ at the first N components, output $(\pi _1, \pi _2, \dots , \pi _N)$.

In Step 2 and 3 of Algorithm 1, we follow the stick-breaking construction of the GEM distribution and sample from its first m components. As $m\rightarrow \infty$, these components become an exact sample of the GEM distribution, and Step 4 returns an exact sample of the Poisson-Dirichlet distribution. However, it is impossible to take m to be infinity in practice, so Algorithm 1 is only an approximation for the $\text {PD}(\alpha )$ distribution.

The rest of the paper is organised as follows. In Sect. 2, we provide some preliminary results for our simulation algorithms and explain their potential applications in Bayesian nonparametric statistics. In Sect. 3, we derive the joint density of the N largest jumps of the gamma and generalised gamma processes, then develop the acceptance-rejection algorithm that samples from these jumps. Section 4 presents the numerical implementations of these algorithms. Section 5 gives some concluding remarks.

2 Preliminary Results

In this section, we illustrate the connection between the (generalised) gamma process and Bayesian nonparametric statistics, and provide some preliminary results that will be used later. The concept of Dirichlet process was first introduced by Ferguson (1973); since then it turns out to be a most notable prior in Bayesian nonparametric statistics. From Theorem 2 of Ferguson (1973), we know that a Dirichlet process can be written as

$$\begin{aligned} G=\sum _{k=1}^{\infty }\pi _k\delta _{\phi _k} , \end{aligned}$$

where $\{ \pi _k \}_{k=1}^{\infty }$ follows the $\text {PD}(\alpha )$ distribution, $\{ \phi _k \}_{k=1}^{\infty }$ is a sequence of i.i.d. random variables with the common distribution $G_0$, and $\delta _{\phi _k}$ is a point mass at $\phi _k$. In Bayesian nonparametric statistics, the latent parameter $\phi _k$ is randomly chosen with probability $\pi _k$, i.e., according to the $\text {PD}(\alpha )$ distribution.

On the other hand, let $\{J_k\}_{k=1}^{\infty }$ be the ranked jumps of a gamma process $\tau _{\alpha }$ on the time interval $[0, \alpha ]$. From Section 4 of Ferguson (1973), we know that the normalised jumps of $\tau _{\alpha }$ has the same law as the Poisson-Dirichlet distribution, i.e.,

$$\begin{aligned} (J_1/\tau _{\alpha }, J_2/\tau _{\alpha }, J_3/\tau _{\alpha }, \dots ) {\mathop {=}\limits ^{law}} (\pi _1, \pi _2, \pi _3, \dots ) . \end{aligned}$$

Then we deduce that to sample from the N largest components of the $\text {PD}(\alpha )$ distribution, it is sufficient to simulate the random vector $(J_1, \dots , J_N, \tau _{\alpha })$, and that is exactly the target of our algorithm.

To simplify the procedure, we define a partial sum $\tau _{\alpha }^{N-}:=\sum _{k=N+1}^{\infty }J_k$, then our task is equivalent to sampling from $(J_1, \dots , J_N, \tau _{\alpha }^{N-})$ because we can revert to $\tau _{\alpha }$ easily by calculating $\sum _{k=1}^{N}J_k+\tau _{\alpha }^{N-}$. But the partial sum is extremely useful because once we have sampled from $(J_1, \dots , J_N)$, the conditional Lévy-Khintchine representation of $\tau _{\alpha }^{N-}$ is

$$\begin{aligned} \mathbb {E}\left( \exp (-\beta \tau _{\alpha }^{N-}) \mid J_1, \dots , J_N \right) = \exp \left( -\alpha \int _{0}^{J_N}(1-e^{-\beta w}) w^{-1}e^{-w}dw \right) . \end{aligned}$$

It follows that $\tau _{\alpha }^{N-}$ is a truncated gamma process, and its exact simulation algorithm has been developed in Dassios et al. (2019). Finally, we can derive the N largest components and the sum of smaller components of $\text {PD}(\alpha )$ from

$$\begin{aligned} \pi _i{\mathop {=}\limits ^{law}}\frac{J_i}{\sum _{k=1}^{N}J_k+\tau _{\alpha }^{N-}} , i=1, \dots , N, \text { and } \sum _{k=N+1}^{\infty }\pi _k {\mathop {=}\limits ^{law}}\frac{\tau _{\alpha }^{N-}}{\sum _{k=1}^{N}J_k+\tau _{\alpha }^{N-}} . \end{aligned}$$

(1)

Another popular prior in Bayesian nonparametric statistics is the generalised Dirichlet process prior. It was first introduced by Hougaard (1986) and Brix (1999), and further studied in Epifani et al. (2003), James et al. (2005), Lijoi et al. (2007) and Ayed et al. (2019). Let $\{J_k\}_{k=1}^{\infty }$ be the ranked jumps of a generalised gamma process $\tau _{\alpha ,\sigma }$ on the time interval $[0, \alpha ]$, then we can express the normalised jump sizes of $\tau _{\alpha ,\sigma }$ as $\left( J_1/\tau _{\alpha ,\sigma }, J_2/\tau _{\alpha ,\sigma }, J_3/\tau _{\alpha ,\sigma }, \dots \right)$. This is again a random probability measure on the set of decreasing positive sequences with sum 1. We denote by $p_k:=J_k/\tau _{\alpha ,\sigma }$ the k-th component of this distribution, then the generalised Dirichlet process prior can be written as $G=\sum _{k=1}^{\infty } p_k \delta _{\phi _k}$.

Our target is to sample from the N largest random weights, $(p_1, \dots , p_N)$, of the generalised Dirichlet process prior. To this end, we first sample from the N largest jumps $(J_1, \dots , J_N)$ of the generalised gamma process, then simulate the partial sum $\tau _{\alpha ,\sigma }^{N-}$$:=\sum _{k=N+1}^{\infty }J_k$, whose conditional Lévy-Khintchine representation is

$$\begin{aligned} \mathbb {E}\left( \exp (-\beta \tau _{\alpha ,\sigma }^{N-}) \mid J_1, \dots , J_N\right) = \exp \left( -\alpha \int _{0}^{J_N}(1-e^{-\beta w}) w^{-\sigma -1}e^{-w} dw \right) . \end{aligned}$$

This turns out to be the Lévy-Khintchine representation of a truncated tempered stable process, and the exact simulation algorithm can be found in Dassios et al. (2020). Finally, we can use the decomposition (1) to derive the N largest components and the sum of smaller components of the generalised Dirichlet process.

3 Simulation Algorithms

In this section, we review the inverse Lévy measure (ILM) algorithm for the gamma and generalised processes, then introduce the acceptance-rejection (AR) algorithm for these processes. We will also extend these algorithms to inhomogeneous processes.

3.1 ILM Algorithm

The ILM algorithm is a straightforward method that samples from the ranked jumps of a Lévy process. We briefly explain the key ideas here and refer the readers to Wolpert and Ickstadt (1998a) and Wolpert and Ickstadt (1998b) for more details. Consider the largest jump $J_1$ of a generalised gamma process $\tau _{\alpha ,\sigma }$. From the basic properties of Poisson random measure, we know

$$\begin{aligned} \begin{aligned} \mathbb {P}(J_1\le x_1)&= \mathbb {P}(\text {Pois}(\alpha v(x_1,\infty ))=0) \\&= \exp (-\alpha v(x_1,\infty ))=\exp \left( -\alpha \int _{x_1}^{\infty } w^{-\sigma -1}e^{-w}dw \right) , \end{aligned} \end{aligned}$$

(2)

where $v(\cdot )$ denotes the Lévy measure. Then we can sample from $J_1$ via the inverse transform method. Let $U_1\sim U(0,1)$ be an uniform random number, then the solution to the equation $U_1 = \exp (-\alpha \int _{x_1}^{\infty } w^{-\sigma -1}e^{-w}dw)$ provides a sample of $J_1$. Conditioning on $J_{k-1}$, we can sample from $J_k$ iteratively by setting $U_k\sim U(0,1)$ and solving the equation $U_k = \exp (-\alpha \int _{x_k}^{J_{k-1}} w^{-\sigma -1}e^{-w}dw)$, for $x_k\in (0, J_{k-1})$. This method is easy to implement, but since the explicit inversion of incomplete gamma integral is unknown, a numerical inversion is required in every iteration. Note that by taking $\sigma =0$, we get the ILM algorithm for a gamma process, and the numerical inversion of an exponential integral is required.

3.2 AR Algorithm for Gamma Process

Next, we derive the joint density of the N largest jumps of a gamma process and develop an acceptance-rejection algorithm to sample from these jumps. Since the size of the $(k+1)$-th largest jump depends on the size of the k-th largest jump, i.e., $J_{k+1}\in (0,J_k)$, it is more convenient to work on the ratio between two consecutive jumps. To this end, we define $R_k:=J_{k+1}/J_k$, $k=1, 2, \dots$, and study the joint density of $(J_1, R_1, \dots , R_{N-1})$.

Theorem 2

Denote by $J_1, \dots , J_N$ the N largest jumps of a gamma process $\tau _{\alpha }$. Let $R_k$$:=J_{k+1}/J_k$ be the ratio between the $(k+1)$-th and k-th largest jumps, then the joint density of $(J_1, R_1, \dots , R_{N-1})$ is

$$\begin{aligned}&\mathbb {P}(J_1\in dx_1, R_1\in dr_1, \dots , R_{N-1}\in dr_{n-1}) \\&=\exp \left( -\alpha \int _{x_1r_1\dots r_{n-1}}^{\infty } w^{-1}e^{-w}dw \right) \alpha ^N (x_1r_1\dots r_{N-1})^{-1} \\&\quad \times e^{-x_1(1+r_1+\dots +r_1r_2\dots r_{N-1})} dr_{N-1}\dots dr_1dx_1 , \end{aligned}$$

where $x_1\in (0,\infty )$ and $r_k\in (0,1)$, for $k=1, \dots , N-1$.

Proof

It follows from Eq. (2) that $J_1$ has the density

$$\begin{aligned} \mathbb {P}(J_1\in dx_1)=\exp \left( -\alpha \int _{x_1}^{\infty } w^{-1}e^{-w}dw \right) \alpha x_1^{-1}e^{-x_1}dx_1 , \end{aligned}$$

where $x_1\in (0,\infty )$. The same argument gives that

$$\begin{aligned} \mathbb {P}(J_k\in dx_k \mid J_{k-1}=x_{k-1}) = \exp \left( -\alpha \int _{x_k}^{x_{k-1}} w^{-1}e^{-w}dw \right) \alpha x_k^{-1}e^{-x_k} dx_k , \end{aligned}$$

where $x_k\in (0,x_{k-1})$. Then we obtain the joint density of $(J_1, \dots , J_N)$ in terms of the product of the density functions above,

$$\begin{aligned}&\mathbb {P}(J_1\in dx_1, \dots , J_N\in dx_N) \\&= \exp \left( -\alpha \int _{x_N}^{\infty } w^{-1}e^{-w}dw \right) \alpha ^N (x_1\dots x_N)^{-1} e^{-(x_1+\dots +x_N)} dx_N\dots dx_1 , \end{aligned}$$

where $x_1>x_2>\dots>x_N>0$. Finally, we make the change of variables $x_k=x_1\prod _{i=1}^{k-1}r_i$, for $k=2, \dots , N$, and the theorem is proved.$\square$

Next, we design an acceptance-rejection algorithm to sample from the random vector $(J_1, \dots , J_N, \tau _{\alpha }^{N-})$. It is Algorithm 3.2 of Dassios et al. (2019) which we refer to as $AlgorithmTG(\cdot , \cdot )$.

Theorem 3

The acceptance-rejection algorithm for $(J_1, \dots , J_N, \tau _{\alpha }^{N-})$.

• 1. Numerically maximising

  $$\begin{aligned} \frac{\exp (-\alpha \int _{x_1r_1\dots r_{N-1}}^{\infty } w^{-1}e^{-w}dw) e^{-x_1(1+r_1+\dots +r_1r_2\dots r_{N-1})}}{\frac{1}{\Gamma (\alpha )0.99^{\alpha }}x_1^{\alpha }e^{-(x_1/0.99)} \alpha ^{-1} (r_1\dots r_{N-1})^{\alpha }} \end{aligned}$$

  with respect to $x_1\in (0,\infty )$ and $r_k\in (0,1)$, for $k=1, \dots , N-1$. Record the maximum value $C_{\alpha , N}$.

• 2. Sample from a gamma distribution $X_1\!\leftarrow \!\text {Gamma}(\alpha ,0.99)$, and for each $k\!=\!1, \dots , N-1$, sample from an uniform distribution $U_k\leftarrow \text {U}(0,1)$, then set $R_k\leftarrow U_k^{1/\alpha }$.

• 3. Sample from an uniform distribution $U\leftarrow \text {U}(0,1)$, if

  $$\begin{aligned} U \le \frac{\exp (-\alpha \int _{X_1R_1\dots R_{N-1}}^{\infty } w^{-1}e^{-w}dw) e^{-X_1(1+R_1+\dots +R_1R_2\dots R_{N-1})}}{C\frac{1}{\Gamma (\alpha )0.99^{\alpha }}X_1^{\alpha }e^{-(X_1/0.99)} \alpha ^{-1} (R_1\dots R_{N-1})^{\alpha }} , \end{aligned}$$

  accept the candidates $(X_1, R_1, \dots , R_{N-1})$ and go to Step 4; otherwise, go to Step 2.

• 4. Set $J_1\leftarrow X_1$, and for each $k=2, \dots , N$, set $J_k\leftarrow J_1 \prod _{i=1}^{k-1}R_i$.

• 5. Set $\tau _{\alpha }^{N-}\leftarrow J_N \times \text {AlgorithmTG}(\alpha , J_N)$.

• 6. Output $(J_1, \dots , J_N, \tau _{\alpha }^{N-})$.

Proof

We apply the acceptance-rejection method to sample from the joint density of $(J_1, R_1, \dots , R_{N-1})$ in Theorem 2 with the envelope

$$\begin{aligned}&\frac{1}{\Gamma (\alpha )b^{\alpha }}x_1^{\alpha -1}e^{-x_1/b}\exp \left( -\alpha \int _{x_1r_1\dots r_{N-1}}^{x_1} w^{-1}dw \right) \alpha ^{N-1} (r_1\dots r_{N-1})^{-1} \\&= \frac{1}{\Gamma (\alpha )b^{\alpha }}x_1^{\alpha -1}e^{-x_1/b} \alpha ^{N-1} (r_1 \dots r_{N-1})^{\alpha -1} . \end{aligned}$$

The first part of the envelope is a gamma density, whose curve should be similar to the density funciton of $J_1$. To this end, we set its shape parameter to be $\alpha$ and scale parameter as close as possible to 1 from below, for example $b=0.99$. The second part can be viewed as the product of $N-1$ number of $\text {Beta}(\alpha ,1)$ density functions $\alpha r_k^{\alpha -1}\mathbbm {1}_{\{0<r_k<1\}}$. Then we can sample from $R_k$ using the inverse transform. Finally, the remaining term $\tau _{\alpha }^{N-}$ has the conditional Laplace transform

$$\begin{aligned} \begin{aligned} \mathbb {E}\left( \exp (-\beta \tau _{\alpha }^{N-}) \mid J_1, \dots , J_N \right) =&\exp \left( -\alpha \int _{0}^{J_N}(1-e^{-\beta y})w^{-1}e^{-w}dw \right) \\ =&\exp \left( -\alpha \int _{0}^{1}(1-e^{-\beta J_N w})w^{-1}e^{-J_N w}dw \right) , \end{aligned} \end{aligned}$$

hence $\tau _{\alpha }^{N-}{\mathop {=}\limits ^{d}}J_NZ_{J_N}(\alpha )$, where $Z_{\mu }(t)$ is a truncated gamma process with Lévy measure $w^{-1}e^{-\mu w}\mathbbm {1}_{\{ 0<w<1 \}}dw$ at time t, and the exact simulation algorithm can be found in Dassios et al. (2019).$\square$

When $\alpha$ is large, the maximum of the ratio between the target density and envelope in Step 1 could be large, making the AR algorithm less efficient or even unfeasible. Next, we design an alternative algorithm that works better for large $\alpha$.

Theorem 4

Alternative acceptance-rejection algorithm for $(J_1, \dots , J_N, \tau _{\alpha }^{N-})$.

• 1. Numerically maximising

  $$\begin{aligned} \frac{\exp (-\int _{x_1}^{\infty }w^{-1}e^{-w}dw) x_1^{-1}e^{-x_1}}{(1/b)e^{-x_1/b}} \end{aligned}$$

  and

  $$\begin{aligned} \frac{\exp (-\alpha \int _{x_1}^{\infty }w^{-1}e^{-w}dw) \alpha x_1^{-1}e^{-x_1}}{\exp (-\int _{x_1}^{\infty }w^{-1}e^{-w}dw) x_1^{-1}e^{-x_1}} \end{aligned}$$

  with respect to $x_1\in (0, \infty )$, record the maximum values as $C_{1,1}$ and $C_{1,2}$ respectively.

• 2. Sample from an exponential distribution $X_1 \leftarrow \text {Exp}(b)$.

• 3. Sample from uniform distributions $V_{1,1}\leftarrow U[0,1]$ and $V_{1,2}\leftarrow U[0,1]$, if both

  $$\begin{aligned} V_{1,1} \le \frac{\exp (-\int _{X_1}^{\infty }w^{-1}e^{-w}dw) X_1^{-1}e^{-X_1}}{C_{1,1}(1/b)e^{-X_1/b}} \end{aligned}$$

  and

  $$\begin{aligned} V_{1,2} \le \frac{\alpha }{C_{1,2}}\exp \biggl ( (1-\alpha )\int _{X_1}^{\infty }w^{-1}e^{-w}dw \biggr ) \end{aligned}$$

  are true, accept $X_1$ and continue; otherwise, go to Step 2.

• 4. For $k=2, \dots , N$, do

  • 1. Numerically maximising

    $$\begin{aligned} \frac{\exp (-\int _{x_k}^{X_{k-1}}w^{-1}e^{-w}dw) x_k^{-1}e^{-x_k}}{1/X_{k-1}} \end{aligned}$$

    and

    $$\begin{aligned} \frac{\exp (-\alpha \int _{x_k}^{X_{k-1}}w^{-1}e^{-w}dw) \alpha x_k^{-1}e^{-x_k}}{\exp (-\int _{x_k}^{X_{k-1}}w^{-1}e^{-w}dw) x_k^{-1}e^{-x_k}} \end{aligned}$$

    with respect to $x_k\!\in \!(0,\! X_{k-1})$, record the maximum values as $C_{k,1}$ and $C_{k,2}$ respectively.

  • 2. Sample from an uniform distribution $X_k \leftarrow U(0, X_{k-1})$.

  • 3. Sample from uniform distributions $V_{k,1}\leftarrow U(0,1)$ and $V_{k,2}\leftarrow U(0,1)$, if both

    $$\begin{aligned} V_{k,1} \le \frac{\exp (-\int _{X_k}^{X_{k-1}}w^{-1}e^{-w}dw) X_k^{-1}e^{-X_k}}{C_{k,1}(1/X_{k-1})} \end{aligned}$$

    and

    $$\begin{aligned} V_{k,2} \le \frac{\alpha }{C_{k,2}} \exp \biggl ( (1-\alpha )\int _{X_k}^{X_{k-1}}w^{-1}e^{-w}dw \biggr ) \end{aligned}$$

    are true, accept $X_k$ and continue; otherwise, go to Step 4(b).

• 4. Denote by $\lfloor \alpha \rfloor$ the largest integer smaller than $\alpha$. For each $i=1, \dots , \lfloor \alpha \rfloor$, sample from a truncated gamma process with time parameter 1,

  $$\begin{aligned} Z_i \leftarrow X_N \times \text {AlgorithmTG}(1, X_N) , \end{aligned}$$

  then sample from a truncated gamma process with time parameter $\alpha -\lfloor \alpha \rfloor$,

  $$\begin{aligned} Z_{\lfloor \alpha \rfloor +1} \leftarrow X_N \times \text {AlgorithmTG}(\alpha -\lfloor \alpha \rfloor , X_N) , \end{aligned}$$

  and set $\tau _{\alpha }^{N-} \leftarrow Z_1+\dots +Z_{\lfloor \alpha \rfloor }+Z_{\lfloor \alpha \rfloor +1}$.

• 5. Set $J_1 \leftarrow X_1, \dots , J_N \leftarrow X_N$, then output $(J_1, \dots , J_N, \tau _{\alpha }^{N-})$.

Proof

To sample from the density of the largest jump $J_1$, we use a two-step acceptance-rejection method. The first step is to maximise

$$\begin{aligned} \frac{\exp (-\int _{x_1}^{\infty }w^{-1}e^{-w}dw) x_1^{-1}e^{-x_1}}{(1/b)e^{-x_1/b}} \end{aligned}$$

for $x_1\in (0, \infty )$, then we can sample from the density in the numerator with an exponential envelope. The second step is to maximise

$$\begin{aligned} \frac{\exp (-\alpha \int _{x_1}^{\infty }w^{-1}e^{-w}dw) \alpha x_1^{-1}e^{-x_1}}{\exp (-\int _{x_1}^{\infty }w^{-1}e^{-w}dw) x_1^{-1}e^{-x_1}} \end{aligned}$$

for $x_1\in (0, \infty )$. When $\alpha >1$, the maximum is approximately $\alpha$. We can then sample from the density in the denominator via the first step, and use it as the envelope to sample from the target density in the numerator, which is the density of $J_1$. The same method applies to the k-th largest jump $J_k$ conditional on $J_{k-1}=x_{k-1}$.

When $\alpha$ is large, the exact simulation algorithm for truncated gamma process could be slow, but we can improve its performance by rewriting the Lévy-Khintchine representation of $\tau _{\alpha }^{N-}$ as

$$\begin{aligned} \begin{aligned}&\mathbb {E} \left( \exp (-\beta \tau _{\alpha }^{N-}) \mid J_1, \dots , J_N \right) \\&=\exp \biggl ( -(\lfloor \alpha \rfloor + (\alpha -\lfloor \alpha \rfloor )) \int _{0}^{1}(1-e^{-\beta J_N w})w^{-1}e^{-J_N w}dw \biggr ) . \end{aligned} \end{aligned}$$

Then we can simulate $\lfloor \alpha \rfloor$ number of independent truncated gamma processes, each at time 1; and a truncated gamma process at time $\alpha -\lfloor \alpha \rfloor$. Their summation is a sample of the truncated gamma process at time $\alpha$.$\square$

3.3 AR Algorithm for Generalised Gamma Process

This section contains the similar results as before but for a generalised gamma process.

Theorem 5

Denote by $(J_1, \dots , J_N)$ the N largest jumps of a generalised gamma process $\tau _{\alpha ,\sigma }$. Let $R_k:=J_{k+1}/J_k$ be the ratio between the $(k+1)$-th and k-th largest jumps, then the joint density of $(J_1, R_1, \dots , R_{N-1})$ is

$$\begin{aligned} \begin{aligned}&\mathbb {P}(J_1\in dx_1, R_1\in dr_1, \dots , R_{N-1}\in dr_{n-1}) \\&=\exp \left( -\alpha \int _{x_1r_1\dots r_{N-1}}^{\infty } w^{-\sigma -1}e^{-w}dw \right) \alpha ^N x_1^{-N\sigma -1}r_1^{-(N-1)\sigma -1}\dots r_{N-1}^{-\sigma -1} \\&\quad \times e^{-x_1(1+r_1+r_1r_2+\dots +r_1r_2\dots r_{N-1})} dr_{N-1}\dots dr_1dx_1 , \end{aligned} \end{aligned}$$

where $x_1\in (0,\infty )$ and $r_k\in (0,1)$, for $k=1, \dots , N-1$.

Proof

This is a repeat of the proof of Theorem 2 with a different Lévy measure, we omit the details.$\square$

Next, we design an acceptance-rejection algorithm to sample from $(J_1, \dots , J_N, \tau _{\alpha ,\sigma }^{N-})$. It is Algorithm 4.4 of Dassios et al. (2020) which we refer to as $AlgorithmTTS(\cdot , \cdot , \cdot )$.

Theorem 6

The acceptance-rejection algorithm for $(J_1, \dots , J_N, \tau _{\alpha ,\sigma }^{N-})$.

• 1. Numerically maximising

  $$\begin{aligned} \frac{\exp (-\alpha \int _{x_1r_1\dots r_{N-1}}^{\infty } w^{-\sigma -1}e^{-w}dw) e^{-x_1(1+r_1+\dots +r_1r_2\dots r_{N-1})}}{\exp (-\alpha (x_1r_1\dots r_{N-1})^{-\sigma }/\sigma )} \end{aligned}$$

  with respect to $x_1\in (0,\infty )$ and $r_k\in (0,1)$, for $k=1, \dots , N-1$. Record the maximum value $C_{\alpha ,\sigma ,N}$.

• 2. Sample from an uniform distribution $U\leftarrow \text {U}(0,1)$, then set

  $$\begin{aligned} X_1\leftarrow (-\sigma \ln (U)/\alpha )^{-1/\sigma } , \end{aligned}$$

  and for each $k=1, \dots , N-1$, sample from an uniform distribution $U_k\leftarrow \text {U}(0,1)$, then set

  $$\begin{aligned} R_k\leftarrow (1-\sigma \ln (U_k)(X_1R_1\dots R_{k-1})^{\sigma }/\alpha )^{-1/\sigma } . \end{aligned}$$

• 3. Sample from an uniform distribution $V\leftarrow \text {U}(0,1)$, if

  $$\begin{aligned} V\le \frac{\exp (-\alpha \int _{X_1R_1\dots R_{N-1}}^{\infty } w^{-\sigma -1}e^{-w}dw) e^{-X_1(1+R_1+\dots +R_1R_2\dots R_{N-1})}}{C_{\alpha ,\sigma ,N} \exp (-\alpha (X_1R_1\dots R_{N-1})^{-\sigma }/\sigma )} , \end{aligned}$$

  accept the candidates $(X_1, R_1, \dots , R_{N-1})$ and go to Step 4; otherwise, go to Step 2.

• 4. Set $J_1\leftarrow X_1$, and for $k=2, \dots , N$, set $J_k\leftarrow J_1 \prod _{i=1}^{k-1}R_i$.

• 5. Set $\tau _{\alpha ,\sigma }^{N-}\leftarrow J_N \times \text {AlgorithmTTS} \left( \sigma , J_N, \alpha J_N^{-\sigma } \right)$.

• 6. Output $(J_1, \dots , J_N, \tau _{\alpha ,\sigma }^{N-})$.

Proof

We apply the acceptance-rejection method to sample from the joint density of $(J_1,$$R_1, \dots , R_{N-1})$ in Theorem 5 with the envelope

$$\begin{aligned} \begin{aligned}&\exp \left( -\alpha \int _{x_1r_1\dots r_{N-1}}^{\infty } w^{-\sigma -1}dw \right) \alpha ^N x_1^{-N\sigma -1}r_1^{-(N-1)\sigma -1}\dots r_{N-1}^{-\sigma -1} \\&=\exp (-\alpha x_1^{-\sigma }/\sigma ) \alpha x_1^{-\sigma -1} \\&\quad \times \prod _{k=1}^{N-1} \exp \left( \alpha (x_1r_1 \dots r_{k-1})^{-\sigma }(1-r_k^{-\sigma })/\sigma \right) \alpha (x_1r_1 \dots r_{k-1})^{-\sigma } r_k^{-\sigma -1} . \end{aligned} \end{aligned}$$

The envelope can be divided into several independent components and each of them can be sampled from using the inverse transform. For the first part, we set

$$\begin{aligned} U = \exp (-\alpha x_1^{-\sigma }/\sigma ) , \end{aligned}$$

and solve for

$$\begin{aligned} X_1 = (-\sigma \ln (U)/\alpha )^{-1/\sigma } . \end{aligned}$$

While for each component in the product term, we set

$$\begin{aligned} U = \exp \left( \alpha (x_1r_1 \dots r_{k-1})^{-\sigma }(1-r_k^{-\sigma })/\sigma \right) , \end{aligned}$$

and solve for

$$\begin{aligned} R_k = (1-\sigma \ln (U)(X_1R_1\dots R_{k-1})^{\sigma }/\alpha )^{-1/\sigma } . \end{aligned}$$

Finally, we know the remaining term $\tau _{\alpha ,\sigma }^{N-}$ has the conditional Laplace transform

$$\begin{aligned} \begin{aligned} \mathbb {E}\left( \exp (-\beta \tau _{\alpha ,\sigma }^{N-}) \mid J_1, \dots , J_N \right) =&\exp \left( -\alpha \int _{0}^{J_N}(1-e^{-\beta w}) w^{-\sigma -1}e^{-w}dw \right) \\ =&\exp \left( -\alpha J_N^{-\sigma } \int _{0}^{1}(1-e^{-\beta J_N w}) w^{-\sigma -1}e^{-J_N w}dw \right) , \end{aligned} \end{aligned}$$

hence $\tau _{\alpha ,\sigma }^{N-}{\mathop {=}\limits ^{d}}J_N Z_{\sigma ,J_N}(\alpha J_N^{-\sigma })$, where $Z_{\sigma ,\mu }(t)$ is a truncated tempered stable process with the Lévy measure $w^{-\sigma -1}e^{-\mu w}\mathbbm {1}_{\{ 0<w<1 \}}dw$ at time t, and the exact simulation algorithm can be found in Dassios et al. (2020).$\square$

For the same reason as before, we provide an alternative algorithm for the generalised gamma process.

Theorem 7

Alternative AR algorithm for $(J_1, \dots , J_N, \tau _{\alpha ,\sigma }^{N-})$.

• 1. Numerically maximising

  $$\begin{aligned} \frac{\exp (-\int _{x_1}^{\infty }w^{-\sigma -1}e^{-w}dw) x_1^{-\sigma -1}e^{-x_1}}{(1/b)e^{-x_1/b}} \end{aligned}$$

  and

  $$\begin{aligned} \frac{\exp (-\alpha \int _{x_1}^{\infty }w^{-\sigma -1}e^{-w}dw) \alpha x_1^{-\sigma -1}e^{-x_1}}{\exp (-\int _{x_1}^{\infty }w^{-\sigma -1}e^{-w}dw) x_1^{-\sigma -1}e^{-x_1}} \end{aligned}$$

  with respect to $x_1\in (0, \infty )$, record the maximum values as $C_{1,1}$ and $C_{1,2}$ respectively.

• 2. Sample from an exponential distribution $X_1 \leftarrow \text {Exp}(b)$.

• 3. Sample from uniform distributions $V_{1,1}\leftarrow U(0,1)$ and $V_{1,2}\leftarrow U(0,1)$, if both

  $$\begin{aligned} V_{1,1} \le \frac{\exp (-\int _{X_1}^{\infty }w^{-\sigma -1}e^{-w}dw) X_1^{-\sigma -1}e^{-X_1}}{C_{1,1}(1/b)e^{-X_1/b}} \end{aligned}$$

  and

  $$\begin{aligned} V_{1,2} \le \frac{\exp (-\alpha \int _{x_1}^{\infty }w^{-\sigma -1}e^{-w}dw) \alpha x_1^{-\sigma -1}e^{-x_1}}{C_{1,2}\exp (-\int _{x_1}^{\infty }w^{-\sigma -1}e^{-w}dw) x_1^{-\sigma -1}e^{-x_1}} \end{aligned}$$

  are true, accept $X_1$ and continue; otherwise, go to Step 2.

• 4. For $k=2, \dots , N$, do

  • 1. Numerically maximising

    $$\begin{aligned} \frac{\exp (-\int _{x_k}^{X_{k-1}}w^{-\sigma -1}e^{-w}dw) x_k^{-\sigma -1}e^{-x_k}}{1/X_{k-1}} \end{aligned}$$

    and

    $$\begin{aligned} \frac{\exp (-\alpha \int _{x_k}^{X_{k-1}}w^{-\sigma -1}e^{-w}dw) \alpha x_k^{-\sigma -1}e^{-x_k}}{\exp (-\int _{x_k}^{X_{k-1}}w^{-\sigma -1}e^{-w}dw) x_k^{-\sigma -1}e^{-x_k}} \end{aligned}$$

    with respect to $x_k\in (0, X_{k-1})$, record the maximum values as $C_{k,1}$ and $C_{k,2}$ respectively.

  • 2. Sample from an uniform distribution $X_k \leftarrow U(0, X_{k-1})$.

  • 3. Sample from uniform distributions $V_{k,1}\leftarrow U(0,1)$ and $V_{k,2}\leftarrow U(0,1)$, if both

    $$\begin{aligned} V_{k,1} \le \frac{\exp (-\int _{X_k}^{X_{k-1}}w^{-\sigma -1}e^{-w}dw) X_k^{-\sigma -1}e^{-X_k}}{C_{k,1}(1/X_{k-1})} \end{aligned}$$

    and

    $$\begin{aligned} V_{k,2} \le \frac{\exp (-\alpha \int _{X_k}^{X_{k-1}}w^{-\sigma -1}e^{-w}dw) \alpha X_k^{-\sigma -1}e^{-X_k}}{C_{k,2}\exp (-\int _{X_k}^{X_{k-1}}w^{-\sigma -1}e^{-w}dw) X_k^{-\sigma -1}e^{-X_k}} \end{aligned}$$

    are true, accept $X_k$ and continue; otherwise, go to Step 4(b).

• 4. For each $i=1, \dots , \lfloor \alpha X_N^{-\sigma } \rfloor$, sample from a truncated tempered stable process with time parameter 1,

  $$\begin{aligned} Z_i \leftarrow X_N \times \text {AlgorithmTTS}(\sigma , X_N, 1) , \end{aligned}$$

  then sample from a truncated tempered stable process with time parameter $\alpha X_N^{-\sigma }$$-\,\lfloor \alpha X_N^{-\sigma } \rfloor$,

  $$\begin{aligned} Z_{\lfloor \alpha X_N^{-\sigma } \rfloor +1} \leftarrow X_N \times \text {AlgorithmTTS}(\sigma , X_N, \alpha X_N^{-\sigma }-\lfloor \alpha X_N^{-\sigma } \rfloor ) , \end{aligned}$$

  and set $\tau _{\alpha ,\sigma }^{N-} \leftarrow Z_1+\dots +Z_{\lfloor \alpha X_N^{-\sigma } \rfloor }+Z_{\lfloor \alpha X_N^{-\sigma } \rfloor +1}$.

• 5. Set $J_1 \leftarrow X_1, \dots , J_N \leftarrow X_N$, then output $(J_1, \dots , J_N, \tau _{\alpha ,\sigma }^{N-})$.

Proof

This is similar to the proof of Algorithm 4, we omit the details.$\square$

3.4 Inhomogeneous Processes

In Corollary 1 of Wolpert and Ickstadt (1998b), the ILM algorithm was extended to inhomogeneous processes. Consider an inhomogeneous generalised gamma process $\tau _{\alpha ,\sigma ,\Pi }$ with the Lévy-Khintchine representation

$$\begin{aligned} \mathbb {E}\left( \exp (-\beta \tau _{\alpha ,\sigma ,\Pi }) \right) = \exp \left( -\int _{\mathcal {S}}\alpha (s)\int _{0}^{\infty }(1-e^{-\beta w}) w^{-\sigma (s)-1}e^{-w} dw\Pi (ds) \right) , \end{aligned}$$

where $\alpha (s)\ge 0$ and $\sigma (s)\ge 0$ are measurable functions on a space $\mathcal {S}$, and $\Pi (ds)$ is a probability measure on $\mathcal {S}$. Then we can sample from the jumps of $\tau _{\sigma ,\alpha ,\Pi }$ using the following algorithm. For $k=1, \dots , N$, we generate independent samples $s_k$ from $\Pi (ds)$ and construct the event times of a Poisson process by setting $T_k:=\sum _{i=1}^{k}e_i$, where $e_i$ are i.i.d. exponential random variables with mean 1. Then we solve the equation $T_k=\int _{J_k}^{\infty }\alpha (s_k)w^{-\sigma (s_k)-1}e^{-w}dw$ to find out $J_k$, for $k=1, \dots , N$. The inhomogeneous generalised gamma process is approximated by $\tau _{\alpha ,\sigma ,\Pi } \leftarrow \sum _{k=1}^{N}J_k$.

To recast the algorithm in terms of the acceptance-rejection method, we notice that Corollary 2 of Wolpert and Ickstadt (1998a) provided the joint density of the jump sizes and locations $\{(J_k,s_k)\}_{k=1}^{N}$ as follows,

$$\begin{aligned} \exp \left( -\alpha (s_N)\int _{J_N}^{\infty }w^{-\sigma (s_N)-1}e^{-w}dw \right) \prod _{k=1}^{N}\left( \alpha (s_k)J_k^{-\sigma (s_k)-1}e^{-J_k} \right) , \end{aligned}$$

(3)

with respect to the product measure $\prod _{k=1}^{N}dJ_k\Pi (ds_k)$ and the constraint

$$\begin{aligned} \alpha (s_k)\int _{J_k}^{\infty }w^{-\sigma (s_k)-1}e^{-w}dw < \alpha (s_{k+1})\int _{J_{k+1}}^{\infty }w^{-\sigma (s_{k+1})-1}e^{-w}dw , \end{aligned}$$

(4)

for every $k<N$.

If the hyperparameters are fixed, i.e., $\alpha (\cdot )\equiv \alpha$ and $\sigma (\cdot )\equiv \sigma$, Eqs. (3) and (4) reduce to the joint density of the N largest jumps of a generalised gamma process, see Theorem 5. However, with the hyperparameters depending on the jump locations, it is hard to develop an acceptance-rejection method directly from (3), especially when the ranges of variables in (4) are not explicit.

To sample from the jumps of the inhomogeneous generalised gamma process via the AR algorithm, we attempt the following procedure. For every $k=1, \dots , N$, we draw a jump location $s_k$ from $\Pi (ds)$, then use the AR algorithm in Sect. 3.3 to sample from the k-th largest jump of a homogeneous generalised gamma process with the Lévy-Khintchine representation

$$\begin{aligned} \exp \left( -\alpha (s_k) \int _{0}^{\infty }(1-e^{-\beta w}) w^{-\sigma (s_k)-1}e^{-w}dw \right) , \end{aligned}$$

and take it as a jump of the inhomogeneous generalised gamma process. The numerical illustration of this algorithm is given in the next section.

4 Numerical Implementation

In this section, we present some numerical results for the algorithms introduced in Sect. 3. The experiments are conducted on an Intel Core i9–10900 CPU @ 2.80GHz processor, 64.0 GB RAM, Windows 10, 64-bit system and performed in Matlab R2023a. Parallel computing is not used throughout the section.

4.1 Jump Mean

We first use the AR algorithms to sample from the five largest jumps of a (generalised) gamma process and compare their sample averages to the true means. To this end, we calculate the mean of these jumps as follows.

Proposition 1

(Mean) The mean of the k-th largest jump of a gamma process is

$$\begin{aligned} \begin{aligned} \mathbb {E}(J_k)&= \int _{0}^{\infty }\int _{0}^{1}\dots \int _{0}^{1} \exp \left( -\alpha \int _{x_1r_1\dots r_{k-1}}^{\infty } w^{-1}e^{-w}dw \right) \\&\quad \times \alpha ^k e^{-x_1(1+r_1+\dots +r_1\dots r_{k-1})} dr_{k-1}\dots dr_1dx_1 , \end{aligned} \end{aligned}$$

and that of a generalised gamma process is

$$\begin{aligned} \begin{aligned} \mathbb {E}(J_k)&=\int _{0}^{\infty }\int _{0}^{1}\dots \int _{0}^{1} \exp \left( -\alpha \int _{x_1r_1\dots r_{k-1}}^{\infty } w^{-\sigma -1}e^{-w}dw \right) \\&\quad \times \alpha ^k x_1^{-k\sigma } r_1^{-(k-1)\sigma } \dots r_{k-1}^{-\sigma } e^{-x_1(1+r_1+\dots +r_1\dots r_{k-1})} dr_{k-1}\dots dr_1dx_1 . \end{aligned} \end{aligned}$$

Proof

These are direct consequences of Theorems 2 and 5.$\square$

Both expectations can be estimated by Monte Carlo method with an exponential variate for $x_1$ and an uniform variate for each $r_i$, $i=1, \dots , k-1$. We record the numerical results in Table 1 and 2. From the tables we can see that the AR algorithms can sample from the jumps exactly. Moreover, when the acceptance rate is high, the AR algorithm would be more efficient than the ILM algorithm. But in general, the ILM algorithm is faster.

Table 1 Jump sizes of the gamma process, $N=5$, sample size is $10^4$. CPU time is rounded to the nearest integer. AR1(GP) and AR2(GP) stand for Theorems 3 and 4 respectively

Table 2 Jump sizes of the generalised gamma process, $N=5$, sample size is $10^4$. CPU time is rounded to the nearest integer. AR1(GGP) and AR2(GGP) stand for Theorems 6 and 7 respectively

Moreover, using the connection between the gamma process and Poisson-Dirichlet distribution in Eq. (1), we can sample from the N largest components of a $\text {PD}(\alpha )$ distribution exactly. We compare the results to the approximation obtained from Algorithm 1. The numerical results are recorded in Table 3.

Table 3 Sample averages of the first 5 components of a Poisson-Dirichlet distribution, $m=50$ for Algorithm 1, sample size is $10^4$

4.2 Jump Covariance

Next, we study the true and empirical covariance between the jumps. The following proposition implies a Monte Carlo method that estimates the true covariance. For simplicity, we assume that $m\ge n$ and focus on the product term $J_mJ_n$ only.

Proposition 2

(Covariance) Assume that $m\ge n\ge 1$, then for a gamma process, the expectation of the product $J_mJ_n$ is

$$\begin{aligned} \begin{aligned} \mathbb {E}(J_mJ_n)&= \int _{0}^{\infty }\int _{0}^{1}\dots \int _{0}^{1} (x_1r_1\dots r_{n-1}) \exp \left( -\alpha \int _{x_1r_1\dots r_{m-1}}^{\infty } w^{-1}e^{-w}dw \right) \\&\quad \times \alpha ^m e^{-x_1(1+r_1+\dots +r_1\dots r_{m-1})} dr_{m-1}\dots dr_1dx_1&, \end{aligned} \end{aligned}$$

and that of a generalised gamma process is

$$\begin{aligned} \begin{aligned} \mathbb {E}(J_mJ_n)&= \int _{0}^{\infty }\int _{0}^{1}\dots \int _{0}^{1} (x_1r_1\dots r_{n-1}) \exp \left( -\alpha \int _{x_1r_1\dots r_{m-1}}^{\infty } w^{-\sigma -1}e^{-w}dw \right) \\&\quad \times \alpha ^m x_1^{-m\alpha } r_1^{-(m-1)\alpha } \dots r_{m-1}^{-\alpha } e^{-x_1(1+r_1+\dots +r_1\dots r_{m-1})} dr_{m-1}\dots dr_1dx_1&. \end{aligned} \end{aligned}$$

Proof

These are direct consequences of Theorems 2 and 5.$\square$

Then we run the AR algorithms and record the empirical covariance in Tables 4 and 5. The data are presented in the format (a, b), where a represents the true covariance obtained from Proposition 9 and b represents the sample average of $J_mJ_n$.

Table 4 Covariance between the jumps of the gamma process, $\alpha =1$, sample size is $10^4$

Table 5 Covariance between the jumps of the generalised gamma process, $\alpha =1$, $\sigma =0.5$, sample size is $10^4$

4.3 Functional Mean

We can also compare the true and empirical Laplace transforms of the gamma and generalised gamma processes. From the Lévy-Khintchine representations, we derive their Laplace transforms explicitly to be $\mathbb {E}(\exp (-\beta \tau _{\alpha }))=(\beta +1)^{-\alpha }$ and $\mathbb {E}(\exp (-\beta \tau _{\alpha ,\sigma }))=\exp (-\alpha \Gamma$$(1-\sigma )( (\beta +1)^{\sigma }-1)/\sigma )$ respectively. On the other hand, we sample from $\tau _{\alpha }$ and $\tau _{\alpha ,\sigma }$ using the AR algorithms and calculate the sample average of $\exp (-\beta \tau _{\alpha })$ and $\exp (-\beta \tau _{\alpha ,\sigma })$ with some specific $\beta$.

In Fig. 1a and b, we plot the true Laplace transform curve in solid line and mark the sample average by a star. The figures show that the AR algorithms are accurate in estimating the Laplace transforms of the gamma and generalised gamma processes.

Fig. 1

True and empirical Laplace transforms, sample size is $10^4$

4.4 Posterior Distribution of the Functional Mean

To illustrate the performance of the AR algorithms in Bayesian nonparametric statistics, we provide another example based on the posterior distribution of the functional mean of a Dirichlet process. For ease of comparison, we consider the same model settings as in Example 1 of Muliere and Tardella (1998), where the target was to study the performance of the $\epsilon$-Dirichlet process.

Assume that we have observed two samples $x_1=0.1$ and $x_2=0.05$ from a Dirichlet process G with concentration parameter $\alpha$ and reference distribution U(0, 1), it is well-known (see, for example, Ferguson 1973) that the posterior distribution of G given $x_1$ and $x_2$ is another Dirichlet process with concentration parameter $\alpha +2$ and reference distribution $(\alpha U(0, 1)+\delta _{x_1}+\delta _{x_2})/(\alpha +2)$. Since the posterior is built based on a Dirichlet process, we can sample from its largest components via the representations in Eq. (1).

Table 6 Posterior distribution of the functional mean of a Dirichlet process, sample size is $10^4$

In Table 6, we use the ILM and AR algorithms to sample from the functional mean of the posterior. We also present the existing results in Muliere and Tardella (1998). From the table we can see that both the ILM and AR algorithms work well in estimating the posterior functional mean.

4.5 Inhomogeneous Generalised Gamma Process

Finally, we illustrate the numerical results for the inhomogeneous generalised gamma process. We set $\alpha (s)=-0.5s+0.6$, $\sigma (s)=0.2\sin (\pi s)+0.4$ and $\Pi (s)=0.4s+0.8$, for $0<s<1$, and sample 100 jumps from the inhomogeneous generalised gamma process. Due to the size of the data, we only present the first 5 jumps in Table 7. We also use the sum of the jumps to approximate the inhomogeneous generalised gamma process; they are compared to the true expectation given by $\mathbb {E}(\tau _{\sigma ,\alpha ,\Pi }) = \int _{0}^{1}\alpha (s) \Gamma (1-\sigma (s)) \Pi (ds) = 0.6393$.

Table 7 Inhomogeneous generalised gamma process with $\alpha (s)=-0.5s+0.6$, $\sigma (s)=0.2\sin (\pi s)+0.4$ and $\Pi (s)=0.4s+0.8$, $0<s<1$. Jump sizes of the generalised gamma process, $N=100$, sample size is $10^4$

5 Concluding Remarks

In this research, we design an acceptance-rejection algorithm that samples from the N largest jumps of gamma and generalised gamma processes. The effectiveness of our algorithms is demonstrated by the empirical mean, covariance and functional mean of the jumps. Moreover, we use the normalised jumps of a gamma process to construct the N largest components of a Poisson-Dirichlet distribution and provide an application in estimating the posterior function mean of a Dirichlet process. We also extend the simulation algorithm to inhomogeneous generalised gamma process. In general, the AR algorithm does not overperform the ILM algorithm in terms of efficiency, but it provides another simulation approach where the numerical inversion of exponential or gamma integral is replaced by an acceptance-rejection step. Specific applications are still to be found in which the AR algorithm is of benefit.

From the Bayesian nonparametrics’ point of view, our algorithms provide a truncation method for the Dirichlet and generalised Dirichlet process priors. Moreover, since our construction is based on a decreasing sequence of random weights, it has the lowest truncation error comparing to other methods, see Campbell et al. (2019) for more details. Apart from that, our algorithms sample from the actual jump sizes $J_k$, not only their weights $\pi _k=J_k/\tau _{\alpha }$. The actual jump sizes are essential in some statistical models. For example, in the Caron-Fox network model (see Caron and Fox 2017), the jump sizes are used to construct an atomic random measure $\sum _{k=1}^{\infty } J_k\delta _{\phi _k}$, which describes the sociability parameters of the nodes in a network. The actual jump sizes are important because it was assumed that the total number of links in the network follows a Poisson distribution with mean $(\sum _{k=1}^{\infty } J_k)^2$, which clearly can not be obtained from the relative weights of the jumps. It would be interesting to investigate the properties of the network model when its nodes are sorted in descending order according to their sociability parameters; we will study this topic in a future work.