First Hitting Time of Brownian Motion on Simple Graph with Skew Semiaxes

Abstract

Consider a stochastic process that lives on n-semiaxes emanating from a common origin. On each semiaxis it behaves as a Brownian motion and at the origin it chooses a semiaxis randomly. In this paper we study the first hitting time of the process. We derive the Laplace transform of the first hitting time, and provide the explicit expressions for its density and distribution functions. Numerical examples are presented to illustrate the application of our results.

1 Introduction

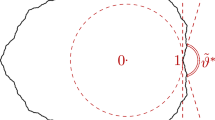
Suppose we have a system of semiaxes emanating from a common origin (a simple graph) and a particle moving on this system. On each semiaxis, the particle behaves as a Brownian motion; and once at the origin, it instantaneously chooses a semiaxis for its next voyage randomly according to a given transition probability. We set an upper boundary on each semiaxis (see Fig. 1), and study the first time that the boundary is hit by the particle.

Fig. 1

A simple graph with five semiaxes and upper boundaries

The study of first hitting time of Brownian motion with linear boundary goes back to Doob (1949). Other types of boundary have also been considered. The second-order boundary was studied by Salminen (1988) using the infinitesimal generator method. The square-root boundary was considered by Breiman (1967) via the Doob’s transform approach. Wang and Pötzelberger (1997) obtained the crossing probability for Brownian motion with a piecewise linear boundary using the Brownian bridge. Scheike (1992) derived an exact formula for the broken linear boundary. Peskir (2002) provided a general result for the continuous boundary using the Chapman-Kolmogorov formula, and gave the probability density function of the first hitting time in terms of a Volterra integral system.

For the first hitting time of Brownian motion with a two-sided boundary, the Laplace transform and density are well-known, see Borodin and Salminen (1996) Section II.1.3. Escribá (1987) studied the crossing problem with two sloping line boundaries. Che and Dassios (2013) used a martingale method to derive the crossing probability with a two-sided boundary involving random jumps. Sacerdote et al. (2014) constructed a Volterra integral system for the probability density function of the first hitting time of Brownian motion with a general two-sided boundary.

In this paper, we are interested in the Brownian motion moving on a simple graph. The construction of Brownian motion on general metric graphs can be seen in Georgakopoulos and Kolesko (2014), Kostrykin et al. (2012) and Fitzsimmons and Kuter (2015). This process contains the Walsh Brownian motion as a special case, which was first considered in the epilogue of Walsh (1978), and further studied by Rogers (1983), Baxter and Chacon (1982), Salisbury (1986) and Barlow et al. (1989). More recently, Karatzas and Yan (2019) introduced a class of planar processes called ‘semimartingales on rays’, which can be viewed as a generalization of the Walsh Brownian motion.

We will study the first hitting time of the Brownian motion on a simple graph. We derive the Laplace transform of the first hitting time, and provide the explicit inverse methods for its density and distribution functions. In particular, our results can be reduced to the first hitting time of Walsh Brownian motion. Papanicolaou et al. (2012) and Yor (1997) Section 17.2.3 derived the Laplace transform of the first hitting time of Walsh Brownian motion when the entering probabilities of the semiaxes are uniformly distributed; Fitzsimmons and Kuter (2015) generalized this result to an arbitrary entering probability.

This paper is motivated by the real-time gross settlement system (RTGS, and known as CHAPS in the UK, see McDonough 1997 and Padoa-Schioppa 2005). The participating banks in the RTGS system are concerned about liquidity risk and wish to prevent the considerable liquidity exposure between two banks. There is evidence suggesting that in CHAPS, banks usually set bilateral or multilateral limits on the exposed position with others (see Becher et al. 2008 and 2008), this mechanism was studied by Che and Dassios (2013) using a Markov model. For a single bank, namely bank A, let a reflected Brownian motion be the net balance between bank A and bank i, and let $u_i$ be the bilateral limit set up by bank A for bank i, Che and Dassios (2013) calculated the probability that the limit is exceeded in a finite time.

We generalize this model by considering an individual bank A and n counterparties. Assume that bank A uses an internal queue to manage its outgoing payments, and once the current payment to bank i is settled, it has probability $P_{ij}$ to make another payment to bank j, where $i, j\in \{1, \dots , n\}$. Let a reflected Brownian motion be the net balance between bank A and bank i. To avoid the considerable exposure to liquidity risk, a limit $b_i$ has been set for the net balance between bank A and bank i (this limit might be set by either the participating banks or the central bank, see Padoa-Schioppa 2005), and they are interested in the first time that such a limit is exceeded. In practice, an individual bank could set multiple limits or even remove the limit on different types of counterparties. This problem can be reduced to the calculation of the first hitting time of Brownian motion on a simple graph. For more details about the RTGS system, see Che (2011) and Soramäki et al. (2007). Applications of the current paper also include the communication in a network, see Deng and Li (2009).

We construct the Brownian motion on the simple graph in Sect. 2, then calculate the Laplace transform of the first hitting time and present some special cases of the result in Sect. 3. Two inverse methods for the Laplace transform are provided in Sect. 4. Numerical examples are presented in Sect. 5. Section 6 proposes a continuous extension of our results. The proofs of the main results are attached in Appendix 1.

2 Construction of the Underlying Process and the First Hitting Time

In this section, we construct the Brownian motion on a simple graph and define the first hitting time we are interested in. Let n be a finite positive integer, we denote by S a simple graph containing n semiaxes emanating from the common origin, i.e., $S:=\{S_1, \dots , S_n\}$, and fix a transition probability matrix $\mathbf{P}:=(P_{ij})_{n\times n}$, so that $\sum _{j=1}^{n}P_{ij}=1$, for $i=1, \dots , n$. We require the Markov chain induced by $\mathbf{P}$ to have only one closed communicating class, so there exists a unique stationary distribution (see Norris 1998).

Consider a planar process X(t) on the simple graph S. We represent the position of X(t) by $(||X(t) ||, \Theta (t))$, where $||X(t) ||$ denotes the distance between X(t) and the origin, and $\Theta (t)\in \{S_1, \dots , S_n\}$ indicates the current semiaxis of the process. Let $||X(t) ||$ have the same distribution as a reflected Brownian motion. We expect $\Theta (t)$ to be constant during each excursion of X(t) away from the origin and have the same distribution as $\mathbf{P}$ when X(t) returns to the origin. To this end, we set

$$\begin{aligned} \mathbb {P}(X(t)=(0, S_j) \mid X(t^-)=(0, S_i))=P_{ij}, \quad i, j\in \{1, \dots , n\} . \end{aligned}$$

Then, X(t) behaves as a Brownian motion on each semiaxis, as long as it does not hit the origin. Once at the origin, it instantaneously chooses a new semiaxis according to $\mathbf{P}$.

There are some special cases of X(t). When $P_{1j}=P_{2j}=\dots =P_{nj}$, for $j=1, \dots , n$, X(t) reduces to a Walsh Brownian motion. When $n=2$, $P_{11}=P_{21}=\alpha$ and $P_{12}=P_{22}=1-\alpha$, for $\alpha \in (0, 1)$, X(t) recovers the skew Brownian motion; we also obtain a standard Brownian motion by setting $\alpha =\frac{1}{2}$. When $n=1$ and $P_{11}=1$, X(t) becomes a reflected Brownian motion.

Next, we define the first hitting time of X(t). On each semiaxis $S_i$, there is a unique upper boundary $b_i>0$, our target is to study the first hitting time $\tau$ defined as

$$\begin{aligned} \tau _i:=\inf \{ t\ge 0; ||X(t) ||=b_i, \Theta (t)=S_i \}, \quad \tau :=\min \limits _{i=1, \dots , n}\tau _i . \end{aligned}$$

(1)

We need to calculate the excursion length of X(t), but the problem is there is no first excursion from zero; before any $t>0$, the process has made an infinite number of small excursions away from the origin. To approximate the dynamic of a Brownian motion, Dassios and Wu (2010) introduced the “perturbed Brownian motion”, we will extend this idea here.

For every $0<\epsilon <\min \limits _{i=1, \dots , n}b_i$, we define a perturbed process $X^{\epsilon }(t)=(||X^{\epsilon }(t) ||, \Theta ^{\epsilon }(t))$ on the simple graph S, where $||X^{\epsilon }(t) ||$ has the same distribution as a reflected Brownian motion starting from $\epsilon$, as long as $X^{\epsilon }(t)$ does not hit the origin. Once at the origin, $X^{\epsilon }(t)$ not only chooses a new semiaxis according to $\mathbf{P}$, but also jumps to $\epsilon$ on the new semiaxis, thus,

$$\begin{aligned} \mathbb {P}(X^{\epsilon }(t)=(\epsilon , S_j) \mid X^{\epsilon }(t^-)=(0, S_i))=P_{ij}, \quad i, j\in \{1, \dots , n\} . \end{aligned}$$

We define the first hitting time $\tau ^{\epsilon }$ similarly as before,

$$\begin{aligned} \tau ^{\epsilon }_i:=\inf \{ t\ge 0; ||X^{\epsilon }(t) ||=b_i, \Theta ^{\epsilon }(t)=S_i \}, \quad \tau ^{\epsilon }:=\min \limits _{i=1, \dots , n}\tau ^{\epsilon }_i . \end{aligned}$$

As $\epsilon \rightarrow 0$, $X^{\epsilon }(t)\rightarrow X(t)$ in a pathwise sense, then $\tau ^{\epsilon }\rightarrow \tau$ in distribution. Hence we will first study the behaviour of $X^{\epsilon }(t)$, then take the limit $\epsilon \rightarrow 0$ to calculate the Laplace transform of the first hitting time $\tau$.

When X(t) starts from a point other than the origin, we denote by $X(0)=(b^*_p, S_p)$ the initial state of X(t), where $p\in \{1, \dots , n\}$ is arbitrary but fixed, and $0<b_p^*<b_p$ (see Fig. 1). We also define the first hitting time of X(t) at the origin as $\delta :=\inf \{ t\ge 0; ||X(t) ||=0 \}$. Then, X(t) behaves as a Brownian motion starting from $b_p^*$ during $[0, \delta )$, i.e., before hitting the origin. Once at the origin, X(t) chooses a new semiaxis according to $\mathbf{P}$, and behaves as a Brownian motion on a simple graph starting from the origin.

We use $\mathbb {E}_{b^*_p}(.)$ for the expectation with respect to the probability measure that X(t) starts from $(b^*_p, S_p)$, and in particular, $\mathbb {E}(.)$ when X(t) starts from the origin.

3 Laplace Transform of $\tau$

We derive the Laplace transform of the first hitting time $\tau$ in this section.

Theorem 1

Let X(t) be a Brownian motion on the simple graph S, where $\mathbf{P} =(P_{ij})_{n\times n}$ and $\{b_i\}_{i=1, \dots , n}$ are the transition probability matrix and upper boundaries of S. When X(t) starts from $(b^*_p, S_p)$, the first hitting time $\tau$ defined in (1) has the Laplace transform

$$\begin{aligned} \mathbb {E}_{b^*_p} \left( e^{-\beta \tau} \right) =\frac{\sinh \left(b_p^*\sqrt{2\beta }\right)}{\sinh \left(b_p\sqrt{2\beta}\right)}+\frac{\sinh \left(\left(b_p-b_p^*\right)\sqrt{2\beta}\right)}{\sinh \left(b_p\sqrt{2\beta }\right)}\frac{\sum _{k=1}^{n}\pi _k\frac{1}{\sinh \left(b_k\sqrt{2\beta }\right)}}{\sum _{k=1}^{n}\pi _k\frac{\cosh \left(b_k\sqrt{2\beta }\right)}{\sinh \left(b_k\sqrt{2\beta }\right)}}, \end{aligned}$$

and the expectation

$$\begin{aligned} \mathbb {E}_{b^*_p}(\tau )=b^*_p \left( b_p-b^*_p \right) +\frac{(b_p-b^*_p)}{b_p}\frac{\sum _{k=1}^{n}\pi _kb_k}{\sum _{k=1}^{n}\frac{\pi _k}{b_k}} , \end{aligned}$$

where $\left( \pi _1,\pi _2,\ldots ,\pi _n \right)$ denotes the stationary distribution of a Markov chain with transition probability matrix $\mathbf{P} =(P_{ij})_{n\times n}$.

We present a special case of Theorem 1 when X(t) starts from the origin.

Corollary 1

When X(t) starts from the origin, the Laplace transform of $\tau$ is

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{\sum _{k=1}^{n}\pi _k\frac{1}{\sinh (b_k\sqrt{2\beta })}}{\sum _{k=1}^{n}\pi _k\frac{\cosh (b_k\sqrt{2\beta })}{\sinh (b_k\sqrt{2\beta })}} , \end{aligned}$$

(2)

and the expectation of $\tau$ is

$$\begin{aligned} \mathbb {E}(\tau )=\frac{\sum _{k=1}^{n}\pi _kb_k}{\sum _{k=1}^{n}\frac{\pi _k}{b_k}} . \end{aligned}$$

Proof

The corollary is proved by setting $b_p^*=0$ in Theorem 1. $\square$

Remark 1

For simplicity, we will concentrate on the case that X(t) starts from the origin in the rest of the paper.

We are also interested in the first hitting time $\tau$ conditional on the event $\{\tau =\tau _i\}$, that is, X(t) hits the upper boundary $b_i$ on the semiaxis $S_i$ before arriving at any other upper boundaries $b_j$, $j\in \{1, \dots , n\}\setminus \{i\}$. Then, we have the following corollary.

Corollary 2

When X(t) starts from the origin, assume that X(t) hits the upper boundary $b_i$ before arriving at any other upper boundaries $b_j$, $j\in \{1, \dots , n\}\setminus \{i\}$, then

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau }\mathbbm {1}_{\{\tau =\tau _i\}} \right) =\frac{\pi _i\frac{1}{\sinh (b_i\sqrt{2\beta })}}{\sum _{k=1}^{n}\pi _k\frac{\cosh (b_k\sqrt{2\beta })}{\sinh (b_k\sqrt{2\beta })}}, \end{aligned}$$

and the probability of the event $\{\tau =\tau _i\}$ is

$$\begin{aligned} \mathbb {P}(\tau =\tau _i)=\frac{\frac{\pi _i}{b_i}}{\sum _{k=1}^{n}\frac{\pi _k}{b_k}}. \end{aligned}$$

Proof

We set $\mathbb {E}\left(e^{-\beta \tau ^{\epsilon }_j}\mathbbm {1}_{\{\tau ^{\epsilon }_j<\delta ^{\epsilon }, \Theta ^{\epsilon }(0)=S_j\}}\right)=0$ for $j\in \{1,\dots ,n\}\setminus \{i\}$, and keep the term $\mathbb {E}\left(e^{-\beta \tau ^{\epsilon }_i}\mathbbm {1}_{\{\tau ^{\epsilon }_i<\delta ^{\epsilon }, \Theta ^{\epsilon }(0)=S_i\}}\right)$ unchanged in the system of Eq. (25). This means the perturbed process $X^{\epsilon }(t)$ will only hit the upper boundary $b_i$. Then we follow the rest of the proof for Theorem 1 to derive the Laplace transform, and take the limit $\beta \rightarrow 0$ to calculate the probability. $\square$  

As in Sect. 2, X(t) can be reduced to some special cases by choosing the parameters accordingly, then we can compare Corollary 1 to the results in the existing literature.

Example 1 (reflected Brownian motion)

When $n=1$ and $P_{11}=1$, X(t) reduces to a reflected Brownian motion. The stationary distribution of $\mathbf{P} =(P_{ij})_{1\times 1}$ is $\pi _1=1$. Let the upper boundary be $b_1>0$, then the first hitting time $\tau$ has the Laplace transform

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{1}{\cosh \left(b_1\sqrt{2\beta }\right)} . \end{aligned}$$

(3)

This is the Laplace transform of the first hitting time of a reflected Brownian motion at $b_1$, see Borodin and Salminen (1996) Section II.3.2.

Example 2 (skew Brownian motion)

When $n=2$, $P_{11}=P_{21}=\alpha$ and $P_{12}=P_{22}=1-\alpha$, for $\alpha \in (0, 1)$, X(t) reduces to a skew Brownian motion (see Lejay 2006). The stationary distribution of $\mathbf{P} =(P_{ij})_{2\times 2}$ is $(\alpha , 1-\alpha )$. Let the upper boundaries be $b_1>0$ and $b_2>0$, then the first hitting time $\tau$ has the Laplace transform

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{\alpha \frac{1}{\sinh (b_1\sqrt{2\beta })}+(1-\alpha )\frac{1}{\sinh (b_2\sqrt{2\beta })}}{\alpha \frac{\cosh (b_1\sqrt{2\beta })}{\sinh (b_1\sqrt{2\beta })}+(1-\alpha )\frac{\cosh (b_2\sqrt{2\beta })}{\sinh (b_2\sqrt{2\beta })}}. \end{aligned}$$

(4)

Moreover, when $\alpha =\frac{1}{2}$, X(t) becomes a standard Brownian motion. In this case, the stationary distribution of $\mathbf{P}$ is $\left(\frac{1}{2}, \frac{1}{2}\right)$, and the first hitting time $\tau$ has the Laplace transform

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{\frac{1}{\sinh (b_1\sqrt{2\beta })}+\frac{1}{\sinh (b_2\sqrt{2\beta })}}{\frac{\cosh (b_1\sqrt{2\beta })}{\sinh (b_1\sqrt{2\beta })}+\frac{\cosh (b_2\sqrt{2\beta })}{\sinh (b_2\sqrt{2\beta })}} . \end{aligned}$$

(5)

This is the Laplace transform of the first exit time of a standard Brownian motion from the two-sided barrier $[-b_1, b_2]$ or $[-b_2, b_1]$, see Borodin and Salminen (1996) Section II.1.3.

Example 3 (Walsh Brownian motion)

When n is a finite positive integer and $P_{1j}=P_{2j}=\dots =P_{nj}=:P_j$, for $j=1, \dots , n$, X(t) becomes a Walsh Brownian motion. The stationary distribution of $\mathbf{P} =(P_{ij})_{n\times n}$ is $(P_1, \dots , P_n)$. Let the upper boundaries be $b_1>0, \dots , b_n>0$, then the first hitting time $\tau$ has the Laplace transform

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{\sum _{k=1}^{n}P_k\frac{1}{\sinh (b_k\sqrt{2\beta })}}{\sum _{k=1}^{n}P_k\frac{\cosh (b_k\sqrt{2\beta })}{\sinh (b_k\sqrt{2\beta })}} . \end{aligned}$$

(6)

This is the Laplace transform of the first hitting time of a Walsh Brownian motion, see Fitzsimmons and Kuter (2015). In particular, when $P_1=\dots =P_n=\frac{1}{n}$, we revert to the main result of Papanicolaou et al. (2012) and Yor (1997) Section 17.2.3.

4 Inverse Laplace Transform

In this section we provide two methods to invert the Laplace transform (2). For simplicity, we denote by g(x, t) and $\Psi (x, t)$ the density and distribution functions of an inverse Gaussian random variable with parameter x:

$$\begin{aligned} g(x, t):=\frac{x}{\sqrt{2\pi t^3}}e^{-\frac{x^2}{2t}} \quad \text {and} \quad \Psi (x, t):=2-2\Phi \left( \frac{x}{\sqrt{t}} \right) , \end{aligned}$$

where $\Phi (\cdot )$ is the standard normal distribution function.

We first present an auxiliary result concerning the poles of the Laplace transform (2), this result will enable us to apply the inverse methods.

Lemma 1

Denote by $-\beta ^*$ the poles of the Laplace transform (2), then $-\beta ^*$ are negative real numbers. Moreover, when $n>1$ and the upper boundaries $\{b_i\}_{i=1, \dots , n}$ are rational numbers, we can find out the poles by solving the equation

$$\begin{aligned} \sum _{i=1}^{n}\pi _i \left( \sum _{k\text { even}}(-1)^{\frac{k}{2}}\left( {\begin{array}{c}C_i\\ k\end{array}}\right) y^k \prod _{j=\{1,\dots , n\}\setminus \{i\}} \left( \sum _{k\text { odd}}(-1)^{\frac{k-1}{2}}\left( {\begin{array}{c}C_j\\ k\end{array}}\right) y^k \right) \right) =0 \end{aligned}$$

with respect to y, and looking for $\beta ^*>0$ which satisfies

$$\begin{aligned} y=\tan \left(\frac{1}{\prod _{j=1}^{n}d_j}\sqrt{2\beta ^*}\right) , \end{aligned}$$

where we have set $b_i=\frac{c_i}{d_i}$, for $i=1, \dots , n$, such that $c_i$ and $d_i$ are positive integers, and $C_i:=c_i\prod _{j=\{1,\dots , n\}\setminus \{i\}}d_j$.

From now on, we denote by $-\beta ^*$ the poles of (2). We sort all the poles in descending order as $-\beta ^*_1>-\beta ^*_2>\dots$, and denote the set of all poles by $\{ -\beta ^*_i\}_{i\in \mathbb {N}}$. We also make the convention that the expressions $\sum _{-\beta ^*}f(-\beta ^*)$ and $\sum _{i\in \mathbb {N}}f(-\beta ^*_i)$ represent the summation with respect to all the poles in descending order.

Next, we apply the convolution method to invert the Laplace transform (2).

Theorem 2

Assume that $b_k$ are rational numbers, then there exist positive integers $c_k$ and $d_k$, such that $b_k=\frac{c_k}{d_k}$, for $k=1, \dots , n$. In this case, the density of the first hitting time $\tau$ is

$$\begin{aligned}f(t)=&{} \left( \sum _{k=1}^{n} \pi _k \frac{\sqrt{2}}{\sqrt{\pi t^5}} \sum _{n=0}^{\infty } \left( (2n+1)^2 b_k^2-t \right) e^{-\frac{(2n+1)^2 b_k^2}{2t}} \right) * \left( \frac{1}{\sqrt{2\pi t}} \right) \\ &{}* \left( \delta (t)-g\left( 2b_1, t \right) \right) *\dots * \left( \delta (t)-g\left( 2b_n, t \right) \right) \\ &{}* \left( \sum _{m=1}^{\infty } A_m \sum _{k=0}^{\infty }(-1)^k g \left( \frac{2k}{d_1\dots d_n}, t \right) \left( -e^{-2\sqrt{-2\beta ^*_m}\frac{1}{d_1\dots d_n}} \right) ^{-1-k} \right) , t>0,\end{aligned}$$

and the distribution of $\tau$ is

$$\begin{aligned}F(t)=&{} \left( \sum _{k=1}^{n} \pi _k \frac{\sqrt{2}}{\sqrt{\pi t^5}} \sum _{n=0}^{\infty } \left( (2n+1)^2 b_k^2-t \right) e^{-\frac{(2n+1)^2 b_k^2}{2t}} \right) * \left( \frac{\sqrt{2t}}{\sqrt{\pi }} \right) \\ &{}* \left( \delta (t)-g\left( 2b_1, t \right) \right) *\dots * \left( \delta (t)-g\left( 2b_n, t \right) \right) \\ &{}* \left( \sum _{m=1}^{\infty } A_m \sum _{k=0}^{\infty }(-1)^k g \left( \frac{2k}{d_1\dots d_n}, t \right) \left( -e^{-2\sqrt{-2\beta ^*_m}\frac{1}{d_1\dots d_n}} \right) ^{-1-k} \right) , t>0, \end{aligned}$$

where $*$ is the convolution notation, $\delta (t)$ denotes the Dirac Delta function, and

$$\begin{aligned} A_m:=\left( \prod _{p\in \mathbb {N}\setminus \{m\}} \left( e^{-2\sqrt{-2\beta ^*_p}\frac{1}{d_1\ldots d_n}}-e^{-2\sqrt{-2\beta ^*_m}\frac{1}{d_1\ldots d_n}} \right) \right) ^{-1}. \end{aligned}$$

In practice, the difficulty in evaluating the convolutions above restricts the usefulness of Theorem 2, so we provide a more explicit way to invert the Laplace transform (2).

Theorem 3

Assume that the upper boundaries $\{b_i\}_{i=1, \dots , n}$ are rational numbers, then the density of the first hitting time $\tau$ is

$$\begin{aligned} f(t)=\sum _{-\beta ^*}e^{-\beta ^* t}\frac{\sum _{k=1}^{n}\pi _k\frac{\sqrt{2\beta ^*}}{\sin (b_k\sqrt{2\beta ^*})}}{\sum _{k=1}^{n}\pi _k b_k+\sum _{k=1}^{n}\pi _k b_k\frac{\cos ^2(b_k\sqrt{2\beta ^*})}{\sin ^2(b_k\sqrt{2\beta ^*})}}, \end{aligned}$$

(7)

and the distribution of $\tau$ is

$$\begin{aligned} F(t)=\sum _{-\beta ^*}\frac{1}{-\beta ^*} \left( e^{-\beta ^* t}-1 \right) \frac{\sum _{k=1}^{n}\pi _k\frac{\sqrt{2\beta ^*}}{\sin (b_k\sqrt{2\beta ^*})}}{\sum _{k=1}^{n}\pi _k b_k+\sum _{k=1}^{n}\pi _k b_k\frac{\cos ^2(b_k\sqrt{2\beta ^*})}{\sin ^2(b_k\sqrt{2\beta ^*})}} . \end{aligned}$$

(8)

Remark 2

Since the poles $-\beta ^*$ are negative real numbers, the series (7) and (8) converge fast when t is large, but slowly when t is small. Inspired by the general Theta function transformation (see Bellman 1961 Section 19), we provide the alternative expressions for the density and distribution functions of $\tau$ that converge fast for small t.

When $\{b_i\}_{i=1, \dots , n}$ are rational numbers, there exist positive integers $c_i$ and $d_i$, such that $b_i=\frac{c_i}{d_i}$, for $i=1,\ldots ,n$. Denote by $x:=e^{-\sqrt{2\beta }\frac{1}{d_1\ldots d_n}}$, then Laplace transform (2) can be written as a quotient of two polynomials M(x)/N(x). The series expansion with respect to x gives

$$\begin{aligned} \frac{M(x)}{N(x)}=\sum _{k=1}^{\infty }a_k x^k=\sum _{k=1}^{\infty }a_k e^{-\sqrt{2\beta }\frac{k}{d_1\dots d_n}}. \end{aligned}$$

(9)

Since $e^{-\sqrt{2\beta }\frac{k}{d_1\ldots d_n}}$ is the Laplace transform of an inverse Gaussian random variable with parameter $\frac{k}{d_1\ldots d_n}$, we can invert (9) term by term to derive the density of $\tau$:

$$\begin{aligned} f(t)=\sum _{k=1}^{\infty }a_k \frac{\frac{k}{d_1\dots d_n}}{\sqrt{2\pi t^3}}e^{-\frac{ \left( \frac{k}{d_1\dots d_n} \right) ^2}{2t}}=\sum _{k=1}^{\infty }a_k g \left( \frac{k}{d_1\dots d_n}, t \right) . \end{aligned}$$

Then integrate the density over (0, t) for the distribution of $\tau$:

$$\begin{aligned} F(t)=\sum _{k=1}^{\infty }a_k \left( 2-2\Phi \left( \frac{\frac{k}{d_1\dots d_n}}{\sqrt{t}} \right) \right) =\sum _{k=1}^{\infty }a_k\Psi \left( \frac{k}{d_1\dots d_n}, t \right) . \end{aligned}$$

We provide some examples to illustrate the use of Theorem 3 and Remark 2.

Example 4 (reflected Brownian motion)

Consider the Laplace transform (3). To find the poles of the Laplace transform, we need to solve the equation $\coth (b_1\sqrt{2\beta })=0$. Set $\beta =-\beta ^*$, we have $\coth (b_1\sqrt{-2\beta ^*})=\cos (b_1\sqrt{2\beta ^*})=0$, and $b_1\sqrt{2\beta ^*}=\frac{2k-1}{2}\pi$, $k\in \mathbb {Z}^+$. Therefore, the Laplace transform (3) has the poles

$$\begin{aligned} -\beta ^*=-\frac{(2k-1)^2}{8b_1^2}\pi ^2, k\in \mathbb {Z}^+ . \end{aligned}$$

Using Theorem 3, we calculate the density and distribution functions of $\tau$ to be

$$\begin{aligned} f(t)=\sum _{k=1}^{\infty }(-1)^{k-1}\pi \frac{(2k-1)}{2b_1^2}e^{-\frac{(2k-1)^2}{8b_1^2}\pi ^2 t}, \end{aligned}$$

$$\begin{aligned} F(t)=\sum _{k=1}^{\infty }(-1)^{k-1}\frac{4}{(2k-1) \pi } \left( 1-e^{-\frac{(2k-1)^2}{8b_1^2}\pi ^2t} \right) . \end{aligned}$$

These expressions converge fast when t is large, but slowly when t is small.

On the other hand, denote by $x:=e^{-\sqrt{2\beta }}$, the negative binomial expansion implies

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{2}{x^{b_1}+x^{-b_1}}=\frac{2x^{b_1}}{x^{2b_1}+1}=2\sum _{k=1}^{n}(-1)^{k-1}x^{(2k-1)b_1}. \end{aligned}$$

For every $k\in \mathbb {Z}^+$, $x^{(2k-1)b_1}=e^{-(2k-1)b_1\sqrt{2\beta }}$ is the Laplace transform of an inverse Gaussian random variable with parameter $(2k-1)b_1$, then Remark 2 gives

$$\begin{aligned} f(t)=2\sum _{k=1}^{\infty }(-1)^{k-1}g \left( (2k-1)b_1, t \right) \quad \text {and} \quad F(t)=2\sum _{k=1}^{\infty }(-1)^{k-1}\Psi \left( (2k-1)b_1, t \right) . \end{aligned}$$

These expressions converge fast for small t, but slowly for large t.

Example 5 (standard Brownian motion)

Let $b_1=1$, $b_2=2$ in Laplace transform (5), then

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{\frac{1}{\sinh (\sqrt{2\beta })}+\frac{1}{\sinh (2\sqrt{2\beta })}}{\frac{\cosh (\sqrt{2\beta })}{\sinh (\sqrt{2\beta })}+\frac{\cosh (2\sqrt{2\beta })}{\sinh (2\sqrt{2\beta })}} . \end{aligned}$$

Using Lemma 1, we can derive the poles of the Laplace transform by solving $y^2-3=0$ and $y=\tan \left(\sqrt{2\beta ^*}\right)$. Thus, the poles are

$$\begin{aligned} -\beta ^*=-\frac{1}{2}\pi ^2\left(k+\frac{1}{3}\right)^2, k\in \mathbb {Z} . \end{aligned}$$

Using Theorem 3, we calculate the density and distribution functions of $\tau$ to be

$$\begin{aligned}f(t)=& \ \frac{\pi }{2\sqrt{3}}\sum _{k=-\infty }^{\infty }e^{-\frac{1}{2}\pi ^2 \left(k-\frac{2}{3} \right) ^2t} \left(k-\frac{2}{3} \right) \left( \left(-1\right)^{k+1}+1 \right) \\ =& \ \frac{\pi }{2\sqrt{3}}\sum _{k=1}^{\infty }e^{-\frac{1}{2}\pi ^2 \left( k-\frac{2}{3} \right) ^2t} \left( k-\frac{2}{3} \right) \left( \left(-1\right)^{k+1}+1 \right) \\ &{}+\frac{\pi }{2\sqrt{3}}\sum _{k=1}^{\infty }e^{-\frac{1}{2}\pi ^2 \left( k-\frac{1}{3} \right) ^2t} \left( k-\frac{1}{3} \right) \left( \left(-1\right)^{k+1}-1 \right), \end{aligned}$$

(10)

and

$$\begin{aligned} F(t)=& \ \frac{1}{\sqrt{3}\pi }\sum _{k=1}^{\infty } \frac{1}{ \left( k-\frac{2}{3} \right) }\left( 1-e^{-\frac{1}{2}\pi ^2 \left( k-\frac{2}{3} \right) ^2t} \right) \left( \left(-1\right)^{k+1}+1 \right) \\ &{}+\frac{1}{\sqrt{3}\pi }\sum _{k=1}^{\infty } \frac{1}{ \left( k-\frac{1}{3} \right) }\left( 1-e^{-\frac{1}{2}\pi ^2 \left( k-\frac{1}{3} \right) ^2 t} \right) \left( \left(-1\right)^{k+1}-1 \right) . \end{aligned}$$

(11)

These expressions converge fast when t is large, but slowly when t is small.

On the other hand, denote by $x:=e^{-\sqrt{2\beta }}$, the negative binomial expansion implies

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{(x-x^{-1})+(x^2-x^{-2})}{x^3-x^{-3}}=\frac{x(x+1)}{x^3+1}=\sum _{k=1}^{\infty }(-1)^{k-1} \left( x^{3k-1}+x^{3k-2} \right) . \end{aligned}$$

For every $k\in \mathbb {Z}^+$, we invert $x^{3k-1}$ and $x^{3k-2}$ using the inverse Gaussian density, then

$$\begin{aligned} f(t)=\sum _{k=1}^{\infty }(-1)^{k-1}g(3k-2, t)+\sum _{k=1}^{\infty }(-1)^{k-1} g(3k-1, t) , \end{aligned}$$

(12)

$$\begin{aligned} F(t)=\sum _{k=1}^{\infty }(-1)^{k-1}\Psi (3k-2, t)+\sum _{k=1}^{\infty }(-1)^{k-1} \Psi (3k-1, t) . \end{aligned}$$

(13)

These expressions converge fast for small t, but slowly for large t.

Example 6 (skew Brownian motion)

Let $\alpha =\frac{1}{3}$ and $b_1=1$, $b_2=2$ in Laplace transform (4), it becomes

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{\frac{1}{3}\frac{1}{\sinh (\sqrt{2\beta })}+\frac{2}{3}\frac{1}{\sinh (2\sqrt{2\beta })}}{\frac{1}{3}\frac{\cosh (\sqrt{2\beta })}{\sinh (\sqrt{2\beta })}+\frac{2}{3}\frac{\cosh (2\sqrt{2\beta })}{\sinh (2\sqrt{2\beta })}} . \end{aligned}$$

Using Lemma 1, we can derive the poles of the Laplace transform by solving $y^2-2=0$ and $y=\tan \left(\sqrt{2\beta ^*}\right)$. Thus, the poles are

$$\begin{aligned} -\beta ^*=-\frac{1}{2}(k\pi +\theta )^2, \quad k\in \mathbb {Z}, \quad \text{where} \quad \theta =\arctan \left(\sqrt{2}\right). \end{aligned}$$

Using Theorem 3, we calculate the density and distribution functions of $\tau$ to be

$$\begin{aligned} f(t)=\frac{1}{2\sqrt{6}}\sum _{k=-\infty }^{\infty }e^{-\frac{1}{2}(\theta +k\pi )^2t}(\theta +k\pi ) \left( \left(-1\right)^k+\sqrt{3} \right) , \end{aligned}$$

(14)

$$\begin{aligned} F(t)=\frac{1}{\sqrt{6}}\sum _{k=-\infty }^{\infty }\frac{1}{(\theta +k\pi )} \left( 1-e^{-\frac{1}{2}(\theta +k\pi )^2t} \right) \left( \left(-1\right)^k+\sqrt{3} \right) . \end{aligned}$$

(15)

These expressions converge fast when t is large, but slowly when t is small.

On the other hand, denote by $x:=e^{-\sqrt{2\beta }}$, the series expansion implies

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{2x+2x^3+4x^2}{3+3x^4+2x^2}=\frac{2}{3}x+\frac{4}{3}x^2+\frac{2}{9}x^3-\frac{8}{9}x^4-\frac{22}{27}x^5-\frac{20}{27}x^6+O\left(x^7\right). \end{aligned}$$

We invert it term by term to derive the density function, then integrate the density for the distribution function:

$$\begin{aligned} f(t)=\frac{2}{3}g(1, t)+\frac{4}{3}g(2, t)+\frac{2}{9}g(3, t)-\frac{8}{9}g(4, t)-\frac{22}{27}g(5, t)-\frac{20}{27}g(6, t)+O\left(g\left(7, t\right)\right) , \end{aligned}$$

(16)

$$\begin{aligned} F(t)=\frac{2}{3}\Psi (1, t)+\frac{4}{3}\Psi (2, t)+\frac{2}{9}\Psi (3, t)-\frac{8}{9}\Psi (4, t)-\frac{22}{27}\Psi (5, t)-\frac{20}{27}\Psi (6, t)+O(\Psi (7, t)) . \end{aligned}$$

(17)

These expressions converge fast for small t, but slowly for large t.

Example 7 (Walsh Brownian motion)

Let $b_1=1$, $b_2=2$, $b_3=3$ and $P_{ij}=\frac{1}{3}$ for $i, j\in \{1, 2, 3\}$ in (6), then the stationary distribution of $\mathbf{P} =(P_{ij})_{3\times 3}$ is $\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right)$, and

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{\frac{1}{3}\frac{1}{\sinh (\sqrt{2\beta })}+\frac{1}{3}\frac{1}{\sinh (2\sqrt{2\beta })}+\frac{1}{3}\frac{1}{\sinh (3\sqrt{2\beta })}}{\frac{1}{3}\frac{\cosh (\sqrt{2\beta })}{\sinh (\sqrt{2\beta })}+\frac{1}{3}\frac{\cosh (2\sqrt{2\beta })}{\sinh (2\sqrt{2\beta })}+\frac{1}{3}\frac{\cosh (3\sqrt{2\beta })}{\sinh (3\sqrt{2\beta })}} . \end{aligned}$$

Using Lemma 1, we can derive the poles of the Laplace transform by solving $y^4-12y^2+11=0$ and $y=\tan (\sqrt{2\beta ^*})$. Thus, we know $\pm 1=\tan (\sqrt{2\beta ^*})$ and $\pm \sqrt{11}=\tan (\sqrt{2\beta ^*})$, and the poles are

$$\begin{aligned} -\beta ^*=-\frac{1}{2} \left( \frac{1}{4}\pi +k\pi \right) ^2 \quad \text {and} \quad -\beta ^*=-\frac{1}{2} \left( \theta +k\pi \right) ^2, \quad k\in \mathbb {Z}, \quad \text {where} \quad \theta =\arctan \left(\sqrt{11}\right) . \end{aligned}$$

Using Theorem 3, we calculate the density and distribution functions of $\tau$ to be

$$\begin{aligned} f(t)=&\frac{1}{10}\sum _{k=-\infty }^{\infty }e^{-\frac{1}{2}\left(\frac{1}{4}\pi +k\pi \right)^2t}\left( 2\sqrt{2}\left(-1\right)^k+1 \right) \left( \frac{1}{4}\pi +k\pi \right) \nonumber \\&+\frac{1}{15}\sum _{k=-\infty }^{\infty }e^{-\frac{1}{2}\left(\theta +k\pi\right)^2t}\left(\left(-1\right)^k\frac{\sqrt{12}}{\sqrt{11}}+\frac{6}{\sqrt{11}}+\left(-1\right)^{k+1}\frac{3\sqrt{3}}{\sqrt{11}} \right) \left( \theta +k\pi \right) , \end{aligned}$$

(18)

$$\begin{aligned} F(t)=&\frac{1}{5}\sum _{k=-\infty }^{\infty }\frac{1}{\left( \frac{1}{4}\pi +k\pi\right)} \left( 1-e^{-\frac{1}{2}\left(\frac{1}{4}\pi +k\pi \right)^2t} \right) \left( 2\sqrt{2}\left(-1\right)^k+1 \right) \nonumber \\&+\frac{2}{15}\sum _{k=-\infty }^{\infty }\frac{1}{\left( \theta +k\pi \right) } \left( 1-e^{-\frac{1}{2}(\theta +k\pi )^2t} \right) \left( \left(-1\right)^k\frac{\sqrt{12}}{\sqrt{11}}+\frac{6}{\sqrt{11}}+\left(-1\right)^{k+1}\frac{3\sqrt{3}}{\sqrt{11}} \right) . \end{aligned}$$

(19)

These expressions converge fast when t is large, but slowly when t is small.

On the other hand, denote by $x:=e^{-\sqrt{2\beta }}$, the series expansion implies

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right)= & {} \frac{2\left( x^{11}+x^{10}+x^9-x^8-2x^7-2x^5-x^4+x^3+x^2+x \right) }{3x^{12}-x^{10}-x^8-2x^6-x^4-x^2+3}\\= & {} \frac{2}{3}x+\frac{2}{3}x^2+\frac{8}{9}x^3-\frac{4}{9}x^4-\frac{22}{27}x^5+\frac{2}{27}x^6+O\left(x^7\right). \end{aligned}$$

We invert it term by term to derive the density function, then integrate the density for the distribution function:

$$\begin{aligned} f(t)=\frac{2}{3}g(1, t)+\frac{2}{3}g(2, t)+\frac{8}{9}g(3, t)-\frac{4}{9}g(4, t)-\frac{22}{27}g(5, t)+\frac{2}{27}g(6, t)+O(g(7, t)) , \end{aligned}$$

(20)

$$\begin{aligned} F(t)=\frac{2}{3}\Psi (1, t)+\frac{2}{3}\Psi (2, t)+\frac{8}{9}\Psi (3, t)-\frac{4}{9}\Psi (4, t)-\frac{22}{27}\Psi (5, t)+\frac{2}{27}\Psi (6, t)+O(\Psi (7, t)) . \end{aligned}$$

(21)

These expressions converge fast for small t, but slowly for large t.

5 Numerical Implementation

In this section, we present the numerical illustration for Examples 5, 6 and 7. We will plot the density and distribution functions in each example, and study the accuracy of these functions.

For Example 5, we first consider the density function when t is large. Since (10) converges fast for large t, we truncate it at a fixed level n. Define the truncated function

$$\begin{aligned} \overline{f}_n(t):= & {} \frac{\pi }{2\sqrt{3}}\sum _{k=1}^{n}e^{-\frac{1}{2}\pi ^2 \left( k-\frac{2}{3} \right) ^2t} \left( k-\frac{2}{3} \right) \left( \left(-1\right)^{k+1}+1 \right) \nonumber \\&+\frac{\pi }{2\sqrt{3}}\sum _{k=1}^{n}e^{-\frac{1}{2}\pi ^2 \left( k-\frac{1}{3} \right) ^2t} \left( k-\frac{1}{3} \right) \left( \left(-1\right)^{k+1}-1 \right) . \end{aligned}$$

(22)

We plot $\overline{f}_2(t)$, $\overline{f}_4(t)$ and $\overline{f}_6(t)$ in Fig. 2a. To demonstrate the accuracy of the truncated functions, we also invert the Laplace transform $\mathbb {E}(e^{-\beta \tau })$ numerically using the Gaver-Stehfest method (see Cohen 2007), and view the resulting curve $\tilde{f}(t)$ as the benchmark in Fig. 2a.

Fig. 2

Density and distribution functions in Example 5

We see from Fig. 2a that, when t is small, $\overline{f}_2(t)$, $\overline{f}_4(t)$ and $\overline{f}_6(t)$ are not accurate because they are far from the benchmark. As t increases, $\overline{f}_6(t)$ converges to $\tilde{f}(t)$ earlier than $\overline{f}_4(t)$ and $\overline{f}_2(t)$. When t is large enough, all the curves converge to $\tilde{f}(t)$.

The difference between $\overline{f}_n(t)$ and $\tilde{f}(t)$ is recorded in Table 1. We denote by $d_n:=|\tilde{f}(t)-\overline{f}_n(t)|$ the truncation error of $\overline{f}_n(t)$, for $n=2, 4, 6$. We also set the error tolerance level to be 0.0001. Then, if $d_n<0.0001$, we say $\overline{f}_n(t)$ is sufficiently accurate; otherwise, it is not sufficiently accurate. From Table 1, we know $d_6<0.0001$ for $t\ge 0.054$, so $\overline{f}_6(t)$ is a sufficiently accurate approximation for the density function of $\tau$ when $t\ge 0.054$.

Table 1 Truncation error of (22) and (23) for $n=2, 4, 6$

For the distribution function (11), we define the truncated function

$$\begin{aligned} \overline{F}_n(t):= & {} \frac{1}{\sqrt{3}\pi }\sum _{k=1}^{n} \frac{1}{ \left( k-\frac{2}{3} \right) }\left( 1-e^{-\frac{1}{2}\pi ^2 \left( k-\frac{2}{3} \right) ^2t} \right) \left( \left(-1\right)^{k+1}+1 \right) \\&+\frac{1}{\sqrt{3}\pi }\sum _{k=1}^{n} \frac{1}{ \left( k-\frac{1}{3} \right) }\left( 1-e^{-\frac{1}{2}\pi ^2 \left( k-\frac{1}{3} \right) ^2 t} \right) \left( \left(-1\right)^{k+1}-1 \right) , \end{aligned}$$

and plot $\overline{F}_2(t)$, $\overline{F}_4(t)$ and $\overline{F}_6(t)$ in Fig. 2b. We also invert the Laplace transform $\frac{\mathbb {E}\left(e^{-\beta \tau }\right)}{\beta }$ numerically, and use the resulting curve $\tilde{F}(t)$ as the benchmark in Fig. 2b.

We see from Fig. 2b that, when t is small, the truncated functions are not parallel to $\tilde{F}(t)$. As t increases, they become parallel to the benchmark. Since the gradient of the distribution curve is the density, when the distribution curve is parallel to the benchmark, we know the approximation is relatively accurate.

Next, we consider the density function when t is small. Since (12) converges fast for small t, we truncate it at a fixed level n. Define the truncated function

$$\begin{aligned} \overline{f}_n(t)=\sum _{k=1}^{n}(-1)^{k-1}g(3k-2, t)+\sum _{k=1}^{n}(-1)^{k-1} g(3k-1, t) , \end{aligned}$$

(23)

we plot $\overline{f}_2(t)$, $\overline{f}_4(t)$ and $\overline{f}_6(t)$ in Fig. 2c. We also use the same benchmark as before, i.e., $\tilde{f}(t)$ obtained by inverting the Laplace transform $\mathbb {E}(e^{-\beta \tau })$ numerically.

We see from Fig. 2c that, when t is small, $\overline{f}_2(t)$, $\overline{f}_4(t)$ and $\overline{f}_6(t)$ are accurate. As t increases, $\overline{f}_2(t)$ diverges from the benchmark earlier than $\overline{f}_4(t)$ and $\overline{f}_6(t)$. When t is large enough, all the curves diverge from the benchmark.

The difference between $\overline{f}_n(t)$ and $\tilde{f}(t)$ is recorded in Table 1. We denote by $e_n:=|\tilde{f}(t)-\overline{f}_n(t)|$ the truncation error of $\overline{f}_n(t)$, for $n=2, 4, 6$. From Table 1 we know, with the error tolerance level 0.0001, $\overline{f}_6(t)$ is sufficiently accurate when $t\le 26.945$.

For the distribution function (13), we define the truncated function

$$\begin{aligned} \overline{F}_n(t)=\sum _{k=1}^{n}(-1)^{k-1}\Psi (3k-2, t)+\sum _{k=1}^{n}(-1)^{k-1} \Psi (3k-1, t) , \end{aligned}$$

and plot $\overline{F}_2(t)$, $\overline{F}_4(t)$ and $\overline{F}_6(t)$ in Fig. 2d. We also invert the Laplace transform $\frac{\mathbb {E}(e^{-\beta \tau })}{\beta }$ numerically, and use the resulting curve $\tilde{F}(t)$ as the benchmark in Fig. 2d. We see from the figure that, when t is small, the truncated functions are accurate. As t increases, the curves diverge from the benchmark. Hence the approximation is relatively accurate for small t.

In conclusion, with the truncation level $n=6$ and the error tolerance level 0.0001, the truncated density function (22) is sufficiently accurate for $t\ge 0.054$; while the truncated density function (23) is sufficiently accurate for $t\le 26.945$.

A similar analysis is conducted for Example 6, with the results recorded in Fig. 3 and Table 2. In conclusion, with the truncation level $n=6$ and the error tolerance level 0.0001, the truncated function of (14) is sufficiently accurate for $t\ge 0.055$; while the truncated function of (16) is sufficiently accurate for $t\le 3.181$.

Fig. 3

Density and distribution functions in Example 6

Table 2 Truncation error of (14) and (16) for $n=2, 4, 6$

For Example 7, the numerical results are recorded in Fig. 4 and Table 3. In conclusion, with the truncation level $n=6$ and the error tolerance level 0.0001, the truncated function of (18) is sufficiently accurate for $t\ge 0.261$; while the truncated function of (20) is sufficiently accurate for $t\le 2.995$.

Fig. 4

Density and distribution functions in Example 7

Table 3 Truncation error of (18) and (20) for $n=2, 4, 6$

6 Continuous Extension

In this section, we extend our results to a graph with infinite but countably many semiaxes. Assume that there are n semiaxes, the stationary distribution of the transition probability matrix is uniform, i.e., $\pi _k=\frac{1}{n}$, for $k=1, \dots , n$. We let the upper boundaries be

$$\begin{aligned}b_k=\frac{k}{n}(a_2-a_1)+a_1, \quad \text{for} \quad 0 < a_1 < a_2, k=1, \dots, n. \end{aligned}$$

Then, Corollary 1 implies that the Laplace transform of the first hitting time is

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{\sum _{k=1}^{n}\frac{1}{n}\frac{1}{\sinh \left(b_k\sqrt{2\beta }\right)}}{\sum _{k=1}^{n}\frac{1}{n}\frac{\cosh \left(b_k\sqrt{2\beta }\right)}{\sinh \left(b_k\sqrt{2\beta }\right)}}= \frac{\sum _{k=1}^{n}\frac{1}{n}\frac{1}{\sinh \left(\left(\frac{k}{n}\left(a_2-a_1\right)+a_1\right)\sqrt{2\beta }\right)}}{\sum _{k=1}^{n}\frac{1}{n}\frac{\cosh \left(\left(\frac{k}{n}\left(a_2-a_1\right)+a_1\right)\sqrt{2\beta }\right)}{\sinh \left(\left(\frac{k}{n}\left(a_2-a_1\right)+a_1\right)\sqrt{2\beta }\right)}} . \end{aligned}$$

Taking $n\rightarrow \infty$, the Laplace transform becomes

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) \rightarrow \frac{\int _{a_1}^{a_2}\frac{1}{\sinh (x\sqrt{2\beta })}dx}{\int _{a_1}^{a_2}\frac{\cosh (x\sqrt{2\beta })}{\sinh (x\sqrt{2\beta })}dx}=\frac{\ln \left( \frac{\tanh (\frac{1}{2}a_2\sqrt{2\beta })}{\tanh (\frac{1}{2}a_1\sqrt{2\beta })} \right) }{\ln \left( \frac{\sinh (a_2\sqrt{2\beta })}{\sinh (a_1\sqrt{2\beta })} \right) } . \end{aligned}$$

(24)

Since the poles of the Laplace transform come from both the numerator and denominator, we derive these poles by solving the equations

$$\begin{aligned} \frac{\tanh \left(\frac{1}{2}a_2\sqrt{2\beta }\right)}{\tanh \left(\frac{1}{2}a_1\sqrt{2\beta }\right)}=0 \text {and}\frac{\sinh \left(a_2\sqrt{2\beta }\right)}{\sinh \left(a_1\sqrt{2\beta }\right)}=1 . \end{aligned}$$

Denote by $-\beta ^*$ the poles of (24), we use the residue theorem to calculate the density of the first hitting time:

$$\begin{aligned} f(t)=\sum _{-\beta ^*}\text {Res}(e^{\beta t}\mathbb {E}(e^{-\beta \tau }), -\beta ^*) . \end{aligned}$$

On the other hand, we denote by $x:=e^{-\sqrt{2\beta }}$, then (24) can be written as

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{\ln \left( \frac{1+x^{a_1}-x^{a_2}-x^{a_1+a_2}}{1-x^{a_1}+x^{a_2}-x^{a_1+a_2}} \right) }{\ln \left( \frac{x^{a_1}-x^{a_1+2a_2}}{x^{a_2}-x^{2a_1+a_2}} \right) } , \end{aligned}$$

we can apply the series expansion with respect to x, and invert the resulting function term by term.

Appendix

This appendix contains the proofs of the main results.

1.1 Proof of Theorem 1

Proof

We first study the behaviour of $X^{\epsilon }(t)$. Assume that $X^{\epsilon }(t)$ starts from semiaxis $S_i$, i.e., $X^{\epsilon }(0)=(\epsilon , S_i)$, then it will either hit the upper boundary $b_i$ or return to the origin in finite time. Let $\delta ^{\epsilon }:=\inf \{ t\ge 0 ; ||X^{\epsilon }(t) ||=0 \}$ be the first time $X^{\epsilon }(t)$ returns to the origin, then we know (see Borodin and Salminen 1996 Section II.1.3),

$$\begin{aligned}&\mathbb {E}\left(e^{-\beta \tau ^{\epsilon }_i}\mathbbm {1}_{\{\tau ^{\epsilon }_i<\delta ^{\epsilon }, \Theta ^{\epsilon }(0)=S_i\}} \right) =\frac{\sinh \left(\epsilon \sqrt{2\beta }\right)}{\sinh \left(b_i\sqrt{2\beta }\right)} ,\\&\mathbb {E} \left( e^{-\beta \delta ^{\epsilon }}\mathbbm {1}_{\{\delta ^{\epsilon }<\tau ^{\epsilon }_i, \Theta ^{\epsilon }(0)=S_i\}} \right) =\frac{\sinh \left(\left(b_i-\epsilon \right)\sqrt{2\beta }\right)}{\sinh \left(b_i\sqrt{2\beta }\right)} . \end{aligned}$$

When $\tau ^{\epsilon }_i<\delta ^{\epsilon }$, $X^{\epsilon }(t)$ hits the upper boundary $b_i$ before returning to the origin, and $\tau ^{\epsilon }=\tau ^{\epsilon }_i$; while for $\delta ^{\epsilon }<\tau ^{\epsilon }_i$, $X^{\epsilon }(t)$ returns to the origin without hitting $b_i$, then jumps to $\left(\epsilon , S_j\right)$ with probability $P_{ij}$ and restarts from semiaxis $S_j$. Using the strong Markov property, we have the following system of equations: for $i=1, \dots , n$,

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau ^{\epsilon }}\mathbbm {1}_{\{\Theta ^{\epsilon }(0)=S_i\}} \right)= & \ {} \mathbb {E} \left( e^{-\beta \tau ^{\epsilon }_i}\mathbbm {1}_{\{\tau ^{\epsilon }_i<\delta ^{\epsilon }, \Theta ^{\epsilon }(0)=S_i\}} \right)\\&+\mathbb {E} \left( e^{-\beta \delta ^{\epsilon }}\mathbbm {1}_{\{\delta ^{\epsilon }<\tau ^{\epsilon }_i, \Theta ^{\epsilon }(0)=S_i\}} \right) \left( \sum _{j=1}^{n}P_{ij}\mathbb {E} \left( e^{-\beta \tau ^{\epsilon }}\mathbbm {1}_{\{\Theta ^{\epsilon }(0)=S_j\}} \right) \right) . \end{aligned}$$

(25)

There are n equations in this system, hence it is possible to solve for $\mathbb {E}\left( e^{-\beta \tau ^{\epsilon }}\mathbbm {1}_{\{\Theta ^{\epsilon }(0)=S_i\}}\right)$. However, we are only interested in the first hitting time $\tau$, then there is no need to solve the whole system. Instead, we apply the series expansion with respect to $\epsilon$ on both sides of (25), we have

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau ^{\epsilon }}\mathbbm {1}_{\{\Theta ^{\epsilon }(0)=S_i\}} \right) =K+\sum _{j=1}^{\infty }\epsilon ^j A_{ij}(\beta ), \end{aligned}$$

where K is the constant term and $A_{ij}(\beta )$ is the j-th coefficient of the expansion. Also,

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau ^{\epsilon }_i}\mathbbm {1}_{\{\tau ^{\epsilon }_i<\delta ^{\epsilon }, \Theta ^{\epsilon }(0)=S_i\}} \right) =\frac{\sinh (\epsilon \sqrt{2\beta })}{\sinh (b_i\sqrt{2\beta })}=\sum _{j=1}^{\infty }\epsilon ^jc_{ij}, \end{aligned}$$

where $c_{ij}$ is the j-th coefficient of the series expansion, and

$$\begin{aligned} \mathbb {E} \left(e^{-\beta \delta ^{\epsilon}}I_{\{\delta ^{\epsilon}<\tau ^{\epsilon }_i, \Theta ^{\epsilon }(0)=S_i\}} \right) =\frac{\sinh \left(\left(b_i-\epsilon \right)\sqrt{2\beta}\right)}{\sinh \left(b_i\sqrt{2\beta }\right)}=1+\sum _{j=1}^{\infty }\epsilon ^jl_{ij}, \end{aligned}$$

where $l_{ij}$ is the j-th coefficient of the series expansion.

Then, we can write (25) as

$$\begin{aligned} K+\sum _{j=1}^{\infty }\epsilon ^j A_{ij}(\beta )= \left( \sum _{j=1}^{\infty }\epsilon ^jc_{ij} \right) + \left( 1+\sum _{j=1}^{\infty }\epsilon ^jl_{ij} \right) \left( \sum _{j=1}^{n}P_{ij} \left( K+\sum _{k=1}^{\infty }\epsilon ^k A_{jk}(\beta ) \right) \right) . \end{aligned}$$

This equation can be expanded to

$$\begin{aligned} \sum _{j=1}^{\infty }\epsilon ^j A_{ij}(\beta )= \left( \sum _{j=1}^{\infty }\epsilon ^jc_{ij} \right) + K\left( \sum _{j=1}^{\infty }\epsilon ^jl_{ij} \right) + \left( 1+\sum _{j=1}^{\infty }\epsilon ^jl_{ij} \right) \left( \sum _{j=1}^{n}P_{ij} \sum _{k=1}^{\infty }\epsilon ^k A_{jk}(\beta ) \right) . \end{aligned}$$

Note that every term in this equation contains $\epsilon$, and those terms with the same power of $\epsilon$ must coincide. Hence for those terms containing $\epsilon ^1$, we have

$$\begin{aligned} \epsilon A_{i1}(\beta )=\epsilon c_{i1}+K\epsilon l_{i1}+\sum _{j=1}^{n}P_{ij} \epsilon A_{j1}(\beta ) . \end{aligned}$$

Since $\epsilon > 0$, we cancel $\epsilon$ on both sides, this gives

$$\begin{aligned} A_{i1}(\beta )=c_{i1}+Kl_{i1}+\sum _{j=1}^{n}P_{ij} A_{j1}(\beta ) , \text {for}i=1, \dots , n. \end{aligned}$$

(26)

We write the system of Eq. (26) in matrix form:

$$\begin{aligned} \begin{pmatrix} A_{11}(\beta )\\ A_{21}(\beta )\\ \ldots \\ A_{n1}(\beta ) \end{pmatrix}= \begin{pmatrix} c_{11}\\ c_{21}\\ ..\\ c_{n1} \end{pmatrix}+ \begin{pmatrix} P_{11} &{} P_{12} &{} .. &{} P_{1n}\\ P_{21} &{} P_{22} &{} .. &{} P_{2n}\\ \ldots &{} \ldots &{} .. &{} \ldots \\ P_{n1} &{} P_{n2} &{} .. &{} P_{nn}\\ \end{pmatrix} \begin{pmatrix} A_{11}(\beta )\\ A_{21}(\beta )\\ \ldots \\ A_{n1}(\beta ) \end{pmatrix}+K \begin{pmatrix} l_{11}\\ l_{21}\\ \ldots \\ l_{n1} \end{pmatrix}, \end{aligned}$$

(27)

where $\mathbf{P} =(P_{ij})_{n\times n}$ is the transition probability matrix. We denote by $\Pi :=(\pi _1, \dots , \pi _n)$ the stationary distribution of $\mathbf{P}$, such that $\sum _{i=1}^{n}\pi _i=1$ and $\Pi \mathbf{P} =\Pi$, and multiply the vector $\Pi$ on both sides of (27), this gives

$$\begin{aligned} K=-\frac{\pi _1c_{11}+\pi _2c_{21}+\ldots +\pi _nc_{n1}}{\pi _1l_{11}+\pi _2l_{21}+\ldots +\pi _nl_{n1}}=\frac{\sum _{k=1}^{n}\pi _k\frac{1}{\sinh (b_k\sqrt{2\beta })}}{\sum _{k=1}^{n}\pi _k\frac{\cosh (b_k\sqrt{2\beta })}{\sinh (b_k\sqrt{2\beta })}} , \end{aligned}$$

where we already know $c_{i1}=\frac{\sqrt{2\beta }}{\sinh (b_i\sqrt{2\beta })}$ and $l_{i1}=-\sqrt{2\beta }\frac{\cosh (b_i\sqrt{2\beta })}{\sinh (b_i\sqrt{2\beta })}$.

But K is the constant term of the series expansion of $\mathbb {E}\left(e^{-\beta \tau ^{\epsilon }}\mathbb {1}_{\{\Theta ^{\epsilon }(0)=S_i\}}\right)$, hence

$$\begin{aligned} \lim \limits _{\epsilon \rightarrow 0}\mathbb {E} \left( e^{-\beta \tau ^{\epsilon }}\mathbbm {1}_{\{\Theta ^{\epsilon }(0)=S_i\}} \right) =K. \end{aligned}$$

(28)

Equation (28) implies that, as $\epsilon \rightarrow 0$, the Laplace transform of $\tau ^{\epsilon }\mathbbm {1}_{\{ \Theta ^{\epsilon }(0)=S_i \}}$ does not depend on the initial semiaxis $S_i$. In fact, as $\epsilon \rightarrow 0$, the initial position of $X^{\epsilon }(t)\mathbbm {1}_{\{ \Theta ^{\epsilon }(0)=S_i \}}$ converges to the origin from semiaxis $S_i$. On the other hand, we know that a Brownian motion will make an infinite number of very small excursions around the origin before any $t>0$. Hence, when the transition probability matrix $\mathbf{P}$ is aperiodic, the limiting process $\lim \limits _{\epsilon \rightarrow 0} X^{\epsilon }(t)\mathbbm {1}_{\{ \Theta ^{\epsilon }(0)=S_i \}}$ will eventually choose the semiaxis according to the limiting distribution of $\mathbf{P}$, which is identical to its stationary distribution $\Pi$ (see Privault 2018). While for a periodic $\mathbf{P}$, after an infinite number of transitions, the limiting process has a uniform probability to be in any semiaxis that belongs to the closed communicating class of $\mathbf{P}$. Hence, the choice of semiaxis is also identical to the stationary distribution $\Pi$. The same argument also applies to the original process X(t).

In the meanwhile, the limiting process $\lim \limits _{\epsilon \rightarrow 0} X^{\epsilon }(t)\mathbbm {1}_{\{ \Theta ^{\epsilon }(0)=S_i \}}$ behaves as a Brownian motion starting from 0 on each semiaxis, which is identical to X(t). Together with the argument above, we know $\lim \limits _{\epsilon \rightarrow 0} X^{\epsilon }(t)\mathbbm {1}_{\{\Theta ^{\epsilon }(0)=S_i\}}\rightarrow X(t)$ in a pathwise sense, then $\lim \limits _{\epsilon \rightarrow 0}\tau ^{\epsilon }\mathbbm {1}_{\{\Theta ^{\epsilon }(0)=S_i\}}\rightarrow \tau$ in distribution, and

$$\begin{aligned} \lim \limits _{\epsilon \rightarrow 0}\mathbb {E} \left( e^{-\beta \tau ^{\epsilon }}\mathbbm {1}_{\{\Theta ^{\epsilon }(0)=S_i\}} \right) =\mathbb {E} \left( e^{-\beta \tau } \right) . \end{aligned}$$

(29)

It follows from (28) and (29) that

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =K. \end{aligned}$$

When $b_p^*\ne 0$, the initial state of X(t) is $X(0)=(b_p^*, S_p)$, for some $p=1, \dots , n$. Then, X(t) will either hit the upper boundary $b_p$ before returning to the origin, or arrive at the origin without hitting $b_p$. Using the similar method as above, we know

$$\begin{aligned} \mathbb {E}_{b^*_p} \left( e^{-\beta \tau } \right) =\frac{\sinh (b_p^*\sqrt{2\beta })}{\sinh (b_p\sqrt{2\beta })}+\frac{\sinh ((b_p-b_p^*)\sqrt{2\beta })}{\sinh (b_p\sqrt{2\beta })}\mathbb {E} \left( e^{-\beta \tau } \right) . \end{aligned}$$

The expectation of $\tau$ can be calculated by applying the moment generating function, then the theorem is proved. $\square$

1.2 Proof of Lemma 1

Proof

The poles of (2) are equivalent to the roots of its denominator. We notice that the Laplace transform (2) has the limit $\lim \limits _{\beta \rightarrow 0}\mathbb {E}(e^{\beta \tau })=1$, hence $\beta =0$ is not a pole of (2). For this reason, we look for the solutions of the equation

$$\begin{aligned} \sum _{k=1}^{n}\pi _k\frac{1}{\sqrt{2\beta }}\frac{\cosh (b_k\sqrt{2\beta })}{\sinh (b_k\sqrt{2\beta })}=0. \end{aligned}$$

(30)

Using the inverse Laplace transform (see Borodin and Salminen 1996 Appendix 2. 11) and the general Theta function transformation (see Bellman 1961 Section 19), we know

$$\begin{aligned} \mathscr{L}^{-1} \left( \frac{\cosh \left(b_k\sqrt{2\beta }\right)}{\sqrt{2\beta }\sinh \left(b_k\sqrt{2\beta }\right)} \right) = \frac{1}{\sqrt{2\pi t}}\sum _{n=-\infty }^{\infty }e^{-\frac{2b_k^2\left(2n+1\right)^2}{t}} = \frac{1}{2b_k}\sum _{n=-\infty }^{\infty }e^{-n^2\pi ^2 \frac{t}{2b_k^2}}, \ t>0. \end{aligned}$$

Then we invert both sides of (30), this gives

$$\begin{aligned} \sum _{k=1}^{n}\frac{\pi _k}{2b_k}\int _{0}^{\infty }e^{-\beta t}\sum _{n=-\infty }^{\infty }e^{-n^2\pi ^2\frac{t}{2b_k^2}}dt=0 . \end{aligned}$$

(31)

We assume that the roots of (31) have the format $x+iy$, for $x, y\in \mathbb {R}$, then

$$\begin{aligned} \sum _{k=1}^{n}\frac{\pi _k}{2b_k}\int _{0}^{\infty }e^{-xt} \left( \cos \left(yt\right)-i\sin \left(yt\right) \right) \sum _{n=-\infty }^{\infty }e^{-n^2\pi ^2 \frac{t}{2b_k^2}}dt=0 . \end{aligned}$$

For the imaginary component of the equation, we calculate the integral

$$\begin{aligned} \int _{0}^{\infty }e^{-xt}\sin (yt)e^{-n^2\pi ^2 \frac{t}{2b_k^2}}dt=\frac{y}{\left( x+n^2\pi ^2 \frac{1}{2b_k^2} \right) ^2+y^2} , \end{aligned}$$

hence we must have $y=0$, for otherwise the imaginary component cannot be zero. This means the roots are real numbers. Next, we set $\beta =x$ in Eq. (30), then we have

$$\begin{aligned} \sum _{k=1}^{n}\frac{\pi _k}{\sqrt{2x}}\coth \left(b_k\sqrt{2x}\right)=0. \end{aligned}$$

Since $\coth (x)>0$, for $x\in \mathbb {R}^+$, this equation cannot hold for any positive real x, this means x must be negative real numbers. We denote by $-\beta ^*$ the roots of Eq. (30), where $\beta ^*>0$, then we have

$$\begin{aligned} \sum _{k=1}^{n}\pi _k\cot (b_k\sqrt{2\beta ^*})=0 . \end{aligned}$$

(32)

Next, we proceed to solve Eq. (32) under the assumption that the upper boundaries $\{b_i\}_{i=1, \dots , n}$ are integers. For any positive integer n, the multiple-angle formula implies

$$\begin{aligned} \cot (n\theta )=\frac{\sum \limits _{k\text { even}}(-1)^{\frac{k}{2}}\left( {\begin{array}{c}n\\ k\end{array}}\right) \tan (\theta )^k}{\sum \limits _{k\text { odd}}(-1)^{\frac{k-1}{2}}\left( {\begin{array}{c}n\\ k\end{array}}\right) \tan (\theta )^k } . \end{aligned}$$

Then, Eq. (32) can be written as

$$\begin{aligned}\sum _{k=1}^{n}\pi _k\cot (b_k\sqrt{2\beta ^*})&= \sum _{i=1}^{n}\pi _i\frac{\sum \limits _{k\text { even}}(-1)^{\frac{k}{2}}\left( {\begin{array}{c}b_i\\ k\end{array}}\right) \tan (\sqrt{2\beta ^*})^k}{\sum \limits _{k\text { odd}}(-1)^{\frac{k-1}{2}}\left( {\begin{array}{c}b_i\\ k\end{array}}\right) \tan (\sqrt{2\beta ^*})^k } \\&=\frac{\sum _{i=1}^{n}\pi _i \left( \sum \limits _{k\text { even}}(-1)^{\frac{k}{2}}\left( {\begin{array}{c}b_i\\ k\end{array}}\right) y^k \prod _{j=\{1,\dots , n\}\setminus \{i\}} \left( \sum \limits _{k\text { odd}}(-1)^{\frac{k-1}{2}}\left( {\begin{array}{c}b_j\\ k\end{array}}\right) y^k \right) \right) }{\prod _{i=1}^{n} \left( \sum \limits _{k\text { odd}}(-1)^{\frac{k-1}{2}}\left( {\begin{array}{c}b_i\\ k\end{array}}\right) y^k \right) }=0 , \end{aligned}$$

(33)

where we denote by $y:=\tan (\sqrt{2\beta ^*})$. Note that $y=0$ is not a solution to this equation, for otherwise Eq. (32) cannot hold. For this reason, we only need to consider the numerator part of (33):

$$\begin{aligned} \sum _{i=1}^{n}\pi _i \left( \sum \limits _{k\text { even}}(-1)^{\frac{k}{2}}\left( {\begin{array}{c}b_i\\ k\end{array}}\right) y^k \prod _{j=\{1,\dots , n\}\setminus \{i\}} \left( \sum \limits _{k\text { odd}}(-1)^{\frac{k-1}{2}}\left( {\begin{array}{c}b_j\\ k\end{array}}\right) y^k \right) \right) =0. \end{aligned}$$

This approach is also sufficient when $\{b_i\}_{i=1, \dots , n}$ are rational numbers. Let $c_i$ and $d_i$ be positive integers, such that $b_i=\frac{c_i}{d_i}$, for $i=1, \dots , n$, then

$$\begin{aligned} b_i\sqrt{2\beta ^*}=\frac{c_i}{d_i}\sqrt{2\beta ^*}=c_i \left( \prod _{j=\{1,\dots , n\}\setminus \{i\}}d_j \right) \theta , \end{aligned}$$

where we denote by $\theta :=\frac{1}{d_1\ldots d_n}\sqrt{2\beta ^*}$. Since $c_i \left( \prod _{j=\{1,\dots , n\}\setminus \{i\}}d_j \right)$ is a positive integer, we can replace $b_i\sqrt{2\beta ^*}$ by $c_i \left( \prod _{j=\{1,\dots , n\}\setminus \{i\}}d_j \right) \theta$ in Eq. (32), and follow the rest of the proof. Then the lemma is proved. $\square$

1.3 Proof of Theorem 2

Proof

We rewrite the Laplace transform (2) as

$$\begin{aligned} \mathbb {E} \left( e^{-\beta \tau } \right) =\frac{\sum _{k=1}^{n}\pi _k\frac{\sqrt{2\beta }}{\sinh (b_k\sqrt{2\beta })}}{\sum _{k=1}^{n}\pi _k\sqrt{2\beta }\frac{\cosh (b_k\sqrt{2\beta })}{\sinh (b_k\sqrt{2\beta })}} . \end{aligned}$$

(34)

From Borodin and Salminen (1996) Appendix 2. 11, we know the inverse Laplace transform

$$\begin{aligned} \mathscr {L}^{-1} \left( \frac{\sqrt{2\beta }}{\sinh (b_i\sqrt{2\beta })} \right) =\frac{\sqrt{2}}{\sqrt{\pi t^5}}\sum _{n=0}^{\infty } \left( \left(2n+1\right)^2b_i^2-t \right) e^{-\frac{\left(2n+1\right)^2 b_i^2}{2t}} , \ t>0, \end{aligned}$$

hence we can invert the numerator of (34) as follows:

$$\begin{aligned} \mathscr {L}^{-1} \left( \sum _{k=1}^{n}\pi _k\frac{\sqrt{2\beta }}{\sinh (b_k\sqrt{2\beta })} \right) =\sum _{k=1}^{n} \left( \pi _k \frac{\sqrt{2}}{\sqrt{\pi t^5}} \sum _{n=0}^{\infty } \left( \left(2n+1\right)^2 b_k^2-t \right) e^{-\frac{(2n+1)^2 b_k^2}{2t}} \right) , \ t>0 . \end{aligned}$$

Next, we proceed to invert the denominator part of (34). Since $b_k$ are rational numbers, there exist positive integers $c_k$ and $d_k$, such that $b_k=\frac{c_k}{d_k}$, for $k=1,\ldots ,n$. We denote by $z:=e^{-2\sqrt{2\beta }\frac{1}{d_1\ldots d_n}}$ and $m_k:=c_k\prod _{p\in \{1,\ldots ,n\}\setminus \{k\}}d_p$, then the denominator can be written as

$$\begin{aligned} \sum _{k=1}^{n}\pi _k\sqrt{2\beta }\frac{\cosh \left(b_k\sqrt{2\beta }\right)}{\sinh \left(b_k\sqrt{2\beta}\right)} &= \sum _{k=1}^{n}\pi _k\sqrt{2\beta }\frac{1+\left(e^{-2\sqrt{2\beta}\frac{1}{d_1\ldots d_n}}\right)^{c_k\prod _{p\in \{1,\ldots ,n\}\setminus \{k\}}d_p}}{1-\left(e^{-2\sqrt{2\beta}\frac{1}{d_1\ldots d_n}}\right)^{c_k\prod _{p\in \{1,\ldots ,n\}\setminus \{k\}}d_p}}\\&=\sum _{k=1}^{n}\pi _k\sqrt{2\beta }\frac{1+z^{m_k}}{1-z^{m_k}}\\&=\sqrt{2\beta}\frac{\sum _{k=1}^{n} \left( \pi _k(1+z^{m_k})\prod _{p\in \{1,\ldots ,n\}\setminus \{k\}}(1-z^{m_p}) \right)}{\prod _{k=1}^{n}\left(1-z^{m_k}\right)}&. \end{aligned}$$

Then inverting the denominator part of (34) is equivalent to inverting the expression:

$$\begin{aligned} \frac{1}{\sqrt{2\beta }} \left( \prod _{k=1}^{n}\left(1-z^{m_k}\right) \right) \frac{1}{\sum _{k=1}^{n} \left( \pi _k(1+z^{m_k})\prod _{p\in \{1,\ldots ,n\}\setminus \{k\}}\left(1-z^{m_p}\right) \right) } . \end{aligned}$$

(35)

This can be viewed as the product of three Laplace transforms, hence we will invert them separately, and present the final result as their convolution.

For the first Laplace transform, we have

$$\begin{aligned} \mathscr {L}^{-1} \left( \frac{1}{\sqrt{2\beta }} \right) = \frac{1}{\sqrt{2\pi t}}, t>0. \end{aligned}$$

For the second Laplace transform, we know

$$\begin{aligned} \mathscr {L}^{-1}(1-z^{m_k})=\mathscr {L}^{-1} \left( 1-e^{-2\sqrt{2\beta }b_k} \right) =\delta (t)-g\left( 2b_k, t \right) , t>0 , \end{aligned}$$

where $\delta (t)$ denotes the Dirac Delta function and g(x, t) represents the inverse Gaussian density with parameter x. Then the inverse of $\prod _{k=1}^{n}\left(1-z^{m_k}\right)$ can be written as the convolution of this result.

For the third Laplace transform, since $m_k$ are integers, the expression

$$\begin{aligned} L(z):=\sum _{k=1}^{n} \left( \pi _k(1+z^{m_k})\prod _{p\in \{1,\ldots ,n\}\setminus \{k\}}(1-z^{m_p}) \right) \end{aligned}$$

can be interpreted as a polynomial with variable z. We notice that all the poles of the Laplace transform come from the roots of this polynomial. On the other hand, these poles have been derived in Lemma 1. Hence we can rewrite the polynomial as

$$\begin{aligned} L(z)= \prod _{m=1}^{\infty } \left( z-e^{-2\sqrt{-2\beta ^*_m}\frac{1}{d_1\ldots d_n}} \right) . \end{aligned}$$

Thus, we have

$$\begin{aligned} \frac{1}{L(z)}&=\prod _{m=1}^{\infty }\frac{1}{z-e^{-2\sqrt{-2\beta ^*_m}\frac{1}{d_1\ldots d_n}}}=\sum _{m=1}^{\infty }\frac{A_m}{z-e^{-2\sqrt{-2\beta ^*_m}\frac{1}{d_1\ldots d_n}}}\\& =\sum _{m=1}^{\infty }A_m \sum _{k=0}^{\infty }(-1)^k z^k \left( -e^{-2\sqrt{-2\beta ^*_m}\frac{1}{d_1\dots d_n}} \right) ^{-1-k}&, \end{aligned}$$

where

$$\begin{aligned} A_m=\left( \prod _{p\in \mathbb {Z}^+\setminus \{m\}} \left( e^{-2\sqrt{-2\beta ^*_p}\frac{1}{d_1\ldots d_n}}-e^{-2\sqrt{-2\beta ^*_m}\frac{1}{d_1\ldots d_n}} \right) \right) ^{-1}. \end{aligned}$$

Then we can invert 1/L(z) term by term:

$$\begin{aligned} \mathscr {L}^{-1} \left( \frac{1}{L(z)} \right) = \sum _{m=1}^{\infty } A_m \sum _{k=0}^{\infty }(-1)^k g \left( \frac{2k}{d_1\dots d_n}, t \right) \left( -e^{-2\sqrt{-2\beta ^*_m}\frac{1}{d_1\dots d_n}} \right) ^{-1-k} . \end{aligned}$$

Finally, the density of $\tau$ can be written as the convolution of the results above.

For the distribution function of $\tau$, we need to invert $\frac{E\left(e^{-\beta \tau }\right)}{\beta }$, but this is equivalent to replacing the term $\frac{1}{\sqrt{2\beta }}$ by $\frac{1}{\sqrt{2\beta ^3}}$ in (35). Since

$$\begin{aligned} \mathscr {L}^{-1}\left( \frac{1}{\sqrt{2\beta ^3}} \right) =\frac{\sqrt{2t}}{\sqrt{\pi }}, t>0, \end{aligned}$$

we only need to change the resulting function accordingly, and the theorem is proved. $\square$

1.4 Proof of Theorem 3

Proof

The poles of the Laplace transform (2) have been derived in Lemma 1, we first show that they are simple poles. The denominator of (2) has the derivative:

$$\begin{aligned} \frac{d}{d\beta } \left( \sum _{k=1}^{n}\pi _k\frac{\cosh (b_k\sqrt{2\beta })}{\sinh (b_k\sqrt{2\beta })} \right) =\frac{1}{\sqrt{2\beta }} \sum _{k=1}^{n}\pi _kb_k \left( 1-\frac{\cosh ^2(b_k\sqrt{2\beta })}{\sinh ^2(b_k\sqrt{2\beta })} \right) , \end{aligned}$$

and the limits of this derivative at the poles are non-zero, i.e.,

$$\begin{aligned} \lim \limits _{\beta \rightarrow -\beta ^*}\frac{d}{d\beta } \left( \sum _{k=1}^{n}\pi _k\frac{\cosh (b_k\sqrt{2\beta })}{\sinh (b_k\sqrt{2\beta })} \right) =\frac{1}{i\sqrt{2\beta ^*}} \sum _{k=1}^{n}\pi _k b_k \left( 1+\frac{\cos ^2(b_k\sqrt{2\beta ^*})}{\sin ^2(b_k\sqrt{2\beta ^*})} \right) \ne 0 , \end{aligned}$$

this implies that $-\beta ^*$ are simple poles.

Next, we introduce an explicit inverse method for the Laplace transform (2). Denote by $\hat{f}(\beta )$ the Laplace transform (2), and f(t) its inverse. From the Bromwich integral (see Lang 2013), we know

$$\begin{aligned} f(t)=\frac{1}{2\pi i}\int _{-i\infty }^{+i\infty }e^{\beta t}\hat{f}(\beta )d\beta . \end{aligned}$$

This integral can be calculated via the residue theorem, that is,

$$\begin{aligned} f(t)=\sum _{-\beta ^*}\text {Res} \left( e^{\beta t}\hat{f}(\beta ), -\beta ^* \right) . \end{aligned}$$

Since the poles of (2) are simple poles, we can calculate the residues by evaluating the limit

$$\begin{aligned} \text {Res} \left( e^{\beta t}\hat{f}(\beta ), -\beta ^* \right) =\lim \limits _{\beta \rightarrow -\beta ^*} \left( \left( \beta -(-\beta ^*) \right) e^{\beta t}\hat{f}(\beta ) \right) , \end{aligned}$$

it follows that

$$\begin{aligned} f(t)=\sum _{-\beta ^*}e^{-\beta ^* t}\frac{\sum _{k=1}^{n}\pi _k\frac{\sqrt{2\beta ^*}}{\sin (b_k\sqrt{2\beta ^*})}}{\sum _{k=1}^{n}\pi _k b_k+\sum _{k=1}^{n}\pi _k b_k\frac{\cos ^2(b_k\sqrt{2\beta ^*})}{\sin ^2(b_k\sqrt{2\beta ^*})}} . \end{aligned}$$

For the distribution function, we integrate f(t) over (0, t), and the theorem is proved. $\square$