Skip to main content
SpringerLink
Log in

Strong Convergence of the Euler-Maruyama Method for Nonlinear Stochastic Convolution Itô-Volterra Integral Equations with Constant Delay

  • Published:
Methodology and Computing in Applied Probability Aims and scope Submit manuscript

Abstract

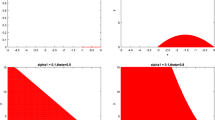
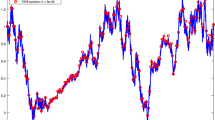
This paper mainly focuses on the strong convergence of the Euler-Maruyama method for nonlinear stochastic convolution Itô-Volterra integral equations with constant delay. It is well known that the strong approximation of the Itô integral usually leads to 0.5-order approximation for stochastic problems. However, in this paper, we will show that 1-order strong superconvergence can be obtained for nonlinear stochastic convolution Itô-Volterra integral equations with constant delay under some mild conditions on the kernel of the diffusion term. Finally, some numerical experiments are given to illustrate our theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Adams RA, Fournier JJF (2009) Sobolev spaces. Academic Press, New York

    MATH  Google Scholar 

  • Bahar A, Mao XR (2004) Stochastic delay Lotka-Volterra model. J Math Anal Appl 292:364–380

    Article  MathSciNet  Google Scholar 

  • Bellour A, Bousselsal M (2014) A Taylor collocation method for solving delay integral equations. Numer Algor 65:843–857

    Article  MathSciNet  Google Scholar 

  • Berger M, Mizel V (1980) Volterra equations with Itô integrals I and II. J Integral Equ 2:187–45 and 319-337

    MATH  Google Scholar 

  • Brunner H (1994) Iterated collocation methods for Volterra integral equations with delay arguments. Math Comp 62:581–599

    Article  MathSciNet  Google Scholar 

  • Brunner H (1994) Collocation and continuous implicit Runge-Kutta methods for a class of delay Volterra integral equations. J Comput Appl Math 53:61–72

    Article  MathSciNet  Google Scholar 

  • Brunner H (2004) Collocation methods for Volterra integral and related function equations. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  • Brunner H (2009) Recent advances in the numerical analysis of Volterra functional differential equations with variable delays. J Comput Appl Math 228:524–537

    Article  MathSciNet  Google Scholar 

  • Cahlon B (1990) On the numerical stability of Volterra integral equations with delay argument. J Comput Appl Math 33(1):97–104

    Article  MathSciNet  Google Scholar 

  • Heydari MH, Hooshmandasl MR, Maalek Ghaini FM, Cattani C (2014) A computational method for solving stochastic Itô-volterra integral equations based on stochastic operational matrix for generalized hat basis functions. J Comput Phys 270:402–415

    Article  MathSciNet  Google Scholar 

  • Itô I (1979) On the existence and uniqueness of solutions of stochastics integral equations of the Volterra type. Kodai Math J 2:158–170

    Article  MathSciNet  Google Scholar 

  • Lamm PK (2000) A survey of regularization methods for first-kind Volterra equations, surveys on solution methods for inverse problems. Springer, Vienna, pp 53–82

    Book  Google Scholar 

  • Liang H, Yang ZW, Gao JF (2017) Strong superconvergence of Euler-maruyama mathod for linear stochastic Volterral integral equations. J Comput Appl Math 317:447–457

    Article  MathSciNet  Google Scholar 

  • Maleknejad K, Khodabin M, Rostami M (2012) Numerical solution of stochastic Volterra integral equations by a stochastic operational matrix based on block pulse functions. Math Comput Model 55:791–800

    Article  MathSciNet  Google Scholar 

  • Mao XR (1997) Stochastic differential equations and their applications. Horwood Publishing Series in Mathematics & Applications, Horwood, Chichester

  • Maruyama G (1955) Continuous Markov processes and stochastic equations. Rend Circ Mat Palermo 4:48–90

    Article  MathSciNet  Google Scholar 

  • Mirzaee F, Hamzeh A (2016) A computational method for solving nonlinear stochastic Volterra integral equations. J Comput Appl Math 306:166–178

    Article  MathSciNet  Google Scholar 

  • Mohammadi F (2015) A wavelet-based computational method for solving stochastic Itô-volterra integral equations. J Comput Phys 298:254–265

    Article  MathSciNet  Google Scholar 

  • Mirzaee F, Hadadiyan E (2014) A collocation technique for solving nonlinear Stochastic Itô-volterra integral equations. Appl Math Comput 247:1011–1020

    MathSciNet  MATH  Google Scholar 

  • Pardoux E, Protter P (1990) Stochastic Volterra equations with anticipating coefficients. Ann. Cambridge University Press, Cambridge, 2004. Probab 18:1635–1655

    MathSciNet  MATH  Google Scholar 

  • Vermiglio R (1992) On the stability of Runge-Kutta methods for delay integral equations. Numer Math 61:561–577

    Article  MathSciNet  Google Scholar 

  • Wen CH, Zhang TS (2011) Improved rectangular method on stochastic Volterra equations. J Comput Appl Math 235:2492–2501

    Article  MathSciNet  Google Scholar 

  • Yang ZW, Ma SF, Liang H Strong convergence of semi-implicit Euler mathod for linear stochastic Volterral integral equations, submitted

  • Zhang XC (2008) Euler schemes and large deviations for stochastic Volterra equations with singular kernels. J Differ Equations 244:2226–2250

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

This work is supported by the Fundamental Research Funds for Central Universities (2572018BC19).

Author information

Authors and Affiliations

  1. Department of Mathematics, Northeast Forest University, Harbin, Heilongjiang, China

    Shu Fang Ma

  2. School of Mathematical Sciences, Harbin Normal University, Harbin, Heilongjiang, China

    Jian Fang Gao

  3. Department of Mathematic, Harbin Institute of Technology, Harbin, Heilongjiang, China

    Zhan Wen Yang

Authors
  1. Shu Fang Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jian Fang Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhan Wen Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jian Fang Gao.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ma, S.F., Gao, J.F. & Yang, Z.W. Strong Convergence of the Euler-Maruyama Method for Nonlinear Stochastic Convolution Itô-Volterra Integral Equations with Constant Delay. Methodol Comput Appl Probab 22, 223–235 (2020). https://doi.org/10.1007/s11009-019-09702-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11009-019-09702-y

Keywords

Mathematics Subject Classification (2010)

Search

Navigation