Skip to main content
SpringerLink
Log in

Telegraph Process with Elastic Boundary at the Origin

  • Published:
Methodology and Computing in Applied Probability Aims and scope Submit manuscript

Abstract

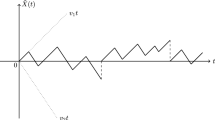
We investigate the one-dimensional telegraph random process in the presence of an elastic boundary at the origin. This process describes a finite-velocity random motion that alternates between two possible directions of motion (positive or negative). When the particle hits the origin, it is either absorbed, with probability α, or reflected upwards, with probability 1−α. In the case of exponentially distributed random times between consecutive changes of direction, we obtain the distribution of the renewal cycles and of the absorption time at the origin. This investigation is performed both in the case of motion starting from the origin and non-zero initial state. We also study the probability law of the process within a renewal cycle.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abramowitz M, Stegun I A (1994) Handbook of Mathematical Functions with Formulas, Graph, and Mathematical Tables Reprint of the 1972 edition. Dover, New York

    MATH  Google Scholar 

  • Acebrón J A, Ribeiro M A (2015) A Monte Carlo method for solving the one-dimensional telegraph equations with boundary conditions. J Comput Phys 305:29–43

    Article  MathSciNet  MATH  Google Scholar 

  • Beghin L, Nieddu L, Orsingher E (2001) Probabilistic analysis of the telegrapher’s process with drift by means of relativistic transformations. J Appl Math Stoch Anal 14:1–25

    Article  MathSciNet  MATH  Google Scholar 

  • Beghin L, Orsingher E (2009) Iterated elastic Brownian motions and fractional diffusion equations. Stoch Proc Appl 119:1975–2003

    Article  MathSciNet  MATH  Google Scholar 

  • Bogachev L, Ratanov N (2011) Occupation time distributions for the telegraph process. Stoch Proc Appl 121:1816–1844

    Article  MathSciNet  MATH  Google Scholar 

  • Buonocore A, Esposito G, Giorno V, Valerio C (2003) Towards dead time inclusion in neuronal modeling. Sci Math Jpn 58:323–334

    MathSciNet  MATH  Google Scholar 

  • Crimaldi I, Di Crescenzo A, Iuliano A, Martinucci B (2013) A generalized telegraph process with velocity driven by random trials. Adv Appl Prob 45:1111–1136

    Article  MathSciNet  MATH  Google Scholar 

  • De Gregorio A, Macci C (2012) Large deviation principles for telegraph processes. Stat Prob Lett 82:1874–1882

    Article  MathSciNet  MATH  Google Scholar 

  • De Gregorio A, Orsingher E (2011) Flying randomly in R d with Dirichlet displacements. Stoch Proc Appl 122:676–713

    Article  MATH  Google Scholar 

  • Di Crescenzo A, Martinucci B (2010) A damped telegraph random process with logistic stationary distribution. J Appl Prob 47:84–96

    Article  MathSciNet  MATH  Google Scholar 

  • Di Crescenzo A, Zacks S (2015) Probability law and flow function of Brownian motion driven by a generalized telegraph process. Methodol Comput Appl Probab 17:761–780

    Article  MathSciNet  MATH  Google Scholar 

  • Dominé M (1995) Moments of the first-passage time of a Wiener process with drift between two elastic barriers. J Appl Prob 32:1007–1013

    Article  MathSciNet  MATH  Google Scholar 

  • Dominé M (1996) First passage time distribution of a Wiener process with drift concerning two elastic barriers. J Appl Prob 33:164–175

    Article  MathSciNet  MATH  Google Scholar 

  • D’Ovidio M, Orsingher E, Toaldo B (2014) Time-changed processes governed by space-time fractional telegraph equations. Stoch Anal Appl 32:1009–1045

    Article  MathSciNet  MATH  Google Scholar 

  • Erdelyi A (1954) Tables of Integral Transforms, vol 1. McGraw-Hill, New York

  • Fontbona J, Guérin H, Malrieu F (2012) Quantitative estimates for the long-time behavior of an ergodic variant of the telegraph process. Adv Appl Prob 44:977–994

    MathSciNet  MATH  Google Scholar 

  • Foong S K (1992) First-passage time, maximum displacement, and Kac’s solution of the telegrapher equation. Phys Rev A 46:R707–R710

    Article  MathSciNet  Google Scholar 

  • Garra R, Orsingher E (2014) Random flights governed by Klein-Gordon-type partial differential equations. Stoch Proc Appl 124:2171–2187

    Article  MathSciNet  MATH  Google Scholar 

  • Giona M, Brasiello A, Crescitelli S (2016) Generalized Poisson–Kac processes: basic properties and implications in extended thermodynamics and transport. J Non-Equilib Thermodyn 41:107–114

    Article  Google Scholar 

  • Giorno V, Nobile A G, Pirozzi E, Ricciardi L M (2006) On the construction of first-passage-time densities for diffusion processes. Sci Math Jpn 64:277–298

    MathSciNet  MATH  Google Scholar 

  • Goldstein S (1951) On diffusion by discontinuous movements, and on the telegraph equation. Quart J Mech Appl Math 4:129–156

    Article  MathSciNet  MATH  Google Scholar 

  • Jacob E (2012) A Langevin process reflected at a partially elastic boundary: I. Stoch Proc Appl 122:191–216

    Article  MathSciNet  MATH  Google Scholar 

  • Jacob E (2013) Langevin process reflected on a partially elastic boundary II. Séminaire de Probabilités XLV:245-275, Lecture Notes in Math, 2078, Springer, Cham

  • Kac M (1974) A stochastic model related to the telegrapher’s equation. Rocky Mountain J Math 4:497–509

    Article  MathSciNet  MATH  Google Scholar 

  • Kolesnik A D, Ratanov N (2013) Telegraph Processes and Option Pricing Springer Briefs in Statistics. Springer, Heidelberg

    Book  MATH  Google Scholar 

  • López O, Ratanov N (2014) On the asymmetric telegraph processes. J Appl Prob 51:569–589

    Article  MathSciNet  MATH  Google Scholar 

  • Masoliver J, Porrà J M, Weiss G H (1992) Solutions of the telegrapher’s equation in the presence of traps. Phys Rev A 45:2222-2227, with erratum in Phys Rev A 46:3574

    Article  Google Scholar 

  • Orsingher E (1990) Probability law, flow function, maximum distribution of wave-governed random motions and their connections with Kirchoff’s laws. Stoch Proc Appl 34:49–66

    Article  MathSciNet  MATH  Google Scholar 

  • Orsingher E (1995) Motions with reflecting and absorbing barriers driven by the telegraph equation. Random Oper Stochastic Equations 3:9–21

    Article  MathSciNet  MATH  Google Scholar 

  • Pogorui A A, Rodríguez-Dagnino RM, Kolomiets T (2015) The first passage time and estimation of the number of level-crossings for a telegraph process. Ukrainian Math J 67:998–1007

    Article  MathSciNet  MATH  Google Scholar 

  • Prudnikov A P, Brychkov Y u A, Marichev O I (1986) Integrals and Series: Elementary Functions, vol 1, Elementary functions. Gordon & Breach Science Publishers, New York

    MATH  Google Scholar 

  • Prudnikov A P, Brychkov Y u A, Marichev O I (1986) Integrals and Series: Special Functions, vol 2, Special functions. Gordon & Breach Science Publishers, New York

    MATH  Google Scholar 

  • Prudnikov A P, Brychkov Y u A, Marichev O I (1990) Integrals and Series: More Special Functions vol 3. Gordon & Breach Science Publishers, New York

    MATH  Google Scholar 

  • Prudnikov A P, Brychkov Y u A, Marichev O I (1992) Integrals and Series: Direct Laplace Transforms vol 4. Gordon & Breach Science Publishers, New York

    MATH  Google Scholar 

  • Prudnikov A P, Brychkov Y u A, Marichev O I (1992) Integrals and Series: Inverse Laplace Transforms vol 5. Gordon & Breach Science Publishers, New York

    MATH  Google Scholar 

  • Ratanov N E (1997) Random walks in an inhomogeneous one-dimensional medium with reflecting and absorbing barriers. Theoret Math Phys 112:857–865

    Article  MathSciNet  MATH  Google Scholar 

  • Ratanov N (2015) Telegraph processes with random jumps and complete market models. Methodol Comput Appl Probab 17:677–695

    Article  MathSciNet  MATH  Google Scholar 

  • Stadje W, Zacks S (2003) Upper first-exit times of compound Poisson processes revisited. Prob Engin Inf Sci 17:459–465

    Article  MathSciNet  MATH  Google Scholar 

  • Stadje W, Zacks S (2004) Telegraph processes with random velocities. J Appl Prob 41:665–678

    Article  MathSciNet  MATH  Google Scholar 

  • Veestraeten D (2006) An alternative approach to modelling relapse in cancer with an application to adenocarcinoma of the prostate. Math Biosci 199:38–54. with Erratum in: (2013) Math Biosci 241:145-146

    Article  MathSciNet  MATH  Google Scholar 

  • Zacks S, Perry D, Bshouty D, Bar-Lev S (1999) Distributions of stopping times for compound Poisson processes with positive jumps and linear boundaries. Comm Statist Stochastic Models 15:89–101

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Matematica, Università degli Studi di Salerno, Via Giovanni Paolo II, 132, 84084, Fisciano, SA, Italy

    Antonio Di Crescenzo & Barbara Martinucci

  2. Department of Mathematical Sciences, Binghamton University, Binghamton, NY, 13902-6000, USA

    Shelemyahu Zacks

Authors
  1. Antonio Di Crescenzo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Barbara Martinucci
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shelemyahu Zacks
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Barbara Martinucci.

Additional information

Research partially supported by the group GNCS of INdAM.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Di Crescenzo, A., Martinucci, B. & Zacks, S. Telegraph Process with Elastic Boundary at the Origin. Methodol Comput Appl Probab 20, 333–352 (2018). https://doi.org/10.1007/s11009-017-9549-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11009-017-9549-4

Keywords

Mathematics Subject Classification (2010)

Search

Navigation