Abstract
We introduce and study a general notion of spatial localization on spacelike smooth Cauchy surfaces of quantum systems in Minkowski spacetime. The notion is constructed in terms of a coherent family of normalized POVMs, one for each said Cauchy surface. We prove that a family of POVMs of this type automatically satisfies a causality condition which generalizes Castrigiano’s one and implies it when restricting to flat spacelike Cauchy surfaces. As a consequence, no conflict with Hegerfeldt’s theorem arises. We furthermore prove that such families of POVMs do exist for massive Klein–Gordon particles, since some of them are extensions of already known spatial localization observables. These are constructed out of positive definite kernels or are defined in terms of the stress–energy tensor operator. Some further features of these structures are investigated, in particular the relation with the triple of Newton–Wigner selfadjoint operators and a modified form of Heisenberg inequality in the rest 3-spaces of Minkowski reference frames.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 The subtle issue of spatial localization of quantum relativistic systems
The study of notions of spatial localization at given time for a quantum relativistic particle can be traced back to the seminal paper by Newton and Wigner [31]. There, spatial localization was referred to the rest 3-space \(\Sigma \), at given time, of an inertial (Minkowskian) reference frame. Later, guided by Mackey’s imprimitivity theory, Wightman established [38] an uniqueness theorem. He proved that the joint (projector-valued) spectral measure \(\textsf{Q}_\Sigma \) on \(\Sigma \) of the triple of Newton–Wigner selfadjoint operators \(N_\Sigma ^1,N_\Sigma ^2,N_\Sigma ^3\) is the unique projector valued measure (PVM) which is covariant with respect to the Euclidean group of isometries of \(\Sigma \) and complies with some further technical hypotheses. If the notion of spatial localization is described in terms of selfadjoint observables, they must be the Newton–Wigner ones necessarily.
Unfortunately, these operators and their common spectral measure (their joint PVM) resulted to be plagued by a number of fundamental issues related to causality. The Hegerfeldt theorem(s) [21, 22] and the Malament theorem [27], with several modern reformulation mainly due to Busch [6] and Halvorson and Clifton [19], proved that some causality requirements and the request of energy positivity are definitely incompatible for quantum particles described as one-particle states of a quantum relativistic field (Wigner particles).
Malament’s result and its modern extensions and reformulations are directly or indirectly related with the description of post-measurement states, in terms of Lüders–von Neuman projection postulate or referring to a Kraus decomposition of the effects of the POVM describing the localization observable. This is a deep and outstanding issue [2] we shall not discuss in this paper.
Conversely, the various versions of the Hegerfeldt theorem only focus on the spatial detection probability of a quantum relativistic particle at given time. The most elementary version is like this. Let us consider the rest 3-space \(\Sigma \) of a Minkowski observer and a quantum relativistic free particle defined according to Wigner classification, with every mass \(m\ge 0\) and every permitted spin s. Suppose that the probability to detect the particle, whose pure quantum state is represented by the normalized vector \(\psi \), vanishes outside a bounded spatial region \(\Delta \) at time \(t=0\). Then, the same state \(\psi \) gives rise to a strictly positive probability to find the particle arbitrarily far from \(\Delta \) and at arbitrarily small time \(t>0\). In other words, superluminal propagation of probability shows up here. The hypotheses leading to Hegerfeldt’s result are quite mild: the crucial one is positivity of energy (more precisely below boundedness) which is embodied in the Wigner’s definition of particle.Footnote 1 In that case, pure states are represented by unit vectors in the one-particle Hilbert space \(\mathcal{H}\) of the Fock space of the associated quantum field. In the proof of the theorem, the detection probability is supposed to be computed through a PVM or, more generally, by means of a POVM (see below) labeled by the sets of a given rest 3-space \(\Sigma \) of an inertial observer in Minkowski spacetime.
The impact on NW operators is evident. Probability distributions which vanish outside a bounded region \(\Delta \) are trivially constructed when adopting a spatial localization notion in terms of a PVM on \(\Sigma \). The position observable are in this case a triple of mutually compatible selfadjoint operators
in the Hilbert space \(\mathcal{H}\). \(\textsf{P}_\Sigma =\textsf{P}_\Sigma (\Delta )\) for \(\Delta \in \mathscr {B}( \Sigma )\) (where henceforth \(\mathscr {B}(\Sigma )\) is the family of Borel sets on \(\Sigma \)) is their joint spectral measure. A normalized vector in \(\psi \in \textsf{P}_\Sigma (\Delta )\mathcal{H}\) immediately yields a probability distribution \(\langle \psi |P(E) \psi \rangle \) which vanishes if \(E \cap \Delta = \varnothing \), fitting the hypothesis of Hegerfeldt’s theorem. If we do not accept superluminal propagation of detection probability, on account of Hegerfeldt achievement, we are committed to reject any description of the spatial localization in terms of PVM, i.e., selfadjoint operators. The first victim of this reasoning is the very triple of Newton–Wigner operators \(X^k=N^k_\Sigma \), \(k=1,2,3\).Footnote 2
Should we rule out spatial localization described by PVMs on the ground of the theoretical evidence of superluminal propagation of probability?
The answer needs a certain analysis. What we can control in laboratories in practice are just macroscopic objects and devices. At macroscopic level, superluminal propagation of information is forbidden. So, a better perspective to tackle this issue is wondering whether or not the superluminal propagation of probability predicted by the Hegerfeldt theorem can be used to propagate superluminal macroscopic information. The answer is positive, in case of states whose probability distribution at \(t=0\) vanishes outside a bounded spatial region. A corresponding ideal experiment was discussed in [30] by one of the authors of this work. The conclusion is that, to describe spatial localization on a rest 3-space \(\Sigma \) at some time of an inertial observer, the use of a suitable normalized positive-operator valued measure (POVM) is compulsory. A \(\mathcal{H}\)-POVM [7] on \(\Sigma \) is a map

such that \(0\le \textsf{A}_\Sigma (\Delta ) \le I\) for every \(\Delta \in \mathscr {B}(\Sigma )\), where  is a complex measure for every \(\psi ,\psi ' \in \mathcal{H}\). \(\textsf{A}_\Sigma \) is normalized if \(\textsf{A}_\Sigma (\Sigma )=I\). If \(\psi \in \mathcal{H}\) is normalized as well, the meaning of \(\langle \psi |\textsf{A}_\Sigma (\Delta ) \psi \rangle \) is the probability to find the system in \(\Delta \), when its state is \(\psi \).
is a complex measure for every \(\psi ,\psi ' \in \mathcal{H}\). \(\textsf{A}_\Sigma \) is normalized if \(\textsf{A}_\Sigma (\Sigma )=I\). If \(\psi \in \mathcal{H}\) is normalized as well, the meaning of \(\langle \psi |\textsf{A}_\Sigma (\Delta ) \psi \rangle \) is the probability to find the system in \(\Delta \), when its state is \(\psi \).
There are POVMs which do not admit probability distributions  localized in bounded regions for any conceivable pure state \(\psi \in \mathcal{H}\). Contrarily to PVMs which always permits probability distributions localized in bounded sets as viewed above. Hegerfeldt’s theorem does not exclude POVMs to describe the spatial localization of relativistic quantum particles. More precisely, it permits the POVMs whose probability distributions to detect the particle is not supported in a bounded region for every pure state \(\psi \in \mathcal{H}\). It is obviously necessary that probability distributions localized in bounded regions can be arbitrarily approximated by permitted distributions. It in fact happens in concrete POVMs describing spatial localization [8, 9, 30].
localized in bounded regions for any conceivable pure state \(\psi \in \mathcal{H}\). Contrarily to PVMs which always permits probability distributions localized in bounded sets as viewed above. Hegerfeldt’s theorem does not exclude POVMs to describe the spatial localization of relativistic quantum particles. More precisely, it permits the POVMs whose probability distributions to detect the particle is not supported in a bounded region for every pure state \(\psi \in \mathcal{H}\). It is obviously necessary that probability distributions localized in bounded regions can be arbitrarily approximated by permitted distributions. It in fact happens in concrete POVMs describing spatial localization [8, 9, 30].
Mathematically speaking, at this juncture, it is convenient to give the following definition, where \(\mathbb {M}\) denotes the Minkowski spacetime and \(\mathscr {C}^{sf}_\mathbb {M}\) is the family of all possible rest 3-spaces \(\Sigma \) of inertial observers at any given instant of their proper time.
Definition 1
Given a quantum system described in the Hilbert space \(\mathcal{H}\), a spatial localization observable of it in \(\mathbb {M}\) is a collection \(\textsf{A}:= \{\textsf{A}_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\), where each \(\textsf{A}_\Sigma \) is a normalized \(\mathcal{H}\)-POVM on \(\mathscr {B}(\Sigma )\) which is absolutely continuous with respect to the Lebesgue measure on \(\Sigma \). \(\blacksquare \)
In principle, a coherence condition should be also imposed if one wants the probability to find the particle in \(\Delta \) be independent of the rest space \(\Sigma \) containing it. One should require that, if \(\Delta \subset \Sigma \cap \Sigma '\), then \(\textsf{A}_\Sigma (\Delta ) = \textsf{A}_{\Sigma '}(\Delta )\). However, the POVMs \(\textsf{A}_\Sigma \) are absolutely continuous with respect to the Lebesgue measure of \(\Sigma \) by hypothesis. Since \(\Delta \subset \Sigma \cap \Sigma '\) has zero measure if \(\Sigma \ne \Sigma '\), we have \(\textsf{A}_\Sigma (\Delta )= 0 = \textsf{A}_{\Sigma '}(\Delta )\) in any cases. Actually, all physically relevant spatial localization observables are also invariant under translations in \(\Sigma \) due to general Poincaré covariance requirements and this fact automatically implies Lebesgue absolute continuity (see (d) Theorem 2.20 in [35]).
Definition 1 is nothing but Definition 18 stated in [30] for a relativistic spatial localization observable without the requirement of \(\mathscr {P}_+\)-covariance.
An important remark is the following one. Consider the case \(\Delta , \Delta ' \in \Sigma \) and \(\Delta \cap \Delta ' = \varnothing \). Referring to quantum relativistic particles (with positive energy), operators \(\textsf{A}_\Sigma (\Delta )\) and \(\textsf{A}_\Sigma (\Delta ')\) cannot commute, although \(\Delta \) and \(\Delta '\) are causally separated in the considered case. That is due to general no-go resultsFootnote 3 [2, 6, 11, 19]. This is a delicate issue somehow related to the Reeh–Schlieder property if embedding all the theoretical description in the framework of local algebras of observables. Roughly speaking, the operators \(\textsf{A}_\Sigma (\Delta )\) cannot belong to a local algebra in the sense of Haag-Kastler. Whether or not this non-commutativity permits superluminal propagation of macroscopic information should be analyzed in a perspective (as in [15, 16]) where measurement instruments are explicitly studied. This analysis would concern post-measurement states which are outside of the goals of this paper.
To get closer to the results achieved in this paper, we observe that there is a more sophisticated version of the Hegerfeldt theorem [22]: If a state \(\psi \in \mathcal{H}\) produces a probability distribution which vanishes sufficiently rapidly at infinity at \(t=0\), then a more specific type of superluminal propagation of probability takes place again at later times.
The modern overall description of the types of violation was only recently formalized by Castrigiano. Let us quickly review the causality condition and the causal time evolution condition, introduced in [8] for localization POVMs in Minkowski spacetime \(\mathbb {M}\), to reformulate the second form of Hegerfeldt’s theorem [22].
In the following, \(\mathscr {L}(\Sigma )\) is the family of Lebesgue sets of \(\Sigma \in \mathscr {C}^{sf}_\mathbb {M}\), and the considered POVMs are defined on this \(\sigma \)-algebra larger than the more usualFootnote 4\(\mathscr {B}(\Sigma )\). Finally, if \(\Sigma ,\Sigma '\in \mathscr {C}^{sf}_\mathbb {M}\) and \(\Delta \in \mathscr {L}(\Sigma )\), we define the region of influence of \(\Delta \) on \(\Sigma '\)
(\(J^\pm (\Delta )\) are the standard causal sets emanated from \(\Delta \) as defined in Sect. 2.) The physical meaning of \(\Delta '\) should be obvious. It is the largest spatial region on \(\Sigma '\) which may have macroscopic causal relations with \(\Delta \subset \Sigma \), when assuming the causal structure of Minkowski spacetime based on the bounded propagation velocity of macroscopic physical signals.
Let us consider a spatial localization observable \(\textsf{A}:= \{\textsf{A}_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\), where \(A_\Sigma : \mathscr {L}(\Sigma )\rightarrow \mathfrak {B}(\mathcal{H})\).
Definition 2
\(\textsf{A}\) satisfies Castrigiano’s causality condition (CC) [8] if
for every \(\Sigma , \Sigma ' \in \mathscr {C}^{sf}_\mathbb {M}\). \(\blacksquare \)
The physical meaning of the condition above is evident: detection probability cannot propagate faster than the light speed. A weaker condition which is implied by CC but does not imply CC, is the causal time evolution. This condition—and not CC—is actually the specific subject of Hegerfeldt’s investigation. It only considers the case where \(\Sigma \) and \(\Sigma '\) are rest spaces of a common inertial observer n, and thus, they are related by means of the time evolution proper of n. Geometrically speaking, that is equivalent to saying that the normal vectors \(n_\Sigma \) and \(n_{\Sigma '}\) coincide (with n).
Definition 3
\(\textsf{A}\) satisfies the causal time evolution condition condition (CT) [8] if
for every \(\Sigma , \Sigma ' \in \mathscr {C}^{sf}_\mathbb {M}\) with \(n_\Sigma =n_{\Sigma '}\).\(\blacksquare \)
The afore-mentioned second version of the Hegerfeldt theorem [22] (see also further formalizations in [9]) can be stated as follows, for a free quantum relativistic particle of any spin and mass \(m\ge 0\). (The result was actually extended [22] to more general relativistic systems in, also self-interacting, but satisfying energy positivity).
Theorem 4
(Hegerfeldt’s theorem on relativistic time evolution [22]) Consider a spatial localization observable \(\textsf{A}\) for a Wigner particle of mass \(m\ge 0\) described in the Hilbert space \(\mathcal{H}\). If there is a unit vector \(\psi \in \mathcal{H}\) such that the associated probability to find the particle outside a ball of radius r in a certain \(\Sigma \) is bounded by \(K_1e^{-K_2r}\), for all \(r>0\) and constants \(K_1\ge 0\) and \(K_2 > 2 \frac{mc}{\hbar }\), then \(\textsf{A}\) fails to satisfy CT.
Remark 5
As consequence, \(\textsf{A}\) fails to satisfy CC as well. \(\blacksquare \)
Castrigiano proved in [8] that spatial localization observables exist which satisfy CC for massive and massless spin 1/2 fermions. Another family of causal—namely satisfying CC—spatial localization observable \(\{\textsf{M}^n_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) was obtained in [30] by one of the authors of this work for scalar, real, massive Klein–Gordon particles. That observable was constructed by generalizing a more specific observable introduced by D. Terno [36] and also studied in [30], where it was rigorously established that it satisfies CT. More recently, D. Castrigiano rigorously proved in [9] that the spatial localization observables for Klein–Gordon particles with causal kernels \(\{\textsf{T}^g_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) introduced in [18, 20] satisfy CC. These three types of causal spatial localization observables also enjoy natural covariance properties with respect to the orthochronous Poincaré group in \(\mathbb {M}\) as expected. In this sense, they are relativistic spatial localization observables (we shall come back to those features later in the paper).
A natural issue, discussed in the first part of this work, is whether or not we can physically admit a spatial localization observable that violates CC. In other words, is it possible to transmit superluminal macroscopic information by exploiting it?
It is not easy to re-adapt the ideal experiment presented in [30] to the case of a POVM and a state whose probability distribution is not supported in a bounded region but vanishes sufficiently fast at infinity to switch on Hegerfeldt’s theorem on relativistic time evolution (Theorem 4), thus violating CT and CC. It seems to the author of [30] that a re-adaptation of the reasoning in [30] should involve some choice about a post-measurement state prescription or about some quantum instrument. As declared before, we do not want to pursue that route in this paper, since we do not intend to deal with more sophisticated theoretical notions than POVMs.
As a matter of fact, CC can be seen as a consequence of a more general causality condition we shall introduce in Sect. 3.
The crucial overall ideaFootnote 5 is to extend the notion of spatial localization to a broader class of 3-dimensional surfaces in Minkowski spacetime. Minkowski spacetime is in fact globally hyperbolic. In other words, it admits certain special 3-dimensional surfaces, called Cauchy surfaces, which can be used as the place where assigning initial data of causal (hyperbolic) PDEs. From the geometric perspective, each of these surfaces is met by all (inextendible) causal curves, exactly once by timelike ones. No macroscopic physical information can be transmitted from a region on a spacelike Cauchy surface to another separated region on the same Cauchy surface. Rest spaces of inertial reference frames at given times are just a special flat case of smooth Cauchy surfaces. From a relativistic perspective, it seems natural to think of spacelike Cauchy surfaces as a generalization of the notion of space at a given time, where to localize quantum systems like particles.Footnote 6 We therefore extend the notion of spatial localization observable to a more general notion where the possible regions \(\Delta \), where a particle can be detected, are subsets of a generic spacelike Cauchy surface S. To this end, each (generally curved) Cauchy surface S is equipped with a normalized POVM \(\textsf{A}_S\).
A spacelike Cauchy localization observable (Definition 21) is the family all these normalized POVMs, when S varies in the collection of all spacelike Cauchy surfaces. An important coherence condition is also imposed: if \(\Delta \subset S\cap S'\), then \(\textsf{A}_S(\Delta ) = \textsf{A}_{S'}(\Delta )\). In other words, the probability to find the particle in \(\Delta \) is independent of the Cauchy surface, but it is a function of \(\Delta \) and the state \(\psi \in \mathcal{H}\) only. Finally we also require that the probability to find a particle in a zero measure set on S vanishes.
At this juncture, a general causality condition GCC (Definition 26) for spacelike Cauchy localization observables can be stated, in the spirit of Definition 2. The general causality condition is just obtained by replacing the flat spacelike Cauchy surfaces \(\Sigma , \Sigma '\) in Definition 2 for generic spacelike Cauchy surfaces \(S,S'\). This general causality condition evidently implies CC when restricting \(\textsf{A}\) to the POVMs \(\textsf{A}_\Sigma \) defined on the subfamily flat Cauchy surfaces \(\Sigma \). A natural issue pops out here:
How is selective the general causality condition?
Quite surprisingly, the answer is that there is no selection at all: every spacelike Cauchy localization observable automatically satisfies the general causality condition (Theorem 32). As a corollary, if a spatial localization observable \(\{\textsf{A}_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) can be extended to a spacelike Cauchy localization observable \(\{\textsf{A}_S\}_{S\in \mathscr {C}^s_\mathbb {M}}\), then the former automatically satisfies CC.
It seems quite remarkable that the result only uses a general, and very natural, notion of localization. The achieved result proves in fact that the general causality relation should not be imposed as an independent postulate because it is physics that asks for it. In summary, the presented result proves that mere localizability implies causality independently of any kinematical argument.
The strategy to prove our main result stated above takes advantage of some general technical facts in Lorentzian geometry on existence of spacelike Cauchy surfaces adapted to given submanifolds with boundary [3, 4].
Other approaches exist where, also considering many particles, one renounces to energy positivity and defines a notion of spatial localization on generic Cauchy surfaces in terms of PVMs [25, 26], finding similar causality conditions. A different general approach to the Born rule for the spatial localization of a particle formulated in a generic spacetime is discussed in [33]. There, a more general notion of 3-space at given time is introduced and analyzed (also relying on technical results in [28]). That notion of space is adapted (transverse) to the considered probability current and, for this reason, it is not necessarily spacelike nor a Cauchy surface.
The second part of the work is mostly devoted to prove that spacelike Cauchy localization observables do exist. Some of them are (uniquely determined) extensions \(\{\textsf{T}^g_S\}_{S\in \mathscr {C}^{s}_\mathbb {M}}\) and \(\{\textsf{M}^n_S\}_{S\in \mathscr {C}^{s}_\mathbb {M}}\) of the respective above-mentioned spatial localization observables \(\{\textsf{T}^g_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) and \(\{\textsf{M}^n_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\). The method to demonstrate the results in the second part uses ideas physically formulated in [18, 20, 23], made rigorous in [9, 30] and here further improved.
Some further results about the interplay of spatial localization observables, the NW operators, and the Heisenberg inequality appear in several spots of the main text and in a cumulative proposition in the last section.
In details, the achievements of this work are as follows.
-
(1)
Theorem 32: Every spacelike Cauchy localization observable satisfies the general causality condition. Corollary 33: If a spatial localization observable can be extended to a spacelike Cauchy localization observable, then it satisfies Castrigiano’s causality condition.
-
(2)
Theorems 49 and 60: Both \(\{\textsf{T}^g_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) and \(\{\textsf{M}^n_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) uniquely extend to corresponding spacelike Cauchy localization observables \(\{\textsf{T}^g_S\}_{S\in \mathscr {C}^{s}_\mathbb {M}}\) and \(\{\textsf{M}^n_S\}_{S\in \mathscr {C}^{s}_\mathbb {M}}\). The former can be even defined for smooth Cauchy surfaces S which are not spacelike.
-
(3)
Theorems 44, 58, Proposition 61: Both \(\{\textsf{T}^g_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) and \(\{\textsf{M}^n_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) give rise to the Newton Wigner operators as their first moments on every inertial rest space \(\Sigma \). The NW operators are the unique selfadjoint operators which satisfy this property. A generalized Heisenberg inequality holds in all cases.
1.2 Structure of the paper
After a list of notations and conventions adopted in this work, Sect. 2 concerns a recap of the causal structure of globally hyperbolic spacetimes and Minkowski spacetime in particular. Section 3, after introducing the relevant definitions, presents our main results about causality: every spacelike Cauchy localization observable is causal. Section 4 collects some technical notions and results necessary to pass to the second set of achievements. These results are established in Sects. 5 and 6: the possibility to extend some relevant spatial localization observables defined in [9] and [30] to corresponding spacelike Cauchy localization observables. In the same section, we shall discuss some features of spatial localization observables. Section 7 is devoted to discuss some general facts about Newton Wigner observables, Heisenberg inequality and spatial localization observables. After a final discussion in Sect. 8, the appendices contain the proofs of several technical lemmata and propositions asserted in the main text.
1.3 General definitions, notations, and conventions
Barring few changes (like the symbol for the flat Cauchy surfaces), we shall adopt the same notation as in [30].
Throughout \(\mathbb {R}_+:= [0,+\infty )\), \(\overline{\mathbb {R}_+}:= \mathbb {R}_+ \cup \{+\infty \}\), and smooth means \(C^\infty \). The light speed is \(c=1\). The normalized Planck constant is \(\hbar =1\). Furthermore, we shall take advantage of the following notation:
if \(f= f(\vec {x})\) is defined on a suitable open domain of \(\mathbb {R}^3\).
The Lebesgue measure (also restricted to the Borel sets) on \(\mathbb {R}^n\) will be denoted by \(d^nx\), when \(x^1,\ldots , x^n\) are orthonormal Cartesian coordinates on \(\mathbb {R}^n\). We use also the notation \(|B|:= \int _B 1 d^nx\). The family of Borel sets on a topological space X will be denoted by \(\mathscr {B}(X)\). The Lebesgue \(\sigma \)-algebra on \(\mathbb {R}^n\) will be indicated by \(\mathscr {L}(\mathbb {R}^n)\).
We assume the following normalization convention concerning volume n-forms in \(\mathbb {R}^n\)
The inner product  in a complex Hilbert space \(\mathcal{H}\) is assumed to be linear in the right entry.
in a complex Hilbert space \(\mathcal{H}\) is assumed to be linear in the right entry.
If \(A: D(A)\rightarrow H\) is an operator in the complex Hilbert space \(\mathcal{H}\) with domain given by the linear subspace \(D(A)\subset \mathcal{H}\), saying that A is positive, written \(A\ge 0\), means \(\langle \phi |A \phi \rangle \ge 0\) for all \(\phi \in D(A)\). Furthermore, if \(D(A)=D(B) \subset H\) for a corresponding pair of operators A, B, then \(A\ge B\) (also written \(B\le A\)) means \(A-B \ge 0\).
\(\mathfrak {B}(\mathcal{H})\) throughout denotes the unital \(C^*\)-algebra of bounded operators [29] \(A: \mathcal{H}\rightarrow \mathcal{H}\), where \(\mathcal{H}\) is a complex Hilbert space.
Let \(\mathscr {M}(X)\) be a \(\sigma \)-algebra on X and \(\mathcal{H}\) a complex Hilbert space. A \(\mathcal{H}\)-POVM (Positive-Operator Valued Measure) on \(\mathscr {M}(X)\) [7] is a map

such that \(0\le \textsf{A}(\Delta )\le I\) and  is a \(\sigma \)-additive complex measure (with finite total variation) for every \(\psi ,\phi \in \mathcal{H}\). It turns out that a POVM is also \(\sigma \)-additive in the strong operator topology. \(\textsf{A}\) is normalized if \(\textsf{A}(X)=I\).
is a \(\sigma \)-additive complex measure (with finite total variation) for every \(\psi ,\phi \in \mathcal{H}\). It turns out that a POVM is also \(\sigma \)-additive in the strong operator topology. \(\textsf{A}\) is normalized if \(\textsf{A}(X)=I\).
A normalized \(\mathcal{H}\)-POVM \(\textsf{A}\) on \(\mathscr {M}(X)\) is a \(\mathcal{H}\)-PVM (Projector Valued Measure) on \(\mathscr {M}(X)\) if \(\textsf{A}(\Delta )^2 = \textsf{A}(\Delta )\) (i.e., \(\textsf{A}(\Delta )\) is an orthogonal projector in \({\mathcal{H}}\)) for every \(\Delta \in \mathscr {M}(X)\). We shall use standard notions and constructions of operator theory and spectral theory (see, e.g., [29]).
An \(\mathcal{H}\)-POVM \(\textsf{A}\) on \(\mathscr {M}(X)\) is absolutely continuous with respect to a positive measure \(\mu : \mathscr {M}(X) \rightarrow \overline{\mathbb {R}_+}\), written \(\textsf{A}<\hspace{-5.0pt}< \mu \), if \(\langle \psi |\textsf{A}(E) \psi \rangle =0\) for every \(\psi \in \mathcal{H}\) when \(\mu (E)=0\), for \(E\in \mathscr {M}(X)\).
2 Causal structures of spacetimes, Minkowski spacetime
This section is devoted to quickly introduce the basic causal structures we shall use in the rest of the paper (see, e.g., [32]). The reader who is already familiar with these notions and wants to achieve the main results soon, may temporarily skip this part, coming back to it when necessary, or for understanding a specific notation or a definition.
2.1 Globally hyperbolic spacetimes and their causal structure
A spacetime is the most general scenario where formulating any macroscopic physical theory according with standard notions of causality (see, e.g., [32]). It is a continuous set of events, a smooth manifold, equipped with geometric structures which account for causal relations. The crucial notion underpinning these notions is the Lorentzian metric tensor field on the spacetime.
Definition 6
A n-dimensional spacetime (M, g) is a connected n-dimensional (\(n\ge 2\)) smooth manifold M equipped with a Lorentzian metric tensor field g. It is a smooth assignment to every \(T^*_pM\otimes T^*_pM\) of non-degenerate symmetric tensors \(g_p\) with constant signature \(-1,+1,\ldots , +1\).
If \(p\in M\), \(v\in T_pM\setminus \{0\}\) is spacelike, timelike, lightlike if, respectively, \(g_p(v,v) >0\), \(g_p(v,v)<0\), \(g_p(v,v)=0\). Causal vectors are both timelike and lightlike. The zero vector \(0\in T_pM\) is spacelike per definition. \(\blacksquare \)
We adopt the same terminology for smooth curves  : they are spacelike, timelike, lightlike, causal according to the character of their tangent vector \(\dot{\gamma }(s)\) supposed to be uniform along \(\gamma \).
: they are spacelike, timelike, lightlike, causal according to the character of their tangent vector \(\dot{\gamma }(s)\) supposed to be uniform along \(\gamma \).
Co-vectors in \(T_p^*M\) are classified as spacelike, timelike, lightlike, causal, according to the associated elements of \(T_pM\) through the natural isomorphism  . The indefinite inner product induced on \(T^*_pM\) by that isomorphism will be denoted by \(g_p^\#\).
. The indefinite inner product induced on \(T^*_pM\) by that isomorphism will be denoted by \(g_p^\#\).
As usual, a \(C^k\) submanifold (\(k=0,1,\ldots , \infty \)) of a given smooth manifold M is a subset \(N\subset M\) equipped with its own structure of \(C^k\) manifold. The submanifold \(N\subset M\) is said to be embeddedFootnote 7 and of dimension \(m\le n:=dim(M)\) if (a) for every \(p\in N\) there is a local chart \((U,\psi )\) of M, such that \(p\in U\) and \(\psi (U\cap S)\) is the intersection of \(\psi (U)\) and \(\mathbb {R}^{m}\) (viewed as a standard m-plane in \(\mathbb {R}^n\)); (b) the topology on N is the one induced by M; and (c) \((U\cap N, \psi |_{U\cap N}: U\cap N \rightarrow \mathbb {R}^m)\) is a local \(C^k\) chart on N. Evidently, \(T_pN\) turns out to be a linear subspace of \(T_pM\) when \(k\ge 1\).
Definition 7
In a n-dimensional spacetime (M, g), an m-dimensional (\(m\le n\)) embedded smooth submanifold S (possibly with boundary) is spacelike if the tangent vectors at every point (including the ones tangent to the boundary if any) are spacelike.
If \(m=n-1\) (and S has no boundary) that is equivalent to saying that the co-normal vector to S is timelike everywhere. \(\blacksquare \)
To go on, observe that the set of timelike vectors in \(T_pM\) is made of two disjoint open cones \(V_p\) and \(V'_p\).
Definition 8
A spacetime (M, g) is time oriented if there exists a continuous timelike vector field T on M. If \(p\in M\),
-
(a)
the open cone \(V^+_p\subset T_pM\) of the pair \(V_p\) and \(V'_p\) which contains \(T_p\) is called the future open cone at p; the causal vectors of \(\overline{V^+_p}\setminus \{0\}\) are said to be future-directed;
-
(b)
the remaining cone \(V^-_p\) is the past open cone at p; the causal vectors of \(\overline{V^-_p}\setminus \{0\}\) are said to be past-directed.
A global continuous choice of \(V_p^+\) for every \(p\in M\) as above is a temporal orientation of (M, g).
A causal co-vector is future-directed or past-directed if it is the image of a, respectively, future-directed or past-directed causal vector through  . \(\blacksquare \)
. \(\blacksquare \)
Remark 9
-
(1)
As M is connected, there are two possible temporal orientations or none.
-
(2)
If \(t\in V^+_p\) and \(u \in T_pM\) is causal, then u future-directed \(\Leftrightarrow g_p(t,u)<0.\) (The same result is valid for t future-directed lightlike and non-parallel to u.) \(\blacksquare \)
Definition 10
Let (M, g) be a time oriented spacetime. If \(A\subset M\),
-
(a)
its chronological future \(I^+(A) \subset M\) is the set of \(q \in M\) such that there is a future-directed timelike smooth curve \(\gamma : (a,b)\rightarrow M\) with \(\gamma (t_1) \in A\) and \(\gamma (t_2) =q\), for \(t_1< t_2\);
-
(b)
its causal future \(J^+(A) \subset M\) is the set of \(q \in M\) such that either \(q\in A\) or there is a future-directed causal smooth curve \(\gamma : (a,b)\rightarrow M\) with \(\gamma (t_1) \in A\) and \(\gamma (t_2) =q\), for \(t_1< t_2\).
The chronological past \(I^-(A)\) and the causal past \(J^-(A)\) are defined similarly.
-
(c)
A is achronal if \(A \cap I^+(A) = A \cap I^-(A) = \varnothing \),
-
(d)
A is acausal if there is no causal smooth curve \(\gamma : (a,b)\rightarrow M\) with \(\gamma (t_1), \gamma (t_2) \in A\) and \(t_1 \ne t_2\). \(\blacksquare \)
Physically speaking, macroscopic physical information is transported along causal (future-directed) curves. The existence of the sets \(J^\pm (p)\) (and also \(V_p^\pm \)) is the mathematical description of the finite propagation speed of physical information exiting (or entering) p.
Definition 11
Let (M, g) be a time oriented spacetime. A future-directed causal smooth curve \(\gamma : (a,b)\rightarrow M\), with \(a,b \in [-\infty ,+\infty ]\), is future, resp. past, inextendible if there is no \(p\in M\) such that, respectively, \(\gamma (s)\rightarrow p\) for \(s\rightarrow b\) or \(s\rightarrow a\).
\(\gamma \) is inextendible if it is both future and past inextendible. \(\blacksquare \)
We shall now focus attention on the so called globally hyperbolic spacetimes. This kind of spacetimes is of the utmost physical interest for many reasons, in particular because a wide family of, roughly speaking, hyperbolic PDEs of great physical relevance—as the Einstein equations, Klein–Gordon equations, Dirac equations—admit existence and uniqueness theorems. Cauchy data are given on special subsets called Cauchy surfaces. Very interestingly, the definition of globally hyperbolic spacetime and Cauchy surface is not related to PDEs, but only relies on the above geometric causal structures. Spacelike Cauchy surfaces are also the natural representation of instantaneous rest spaces of globally extended observers.
Definition 12
A time oriented spacetime (M, g) is said to be globally hyperbolic (e.g., see [3]) if it includes a Cauchy surface. That is a set \(S\subset M\) which intersects every inextendible timelike smooth curve exactly once. \(\blacksquare \)
Remark 13
There are features of Cauchy surfaces in a n-dimensional globally hyperbolic spacetime (M, g) which deserve mention also because they are technically important for this paper.
-
(a)
Every Cauchy surface is in particular achronal. It is also met by every causal inextendible curve, but not necessarily once [32].
-
(b)
As it was established by Geroch, a Cauchy surface S is a closed (in M) \(C^0\) embedded submanifold of co-dimension 1 of M which, in turn, is homeomorphic to \(\mathbb {R}\times S\). All Cauchy surfaces are homeomorphic. [32].
-
(c)
If a Cauchy surface S is also a smooth embedded co-dimension 1 submanifold of M, then its tangent vectors at each point must be either spacelike or lightlike, since S does not contain timelike curves. These Cauchy surfaces are said smooth Cauchy surfaces.
-
(d)
As established by Bernal and Sánchez [3], every globally hyperbolic spacetime admits spacelike smooth Cauchy surfaces (necessarily closed in M for (b)). In turn, M is diffeomorphic to \(\mathbb {R}\times S\). The following further facts are of crucial interest to our work.
-
(d1)
(Proposition 5.18 in [4]) Let \(S_-,S_+\) be disjoint spacelike smooth Cauchy surfaces of (M, g) with \(S_- \subset I^-(S_+)\). If \(S \subset I^+(S_-)\cap I^-(S_+)\) is a closed (in M) connected spacelike smooth embedded 1-codimensional submanifold of M, then S is a Cauchy surface of (M, g) as well.
-
(d2)
(Theorem 1.1 and Remark 4.14 of [4]) If \(K\subset M\) is a compact spacelike acausal smooth p-dimensional (\(p=1,2,\ldots , n-1\)) (embedded) submanifold with boundaryFootnote 8of (M, g) not necessarily connected, then there is a spacelike smooth Cauchy surface \(S\supset K\).
-
(d1)
-
(e)
A spacelike smooth Cauchy surface S meets exactly once also every inextendible causal curve [3]. In particular, S is therefore acausal. \(\blacksquare \)
Remark 14
\(\mathscr {C}_M\) will henceforth denote the family of all smooth Cauchy surfaces of (M, g).\(\blacksquare \)
2.2 Minkowski spacetime geometric and causal structures
Definition 15
Minkowski spacetime \((\mathbb {M}, \textsf{V}, \textbf{g})\) is a 4-dimensional real affine space whose space of translation—denoted by \(\textsf{V}\)—is equipped with a Lorentzian inner product with signatureFootnote 9\((-1,+1,+1,+1)\) indicated by  . \(\blacksquare \)
. \(\blacksquare \)
This definition is consistent with Definition 8 because \(\mathbb {M}\) is automatically a smooth 4-dimensional manifold with respect to the natural smooth structure induced by its affine structure. It is defined by requiring that, upon the choice of an origin \(o\in \mathbb {M}\), the bijective map  is a diffeomorphism. \(\imath _p:= dI^o_p:T_p\mathbb {M}\rightarrow \textsf{V}\) is a natural isomorphism independent of the choice of o. \(\textbf{g}\) can therefore be exported to each tangent space \(T_p\mathbb {M}\) as \(g_p(u,v):= \textbf{g}(\imath _p u, \imath _p v)\). The construction defines a smooth manifold diffeomorphic to \(\mathbb {R}^4\) endowed with a Lorentzian metric tensor field—called Minkowski metric—still denoted by \(\textbf{g}\). In the rest of the paper, for \(u,v \in T_p\mathbb {M}\), we use the notation \(\textbf{g}(u,v):=u\cdot v:=g_p(u,v)\).
is a diffeomorphism. \(\imath _p:= dI^o_p:T_p\mathbb {M}\rightarrow \textsf{V}\) is a natural isomorphism independent of the choice of o. \(\textbf{g}\) can therefore be exported to each tangent space \(T_p\mathbb {M}\) as \(g_p(u,v):= \textbf{g}(\imath _p u, \imath _p v)\). The construction defines a smooth manifold diffeomorphic to \(\mathbb {R}^4\) endowed with a Lorentzian metric tensor field—called Minkowski metric—still denoted by \(\textbf{g}\). In the rest of the paper, for \(u,v \in T_p\mathbb {M}\), we use the notation \(\textbf{g}(u,v):=u\cdot v:=g_p(u,v)\).
Minkowski spacetime \((\mathbb {M},\textbf{g})\) is assumed to be time oriented and \(d\imath _p(V_p^+)=: \textsf{V}_+\subset \textsf{V}\) (which does not depend on p) is the future open cone in \(\textsf{V}\) by definition.
The orthochronous Poincaré group \(\mathscr {P}_+\) is the group of time-orientation preserving isometries of \((\mathbb {M}, \textbf{g})\). \(\mathscr {P}_+\) turns out to be the semidirect product \(\textsf{V}\rtimes \mathscr {L}_+\) of \(\textsf{V}\) (the abelian group of displacements of \(\mathbb {M}\)) and the orthochronous Lorentz group \(\mathscr {L}_+\) consisting of the \(\textsf{V}_+\)-preserving linear isometries of \((\textsf{V}, \textbf{g})\). Upon the choice of an origin \(o\in \mathbb {M}\) and referring to the map \(I^o_p\) above, the action of \((v,\Lambda ) \in \mathscr {P}_+\) is

This action also defines the structure of semidirect product \(\mathscr {P}_+ = \textsf{V}\rtimes \mathscr {L}_+\).
A Minkowski reference frame, physically corresponding to an inertial observer, is defined by a future-directed timelike unit vector n. The set of these unit vectors will be denoted by \(\textsf{T}_+\subset \textsf{V}_+\). Take \(o\in \mathbb {M}\) and a Minkowski basis, i.e., \(e_0,e_1,e_2,e_3 \in \textsf{V}\) such that \(e_0\in \textsf{T}_+\) and \(\textbf{g}(e_\mu ,e_\nu )=\eta _{\mu \nu }\), where \([\eta _{\mu \nu }]_{\mu ,\nu =0,1,2,3}:= \text{ diag }(-1,1,1,1)\). The global (bijective Cartesian) chart  is a Minkowski chart on \(\mathbb {M}\) (with origin o and axes \(e_0,e_1,e_2,e_3\)) by definition. The vectors \(\partial _{x^\mu }|_p \in T_p\mathbb {M}\) of the local bases associated to the coordinates are mapped to \(e_\mu \) by \(\imath _p\) and it holds both \(\textbf{g}(\partial _{x^\mu },\partial _{x^\nu }) = \eta _{\mu \nu }\) and \(\textbf{g}^\#({\text {d}}x^\mu ,{\text {d}}x^\nu ) =\eta ^{\mu \nu }:= \eta _{\mu \nu }\) constantly everywhere. These identities imply in particular that the metric tensor field \(\textbf{g}\) is globally flat. A Minkowski chart \(x^0,x^1,x^2,x^3\) is adapted to a Minkowski reference frame \(n\in \textsf{T}_+\) if \(\partial _{x^0}=n\) everywhere (where again the natural isomorphism \(\imath _p\) is understood).
is a Minkowski chart on \(\mathbb {M}\) (with origin o and axes \(e_0,e_1,e_2,e_3\)) by definition. The vectors \(\partial _{x^\mu }|_p \in T_p\mathbb {M}\) of the local bases associated to the coordinates are mapped to \(e_\mu \) by \(\imath _p\) and it holds both \(\textbf{g}(\partial _{x^\mu },\partial _{x^\nu }) = \eta _{\mu \nu }\) and \(\textbf{g}^\#({\text {d}}x^\mu ,{\text {d}}x^\nu ) =\eta ^{\mu \nu }:= \eta _{\mu \nu }\) constantly everywhere. These identities imply in particular that the metric tensor field \(\textbf{g}\) is globally flat. A Minkowski chart \(x^0,x^1,x^2,x^3\) is adapted to a Minkowski reference frame \(n\in \textsf{T}_+\) if \(\partial _{x^0}=n\) everywhere (where again the natural isomorphism \(\imath _p\) is understood).
A rest space \(\Sigma _n\) of \(n\in \textsf{T}_+\) is any 3-dimensional plane orthogonal to n. Rest spaces are smooth spacelike 3-dimensional embedded submanifolds. The surjective coordinate function \(x^0: \mathbb {M}\rightarrow \mathbb {R}\) of a Minkowski chart adapted to n defines a global time coordinate of n. The possible global time coordinates of n are defined up to an arbitrary additive constant. If a Minkowski chart \(x^0,x^1,x^2,x^3\) is adapted to n, the time slices
at constant time \(x^0=x_0^0\) are the coordinate representation of the rest spaces \(\Sigma _{n, x^0_0}\) of n (adopting the notation used in [30]). The rest spaces of n are, in fact, bijectively labeled by the values of \(x^0\) itself and the remaining coordinates \(x^1,x^2,x^3\) define an admissible global chart on each submanifold \(\Sigma _{n,x^0}\). This chart is an orthogonal Cartesian coordinate system on \(\Sigma _{n,x^0}\) with respect to the (Euclidean) metric induced by \(\textbf{g}\) on \(\Sigma _{n,x^0}\) and the affine structure induced by the one of \(\mathbb {M}\). So that, for instance, the Lebesgue \(\sigma \)-algebra \(\mathscr {L}(\Sigma _{n,x^0})\) and the Lebesgue measure are univocally defined on each \(\Sigma _{n,x^0}\) independently of the Minkowski chart adapted to n. The Lebesgue measure on \(\Sigma _{n,x^0}\) coincides with the completion of the Borel measure canonically induced by \(\textbf{g}\) on its embedded submanifolds of \(\mathbb {M}\) (see (10)).
Given Minkowski chart \(x^0,x^1,x^2,x^3\), the spatial components of \(k\in T_p\mathbb {M}\equiv \textsf{V}\) along the local basis \(\partial _{x^0}|_p, \partial _{x^1}|_p,\partial _{x^2}|_p,\partial _{x^3}|_p \in T_pM\) (i.e., the Minkowski basis \(e_0,e_1, e_2,e_3\in \textsf{V}\) associated to the said Minkowski chart) are \(\vec {k}:=(k^1,k^2,k^3)\) and the temporal component is \(k^0\). Referring to the spatial components of \(k,p \in \textsf{V}\), their inner product in \(\mathbb {R}^3\) is again denoted by the dot \(\vec {k}\cdot \vec {h}\).
An important feature of Minkowski spacetime \(\textsf{M}\) is that the structure of \(J^\pm (A)\) and \(I^\pm (A)\) simplify because \(\mathbb {M}\) is a globally flat spacetime. The following result is true, whose elementary proof is left to the reader.
Proposition 16
If \(A\subset \textsf{M}\), the following holds.
-
(a)
\(I^+(A)\) is made of the points \(q \in \textsf{M}\) such that there is \(p\in A\) for that the \(q-p\in \textsf{V}_+\).
-
(b)
\(J^+(A) \) is made of the points \(q \in \textsf{M}\) such that there is \(p\in A\) for that \(q-p\in \overline{\textsf{V}_+}\) (so \(p=q\) is admitted).
Analogous facts are true for \(J^-(A)\) and \(I^-(A)\).
Proposition 17
([32]) Minkowski spacetime is globally hyperbolic since the rest spaces of every Minkowski reference frame are (spacelike) Cauchy surfaces.
Definition 18
A spacelike Cauchy surface in \(\mathbb {M}\) is a spacelike smooth Cauchy surface of \((\mathbb {M}, \textbf{g})\). Their family is denoted by \(\mathscr {C}^s_\mathbb {M}\).
A spacelike flat Cauchy surfaces in \(\mathbb {M}\) is a rest space of any Minkowski reference frame. Their family will be denoted by \(\mathscr {C}^{sf}_\mathbb {M}\). \(\blacksquare \)
Remark 19
In the following, S will denote a smooth Cauchy surface of \(\mathbb {M}\), i.e., an element of \(\mathscr {C}_\mathbb {M}\). However, in case S is flat and spacelike, i.e., \(S\in \mathscr {C}^{sf}_\mathbb {M}\), we shall very often use the symbol \(\Sigma \) in place of S, especially when viewing them as 3-rest spaces of inertial observers according to the notation of [30]. \(\blacksquare \)
In addition to spacelike flat Cauchy surfaces, there are many other types of smooth Cauchy surfaces in \(\mathbb {M}\). The following proposition concern their description.
Proposition 20
Consider a given Minkowski chart \(x^0,x^1,x^2,x^3\) and \(S\in \mathscr {C}_\mathbb {M}\).
-
(a)
S is determined by a smooth map \(x^0 = t_S(\vec {x})\), \(\vec {x}\in \mathbb {R}^3\) with
$$\begin{aligned} |\nabla t_S(\vec {x})| \le 1\quad \text{ for } \text{ every } \vec {x}\in \mathbb {R}^. \text{ Here }, < \text{ replaces } \le \text{ if } S \text{ is } \text{ spacelike }. \end{aligned}$$(7) -
(b)
S is diffeomorphic to \(\mathbb {R}^3\) as the coordinates \((x^1,x^2,x^3)\in \mathbb {R}^3\) define a global chart on it.
Proof
See Appendix 1. \(\square \)
Let us now focus on the case where \(S\in \mathscr {C}^s_\mathbb {M}\), i.e., the smooth Cauchy surface S is spacelike.
-
(1)
The future-directed unit normal vector and co-vector to S at \((t_S(\vec {x}), \vec {x})\) are, respectively,
$$\begin{aligned} n_S(\vec {x}):= \frac{\partial _{x^0} + \sum _{k=1}^3 \frac{\partial t_S}{\partial x^k} \partial _{x^k}}{\sqrt{1 - |\nabla t_S(\vec {x})|^2}}, \quad \textbf{g}(n_S, \cdot )(\vec {x}):= \frac{-{\text {d}}x^0 + \sum _{k=1}^3 \frac{\partial t_S}{\partial x^k} {\text {d}}x^k}{\sqrt{1 - |\nabla t_S(\vec {x})|^2}}.\end{aligned}$$(8) -
(2)
The Riemannian metric \(h^S\) induced on S and represented in terms of the local coordinates \(\vec {x} \in \mathbb {R}^3\) is the pullback of \(\textbf{g}\) through the embedding function. It reads
$$\begin{aligned} h^S_{ab}:= \sum _{\alpha \beta =0}^3 \eta _{\alpha \beta } \frac{\partial x^\alpha }{\partial x^a} \frac{\partial x^\beta }{\partial x^b} = \delta _{ab} - \frac{\partial t_S}{\partial x^a} \frac{\partial t_S}{\partial x^b}\end{aligned}$$(9)where \(a,b =1,2,3\) and \(x^0= t_S(\vec {x})\).
-
(c)
Correspondingly, the Borel measure on S induced by the metric is equivalent to the Lebesgue measure \(d^3x\) on \(\mathbb {R}^3\) (restricted to the Borel sets) and readsFootnote 10
$$\begin{aligned} \nu _S(A):= \int _{A} \sqrt{\text{ det }h^S} d^3 x = \int _{A} \sqrt{1- |\nabla t_S(\vec {x})|^2}\, d^3 x \quad \text{ for } \text{ every } A\in \mathscr {B}(S),\end{aligned}$$(10)where (and occasionally henceforth) the integration region A in the integrals actually denotes the projection of \(A\in \mathscr {B}(S)\) onto \(\mathbb {R}^3\).
In case the smooth Cauchy surface S is generic, we can still define non-vanishing, causal and future-directed normal vectors and co-vectors to S at \((t_S(\vec {x}), \vec {x})\) but, generally speaking, we cannot normalize them
The induced metric turns out to be degenerate where these vectors are lightlike.
3 Spacelike Cauchy localization observables in \(\mathbb {M}\) and a general causality condition
We pass to present our generalized notion of spatial localization and a corresponding generalized causality condition. The latter extends CC stated in Definition 2. The general notion of spatial localization will be given in terms of families of POVMs on spacelike Cauchy surfaces. This notion extends the analogous Definition 1, where only flat Cauchy surfaces were considered.
3.1 A general notion of spatial localization in terms of POVMs
The POVMs we shall use will be defined on a completion of the Borel \(\sigma \)-algebra on \(S\in \mathscr {C}_\mathbb {M}^s\). This is necessary because the region of influence \(\Delta ' \subset S'\) of a set \(\Delta \in \mathscr {B}(S)\) is not necessarily in \(\mathscr {B}(S')\), but it necessarily stays in the \(\nu _{S'}\) completion of \(\mathscr {B}(S')\) (see below). This fact was already true [8, 9, 30] when dealing with flat Cauchy surfaces \(\Sigma \), where the said completion of \(\mathscr {B}(\Sigma )\) was nothing but the Lebesgue \(\sigma \)-algebra. If \(S\in \mathscr {C}_\mathbb {M}^s\), we denote by
the completion \(\sigma \)-algebra of \(\mathscr {B}(S)\) and the completion measure of \(\nu _S\) with respect to the positive Borel measure \(\nu _S\) (10) induced on S by the spacetime metric.
Definition 21
Consider a quantum system described in the Hilbert space \(\mathcal{H}\). A spacelike Cauchy localization observable (for short spacelike Cauchy localization) of the system in \(\mathbb {M}\) is a family of normalized \(\mathcal{H}\)-POVMs \(\textsf{A}:=\{\textsf{A}_S\}_{S\in \mathscr {C}_\mathbb {M}^s}\) where \(\textsf{A}_S: \mathscr {M}(S) \rightarrow \mathfrak {B}(\mathcal{H})\), such that
-
(a)
\(\textsf{A}\) satisfies the coherence condition
$$\begin{aligned} \textsf{A}_S(\Delta ) = \textsf{A}_{S'}(\Delta ) \quad \text{ if } S,S'\in \mathscr {C}^s_\mathbb {M}, \Delta \subset S\cap S' \text{ and } \Delta \in \mathscr {M}(S) \cap \mathscr {M}(S'); \end{aligned}$$(13) -
(b)
\(\textsf{A}_S\) is absolutely continuous with respect to \(\overline{\nu _S}\), for every \(S\in \mathscr {C}_\mathbb {M}^s\) (in formulae \(\textsf{A}_S<\hspace{-5.0pt}< \overline{\nu _S}\)).\(\blacksquare \)
Physically speaking, requirement (b) \(\textsf{A}_S<\hspace{-5.0pt}< \overline{\nu _S}\) means that there is no chance to find a particle in a spatial region with zero measure. This condition will play a crucial technical role in establishing Theorem 32. This property is closely related to the analogous property of measures associated to spatial localization observables as \(\overline{\nu _S}\) is equivalent to the image of the Lebesgue measure on \(\mathbb {R}^3\).
When restricting to flat Cauchy surfaces, the definition of spacelike Cauchy localization observable boils down to the definition of spatial localization observable as in Definition 1.
Remark 22
-
(1)
Definition 21, in principle, is valid for a generic quantum system and not necessarily for a Wigner particle.
-
(2)
A different approach [10] in defining our localization observable would concern an assignment of effects on a suitable family of acausal subsets of \(\mathbb {M}\), without declaring that they gives rise to families of POVMs on the Cauchy surfaces of \(\mathscr {C}^s_\mathbb {M}\), but recovering this fact at a more advanced stage of the theory. This physically deeper approach would avoid to impose the coherence condition (13), since it would be encapsulated in the formalism automatically. On the other hand, this perspective would turn out technically involved when proving Theorem 32, in view of used mathematical technology which relies upon features of smooth spacelike Cauchy surfaces.\(\blacksquare \)
Since the examples of POVMs we shall consider later are initially defined on \(\mathscr {B}(S)\), the following extension results are of relevance to our work.
Proposition 23
Let \(\textsf{A}_S\) be a normalized \(\mathcal{H}\)-POVM defined on \(\mathscr {B}(S)\) for \(S\in \mathscr {C}_\mathbb {M}^s\). If \(\textsf{A}_S<\hspace{-5.0pt}< \nu _S\), then there exists a unique normalized \(\mathcal{H}\)-POVM \(\tilde{\textsf{A}}_S\) on \(\mathscr {M}(S)\) which extends \(\textsf{A}_S\) and such that \(\tilde{\textsf{A}}_S<\hspace{-5.0pt}< \overline{\nu _S}\).
Proof
See Appendix 1. \(\square \)
Proposition 24
Suppose that the family of POVMs \(\{\textsf{A}_S\}_{S\in \mathscr {C}_\mathbb {M}^s}\), where \(\textsf{A}_S: \mathscr {B}(S) \rightarrow \mathfrak {B}(\mathcal{H})\), satisfies
-
(a)
\(\textsf{A}_S(\Delta ) = \textsf{A}_{S'}(\Delta )\) for every \(\Delta \in \mathscr {B}(S) \cap \mathscr {B}(S')\);
-
(b)
\(\textsf{A}_S<\hspace{-5.0pt}< \nu _S\).
Then, extending each POVM according to Proposition 23, we obtain a spacelike Cauchy localization observable \(\{\tilde{\textsf{A}}_S\}_{S\in \mathscr {C}_\mathbb {M}^s}\).
Remark 25
In the rest of the paper, we shall use the same symbol \(\textsf{A}_S\) also for the extension to \(\mathscr {M}(S)\) above denote by \(\tilde{\textsf{A}}_S\). \(\blacksquare \).
In principle, it would be possible to define from scratch a notion of Cauchy localization for smooth Cauchy surfaces S which are not necessarily spacelike on the corresponding Borel \(\sigma \)-algebra \(\mathscr {B}(S)\). As a matter of fact, we shall define such type of families of POVMs \(\textsf{T}^g\) in Sect. 5. However, Theorem 32 needs several general results about spacelike smooth Cauchy surfaces. The generalization of the results presented in this section to families of POVMs defined on generic Cauchy surfaces (also non-smooth) will be investigated elsewhere.
3.2 The general causality condition for spacelike Cauchy localization observables
We can state a natural generalization of CC.
Definition 26
If \(S,S'\in \mathscr {C}_\mathbb {M}^s\) and \(\Delta \in \mathscr {M}(S)\), its region of influence on \(S'\) is
A spacelike Cauchy localization \(\textsf{A}\) satisfies the general causality condition (GCC) if, for every \(S, S' \in \mathscr {C}_\mathbb {M}^s\),
when \(\Delta \in \mathscr {M}(S)\) satisfies
\(\blacksquare \)
If \(S =\Sigma \) and \(S'= \Sigma '\) are spacelike flat Cauchy surfaces of Minkowski spacetime, the completed measures \(\overline{\nu _\Sigma }\) and \(\overline{\nu _{\Sigma '}}\) are nothing but the Lebesgue measures on \(\Sigma \) and \(\Sigma '\). In this situation, as already said, it turns out that [8] \(\Delta ' \in \mathscr {M}(\Sigma ')\) whenever \(\Delta \in \mathscr {M}(\Sigma )\). We do not known if this fact is general. It is, however, possible to prove the following fact, whose proof is inspired by analogous ideas and proofs in [10]. To this end, we observe that \(S\in \mathscr {C}_\mathbb {M}\) is a Polish space [12]. It can be proved in various ways, the most economic way is to use the diffeomorphism of S and \(\mathbb {R}^3\) according to Proposition 20.
Proposition 27
Consider \(S,S'\in \mathscr {C}_\mathbb {M}^s\). If \(\Delta \in \mathscr {B}(S)\), then \(\Delta ' \in \mathscr {M}(S')\).
Proof
Define the following continuous function

The set \(\Delta \times (-\infty , 0]\) is in \(\mathscr {B}(S \times \mathbb {R})\) trivially. Since \(\eta \) is Borel measurable (as it is continuous),
is in \(\mathscr {B}(S\times S')\). A this point, we can use Proposition 8.4.4 in [12] obtaining that the projection of the above set onto \(S'\) is universally measurable: it stays in the \(\sigma \)-algebra obtained by completing \(\mathscr {B}(S')\) with respect to any positive finite Borel measure on \(S'\). To conclude we prove that \(\Delta '\) must therefore belong to \(\mathscr {M}(S')\). Upon the identification of \(S'\) with \(\mathbb {R}^3\) through the global chart defined in (b) of Proposition 20, consider the Borel finite measure \(\nu _n(E) = \int _{E} \chi _{B_n} \sqrt{1- |\nabla t_{S'}|^2} d^3x\), where \(B_n\) is the open ball of radius \(n\in \mathbb {N}\) and center the origin of \(\mathbb {R}^3\). \(\nu _n|_{\mathscr {B}(B_n)}\) is equivalent to the \(\mathbb {R}^3\) Lebesgue measure restricted to \(B_n\). Since \(\Delta '\cap B_n \in \overline{\mathscr {B}(S')}^{\nu _n}\), due to Lemma 62, it must be \(\Delta '\cap B_n = E_n \cup N_n\) where \(E_n \in \mathscr {B}(B_n) \subset \mathscr {B}(S')\) and \(N_n \subset Z_n\) with \(Z_n \in \mathscr {B}(B_n) \subset \mathscr {B}(S')\) and \(|Z_n|=0\), that is \(\nu _{S'}(Z_n)=0\). In summary, \(\Delta ' = \cup _{n\in \mathbb {N}} E_n \cup N_n = ( \cup _{n\in \mathbb {N}} E_n) \cup (\cup _{n\in \mathbb {N}} N_n)\) with \(\cup _{n\in \mathbb {N}} E_n \in \mathscr {B}(S')\) and \(\cup _{n\in \mathbb {N}} N_n\subset \cup _{n\in \mathbb {N}} Z_n \in \mathscr {B}(S')\), where \(0\le \nu _{S'}(\cup _{n\in \mathbb {N}} Z_n ) \le \sum _{n} \nu _{S'}(Z_n)=0\), so that \(\nu _{S'}(\cup _{n\in \mathbb {N}} Z_n )=0\). By construction \(\Delta ' \in \overline{\mathscr {B}(S')}^{\nu _{S'}}=: \mathscr {M}(S')\). \(\square \)
3.3 The general causality condition is valid for every spacelike Cauchy localization observable
We pass to prove that GCC is actually valid for every spacelike Cauchy localization. The proof consists of some steps. The general structure of the demonstration enjoys many similarities with some proofs originally introduced in [30] and later generalized in [9]. However, to extend these constructions to generic spacelike Cauchy surfaces, we shall also take advantage of some fundamental achievements by Bernal and Sánchez [3, 4] here specialized to Cauchy surfaces of Minkowski spacetime.
Lemma 28
Consider a Minkowski chart on \(\mathbb {M}\) and consider a pair of spacelike smooth 3-dimensional embedded manifolds \(S,S'\), respectively, described as the sets
for a pair of smooth functions \(t_S: \mathbb {R}^3 \rightarrow \mathbb {R}\) and \(t_{S'}: \mathbb {R}^3 \rightarrow \mathbb {R}\) (where necessarily \(|\nabla t_S|<1\) and \(|\nabla t_S|<1\) everywhere). If \(S\in \mathscr {C}_\mathbb {M}^s\) and \(t_{S'}(\vec {x})= t_S(\vec {x})\) outside a compact set in \(\mathbb {R}^3\), then \(S'\in \mathscr {C}_\mathbb {M}^s\) as well.
Proof
\(S'\) is diffeomorphic to \(\mathbb {R}^3\) through the projection map  . Therefore \(S'\) is connected and closed as it is the preimage of the closed set \(\{0\}\) according to the continuous (actually smooth) map
. Therefore \(S'\) is connected and closed as it is the preimage of the closed set \(\{0\}\) according to the continuous (actually smooth) map  . Let us define \(T= \max \{ |t_S(\vec {x})- t_{S'}(\vec {x})| | \vec {x} \in \mathbb {R}^3\}\). Notice that T is finite because the function is continuous and compactly supported. Since the curves tangent to the \(x^0\) axis are timelike, we have that \(S' \subset I^+(S_{-2T}) \cap I^-(S_{2T})\), where
. Let us define \(T= \max \{ |t_S(\vec {x})- t_{S'}(\vec {x})| | \vec {x} \in \mathbb {R}^3\}\). Notice that T is finite because the function is continuous and compactly supported. Since the curves tangent to the \(x^0\) axis are timelike, we have that \(S' \subset I^+(S_{-2T}) \cap I^-(S_{2T})\), where
Similarly, \(S_{-2T} \subset I^-(S_{2T})\) and also \(S_{\pm 2T}\) are spacelike Cauchy surfaces because they are obtained trough isometries out of the spacelike Cauchy surface S. According to (d1) in Remark 13, \(S'\) is a spacelike Cauchy surface. \(\square \)
Proposition 29
If \(\textsf{A}\) is a spacelike Cauchy localization, then (16) and (15) are true when \(\Delta \subset S \in \mathscr {C}_\mathbb {M}\) is a spacelike (embedded) compact smooth 3-submanifold with boundary.
Proof
We henceforth choose a Minkowski global chart and we describe S and \(S'\) through the global chart as in (b) of Proposition 20. In particular  will be denote the said global chart on \(S'\).
will be denote the said global chart on \(S'\).
As \(\Delta \) is compact, it belongs to \(\mathscr {M}(S)\). Furthermore, \(\Delta ' = (J^+(\Delta ) \cup J^-(\Delta )) \cap S' \) is compact as well (Corollary A.5.4 [1]), so that it belongs to \(\mathscr {M}(S')\). Next we consider a sequence of open sets \(F'_n \subset S'\) such that (a) \( \partial F'_n \cap \Delta ' = \varnothing \), (b) \(\overline{F'_{n+1}}\subset F'_n\), and (c) \(\cap _{n\in \mathbb {N}} F'_n = \Delta '\). This sequence is recursively constructed by extracting a finite subcovering of a covering of \(\Delta '\) made of coordinate open balls \(\psi '^{-1}(B_{r_n}(\psi '(p_i)))\) of radius \(r_n\), \(p_i \in \Delta '\), where \(r_n \rightarrow 0\) for \(n\rightarrow +\infty \), and \(r_{n+1} < \text{ dist }(\Delta ', \partial F'_n)\), where \(\text{ dist }(A,B):= \inf _{(x,y)\in A\times B} \text{ dist }(\psi '(x),\psi '(y))\) for \(A,B\subset S'\). The latter distance being the standard distance of couples of points in \(\mathbb {R}^3\) (notice that \( \text{ dist }(\Delta ', \partial F'_n)\) is strictly positive and finite by construction). The boundary of each \(F'_n \subset S'\) is a \(C^0\) submanifold which is also smooth up to a zero-measure subset of the boundary of the balls made of part of the intersections of the boundaries of a finite number of open balls. Each \(\partial F'_n\) can be therefore slightly locally smoothed in order to transform each \(F'_n\) to a corresponding open set \(R'_n\), such that \(\overline{R'_n}\) is a compact smooth submanifold with boundary of the spacelike Cauchy surface \(S'\) and, as before, \(\Delta ' \cap \partial R'_n=\varnothing \), (b) \(\overline{R'_{n+1}}\subset R'_n\), and (c) \(\cap _{n\in \mathbb {N}} R'_n = \Delta '\). Let us now focus on the further family of open relatively compact sets
\(\overline{dR'_n}\) is a compact smooth submanifold with boundary of \(S'\) and \(\overline{dR'_n}\) has no intersection with \(J^+(\Delta ) \cup J^-(\Delta )\) by construction. Since \(\Delta \) is a smooth submanifold with boundary of the spacelike Cauchy surface S, we conclude that \(\Delta \cup \overline{dR_n'}\) is a (non-connected) spacelike and acausal compact smooth 3-submanifold with boundary of \(\mathbb {M}\). According to (d2) in Remark 13, there is a spacelike Cauchy surface \(S''_n\) which includes \(\Delta \cup \overline{dR_n'}\). Finally consider the set
where the map \(t_{S_n}: \mathbb {R}^3 \rightarrow \mathbb {M}\) is constructed as follows:
This map is smooth by construction and \(|\nabla t_{S_n}(\vec {x})| <1 \) everywhere, in particular \({\text {d}}x^0 - t_{S_n} \ne 0\) everywhere, so that the \(S_n\) of \(t_{S_n}\) is a spacelike smooth submanifold. This is a spacelike compact deformation of the Cauchy surface \(S'\) as it coincides to it outside the compact \(\overline{R'}_n\). According to Lemma 28, \(S_n\) is a spacelike Cauchy surface as well.
To go on, we pass to consider the two normalized \(\mathcal{H}\)-POVM \(\textsf{A}_S\) and \(\textsf{A}_{S'}\). We can decompose
where \(\psi ''_n: S''_n \rightarrow \mathbb {R}^3\) is the global chart on \(S''_n\) according to (b) of Proposition 20. Similarly,
We know that \(S_n {\setminus } {\psi ''_n}^{-1}\circ \psi '\left( R'_n\right) =S' {\setminus } R'_n\) because \(S'\) and \(S_n\) coincide thereon. As a consequence of the coherence condition (13), \( \textsf{A}_{S'}(S' \setminus R'_n)=\textsf{A}_{S_n}({S_n \setminus \psi ''_n}^{-1}\circ \psi '( R'_n))\) so that,
Using again the coherence condition with \(\Delta \subset S \cap S_n\), we have obtained that
so that, for every \(\psi \in \mathcal{H}\), we achieve the relation between positive finite measures
At this juncture, \(\langle \psi |\textsf{A}_{S'}(R'_n)\psi \rangle <+\infty \), \(\cap _{n\in \mathbb {N}} R'_n = \Delta '\), \(R'_{n+1}\subset R'_n\), and external continuity yield
As \(\inf _{n\in \mathbb {N}}\langle \psi | \textsf{A}_{S_n}({\psi ''_n}^{-1}\circ \psi '(R'_n\setminus \Delta ))\psi \rangle \ge 0\), we have proved that
This is the thesis by arbitrariness of \(\psi \in \mathcal{H}\). \(\square \)
Proposition 30
If \(\textsf{A}\) is a spacelike Cauchy localization, then (16) and (15) are true when \(\Delta \subset S \in \mathscr {C}^s_\mathbb {M}\) is open.
Proof
Consider \(S,S' \in \mathscr {C}^s_\mathbb {M}\) and refer to the definition (14) of \(\Delta '\). Generally speaking, if \(\Delta \subset S\) is open set, from Proposition 16 and the fact that S is a smooth submanifold (a \(C^0\) embedded submanifold is enough actually), it is not difficult to prove that \(J^\pm (\Delta )\) are open setsFootnote 11 in \(\mathbb {M}\). Hence, \(\Delta ' \subset S'\) is open as well. Therefore (16) is true in the considered case.
Let us denote by \(\psi : S \rightarrow \mathbb {R}^3\) the global chart on S constructed through a function \(t_S\) in a Minkowski chart \(x^0,\vec {x}\) as prescribed in (b) of Proposition 20. We shall use this identification to see the points of S as points of \(\mathbb {R}^3\). This identification enjoys an important property. The completed measures \(\overline{\nu }_S\) and the standard Lebesgue measure on \(\mathbb {R}^3\) turn out to be equivalent through the identification \(\psi \) as a straightforward consequence of the fact that, in (10), the map  is continuous and strictly positive. The impact of this remark relies upon the following known result (Theorem 1.26 in [14]). If \(A \subset \mathbb {R}^n\) is open, \(\delta >0\), there exist a countable collection \(\{B_j\}_{j=1,2,\ldots }\) of disjoint (non-empty) closed balls \(B_j \subset A\) with diameter less than \(\delta \), such that
is continuous and strictly positive. The impact of this remark relies upon the following known result (Theorem 1.26 in [14]). If \(A \subset \mathbb {R}^n\) is open, \(\delta >0\), there exist a countable collection \(\{B_j\}_{j=1,2,\ldots }\) of disjoint (non-empty) closed balls \(B_j \subset A\) with diameter less than \(\delta \), such that
the bar denoting the Lebesgue measure on \(\mathbb {R}^3\). Passing to S, it means that (for every \(\delta >0\)) there exist a countable family of pairwise disjoint compact smooth spacelike submanifolds with boundary \(\Delta _j:= \psi ^{-1}(B_j) \subset \Delta \subset S\), such that
Therefore, since the positive measure \(\langle \psi |\textsf{A}_S(\cdot )\psi \rangle \) is finite and is absolutely continuous with respect to \(\nu _S\) according to Proposition 23:
if \(\psi \in \textsf{H}\). If we define the compact set \(\Delta _N:= \bigcup _{j=0}^N \Delta _j \subset \Delta \) and \(\Delta '_N\) correspondingly, we can apply Proposition 29 obtaining that, for every \(\psi \in \mathcal{H}\),
As both sequences are non-decreasing, the limit for \(N\rightarrow +\infty \) exist and, using inner continuity, (17), and monotony, we find
This is the thesis by arbitrariness of \(\psi \in \mathcal{H}\).\(\square \)
Proposition 31
If \(\textsf{A}\) is a spacelike Cauchy localization, then (16) and (15) are true when \(\Delta \subset S \in \mathscr {C}_\mathbb {M}\) is compact.
Proof
(16) is valid just because, as already observed in the proof of Proposition 29, \(\Delta '\) is compact if \(\Delta \) is. So we have to establish the validity of (15) only. We refer to a global chart \(\psi : S \rightarrow \mathbb {R}^3\) on S constructed out of the map \(t_S\) in a Minkowski chart \(x^0,\vec {x}\) as in (b) of Proposition 20. If \(\Delta \subset S\) is compact we can construct a sequence of open sets \(F_n \supset \Delta \) such that \(F_{n+1} \subset F_n\) and \(\cap _{n\in \mathbb {N}} F_n = \Delta \). \(F_n\) is the finite union of coordinate balls of radius \(r_n \rightarrow 0\) such that \(r_{n+1}<\text{ dist }(\Delta , F_n)\) where we adopted the same notation as in the proof of Proposition 29. In view of Prof 31, taking account of the external continuity of the involved measures
The proof ends if proving that \(\cap _{n\in \mathbb {N}} F'_n= \Delta '\). In, fact, obviously \(\cap _{n\in \mathbb {N}} F_n\supset \Delta '\). On the other hand, if \(p \in \cap _{n\in \mathbb {N}} F'_n\), then there is a causal segment from p to \(q_n\in F_n \subset \overline{F_0}\) which is compact and stays in S because it is closed. As a consequence there is a subsequence \(q_{n_k} \rightarrow q \in \overline{F_0}\) for \(k\rightarrow +\infty \). It is easy to see that \(q\in \Delta \) (otherwise q would stay at some distance from the compact \(\Delta \) and this is not admitted in view of the very construction of the sets  ). The limit \(p-q\) of the causal segments \(p-q_n\) is still causal or 0 (as the set of causal vectors and \(\{0\}\) is closed). We conclude that \(p \in (J^+(\Delta ) \cup J^-(\Delta ))\cap S = \Delta '\). We have established that \(\cap _{n\in \mathbb {N}} F_n\subset \Delta '\), so that \(\cap _{n\in \mathbb {N}} F_n= \Delta '\) concluding the proof. \(\square \)
). The limit \(p-q\) of the causal segments \(p-q_n\) is still causal or 0 (as the set of causal vectors and \(\{0\}\) is closed). We conclude that \(p \in (J^+(\Delta ) \cup J^-(\Delta ))\cap S = \Delta '\). We have established that \(\cap _{n\in \mathbb {N}} F_n\subset \Delta '\), so that \(\cap _{n\in \mathbb {N}} F_n= \Delta '\) concluding the proof. \(\square \)
We are in a position to prove the first main result of this work: spacelike Cauchy localizations always satisfy the Cauchy causality requirement in Definition 26. Thus, in particular, also Castrigiano’s causal requirement when restricting to spacelike flat Cauchy surfaces.
Theorem 32
Let \(\textsf{A}:= \{\textsf{A}_S\}_{S\in \mathscr {C}^s_\mathbb {M}}\) be a spacelike Cauchy localization observable, then it satisfies the general causal condition in Definition 26.
More generally, if \(S,S' \in \mathscr {C}_\mathbb {M}^s\), \(\Delta \in \mathscr {M}(S)\), and \(\psi \in \mathcal{H}\), then
even if \(\Delta ' \not \in \mathscr {M}(S')\). (Above \(K':= (J^+(K) \cup J^-(K)) \cap S'\) as usual.)
Proof
The positive Borel measure  is regular (because S is Hausdorff, locally compact and every open set is a countable union of compacts with finite measure, according to Theorem 2.18 in [35]). As a consequence, the completion measure
is regular (because S is Hausdorff, locally compact and every open set is a countable union of compacts with finite measure, according to Theorem 2.18 in [35]). As a consequence, the completion measure  is regular as well (Proposition 1.59 in [12]). If \(\Delta \in \mathscr {M}(S)\), internal regularity yields
is regular as well (Proposition 1.59 in [12]). If \(\Delta \in \mathscr {M}(S)\), internal regularity yields
At this juncture Proposition 31 entails (19).
If we also know that \(\Delta ' \in \mathscr {M}(S')\), noticing that the sets \(K'\) are compact and satisfy \(K'\subset \Delta '\), but they are not necessarily all compact sets in \(S'\) satisfying the latter condition, internal regularity entails
However, Proposition 31 implies
Therefore \( \langle \psi | \textsf{A}_S(\Delta ) \psi \rangle \le \langle \psi | \textsf{A}_{S'}(\Delta ') \psi \rangle \). This is just (15) due to arbitrariness of \(\psi \in \mathcal{H}\). \(\square \)
Corollary 33
If a spatial localization observable \(\{\textsf{A}_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) can be extended to a spacelike Cauchy localization observable \(\{\textsf{A}_S\}_{S\in \mathscr {C}^s_\mathbb {M}}\), then the former automatically satisfies CC in Definition 2.
Proof
Consider only spacelike flat Cauchy surfaces, noticing that there \(\mathscr {M}(\Sigma )= \mathscr {L}(\Sigma )\) and that \(\Delta ' \in \mathscr {L}(\Sigma ')\) for every \(\Delta \subset \Sigma \) (even if \(\Delta \not \in B(\Sigma )\)!) as established in [8]. In that case GCC in Definition 26 boils down to CC in Definition 2. \(\square \)
Remark 34
In the proof of Theorem 32, the coherence condition (13) of Definition 21 is of utmost relevance. This is one of the reasons why we inserted that requirement already in Definition 21. However, an alternative approach would consist of removing this condition from the Definition 21 and to directly add it in the hypotheses of Theorem 32, proving again the validity of GCC. At this juncture it is worth stressing that GCC trivially implies the coherence condition 13 (since \(\Delta = \Delta '\) if \(\Delta \subset S \cap S'\)). The conclusion is that, if using from scratch a weaker version of Definition 21, i.e., without the requirement of coherence (13), the general causal conditions (15)–(16) and the coherence condition (13) would be equivalent.Footnote 12\(\blacksquare \)
4 Massive KG particles, conserved currents
In this section, we shall introduce some basic notion and results to construct examples of spatial Cauchy localization observables. The former section is a recap about the one-particle structure of the massive real Klein–Gordon particle. The latter deals with some general properties of conserved currents and associated exact volume 3-forms.
4.1 One-particle Hilbert space of real massive KG particles in \(\mathbb {M}\)
According to Sect. 2.2, we fix a preferred origin \(o\in \mathbb {M}\), so that the map  defines a one-to-one correspondence between points of \(\mathbb {M}\) and vectors in \(\textsf{V}\) (the differential of this map being \(\imath _p\)). This identification is very useful when dealing with the Fourier transformation on \(\mathbb {M}\), where the product \(p\cdot x\) enters the play. All the theory developed in this work does not depend on the choice of o. With this structure, the active action (6) of \((y, \Lambda ) \in \mathscr {P}_+\) on \(\mathbb {M}\) takes the form
defines a one-to-one correspondence between points of \(\mathbb {M}\) and vectors in \(\textsf{V}\) (the differential of this map being \(\imath _p\)). This identification is very useful when dealing with the Fourier transformation on \(\mathbb {M}\), where the product \(p\cdot x\) enters the play. All the theory developed in this work does not depend on the choice of o. With this structure, the active action (6) of \((y, \Lambda ) \in \mathscr {P}_+\) on \(\mathbb {M}\) takes the form  . Given a mass constant \(m>0\), the future mass-shell in \(\textsf{V}\) is \(\textsf{V}_{m,+}:= \{k\in V_+ | k\cdot k = -m^2\}\). For every Minkowski chart \(x^0,x^1,x^2,x^3\),
. Given a mass constant \(m>0\), the future mass-shell in \(\textsf{V}\) is \(\textsf{V}_{m,+}:= \{k\in V_+ | k\cdot k = -m^2\}\). For every Minkowski chart \(x^0,x^1,x^2,x^3\),
The one-particle Hilbert space of a Klein–Gordon particle of mass \(m>0\) is isomorphic to \(L^2(\mathbb {R}^3, d^3p)\) upon the choice of a Minkowski chart \(x^0,x^1,x^2,x^3\). Here \(\mathbb {R}^3\), is the space of momenta \(\vec {p}\) and the momentum representation wavefunctions \(\phi =\phi (\vec {p})\) are normalized elements of \(L^2(\mathbb {R}^3, d^3p)\). To have a completely covariant formulation, one takes advantage of the canonical Hilbert space isomorphism

There,
is the (covariant) one-particle Hilbert space of a real Klein–Gordon particle with mass \(m>0\), where \(\mu _m\) is the \(\mathscr {P}_+\)-invariant measure on the mass shell \(\textsf{V}_{m,+}\). Covariance is here manifest because, the standard unitary representation of \(\mathscr {P}_+\) on the one-particle space

takes the equivariant form
For future convenience, we define the dense subspaces \(\mathcal{D}(\mathcal{H}) \subset \mathcal{S}(\mathcal{H}) \subset \mathcal{H}\)
where \({\mathscr {S}}(\mathbb {R}^3)\) is the usual Schwartz space on \(\mathbb {R}^3\). It easy to prove that, in view of (24), the definition of \(\mathcal{D}(\mathcal{H})\) and \(\mathcal{S}(\mathcal{H})\) do not depend on the choice of the Minkowski chart used to construct F. If \(\psi \in \mathcal{D}(\mathcal{H})\), or more generally \(\psi \in \mathcal{S}(\mathcal{H})\), the associated (complex) covariant wavefunction is
Notice that \(\varphi _\psi \in C^\infty (\mathbb {M})\), it is also bounded with all of its derivatives, and it solves the Klein–Gordon equation in \(\mathbb {M}\)
Furthermore, the action of U on \(\varphi _\psi \) is straightforward and explains the adjective ”covariant”:
Due to (26),(27) and Proposition 37 applied to the bounded conserved smooth current
we have that the scalar product of \(\mathcal{H}\) satisfies, for \(\psi ,\psi ' \in \mathcal{S}(\mathcal{H})\),
for every spacelike smooth Cauchy surface S in \(\mathbb {M}\). An analogous formula for generic smooth Cauchy surfaces can be established on account of Propositions 36 and 37.
Various issues concerning the possibility to directly or indirectly interpret \(\varphi _\psi \) as a wavefunction in classical sense somehow related to notions of spatial localization, and the failure of these expectations accumulated over the years, were discussed in [30].
4.2 Conserved quantities on generic smooth Cauchy surfaces of \(\mathbb {M}\)
From now on, we assume that \(\mathbb {M}\) is oriented. Consider a smooth vector field J in \(\mathbb {M}\). We can associate a 3-form to it,Footnote 13where we henceforth take advantage of the summation convention over repeated Greek indices,
Above \(\epsilon _{\delta \alpha \beta \gamma }\) is the Levi-Civita (pseudo)tensor which, in Minkowski coordinates, coincides to the sign of the permutation \((\delta , \alpha ,\beta , \gamma )\) of (0, 1, 2, 3), or vanishes in case of repetitions.
Let S be a smooth Cauchy surface determined by the map \(t_S:\mathbb {R}^3 \rightarrow \mathbb {R}\) in Minkowski coordinates \(x^0,x^1,x^2,x^3\) where \(v_S\) is the future-directed normal vector to S as in (11). If \(J \equiv (J^0, \vec {J})\) is either zero or causal and future directed depending on \(x\in \mathbb {M}\), then we define
In the last two integrals, A is interpreted as a subset of \(\mathbb {R}^3\) according to the canonical projection  and the integrals are well defined in \([0,+\infty ]\) because
and the integrals are well defined in \([0,+\infty ]\) because
Remark 35
The integral of the form \(\omega ^J\) as defined by the right-most term in (31) is a standard integral in the sense of measure theory for a generic Borel set A. This fact permits to use standard arguments of measure theory. On the other hand, if A is compact, the definition agrees with the standard integral of smooth n-forms on compact sets and we can take advantage of standard results in this context as the Poincaré theorem. \(\blacksquare \)
We have a preliminary proposition whose elementary proof is left to the reader.
Proposition 36
If J is a smooth vector field on \(\mathbb {M}\) and \(\omega ^J\) is defined as in (30), then the following facts are valid (where (5) has been taken into account)
-
(1)
J is conserved iff \(\omega ^J\) is closed:
$$\begin{aligned} \partial _\alpha J^\alpha (x) =0 \quad \Leftrightarrow \quad d \omega ^J(x) =0. \end{aligned}$$(33) -
(2)
If \(S\in \mathscr {C}_\mathbb {M}^s\), then
$$\begin{aligned} \int _A \omega ^J = -\int _A J\cdot n_S \, d\nu _S . \end{aligned}$$(34)
We pass now to state a folklore statement which is actually technically very useful. The unexpectedly technical proof is in the appendix.
Proposition 37
Let J be a smooth vector field on \(\mathbb {M}\) such that
-
(1)
it is conserved, i.e., \(\partial _\alpha J^\alpha =0\) everywhere;
-
(2)
if \(x\in \mathbb {M}\), then either \(J(x)=0\) or J(x) is causal and future-directed, i.e., \(J(x) \in \overline{\textsf{V}_+}\);
-
(3)
it is bounded, i.e., its components in a (thus every) Minkowski chart are bounded functions.
Then, if \(S,S' \in \mathscr {C}_\mathbb {M}\),
If, e.g., \(S'\in \mathscr {C}^s_\mathbb {M}\), then the above identity can be re-written as
Proof
See Appendix 1. \(\square \)
5 Spacelike Cauchy localization observables out of causal kernels of massive KG particles
We now pass to make contact with a family of normalized POVMs, for a massive real Klein–Gordon particle, defined on spacelike flat Cauchy surfaces and introduced by Gerlach, Gromes and Petzold [18] and Henning, Wolf [20] and, much more recently, rigorously studied by Castrigiano in [9], proving in particular that these POVMs satisfy CC. Next we pass to extend these POVMS to the full family of smooth Cauchy surfaces showing that, when considering only the spacelike Cauchy surfaces, they induce corresponding spacelike Cauchy localization observables. Before, we have to recall some basic definitions.
Remark 38
We stress that the localization observable we shall construct is more general than the notion of spacelike Cauchy localization. In fact the POVMs we shall construct are also defined for smooth Cauchy surfaces which are not spacelike. This feature may have some consequences in the analysis of the structure of causal regions of \(\mathbb {M}\) in terms of orthocomplemented lattices [8]. \(\blacksquare \)
5.1 A notion of spatial localization for massive KG particles out of causal kernels
Consider a Minkowski chart \(x^0,x^1,x^2,x^3\). We want to introduce an \(L^2(\mathbb {R}^3, d^3p)\) POVM rigorously discussed in [9]—there named POL—on the rest space at time \(x^0\) denoted below by \(\mathbb {R}^3_{x^0}\). The POVM \(\textsf{T}_{\mathbb {R}^3_{x^0}}\) defines the position in \(\mathbb {R}^3_{x^0}\) of a scalar real Klein Gordon particle of mass \(m>0\)—whose pure states are defined by functions \(\phi =\phi (\vec {p})\) in momentum representation with Hilbert space \(L^2(\mathbb {R}^3, d^3p)\). It satisfies the condition
Above, \(\vec {x}:= (x^1,x^2,x^3)\), the components \(k^0\) and \(p^0\) are determined by \(\vec {k}, \vec {p} \in \mathbb {R}^3\) as prescribed in (20) and the vectors \(\phi \) stay in a suitable dense subspace of \(L^2(\mathbb {R}^3, d^3p)\). More specifically, referring to the discussion of Sect 11 [9]:
Definition 39
Consider a Minkowski chart \(x^0,x^1,x^2, x^3\) on \(\mathbb {M}\). A POL with causal kernelFootnote 14 on \(\mathbb {R}^3_{x^0}\) is a normalized \(L^2(\mathbb {R}^3, d^3p)\)-POVM \(T^g_{\mathbb {R}^3_{x^0}}\) such thatFootnote 15
-
(a)
(37) is valid when \(\phi \in L^1(\mathbb {R}^3, dk^3)\cap L^2(\mathbb {R}^3, dk^3)\);
-
(b)
\(K:=K_g\) is a causal kernel, i.e., it has the structure
$$\begin{aligned} K_g(\vec {k},\vec {p}):=(k^0+p^0) g(-k\cdot p),\quad k,p \in \textsf{V}_{m,+} \end{aligned}$$(38)for \(g: [m^2,+\infty ) \rightarrow \mathbb {R}\) which is continuous, normalized to \(g(m^2)=1\) and it is such that \(K_g: \mathbb {R}^3 \times \mathbb {R}^3 \rightarrow \mathbb {C}\) is positive definite. \(\blacksquare \)
Remark 40
-
(1)
We recall the reader that \(K: X\times X \rightarrow \mathbb {C}\) is a positive definite kernel if
$$\begin{aligned} \sum _{i,j=1}^N \overline{c_i}c_j K(k_i, k_j) \ge 0, \forall \{c_j\}_{j=1,\ldots , N}\subset \mathbb {C}, \forall \{k_j\}_{j=1,\ldots , N}\subset X , \forall N=1,2,\ldots .\end{aligned}$$(39)Notice that a positive definite kernel is necessarily Hermitian: \(K(p,q)= \overline{K(q,p)}\).
-
(2)
We stress that in (38), \(k = (k^0(\vec {k}), \vec {k})\) and \(p = (p^0(\vec {p}), \vec {p})\) in accordance with (20), so that we can see \(K_g\) either as a function on \(\mathbb {R}^3\times \mathbb {R}^3\) or on \(\textsf{V}_{m,+}\times \textsf{V}_{m,+}\) indifferently. \(\blacksquare \)
It is possible to prove (see [9] for details) that \(\mathscr {P}_+\)-covariant localization POVMs with causal kernel do exist. In particular, a family of functions g as in the above definition which give rise to corresponding \(\mathscr {P}_+\)-covariant POVM with causal kernel is
Finite convex combinations of functions \(g_r\) also define causal kernels. Even some pointwise limits of these convex combinations do the job as discussed in [18] and [20]:

It is convenient to re-write the POVM \(\textsf{T}^g_{\mathbb {R}^3_{x^0}}\) of Definition 39 into a different form, where (a) the dependence on a chart disappears, (b) the spacelike flat Cauchy surface normal to a reference frame remains, and (c) some covariance properties explicitly show up. A similar reformulation already appeared in [9], but we use here a slightly different approach and notation, more useful for our final goals. To this end, as in [9], we first define a current \(j_g(k,p) \in \textsf{V}_+\) by means of
so that (37) can be rephrased to an equivalent form
Above, the Minkowski chart \(x^0,x^1,x^2,x^3\) is adapted to \(n:= \partial _{x^0}\). Furthermore, up to a spacetime displacement of the origin of the coordinates, we can always assume that (0, 0, 0, 0) corresponds to the origin \(o\in \mathbb {M}\) initially fixedFootnote 16 (beginning of Sect. 5). The vector \(x\in \textsf{V}\) in the exponent in (42) is such that the point \(o+x \in \mathbb {M}\) has coordinates \(x^0,x^1,x^2,x^3\). We might therefore write \(d\mu _{\mathbb {R}^3_{x^0}}(o+x)\) rather than \(d\mu _{\mathbb {R}^3_{x^0}}(x)\). However, this misuse of notation does not produces troubles because the map  is one-to-one. The factor \(1/\sqrt{p^0k^0}\) in (42) stems from the choice of the Hilbert space \(L^2(\mathbb {R}^3,d^3p)\). It can be removed by passing to covariant one-particle Hilbert space \(\mathcal{H}:= L^2(\textsf{V}_{m,+}, \mu _m)\) (22). With this prescription, if \(\Sigma \in \mathscr {C}_\mathbb {M}^{sf}\), (42) can be rephrased to
is one-to-one. The factor \(1/\sqrt{p^0k^0}\) in (42) stems from the choice of the Hilbert space \(L^2(\mathbb {R}^3,d^3p)\). It can be removed by passing to covariant one-particle Hilbert space \(\mathcal{H}:= L^2(\textsf{V}_{m,+}, \mu _m)\) (22). With this prescription, if \(\Sigma \in \mathscr {C}_\mathbb {M}^{sf}\), (42) can be rephrased to
It is now evident that no choice of a Minkowski chart enters (43) and the only spot where a Minkowski reference frame \(n_\Sigma \) takes place is when assigning the spacelike flat Cauchy surface \(\Sigma \), since \(n_\Sigma \) is the future directed unit normal vector to \(\Sigma \). The vectors x entering the exponential satisfy \(o+x\in S\), which, in turn, is the integration space of the external integral.
5.2 Properties of \(\textsf{T}^g_\Sigma \), for spacelike flat Cauchy surfaces \(\Sigma \): covariance, causality, no strict localizability, Newton–Wigner, Heisenberg inequality
If we fix a function g as in Definition 39, the arising spatial localization observable \(\{\textsf{T}^g_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) is \(\mathscr {P}_+\)-covariant in the sense discussed in [9]: If U is the unitary representation of \(\mathscr {P}_+\) in the one-particle space introduced in (23) and (24), it holds
Notice that \(h\Sigma \) is an analogous spacelike flat Cauchy surface normal to \(n_{h\Sigma }= \Lambda _hn_\Sigma \) if \(h=(y_h,\Lambda _h)\). We do not enter into the details of these properties because we shall not use them in the rest of the paper. The spatial localization observable \(\{\textsf{T}^g_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) complies with the definition of relativistic spatial localization observable proposed in [30] (Definition 18 therein). Denoting the POVMs extended from \(\mathscr {B}(\Sigma )\) to \(\mathscr {L}(\Sigma )\) with the same symbol \(\textsf{T}^g_\Sigma \), we can prove the following result.
Theorem 41
([9]) If \(g: [m^2,+\infty ) \rightarrow \mathbb {R}\) continuous,Footnote 17 normalized to \(g(m^2)=1\) such that the kernel \(K_g: \mathbb {R}^3 \times \mathbb {R}^3 \rightarrow \mathbb {C}\) in (38) is positive definite, then spatial localization observable \(\{ \textsf{T}^g_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) satisfies CC in Definition 2.
Proof
Theorem 56 [9]. \(\square \)
Corollary 42
If \(\psi \in \mathcal{H}\), the localization probability associated to the spatial localization observable \(\{ \textsf{T}^g_\Sigma \}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) cannot be zero outside a bounded set in \(\Sigma \).
Proof
If localized states as above exist, CT would fail as a consequence of Hegerfeldt’s theorem on relativistic time evolution (Theorem 4) and thus also CC would be false. (See [30] for a discussion on this point.) \(\square \)
Remark 43
In spite of this obstruction, it is possible to show [9] that probability distributions localized in bounded sets can be arbitrarily well approximated by probability distributions arising by suitable sequences of state \(\psi _n\). In the case of causal kernels it is an important open problem whether there are point localized sequences of states, i.e., roughly speaking whether the system can be localized within a bounded region as accurately as desired. This problem is discussed in [9] sec. 18 Discussion. \(\blacksquare \)
There is an interesting relation between the first moment of the POVM \(\textsf{T}^g_\Sigma \) on a spacelike flat Cauchy surface \(\Sigma \) and the Newton–Wigner selfadjoint operators \(N_\Sigma ^1,N_\Sigma ^2,N_\Sigma ^3\) [30] associated to a Minkowski chart \(x^0,x^1,x^2,x^3\) such that the slice \(x^0=0\) coincides with \(\Sigma \). Similarly to Thm 26 in [30], one sees that the following result is valid. Below \(\Delta _\psi x^a_{\textsf{T}^g_\Sigma }\) denotes the standard deviation for the coordinate \(x^a\) referred to the probability distribution \(\langle \psi | \textsf{T}^g_\Sigma (\cdot ) \psi \rangle \) constructed out of the POVM \(\textsf{T}^g_\Sigma \) in the state defined by the unit vector \(\psi \).
Theorem 44
Suppose that g in the definition of \(\textsf{T}^g_\Sigma \) is real, bounded, and smooth, then the following is true.
-
(a)
The a-first moment of \(\textsf{T}^g_\Sigma \) is defined for every \(\psi \in \mathcal{D}(\mathcal{H})\) with \(||\psi ||=1\) and
$$\begin{aligned} \int _{\Sigma } x^a \langle \psi | \textsf{T}^g_\Sigma (d^3x) \psi \rangle = \langle \psi | N_\Sigma ^a \psi \rangle ,\quad \text{ where } a=1,2,3. \end{aligned}$$(45)In particular, \(N^a_\Sigma \) is the unique selfadjoint operator in \(\mathcal{H}\) which satisfies the identity above.
-
(b)
The Heisenberg inequality turns out to be corrected as, for \(\psi \in \mathcal{D}(\mathcal{H})\),
$$\begin{aligned}\Delta _\psi x_{\textsf{T}^g_\Sigma }^a \Delta _\psi P_a \ge \frac{\hbar }{2} \sqrt{1+4 (\Delta _\psi P_a)^2 \langle \psi |\textsf{K}^{\textsf{T}^g_\Sigma }_{a} \psi \rangle }, \quad a=1,2,3.\end{aligned}$$\(\textsf{K}^{\textsf{T}^g_\Sigma }_{a}\in \mathfrak {B}(\mathcal{H})\) is a selfadjoint operator, which is a (spectral) function of the four momentum observable P with the form (79), such that \(\textsf{K}^{\textsf{T}^g_\Sigma }_{a}\ge 0\).
-
(c)
If g is of the form (40), or convex combinations of them, then (a) and (b) also hold for \(\psi \in \mathcal{S}(\mathcal{H})\).
Proof
See Appendix 1. \(\Box \)
Notice that the left-hand side of (45) does not depend on g.
Remark 45
-
(1)
If also the identity
$$\begin{aligned} \int _{\Sigma } (x^a)^2 \langle \psi | \textsf{T}^g_{\Sigma }(d^3x) \psi \rangle = \langle \psi | (N^a_\Sigma )^2\psi \rangle \, \quad \text{(false!) },\end{aligned}$$were valid one could apply a known theorem by Naimark about the decomposition of maximally symmetric operators (here \(N^a_\Sigma \)) in terms of POVMs (see Theorem 23 in [13] and the discussion about it) obtaining \(\textsf{T}^g_\Sigma = \textsf{Q}_{\Sigma }\). This is obviously false and it is also reflected by the appearance of the term \( \langle \psi |\textsf{K}^{\textsf{T}^g_\Sigma }_{a} \psi \rangle \) in the modified Heisenberg inequality.
-
(2)
If \(U^{(n)}_t\) is the unitary time evolutor corresponding to the time evolution along n in \(\mathbb {M}\), it is easy to see that the Heisenberg evolution \(U^{(n)}_t N_\Sigma ^a U^{(n)\dagger }_t\) of \(N_\Sigma ^a\) on the right-hand side of (45) equals the integral on the left-hand side over the correspondingly temporally translated time slice \(\Sigma _t\). As already observed in [30], this fact implies that the worldline
 is timelike (Corollary 14 in [30]) as expected by massive particles. \(\blacksquare \)
is timelike (Corollary 14 in [30]) as expected by massive particles. \(\blacksquare \)
5.3 A spacelike Cauchy localization observable \(\textsf{T}^g= \{\textsf{T}^g_S\}_{S\in \mathscr {C}_\mathbb {M}^s}\) for a massive KG particle
Let us focus again on the POVM \(T_{g, \mathbb {R}^3_{x^0}}\) satisfying (37). The equivalent form (43) of (37) is actually already prompt to be generalized to any smooth Cauchy surface S. Heuristically, if \(S\subset \mathbb {M}\) is a spacelike Cauchy surface defined by \(x^0=t_S(\vec {x})\), we expect that the current \(j_{g}\) also defines a normalized POVM whose expectation value on \(\Delta \in \mathscr {B}(S)\) is:
when \(\psi \) belongs to a suitable subspace of \(\mathcal{H}\) and where \(n_S\) is the normal future-directed unit vector to S. In case S is smooth but not spacelike, we can expect the version in terms of forms be valid
where
As we shall see shortly, this current is conserved: \(\partial _\mu J_{g, \psi }^\mu =0\), so that \(d \omega ^{J_{g,\phi }}=0\) and that it is zero or causal and future directed at each point of \(\mathbb {M}\).
To extend the definition of \(\textsf{T}^g_S\) to every smooth Cauchy surface of \(\mathbb {M}\), we cannot directly follow the approach of [9]—based on a smart decompositions of \(\textsf{T}(\Delta )\) in terms of isometries and the standard PVM of the position observable on \(\mathbb {R}^3\)—because of the appearance of various spurious terms containing \(t_S(\vec {x})\) and \(\nabla t_S(\vec {x})\) in the expression of \(\omega ^{J_{g,\psi }}\). Nevertheless, the wanted extension is feasible through a more indirect way.
There are various lemmata we shall exploit to achieve the wanted result.
Lemma 46
Consider \(g: [m^2,+\infty ) \rightarrow \mathbb {R}\) continuous, normalized to \(g(m^2)=1\) such that the kernel \(K_g: \mathbb {R}^3 \times \mathbb {R}^3 \rightarrow \mathbb {C}\) in (38) is positive definite.
If \(\psi \in \mathcal{D}(\mathcal{H})\) then the current \(J_{g,\psi }\) defined in (48) is smooth, bounded, conserved, and zero or causal and future-directed at any point of \(\mathbb {M}\).
Proof
Fix a Minkowski chart \(x^0,x^1,x^2,x^3\). Let us take \(\phi \in C_c^\infty (\mathbb {R}^3) \subset L^2(\mathbb {R}^3, d^3k)\) and let us consider the vector field in \(\mathbb {M}\) defined in (48), now in equivalent terms of \(\phi \) instead of \(\psi \) according to (21),
With the said hypotheses on \(\phi \), a direct use of the Lebesgue dominate convergence theorem permit us to pass the \(x^\nu \) derivatives of every order under the integration symbol proving that J is bounded and smooth. However, the first derivative yields
since \((p^\mu +k^\mu )(p_\mu -k_\mu ) = -m^2+m^2 +k^\mu p_\mu - p^\mu k_\mu =0\). Finally, as established in [9], J(x) is either zero or causal and future-directed for every \(x\in \mathbb {M}\) (see Theorem 52 in [9] and (c) in its proof). \(\square \)
Lemma 47
Consider g as in Lemma 46. If S is a smooth Cauchy surface, it holds
for every \(\psi \in \mathcal{D}(\mathcal{H})\).
Proof
In view of Lemma 46, since \(J_{g,\psi }\) satisfies all required hypotheses, we can apply Proposition 37 for \(S'\) given by the time-slice at \(x^0=0\), taking (31) into account and finally obtaining that
which is the thesis. The last identity is due to the fact that, as established in [9], the last integral is nothing but \(\langle \phi | \textsf{T}_{\mathbb {R}^3_0}(\mathbb {R}^3) \phi \rangle \) where  is a normalized POVM in \(\mathbb {R}^3_{x^0=0}\), because is a POVM defined as in Definition 39.\(\square \)
is a normalized POVM in \(\mathbb {R}^3_{x^0=0}\), because is a POVM defined as in Definition 39.\(\square \)
Lemma 48
Let \(\mathcal{K}\) be a complex Hilbert space and \(D\subset \mathcal{K}\) a dense subspace. Consider a Hermitian form \(\Lambda : D \times D \rightarrow \mathbb {C}\) such that \(|\Lambda (x,x)| \le C||x||^2\) for some constant \(C\ge 0\) and \(\Lambda (x,x) \ge 0\) for every \(x\in D\). Then, a unique operator \(A \in \mathfrak {B}(\mathcal{K})\) exists such that \(\Lambda (x, x) = \langle x | A x \rangle \) for all \(x \in D\). Furthermore, \(||A|| \le C\) and \(A\ge 0\).
Proof
The Cauchy–Schwarz inequality implies \(|\Lambda (x,y)| \le C ||x||\, ||y||\) if \(x,y \in D\). Thus, \(\Lambda \) is continuous and, since \(D\subset \mathcal{H}\) is dense, \(\Lambda \) continuously extends to a Hermitian form on \(\mathcal{H}\times \mathcal{H}\) satisfying the same bound as above, as the reader easily proves. The proof ends by direct application of Corollary after Theorem II.4 in [34]. \(\square \)
We are in a position to prove that a normalized POVM induced by the operators \(\textsf{T}^g_S(\Delta )\) exists on every smooth Cauchy surface of \(\mathbb {M}\) and satisfies the natural coherence requirement (13) also in that case.
Theorem 49
Let \(S\in \mathscr {C}_\mathbb {M}\) and suppose that \(g: [m^2,+\infty ) \rightarrow \mathbb {R}\) is continuous, \(g(m^2)=1\) and the kernel in (38) is positive definite. Then,
-
(a)
there is a unique \(\mathcal{H}\)-POVM, still indicated by \(\{\textsf{T}^g_S(\Delta )\}_{\Delta \in \mathscr {B}(S)}\), which satisfies (47) when \(\psi \in \mathcal{D}(\mathcal{H})\):
$$\begin{aligned} \langle \psi | \textsf{T}^g_S(\Delta ) \psi \rangle =\int _\Delta \omega ^{J_{g,\psi }}, \quad \Delta \in \mathscr {B}(S) , \end{aligned}$$so that, \(\textsf{T}^g_S< \hspace{-5.0pt}< \nu _S\) if \(S \in \mathscr {C}_\mathbb {M}^s\) due to (34).
-
(b)
\(\textsf{T}^g_S\) is normalized: \(\textsf{T}^g_S(S)=I\);
-
(c)
\(\textsf{T}^g_S\) satisfies Definition 39 (i.e., it is a POL with causal kernel according to [9]) when \(S=\Sigma \) is a time slice of a Minkowski coordinate system;
-
(d)
if \(\Delta \in S\cap S'\) is a Borel set, where \(S'\in \mathscr {C}_\mathbb {M}\), then
$$\begin{aligned}\textsf{T}^g_S(\Delta ) =\textsf{T}^g_{S'}(\Delta ).\end{aligned}$$
The family \(\textsf{T}^g:= \{\textsf{T}^g_S\}_{S\in \mathscr {C}^s_\mathbb {M}}\), where we extend each POVMs to \(\mathscr {M}(S)\) according to Proposition 23, is a spacelike Cauchy localization observable in the sense of Definition 21.
Proof
Item (c) is a trivial consequence of (a),(b), and [9], so we prove (a), (b), and (d). The last statement is evident in view of the items (a), (b), (d) and Definition 21
We prove (a) and (b) together. Let \(x^0=t_S(\vec {x})\) be the map which defines S by identifying it with the spatial \(\mathbb {R}^3\) in a given Minkowski system of coordinates \(x^0, \vec {x}\) according to Proposition 20. To make easier the notation we shall omit \(^g\) in \(\textsf{T}^g_S\). If \(\Delta \in \mathscr {B}(\mathbb {R}^3)\) is bounded, so that the integral below is defined, consider the Hermitian form
for \(\psi ,\psi ' \in \mathcal{D}(\mathcal{H})\) and \(\phi _\psi , \phi _{\psi '}\) are the corresponding elements in the isomorphic Hilbert space \(L^2(\mathbb {R}^3,d^3p)\). Since (use (31))
we conclude that
The former inequality arises from the last identity in (31) when remembering that \(J_{g,\psi }\) is zero or causal and future directed for Lemma 46. The latter inequality in (50) is consequence of the positivity of the integrand \( \omega ^{J_{g,\psi }}\) in coordinates (again for (31)) and of Lemma 47. We can finally apply Lemma 48 proving that there exists \(\textsf{T}_S(\Delta ) \in \mathfrak {B}(\mathcal{H})\) such that \(0\le T_S(\Delta )\le I\) and
Eq. (47) is therefore satisfied for \(\Delta \) bounded. To go on we define \(\mathscr {F}(S)\) as the ring of Borel sets of S which are bounded in \(\mathbb {R}^3\). It is clear that the \(\sigma \)-algebra generated by \(\mathscr {F}(S)\) is \(\mathscr {B}(S)\) itself. For the elements \(\Delta \in \mathscr {F}(S)\) we can use the positive operatorFootnote 18\(\textsf{T}_S(\Delta ): \mathcal{H}\rightarrow \mathcal{H}\) bounded by I defined above. We want to prove that, if \(\psi \in \mathcal{H}\), the map

is a \(\sigma \)-additive premeasure on \(\mathscr {F}(S)\). We stress that \(\sigma \)-additivity is guaranteed by the monotone convergence theorem referred to the integral in (51)—using the fact that the integrand is positive. However, this argument works only when \(\psi \in \mathcal{D}(\mathcal{H})\) since (51) is given for this type of functions. On the other hand, the very structure of (51) implies (simple) additivity of \(\nu _\psi \) for \(\psi \in \mathcal{H}\) just by the continuity of \(\textsf{T}_S(\Delta )\). To prove \(\sigma \)-additivity for the general \(L^2\) case, consider \(\Delta \in \mathscr {F}(S)\) which is the countable union of pairwise-disjoint sets \(\Delta _n \in \mathscr {F}(S)\). If \(\psi \in \mathcal{H}\), since all operators \(\textsf{T}_S(\Delta _n)\) are positive and additivity holds, we conclude that
The latter inequality arises from \(\textsf{T}_N = \textsf{T}_S(\cup _{n=0}^N \Delta _n)\le I\). A known result on increasing sequences of positive operators (Proposition 3.76 [29]) proves that there exist a bounded operator \(P: \mathcal{H}\rightarrow \mathcal{H}\) such that \(0\le P \le I\) and
However, \(\sigma \)-additivity for \(\psi \in \mathcal{D}(\mathcal{H})\) guarantees that
Comparing the found limits, we conclude that \( \langle \psi | \textsf{T}_S(\Delta ) \psi \rangle = \langle \psi | P \psi \rangle \) for every \(\psi \in \mathcal{D}(\mathcal{H})\). By continuity of P and \(\textsf{T}_S(\Delta )\), this identity extends to \(\psi \in \mathcal{D}(\mathcal{H})\) which, in turn, yields \(\textsf{T}_S(\Delta )= P\) since the Hilbert space is complex. In summary, (52) can be rephrased to
that is the wanted \(\sigma \)-additivity property for \(\nu _\phi \). As a consequence of the Carathéodory extension theorem, there is a positive \(\sigma \)-additive measure \(\overline{\nu _\phi }: \mathscr {B}(S) \rightarrow [0,+\infty ]\) which extends \(\nu _\phi \), for every given \(\phi \in L^2(\mathbb {R}^3, d^3k)\). This measure is unique because S is countable union of sets in \(\mathscr {F}(S)\) thus with premeasure \(\nu _\phi \) finite. \(\overline{\nu _\phi }\) is finite by inner continuity: If \(\Delta _n \in \mathscr {F}(S)\) satisfy \(\Delta _n \subset \Delta _{n+1}\) and \(\cup _{n\in \mathbb {N}} \Delta _n = S\), we have
Now we use \(\nu _\phi \) to extend the definition of \(\textsf{T}_S(\Delta )\) to the case of \(\Delta \in \mathscr {B}(S)\) without the constraint \(\Delta \in \mathscr {F}(S)\).
Consider \(\Delta \in \mathscr {B}(S)\) and a sequence \(\Delta _n \in \mathscr {F}(S)\) such that \(\Delta _{n} \subset \Delta _{n+1} \subset \Delta \) and \(\cup _{n\in \mathbb {N}} \Delta _n = \Delta \). For instance, \(\Delta _n = \Delta \cap B_n(0)\), where \(B_n(0)\) is the open ball of radius n centered at the origin of \(\mathbb {R}^3\equiv S\). By construction, using additivity, \(0\le \textsf{T}_S(\Delta _n) \le \textsf{T}_S(\Delta _{n+1})\le I\). Therefore, again for Proposition 3.76 [29], there exists a bounded everywhere defined operator
such that \(0\le \textsf{T}_S(\Delta ) \le I\). With an argument strictly similar to the one used before, this operator satisfies
This identity proves both that \(\textsf{T}_S(\Delta )\) extends the definition for \(\Delta \in \mathscr {F}(S)\) and that \(\textsf{T}_S(\Delta )\) does not depend on the used sequence of sets \(\Delta _n\in \mathscr {F}(S)\) to define it. Now fix \(\Delta \in \mathscr {B}(S)\) with \(\Delta \) unbounded. Taking advantage of a sequence \(\Delta _n:= \Delta \cap B_n(0)\), according to (53) and (51), we can prove that (47) is valid also if \(\Delta \) unbounded for \(\psi \in \mathcal{D}(\mathcal{H})\):
In the last limit, we exploited the monotone convergence theorem (the integrand being positive). Finally, let us consider the case \(\Delta = S\equiv \mathbb {R}^3\). Again, if \(\psi \in \mathcal{D}(\mathcal{H})\)
The last limit, due to the monotone convergence theorem (the integrand being positive) coincides to the integral on the whole S which is \(\langle \psi |\psi \rangle \) according to Lemma 47. Hence, \(\langle \psi |\textsf{T}_S(S)-I)\psi \rangle =0\) for every \(\psi \in \mathcal{D}(\mathcal{H})\). The standard density and continuity argument (in a complex Hilbert space) permits to conclude that \(\textsf{T}_S(S) =I\). This result also proves (b) if \(\textsf{T}_S\) satisfies the other requirements of a POVM. To end the proof, it is sufficient to prove that \(\{\textsf{T}_S(\Delta )\}_{\Delta \in \mathscr {B}(S)}\) is a POVM in all cases. It is equivalent to prove that \(\{\langle \psi |\textsf{T}_S(\Delta )\phi \rangle \}_{\Delta \in \mathscr {B}(S)}\) is a complex measure for every choice of \(\phi ,\psi \in \mathcal{D}(\mathcal{H})\). The only fact to be proved is that  is \(\sigma \)-additive. This fact immediately arise by \(\sigma \)-additivity of the positive Borel measure
is \(\sigma \)-additive. This fact immediately arise by \(\sigma \)-additivity of the positive Borel measure  , by choosing \(\chi = \psi \pm \phi \) and \(\chi = \psi \pm i\phi \) and taking advantage of the polarization identity.
, by choosing \(\chi = \psi \pm \phi \) and \(\chi = \psi \pm i\phi \) and taking advantage of the polarization identity.
The proof of (d) is trivial due to (a), polarization, and an obvious density argument.
The last statement of the thesis immediately arises from Proposition 24. \(\square \)
6 Spacelike Cauchy localization observables out of the stress–energy tensor of massive KG particles
In the final Sect 7 of [30], a second type of spatial localization observable was introduced by generalizing an idea by D. Terno [36] also analyzed in the first part of [30]. These POVMs denoted by \(\textsf{M}^{n'}_{n,t}\) (with \(n, n'\in \textsf{T}_+\)) were constructed on spacelike flat Cauchy surfaces out of the stress energy tensor of the Klein Gordon field.
The goal of the remaining part of this section is to prove that this different notion of POVM can be defined on spacelike Cauchy surfaces of \(\mathbb {M}\), giving rise to a Cauchy localization according to Definition 21. We expect that the construction can be generalized to any static (or stationary) globally hyperbolic spacetime referring to the Hadamard static vacuum, since the theoretical construction does not depend on the use of Fourier transform, at least at heuristic level. This conjecture will be analyzed elsewhere.
6.1 The POVM \(\textsf{M}^n_{\Sigma }\) for massive KG particles
In Sect. 7 of [30], extending a notion introduced by D. Terno [36], a family of POVMs was introduced on all spacelike flat Cauchy surfaces \(\Sigma \) of \(\mathbb {M}\) for a common choice of a reference frame \(n\in \textsf{T}_+\). (If \(n=n_\Sigma \) one obtains the very notion introduced by Terno, studied and made rigorous in the first part of [30] that is a special case of the following discussion. A rigorous proof of CT for that observable appears in [30]).
At the level of 2nd quantization of the massive real Klein–Gordon field, the considered POVM is formally defined as follows on \(\Sigma \in \mathscr {C}^{sf}_\mathbb {M}\) (we readapt the notation to the choices of the present work)
where \(P_1: \mathfrak {F}_+(\mathcal{H}) \rightarrow \mathcal{H}\) is the orthogonal projector onto the one-particle space of the symmetric Fock space \(\mathfrak {F}_+ (H)\) constructed upon the Minkowski vacuum state with the Hilbert space \(\mathcal{H}\) defined as in (22) as the one-particle subspace. \(:\hspace{-3.0pt}\hat{T}_{\mu \nu }\hspace{-3.0pt}:\hspace{-3.0pt}(x)\) is the normally ordered stress energy tensor operator. \(H_n\) is the Hamiltonian operator of the quantum field in the reference frame \(n\in \textsf{T}_+\). \(\Sigma \) is a flat spacelike Cauchy surface orthogonal with constant normal unit vector \(n_\Sigma \in \textsf{T}_+\).
The overall idea at the basis of [36] and [30] is that a physical procedure to detect a particle in a region of a flat Cauchy surface may exploit the energy of the particle. However, we have many ways to synchronize a net of detectors and, as discussed in [30]: \(\langle \psi |\textsf{M}^n_{\Sigma }(\Delta )\psi \rangle \) accounts for the probability to find a particle of state \(\psi \) in \(\Delta \subset \Sigma \) using a net of detectors which are (a) at rest in n but (b) synchronized on \(\Sigma \). This possibility naturally arises from the observation [30] that
for every choice of \(n,n_\Sigma \in \textsf{T}_+\) and \(\Delta \in \mathscr {L}(\Sigma )\), even if positivity fails when removing the one-particle space projectors \(P_1\).
Remark 50
A similar local positivity property does not hold when dealing with massive Dirac particles, even if \(n=n_\Sigma \) [37]: A localization POVM cannot be constructed for this type of fermions in terms of energy on a given rest space of a Minkowski reference frame according to the approach of [30, 36]. The natural physical object, useful to this goal, is instead the fermionic current operator \(:\hspace{-3.0pt}\hat{J}^\mu \hspace{-3.0pt}: \hspace{-3.0pt}(x)\) [8]. \(\blacksquare \)
The rigorous definition of the normalized POVM \(\textsf{M}^n_{\Sigma }\) in \(\mathcal{H}\) corresponding to the formal object (54) was given in Thm 37 of [30] in terms of a kinematic deformation of the PVM \(\textsf{Q}_\Sigma (\Delta )\) of the Newton–Wigner position operator [30] (see (57)) on the spacelike flat Cauchy surface \(\Sigma \):
Above \(\Delta \in \mathscr {L}(\Sigma )\), \(H_r:= -P \cdot r\) (for \(r\in \textsf{T}_+\)) is the Hamiltonian in the Minkowski reference frame r.
The various everywhere-defined bounded composite operators \(H_n/H_{n_\Sigma }\), \(P_{\nu }/H_{n_\Sigma }\), etc., are defined in terms of the joint spectral measure of the four momentum operator \(P^\mu \) and standard spectral calculus. The components \(P^\mu \) are referred to a Minkowski chart adapted to n.
6.2 Properties of \(\textsf{M}_\Sigma ^n\) for spacelike flat Cauchy surfaces \(\Sigma \): covariance, causality, no strict localizability, Newton–Wigner, Heisenberg inequality
Though it is clear from (56) that \(\textsf{M}^n_{\Sigma }(\Delta )\in \mathfrak {B}(\mathcal{H})\) and that \(\textsf{M}^n_{\Sigma }(\Sigma )=I\) (notice that \( \textsf{Q}_{n_\Sigma }(\Sigma )=I\) and \(P_\mu P^\mu + m^2I=0\)), it is not evident that \(\textsf{M}^n_{\Sigma }(\Delta )\ge 0\), nor the connection between (56) and (54) seems straightforward. We spend this section about these issues because the discussion will turn out useful when we shall generalize \(\textsf{M}^n_\Sigma \) to generally curved spacelike Cauchy surfaces S.
From Eq. (17) in [30], we know that, if \(\Sigma \in \mathscr {C}^{sf}_\mathbb {M}\),
We adopted the notation
(\(E_r(p)\) is nothing but the component \(p^0\) of \(p\in \textsf{V}\) in any Minkowski chart adapted to r.) At this juncture, it is not difficult to see from (56) that, if \(\psi \in \mathcal{D}(\mathcal{H})\) or more generally \(\psi \in \mathcal{S}(\mathcal{H}) (\supset \mathcal{D}(\mathcal{H}))\) as used in [30], then
Conversely, since \(\mathcal{D}(\mathcal{H})\) and \(\mathcal{S}(H)\) are dense in \(\mathcal{H}\) and \(\textsf{M}^n_{\Sigma }(\Delta ) \in \mathfrak {B}(\mathcal{H})\), identity (59) completely determines \(\textsf{M}^n_{\Sigma }(\Delta )\) by polarization, density, and continuity.
First of all, we prove that (59) can be written into an equivalent form already used in [30], which eventually leads to both the requested positivity condition and the relation with (54).
Lemma 51
If \(\psi \in \mathcal{S}(\mathcal{H})\), the right-hand side of (59) can be equivalently written with the first two integrals interchanged:
Proof
See Appendix 1. \(\square \)
To go no, if \(\psi \in \mathcal{D}(\mathcal{H})\) (or more generally, \(\psi \in \mathcal{S}(\mathcal{H})\)) and \(n\in \textsf{T}_+\), we define the solution of the Klein–Gordon equation
\(\Phi ^\psi _n=\Phi ^\psi _n(x)\) is smooth on \(\mathbb {M}\) and bounded with all of its derivatives. More strongly \(\Phi _n^\psi \in \mathscr {S}(\Sigma )\) for every flat \(\Sigma \in \mathscr {C}^{sf}_\mathbb {M}\), where \(\mathscr {S}(\Sigma )\) is the usual Schwartz space on \(\mathbb {R}^3\equiv \Sigma \) referring to any Minkowski chart adapted to \(n_\Sigma \). We stress that (61) is not the standard covariant Klein–Gordon wavefunction \(\varphi _\psi \) (26) associated to a state \(\psi \in \mathcal{H}\), since the integrand above includes a further ”anomalous” factor \(E_p^{-1/2}(p)\). This latter can be traced back to the factors \(H_n^{1/2}\) in (55).
Definition 52
If \(\psi \in \mathcal{D}(\mathcal{H})\) and \(n\in \textsf{T}_+\), the n-normalized stress energy operator is, in components of a Minkowski chart,
and the associated current
\(\blacksquare \)
Lemma 53
With the said definitions, for \(\psi \in \mathcal{D}(\mathcal{H})\) and \(n\in \textsf{T}_+\),
-
(a)
\(J^{\psi }_{n}\) is smooth, belongs to \(\mathscr {S}(\Sigma )\) for every \(\Sigma \in \mathscr {C}^{sf}_\mathbb {M}\), and is bounded;
-
(b)
\(J^{\psi }_{n}\) is conserved;
-
(c)
\(J^{\psi }_{n}(x)\) is either zero or causal and past-directed if \(x\in \mathbb {M}\), so that
$$\begin{aligned} J_n^{\psi }(x) \cdot r \ge 0 \quad \forall x\in \mathbb {M}\;, \forall r \in \textsf{T}_+. \end{aligned}$$(64)
Proof
(a) is a trivial consequence of the definition. (b) Follows from the Klein Gordon equation which is satisfied by \(\Phi ^\psi _n\). (c) was established in Proposition 30 [30].\(\square \)
We are prompt to prove that \(\textsf{M}^n_{\Sigma }\) is a normalized POVM when \(\Sigma \) is a spacelike flat Cauchy surface. In particular \(\textsf{M}^n_\Sigma (\Delta )\ge 0\).
Theorem 54
If \(\Sigma \subset \mathbb {M}\) is a spacelike flat Cauchy surface, the family of operators (56), when \(\Delta \in \mathscr {L}(\Sigma )\), defines a normalized \(\mathcal{H}\)-POVM. Furthermore, if \(\psi \in \mathcal{D}(\mathcal{H})\) (or more generally \(\psi \in \mathcal{S}(\mathcal{H})\)),
Proof
First of all \(\langle \psi |\textsf{M}^n_{\Sigma }(\Delta )\psi \rangle \ge 0\) if \(\psi \in \mathcal{S}(\mathcal{H})\). Indeed, from Lemma 51 and expanding (62) as prescribed in (61), we find
on account of (64) and where the integral is finite because \(J_n^{\psi } \in \mathscr {S}(\Sigma )\). (The found identity also establishes (65).) As a consequence \(\textsf{M}^n_{\Sigma }(\Delta ) \ge 0\) because, as already observed, \(\langle \psi |\textsf{M}^n_{\Sigma }(\Delta )\psi \rangle \) is the limit of analogous matrix elements with \(\psi \in \mathcal{D}(\mathcal{H})\) or \(\mathcal{S}(\mathcal{H})\). Normalization of the POVM has been already discussed beforehand, and (56) itself implies weak \(\sigma \)-additivity from the analogous property of \(\textsf{Q}_\Sigma \). \(\square \)
Regarding the connection between (56) and (54), from \(E_p^{-1/2}(p)\) in (61) and the expression (62) of the stress energy tensor, it is not difficult to see that (65) is nothing but the matrix element of (54) with respect a one-particle state \(\psi \in \mathcal{H}\).
Referring to the spatial localization observable \(\{\textsf{M}^n_\Sigma \}_{n\in \textsf{T}_+, \Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\), the \(\mathscr {P}_+\)-covariance relations analogous to (44) are valid (Thm 37 in [30])
The validity of these relations is actually required in the spirit of the very definition of relativistic spatial localization observable assumed in [30] (Definition 18 therein). And, in fact, \(\{\textsf{M}^n_\Sigma \}_{n\in \textsf{T}_+, \Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) satisfies that definition in a broader sense, due to the presence of the further specificationFootnote 19\(n\in \textsf{T}_+\).
Let us pass to discuss causality properties.
Theorem 55
([30]) For a given choice of \(n\in \textsf{T}_+\), the spatial localization observable \(\{\textsf{M}^{n}_{\Sigma }\}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) satisfies the CC in Definition 2.
Proof
Theorem 39 [30].\(\square \)
Corollary 56
If \(\psi \in \mathcal{H}\), the localization probability associated to the spatial localization observable \(\{\textsf{M}^{n}_{\Sigma }\}_{\Sigma \in \mathscr {C}^{sf}_\mathbb {M}}\) cannot be zero outside a bounded set in \(\Sigma \).
Proof
If states producing localized probability distributions as above exist CT would fail as a consequence of Hegerfeldt’s theorem on relativistic time evolution (Theorem 4) and thus also CC would be false. (See [30] for a discussion on this point.) \(\square \)
Remark 57
In spite of this obstruction, it is possible to show [30] that probability distributions localized in bounded sets can be arbitrarily well approximated by probability distributions arising by suitable sequences of state \(\psi _k\) when \(n=n_\Sigma \). However it is not difficult to generalize this result to \(n\ne n_\Sigma \). \(\blacksquare \)
As already observed for the POVMs \(\textsf{T}^g_\Sigma \), there is again the interesting relation between the first moment of the POVM \(\textsf{M}^n_\Sigma \) on a spacelike flat Cauchy surface \(\Sigma \) and the Newton–Wigner selfadjoint operators \(N_\Sigma ^1,N_\Sigma ^2,N_\Sigma ^3\) [30] associated to a Minkowski chart \(x^0,x^1,x^2,x^3\) such that the slice \(x^0=0\) coincides with \(\Sigma \). Generalizing Thm 26 in [30], one sees that the following theorem is true. Below, \(\Delta _\psi x^a_{\textsf{M}^n_\Sigma }\) denotes the standard deviation for the coordinate \(x^a\) referred to the probability distribution \(\langle \psi | \textsf{M}^n_\Sigma (\cdot ) \psi \rangle \) constructed out of the POVM \(\textsf{M}^n_\Sigma \) in the state defined by the unit vector \(\psi \).
Theorem 58
Referring to the POVM \(\textsf{M}^n_\Sigma \) for \(\Sigma \in \mathscr {C}^{sf}_\mathbb {M}\), the following facts are true.
-
(a)
The a-first moment of \(\textsf{M}^n_\Sigma \) is defined for every \(\psi \in \mathcal{S}(\mathcal{H})\) with \(||\psi ||=1\) and
$$\begin{aligned} \int _{\Sigma } x^a \langle \psi | \textsf{M}^n_\Sigma (d^3x) \psi \rangle = \langle \psi | N_\Sigma ^a \psi \rangle \quad \text{ for } a=1,2,3. \end{aligned}$$(67)In particular, \(N^a_\Sigma \) is the unique selfadjoint operator in \(\mathcal{H}\) which satisfies the identity above.
-
(b)
The Heisenberg inequality turns out to be corrected as, for \(\psi \in \mathcal{S}(\mathcal{H})\),
$$\begin{aligned}\Delta _\psi x_{\textsf{M}^n_\Sigma }^a \Delta _\psi P_a \ge \frac{\hbar }{2} \sqrt{1+4 (\Delta _\psi P_a)^2 \langle \psi |\textsf{K}^{\textsf{M}^n_{\Sigma }}_{a} \psi \rangle }, \quad a=1,2,3 \end{aligned}$$where \(\textsf{K}^{\textsf{M}^n_{\Sigma }}_{a}\in \mathfrak {B}(\mathcal{H})\) is a selfadjoint operator which is a (spectral) function of the four momentum observable P with the form (79) and \(\textsf{K}^{\textsf{M}^n_{\Sigma }}_{a}\ge 0\).
Proof
See Appendix 1. \(\square \)
Observe that the result in (67) does not depend on n.
Remark 59
-
(1)
If also the identity
$$\begin{aligned} \int _{\Sigma } (x^a)^2 \langle \psi | \textsf{M}^n_{\Sigma }(d^3x) \psi \rangle = \langle \psi | (N^a_\Sigma )^2\psi \rangle \quad \text{(false!) },\end{aligned}$$were valid one could apply a known theorem by Naimark about the decomposition of maximally symmetric operators (here \(N^a_\Sigma \)) in terms of POVMs (see Theorem 23 in [13] and the discussion about it) obtaining \(\textsf{M}^n_\Sigma = \textsf{Q}_{\Sigma }\). This is obviously false and it is also reflected by the presence of the term \( \langle \psi |\textsf{K}^{\textsf{M}^n_\Sigma }_{a} \psi \rangle \) in the modified Heisenberg inequality.
-
(2)
If \(U^{(n)}_t\) is the unitary time evolutor corresponding to the time evolution along n in the spacetime \(\mathbb {M}\), it is easy to see that the Heisenberg evolution \(U^{(n)}_t N_\Sigma ^a U^{(n)\dagger }_t\) of \(N_\Sigma ^a\) on the right-hand side of (67) equals the integral on the left-hand side over the correspondingly temporally translated time slice \(\Sigma _t\). As already observed in [30], this fact implies that the worldline
 is timelike (Corollary 14 in [30]) as expected by massive particles. \(\blacksquare \)
is timelike (Corollary 14 in [30]) as expected by massive particles. \(\blacksquare \)
6.3 A spacelike Cauchy localization observable \(\textsf{M}^n= \{\textsf{M}^n_S\}_{S\in \mathscr {C}_\mathbb {M}^s}\) for massive KG particles
We are in a position to prove that a normalized POVM \(\textsf{M}^n_S\) exists on every spacelike Cauchy surface S of \(\mathbb {M}\). We shall also obtain that the elements of the POVMs do not depend on the Cauchy surface they belong to. In other words, we have a spacelike Cauchy localization \(\textsf{M}^n\).
Theorem 60
Consider \(S\in \mathscr {C}^s_\mathbb {M}\) and \(n\in \textsf{T}_+\). Then,
-
(a)
there is a unique \(\mathcal{H}\)-POVM, still indicated by \(\{\textsf{M}^g_S(\Delta )\}_{\Delta \in \mathscr {B}(S)}\), which satisfies (65) also for generic spacelike Cauchy’s surface S when \(\psi \in \mathcal{D}(\mathcal{H})\):
$$\begin{aligned} \langle \psi |\textsf{M}^n_{S}(\Delta )\psi \rangle = \int _\Delta T^{\psi }_{\mu \nu }(x)_n n^\mu n^\nu _S d\nu _S(x),\quad \Delta \in \mathscr {B}(S), \end{aligned}$$(68)so that, \(\textsf{M}^n_S< \hspace{-5.0pt}< \nu _S\).
-
(b)
\(\textsf{M}^n_S\) is normalized: \(\textsf{M}^n_S(S)=I\);
-
(c)
\(\textsf{M}^n_\Sigma \) satisfies (56) when \(\Sigma \in \mathscr {C}_\mathbb {M}^{sf}\);
-
(d)
if \(\Delta \in S\cap S'\) is a Borel set, where \(S\in \mathscr {C}^s_\mathbb {M}\), then
$$\begin{aligned}\textsf{M}^n_S(\Delta ) =\textsf{M}^n_{S'}(\Delta ).\end{aligned}$$
The family \(\textsf{M}^n:= \{\textsf{M}^n_S\}_{S\in \mathscr {C}^s_\mathbb {M}}\), where we extend each POVMs to \(\mathscr {M}(S)\) according to Proposition 23, is a spacelike Cauchy localization observable according to Definition 21.
Proof
Item (c) is a trivial consequence of (a) and (b), so we prove (a), (b), and (d).
Let \(x^0=t_S(\vec {x})\) be the map which defines S by identifying it with the spatial \(\mathbb {R}^3\) in a given Minkowski system of coordinates \(x^0, \vec {x}\) according to Proposition 20. If \(\Delta \in \mathscr {B}(\mathbb {R}^3)\) is bounded consider the Hermitian form
where, taking (61) into account,
and
As \(\Delta \) is bounded, the integral is well defined. Since (use (31)) we conclude that
The former inequality arises from the last identity in (31) when observing that (see (63)) \(J^{\psi \psi }_n= J^{\psi }_n\) is zero or causal and future directed as established in Lemma 53. The latter inequality in (71) is consequence of the positivity of the integrand \( \omega ^{J^{\psi }_n}\) in coordinates (again for (31)) and (64) which first of all imply (we write \(J^{\psi }_n= J^{\psi \psi }_n\))
On the other hand
because we can apply Proposition 36 (since \(J^{\psi }_n\) is also smooth, bounded, and conserved according to Lemma 53) choosing a spacelike flat surface \(S'\), obtaining
The last identity is due to the fact that the last integral is nothing but \(\langle \psi |\textsf{M}^n_{S'}(S')\psi \rangle = \langle \psi | \psi \rangle \) due to Theorem 54.
We can finally apply Lemma 48 proving that there exists \(\textsf{M}^n_S(\Delta ) \in \mathfrak {B}(\mathcal{H})\) such that \(0\le M^n_S(\Delta )\le I\) and
so that (68) is satisfied for \(\Delta \) bounded. From this point on, the proof is identical to the one of Theorem 49. In particular, the normalization condition (b) follows now from (72). The last statement of the thesis immediately arises from Proposition 24. \(\square \)
7 Moments of \(\textsf{T}^g_\Sigma \) and \(\textsf{M}^n_\Sigma \), Newton–Wigner operator, and Heisenberg inequality
We address the reader to the discussion and references in [30] about the Newton–Wigner observables for a massive spinless particle.
Referring to the representation \(L^2(\mathbb {R}^3, d^3p)\) (see Sect. 4.1) of the one-particle space \(\mathcal{H}\) through the Hilbert space isomorphism (21) \(F:\mathcal{H}\rightarrow L^2(\mathbb {R}^3, d^3p)\), the joint PVM of the selfadjoint Newton Wigner operators \(N^1,N^2,N^3\) for a massive spinless particle, associated to the coordinates \(\vec {x}=(x^1,x^2,x^3)\) on \(\mathbb {R}^3\) in a Minkowski frame \(x^0,x^1,x^2,x^3\) at time \(x^0=0\), is given by
It extends by continuity to the whole Hilbert space. Notice that \(\mathcal{S}(\mathcal{H}) = F(\mathscr {S}(\mathbb {R}^3))\) and \(\mathcal{D}(\mathcal{H}) = F(C_c^\infty (\mathbb {R}^3))\) are invariant spaces and cores for each \(N^a\) and thereon they are unitarily equivalent to the respective differential operator \(FN^a|_{\mathscr {S}(\mathbb {R}^3)}F^{-1} = i \frac{\partial }{\partial p_a}\).
Theorems 44 and 58 are subcases of the following result.
Proposition 61
Consider a normalized POVM on \(\mathbb {R}^3\) satisfying (with \(\phi _\psi := F\psi \))
where \(K_\textsf{A}\) is a positive definite kernel which satisfies \(K_\textsf{A}(\vec {p}, \vec {p})=1\) for every \(\vec {p} \in \mathbb {R}^3\).
-
(a)
If \(K_\textsf{A}\) is real and smooth, then
$$\begin{aligned} \int _{\mathbb {R}^3} x^a \langle \psi | \textsf{A}(d^3x)\psi \rangle = \langle \psi |N^a \psi \rangle \quad \text{ for } a=1,2,3 \text{ and } \psi \in \mathcal{D}(\mathcal{H}), \text{ with } ||\psi ||=1,\end{aligned}$$(76)where \(N^a\) is the unique selfadjoint operator in \(\mathcal{H}\) which satisfies the identity above. More generally, if \(\alpha := (\alpha _1,\alpha _2,\alpha _3)\) is a multi-index, so that \(x^\alpha := (x^1)^{\alpha _1} (x^2)^{\alpha _2} (x^3)^{\alpha _3}\),
$$\begin{aligned}{} & {} \int _{\mathbb {R}^3}(x^1)^{\alpha _1}(x^2)^{\alpha _2} (x^3)^{\alpha _3} \langle \psi |A(d^3x)\psi \rangle =\langle \psi |(N^1)^{\alpha _1}(N^2)^{\alpha _2}(N^3)^{\alpha _3}\psi \rangle \nonumber \\{} & {} \quad +\sum _{1<|\beta |, \beta \le \alpha }\left( {\begin{array}{c}\alpha \\ \beta \end{array}}\right) \int _{\mathbb {R}^3}\left( i^{|\alpha |-|\beta |}\frac{\partial ^{|\alpha |-|\beta |}\overline{\phi _\psi (\vec {p})}}{\partial p^{\alpha -\beta }}\right) \left. \left( i^{|\beta |}\frac{\partial ^{|\beta |}K_\textsf{A}(\vec {p},\vec {q})}{\partial p^\beta }\right) \right| _{\vec {q}=\vec {p}}\phi _\psi (\vec {p})d^3p.\nonumber \\ \end{aligned}$$(77) -
(b)
If \(K_\textsf{A}\) is real, smooth, and has polynomial growth with all of its derivatives of any order, then (75), (76), (77) are also valid for \(\psi \in \mathcal{S}(\mathcal{H})\).
-
(c)
If \(K_\textsf{A}\) is as in (b), a formula for the second moment holds for \(\psi \in \mathcal{S}(\mathcal{H})\) with \(||\psi ||=1\)
$$\begin{aligned} \int _{\mathbb {R}^3} (x^a)^2 \langle \psi | \textsf{A}(d^3x)\psi \rangle = \langle \psi |(N^a)^2 \psi \rangle + \langle \psi |\textsf{K}^{\textsf{A}}_{a} \psi \rangle \quad \text{ for } a=1,2,3. \end{aligned}$$(78)\(\textsf{K}^{\textsf{A}}_{a} \ge 0\) is the (generally unbounded) multiplicative selfadjoint operator
$$\begin{aligned} \left( \textsf{K}^{\textsf{A}}_{a} \psi \right) (p):= \sqrt{p^0} \left( \left. \frac{\partial }{\partial q_a}\frac{\partial }{\partial p_a}K_\textsf{A}(\vec {q}, \vec {p})\right| _{\vec {p}=\vec {q}} \right) \frac{\psi (p)}{\sqrt{p^0}}, \quad \psi \in D(\textsf{K}^{\textsf{A}}_{a}) ,\end{aligned}$$(79)with \(\textsf{K}^{\textsf{A}}_{a}\in \mathfrak {B}(\mathcal{H})\) if
 is bounded.
is bounded. -
(d)
If \(K_\textsf{A}\) is as in (b), a modified Heisenberg inequality holds for \(\psi \in \mathcal{S}(\mathcal{H})\) with \(||\psi ||=1\) (restoring Plank’s constant),
$$\begin{aligned} \Delta _\psi x_\textsf{A}^a \Delta _\psi P_a \ge \frac{\hbar }{2} \sqrt{1+4 (\Delta _\psi P_a)^2 \langle \psi |\textsf{K}^{\textsf{A}}_{a} \psi \rangle }, \quad a=1,2,3. \end{aligned}$$(80)Above, \(\Delta _\psi x_\textsf{A}^a\) is the standard deviation of the probability distribution \(\langle \psi |\textsf{A}(\cdot )\psi \rangle \), \(\Delta _\psi P_a\) is the standard deviation of the probability distribution of the a-component of the momentum observable in the state \(\psi \).
-
(e)
Suppose that \(K_\textsf{A}\) is not necessarily real but is finite according to [9]. In other words, it has the form, for \(N< +\infty \) suitable measurable functions \(u_j\)
$$\begin{aligned}K_\textsf{A}(\vec {p}, \vec {q}) = \sum _{j=1}^N \overline{u_j(\vec {p})} u_j(\vec {q}).\end{aligned}$$In addition, assume that the N functions \(u_j: \mathbb {R}^3 \rightarrow \mathbb {C}\) are smooth with polynomial growth with all of their derivatives of any order. Then, the standard Heisenberg inequality holds in any cases for \(\psi \in \mathcal{S}(\mathcal{H})\) with \(||\psi ||=1\)
$$\begin{aligned}\Delta _\psi x_\textsf{A}^a \Delta _\psi P_a \ge \frac{\hbar }{2}.\end{aligned}$$
Proof
See Appendix 1. \(\square \)
8 Discussion
The major achievement of this work (Theorem 32) is the result that, if we use POVMs to describe the probability of spatial localization of quantum systems in a sufficiently general way, then spatial localization, in the sense of a spacelike Cauchy localization observable Definition 21, implies causality, in the terms of our general causal condition GCC in Definition 26. The physical postulates at the ground of this implication, encapsulated in the notion of spacelike Cauchy localization observable, are the following ones.
-
(1)
It is supposed that every spacelike Cauchy surface can be used to localize the system. In other words, if we fill a spacelike Cauchy surface with a net of detectors, we must find somewhere the quantum system on that 3-space.
-
(2)
If, for a given spacelike Cauchy localization observable, i.e., for a specific type of detectors, a pair of Cauchy surface coincide in a region, then they share the same detectors therein.
-
(3)
There is no chance to detect the quantum system in a spatial region with zero measure on a spacelike Cauchy surface.
An observation about the need for condition (2), we named coherence condition, is important. As we have seen in Remark (34), condition (2) can be removed from the definition of spacelike Cauchy localization observable and inserted as a further hypothesis of Theorem 32. Within this scheme, the coherence condition would be recovered as a corollary of Theorem 32. In other words, if (1) and (3) are valid for a family of POVMs, then the coherence condition is equivalent to GCC.
We also proved, as a second achievement in double form (Theorems 49 and 60): The above general notions of localization exist at theoretical level. In fact, we presented two of them for massive Klein–Gordon particles. In the second case the localization observable was constructed in terms of physical quantities of the system (its energy). There is no evident obstruction to construct similar spacelike Cauchy localization observables for other types of particles like fermions considered in [8]. The basic ingredient to construct these observables is a conserved causal current constructed out of the state of the system. It seems plausible that spacelike Cauchy localization observables can be built up also in a more general spacetime (referring to the one-particle structure of quantum field Gaussian states) provided the spacetime is globally hyperbolic. This is because the central technology to produce the former achievement, some technical results about Cauchy surfaces [3, 4] are at disposal in generic globally hyperbolic spacetimes. On the other hand the explicit structure of spacelike Cauchy localization observable relies upon notions, like conserved currents, which can be generalized to every globally hyperbolic spacetime. The only mathematically delicate issue which deserves attention is the fact that the region of influence \(\Delta '\) of a Borel set \(\Delta \) is again Borel or in a natural completion of that \(\sigma \)-algebra.
When coming back to flat Cauchy surfaces, i.e., rest frames of inertial observers, the resulting spatial localization observables show interesting features. Since causality is not violated by the distribution of probability of a Klein–Gordon massive particle, the no-go Hegerfeldt theorem is made harmless. There is a price to pay however: no strictly localized (in bounded spatial sets) probability distributions are permitted. Another interesting fact, already evident in [30], is that the Newton–Wigner operators insist to play some role in this much less naive picture, in spite of the fact that the Hegerfeldt no go results seemed to have ruled out them long time ago. Even if they no longer represent observables, they account for the timelike spacetime evolution of the first moment of a massive particle.
A widely open issue is the relation between the constructed POVMs and their decompositions in terms of Kraus operators or quantum instruments. Related to this issue is the fact that the effects of the presented POVMs do not commute even when are localized in causally separated sets. This is an urgent problem when analyzing all the construction from the perspective of the local operator algebras theory. These outstanding problems will be investigated elsewhere.
Data availability
All data generated or analyzed during this study are contained in this document.
Notes
As already found in [30], in the new picture arising from modern achievements as the present work, the Newton–Wigner observable is, however, recovered in terms of the first moments of permitted localization observables which are described in terms of POVMs.
See Lemma 4 on p.13 of [11] and its proof in particular.
The use of the Lebesgue \(\sigma \)-algebra \(\mathscr {L}(\Sigma )\) in place of the Borel one \(\mathscr {B}(\Sigma )\) is compulsory here. In fact, as discussed in [8], if defining the relevant POVMs on \(\mathscr {B}(\Sigma )\) rather than on \(\mathscr {L}(\Sigma )\) it is not guaranteed that \(\Delta ' \in \mathscr {B}(\Sigma ')\) when \(\Delta \in \mathscr {B}(\Sigma )\), making meaningless (3). It is, however, true that \(\Delta ' \in \mathscr {L}(\Sigma ')\) for every \(\Delta \subset \Sigma \) (even if \(\Delta \not \in B(\Sigma )!\)) as established in [8]. The use of \(\mathscr {L}(\Sigma )\) is not a serious issue, even if initially dealing with POVMs defined on the Borel sets, since the standard completion procedure uniquely extends them to POVMs on \(\mathscr {L}(\Sigma )\).
D. Castrigiano communicated to V.M. that R.F. Werner independently had a similar idea to prove CC.
However, see [33] and below in the text for a different viewpoint on this issue.
We shall not consider immersed submanifolds in this work.
We refer to [24] for the notion and the use of manifold with boundary.
We take advantage of \(\text{ det }(I + cd^t) = 1+ d^tc\) for \(c,d \in \mathbb {R}^n\) and I the identity of \(M(n,\mathbb {R})\).
This is generally false in other spacetimes!
We are grateful to D.P.L. Castrigiano for this observation.
\(\omega ^J\) can equivalently be written as the interior product of J and the volume 4-form of \((\mathbb {M}, \textbf{g})\).
According to [9].
Changes of the origin \(o\in \mathbb {M}\) can be re-absorbed in the definition of wavefunctions through an obvious unitary transformation.
Actually continuity of g already follows from measurability of g, see [9] (55) Corollary.
If \(n=n_\Sigma \), giving rise to the Terno spatial localization observable studied in first part of [30], it fully satisfies that definition.
Indeed, \(\phi ^Y_s: \mathbb {M}\rightarrow \mathbb {M}\) is a diffeomorphism and thus it transforms the embedded submanifold \(S'\equiv \mathbb {R}^3\) transverse to \(Y|_{S'}\) into the embedded submanifold \(\phi ^Y_s(S')\) transverse to \(d\phi ^Y|_{S'} Y= Y|_{\phi _s^Y(S')}\), in particular, \(d\phi ^Y_s\) bijectively transforms the tangent spaces of these manifolds accordingly.
References
Bär, C., Ginoux, N., Pfäffle, F.: Wave Equations on Lorentzian Manifolds and Quantization, ESI Lectures in Mathematics and Physics. EMS Publishing House (2007)
Beck, C.: Localization Local Quantum Measurement and Relativity, Dissertation an der Fakultät für Mathematik, Informatik und Statistik der Ludwig-Maximilian-Universität München (2020)
Bernal, A.N., Sánchez, M.: On smooth Cauchy hypersurfaces and Geroch’s splitting theorem. Commun. Math. Phys. 243, 461–470 (2003)
Bernal, A.N., Sánchez, M.: Further results on the smoothability of Cauchy hypersurfaces and Cauchy time functions. Lett. Math. Phys. 77, 183–197 (2006)
Brezis, H.: Functional Analysis. Sobolev Spaces and Partial Differential Equations. Springer, Berlin (2010)
Busch, P.: Unsharp localization and causality in relativistic quantum theory. J. Phys. A Math. Gen. 32(37), 6535 (1999)
Busch, P., Lahti, P., Pellonpää, J.-P., Ylinen, K.: Quantum Measurement. Springer, Berlin (2016)
Castrigiano, D.P.L.: Dirac and Weyl Fermions—The Only Causal Systems (2017). arXiv:1711.06556
Castrigiano, D.P.L.: Causal localizations of the massive scalar Boson. Lett. Math. Phys. 114, 2 (2024)
Castrigiano, D.P.L.: Private communication (2024)
Castrigiano, D.P.L., Leiseifer, A.D.: Causal localizations in relativistic quantum mechanics. J. Math. Phys. 56, 072301 (2015)
Cohn, D.: Measure Theory. Birkhäuser, Boston (1980)
Drago, N., Moretti, V.: The notion of observable and the moment problem for \(*\)-algebras and their GNS representations. Lett. Math. Phys. 110(7), 1711–1758 (2020)
Evans, L.C., Gariepy, R.F.: Measure Theory and Fine Properties of Functions, Revised CRC Press Taylor & Francis Group, Boca Raton (2015)
Fewster, C.J., Verch, R.: Quantum fields and local measurements. Commun. Math. Phys. 378, 851–889 (2020)
Fewster, C.L., Jubb, I., Ruep, M.H.: Asymptotic measurement schemes for every observable of a quantum field theory. Ann. Henri Poincaré 6, 66 (2022)
Finster, F., Paganini, C.F.: Incompatibility of frequency splitting and spatial localization: a quantitative analysis of Hegerfeldt’s theorem. Ann. Henri Poincaré 24, 413–467 (2023)
Gerlach, B., Gromes, D., Petzold, J.: Konstruktion definiter Ausdrücke für die Teilchendichte des Klein–Gordon–Feldes. Z. Phys. 204, 1–11 (1967)
Halvorson, H., Clifton, R.: No place for particles in relativistic quantum theories? In: Kuhlmann, M., Lyre, H., Wayne, A. (Eds.) Ontological Aspects of Quantum Field Theory. World Scientific (2002)
Henning, J.J., Wolf, W.: Positive definite particle densities for the positive frequency solutions of the Klein Gordon equation with arbitrary mass. Z. Phys. 242, 12–20 (1971)
Hegerfeldt, G.C.: Remark on causality and particle localization. Phys. Rev. D 10, 3320 (1974)
Hegerfeldt, G.C.: Violation of causality in relativistic quantum theory? Phys. Rev. Lett. 54, 2395 (1985)
Jancewicz, B.: Operator density current and relativistic localization problem. J. Math. Phys. 18, 2487 (1977)
Lee, J.M.: Introduction to Smooth Manifolds, 2nd edn. Springer, Berlin (2013)
Lienert, M., Tumulka, R.: Born’s rule for arbitrary Cauchy surfaces. Lett. Math. Phys. 110, 753–804 (2020)
Lill, S., Tumulka, R.: Another proof of Born’s rule on arbitrary Cauchy surfaces. Ann. Henri Poincaré 23, 1489–1524 (2022)
Malament. D.: In defense of dogma: Why there cannot be a relativistic quantum mechanics of (localizable) particles. In: Clifton, R. (Ed.) Perspectives on Quantum Reality, pp. 1–11. Kluwer, Dordrecht (1996)
Miller, T., Eckstein, M., Horodecki, P., Horodecki, R.: Generally covariant N-particle dynamics. J. Geom. Phys. 160, 103990 (2021)
Moretti, V.: Spectral Theory and Quantum Mechanics, 2nd edn. Springer, Berlin (2017)
Moretti, V.: On the relativistic spatial localization for massive real scalar Klein–Gordon quantum particles. Lett. Math. Phys. 113, 66 (2023)
Newton, T.D., Wigner, E.P.: Localized states for elementary systems. Rev. Mod. Phys. 21, 400–406 (1949)
O’Neill, B.: Semi Riemannian Geometry With Applications to Relativity, 1st edn. Academic Press, London (1983)
Reddiger, M., Poirier, B.: Towards a Probabilistic Foundation of Relativistic Quantum Theory: The One-Body Born Rule in Curved Spacetime. arXiv:2012.05212
Reed, M., Simon, B.: Functional Analysis I, Revised and Enlarged Edition, enlarged Academic Press, London (1980)
Rudin, W.: Real and Complex Analysis, 3d edn. McGraw-Hill, New York (1986)
Terno, D.R.: Localization of relativistic particles and uncertainty relations. Phys. Rev. A 89, 042111 (2014)
Vollick, D.N.: Negative energy density states for the Dirac field in flat spacetime. Phys. Rev. D 57, 3484 (1998)
Wightman, A.S.: On the localizability of quantum mechanical systems. Rev. Mod. Phys. 34, 845–872 (1962)
Acknowledgements
V.M. is very grateful to D.P.L.Castrigiano for various remarks, suggestions, and discussions about several issues appearing in this paper. We are grateful to an anonymous referee for useful remarks and comments. We thank N.Pinamonti and M.Sánchez for helpful discussions on some technical problems, and S. Lill and M. Reddiger for pointing out some relevant literature. This work has been written within the activities of INdAM-GNFM.
Funding
Open access funding provided by Università degli Studi di Trento within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Proof of some propositions
Proof of Proposition 20
Every coordinate curve  is smooth timelike, and thus, it intersects S exactly once for a corresponding value \(x^0= t_S(\vec {x})\); therefore, it defines a map
is smooth timelike, and thus, it intersects S exactly once for a corresponding value \(x^0= t_S(\vec {x})\); therefore, it defines a map  . In the rest of the proof write t in place of \(t_S\) for shortness. By definition \(S \equiv \{(t(\vec {x}), \vec {x})| \vec {x} \in \mathbb {R}^3 \}\). Since S is an embedded co-dimension 1 submanifold, it must be locally described as the locus \(f(x^0,x^1,x^2,x^3)=0\) of a smooth map with \(\textbf{g}(df, df) \le 0\) because the g-normal vectors to df are spacelike or lightlike and thus df is timelike or lightlike. It must be in particular \(\partial _{x^0}f \ne 0\). As a consequence of the implicit function theorem, in a neighborhood of every \(p\in S\), we can represent S as a smooth map \(x^0=t'(\vec {x})\). Therefore \(t(\vec {x}) = t'(\vec {x})\) is locally smooth and thus smooth. Finally, as S is the locus of \(g(x^0,x^1,x^2,x^3)=0\) for \(g(x^0,x^1,x^2,x^3) = x^0 - t(\vec {x})\), a normal co-vector to S is \(v={\text {d}}x^0 - \sum _{k=1}^3 \frac{\partial t}{\partial x^k} {\text {d}}x^k\). If S is spacelike, then its normal vector is timelike, written as \(\textbf{g}(v,v)<0\), is equivalent to \(|\nabla t| <1\). In the other cases v can also be lightlike \(\textbf{g}(v,v) \le 0\) which is equivalent to \(|\nabla t| \le 1\).
. In the rest of the proof write t in place of \(t_S\) for shortness. By definition \(S \equiv \{(t(\vec {x}), \vec {x})| \vec {x} \in \mathbb {R}^3 \}\). Since S is an embedded co-dimension 1 submanifold, it must be locally described as the locus \(f(x^0,x^1,x^2,x^3)=0\) of a smooth map with \(\textbf{g}(df, df) \le 0\) because the g-normal vectors to df are spacelike or lightlike and thus df is timelike or lightlike. It must be in particular \(\partial _{x^0}f \ne 0\). As a consequence of the implicit function theorem, in a neighborhood of every \(p\in S\), we can represent S as a smooth map \(x^0=t'(\vec {x})\). Therefore \(t(\vec {x}) = t'(\vec {x})\) is locally smooth and thus smooth. Finally, as S is the locus of \(g(x^0,x^1,x^2,x^3)=0\) for \(g(x^0,x^1,x^2,x^3) = x^0 - t(\vec {x})\), a normal co-vector to S is \(v={\text {d}}x^0 - \sum _{k=1}^3 \frac{\partial t}{\partial x^k} {\text {d}}x^k\). If S is spacelike, then its normal vector is timelike, written as \(\textbf{g}(v,v)<0\), is equivalent to \(|\nabla t| <1\). In the other cases v can also be lightlike \(\textbf{g}(v,v) \le 0\) which is equivalent to \(|\nabla t| \le 1\).
The final statement is now obvious, since the wanted diffeomorphism is the identity map  when adopting on S the coordinates \(\vec {x}\). \(\Box \)
when adopting on S the coordinates \(\vec {x}\). \(\Box \)
Proof of Proposition 23
We refer to [12] for the definition of completion of a \(\sigma \)-algebra and a positive measure on it. We divide the main proof into some further lemmata. \(\square \)
Lemma 62
Let \(\mu :\mathscr {B}\rightarrow \overline{\mathbb {R}}_+\) be a positive measure on a \(\sigma \)-algebra \(\mathscr {B}\) on X, \(\overline{\mathscr {B}}^\mu \) be the completion of \(\mathscr {B}\) with respect to \(\mu \), and let us denote by \(\overline{\mu }\) the completion measure on \(\overline{\mathscr {B}}^\mu \).
Then, \(\Delta \in \overline{\mathscr {B}}^\mu \) if and only if \(\Delta = \Delta _0 \cup N\) with \(\Delta _0 \in \mathscr {B}\) and \(N \subset N_0 \in \mathscr {B}\) with \(\mu (N_0)=0\). Furthermore, for every decomposition of \(\Delta \) as above, \(\overline{\mu }(\Delta )= \mu (\Delta _0)\).
Proof
Direct inspection. \(\square \)
Lemma 63
Let \(\mu :\mathscr {B}\rightarrow \overline{\mathbb {R}}_+\) be a positive measure on a \(\sigma \)-algebra \(\mathscr {B}\) on X and \(\mathscr {L}:= \overline{\mathscr {B}}^\mu \) be the completion of \(\mathscr {B}\) with respect to \(\mu \). Let \(\nu :\mathscr {B}\rightarrow \overline{\mathbb {R}_+}\) be a positive measure such that \(\nu<\hspace{-5.0pt}<\mu \). Then, the completion \(\overline{\mathscr {B}}^\nu \) of \(\mathscr {B}\) respect to \(\mu \) satisfies \(\mathscr {L}\subset \overline{\mathscr {B}}^\nu ,\) and there exists a unique positive measure \(\tilde{\nu }\) which extends \(\nu \) on \(\mathscr {L}\) and \(\tilde{\nu }<\hspace{-5.0pt}<\overline{\mu }\), where \(\overline{\mu }\) is the completion of \(\mu \) on \(\mathscr {L}\). Finally, \(\tilde{\nu }(X)= \nu (X)\).
Proof
(Uniqueness) By Lemma 62, if \(\Delta \in \mathscr {L}\) we can decompose \(\Delta =\Delta '\cup N\) where \(\Delta \in \mathscr {B}\) and \(N\subset \tilde{N}\in \mathscr {B}\) is such that \(\mu (\tilde{N})=0\). Suppose that \(\tilde{\nu }\) extends \(\nu \) on \(\mathscr {L}\). Sub-additivity and monotony yield
where, in the last step, we used \(\nu< \hspace{-5.0pt}<\mu \). By monotony \(\tilde{\nu }(\Delta )\ge \tilde{\nu }(\Delta ')=\nu (\Delta ')\), therefore \(\tilde{\nu }(\Delta )=\nu (\Delta ')\). In summary, an extension has to be absolutely continuous with respect to \(\overline{\mu }\). Indeed \(\overline{\mu }(\Delta )=0\) implies \(\mu (\Delta ')=0\) and therefore \(\tilde{\nu }(\Delta )=\nu (\Delta ')=0\).
(Existence) Let \(\overline{\mathscr {B}}^\nu \) be the completion of \(\mathscr {B}\) with respect to \(\nu \) and \(\overline{\nu }\) the completion of \(\nu \) on \(\overline{\mathscr {B}}^\nu \). Notice that \(\mathscr {L}\subset \overline{\mathscr {B}}^\nu \), indeed \(\mu (\tilde{N})=0\) implies \(\nu (\tilde{N})=0\). Therefore \(\tilde{\nu }:=\overline{\nu }\left| \right. _\mathcal {L}\) is a well defined finite measure which extends \(\nu \) on \(\mathcal {L}\). Since \(X \in \mathscr {B}\cap \overline{\mathscr {B}}^\nu \), we finally have \(\tilde{\nu }(X)= \nu (X)\). \(\square \)
In the following, if \(\textsf{E}: \mathscr {B}\rightarrow \mathfrak {B}(\mathcal{H})\) is a \(\mathcal{H}\)-POVM and \(\psi ,\phi \in \mathcal{H}\), \(\mu ^\textsf{E}_{\psi ,\phi }(\Delta ):= \langle \psi |\textsf{E}(\Delta ) \phi \rangle \) for \(\Delta \in \mathscr {B}\). Furthermore, \(\mu ^\textsf{E}_{\psi }(\Delta ):= \mu ^\textsf{E}_{\psi ,\psi }(\Delta )\).
Lemma 64
Let \(\textsf{A}: \mathscr {B}\rightarrow \mathfrak {B}(\mathcal{H})\) be a normalized \(\mathcal{H}\)-POVM and \(\mu :\mathscr {B}\rightarrow \overline{\mathbb {R}}_+\) be a positive measure on a \(\sigma \)-algebra \(\mathscr {B}\) such that, for every \(\psi \in \textsf{H}\), \(\mu ^\textsf{A}_\psi<\hspace{-5.0pt}<\mu \). Then, there exists a unique normalized \(\mathcal{H}\)-POVM \(\tilde{\textsf{A}}\) on \(\mathscr {L}:= \overline{\mathscr {B}}^\mu \) which extends \(\textsf{A}\) and such that for every \(\mu ^{\tilde{A}}_\psi<\hspace{-5.0pt}<\overline{\mu }\).
Proof
Taking advantage of Lemma 63, for every \(\psi \in \textsf{H}\), we can extend \(\mu ^\textsf{A}_\psi \) to \(\widetilde{\mu ^\textsf{A}_\psi }\) on \(\mathscr {L}\). Then, we define
For a fixed \(\Delta \in \mathscr {L}\)—\(\Delta = \Delta ' \cup N\) as in the proof of Lemma 63—the map  is sesquilinear and continuous since \(\widetilde{\mu ^\textsf{A}_{\phi ,\psi }}(\Delta )= {\mu ^\textsf{A}_{\phi ,\psi }}(\Delta ')\). As a consequence, for \(\Delta \in \mathscr {L}\), the map
is sesquilinear and continuous since \(\widetilde{\mu ^\textsf{A}_{\phi ,\psi }}(\Delta )= {\mu ^\textsf{A}_{\phi ,\psi }}(\Delta ')\). As a consequence, for \(\Delta \in \mathscr {L}\), the map  is a linear and continuous functional with norm bounded \(||\psi ||\). A straightforward use of the Riesz lemma gives that there is a unique operator \(\tilde{A}(\Delta ): \mathcal{H}\rightarrow \mathcal{H}\) such that \(\langle \psi |\tilde{A}(\Delta ) \phi \rangle = \widetilde{\mu ^A_{\phi ,\psi }}(\Delta )\). \(\tilde{A}(\Delta )\)is positive because \(\mu ^{\tilde{A}}_\psi \) is positive. Bu construction
is a linear and continuous functional with norm bounded \(||\psi ||\). A straightforward use of the Riesz lemma gives that there is a unique operator \(\tilde{A}(\Delta ): \mathcal{H}\rightarrow \mathcal{H}\) such that \(\langle \psi |\tilde{A}(\Delta ) \phi \rangle = \widetilde{\mu ^A_{\phi ,\psi }}(\Delta )\). \(\tilde{A}(\Delta )\)is positive because \(\mu ^{\tilde{A}}_\psi \) is positive. Bu construction  defines a normalized POVM. Normalization arises from \(\langle \phi | \tilde{\textsf{A}}(S) \psi \rangle = \widetilde{\mu ^\textsf{A}_{\phi ,\psi }}(S) = \mu ^A_{\phi ,\psi }(S) = \langle \phi |\psi \rangle \). Finally, \(\mu ^{\tilde{\textsf{A}}}_\psi =\widetilde{\mu ^\textsf{A}_\psi }< \hspace{-5.0pt}<\overline{\mu }\). \(\square \)
defines a normalized POVM. Normalization arises from \(\langle \phi | \tilde{\textsf{A}}(S) \psi \rangle = \widetilde{\mu ^\textsf{A}_{\phi ,\psi }}(S) = \mu ^A_{\phi ,\psi }(S) = \langle \phi |\psi \rangle \). Finally, \(\mu ^{\tilde{\textsf{A}}}_\psi =\widetilde{\mu ^\textsf{A}_\psi }< \hspace{-5.0pt}<\overline{\mu }\). \(\square \)
We can now conclude the proof of the main proposition. If \(S\in \mathscr {C}^s_{\mathbb {M}}\), set \(\mathscr {B}=\mathscr {B}(S)\), \(\textsf{A}:= \textsf{A}_S: \mathscr {B}(S) \rightarrow \mathfrak {B}(\mathcal{H})\) and \(\mu =\nu _S\) in Lemma 64. The map  defines the wanted extension. It is unique because every extension of the considered type is completely determined by the positive measure \(\widetilde{\mu ^\textsf{A}_{\psi }}\) which is uniquely determined by \(\mu ^\textsf{A}_{\psi }\), thus by \(\textsf{A}\) itself. \(\Box \)
defines the wanted extension. It is unique because every extension of the considered type is completely determined by the positive measure \(\widetilde{\mu ^\textsf{A}_{\psi }}\) which is uniquely determined by \(\mu ^\textsf{A}_{\psi }\), thus by \(\textsf{A}\) itself. \(\Box \)
Proof of Proposition 24
We have only to prove that the extended POVMs satisfy the coherence condition (13). Take \(\psi \in \mathcal{H}\). If \(\Delta \in \mathscr {M}(S)\) then, according to the construction in the proof of Proposition 23, there exists a decomposition \(\Delta = \Delta _0 \cup N\) with \(\Delta _0\in \mathscr {B}(S)\) and \(N\subset N_0 \in \mathscr {B}(S)\), and finally \(\langle \psi |\textsf{A}_S(N_0)\psi \rangle =0\), \(\langle \psi |\tilde{\textsf{A}}_S(\Delta )\psi \rangle = \langle \psi |\textsf{A}_S(\Delta _0)\psi \rangle \). These last two identities do not depend on the decomposition of \(\Delta \) as \(\Delta _0\cup N\). Since \(\Delta _0,N,N_0 \subset \Delta \subset S\cap S'\), we can repeat everything for \(\langle \psi |\textsf{A}_{S'}(\Delta )\psi \rangle \) with the same decomposition of \(\Delta \), proving that
where we used the fact that \(\textsf{A}\) satisfies the coherence condition on the Borel sets \(\Delta _0, N_0\subset S\cap S'\) by hypothesis. In particular \(\langle \psi |\tilde{\textsf{A}}_{S'}(\Delta )\psi \rangle =\langle \psi |\tilde{\textsf{A}}_{S}(\Delta )\psi \rangle \). Arbitrariness of \(\psi \), using polarization and the fact that \(\mathcal{H}\) is complex, proves the validity of the coherence condition for the extended POVMs ending the proof. \(\Box \)
Proof of Proposition 37
Notice that (36) is nothing but (35) when exploiting (34). Evidently, it is sufficient to establish the thesis when \(S'\) is a Minkowski time slice and S is a generic smooth Cauchy surface. From now on, we consider a Minkowski coordinate frame \(x^0,x^1,x^3,x^4\) and describe S in terms of a smooth function \(x^0=t(\vec {x})\), taking \(S'\) as the time-slice \(x^0=0\). Define the auxiliary vector field
By construction K is conserved, everywhere non-vanishing, timelike, and future-directed. Finally,
Define \(B'_R\) as the open ball in \(S'\equiv \mathbb {R}^3\) centered at the origin and with finite radius \(R>0\). Correspondingly \(B_R \subset S\) is the open set in S defined by \(x^0= t(\vec {x})\), \(\vec {x} \in B'_R\). Let \(T_R\subset \mathbb {M}\) be the closed (compact) cylinder with bases \(\overline{B_R}\) and \(\overline{B'_R}\) and lateral surface parallel to K (i.e., to \(\partial _{x^0}\)). We are explicitly assuming that the closures of \(B'_R\) and \(B_R\) have no intersection for now and we shall treat later the case where the two surfaces intersect. As K is conserved, \(d\omega ^K=0\) for (1) Proposition 36. Furthermore, \(\partial T_R\) is an orientable smooth embedded submanifold up to zero-measure subsets, we can apply the Poincaré theorem, proving that \(\int _{\partial T_R} \omega ^K =\int _{T_R} d\omega ^K = 0\). Since the lateral surface gives no contribution as easily arises from (30) using the fact that J is parallel to that surface, the identity boils down to
This identity is valid also when \(B'_R\) and \(B_R\) have intersection (just because S and \(S'\) do and \(B'_R\) passes through that intersection). In that case, as R is finite so that \(t(\vec {x})\) is bounded for \(\vec {x} \in B'_R \subset S' \equiv \mathbb {R}^3\), we can move \(S'\) parallelly to \(\partial _{x^0}\) till to another \(x^0\)-slice \(S''\) in the past of \(S'\), in order that \(B_R\) and \(B''_R\) (the projection of \(B'_R\) onto \(S''\)) do not meet. By construction, using the above argument once again for the relevant embedded submanifolds with orientable boundary, since now the bases do not touch each other,
and also
In summary
is valid even if \(B_R\) and \(B'_R\) have intersection.
Taking \(R\rightarrow +\infty \), a direct application of the monotone convergence theorem (as the integrals can be written as Lebesgue integrals in \(\mathbb {R}^3\) of non-negative functions according to (31) proves that
where we also used (81).
To go on, define \(Y:= J+K\) noticing that this smooth conserved vector field is everywhere timelike and future directed. Since it is also bounded, its flow is global and defines a smooth one-parameter group of diffeomorphisms \(\{\phi ^{Y}_{s}\}_{s\in \mathbb {R}}\) of \(\mathbb {M}\). Finally, the integral curves of Y are future directed and inextendible. In fact, suppose that \(\gamma (s)\rightarrow q\in \mathbb {M}\) for \(s\rightarrow +\infty \), i.e., the curve is not future inextendible (the same argument applies for \(s\rightarrow -\infty )\). If \(Y^k(q)\ne 0\) for some \(k=0,1,2,3\), then it happens in a connected neighborhood U of q where the sign of \(Y^k= \frac{{\text {d}}x^k}{ds}\) is therefore fixed. There we can use \(z=x^k\) to parametrize \(\gamma \) obtaining \(s(z) = \int _0^{z} \frac{{\text {d}}x^k}{Y^k(\gamma (x^k))}\). However, since s varies till \(+\infty \) when \(\gamma \) approaches q in U, then \(Y^k(\gamma (x^k))\) must vanish as \(x^k \rightarrow x^k(q)\) contrarily to the hypothesis. Hence, all components of Y must vanish at q but this was excluded a priori.
As a consequences of these properties, the map

turns out to be a diffeomorphism as well. In fact, \(\Phi \) is injective because \(\phi ^Y_s(p)=\phi ^Y_{s'}(p')\) implies \(p = \phi ^Y_{s'-s}(p')\) but this would mean that the integral curve of Y through p touches twice \(S'\), and this is not possible unless \(s=s'\) and thus \(p=p'\); surjectivity of \(\Phi \) follows from the fact that, if \(q\in \mathbb {M}\) there is an integral line of Y through q at \(s=0\) and, it being timelike and inextendible, it must intersect \(S'\) at some \(q'\) for \(s=T_q\) because \(S'\) is a Cauchy surface. Therefore \(\Phi (-T_q,q')=q\); finally \(d\Phi \ne 0\) everywhere, because (a) \(d\Phi (s,p) e_0 = Y(\phi ^Y_s(p))\) and (\(e_0, e_1,e_2,e_3\) denoting the canonical basis of \(\mathbb {R}\times \mathbb {R}^3 \equiv \mathbb {R}\times S'\)) (b) \(d\Phi (s,p) e_k = d\phi ^Y_s(p) e_k\) defines a basis of the tangent space at \(\phi ^Y_s(p)\) of the embedded 3D submanifold \(\phi ^Y_s(S')\)Footnote 20 that is transverse to \(Y(\phi ^Y_s(p)) = d\phi ^Y_s Y(p)\) by construction. In summary, \(d\Phi (s,p)\) sends the canonical basis of \(\mathbb {R}^4 = \mathbb {R}\times \mathbb {R}^3 \equiv \mathbb {R}\times S'\) to a basis of \(T_{\phi _s(p)}\mathbb {M}\) and it is therefore bijective. The situation is identical to the one of the vector K, with the only difference that we have replaced K for Y and \(x^0\) for the global parameter s. Now \(s,x^1,x^2,x^3\)—where the latter three coordinates are taken on \(S'\)—define a global chart on \(\mathbb {M}\). In these coordinates, the action of \(\phi ^Y\) is trivial  .
.
Taking advantage of the diffeomorphism \(\Phi \), one easily proves the following facts whose details are left to the reader. If \(B'_R \subset S'\equiv \mathbb {R}^3\) is as before an open ball of radius \(R>0\), \(\Gamma _R:= \Phi (\mathbb {R}\times \overline{B'_R})\) is a smooth 4-manifold with orientable boundary embedded in \(\mathbb {M}\). The boundary \(\partial \Gamma _R\) is made of the integral lines of Y exiting \(\partial B'_R\). We extract from \(\Gamma _R\) the compact cylinder \(T_R\) with bases given by the closures of \(B'_R\) and the closure of the smooth embedded submanifold
(which is not a ball in general now!). As before we assume that the closures of \(B_R\) and \(B'_R\) have no intersection and the case of non-empty intersection can be treated exactly as before in the representation \(\mathbb {R}\times \mathbb {R}^3\) where \(s\in \mathbb {R}\) and \(\mathbb {R}^3 \equiv S'\). Notice that \(B_R \subset B_{R'} \subset S\) if \(R< R'\) by construction and also
This identity is valid because, for every \(p\in S\), there is \(R'>0\) such that \(p \in B_{R'}\). (In fact, as before, there is an integral curve of Y passing through p and, since this curve is timelike and inextendible, there must be \(p'\in S'\) such that \(\phi ^Y_s(p')=p\) for some s because \(S'\) is Cauchy. Since the union of the sets \(B'_R\) covers \(S'\), then \(p'\in B'_{R'}\) for some \(R'>0\) sufficiently large and so \(p\in B_{R'}\).) \(\partial T_R\) is an orientable smooth embedded submanifold up to zero-measure sets and we can apply the Poincaré theorem as before, obtaining
where we have disregarded the contribution of the lateral surface because it is made of integral lines of Y itself and no contribution to the boundary integral arises according to (30). Taking the limit for \(R\rightarrow +\infty \) on both sides, the monotone convergence theorem (taking positivity of integrands into account according to (2) Proposition 36 and (83)) yields
Namely,
On the ground of the validity of (82), this identity boils down to
In particular both integrals converge or diverge simultaneously. \(\Box \)
Proof of Lemma 51
Passing to a Minkowski chart adapted to \(n_\Sigma \), the right-hand side of (59) is a finite linear combination of integrals of the form
where \(f,g \in \mathcal{\Sigma }(\mathbb {R}^3)\) and the exponentials containing \(x^0\) are embodied in these functions. Therefore, proving the thesis for I is enough for ending the proof of the theorem. We have,
Above, \(\chi _\Delta \cdot \hat{g}\in L^1(\mathbb {R}^3, d^3x) \cap L^2(\mathbb {R}^3, d^3x)\) because \(\chi _\Delta \) is bounded and \( \hat{g}\) Schwartz, and in the last identity we exploited the Plancherel theorem in \(L^2\). From the very definition of Fourier transform, we finally have
Last identity concludes the proof. \(\Box \)
Proof of Proposition 61
(a) and (b). We adopt throughout the easier notation \(\phi := \phi _\psi \). We start by observing that the function  is \(\mathscr {S}(\mathbb {R}^6)\) in both cases (a) and (b), and thus
is \(\mathscr {S}(\mathbb {R}^6)\) in both cases (a) and (b), and thus

is in \(\mathscr {S}(\mathbb {R}^3)\) as it can be proved by direct inspection. Notice that, in the case (b), (75) must be valid also for \(\phi \in \mathscr {S}(\mathbb {R}^3)\) since, for a fixed \(\phi \in \mathscr {S}(\mathbb {R}^3)\), there is a sequence of functions  pointwise and \(|\phi _n|\le \phi \). Hence, we can take the limit on both sides of (75) by using continuity of \(\textsf{A}(\Delta )\) on the left-hand side and the dominated convergence theorem on the right-hand side.
pointwise and \(|\phi _n|\le \phi \). Hence, we can take the limit on both sides of (75) by using continuity of \(\textsf{A}(\Delta )\) on the left-hand side and the dominated convergence theorem on the right-hand side.
We pass to compute the various moments of the probability measure \(\langle \psi |\textsf{A}(\cdot ) \psi \rangle \) taking advantage of the theory of Fourier transformation of distributions in \(\mathscr {S}'(\mathbb {R}^n)\). If \(\alpha := (\alpha _1,\alpha _2,\alpha _3)\) is a multi-index, so that \(x^\alpha := (x^1)^{\alpha _1} (x^2)^{\alpha _2} (x^3)^{\alpha _3}\), we can write
where \(M^\alpha \) is the multiplicative operator with \(x^\alpha \) and \(f \in \mathscr {S}(\mathbb {R}^3)\) is defined above. Changing variables to \(\vec {u}:=\vec {q}-\vec {p}\) and \(\vec {v}:=\vec {q}\) we have,
with is the inverse Fourier transform, always in \(\mathscr {S}(\mathbb {R}^3)\), of
Therefore
To go on, defining \(l(\vec {p},\vec {q}):=(\vec {p},\vec {p})\), since \(K_\textsf{A}(\vec {p}, \vec {p})=1\), we have that \(0=\partial ^{\alpha }(K_\textsf{A}\circ l)=(\partial ^\alpha K_\textsf{A})\circ l\) for \(|\alpha |=1\). Therefore, we obtain the general expression for the \(\alpha \)-th moment (77),
In particular, for \(|\alpha |=1\), we find (76)
Every other selfadjoint operator B in \(\mathcal{H}\) which satisfies the identity above must also satisfy (from polarization and density)
(also replacing \(\mathcal{D}(\mathcal{H})\) for \(\mathcal{S}(\mathcal{H})\)). Since \(\mathcal{D}(\mathcal{H})\) (resp. \(\mathcal{S}(\mathcal{H})\)) is a core for \(N^a\):
Since a selfadjoint operator (here \(N^a\)) is maximally symmetric, it must hold \(N^a = B\). This ends the proof of (a) and (b).
We can pass to prove (c) and (d). For \(|\alpha |=2\), the formula above for the \(\alpha \)-th moment yields
However, taking advantage of \(\frac{\partial ^{|\alpha |}K_\textsf{A}}{\partial p^\alpha }\circ l=-\frac{\partial ^{|\alpha |}K_\textsf{A}}{\partial q^{\alpha _1}\partial p^{\alpha _2}}\circ l\) for \(|\alpha |=2\) and when only a component of \(\alpha \) does not vanish, we can rephrase the found result as
The multiplicative operator \(\textsf{K}^{\textsf{A}}_a\) defined in (79), here viewed in \(L^2(\mathbb {R}^3, d^3p)\), defined by the function \(\left. \frac{\partial }{\partial p_a}\frac{\partial }{\partial q_a} K_\textsf{A}(\vec {p}, \vec {q})\right| _{\vec {p}= \vec {q}}\) is a selfadjoint operator which is a spectral function of the four momentum operator P as this function is real (see, e.g., [29]). The domain of the operator trivially includes \(C_c^\infty (\mathbb {R}^3)\), but also \(\mathscr {S}(\mathbb {R}^3)\) when \(K_\textsf{A}(\vec {p}, \vec {q})\) has polynomial growth with all of its derivatives. Evidently \(\textsf{K}^{\textsf{A}}_a\) is also bounded, and thus in \(\mathfrak {B}(\mathcal{H})\), if the function \(\left. \frac{\partial }{\partial p_a}\frac{\partial }{\partial q_a} K_\textsf{A}(\vec {p}, \vec {q})\right| _{\vec {p}= \vec {q}}\) is bounded. Finally the operator \(\textsf{K}^{\textsf{A}}_a\) is positive just because
This can be proved as follows. Consider a real smooth mollificator (with a common compact support) such that \(\psi _{n}(\vec {x}-\vec {x_0}) \rightarrow \delta (\vec {x}-\vec {x}_0)\) weakly for \(n\rightarrow +\infty \). As \(K_\textsf{A}\) is positive definite, we have
uniformly as a function of \(\vec {k}\) because \(K_\textsf{A}\) is continuous (Proposition 4.21 [5]) so that the resulting function of \(\vec {k}\) is non-negative as well. In summary,
Multiplying both sides of the found identity with \((\Delta _\psi P_a)^2\) and taking the standard Heisenberg inequality into account we get the thesis:
where the second factor \(\hbar ^2\) arises when restoring the Planck constant in the exponentials \(e^{i (\vec {q}-\vec {p})\cdot {\vec {x}}/\hbar }\) so that the representation of \(N^a\) on \(\mathscr {S}(\mathbb {R}^3)\) in the \(L^2(\mathbb {R}^3,d^3p)\) space is \(i\hbar \frac{\partial }{\partial p_a}\).
(e) \(\mathcal{H}_N:= \oplus _{j=1}^N \mathcal{H}\) is the complex Hilbert space of vectors of measurable complex valued functions \(\Psi := (\psi _1,\ldots , \psi _N)\) equipped with the Hilbert space structure arising from the Hermitian scalar product
If \(\psi \in \mathcal{S}(\mathcal{H})\), define \(\Phi _\psi := N^{-1/2}(\phi _\psi u_1, \ldots , \phi _\psi u_N)\). Each component is in \(\mathscr {S}(\mathbb {R}^3)\) in our hypotheses. Finally, using \(K_\textsf{A}(\vec {p},\vec {p}) =1\)
With the same procedure as in the proof of (c) and (d), one sees that, for every constant \(c\in \mathbb {R}\)
where we have used the fact that \(i\partial _{p_a}-c\), acting componentwise, is symmetric on \(\oplus _{j=1}^N \mathscr {S}(\mathbb {R}^3)\). Similarly
Where the multiplicative operator \(p_a-d\), acting componentwise, is symmetric on \(\oplus _{j=1}^N \mathscr {S}(\mathbb {R}^3)\). Cauchy–Schwarz inequality and (84) yield
Restoring \(\hbar \), we have found that, for \(||\psi ||=1\)
This is the thesis when replacing c for \(\int _{\mathbb {R}^3} x^a \langle \psi | \textsf{A}(d^3x)\psi \rangle \) and and b for \(\langle \psi |P_a \psi \rangle \). \(\Box \)
Proof of Theorems 44 and 58
Those theorems are easy consequences of Proposition 61. Both \(\textsf{M}^n_\Sigma (\Delta )\) and \(\textsf{T}^g_\Sigma (\Delta )\), for g real and smooth, have the expression (75) if \(\Sigma \) coincides with the slice at \(x^0=0\) of a Minkowski chart (see (42) and (59) for \(x^0=0\)). In details,
and
These kernels are positive definite, respectively, in view of Definition 39 and Thm. 54.
The kernels \(K_{\textsf{M}^n_{\Sigma }}(\vec {q}, \vec {p})\), and \(K_{\textsf{T}^g_{\Sigma }}(\vec {q}, \vec {p})\) when g has the form (40) and convex combinations of these functions, have polynomial growth with all of their derivatives, so the case (b) of the proposition applies to these cases.
It is not difficult to prove in particular that the functions of \(\vec {p}\) given by \(\frac{\partial }{\partial q_a}\frac{\partial }{\partial p_a}K_{\textsf{M}^n_{\Sigma }}(\vec {q}, \vec {p})\Big |_{\vec {p}=\vec {q}}\) and \(\left. \frac{\partial }{\partial q_a}\frac{\partial }{\partial p_a}K_{\textsf{T}^g_{\Sigma }}(\vec {q}, \vec {p})\right| _{\vec {p}=\vec {q}}\) are bounded (in the second case for every smooth g, it is not necessary the form (40)) and therefore the corresponding operator in (79) is a positive selfadjoint operator in \(\mathfrak {B}(\mathcal{H})\). \(\Box \)
B Conditions for positive-definite kernels on \(\mathbb {R}^n\)
We prove here a useful property of positive definite kernels.
Proposition 65
Let \(K: \mathbb {R}^n\times \mathbb {R}^n \rightarrow \mathbb {C}\) be continuous, the following facts are equivalent.
-
(a)
Every \(N\times N\) matrix \([K(k_i,k_j)]_{i,j=1,\ldots , N}\) for every choice of \(k_1,\ldots , k_N \in \mathbb {R}^n\) and \(N=1,2,\ldots \) are positive semidefinite (in particular Hermitian);
-
(b)
K is positive definite according to (39);
$$\begin{aligned} \sum _{i,j=1}^N \overline{c_i}c_j K(k_i, k_j) \ge 0, \quad \forall \{c_j\}_{j=1,\ldots , N}\subset \mathbb {C}, \forall \{k_j\}_{j=1,\ldots , N}\subset X , \forall N=1,2,\ldots \,; \quad \quad \,\, (39)\end{aligned}$$ -
(c)
the bilinear functional induced by K on \(C_c(\mathbb {R}^n)\) is positive:
$$\begin{aligned} \int _{\mathbb {R}^n\times \mathbb {R}^n} \overline{f(p)} K(p,q) f(q) d^npd^nq \ge 0, \quad \forall f \in C_c(\mathbb {R}^n) . \end{aligned}$$(85)
Proof
Evidently (a) and (b) are equivalent, so we only prove that (b) and (c) are equivalent. We start by establishing that K positive definite implies (85). Define a compactly supported continuous function on \(\mathbb {R}^{2n}\) as \(g(p,q)=\overline{f}(p)K(p,q)f(q)\) and let \(Q\subset \mathbb {R}^{2 n}\) be an open, 2n-square such that \(supp (g)\subset Q\). Then, for any \(N\in \mathbb {N}\) there exist a family of \(N^{2n}\) pairwise-disjoint open 2n-squares \(Q_i^N\subset Q\), \(i=1,\ldots , N^{2n}\), with common (Lebesgue) measure \(\left| Q_i^N\right| =\frac{\left| Q\right| }{N^{2n}}\) and \( \overline{Q}=\bigcup _{i=1}^{N^{2n}}\overline{Q_i^{N}}\). Choosing \(x_i^N\in Q_i^N\) with \(i=1,\ldots ,N^{2n}\) for every given N, we can define the family of simple functions \( g_N(x)=\sum _{i=1}^{N^{2n}}g(x_i^N)\chi _{Q_i^N}(x).\) Since \(diam(Q_i^N)\)=\(\sqrt{2 d}\frac{\left| Q\right| ^{\frac{1}{2 d}}}{N}\), uniform continuity of g on the compact \(\overline{Q}\) implies that for \(\epsilon >0\) there is \(N_{\epsilon }\) such that \(\left| g(x_i^N)-g(x)\right| <\epsilon \text { if }x\in Q_i^N\) and \(N>N_{\epsilon }\) and for \(i=1,\ldots , N^{2n}\). Therefore, if \(N>N_{\epsilon }\) and \(x\in Q\), \(\left| g_N(x)-g(x)\right| \le \sum _{i=1}^{N^{2n}}\left| g(x_i^N)-g(x)\right| \chi _{Q_i^N}(x)<\epsilon \), so that \(g_N\) converges to g on Q uniformly and also in \(L^1\) since \(|Q|< +\infty \). The proof is over because
We eventually prove that (85) entails that the continuous kernel K is positive definite. To this end, we can choose \(c_1,\ldots , c_N \in \mathbb {C}\), \(p_1,\ldots , p_N \in \mathbb {R}^n\) and a \(L\in (1,+\infty )\) parametrized family of functions
where \(h: \mathbb {R}^n \rightarrow [0, +\infty )\) is continuous, compactly supported, \(h(0)=1\), and \(\int _{\mathbb {R}^n} h d^nx =1\). In this case, it is easy to prove that
for every continuous function \(g: \mathbb {R}^n \times \mathbb {R}^n \rightarrow \mathbb {C}\). Replacing the function f for \(f_L\) in (85), the limit as \(L \rightarrow +\infty \) implies (39), ending the proof. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
De Rosa, C., Moretti, V. Quantum particle localization observables on Cauchy surfaces of Minkowski spacetime and their causal properties. Lett Math Phys 114, 72 (2024). https://doi.org/10.1007/s11005-024-01817-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11005-024-01817-9
Keywords
- Relativistic quantum localization
- Cauchy surface
- Hegerfeldt theorem
- Positive-operator-valued measures
- Klein-gordon equation
- Positive-definite kernel
- Stress-energy tensor
- Newton–Wigner localization



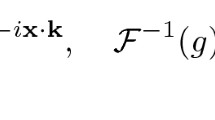

 is timelike (Corollary 14 in [
is timelike (Corollary 14 in [ is timelike (Corollary 14 in [
is timelike (Corollary 14 in [ is bounded.
is bounded.