Matrix product operator algebras II: phases of matter for 1D mixed states

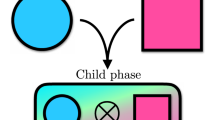
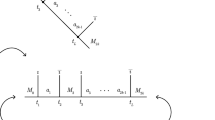
Abstract

The mathematical classification of topological phases of matter is a crucial step toward comprehending and characterizing the properties of quantum materials. In this study, our focus is on investigating phases of matter in one-dimensional open quantum systems. Our goal is to elucidate the emerging phase diagram of one-dimensional tensor network mixed states that act as renormalization fixed points. These operators hold special significance since, as we prove, they manifest as boundary states of two-dimensional topologically ordered states, encompassing all known two-dimensional topological phases. To achieve their classification we begin by constructing families of such states from C*-weak Hopf algebras, which are algebras with fusion categories as their representations, and we present explicit local fine-graining and coarse-graining quantum channels defining the renormalization procedure. Lastly, we prove that a subset of these states, originating from C*-Hopf algebras, are in the trivial phase.

Appendices

Diagrammatic Language for Tensor Networks

In this section, we introduce a slightly adapted version of the usual graphical notation from the literature of tensor networks. From now on, let V be a finite-dimensional complex vector space. First, a vector $v\in V$ is depicted by a shape (e.g., a circle) and a line sticking out of it, associated to the vector space and labeled accordingly; we convey to draw the arrow outgoing from the shape. Second, any element $\phi \in V^*$ is a vector in $V^*$ or a linear functional defined on V, and we alternatively draw it with an arrow ingoing to the shape. Pictorially,

Note that, although we have represented the previous elements using straight horizontal lines, no reading order has been prescribed. Here, we identify each finite-dimensional complex vector space V and its double dual $V^{**}$, which are canonically isomorphic. Therefore, one can regard any vector $v\in V$ as a linear functional on $V^*$ and thus, exchange the orientation of any line by labeling the dual:

Now, let V and W be two finite-dimensional complex vector spaces. Any vector $v\in V\otimes W$ in the tensor product is depicted by a shape with two lines, e.g.,

By virtue of the previous identification, one can rewrite

In addition, the tensor product of two vectors $v\in V$ and $w\in W$ is depicted by placing both representations in the same picture, next to each other:

Note that, although the labels V and W should allow to identify the corresponding indices, even if $V = W$, it may not be enough. One solution, used in this paper, consists on prescribing colors to each index. Additionally, note that we have implicitly identified $V\otimes W$ and $W\otimes V$, since no order is prescribed in the previous picture. However, these are again canonically isomorphic and no preference is considered here. In this context, it is natural to represent the action of the canonical pairing by joining the corresponding lines, i.e.,

On the other hand, since $\textrm{Hom}(V,W)$ is canonically isomorphic to $V^*\otimes W$, we can also represent any linear map $F: V \rightarrow W$ in the following form:

Remarkably, the distinction between $F:V \rightarrow W$ and its transpose $F^{\textrm{t}}: W^* \rightarrow V^*$, is only reflected in the diagram by the arrows and their labels.

The canonical regular element

Here we recall additional results on the framework of C*-weak Hopf algebra not introduced in the main text. As a matter of fact, we are interested in describing the canonical regular element in terms of these. First, it is well known that in any C*-weak Hopf algebra A there exists a unique non-degenerate two-sided normalized integral $h\in A$, known as the Haar integral of A; see Definition 3.24 and Theorem 4.5 in [5]. In particular,

$$\begin{aligned} h^2 = h^* = h = S(h). \end{aligned}$$

(51)

By self-duality, let $\hat{h}\in A^*$ denote the Haar integral of the dual C*-weak Hopf algebra. We also recall the existence of $\Lambda \in A$, known as the dual left-integral of $\hat{h}$, such that

$$\begin{aligned} \Lambda _{(1)} \, \hat{h} ( \Lambda _{(2)} )= 1 \;\,\text { and }\;\, S(\Lambda _{(1)}) \otimes \Lambda _{(2)} = \Lambda _{(2)}\otimes \Lambda _{(1)}; \end{aligned}$$

(52)

see, e.g., Theorem 3.18 and Lemma 3.20 in [5]. Second, there is a unique positive element $g\in A$ implementing the antipode squared as an inner automorphism, i.e.,

$$\begin{aligned} S^2(x) = g x g^{-1} \end{aligned}$$

(53)

for all $x\in A$, among other properties, known as the canonical group-like element of A; see Proposition 4.9 in [5]. As its name implies, it is a group-like element, i.e., it satisfies the following property:

$$\begin{aligned} g_{(1)}\otimes g_{(2)} = g 1_{(1)}\otimes g1_{(2)} = 1_{(1)}g\otimes 1_{(2)}g. \end{aligned}$$

(54)

Moreover, it can be decomposed in the form $g = g_L g_R^{-1}$ for $g_L,g_R > 0$ given by

$$\begin{aligned} g_L:= ( \hat{h}(h_{(1)}) h_{(2)} )^{1/2}\in A^L, \quad g_R := S(g_L) = S^{-1}(g_L) \in A^R. \end{aligned}$$

(55)

By self-duality, we denote by $\hat{g}\in A^*$ the canonical group-like element of the dual C*-weak Hopf algebra. Finally, let us recall the following formula.

Proposition B.1

For any C*-weak Hopf algebra,

$$\begin{aligned} x_{(1)} \, \hat{g}( x_{(2)} ) = g_R x g_R^{-1} \;\;\text { and }\;\; \hat{g} ( x_{(1)} ) \, x_{(2)} = g_L x g_L^{-1} \end{aligned}$$

for all $x\in A$. In particular,

$$ 1_{(1)} \, \hat{g} ( 1_{(2)} ) = 1 = \hat{g} ( 1_{(1)} ) \, 1_{(2)}. $$

Proof

See Scholium 2.7 and Lemma 4.13 in [5] for a proof. $\square$

Proposition B.2

(see [35]) For any biconnected C*-weak Hopf algebra A,

$$\begin{aligned} \chi _\alpha (g) = \varepsilon (1) \, \delta _\alpha , \end{aligned}$$

(56)

for all sectors $\alpha = 1,\ldots ,s$.

Proposition B.3

For any biconnected C*-weak Hopf algebra

$$\begin{aligned} \omega (x) = \frac{1}{\mathcal {D}^{2}\varepsilon (1)} \hat{h}(g_L^{-1} g_R^{-1} x) = \frac{1}{\mathcal {D}^{2}\varepsilon (1)} \hat{h}(x g_L^{-1} g_R^{-1}) \end{aligned}$$

(57)

for all $x\in A$ and

$$\begin{aligned} \Omega = \frac{1}{\mathcal {D}^{2}\varepsilon (1)} \, \Lambda _{(1)} \, \hat{g}^{-1}(\Lambda _{(2)}) = \frac{1}{\mathcal {D}^{2}\varepsilon (1)} \, \hat{g}^{-1} ( \Lambda _{(1)} ) \, \Lambda _{(2)}. \end{aligned}$$

(58)

Proof

There exists a well-known element, called the S-invariant trace functional of A [5], given by the expression $\chi _1(g^{-1})\chi _1 + \cdots + \chi _s(g^{-1})\chi _s$. By virtue of Theorem 2.8 and Proposition B.2, one easily checks that both elements are proportional. $\square$

We make use of the explicit expression of the linear map T in Theorem 2.8:

$$\begin{aligned} T(x) = S(x_{(1)}) \, \hat{g} ( x_{(2)} ) = \hat{g} ( x_{(1)} ) S^{-1}(x_{(2)}), \end{aligned}$$

(59)

and the fact that $\omega$ is invariant under both this map and the antipode:

$$\begin{aligned} \omega \circ T =\omega \circ S = \omega . \end{aligned}$$

(60)

See Ref. [33] for proofs of both results.

Finally, let us particularize the previous notions and results in the context of C*-Hopf algebras. We refer the reader to Ref. [34] for more details.

Proposition B.4

Let A be a C*-Hopf algebra. Then, the following hold:

• (1) $S^2 = \textrm{Id}$ and the canonical grouplike element is $g = 1$;

• (2) $\delta _\alpha = \dim _{\mathbb {C}}(V_\alpha )$ for all sectors $\alpha =1,\ldots , s$;

• (3) the dual left integral of the Haar measure $\hat{h}\in A^*$ is $\textrm{t} = \mathcal {D}^2 \Omega$;

• (4) the canonical regular element and the Haar integral coincide, i.e., $\Omega = h$;

• (5) the linear map $T:A \rightarrow A$ coincides with the antipode;

• (6) $g_L = g_R = \mathcal {D}^{-1} 1$.

Proof

(1) It is a well-known result that for C*-Hopf algebras it holds that $S^2 = \textrm{Id}$ [28, 29]. Since $1\in A$ satisfies the defining properties of the canonical group-like element too, which is unique, $g = 1$. (2) Recall that $\varepsilon (1) = 1$ by hypothesis and hence by Proposition B.2 it follows that

$$\begin{aligned} \dim _{\mathbb {C}}(V_\alpha ) = \chi _\alpha (1) = \chi _\alpha (g) = \varepsilon (1)\, \delta _\alpha = \delta _\alpha \end{aligned}$$

for all $\alpha =1,\ldots , s$. (3) Since C*-Hopf algebras are self-dual, $\hat{g} = \varepsilon$, and therefore $\Omega = \mathcal {D}^{-2}\varepsilon (1)^{-1} \textrm{t} = \mathcal {D}^{-2} \textrm{t}$, where the first expression follows from Proposition B.3. (4) Every C*-Hopf algebra is unimodular, see [34], i.e., every left integral is a two-sided integral, and the subspace of two-sided integrals is one-dimensional. Hence, $\textrm{t} = \eta h$ for some $\eta \in \mathbb {C}$. Since both $\Omega$ and h are projectors, $\eta = \mathcal {D}^{2}$. (5) This follows trivially as a consequence of Eq. 59 since $\hat{g} =\varepsilon$. (6) Recall the definition of $g_L$ and $g_R$ in Eq. 55 and consider both (3) and (4). $\square$

Proof of Lemma 3.5

Here we restate and prove the following result.

Lemma 3.5

Let A be a biconnected C*-weak Hopf algebra. Then,

$$\begin{aligned} \omega ( \xi T(\Omega _{(1)}) ) \, \Omega _{(2)} = 1 \end{aligned}$$

(30)

for some $\xi \in A$. Furthermore, $\xi$ is uniquely determined, positive, invertible and

$$\begin{aligned} \xi ^{-1} = \omega ( \Omega _{(1)} ) \, \Omega _{(2)} = \omega ( T(\Omega _{(1)}) ) \, \Omega _{(2)}; \end{aligned}$$

(31)

it is invariant under $T:A\rightarrow A$ and satisfies the relation

$$\begin{aligned} T(x)^* = \xi \, T(x^*) \, \xi ^{-1} \end{aligned}$$

(32)

for all $x\in A$. In addition,

$$\begin{aligned} \chi _\alpha (\xi ^{-1}) = \delta _\alpha \, \omega (\Omega ) \end{aligned}$$

(33)

for all $\alpha = 1, \ldots , s$. Moreover, $\xi = \xi _L \xi _R$ for two positive elements

$$\begin{aligned} \xi _L\in A^L, \quad \xi _R = S(\xi _L) = S^{-1}(\xi _L) \in A^R. \end{aligned}$$

(34)

Dually, let us denote $\hat{\xi } = \hat{\xi }_L \hat{\xi }_R \in A^*$ their dual counterparts, then

$$\begin{aligned} x_{(1)} \, \hat{\xi }_L ( x_{(2)} ) = \xi _R^{-1} \, x, \quad x_{(1)} \, \hat{\xi }_R^{-1} ( x_{(2)} ) = x \, \xi _R^{-1}, \end{aligned}$$

(35)

for all $x\in A$. Finally, if A is a C*-Hopf algebra, then

$$\begin{aligned} \xi _L^2 = \xi _R^2 = \xi = \mathcal {D}^2\,\varepsilon (1) \, 1 = \omega (\Omega )^{-1} \, 1. \end{aligned}$$

(36)

Proof

Since $\Omega \in A$ is non-degenerate there exists $f\in A^*$ such that

$$\begin{aligned} f ( \Omega _{(1)} ) \, \Omega _{(2)} = 1. \end{aligned}$$

(61)

On the other hand, since $\omega \in A^*$ is non-degenerate,

$$\begin{aligned} \omega ( \xi x ) = (f \circ T)(x) \end{aligned}$$

(62)

for all $x\in A$, for some $\xi \in A$. Therefore,

$$\begin{aligned} \omega ( \xi T( \Omega _{(1)}) ) \, \Omega _{(2)} = ( f\circ T ) ( T(\Omega _{(1)}) ) \, \Omega _{(2)} = f ( \Omega _{(1)} ) \, \Omega _{(2)} = 1, \end{aligned}$$

(63)

where in the second equality we have used that T is involutive. Recall that $\omega \in A^*$ is a trace-like linear functional of $A^*$. It follows by Eq. 15 that

$$\begin{aligned} 1 = \omega ( \xi T(\Omega _{(1)}) ) \, \Omega _{(2)} = \omega ( T(\Omega _{(1)})\,\xi ) \, \Omega _{(2)} = (\omega \circ T)(\Omega _{(1)}) \, \xi \, \Omega _{(2)}, \end{aligned}$$

(64)

and hence $\xi \in A$ is invertible. Its inverse is then trivially given by the expression

$$\begin{aligned} \xi ^{-1} = \omega ( T(\Omega _{(1)}) ) \, \Omega _{(2)} = \omega ( \Omega _{(1)} ) \, \Omega _{(2)}. \end{aligned}$$

(65)

where the last equality follows from Eq. 60. Let us prove now Eq. 34. By virtue of Proposition B.3, it is easy to conclude from Eq. 30 that $\xi \in A$ is necessarily given by the expression

$$\begin{aligned} \xi = \mathcal {D}^4 \, \varepsilon (1)^2 \, g_L \, g_R. \end{aligned}$$

(66)

Consequently, a natural choice of positive elements $\xi _L\in A^L$ and $\xi _R\in A^R$ is

$$\begin{aligned} \xi _L := \mathcal {D}^2 \, \varepsilon (1) \, g_L \;\,\text { and }\;\, \xi _R := \mathcal {D}^2 \, \varepsilon (1) \, g_R = S(\xi _L). \end{aligned}$$

(67)

Since $g_L,g_R > 0$, $\xi$ is strictly positive, as we wanted to prove. We now prove that $T(\xi ) = \xi$. Note by the previous expressions that it turns out to be enough to check that $T(g_L) = g_R$ and $T(g_R) = g_L$. We refer to Eqs. 75 and 76 below for elementary proofs of these facts. In addition, note that Eq. 33 is straightforward by the eigenvalue identity in Eq. 16. See Scholium 2.7 and Lemma 4.13 from [5] for a proof of Eq. 35. Let us now move to the proof of Eq. 32. For simplicity, we prove the equivalent formula

$$\begin{aligned} \xi \, T(x) \, \xi ^{-1} = T(x^*)^* \end{aligned}$$

for all $x\in A$. To this end, we recall first that

$$\begin{aligned} \xi \, y \, \xi ^{-1} = g_L \, g_R \, y \, g_L^{-1}\, g_R^{-1} = \hat{g} ( y_{(1)} ) \, y_{(2)} \, \hat{g} ( y_{(3)} ) \end{aligned}$$

(68)

for all $y\in A$, see Proposition B.1. On the other hand,

$$\begin{aligned} \hat{g}^{-1} ( y ) = \hat{g} ( S^{-1}(y) ) = \hat{g}^* ( S^{-1}(y) ) = \overline{ \hat{g} ( S(S^{-1}(y))^* ) } = \overline{ \hat{g} ( y^* ) } \end{aligned}$$

(69)

for all $y\in A$. Thus,

for all $x\in A$, as we wanted to prove. Finally, if A is a C*-Hopf algebra, it is already known by Proposition B.4 that $g_L = g_R = \mathcal {D}^{-1} 1$. This, together with the definition of $\xi$ in Lemma 3.5 and the fact that $\varepsilon (1) = 1$, leads to the expressions

$$\xi _L = \xi _R = \mathcal {D} 1 \quad \text { and }\quad \xi = \mathcal {D}^2 1, $$

as we wanted to prove. $\square$

Proof of Lemma 5.2

In this appendix, we present a proof of Lemma 5.2. To begin, we establish the following auxiliary result, which is connected to the trace-preserving condition of the gluing map.

Lemma D.1

Let A be a C*-Hopf algebra. Then,

$$\begin{aligned} x_{(1)}\otimes \omega ( x_{(2)} ) x_{(3)} = \omega ( x ) 1\otimes 1 \end{aligned}$$

for all $x\in A$.

Proof

Fix $x\in A$, since $\Omega \in A$ is non-degenerate, there exists $f\in A^*$ such that

$$\begin{aligned} x = \Omega _{(1)} \, f(\Omega _{(2)}) \end{aligned}$$

(70)

As an immediate consequence,

$$\begin{aligned} \omega (x) = \omega ( \Omega _{(1)} ) \, f ( \Omega _{(2)} ) = \frac{1}{\mathcal {D}^{2}} \, f(1), \end{aligned}$$

(71)

where the last equality follows from Lemma 3.5. Then, it is easy to conclude that

as we wanted to prove. $\square$

Lemma 5.2

For all C*-Hopf algebras A and all positive non-zero $x\in A$, there exists a quantum channel $\mathcal {F}_x:\textrm{End}(V\otimes V)\rightarrow \textrm{End}(V\otimes V)$ such that

$$\begin{aligned} (\textrm{Id}^{\otimes m-1}\otimes \mathcal {F}_x \otimes \textrm{Id}^{\otimes n-1}) (\varrho _m(\Omega )\otimes \varrho _n(\Omega )) = \varrho _{m+n}(x) \end{aligned}$$

(49)

for all $m,n \ge 1$.

Proof

Fix any positive non-zero $x\in A$. We recall first the definition of the gluing map previously given in Sect. 5. For the sake of simplicity, let

$$\mathcal {F}_x:= \mathcal {T}\circ \mathcal {F}$$

for the linear map $\mathcal {F}:\textrm{End}(V\otimes V)\rightarrow \textrm{End}(V)$ defined by the expression

$$\begin{aligned} \mathcal {F}(X\otimes Y) := \frac{1}{\omega ( x )} \, \textrm{Tr}((\Phi \circ S)(x_{(1)}) X) \, b(\omega )\, \Phi (x_{(2)}) \, \textrm{Tr}((\Phi \circ S)(x_{(3)}) Y) \end{aligned}$$

(72)

for all $X,Y\in \textrm{End}(V)$. Then, it is enough to check that

$$\begin{aligned} (\textrm{Id}\otimes \mathcal {F} \otimes \textrm{Id})(\varrho _2(\Omega )\otimes \varrho _2(\Omega )) = \varrho _3(\Omega ). \end{aligned}$$

To this end, let us recall that, in the case of C*-Hopf algebras,

$$\begin{aligned} \omega ( \Omega _{(1)} ) \, \Omega _{(2)} = \frac{1}{\mathcal {D}^{2}} \, 1 = \omega ( \Omega ) \,1, \end{aligned}$$

(73)

where the first equality is stated in Lemma 3.5 and the second equality follows by applying the counit in the first one, since $\varepsilon (1) = 1$. Then,

$$\begin{aligned} (\textrm{Id} \otimes {}&{} \mathcal {F} \otimes \textrm{Id})(\varrho _2(\Omega )\otimes \varrho _2(\Omega )) \\&= \frac{1}{\omega (x)}\frac{1}{\omega ( \Omega )^2} b(\omega )\,\Phi (\Omega _{(1)} ) \otimes \omega ( S(x_{(1)} ) \Omega _{(2)}) \, b(\omega )\,\Phi ( x_{(2)}) \\ {}&\hspace{3cm} \otimes \omega ( S(x_{(3)})\Omega _{(1')} ) \, b(\omega )\,\Phi (\Omega _{(2')}) \\ {}&= \frac{1}{\omega (x)}\frac{1}{\omega ( \Omega ) ^2} b(\omega )\,\Phi ( x_{(1)} \Omega _{(1)} ) \otimes \omega ( \Omega _{(2)} ) \, b(\omega )\,\Phi ( x_{(2)}) \\ {}&\hspace{3cm} \otimes \omega ( S(x_{(3)})\Omega _{(1')} ) \, b(\omega )\,\Phi ( \Omega _{(2')}) \\&= \frac{1}{\omega (x)}\, \frac{1}{\omega ( \Omega ) ^2} b(\omega )\,\Phi (x_{(1)} \Omega _{(1)} ) \otimes \omega ( \Omega _{(2)} ) \, b(\omega ) \, \Phi (x_{(2)}) \\ {}&\hspace{3cm} \otimes \omega ( \Omega _{(1')} )\, b(\omega )\,\Phi ( x_{(3)}\Omega _{(2')}) \\ {}&= \frac{1}{\omega (x)} b(\omega )\, \Phi ( x_{(1)} 1 )\otimes b(\omega )\,\Phi ( x_{(2)}) \otimes b(\omega )\,\Phi (x_{(3)}1 ) = \varrho _3(x). \end{aligned}$$

This calculation can be explained as follows. In the first place, we have replaced the trace with the canonical regular element $\omega \in A^*$ since is cocentral, the weight $b(\omega )$, which is central, defines a linear extension of $\omega$ to the representation space. In the second and third steps we have applied the pulling-through identity; see Eq. 15. Finally, we apply twice Eq. 73 to get rid of $\Omega$ and the coefficients $\omega ( \Omega )^{-1}$. As an aside, note that $\omega ( \Omega _{(1)} ) \, \Omega _{(2)} = \Omega _{(1)} \, \omega ( \Omega _{(2)} )$ since $\Omega$ is cocentral. Since $\mathcal {T}$ is a quantum channel it only remains to prove that $\mathcal {F}$ is also a quantum channel. On the one hand, that $\mathcal {F}$ is trace-preserving is a straightforward consequence of Lemma D.1:

for all $X,Y\in \textrm{End}(V)$. On the other hand, in order to prove that $\mathcal {F}$ is completely positive, let $x = y y^*$ for some $y\in A$. Then, we can rewrite it as follows

$$\begin{aligned} \mathcal {F}( X\otimes Y)&= \frac{1}{\omega (x)} \, \textrm{Tr}(\Phi (S((yy^*)_{(1)})) X) \\&\hspace{2cm} b(\omega )\,\Phi ( (y y^*)_{(2)}) \, \textrm{Tr}(\Phi (S(y y^*)_{(3)}) Y) \\ {}&= \frac{1}{\omega (x)} \, \textrm{Tr}(\Phi (S(y_{(1)} y_{(1')}^*)) X) \\&\hspace{2cm} b(\omega )\,\Phi ( y_{(2)} y_{(2')}^*) \, \textrm{Tr}(\Phi (S( y_{(3)} y_{(3'}^*)) Y) \\ {}&= \frac{1}{\omega (x)} \, \textrm{Tr}(\Phi (S(y_{(1')}^*) S(y_{(1)})) X) \\&\hspace{2cm} b(\omega )\,\Phi (y_{(2)} y_{(2')}^*) \, \textrm{Tr}(\Phi (S(y_{(3')}^*) S( y_{(3)} )) Y) \\ {}&= \frac{1}{\omega (x)} \, \textrm{Tr}(\Phi (S(y_{(1')})^*S(y_{(1)})) X) \\&\hspace{2cm} b(\omega )\,\Phi (y_{(2)} y_{(2')}^*) \, \textrm{Tr}(\Phi (S(y_{(3')})^* S( y_{(3)} )) Y) \\ {}&= \frac{1}{\omega (x)} \, \textrm{Tr}(\Phi (S(y_{(1)})) \, X \, \Phi (S(y_{(1')})^*)) \\&\hspace{2cm} b(\omega )\,\Phi (y_{(2)} y_{(2')}^*) \, \textrm{Tr}(\Phi ( S( y_{(3)} )) \, Y \, \Phi (S(y_{(3')})^*)) \\ {}&= \textrm{Tr}_{1,3} (Q (X\otimes \textrm{Id}\otimes Y) Q^\dagger ) \end{aligned}$$

where we have defined

$$\begin{aligned} Q := \frac{1}{\omega ( x)^{1/2}} (\Phi \circ S)(y_{(1)}) \otimes b(\omega )^{1/2} \, \Phi (y_{(2)}) \otimes (\Phi \circ S)(y_{(3)}). \end{aligned}$$

(74)

Therefore, $\mathcal {F}$ is completely positive. Indeed, in the first step we have applied that the comultiplication is multiplicative and the $*$-operation is a coalgebra homomorphism; see Definitions 2.1. In the second and third steps we have used that $S:A\rightarrow A$ is an algebra anti-homomorphism and the relation between the antipode and the $*$-operation; see Eq. 11. Note that, for C*-Hopf algebras, $S = S^{-1}$; see Proposition B.4. The fourth step is a simple consequence of the fact that $\Phi$ is a $*$-representation and the cyclic property of the trace. Finally, the middle term can be rewritten in the form

$$ b(\omega )\, \Phi (y_{(2)} y_{(2')}^*) = b(\omega ) \, \Phi ( y_{(2)}) \, (b(\omega ) \, \Phi (y_{(2')}))^\dagger $$

since $b(\omega )$ is positive and central and $\Phi$ is a $*$-representation. $\square$

Proofs of Remark 5.4 and Lemma 5.6

In this appendix we prove Remark 5.4 and Lemma 5.6. In order to provide an analogous construction of this gluing map to the one given in the C*-Hopf algebra case, we first derive an appropriate version of the usual pulling-through identity in Eq. 15 to the trivial sector.

Lemma E.1

Let A be a biconnected C*-weak Hopf algebra. Then,

$$\begin{aligned} x_L S(1_{(1)}) \otimes 1_{(2)} \otimes S(1_{(3)}) y_R = S(1_{(1)}) \otimes y_R 1_{(2)} x_L \otimes S(1_{(3)}) \end{aligned}$$

for all $x_L\in A^L$ and $y_R\in A^R$.

Proof

First, recall Equations 2.31a and 2.31b from [5]:

$$\begin{aligned} x_L S(1_{(1)}) \otimes 1_{(2)}&= S(1_{(1)}) \otimes 1_{(2)} x_L, \\ y_R 1_{(1)} \otimes S(1_{(2)})&= 1_{(1)} \otimes S(1_{(2)}) y_R. \end{aligned}$$

for all $x_L\in A^L$ and $y_R\in A^R$. This, together with Definitions 2.7, leads by taking coproducts accordingly to the following identities:

$$\begin{aligned}&x_L S(1_{(1)}) \otimes 1_{(2)} \otimes 1_{(3)} = S(1_{(1)}) \otimes 1_{(2)} x_L\otimes 1_{(3)}, \\&1_{(1)}\otimes y_R 1_{(2)}\otimes S(1_{(3)}) = 1_{(1)} \otimes 1_{(2)} \otimes S(1_{(3)}) y_R, \end{aligned}$$

respectively, for all $x_L\in A^L$ and $y_R\in A^R$. Finally, since $A^L$ and $A^R$ commute, we conclude the result by combining both identities. $\square$

In addition, we adapt slightly Lemma 3.5 to the trivial sector, which is a key property concerning complete positivity of the gluing map in Lemma 5.6. The following result solves this problem.

Lemma E.2

Let A be a biconnected C*-weak Hopf algebra. Then,

$$\begin{aligned} \xi _R S( x_L^* ) = S( x_L )^* \xi _R \;\,\text { and }\;\, S( y_R ) \xi _L = \xi _L S( y_R^* )^* \end{aligned}$$

for all $x_L\in A^L$ and $y_R\in A^R$.

Proof

In the first place, note that $T:A\rightarrow A$ coincides with S and $S^{-1}$ restricted to $A^L$ and $A^R$, respectively. Indeed, by virtue of Eq. 59, Proposition B.1 and Eq. 11,

$$\begin{aligned} T(x_L)&= S(x_L 1_{(1)}) \, \hat{g} ( 1_{(2)} ) = S(x_L), \end{aligned}$$

(75)

$$\begin{aligned} T(y_R)&= \hat{g} ( 1_{(1)} )\, S^{-1}(1_{(2)}y_R) = S^{-1}(y_R) = S(y_R^*)^*, \end{aligned}$$

(76)

for all $x_L\in A^L$ and $y_R\in A^R$. Then, recall Lemma 3.5 to conclude that

$$\begin{aligned} S(x_L^*) = T(x_L^*) = \xi _L^{-1}\xi _R^{-1} T(x_L)^* \xi _L\xi _R = \xi _L^{-1}\xi _R^{-1} S(x_L)^* \xi _L \xi _R = \xi _{R}^{-1}S(x_L)^* \xi _R, \end{aligned}$$

where in the last step we have used that $S(x_L)\in A^R$ and $A^L$ and $A^R$ commute. The remaining identity is proved similarly. $\square$

The following auxiliary results arise naturally in the course of the derivation of the properties of the gluing map.

Lemma E.3

Let A be a biconnected C*-weak Hopf algebra. Then,

$$\begin{aligned} \hat{h}(\Omega _{(1)}) \, \Omega _{(2)} = \frac{1}{\mathcal {D}^{2}\varepsilon (1)} 1. \end{aligned}$$

Proof

It is easy to check that

$$\begin{aligned} \mathcal {D}^2 \, \varepsilon (1) \, \hat{h}(\Omega _{(1)}) \, \Omega _{(2)} = \hat{h}(t_{(1)} ) \, t_{(2)} \, \hat{g}(t_{(3)}) = 1_{(1)} \, \hat{g}(1_{(2)} ) = 1, \end{aligned}$$

where the first step is a consequence of Proposition B.3, the second follows from the definition of dual left integral in Eq. 52 and the third equality is due to Proposition B.1. $\square$

Lemma E.4

Let A be a biconnected C*-weak Hopf algebra. Then,

$$\begin{aligned} 1_{(1)}\, \hat{h}(1_{(2)})\otimes 1_{(3)} = \frac{1}{\varepsilon (1)} \, 1\otimes 1. \end{aligned}$$

(77)

Proof

Equivalently, we will check that

$$\begin{aligned} (\phi \hat{h} \psi )(1) = \frac{1}{\varepsilon (1)} \, \phi (1) \, \psi (1) \end{aligned}$$

(78)

for all $\phi ,\psi \in A^*$. Recall that ${\hat{h}}\in A^*$ is a one-dimensional projector supported on the trivial sector [5, Lemma 4.8]. Hence,

$$\begin{aligned} (\phi \hat{h}\psi \hat{h})(\textrm{x}_{1}) = (\phi \hat{h})(\textrm{x}_1) \, (\psi \hat{h})(\textrm{x}_1) \;\,\text { and }\;\, (\phi \hat{h})(\textrm{x}_a) = \delta _{a 1} \end{aligned}$$

(79)

for all $\phi ,\psi \in A^*$ and all sectors $a=1,\ldots ,r$. In particular

$$\begin{aligned} (f\hat{h})(\textrm{x}_1) = (f\hat{h})(d_1\textrm{x}_1+\cdots +d_r\textrm{x}_r ) = \mathcal {D}^2 (f\hat{h})(\Omega ) = \frac{1}{\varepsilon (1)} \, f(1) \end{aligned}$$

(80)

for all $f\in A^*$. Thus, we conclude that:

$$\begin{aligned} \frac{1}{\varepsilon (1)} \, (\phi \hat{h}\psi )(1) = (\phi \hat{h} \psi \hat{h})(\textrm{x}_1) = ( \phi {\hat{h}} )(\textrm{x}_1) \, ( \psi {\hat{h}} )( \textrm{x}_1) = \frac{1}{ \varepsilon (1)^{2} }\, \phi (1) \, \psi (1) \end{aligned}$$

(81)

where the first equality follows from Eq. 80 using $f:= \phi \hat{h}\psi$, the second equality is simply Eq. 79 and the third equality follows from Eq. 80 considering $f:= \phi ,\psi$. $\square$

Lemma E.5

Let A be a biconnected C*-weak Hopf algebra. Then,

$$\begin{aligned} 1_{(1)} \otimes \omega (1_{(2)}) \, 1_{(3)} = \mathcal {D}^{2} \, \xi _R^{-1}\otimes \xi _L^{-1}. \end{aligned}$$

Proof

As a consequence of Definitions 2.7 and Lemma 3.5,

$$\begin{aligned} (\xi ^{-1})_{(1)} \otimes (\xi ^{-1})_{(2)} \otimes (\xi ^{-1})_{(3)} = \xi _L^{-1} 1_{(1)} \otimes 1_{(2)}\otimes \xi _R^{-1} 1_{(3)} \end{aligned}$$

(82)

Then, the statement follows from the following calculation:

as we wanted to prove. $\square$

Lemma E.6

Let A be a biconnected C*-weak Hopf algebra. Then,

$$\begin{aligned} \omega (1_{(1)}) \, 1_{(2)} \, \omega (1_{(3)}) = \mathcal {D}^2 \, \omega (1) \, \xi ^{-1}. \end{aligned}$$

(83)

Proof

First, let us compute the constant $\omega (1)$ in a more operative way. The following calculation is an immediate consequence of Proposition B.3 and Eq. 67:

$$\begin{aligned} \omega (1) = \frac{1}{\mathcal {D}^2 \varepsilon (1)} \, \hat{h}(g_L^{-1} g_R^{-1}) = \frac{\mathcal {D}^4 \varepsilon (1)^2}{\mathcal {D}^2 \varepsilon (1)} \, \hat{h}(\xi _L^{-1}\xi _R^{-1}) = \mathcal {D}^2 \, \varepsilon (1) \, \hat{h}(\xi _L^{-1}\xi _R^{-1}). \end{aligned}$$

(84)

Now, by an analogous reasoning as in the previous proof:

as we wanted to prove. $\square$

Remark 5.4

There are no trace-preserving gluing maps for general biconnected C*-weak Hopf algebras such that Eq. 49 holds for all $x\in A$.

Proof

Suppose by contradiction that there exists a trace-preserving linear map $\mathcal {F}:\textrm{End}(V\otimes V)\rightarrow \textrm{End}(V\otimes V)$ that is a gluing map. In particular,

$$\begin{aligned} (\textrm{Id} \otimes \mathcal {F} \otimes \textrm{Id}) (\varrho _2(\Omega ) \otimes \varrho _2(\Omega )) = \varrho _4(\Omega ). \end{aligned}$$

On the one hand, after performing a partial trace on the second and third subsystems, the left-hand side would be trivially given by the product state

$$\begin{aligned} \textrm{Tr}_{2,3}(\varrho _2(\Omega )\otimes \varrho _2(\Omega ))&= \frac{1}{\omega (\Omega )^{2} } \, b(\omega ) \, \Phi (\Omega _{(1)}) \, \omega ( \Omega _{(2)} ) \otimes \omega (\Omega _{(1')} ) \, b(\omega )\, \Phi (\Omega _{(2')}) \\ {}&= \frac{1}{\omega (\Omega )^{2} } b(\omega ) \, \Phi ( \xi ^{-1})\otimes b(\omega ) \, \Phi ( \xi ^{-1}) \end{aligned}$$

by virtue of Lemma 3.5. However, the right-hand side would take the form

$$\begin{aligned} \textrm{Tr}_{2,3}(\varrho _4(\Omega ))&= \frac{1}{\omega (\Omega )^{2}} \, b(\omega ) \, \Phi ( \Omega _{(1)}) \otimes \omega (\Omega _{(2)}) \, \omega (\Omega _{(3)} ) \, b(\omega ) \, \Phi (\Omega _{(4)}) \\ {}&= \frac{1}{\omega (\Omega )^{2}} \, b(\omega )\, \Phi ( \Omega _{(1)}) \otimes \omega (\Omega _{(2)}) \, b(\omega )\, \Phi ( \Omega _{(3)}) \\ {}&= \frac{1}{\omega (\Omega )^{2}}\, b(\omega )\, \Phi ( \Omega _{(2)}) \otimes \omega ( \Omega _{(3)}) \, b(\omega )\, \Phi ( \Omega _{(1)}) \\ {}&= \frac{1}{\omega (\Omega )^{2}} \, b(\omega )\, \Phi (\xi _R^{-1}1_{(2)})\otimes b(\omega )\, \Phi ( \xi _L^{-1}1_{(1)}), \end{aligned}$$

which is not a product state. This contradicts the previous equation. $\square$

Lemma 5.6

For all biconnected C*-weak Hopf algebras, there exists a quantum channel $\mathcal {F}_1:\textrm{End}(V\otimes V)\rightarrow \textrm{End}(V\otimes V)$ such that

$$\begin{aligned} (\textrm{Id}^{\otimes m-1}\otimes \mathcal {F}_1 \otimes \textrm{Id}^{\otimes n-1}) (\varrho _m(1)\otimes \varrho _n(1)) = \varrho _{m+n}(1) \end{aligned}$$

(50)

for all $m,n\ge 1$.

Proof

Let

$$\mathcal {F}_1:= \mathcal {T}\circ \mathcal {F},$$

where $\mathcal {T}$ stands for the local coarse-graining quantum channel and $\mathcal {F}$ is given by

$$\begin{aligned} \mathcal {F}(X\otimes Y) := \frac{1}{\mathcal {D}^2} \, \textrm{Tr}(\Phi (S(1_{(1)})\xi _L) X)\, b(\omega ) \, \Phi (1_{(2)} )\, \textrm{Tr}(\Phi (\xi _R S(1_{(3)})) Y) \end{aligned}$$

for all $X,Y\in \textrm{End}(V)$. Assume $m = n = 2$ for simplicity and let us check that

$$\begin{aligned} (\textrm{Id}\otimes \mathcal {F}\otimes \textrm{Id})(\varrho _2(1)\otimes \varrho _2(1)) = \varrho _3(1). \end{aligned}$$

To this end, it turns out to be enough to prove that

$$\begin{aligned} \mathcal {F}(b(\omega )\,\Phi (x_L )\otimes b(\omega ) \, \Phi ( x_R)) = \omega (1) \, b(\omega ) \, \Phi (x_L x_R) \end{aligned}$$

(85)

for all $x_L\in A^L$ and $x_R\in A^R$. Indeed, in that case,

$$\begin{aligned}&(\textrm{Id}\otimes \mathcal {F}\otimes \textrm{Id})(\varrho _2(1) \otimes \varrho _2(1) ) \\&\hspace{1cm} = \frac{1}{\omega (1)^2} \, b(\omega ) \Phi ( 1_{(1)}) \otimes \mathcal {F}(b(\omega ) \, \Phi ( 1_{(2)})\otimes b(\omega )\, \Phi ( 1_{(1')})) \otimes b(\omega )\, \Phi ( 1_{(2')}) \\&\hspace{1cm}= \frac{1}{\omega (1)}\, b(\omega ) \, \Phi ( 1_{(1)}) \otimes b(\omega ) \, \Phi ( 1_{(2)} 1_{(1')}) \otimes b(\omega ) \, \Phi ( 1_{(2')}) \\&\hspace{1cm}= \frac{1}{\omega ( 1 )} \, b(\omega ) \, \Phi (1_{(1)}) \otimes b(\omega ) \, \Phi (1_{(2)}) \otimes b(\omega ) \, \Phi ( 1_{(3)}) = \varrho _3(1). \end{aligned}$$

by the weak comultiplicativity of the counit and the fact that $1_{(1)}\otimes 1_{(2)} \in A^R\otimes A^L$ [5]. Thus, let us move to the proof of Eq. 85:

Additionally, $\mathcal {F}$ is trace-preserving as an immediate consequence of Lemma E.5:

Finally, in order to check that $\mathcal {F}$ is a completely positive linear map, let us first consider the following two calculations:

for all $x_R,y_R\in A^R$ and, analogously,

$$\begin{aligned} \textrm{Tr}(\Phi (\xi _R) \, (\Phi \circ S)(x_L y_L^*)) \, Y) = \textrm{Tr}(\Phi (\xi _R^{1/2} \, S(x_L)) \, Y \, \Phi ( \xi _R^{1/2} \, S(y_L))^\dagger ) \end{aligned}$$

for all $x_L, y_L\in A^L$. Now, recall that $1_{(1)}\otimes 1_{(2)}\otimes 1_{(3)}\in A^R\otimes A\otimes A^L$; see [5]. This allows us to rewrite $\mathcal {F}$ in the following form:

where the last step follows from the previous calculations, and we have defined

$$\begin{aligned} Q:= \frac{1}{\mathcal {D}} \, \Phi (\xi _L^{1/2}\,S(1_{(1)}^*) ) \otimes b(\omega )^{1/2}\,\Phi ( 1_{(2)}) \otimes \Phi (\xi _R^{1/2}\,S(1_{(3)})). \end{aligned}$$

(86)

This concludes the proof. $\square$