Bananas: multi-edge graphs and their Feynman integrals

Abstract

We consider multi-edge or banana graphs $b_n$ on n internal edges $e_i$ with different masses $m_i$. We focus on the cut banana graphs $\Im (\Phi _R(b_n))$ from which the full result $\Phi _R(b_n)$ can be derived through dispersion. We give a recursive definition of $\Im (\Phi _R(b_n))$ through iterated integrals. We discuss the structure of this iterated integral in detail. A discussion of accompanying differential equations, of monodromy and of a basis of master integrals is included.

1 Introduction

We define a banana graph $b_n$ by two vertices $v_1,v_2$ connected by n edges forming a multi-edge.¹ Furthermore, $v_1,v_2$ are both $n+1$ valent vertices so that $b_n$ has an external edge at each vertex.

Fig. 1

Banana graphs $b_n$ on $|b_n|=(n-1)$ loops. We indicate momenta at internal edges $e_1,\ldots e_n$ labelling from top to bottom. We assign mass square $m_i^2$ to edge $e_i$. A positive infinitesimal imaginary part is understood in each propagator. Both vertices have an external edge with incoming momenta $k_n$ and $-k_n$. Note that edges $e_1, \ldots ,e_j$, $n>j\ge 2$ constitute a banana graph $b_j$ with external momentum $k_{j}$ flowing through. It is a $(j-1)$-loop subgraph of $b_n$. In particular, we have a sequence $b_2\subset b_3\subset \cdots \subset b_n$ of graphs which gives rise to an iterated integral

1.1 General considerations

We study associated banana integrals $\Phi _R^D(b_n)$. The case $n=3$ has been intensively studied and initiated a detailed analysis of elliptic integrals in Feynman amplitudes, see, for example, [1,2,3,4,5,6,7,8,9,10,11]. Evaluation at masses $m_i^2\in \{0,1\}\ni k_n^2$ was recognized to provide a rich arena for an analysis of periods in Feynman diagrams [12] including the appearance of elliptic trilogarithms at sixth root of unity in the evaluation of $b_4$ [8].

Let us pause and put the problem into context.

1.1.1 Recursion and splitting in phase-space integrals

The imaginary part $\Im \left( \Phi _R^D(b_n)\right)$ of $\Phi _R^D(b_n)$ has been a subject of interest for almost seventy years at least [13,14,15]. This imaginary part has the interpretation of a phase space integral. Our attempt below to express it recursively by an iterated integral can be traced back to this early work. In fact, computing $\Im \left( \Phi _R^D(b_n)\right)$ by identifying an imaginary part $\Im \left( \Phi _R^D(b_{n-1})\right)$ as a subintegral amounts to a split in the phase-space integral and this recurses over n.

1.1.2 Banana integrals and monodromy

In the more recent literature, the graphs $b_n$ were studied in an attempt to interpret the monodromies of the associated functions depending on momenta and masses $\Phi _R^D(b_n)(s,s_0,\{m_i^2\})$ as a generalization of the situation familiar from the study of polylogarithms. This role of elliptic functions was prominent already in the historical work cited in Sect. 1.1.1 and continued to give insights into the structure of phase space systematically [5, 9]. Recently, the aim shifted to explore it in the spirit of modern mathematics. This brought concepts developed in algebraic geometry—motives, Hodge theory, co-actions, symbols and such—to the forefront [7, 8, 11, 16,17,18,19]. For us, the focus is less on elliptic integrals and elliptic polylogarithms prominent in recent work. Rather, we focus on the recursive structure of $\Im \left( \Phi _R^D(b_n)\right)$ as it has a lot to offer still for mathematical analysis.

1.2 Iterated integral structure for $b_n$

Our task is to find iterated integral representations for $\Im \left( \Phi _R^D(b_n)\right)$ which give insight into their structure for all n. We will use $\Im \left( \Phi _R^D(b_2)\right)$ as a seed for the iteration. $\Im \left( \Phi _R^D(b_3)\right)$ which has $\Im \left( \Phi _R^D(b_2)\right)$ as a subintegral then gives a complete elliptic integral as expected, see Sect. 2.3. Already, the computation of $b_4$ indicates more subtle functions to appear as Sect. 2.5 and Eq. (2.11) demonstrate. Nevertheless, it turns out that such functions are very nicely structured as we explore in Sect. 2.6.

We want to understand the function $\Phi _R^D(b_n)$ obtained from applying renormalized Feynman rules $\Phi _R^D$ in D dimensions

$$\begin{aligned} \Phi _R^D(b_n)=S_R^\Phi \star \Phi ^D(b_n)(s,s_0), \end{aligned}$$

to the graph $b_n$.

We will study in particular the imaginary part $\Im \left( \Phi _R^D(b_n)\right)$ having in mind that $\Phi _R^D(b_n)$ can be obtained from $\Im \left( \Phi _R^D(b_n)\right)$ by a dispersion integral.

We will mostly work with a kinematic renormalization scheme in which tadpole integrals evaluate to zero. This is particularly well suited for the use of dispersion. Indeed, $\Im \left( \Phi _R^D(b_n)\right)$ is free of short-distance singularities as the n constraints putting n internal propagators on-shell fix all non-compact integrations.

This reduces renormalization of $b_n$ to a mere use of sufficiently subtracted dispersion integrals. Correspondingly, in kinematic renormalization we can work in a Hopf algebra $H_R=H/I_{\textrm{tad}}$ of renormalization which divides by the ideal $I_\textrm{tad}$ spanned by tadpole integrals rendering the graphs $b_n$ primitive:

$$\begin{aligned} \Delta _{H_R}(b_n)=b_n\otimes \mathbb {I}+\mathbb {I}\otimes b_n. \end{aligned}$$

Therefore,

$$\begin{aligned} S_R^{\Phi ^D}\star \Phi ^D(b_n)=\Phi ^D(b_n)(s)- T ^{(j)}\Phi ^D(b_n)(s,s_0). \end{aligned}$$

$\Phi ^D$ are the unrenormalized Feynman rules in dimensional regularization and $T ^{(j)}$ is a suitable Taylor operator.

Nevertheless, there is no necessity to regulate Feynman integrals in our approach as we can subtract on the level of integrands. Indeed, $T ^{(j)}$ can be chosen to subtract in the integrand. We implement it in Eq. (1.1) using the dispersion integral. Our conventions for Feynman rules are in “App. A”.

Our interest lies in a compact formula for

$$\begin{aligned} \Im \left( \Phi _R^D(b_n)\right) \left( s,\{m_i^2\}\right) =\int _{\mathbb {M}_n}I_{\textrm{cut}}(b_n), \end{aligned}$$

with $I_{\textrm{cut}}(b_n)$ given in Eq. (A.1). We will succeed by giving it as an iterated integral in Eq. (2.14) which is part of Thm. (2.2).

Results for $\Phi _R^D(b_n)(s,s_0,\{m_i^2\})$ then follow by (subtracted at $s_0$) dispersion which implements $T ^{(\frac{D}{2}-1)(n-1)}$:

$$\begin{aligned} \Phi _R^D(b_n)\left( s,s_0,\{m_i^2\}\right) =\frac{(s-s_0)^{(\frac{D}{2}-1)(n-1)}}{\pi }\int _{\left( \sum _{j=1}^n m_j\right) ^2}^\infty \frac{\int _{\mathbb {M}_n}I_{\textrm{cut}}(b_n)(x)}{(x-s)(x-s_0)^{(\frac{D}{2}-1)(n-1)}}\textrm{d}x. \end{aligned}$$

(1.1)

Note that in the Taylor expansion of $\Phi _R^D(b_n)(s,s_0,\{m_i^2\})$ around $s=s_0$, the first $(\frac{D}{2}-1)(n-1)$ coefficients vanish. These are our kinematic renormalization conditions.

For example, $\Phi _R^4(b_2)(s_0,s_0)=0$. On the other hand, $\Phi _R^2(b_2)(s,s_0)=\Phi _R^2(b_2)(s)$ as it does not need subtraction at $s_0$ as it is ultraviolet convergent. So, $s_0$ disappears from its definition and the dispersion integral is unsubtracted as $(\frac{D}{2}-1)(n-1)=0$ and for $D=6$, $\Phi _R^6(b_2)(s_0,s_0)=0 =\partial _s\Phi _R^6(b_2)(s,s_0)_{|s=s_0}$.

1.3 Normal and pseudo-thresholds for $b_n$

To understand possible choices for $s_0$, define a set $\textbf{thresh}$ of $2^{n-1}$ real numbers by

$$\begin{aligned} \textbf{thresh}=\left\{ (\pm m_1\pm \cdots \pm m_n)^2 \right\} , \end{aligned}$$

and set

$$\begin{aligned} s_{\textbf{min}}:=\min \{x\in \textbf{thresh}\}. \end{aligned}$$

Note that the maximum is achieved by $s_{\textbf{normal}}:=\left( \sum _{j=1}^n m_j\right) ^2$. Our requirement for $s_0$ is

$$\begin{aligned} s_0\lneq s_{\textbf{min}}. \end{aligned}$$

(1.2)

This ensures that the renormalization at $s_0$ does not produce contributions to the imaginary part of the renormalized $\Phi _R^D(b_n)(s,s_0)$ as $\Im (\Phi ^D(b_n)(s_0))=0$.

We call $s_{\textbf{normal}}$ normal threshold and the $2^{-1}-1$ other elements of $\textbf{thresh}$ pseudo-thresholds.

Also we call $m_{\textbf{normal}}^n:=\sum _{j=1}^n m_j$ the normal mass of $b_n$ and any of the other $2^{n-1}-1$ numbers $|\pm m_1\cdots \pm m_n|$ a pseudo-mass of $b_n$. For any ordering o of the edges of $b_n$, we get a flag $b_2\subset \cdots b_{n-1}\subset b_n$ such that

$$\begin{aligned} m_{\textbf{normal}}^{j+1}=m_{\textbf{normal}}^j+m_{j+1},\,j\le n-1. \end{aligned}$$

On the other hand, for any chosen fixed pseudo-mass there exists at least one ordering o of edges of $b_n$ for which the pseudo-mass is $m_1-m_2\pm \cdots$.

Remark 1.1

By the Coleman–Norton theorem [20] (or by an analysis of the second Symanzik polynomial $\varphi (b_n)$, see Eq. (D.1) in “App. D”), the physical threshold of $b_n$ is when the energy $\sqrt{s}$ of the incoming momenta $k_n=(k_{n;0},\vec {0})^T$ equals the normal mass

$$\begin{aligned} \sqrt{s}=m_{\textbf{normal}}^n. \end{aligned}$$

The imaginary part $\Im \left( \Phi _R^D(b_n)\right)$ is then given by the monodromy associated with that threshold and is supported at $s\ge m_{\textbf{normal}}^n$.

In this paper, we are mainly interested in the principal sheet monodromy of $b_n$ and hence in the monodromy at $\sqrt{s}=m_{\textbf{normal}}^n$ which gives $\Im (\Phi _R^D(b_n))$. Pseudo-masses are needed to understand monodromy from pseudo-thresholds off the principal sheet.

They can always be expressed as iterated integrals starting possibly from a pseudo-threshold of $\Phi _R^D(b_2)$. Such non-principal sheet monodromies need to be studied to understand the mixed Hodge theory of $\Phi _R^D(b_n)$ as a multi-valued function in future work. See [21] for some preliminary considerations.

In preparation to such future work, we note that iterated integral representations can also be obtained for pseudo-thresholds in quite the same manner as in Eq. (2.14) by changing signs of masses (not mass squares) in Eq. (2.13) as given in Eq. (D.2) and correspondingly in the boundaries of the dispersion integral. This dispersion will then reconstruct variations on non-principal sheets. We collect these integral representations in “App. D” (Fig. ). |

2 Banana integrals $\Im \left( \Phi _R^D(b_n)\right)$

2.1 Computing $b_2$

We start with the two-edge banana $b_2$, a bubble on two edges with two different internal masses $m_1,m_2$, indicated by two different colours in Fig. .

Fig. 2

The bubble $b_2$. It gives rise to a function $\Phi _R^D(b_2)(k_2^2,m_1^2,m_2^2)$. We compute its imaginary part $\Im \left( \Phi _R^D(b_2)(k_2^2,m_1^2,m_2^2)\right)$ below. It starts an induction leading to the desired iterated integral for $\Im (\Phi _R^D(b_n))$. The edges $e_1,e_2$ are given in red or blue. Shrinking one of them gives a tadpole integral $\Phi _R^D(t_1)(m_1^2)$ (red) or $\Phi _R^D(t_2)(m_2^2)$ (blue) (colour figure online)

The incoming external momenta at the two vertices of $b_2$ are $k_2,-k_2$ which can be regarded as momenta assigned to leaves at the two three-valent vertices.

We discuss the computation of $b_2$ in detail as it gives a start of an induction which leads to the computation of $b_n$. The underlying recursion goes long way back as discussed in Se. (1.1.1) above, see [15] in particular. More precisely, it allows to express $\Im (\Phi _R^D)(b_n)$ as an iterated integral with the integral $\Im (\Phi _R^D)(b_2)$ as the start so that $b_n$ is obtained as a $(n-2)$-fold iterated one-dimensional integral.

For the Feynman integral $\Phi _R^D(b_2)$, we implement a kinematic renormalization scheme by subtraction at $s_0\equiv \mu ^2\lneq (m_1-m_2)^2$ in accordance with Eq. (1.2). This implies that the subtracted terms do not have an imginary part, as $\mu ^2$ is below the pseudo-threshold $(m_1-m_2)^2$. For example, for $D=4$

$$\begin{aligned} \Phi _R^4(b_2)(s,s_0,m_1^2,m_2^2)=\int d^Dk_1 \left( \frac{1}{\underbrace{k_1^2-m_1^2}_{Q_1}}\frac{1}{\underbrace{(k_2-k_1)^2-m_2^2}_{Q_2} }- \{k_2^2\rightarrow \mu ^2\}\right) . \end{aligned}$$

We have $s:=k_2^2$. For $D=6,8,\ldots$, subtractions of further Taylor coefficients at $s=\mu ^2$ are needed.

As the D-vector $k_2$ is assumed timelike (as $s>0$), we can work in a coordinate system where $k_2=(k_{2;0},\vec {0})^T$ and get

$$\begin{aligned} \Phi _R^D(b_2)= & {} \omega _{\frac{D}{2}} \int _{-\infty }^\infty dk_{1;0}\int _0^\infty \sqrt{t_1}^{D-3}dt_1 \\{} & {} \times \left( \frac{1}{k_{1;0}^2-t_1-m_1^2}\frac{1}{(k_{2;0}-k_{1;0})^2-t-m_2^2}- \{s\rightarrow s_0\}\right) . \end{aligned}$$

We define the Källen function, actually a homogeneous polynomial,

$$\begin{aligned} \lambda (a,b,c):=a^2+b^2+c^2-2(ab+bc+ca), \end{aligned}$$

and find by explicit integration, for example, for $D=4$,

$$\begin{aligned}{} & {} \Phi _R^4(b_2)(s,s_0;m_1^2,m_2^2) \\{} & {} \quad = \left( \underbrace{ \frac{\sqrt{\lambda (s,m_1^2,m_2^2)}}{2s}\ln \frac{m_1^2+m_2^2-s -\sqrt{\lambda (s,m_1^2,m_2^2)}}{m_1^2+m_2^2-s+\sqrt{\lambda (s,m_1^2,m_2^2)}} - \frac{m_1^2-m_2^2}{2s}\ln \frac{m_1^2}{m_2^2}}_{W_2^4(s)} -\underbrace{\{s\rightarrow s_0\}}_{W_2^4(s_0)}\right) . \end{aligned}$$

The principal sheet of the above logarithm is real for $s\le (m_1+m_2)^2$ and free of singularities at $s=0$ and $s=(m_1-m_2)^2$. It has a branch cut for $s\ge (m_1+m_2)^2$. See, for example, [5, 21] for a discussion of its analytic structure and behaviour off the principal sheet.

The threshold divisor defined by the intersection $L_1\cap L_2$ where the zero loci

$$\begin{aligned} L_i:\,Q_i=0, \end{aligned}$$

of the two quadrics meet is at $s=(m_1+m_2)^2$. This is an elementary example of the application of Picard–Lefschetz theory [22].

Off the principal sheet, we have a pole at $s=0$ and a further branch cut for $s\le (m_1-m_2)^2$.

It is particularly interesting to compute the variation—the imaginary part—of $\Phi _R(b_2)$ using Cutkosky’s theorem [22]. For all D,

$$\begin{aligned} \Im (\Phi _R^{D}(b_2))= & {} \omega _{\frac{ D}{2}}\int _{0}^\infty \sqrt{t_1}^{D-3}dt \int _{-\infty }^\infty dk_{1;0}\delta _+\left( k_{1;0}^2-t_1-m_1^2\right) \\{} & {} \delta _ +\left( (k_{2;0}-k_{1;0})^2-t_1-m_2^2\right) . \end{aligned}$$

We have

$$\begin{aligned} \delta _+\left( (k_{2;0}-k_{1;0})^2-t_1-m_2^2\right) =\Theta (k_{2;0}-k_{1;0})\delta \left( (k_{2;0}-k_{1;0})^2-t_1-m_2^2\right) , \end{aligned}$$

and

$$\begin{aligned}{} & {} \delta \left( (k_{2;0}-k_{1;0})^2-t_1-m_2^2\right) \\ {}{} & {} \qquad = \frac{1}{2|k_{2;0}-k_{1;0}|}_{|k_{1;0}=k_{2;0} +\sqrt{t_1+m_2^2}}\times \delta \left( k_{1;0}-k_{2;0}-\sqrt{t_1+m_2^2}\right) \\{} & {} \qquad \quad + \frac{1}{2|k_{2;0}-k_{1;0}|}_{|k_{1;0}=k_{2;0}-\sqrt{t_1+m_2^2}}\times \delta \left( k_{1;0}-k_{2;0}+\sqrt{t_1+m_2^2}\right) . \end{aligned}$$

In summary,

$$\begin{aligned}{} & {} \delta _+\left( (k_{2;0}-k_{1;0})^2-t_1-m_2^2\right) \\ {}{} & {} \quad = \Theta (k_{2;0}-k_{1;0})\delta \left( (k_{2;0}-k_{1;0})^2-t_1-m_2^2\right) \\{} & {} \quad = \frac{1}{2|k_{2;0}-k_{1;0}|}_{|k_{1;0}=k_{2;0}-\sqrt{t_1+m_2^2}}\delta \left( k_{1;0}-k_{2;0}+\sqrt{t_1+m_2^2}\right) , \end{aligned}$$

and therefore,

$$\begin{aligned} \Im (\Phi _R(b_2))=\omega _{\frac{D}{2}}\int _0^\infty \sqrt{t_1}^{D-3}dt_1 \delta \left( s-2\sqrt{s}\sqrt{t_1+m_2^2}+m_2^2-m_1^2\right) \frac{1}{\sqrt{t_1+m_2^2}}. \end{aligned}$$

We have from the remaining $\delta$-function,

$$\begin{aligned} \delta \left( s-2\sqrt{s}\sqrt{t_1+m_2^2}+m_2^2-m_1^2\right) =\frac{\sqrt{t_1+m_2^2}}{\sqrt{s}} \delta \left( t_1-\frac{\lambda (s,m_1^2,m_2^2)}{4s}\right) , \end{aligned}$$

and hence,

$$\begin{aligned} 0\le t_1 =\frac{\lambda (s,m_1^2,m_2^2)}{4s}, \end{aligned}$$

whenever the Källen function $\lambda (s,m_1^2,m_2^2)$ is positive, so for $s>(m_1+m_2)^2$ (normal threshold, on the principal sheet) or for $0<s<(m_1-m_2)^2$ (pseudo-threshold, off the principal sheet).

The integral then gives

$$\begin{aligned} \Im \left( \Phi _R^D(b_2)\right) \left( s,m_1^2,m_2^2\right) =\overbrace{\omega _{\frac{D}{2}}\left( \frac{\left( \sqrt{\lambda (s,m_1^2,m_2^2)}\right) ^{D-3}}{(2s)^{\frac{D}{2}-1}}\right) }^{=:V_{2}^{D}(s;m_1^2,m_2^2)}\times \Theta \left( s-(m_1+m_2)^2\right) , \end{aligned}$$

with $\omega _{\frac{D}{2}}$ given in Eq. (A.2). We emphasize that $V_{2}^D$ has a pole at $s=0$ with residue $|m_1^2-m_2^2|/2$ and note $\lambda (s,m_1^2,m_2^2)=(s-(m_1+m_2)^2)(s-(m_1-m_2)^2)$.

We regain $\Phi _R^D(b_2)$ from $\Im (\Phi _R^D(b_2))$ by a subtracted dispersion integral, for example, for $D=4$:

$$\begin{aligned} \Phi _R^4(b_2)(s,s_0)=\frac{s-s_0}{\pi }\int _0^\infty \frac{\Im \left( \Phi _R^4(b_2)\right) (x)}{(x-s)(x-s_0)}\textrm{d}x. \end{aligned}$$

Here, the renormalization condition implemented in the once-subtracted dispersion imposes $\Phi _R^D(b_2)(s_0,s_0)=0$ for $D=4$.

Finally, we note that for on-shell edges $(k_2-k_1)^2=m_2^2$ so

$$\begin{aligned} k_2\cdot k_1= & {} \frac{k_2^2-m_2^2+m_1^2}{2},\\ k_1^2= & {} m_1^2. \end{aligned}$$

2.2 Computing $b_3$

We now consider the three-edge banana $b_3$ on three different masses.

We start by using the fact that we can disassemble $b_3$ in three different ways into a $b_2$ subgraph, with a remaining edge providing the co-graph. Using Fubini, the three equivalent ways to write it in accordance with the flag structure $b_2\subset b_3$ are:

$$\begin{aligned} \Im (\Phi _R^D(b_3))= & {} \int d^Dk_2 \Im \Big (\Phi _R^D(b_2)\Big )\Big (k_2^2,m_1^2,m_2^2\Big ) \delta _+\Big ((k_3-k_2)^2-m_3^2\Big ), \end{aligned}$$

(2.1)

$$\begin{aligned} \Im \Big (\Phi _R^D(b_3)\Big )= & {} \int d^Dk_2 \Im \Big (\Phi _R^D(b_2)\Big )\Big (k_2^2,m_2^2,m_3^2\Big ) \delta _+\Big ((k_3-k_2)^2-m_1^2\Big ), \end{aligned}$$

(2.2)

$$\begin{aligned} \Im \Big (\Phi _R^D(b_3)\Big )= & {} \int d^Dk_2 \Im \Big (\Phi _R^D(b_2)\Big )\Big (k_2^2,m_3^2,m_1^2\Big ) \delta _+\Big ((k_3-k_2)^2-m_2^2\Big ). \end{aligned}$$

(2.3)

In any of these cases for $\Im (\Phi _R^D(b_3))$, we integrate over the common support of the distributions

$$\begin{aligned} \Im \Big (\Phi _R^D(b_2)\Big )\Big (k_2^2,m_i^2,m_j^2\Big )\sim \Theta \Big (k_2^2-(m_i+m_j)^2\Big )\,\,{\text {and}}\,\,\delta _+\Big ((k_3-k_2)^2-m_k^2\Big ), \end{aligned}$$

generalizing the situation for $\Im (\Phi _R^D(b_2))$ where we integrated over the common support of

$$\begin{aligned} \delta _+\big (k_1^2-m_1^2\big )\,\,{\text {and}}\,\,\delta _+\Big ((k_2-k_1)^2-m_2^2\Big ). \end{aligned}$$

The integral Eqs. (2.1, 2.2, 2.3) are well defined and on the principal sheet they are equal and give the variation (and hence imaginary part) $\Im (\Phi _R^D(b_3))$ of $\Phi _R^D(b_3)$.

$\Phi _R^D(b_3)$ itself can be obtained from it by a sufficiently subtracted dispersion integral which reads for $D=4$

$$\begin{aligned} \Phi _R^4(b_3)(s,s_0)=\frac{(s-s_0)^2}{\pi }\int _0^\infty \frac{\Im (\Phi _R^4(b_3)(x))}{(x-s)(x-s_0)^2}\textrm{d}x. \end{aligned}$$

For general D, $\Phi _R^D(b_3)$ is well-defined no matter which of the two edges we choose as the subgraph, and Cutkosky’s theorem defines a unique function $V_{3}^D(s)$,

$$\begin{aligned} \Im (\Phi _R^D(b_3)(s))=:V_{3}^D(s)\Theta (s-(m_1+m_2+m_3)^2). \end{aligned}$$

Remark 2.1

Below when we discuss master integrals for $b_n$, we find that by breaking symmetry through a derivative $\partial _{m_i^2}$, we obtain four master integrals for $b_3$. $\Phi _R^D(b_3)$ itself, and by applying $\partial _{m_i^2}$ to any of Eqs. (2.1, 2.2, 2.3). $|$

Let us compute $V_3^D$ first. We consider edges $e_1,e_2$ as a $b_2$ subgraph with an external momentum $k_2$ flowing through.

We let $k_3$ be the external momentum of $\Im (\Phi _R^D(b_3))$, $0<k_3^2=:s$. For the $k_2$-integration, we put ourselves in the restframe $k_3=(k_{3;0},\vec {0})^T$.

Consider then

$$\begin{aligned} \Im \left( \Phi _R^D(b_3)\right) (s)= & {} \int d^Dk_2 \Theta (k_2^2-(m_1+m_2)^2) \delta _+((k_3-k_2)^2)-m_3^2)\\{} & {} V_2^D(k_2^2,m_1^2,m_2^2). \end{aligned}$$

The $\delta _+$-distribution demands that $k_{3;0}-k_{2;0}>0$, and therefore, we get

$$\begin{aligned} \Im \left( \Phi _R^D(b_3)\right) (s)= & {} \omega _{\frac{D}{2}}\int _{-\infty }^{k_{3;0}} dk_{2;0}\int _0^\infty dt_2\sqrt{t_2}^{D-3}\Theta (k_{2;0}^2-t_2-(m_1+m_2)^2)\\{} & {} \quad \times V_2^D(k_{2;0}^2-t,m_1^2,m_2^2) \delta ((k_{3;0}-k_{2;0})^2-t_2-m_3^2). \end{aligned}$$

As a function of $k_{2;0}$, the argument of the $\delta$-distribution has two zeros:

$$\begin{aligned} k_{2;0}=k_{3;0}\pm \sqrt{t_2+m_3^2}. \end{aligned}$$

As $k_{3;0}-k_{2;0}>0$, it follows $k_{2;0}=k_{3;0}-\sqrt{t_2+m_3^2}$. Therefore, $k_{2;0}^2-t_2=k_{3;0}^2+m_3^2-2k_{3;0}\sqrt{t_2+m_3^2}$.

For our desired integral, we get

$$\begin{aligned} \Im \left( \Phi _R^D(b_3)\right) (s)= & {} \omega _{\frac{D}{2}}\int _0^\infty dt_2 \sqrt{t_2}^{D-3} \Theta \left( k_{3;0}^2+m_3^2-2k_{3;0}\sqrt{t_2+m_3^2}-(m_1+m_2)^2\right) \\{} & {} \quad \times \frac{ V_2^D\left( k_{3;0}^2+m_3^2-2k_{3;0}\sqrt{t_2+m_3^2},m_1^2,m_2^2\right) }{\sqrt{t_2+m_3^2}}. \end{aligned}$$

The $\Theta$-distribution requires

$$\begin{aligned} k_{3;0}^2+m_3^2-(m_1+m_2)^2\ge 2k_{3;0}\sqrt{t_2+m_3^2}. \end{aligned}$$

Solving for $t_2$, we get

$$\begin{aligned} 0\le t_2\le \frac{\lambda \left( s,m_3^2,(m_1+m_2)^2\right) }{4s}. \end{aligned}$$

As $t_2\ge 0$, we must have for the physical threshold $s>(m_3+m_1+m_2)^2$ which is indeed completely symmetric under permutations of 1, 2, 3, in accordance with our expectations for $\Im (\Phi _R^D(b_3)(s))$. We then have

$$\begin{aligned} \Im \left( \Phi _R^D(b_3)(s)\right)= & {} \Theta \left( s-(m_1+m_2+m_3)^2\right) \omega _{\frac{D}{2}}\int _0^{\frac{\lambda \left( s,m_3^2,(m_1+m_2)^2\right) }{4s}}\\{} & {} \quad \times \frac{V_2^D\left( s+m_3^2-2\sqrt{s}\sqrt{t_2+m_3^2},m_1^2,m_2^2\right) }{\sqrt{t_2+m_3^2}} \sqrt{t_2}^{D-3}\textrm{d}t_2. \end{aligned}$$

There is also a pseudo-threshold off the principal sheet at $s<(m_3-m_1-m_2)^2$, see Sect. 2.

Note that the integrand vanishes at the upper boundary $\frac{\lambda (s,m_k^2,(m_i+m_j)^2)}{4s}$ as

$$\begin{aligned}{} & {} \lambda \left( s+m_3^2-2\sqrt{s}\sqrt{t_2+m_3^2},m_1^2,m_2^2\right) _{\mid t_2=\frac{\lambda \left( s,m_3^2,(m_1+m_2)^2\right) }{4s}}\\{} & {} \quad =\lambda \left( (m_1+m_2)^2,m_1^2,m_2^2\right) =0. \end{aligned}$$

Let us now transform variables.

$$\begin{aligned} y_2:= & {} \sqrt{t_2+m_{3}^2},\\ t_2= & {} y_2^2-m_{3}^2,\\ dt_2= & {} 2y_2 dy_2,\\ \int _0^{\frac{\lambda }{4s}}\rightarrow & {} \int _{m_{3}}^{\frac{s+m_{3}^2-(m_1+m_2)^2}{2\sqrt{s}}}. \end{aligned}$$

We get

$$\begin{aligned} \Im \left( \Phi _R^D(b_3)(s)\right)= & {} \Theta \left( s-(m_1+m_2+m_3)^2\right) \nonumber \\{} & {} \quad \times \underbrace{\omega _{\frac{D}{2}}\int _{m_3}^{\frac{s+m_{3}^2-(m_1+m_2)^2}{2\sqrt{s}}} V_2^D\left( \overbrace{s+m_3^2-2\sqrt{s}y_2}^{s_3^1(y_2,m_3^2)},m_1^2,m_2^2\right) \sqrt{y_2-m_3^2}^{D-3} dy_2}_{V_3^{D}(s,m_1^2,m_2^2,m_3^2)}. \nonumber \\ \end{aligned}$$

(2.4)

Had we chosen $e_2,e_3$ or $e_3,e_1$ instead of $e_1,e_2$ for $b_2$, we would find in accordance with Eqs. (2.1, 2.2, 2.3)

$$\begin{aligned} \Im \left( \Phi _R^D(b_3)(s)\right)= & {} \Theta \left( s-(m_1+m_2+m_3)^2\right) \nonumber \\{} & {} \quad \times \underbrace{\omega _{\frac{D}{2}}\int _{m_1}^{\frac{s+m_{1}^2-(m_2+m_3)^2}{2\sqrt{s}}} V_2^D\left( \overbrace{s+m_1^2-2\sqrt{s}y_2}^{s_3^1(y_2,m_1^2)},m_2^2,m_3^2\right) \sqrt{y_2-m_1^2}^{D-3} dy_2}_{V_3^{D}(s,m_1^2,m_2^2,m_3^2)}, \nonumber \\ \end{aligned}$$

(2.5)

or

$$\begin{aligned} \Im \left( \Phi _R^D(b_3)(s)\right)= & {} \Theta \left( s-(m_1+m_2+m_3)^2\right) \nonumber \\{} & {} \quad \times \underbrace{\omega _{\frac{D}{2}}\int _{m_2}^{\frac{s+m_{2}^2-(m_3+m_1)^2}{2\sqrt{s}}} V_2^D\left( \overbrace{s+m_2^2-2\sqrt{s}y_2}^{s_3^1(y_2,m_2^2)},m_3^2,m_1^2\right) \sqrt{y_2-m_2^2}^{D-3} dy_2}_{V_3^{D}(s,m_1^2,m_2^2,m_3^2)}. \nonumber \\ \end{aligned}$$

(2.6)

with three different $s_3^1(y_2)=s_3^1(y_2,m_i^2)$.

We omit this distinction in the future as we will always choose a fixed order of edges and call the edges in the innermost bubble $b_2$ edges $e_1,e_2$.

Finally, we note

$$\begin{aligned} k_{2,0}= & {} k_{3,0}-y_2,\\ k_2^2= & {} k_{3,0}^2-2k_{3,0}y_2+m_3^2,\\ |\vec {k_2}|= & {} \sqrt{y_2^2-m_3^2}. \end{aligned}$$

Written in invariants this is

$$\begin{aligned} k_3\cdot k_{2}= & {} \sqrt{s}(\sqrt{s}-y_2),\\ k_2^2= & {} s-2\sqrt{s}y_2+m_3^2,\\ |\vec {k_2}|= & {} \sqrt{y_2^2-m_3^2}. \end{aligned}$$

2.3 $b_3$ and elliptic integrals

Note that for $D=2$ (the case $D=4$ can be treated similarly as in [5]) and using Eq. (2.4),

$$\begin{aligned} V_3^2(s)= \omega _{1}\int _{m_3}^{\frac{s+m_{3}^2-(m_2+m_1)^2}{2\sqrt{s}}} \frac{1}{\sqrt{U(y_2)}} \textrm{d}y_2, \end{aligned}$$

with

$$\begin{aligned} U(y_2)= & {} \lambda \left( {s+m_3^2-2\sqrt{s}y_2},m_2^2,m_1^2\right) (y_2^2-m_3^2) \\= & {} s(y_2-m_3)(y_2+m_3)(y_2-y_+)(y_2-y_-), \end{aligned}$$

a quartic polynomial so that $V_3^2$ defines an elliptic integral following, for example, [5]. Here,

$$\begin{aligned} y_\pm =\frac{(s+m_3^2-m_1^2-m_2^2)\pm 2\sqrt{m_1^2m_2^2}}{2\sqrt{s}}. \end{aligned}$$

So, indeed

$$\begin{aligned} V_3^2(s)=\frac{2\omega _1}{(y_++m_3)(y_--m_3)}K\left( \frac{(y_-+m_3)(y_+-m_3)}{(y_--m_3)(y_++m_3)}\right) , \end{aligned}$$

(2.7)

with K the complete elliptic integral of the first kind. Finally,

$$\begin{aligned} \Phi _R^2(b_3)(s)=\frac{1}{\pi }\int _{(m_1+m_2+m_3)^2}^\infty \frac{V_3^2(x)}{(x-s)} \textrm{d}x, \end{aligned}$$

(2.8)

gives the full result for $b_3$ in terms of elliptic dilogarithms in all its glory [6, 7, 16] for $D=2$. For arbitrary D, we get

$$\begin{aligned} \Phi _R^D(b_3)(s,s_0)=\frac{(s-s_0)^{D-2}}{\pi }\int _{(m_1+m_2+m_3)^2}^\infty \frac{V_3^D(x)}{(x-s)(x-s_0)^{D-2}} \textrm{d}x. \end{aligned}$$

(2.9)

To compare our result Eq. (2.7) with the result in [5] say, note that we can write

$$\begin{aligned} U(y_2)=\frac{1}{4}\lambda \left( s,s_3^1,m_3^2\right) \lambda \left( s_3^1,m_1^2,m_2^2\right) , \end{aligned}$$

as

$$\begin{aligned} \lambda \left( s,s_3^1,m_3^2\right) =\left( s_3^1-\left( \sqrt{s}-m_3\right) ^2\right) \left( s_3^1-\left( \sqrt{s}+m_3\right) ^2\right) =4s\left( y_2^2-m_3^2\right) , \end{aligned}$$

with $s_3^1=s-2\sqrt{s}y_2+m_3^2$, and use $b=s_3^1$, $db=-2\sqrt{s}dy_2$ to compare.

2.4 Computing $b_4$

Above we have expressed $V_3^D$ as an integral involving $V_2^D$. We can iterate this procedure.

Let us compute $V_4^D$ next repeating the computation which led to Eq. (2.4). We consider edges $e_1,e_2,e_3$ as a $b_3$ subgraph with an external momentum $k_3$ flowing through.

We let $k_4$ be the external momentum of $\Im (\Phi _R^D(b_4))$, $0<k_4^2=s$. We put ourselves in the restframe $k_4=(k_{4;0},\vec {0})^T$ for the $k_3$-integration.

Consider then

$$\begin{aligned}{} & {} \Im \left( \Phi _R^D(b_4)\right) (s)=\int d^Dk_3 \Theta \left( k_3^2-(m_1+m_2+m_3)^2\right) \\{} & {} \delta _+\left( (k_4-k_3)^2\right) -m_4^2)V_3^D\left( k_3^2,m_1^2,m_2^2,m_3^2\right) . \end{aligned}$$

The $\delta _+$ distribution demands that $k_{4;0}-k_{3;0}>0$, and therefore, we get

$$\begin{aligned} \Im \left( \Phi _R^D(b_4)\right) (s)= & {} \omega _{\frac{D}{2}}\int _{-\infty }^{k_{4;0}} \textrm{d}k_{3;0}\int _0^\infty \textrm{d}t_3\sqrt{t_3}^{D-3}\Theta \left( k_{3;0}^2-t_3-(m_1+m_2+m_3)^2\right) \\{} & {} \quad V_3^D\left( k_{3;0}^2-t_3,m_1^2,m_2^2,m_3^2\right) \delta \left( (k_{4;0}-k_{3;0})^2-t_3-m_4^2\right) . \end{aligned}$$

As a function of $k_{3;0}$, the argument of the $\delta$-distribution has two zeros: $k_{3;0}=k_{4;0}\pm \sqrt{t_3+m_4^2}$.

As $k_{4;0}-k_{3;0}>0$, it follows $k_{3;0}=k_{4;0}-\sqrt{t_3+m_4^2}$. Therefore, $k_{3;0}^2-t_3=k_{4;0}^2+m_4^2-2k_{4;0}\sqrt{t_3+m_4^2}$.

For our desired integral, we get

$$\begin{aligned} \Im \left( \Phi _R^D(b_4)\right) (s)= & {} \omega _{\frac{D}{2}}\int _0^\infty dt_ 3 \sqrt{t_3}^{D-3} \Theta \left( k_{4;0}^2+m_4^2-2k_{4;0}\sqrt{t_3+m_4^2}-(m_1+m_2+m_3)^2\right) \\{} & {} \quad \times \frac{ V_3^D\left( k_{4;0}^2+m_4^2-2k_{4;0}\sqrt{t_3+m_4^2},m_1^2,m_2^2,m_3^2\right) }{\sqrt{t_3+m_4^2}}. \end{aligned}$$

The $\Theta$-distribution requires

$$\begin{aligned} k_{4;0}^2+m_4^2-(m_1+m_2+m_3)^2\ge 2k_{4;0}\sqrt{t_3+m_4^2}. \end{aligned}$$

Solving for $t_3$, we get

$$\begin{aligned} 0\le t_3\le \frac{\lambda (s,m_4^2,(m_1+m_2+m_3)^2)}{4s}. \end{aligned}$$

As $t_3\ge 0$, we must have for the physical threshold $s>(m_4+m_3+m_1+m_2)^2$. We then have

$$\begin{aligned} \Im \left( \Phi _R^D(b_4)(s)\right)= & {} \Theta \left( s-(m_1+m_2+m_3+m_4)^2\right) \omega _{\frac{D}{2}}\int _0^{\frac{\lambda (s,m_4^2,(m_1+m_2+m_3)^2)}{4s}}\\{} & {} \times \frac{V_3^D(s+m_4^2-2\sqrt{s}\sqrt{t_3+m_4^2},m_1^2,m_2^2,m_3^2)}{\sqrt{t_3+m_4^2}} \sqrt{t_3}^{D-3}dt_3. \end{aligned}$$

Let us now transform variables again.

$$\begin{aligned} y_3:= & {} \sqrt{t_3+m_{4}^2},\\ t_3= & {} y_3^2-m_{4}^2,\\ \textrm{d}t_3= & {} 2y_3 dy_3,\\ \int _0^{\frac{\lambda }{4s}}\rightarrow & {} \int _{m_{4}}^{\frac{s+m_{4}^2-(m_1+m_2+m_3)^2}{2\sqrt{s}}}. \end{aligned}$$

We get

$$\begin{aligned} \Im (\Phi _R^D(b_4)(s))= & {} \Theta \left( s-(m_1+m_2+m_3+m_4)^2\right) \\{} & {} \times \underbrace{\omega _{\frac{D}{2}}\int _{m_4}^{\frac{s+m_{4}^2-(m_1+m_2+m_3)^2}{2\sqrt{s}}} V_3^D(\overbrace{s+m_4^2-2\sqrt{s}y_3}^{s_4^1(y_3)},m_1^2,m_2^2,m_3^2)\sqrt{y_3-m_4^2}^{D-3} dy_3}_{V_4^{D}(s,m_1^2,m_2^2,m_3^2,m_4^2)}. \end{aligned}$$

We have thus expressed $V_4^D$ as an integral involving $V_3^D$. As we can express $V_3^D$ by $V_2^D$, we get the iterated integral,

$$\begin{aligned} V_4^D\left( s,m_1^2,m_2^2,m_3^2,m_4^2\right)= & {} \omega _{\frac{D}{2}}^2\int _{m_4}^{\frac{s+m_{4}^2-(m_1+m_2+m_3)^2}{2\sqrt{s}}} \Biggl (\int _{m_3}^{\frac{s_4^1(y_3)+m_{3}^2-(m_1+m_2)^2}{2\sqrt{s_4^1(y_3)}}} \nonumber \\{} & {} \quad \times V_2^D\left( s_4^2(y_2,y_3),m_1^2,m_2^2\right) \sqrt{y_2-m_3^2}^{D-3}dy_2\Biggr )\nonumber \\{} & {} \quad \times \sqrt{y_3-m_4^2}^{D-3}dy_3. \end{aligned}$$

(2.10)

We abbreviated

$$\begin{aligned}{} & {} s_4^2(y_2,y_3):=s_4^1(y_3)-2\sqrt{s_4^1(y_3)}y_2+m_3^2 \\{} & {} \quad =s_4^0-2\sqrt{s_4^0}y_3+m_4^2-2\sqrt{s_4^0-2\sqrt{s_4^0}y_3+m_4^2}y_2+m_3^2, \end{aligned}$$

$s_4^0:=s$.

2.5 Beyond elliptic integrals for $b_4$

Note that $V_4^2$ cannot be read as a complete elliptic integral of any kind. It is a double integral over the inverse square root of an algebraic function. $V_3^2$ was in contrast a single integral over the inverse square root of a mere quartic polynomial. Concretely, the relevant integrand is

$$\begin{aligned} \frac{1}{\sqrt{(y_3^2-m_4^2)^2(y_2^2-m_3^2)v_4(y_2,y_3)}}. \end{aligned}$$

In fact, the innermost $y_2$ integral can still be expressed as a complete elliptic integral of the first kind as in Eq. (2.7), as $v_4$ is a quadratic polynomial in $y_2$ so that

$$\begin{aligned} (y_2^2-m_3^2)v_4=(y_2-m_3)(y_2+m_3)(y_2-y_{2,+})(y_2-y_{2,-}) \end{aligned}$$

is a quartic in $y_2$ albeit with coefficients $y_{2,\pm }$ which are algebraic in $y_3$. We have

$$\begin{aligned} y_{2,\pm }(y_3)=\frac{(m_1^2+m_2^2-m_3^2-s_4^1(y_3)) \pm 2\sqrt{m_1^2m_2^2}}{2 \sqrt{s_4^1(y_3)}}. \end{aligned}$$

We get the more than elliptic integral over an elliptic integral of the first kind,

$$\begin{aligned} V_4^2(s)= & {} \omega _1\int _{m_4}^{\frac{s+m_{4}^2-(m_1+m_2+m_3)^2}{2\sqrt{s}}}\frac{2\omega _1}{(y_{2,+}(y_3)+m_4)(y_{2,-}(y_3)-m_4)}\nonumber \\{} & {} \quad \times K\left( \frac{(y_{2,-}(y_3)+m_4)(y_{2,+}(y_3)-m_4)}{(y_{2,-}(y_3)-m_4)(y_{2,+}(y_3)+m_4)}\right) \frac{1}{\sqrt{y_3^2-m_4^2}}dy_3. \end{aligned}$$

(2.11)

2.6 Computing $b_n$ by iteration

Iterating the computation which led to Eq. (2.10), we get

Theorem 2.2

Let $b_n$ be the banana graph on n edges and two leaves (at two distinct vertices) with masses $m_i$ and momenta $k_n,-k_n$ incoming at the two vertices in D dimensions.

• (i) it has an imaginary part determined by a normal threshold as

  $$\begin{aligned} \Im \left( \Phi _R^D(b_n)\right) (s)=\Theta \left( s-\left( \sum _{j=1}^n m_j\right) ^2\right) V_n^D(s,\{m_i^2\}), \end{aligned}$$

  and with a recursion ($n\ge 3$)

  $$\begin{aligned} V_n^D(s;\{m_i^2\})= & {} \omega _{\frac{D}{2}}\int _{m_n}^{\frac{s+m_n^2-(\sum _{j=1}^{n-1}m_j)^2}{2\sqrt{s_n^0}}}V_{n-1}^D(s_n^0-2\sqrt{s_n^0}y_{n-1}+m_n^2,m_1^2,\ldots ,m_{n-1}^2)\\{} & {} \quad \times \sqrt{y_{n-1}^2-m_n^2}^{D-3}dy_{n-1}. \end{aligned}$$

Remark (i) This imaginary part is the variation in s of $\Phi _R^D(b_n)(s)$ in the principal sheet. Variations on other sheets are collected in “App. D”. See [21] for an introduction to a discussion of the role of such pseudo-thresholds.|

Theorem

• (ii) Define for all $n\ge 2$, $0\le j\le n-2$,

  $$\begin{aligned} s_n^0:=s, \end{aligned}$$

and for $n-2\ge j\ge 1$, $s_n^j=s_n^j(y_{n-j},\ldots ,y_{n-1};m_n,\ldots ,m_{n-j+1})$,

$$\begin{aligned} s_n^j =s_n^{j-1}-2\sqrt{s_n^{j-1}}y_{n-j}+m^2_{n-j+1}. \end{aligned}$$

(2.12)

Define

$$\begin{aligned} \textrm{up}_n^j:=\frac{s_n^j+m_{n-j}^2-\left( \sum _{i=1}^{n-j-1}m_i\right) ^2}{2\sqrt{s_n^{j}}}, \end{aligned}$$

(2.13)

then $V_n^D$ is given by the following iterated integral:

$$\begin{aligned} V_n^D(s,m_1^2,\ldots ,m_n^2):= & {} \omega _{\frac{D}{2}}^{n-2}\int _{m_n}^{\textrm{up}_n^0}\Biggl (\int _{m_{n-1}}^{\textrm{up}_n^1(y_{n-1})}\Biggl ( \int _{m_{n-2}}^{\textrm{up}_n^2(y_{n-1},y_{n-2})}\nonumber \\{} & {} \cdots \Biggl (\int _{m_3}^{\textrm{up}_n^{n-3}(y_3,\ldots ,y_{n-1})} V_2^D(s_n^{n-2}(y_2,\ldots ,y_{n-1}),m_1^2,m_2^2)\nonumber \\{} & {} \quad \times \sqrt{y_2^2-m_{3}^2}^{D-3}dy_2 \Biggr )\cdots \sqrt{y_{n-2}^2-m_{n-1}^2}^{D-3} dy_{n-2}\Biggr ) \nonumber \\{} & {} \quad \times \sqrt{y_{n-1}^2-m_{n}^2}^{D-3} dy_{n-1}. \end{aligned}$$

(2.14)

Here, $V_2^D(a,b,c)=\frac{\lambda (a,b,c)^{\frac{D-3}{2}}}{a^{\frac{D}{2}-1}},$ so that

$$\begin{aligned} V_2^D\left( s_n^{n-2}(y_2,\ldots ,y_{n-1}),m_1^2,m_2^2\right) =\omega _{\frac{D}{2}}\frac{\lambda \Bigl (s_n^{n-2}(y_2,\ldots ,y_{n-1}),m_1^2,m_2^2\Bigr )^{\frac{D-3}{2}}}{\Bigl (s_n^{n-2}(y_2,\ldots ,y_{n-1})\Bigr )^{\frac{D}{2}-1}}. \end{aligned}$$

Remark (ii) We solve the recursion in terms of an iteration of one-dimensional integrals. $V_2^D(b_2)$ serves as the seed, $V_2^D=\omega _{\frac{D}{2}}\lambda (s_n^{n-2},m_1^2,m_2^2)/s^{\frac{D}{2}-1}$) and $s_n^{n-2}=s_n^{n-2}(y_{n-1},\ldots ,y_2;m_3^2,\ldots ,m_n^2)$ depends on integration variables $y_j$ and on mass squares $m_{j+1}^2$, $j=2,\ldots ,n-1$. For $b_3$, we need a single integration; for $b_n$, we need to iterate $(n-2)$ integrals. Note that we could always do the innermost $y_2$-integral in terms of a complete elliptic integral (replacing $s_4^1\rightarrow s_n^{n-3}$ in Eq. (2.11), etc.) and use that as the seed.|

Theorem

(iii) We have the following identities:

$$\begin{aligned} V_n^D\left( \left( \sum _{j=1}^nm_j\right) ^2;\{m_i^2\}\right)= & {} 0, \end{aligned}$$

(2.15)

$$\begin{aligned} \textrm{up}_n^1(y_{n-1})_{|y_{n-1}=\textrm{up}_n^0}= & {} m_{n-1}, \end{aligned}$$

(2.16)

$$\begin{aligned} \textrm{up}_n^j(y_{n-j},\ldots , y_{n-1})_{|y_{n-j}=\textrm{up}_n^{j-1}}= & {} m_{n-j}, \end{aligned}$$

(2.17)

$$\begin{aligned} \textrm{up}_n^{n-3}(y_{3},\ldots , y_{n-1})_{|y_{3}=\textrm{up}_n^{n-4}}= & {} m_3, \end{aligned}$$

(2.18)

$$\begin{aligned} V_2^D(s_n^{n-2},m_1^2,m_2^2)_{|y_{2}=\textrm{up}_n^{n-3}}= & {} 0. \end{aligned}$$

(2.19)

Remark (iii) Equation (2.15) ensures that the dispersion integrand vanishes at the lower boundary $x=(m_1+\cdots +m_n)^2$ (the normal threshold) as it should. Following Eqs. (2.16–2.18) for any $y_j$-integration but the innermost integration the integrand vanishes at the lower and upper boundaries. By Eq. (2.19) for the innermost $y_{n-1}$ integral this holds for $D\gneq 2$.

At $D=2$, the result can be achieved by considering

$$\begin{aligned} \lim _{\eta \rightarrow 0}\int _{m_3+\eta }^{\textrm{up}_n^{n-3}-\eta }\cdots dy_{n-1}. \end{aligned}$$

In the limit $\sqrt{s}\rightarrow m_{\textbf{normal}}^n$ for which $\textrm{up}_n^{n-3}\rightarrow m_3$, one confirms the analysis in [5] that a finite value at threshold remains.

Summarizing for any D this amounts to compact integration as we have in any $y_j$ integration a resurrection of Stokes formula

$$\begin{aligned} \int _{m_{j+1}}^{\textrm{up}_n^{j+1}}\partial _{y_j}f(y_j)\cdots dy_{j}=0, \end{aligned}$$

(2.20)

for any rational function $f(y_j)$ inserted as a coefficient of $V_2^D$. The dots correspond to the other iterations of integrals in the $y_j$ variables. These are integration-by-parts identities.

This reflects the fact that the n $\delta$-functions in a cut banana $b_n$ constrain the $(n-1)$ integrations of $k_{j;0}$, $j=1,\ldots ,n-1$ and also the total integration over $r=\sum _{j=1}^{n-1}|\vec {k_j}|$. Here, we can set $|\vec {k_j}|=r u_j$, and the $u_j$ parameterize a $(n-1)$-simplex and hence a compactum. Angle integrals are over compact surfaces $S^{D-2}$. Only integrations over boundaries remain.|

Theorem

• (iv) We have

  $$\begin{aligned} \partial _{y_{k}} s_n^j=-2\sqrt{s_n^{n-k-1}}\partial _{m^2_{k+1}}s_n^j,\forall (n-j)\le k\le (n-1), \end{aligned}$$

  (2.21)

if all masses are different. The case of some equal masses is left to the reader.

Also,

$$\begin{aligned} \left( \prod _{j=0}^{i-1}\sqrt{s_n^j}\right) \partial _{s}s_n^i=2\prod _{j=0}^{i-1} \left( \sqrt{s_n^{j}}-y_{n-j-1}\right) . \end{aligned}$$

(2.22)

For derivatives with respect to masses, we have for $0\le r\lneq k-1$,

$$\begin{aligned} \partial _{m_{n-r}^2}s_n^k=\prod _{j=r+1}^{k-1}\frac{\sqrt{s_n^{j}}-y_{n-(j+1)}}{\sqrt{s_n^{j}}}, \end{aligned}$$

(2.23)

while $\partial _{m_{n-k+1}^2}s_n^k=1$. Furthermore, for $1\le i\le n-2-r$, $0\le r\le n-3$,

$$\begin{aligned} \partial _{y_{n-i}}s_{n}^{n-2-r}=-2\sqrt{s_n^{i-1}}\prod _{j=2+r}^{n-1-i}\frac{s_n^{n-j-1}-y_{j}}{s_n^{n-j-1}}. \end{aligned}$$

(2.24)

Remark (iv) These formulae allow to trade $\partial _{y_j}$ derivatives with $\partial _{m_{j+1}^2}$ derivatives and to treat $\partial _s$ derivatives. This is useful below when discussing differential equation, integration-by-parts and master integrals for $\Phi _R^D(b_n)$.|

Theorem

• (v) Dispersion. Let $|[n,\nu ]|-1$ (see Eq. (C.2)) be the degree of divergence of $\Phi _R^D(b_n)_\nu$. Then,

  $$\begin{aligned} \Phi _R^D(b_n)_\nu (s,s_0)=\frac{(s-s_0)^{|[n,\nu ]|}}{\pi }\int _{\left( \sum _{j=1}^n m_j\right) ^2}^\infty \frac{V_{[n,\nu ]}^D(x,\{m_i^2\})}{(x-s)(x-s_0)^{|[n,\nu ]|}}\textrm{d}x, \end{aligned}$$

is the renormalized banana graph with renormalization conditions

$$\begin{aligned} \Phi _R^D(b_n)_\nu ^{(j)}(s_0,s_0)=0,\, j\le |[n,\nu ]|-1, \end{aligned}$$

where $\Phi _R^D(b_n)_\nu ^{(j)}(s_0,s_0)$ is the jth derivative of $\Phi _R^D(b_n)_\nu (s,s_0)$ at $s=s_0$.

Remark (v) This gives $\Phi _R^D(b_n)_\nu$ from $V_{[n,\nu ]}^D$ in kinematic renormalization. See “App. C” for notation. For a result in dimensional integration with MS, use an unsubtracted dispersion

$$\begin{aligned} \Phi _{MS}^D(b_n)_\nu (s)=\frac{1}{\pi }\int _{\left( \sum _{j=1}^n m_j\right) ^2}^\infty \frac{V_{[n,\nu ]}^D(x,\{m_i^2\})}{(x-s)}\textrm{d}x, \end{aligned}$$

and then renormalize by Eq. (B.1) as tadpoles do not vanish in MS.|

Theorem

• (vi) Tensor integrals (see “App. C”). We have

  $$\begin{aligned} k_{j+1}\cdot k_j= & {} m_{j+1}^2-s_n^{n-j-1}-s_n^{n-j}\\ \nonumber= & {} -\sqrt{s_n^{n-j-1}}\left( \sqrt{s_n^{n-j-1}}-y_{n-j}\right) ,\,j\ge 2, \end{aligned}$$

  (2.25)
  $$\begin{aligned} k_2\cdot k_{1}= & {} \frac{k_2^2-m_2^2+m_1^2}{2}, \end{aligned}$$

  (2.26)
  $$\begin{aligned} k_j^2= & {} s_n^{n-j},\,\,{\text {in particular}} \,\,k_2^2=s_n^{n-2}, \end{aligned}$$

  (2.27)
  $$\begin{aligned} k_{j}\cdot k_l= & {} \frac{k_l\cdot k_{l+1}k_{l+1}\cdot k_{l+2}\cdots k_{j-1}\cdot k_j}{{k_{l+1}^2}\cdots {k_{j-1}^2}}\nonumber \\= & {} \frac{\sqrt{s_n^{n-j-1}}}{\sqrt{s_n^{n-l-1}}}\prod _{i=l+1}^j \left( \sqrt{s_n^{n-i}}-y_{i+1}\right) ,\,j-l\gneq 1,\, j>l, l\gneq 1,\qquad \quad \end{aligned}$$

  (2.28)
  $$\begin{aligned} k_{j}\cdot k_1= & {} \frac{k_l\cdot k_{l+1}k_{l+1}\cdot k_{l+2}\cdots k_{j-1}\cdot k_j}{{k_{l+1}^2}\cdots {k_{j-1}^2}}\nonumber \\= & {} \frac{\sqrt{s_n^{n-j-1}}}{\sqrt{s_n^{n-2}}}\frac{s_n^{n-2}-m_2^2+m_1^2}{\sqrt{s_n^{n-2}}}\prod _{i=2}^j \left( \sqrt{s_n^{n-i}}-y_{i+1}\right) ,\,j-1\gneq 1. \nonumber \\ \end{aligned}$$

  (2.29)

Furthermore, $V^D_{[n,\nu ]}$ is obtained by using Eqs. (2.25–2.29) to insert tensor powers as indicated by $\nu$ in the integrand of $V_2^D(s_n^{n-2},m_1^2,m_2^2)$ and apply derivatives with respect to mass squares accordingly.

Remark (vi) We first give in Fig.  with $k_j^2=s_n^{n-j}$ also the irreducible squares of internal momenta (there is no propagator $k_j^2-m_j^2$ in the denominator of $b_n$).

Fig. 3

We indicate momenta and masses at internal edges from top to bottom. We now also indicate momentum $s_n^j$ for edges $e_2,\ldots , e_n$. The mass-shell conditions encountered in the computation of $V_n^D$ enforce $k_j^2=s_n^{n-j}$ for $2\le j\le n$. Equation (2.25) simply expresses the fact that $-2k_j\cdot k_{j+1}=(k_{j+1}-k_j)^2-k_{j+1}^2-k_j^2$ with $(k_{j+1}-k_j)^2=m_{j+1}^2$

Equation (2.26) is needed as Eq. (2.25) cannot cover the case $j=1$, due to the fact that for the $b_2$ integration $d^Dk_1$ both edges are constrained by a $\delta _+$-function, while each other loop integral gains only one more constraint, giving us a $y_j$ variable.

Equations (2.25–2.29) allow to treat tensor integrals involving scalar products of irreducible numerators. Irreducible as there is no propagator $1/(k_j^2-m_{j+1}^2)$ in our momentum routing for $b_n$, see Fig. 3.

Equations (2.28, 2.29) for irreducible scalar products follow by integrating tensors in the numerator in the order of iterated integration. For example, for the case of $b_3$,

$$\begin{aligned} \int \int k_1\cdot k_3\frac{1}{\cdots }d^Dk_1d^Dk_2 =\int A(k_2^2)k_2\cdot k_3\frac{1}{\cdots } d^D k_2=C(k_3^2), \end{aligned}$$

and

$$\begin{aligned} \int \int \frac{k_1\cdot k_2 k_2\cdot k_3}{k_2^2}\frac{1}{\cdots }d^Dk_1d^Dk_2 =\int A(k_2^2)\frac{k_2^2 k_2\cdot k_3}{k_2^2}\frac{1}{\cdots } d^D k_2=C(k_3^2), \end{aligned}$$

using

$$\begin{aligned} \int \frac{{k_1}_\mu }{\cdots }d^Dk_1= A(k_2^2){k_2}_\mu , \end{aligned}$$

and dots $\cdots$ correspond to the obvious denominator terms. |

Proof

(i) and (ii) follow from the derivation of Eq. (2.10) upon setting $4\rightarrow n$, $3\rightarrow n-1$ in an obvious manner.

(iii) follows from inspection of Eq. (2.6): For example,

$$\begin{aligned} \textrm{up}_n^0=\frac{s+m_n^2-(m_1+\cdots +m_{n-1})^2}{2\sqrt{s}},\\ \textrm{up}_n^1(y_{n-1})=\frac{s_n^1+m_{n-1}^2-(m_1+\cdots +m_{n-2})^2}{2\sqrt{s_n^1}}, \end{aligned}$$

with

$$\begin{aligned} s_n^1(y_{n-1})=s-2\sqrt{s}y_{n-1}+m_n^2. \end{aligned}$$

Then,

$$\begin{aligned} \textrm{up}_n^1(\textrm{up}_n^0)=\frac{(m_1+\dots +m_{n-1})^2+m_{n-1}^2 -(m_1+\cdots +m_{n-2})^2}{2(m_1+\cdots +m_{n-1})}=m_{n-1}, \end{aligned}$$

and so on.

(iv) straight from the definition Eq. (2.12) of $s_n^j$. For example,

$$\begin{aligned} \partial _{m_n^2} s_n^3=\frac{\left( \sqrt{s_n^1}-y_{n-2}\right) \left( \sqrt{s_n^2}-y_{n-3}\right) }{\sqrt{s_n^1}\sqrt{s_n^2}} \end{aligned}$$

(v) This is the definition of dispersion in kinematic renormalization conditions.

(vi) For tensor integrals, we collect variables $k_{j;0}$ and $t_j$ in any step of the computation in terms of $y_j=\sqrt{t_j+m_{j+1}^2}$. $\square$

2.6.1 $s_n^j$: iterating square roots

Choose an order o of the edges which fixes

$$\begin{aligned} b_2\subset b_3\subset \cdots \subset b_{n-1}\subset b_n. \end{aligned}$$

Here, we label

$$\begin{aligned} E_{b_2}=: \{e_1,e_2\},\,E_{b_3}=\{e_1,e_2,e_3\},\ldots ,E_{b_n}=\{E_{b_{n-1}}\cup e_n\}. \end{aligned}$$

Then,

$$\begin{aligned} s_n^1(y_{n-1})= & {} s-2\sqrt{s}y_{n-1}+m_n^2,\\ s_n^2(y_{n-1},y_{n-2})= & {} s-2\sqrt{s}y_{n-1}+m_n^2-2\sqrt{s-2\sqrt{s}y_{n-1}+m_n^2}y_{n-2}+m_{n-1}^2,\\ s_n^3(y_{n-1},y_{n-2},y_{n-3})= & {} s-2\sqrt{s}y_{n-1}+m_n^2 - 2\sqrt{s-2\sqrt{s}y_{n-1}+m_n^2}y_{n-2}+m_{n-1}^2\\{} & {} \quad - 2 \sqrt{s-2\sqrt{s}y_{n-1}+m_n^2 - 2\sqrt{s-2\sqrt{s}y_{n-1}+m_n^2}y_{n-2}+m_{n-1}^2}\\ {}{} & {} \quad \times y_{n-3}+m_{n-2}^2,\\{} & {} \cdots ,\\ s_n^{n-2}(y_{n-1},\ldots ,y_3,y_2)= & {} s_n^{n-3}(y_{n-1},\ldots ,y_3)-2\sqrt{s_n^{n-3}(y_{n-1},\ldots ,y_3)}y_2+m_3^2. \end{aligned}$$

Remark 2.3

The iteration of square roots in particular for $s_n^{n-2}$ which is the crucial argument in $V_n^D(s_n^{n-2},m_1^2,m_2^2)$ is hopefully instructive for a future analysis of periods which emerge in the evaluation of that function [11]. This iteration of square roots points to the presence of a solvable Galois group with successive quotients ${{\mathbb {Z}}}/2{{\mathbb {Z}}}$ reflecting iterated double covers in momentum space. Thanks to Spencer Bloch for pointing this out. |

3 Differential equations and related considerations

This section collects some comments with respect to the results above with regard to:

• Dispersion. We want to discuss in some detail why raising powers of propagators is well defined in dispersion integrals even if a higher power of a propagator constitutes a product of distributions with coinciding support.

• Integration by parts (ibp) [23]. We do not aim at constructing algorithms which can compete with the established algorithms in the standard approach [24]. But at least we want to point out how ibp works in our iterated integral set-up.

• Differential equations. Here, we focus on systems of linear first-order differential equations for master integrals [25]. We also add a few comments on higher-order differential equation for assorted master integrals which emerge as Picard–Fuchs equations [6, 7, 10, 19].

• Master integrals. Master integrals are assumed independent by definition with regard to relations between them with coefficients which are rational functions of mass squares and kinematic invariants [26, 27]. We will remind ourselves that such a relation can still exist for their imaginary parts [5]. We trace this phenomenon back to the degree of subtraction needed in dispersion integrals to construct their real part from their imaginary parts. Furthermore, we will offer a geometric interpretation of the counting of master integrals for graphs $b_n$.

3.1 Dispersion and derivatives

As we want to obtain full results from imaginary parts by dispersion, we have to discuss the existence of dispersion integrals in some detail. There are subtleties when raising powers of propagators. It is sufficient to discuss the example of $b_2$.

With $\Phi _R^D(b_2)$ given, consider a derivative with respect to a mass square such that a propagator is raised to second power,

$$\begin{aligned} \Phi _R^D(b_2)_{2,1}:=\partial _{m_1^2}\Phi _R^D(b_2)(s,m_1^2,m_2^2). \end{aligned}$$

Similar to the imaginary part,

$$\begin{aligned} \Im \left( \Phi _R^D(b_2)_{2,1}\right) :=\partial _{m_1^2}\Im \left( \Phi _R^D(b_2)\right) (s,m_1^2,m_2^2). \end{aligned}$$

We have (for $D=4$ say)

$$\begin{aligned} \Im \left( \Phi _R^4(b_2)_{2,1}\right) =\frac{s-s_0}{\pi }\int _0^{\infty }\frac{ \partial _{m_1^2}\left( \Theta (x-(m_1+m_2)^2) V_2^4(x,m_1^2,m_2^2)\right) }{(x-s)(x-s_0)}\textrm{d}x. \end{aligned}$$

There is an issue here. It concerns the fact that to a propagator, itself a distribution,

$$\begin{aligned} Q(r,m)=\frac{1}{r^2-m^2}\,=\mathrm {P.V.}\frac{1}{r^2-m^2}+ i\pi \delta (r^2-m^2), \end{aligned}$$

(using Cauchy’s principal value and the $\delta$-distribution) we can associate a well-defined distribution by ‘cutting’ the propagator:

$$\begin{aligned} \frac{1}{Q(r,m)}\rightarrow \delta _+(Q(r,m))=\Theta (r_0)\delta (r^2-m^2). \end{aligned}$$

The expression

$$\begin{aligned} 2\frac{\delta _+(Q(r,m))}{Q}, \end{aligned}$$

obtained from cutting any one of the two factors in the squared propagator,

$$\begin{aligned} -\partial _{m^2}\frac{1}{Q(r,m)}=\frac{1}{Q^2(r,m)} \rightarrow 2\frac{\delta _+(Q(r,m))}{Q}, \end{aligned}$$

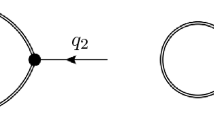
is ill defined as the numerator forces the denominator to vanish. Hence, higher powers of propagators are subtle when it comes to cuts on any one of their factors (Fig. ).

Fig. 4

The doubling of propagators indicated by a dot on the edge creates a problem

Remarkably, dispersion still works despite the fact that derivatives like $\partial _{m_1^2}$ do just that: generating such higher powers.

We have

$$\begin{aligned} \partial _{m_1^2}\Im (\Phi _R^D(b_2))= & {} \delta (s-(m_1+m_2)^2)V_2^D(s,m_1^2,m_2^2) \left( 1+\frac{m_2}{m_1}\right) \\{} & {} \quad + \Theta (s-(m_1+m_2)^2)\partial _{m_1^2}V_2^D(s,m_1^2,m_2^2), \end{aligned}$$

where

$$\begin{aligned} \left( 1+\frac{m_2}{m_1}\right) =\partial _{m_1^2} (m_1+m_2)^2. \end{aligned}$$

Using

$$\begin{aligned} V_2^D(s,m_1^2,m_2^2)=\frac{\sqrt{\lambda (s,m_1^2,m_2^2)}^{D-3}}{s^{\frac{D}{2}-1}}, \end{aligned}$$

the above is singular at $s=(m_1+m_2)^2$. Indeed, both terms on the rhs are ill defined, but their sum can be integrated in the dispersion integral

$$\begin{aligned} \partial _{m_1^2}\phi _R^D(b_2)= & {} \frac{(s-s_0)}{\pi }\int _0^\infty \left( \delta (x-(m_1+m_2)^2)V_2^D(x,m_1^2,m_2^2) \left( 1+\frac{m_2}{m_1}\right) \right. \\{} & {} \quad + \left. \Theta (x-(m_1+m_2)^2)\partial _{m_1^2}V_2^D(x,m_1^2,m_2^2)\right) \frac{1}{(x-s)(x-s_0)}\textrm{d}x, \end{aligned}$$

so that the singularity drops out for all D by Taylor expansion of

$$\begin{aligned} \partial _{m_1^2}\lambda (x,m_1^2,m_2^2)=\partial _{m_1^2}\left( (x-(m_1+m_2)^2)(x-(m_1-m_2)^2)\right) , \end{aligned}$$

near the point $x=(m_1+m_2)^2$.

We are not saying that it is meaningful to replace

$$\begin{aligned} \frac{1}{Q^2}\rightarrow \frac{\delta _+(Q)}{Q}, \end{aligned}$$

to come to dispersion relations.

Instead, we can exchange either:

• (i) Taking derivatives wrt masses on an imaginary part $\Im \left( \Phi _R^D(b_n)_\nu \right)$ first and then doing the dispersion integral, or,

• (ii) Doing the dispersion integral first and then taking derivatives.

3.2 Integration-by-parts

Integration-by-parts ($\textrm{ibp}$) is a standard method employed in high energy physics computations.

It starts from an incarnation of Stoke’s theorem in dimensional regularization

$$\begin{aligned} 0=\int d^Dk \frac{\partial }{\partial k_\mu } v_\mu F(\{k\cdot r\}), \end{aligned}$$

where F is a scalar function of loop momentum k and other momenta and $v_\mu$ is a linear combination of such momenta employing a suitable definition of D-dimensional integration for $D\in \mathbb {C}$.

We want to discuss ibp and Stokes theorem from the viewpoint of the $y_i$-integrations in our iterated integral.

We let $\textbf{Int}_{b_n}$ be the integrand in Eq. (2.14). It is made from three factors:

$$\begin{aligned} \textbf{Int}_{b_n}={\textbf{Y}}_n^{D-3}\times \mathbf {\Lambda }_n^{D-3}\times {\sigma }_n^{1-\frac{D}{2}}, \end{aligned}$$

with ${\textbf{Y}}_n,\mathbf {\Lambda }_n,{\sigma }_n$ defined by,

$$\begin{aligned} {\textbf{Y}}_n^{D-3}= & {} \prod _{j=2}^{n-1}\sqrt{y_j^2-m_{j+1}^2}^{D-3},\\ \mathbf {\Lambda }_n^{D-3}= & {} \sqrt{\lambda (s_n^{n-2}(y_2,\ldots ,y_{n-1}),m_1^2,m_2^2)}^{D-3},\\ {\sigma }_n^{1-\frac{D}{2}}= & {} \frac{1}{\left( s_n^{n-2}(y_2,\ldots ,y_{n-1})\right) ^{\frac{D}{2}-1}}. \end{aligned}$$

We have the following identities which allow to trade derivatives with respect to $y_j$ with derivatives with respect to $m_{j+1}^2$ or s,

$$\begin{aligned} \partial _{y_j}{\textbf{Y}}_n= & {} y_j\frac{1}{y_j^2-m_{j+1}^2}{\textbf{Y}}_n = -2y_j\partial _{m_{j+1}^2}{\textbf{Y}}_n, \end{aligned}$$

(3.1)

$$\begin{aligned} \partial _{y_j}\mathbf {\Lambda }_n= & {} \frac{s_n^{n-2}-m_1^2-m_2^2}{\lambda (s_n^{n-2}(y_2,\ldots ,y_{n-1}),m_1^2,m_2^2)}(\partial _{y_j} s_n^{n-2})\mathbf {\Lambda }_n\nonumber \\= & {} \left( \partial _{s}\mathbf {\Lambda }_n\right) \left( \frac{-2\sqrt{s}}{\sqrt{s-y_{n-1}}} \prod _{k=1}^{n-j-1}\frac{s_n^k}{s_n^{k}-y_{n-k-1}}\right) \end{aligned}$$

(3.2)

$$\begin{aligned}= & {} -2\sqrt{s_n^{n-j-1}}\partial _{m_{j+1}^2}\mathbf {\Lambda }_n,\nonumber \\ \partial _{y_j} {\sigma }_n= & {} \partial _{y_{j}}s_{n}^{n-2}=-2\sqrt{s_n^{n-j-1}}\prod _{l=2}^{j-1}\frac{s_n^{n-l-1}-y_{l}}{s_n^{n-l-1}}\nonumber \\= & {} -2\sqrt{s_n^{n-j-1}} \partial _{m_{j+1}^2}{\sigma }_n \nonumber \\= & {} \partial _{s}{\sigma }_n \left( \frac{-2\sqrt{s}}{\sqrt{s-y_{n-1}}} \prod _{k=1}^{n-j-1}\frac{s_n^k}{s_n^{k}-y_{n-k-1}}\right) . \end{aligned}$$

(3.3)

We also note that

$$\begin{aligned} \partial _{m_{j+1}^2}\mathbf {\Lambda }_n = (\partial _{m_{j+1}^2}s_n^{n-2})\frac{1}{m_1^2-m_2^2} \left( m_1^2\partial _{m_1^2}-m_2^2\partial _{m_2^2}\right) \mathbf {\Lambda }_n, \end{aligned}$$

(3.4)

and

$$\begin{aligned} \partial _{s}\mathbf {\Lambda }_n = (\partial _{s}s_n^{n-2})\frac{1}{m_1^2-m_2^2}\left( m_1^2\partial _{m_1^2}-m_2^2\partial _{m_2^2}\right) \mathbf {\Lambda }_n. \end{aligned}$$

(3.5)

Furthermore, insertion of tensor structure given by $\nu$ following Sect. 1 and Eqs. (2.25–2.29) define an integrand $\textbf{Int}_{{b_n},\nu }$.

Now, using Eq. (2.20) we have for any such integrand,

$$\begin{aligned} \int _{m_{j+1}}^{\textrm{up}_n^{j+1}}\partial _{y_j}\left( \textbf{Int}_{{b_n},\nu }\right) dy_{j}=0,\,\forall j,\, 2\le j\le (n-1). \end{aligned}$$

Proposition 3.1

The above evaluates to an identity of the form,

$$\begin{aligned} \sum _j \textbf{Int}_{{b_n},\nu _j}=0, \end{aligned}$$

between tensor integrals $\textbf{Int}_{{b_n},\nu _j}$ for some tensor structures $\nu _j$.

Proof

Derivatives with respect to $y_j$ can be traded for derivatives with respect to masses and with respect to the scale s using Eqs. (3.1, 3.3, 3.1). Starting with $\nu$, this creates suitable new tensor structures $\nu _j$. Homogeneity of $\lambda$ allows to replace the $\partial _s$ derivatives by $\textbf{Int}_{{b_n},\tilde{\nu }_j}$ with once-more modified tensor structures $\tilde{\nu }_j$. $\square$

3.3 Differential equations

Functions $\Phi _R^D(G)(\{k_i\cdot k_j\},\{m_e^2\})$ for a chosen Feynman graph G fulfil differential equations with respect to suitable kinematical variables [25]. Those variables are given by scalar products $k_i\cdot k_j$ of external momenta. For $G=b_n$, these are differential equations in the sole scalar product $s=k_n\cdot k_n$ of external momenta.

$\Phi _R^D(b_n)(s,\{m_e^2\})$ is a solution to an inhomogeneous differential equation, and the imaginary part $\Im \left( \Phi _R^D(b_n)\right) (s,\{m_e^2\})$ solves the corresponding homogeneous one.

More precisely, there is a set of master integrals $\{b_n\}_M$ defined as a class of Feynman graphs such that any given graph $b_n$, giving rise to integrals $\Phi _R^D(b_n)_\nu (s,s_0,\{m_e^2\})$—so with all its corresponding tensor integrals and arbitrary integer powers of propagators—can be expressed as linear combinations of elements of $\{b_n\}_M$.

Let us consider the column vector $S_{b_n}$ formed by the elements of $\{b_n\}_M$. One searches for a first-order system

$$\begin{aligned} \partial _s S_{b_n}(s)=A S_{b_n}(s)+T, \end{aligned}$$

with $A=A(s,\{m_e^2\})$ a matrix of rational functions and $T=T(\{m_e^2\})$ the inhomogeneity provided by the minors of $b_n$. Those are $(n-1)$-loop tadpoles $t_e$ obtained from shrinking an edge e, $t_e=b_n/e$.

One then has

$$\begin{aligned} \partial _s \Im (S_{b_n})(s)=A \Im (S_{b_n})(s), \end{aligned}$$

where $\Im (S_{b_n})$ is formed by the imaginary parts of entries of $S_{b_n}$ and $\Im (\Phi _R^D(t_e))=0$.

For $b_3$, for example, one has $S_{b_3}=(F_0,F_1,F_2,F_3)^T$, with $F_0=\Phi _R^D(b_3)$, $F_i=\partial _{m_i^2}\Phi _R^D(b_3)$, $i\in \{1,2,3\}$.

The $4\times 4$ matrix A and the four-vector T for that example are well-known, see [10].

From such a first-order system for the full set of master integrals, one often derives a higer-order differential equation for a chosen master integral. For $b_3$ or $b_4$, it is a Picard–Fuchs equation [10].

For banana graphs $b_n$, it is a differential equation of order $(n-1)$:

$$\begin{aligned} \sum _{j=0}^{n-1}\left( Q_{b_n}^{(j)}\partial _s^j\right) \Phi _R^D(b_n)(s)=T_n(s), \end{aligned}$$

(3.6)

where $Q_{b_n}^{(j)}$ are rational functions in $s,\{m_e^2\}$ and one can always set $Q_{b_n}^{(n-1)}=1$. It has been studied extensively [6, 7, 10, 11, 19].

We want to outline how our iterated integral approach relates to such differential equations, to master integrals and to the integration-by-parts (ibp) identities which underlay such structures.

Our first task is to remind ourselves how to connect the homogeneous and inhomogeneous differential equations, and we turn to $b_2$ for some basic considerations.

3.3.1 Differential equation for $b_2$

We set $D=2$ for the moment. Consider the imaginary part of the bubble

$$\begin{aligned} \Im (\Phi _R^2(b_2))(s)=\frac{1}{\sqrt{\lambda (s,m_1^2,m_2^2)}}\Theta (s-(m_1+m_2)^2). \end{aligned}$$

We can recover $\Phi _R^2(b_2)$ by dispersion which reads for $D=2$,

$$\begin{aligned} \Phi _R^2(b_2)(s)=\frac{1}{\pi }\int _{(m_1+m_2)^2}^\infty \frac{\Im (\Phi _R^2(b_2))(x)}{(x-s)}\textrm{d}x. \end{aligned}$$

We now use this representation to analyse the well-known differential equation [6] for $b_2$ given in

Proposition 3.2

$$\begin{aligned} \left( \lambda (s,m_1^2,m_2^2)\frac{\partial }{\partial s}+(s-m_1^2-m_2^2)\right) \Phi _R^2(b_2)(s)=\frac{1}{\pi }, \end{aligned}$$

(3.7)

and for the imaginary part

$$\begin{aligned} \left( \lambda (s,m_1^2,m_2^2)\frac{\partial }{\partial s}+(s-m_1^2-m_2^2)\right) \Im \left( {\Phi _R^2(b_2)(s)}\right) =0. \end{aligned}$$

(3.8)

Note that Eq. (3.8) is the homogeneous equation associated with Eq. (3.7) as it must be [25].

The following proof aims at deriving Eq. (3.7) from the dispersion integral.

Proof

Let us first prove Eq. (3.8).

$$\begin{aligned}{} & {} \lambda \left( s,m_1^2,m_2^2\right) \frac{\partial }{\partial s}\frac{1}{\sqrt{\lambda \left( s,m_1^2,m_2^2\right) }}\Theta \left( s-(m_1+m_2)^2\right) \\{} & {} \quad = \frac{-\left( s+m_1^2+m_2^2\right) }{\sqrt{\lambda \left( s,m_1^2,m_2^2\right) }}\Theta \left( s-(m_1+m_2)^2\right) \\{} & {} \qquad + \sqrt{\lambda \left( s,m_1^2,m_2^2\right) }\delta \left( s-(m_1+m_2)^2\right) \\{} & {} \quad = \frac{-\left( s+m_1^2+m_2^2\right) }{\sqrt{\lambda \left( s,m_1^2,m_2^2\right) }}\Theta \left( s-(m_1+m_2)^2\right) \\{} & {} \quad = -\left( s+m_1^2+m_2^2\right) \Im \left( \Phi _R^2(b_2)\right) (s), \end{aligned}$$

as desired. We use $\lambda ((m_1+m_2)^2,m_1^2,m_2^2)=0$.

Now, for Eq. (3.7). Evaluating the lhs gives

$$\begin{aligned} \textrm{LHS}= & {} \lambda (s,m_1^2,m_2^2)\frac{1}{\pi }\int _{(m_1+m_2)^2}^\infty \frac{1}{\sqrt{\lambda (x,m_1^2,m_2^2)}(x-s)^2}\textrm{d}x \end{aligned}$$

(3.9)

$$\begin{aligned}{} & {} \quad + \frac{1}{\pi }\int _{(m_1+m_2)^2}^\infty \frac{(s-m_1^2-m_2^2)}{\sqrt{\lambda (x,m_1^2,m_2^2)}(x-s)}\textrm{d}x. \end{aligned}$$

(3.10)

A partial integration in the first term (3.9) delivers

$$\begin{aligned} \textrm{LHS}= & {} -\lambda (s,m_1^2,m_2^2)\frac{1}{2\pi }\int _{(m_1+m_2)^2}^\infty \frac{\partial _x \lambda (x,m_1^2,m_2^2)}{\sqrt{\lambda (x,m_1^2,m_2^2)}^3(x-s)}\textrm{d}x\\{} & {} \quad +\frac{1}{\pi }\int _{(m_1+m_2)^2}^\infty \frac{(s-m_1^2-m_2^2)}{\sqrt{\lambda (x,m_1^2,m_2^2)}(x-s)}\textrm{d}x\\{} & {} \quad - \lambda (s,m_1^2,m_2^2)\left[ \frac{1}{\pi }\frac{1}{\sqrt{\lambda (x,m_1^2,m_2^2)}(x-s)}\right] ^\infty _{(m_1+m_2)^2}. \end{aligned}$$

We have

$$\begin{aligned} \partial _x \lambda \left( x,m_1^2,m_2^2\right) =2\left( x-m_1^2-m_2^2\right) =:v_1(x),\, v_1(x)-v_1(s)=2(x-s), \end{aligned}$$

(3.11)

and

$$\begin{aligned} \lambda \left( s,m_1^2,m_2^2\right) -\lambda \left( x,m_1^2,m_2^2\right) =(s-x)\left( (s+x)-2(m_1^2+m_2^2)\right) =:w(x,s)(s-x). \end{aligned}$$

(3.12)

Using this the lhs of Eq. (3.7) reduces to a couple of boundary terms. We collect

$$\begin{aligned}+ & {} \frac{1}{\pi }\left[ \frac{x}{\sqrt{\lambda _x}}\right] ^\infty _{(m_1+m_2)^2}\\+ & {} \frac{s-2(m_1^2+m_2^2)}{\pi }\left[ \frac{1}{\sqrt{\lambda _x}}\right] ^\infty _{(m_1+m_2)^2}\\+ & {} \left[ \frac{1}{\pi }\frac{(s-x)w(s,x)+\lambda _x}{\sqrt{\lambda _x}(x-s)}\right] ^\infty _{(m_1+m_2)^2}\\= & {} \frac{1}{\pi }, \end{aligned}$$

as desired.

Indeed, using that $w(s,x)=s+x-2(m_1^2+m_2^2)$ we see that the term $\sim w$ in the third line cancels the first and second lines. The remaining term is

$$\begin{aligned} \left[ \frac{1}{\pi }\frac{\lambda _x}{\sqrt{\lambda _x}(x-s)}\right] ^\infty _{(m_1+m_2)^2}=\frac{1}{\pi }, \end{aligned}$$

as $\sqrt{\lambda ((m_1+m_2)^2,m_1^2,m_2^2)}=0$ and $\lim _{x\rightarrow \infty }\sqrt{\lambda (x,m_1^2,m_2^2)}=x$. $\square$

Remark 3.3

So, for $b_2$ we have by Eqs. (3.12, 3.11)

$$\begin{aligned} Q_0(x)=\frac{2(s-m_1^2-m_2^2)}{\lambda (s,m_1^2,m_2^2)} {\text { and }} Q_1(x)=1. \end{aligned}$$

This is a trivial incarnation of Eq. (3.6). As $(Q_0(x)-Q_0(s))\sim (x-s)$, we cancel the denominator $1/(x-s)$ in the dispersion integral and we are left with boundary terms which constitute the inhomogeneous terms.

Remark 3.4

The non-rational part $\Phi _R^D(b_2)_\textbf{Transc}$ of $\Phi _R^D(b_2)$ is divisible by $V_2^D$ and gives a pure function in the parlance of [2]. Indeed, one wishes to identify such pure functions in the non-rational parts of $\Phi _R^D(b_n)(s,s_0)$.

For example, for $D=4$ (ignoring terms in $\Phi _R^4(b_2)(s)$ which are rational in s)

$$\begin{aligned} \Phi _R^4(b_2)(s)_\textbf{Transc}/V_2^4(s)=\ln \frac{m_1^2+m_2^2-s -\sqrt{\lambda (s,m_1^2,m_2^2)}}{m_1^2+m_2^2-s+\sqrt{\lambda (s,m_1^2,m_2^2)}}. \end{aligned}$$

This follows also for all $b_n$, $n>2$, as long as the inhomogenuity $T_n(s)$ fulfils

$$\begin{aligned} \Im (T_n(s))=0, \end{aligned}$$

which is certainly true for the case $b_2$ with $T_2(s)=1/\pi$. Indeed, for f(s) a solution of the homogeneous

$$\begin{aligned} \left( \sum _{j=0}^{n-1} Q_j(s)\partial ^j_s\right) f(s)=0, \end{aligned}$$

the inhomogeneous Picard–Fuchs equation

$$\begin{aligned} \left( \sum _{j=0}^{n-1} Q_j(s)\partial ^j_s\right) g(s)=T_n(s), \end{aligned}$$

can be solved by setting $g(s)=f(s)h(s)$. Using Leibniz’ rule, this determines h(s) as a solution of an equation

$$\begin{aligned} \sum _{k=1}^{n-1} h^{(k)}(s)\left( \sum _{j=k}^{n-1} \left( {\begin{array}{c} {j}\\ {k} \end{array}} \right) a_j(s) f^{(j-k)}(s)\right) =u(s), \end{aligned}$$

with $f^{(j-k)}(s)=\partial _s^{j-k}f(s)$ and similarly for $h^{(k)}(s)$. Note $f^{(j-k)}(s)$ are given by solving the homogeneous equation. Hence, g(s) indeed factorizes as desired.²

This relates to co-actions and cointeracting bialgebras [28, 29] and will be discussed elsewhere.

3.3.2 Systems of linear differential equations for $b_n$

To find differential equations for the iterated $y_j$-integrations of Eq. (2.14), we first systematically shift all $y_j$-derivatives acting on $\sqrt{y_j^2-m_{j+1}^2}$ to act on $V_2^D(s_n^2,m_1^2,m_2^2)$ using partial integration. We can ignore boundary terms by Thm. (2.2(iii)). We use

$$\begin{aligned} \left( \partial _{m_j^2}\frac{1}{\sqrt{y_{j-1}-m_j^2}}\right) F= & {} \frac{1}{2\sqrt{y_{j-1}-m_j^2}^3}F\\= & {} \left( -\frac{y_{j-1}^2-m_j^2}{2m_j^2\sqrt{y_{j-1}-m_j^2}^3} +\frac{y_{j-1}^2}{2m_j^2\sqrt{y_{j-1}-m_j^2}^3}\right) F\\= & {} \left( -\frac{1}{2m_j^2\sqrt{y_{j-1}-m_j^2}} -y\left( \partial _{y_{j-1}}\frac{1}{2m_j^2\sqrt{y_{j-1}-m_j^2}}\right) \right) F\\= & {} -\frac{1}{2m_j^2\sqrt{y_{j-1}-m_j^2}}F +\frac{1}{2m_j^2\sqrt{y_{j-1}-m_j^2}}\left( \partial _{y_{j-1}}y_{j-1}F\right) \\= & {} +\frac{1}{2m_j^2\sqrt{y_{j-1}-m_j^2}}y_{j-1}\left( \partial _{y_{j-1}} F\right) \\= & {} +\frac{1}{m_j^2\sqrt{y_{j-1}-m_j^2}}y_{j-1}\left( \sqrt{s_n^{j-1}}\partial _{m^2_{j}} F\right) . \end{aligned}$$

We could trade a derivative wrt $y_{j-1}$ for a derivative wrt $m_j^2$ thanks to Thm. (2.2(iv)). This holds under the proviso that all masses are different. Else, we use the penultimate line as our result:

$$\begin{aligned} \left( \partial _{m_j^2}\frac{1}{\sqrt{y_{j-1}-m_j^2}}\right) F= +\frac{1}{2m_j^2\sqrt{y_{j-1}-m_j^2}}y_{j-1}\left( \partial _{y_{j-1}} F\right) . \end{aligned}$$

We can iterate this and shift higher than first derivatives

$$\begin{aligned} \left( \partial _{m_j^2}^k\frac{1}{\sqrt{y_{j-1}-m_j^2}}\right) F \end{aligned}$$

to derivatives on F.

We note that from the definition of $\lambda (s_n^{n-2},m_2^2,m_1^2)$ we have

$$\begin{aligned} \lambda \left( s_n^{n-2},m_2^2,m_1^2\right)= & {} s_n^{n-2}\left( s_n^{n-2}-2\left( m_1^2+m_2^2\right) \right) \\{} & {} +\left( m_1^2-m_2^2\right) ^2. \end{aligned}$$

By Euler ($\lambda$ is homogeneous of degree two),

$$\begin{aligned} 2\lambda \left( s_n^{n-2},m_2^2,m_1^2\right)= & {} \partial _{s_n^{n-2}}\lambda \left( s_n^{n-2},m_2^2,m_1^2\right) +\partial _{m_1^2}\lambda \left( s_n^{n-2},m_2^2,m_1^2\right) \\{} & {} \quad +\partial _{m_2^2}\lambda \left( s_n^{n-2},m_2^2,m_1^2\right) . \end{aligned}$$

Also,

$$\begin{aligned} \partial _{m_1^2}\lambda \left( s_n^{n-2},m_2^2,m_1^2\right)= & {} 2\left( m_1^2-m_2^2-s_n^{n-2}\right) ,\\ \partial _{m_2^2}\lambda \left( s_n^{n-2},m_2^2,m_1^2\right)= & {} 2\left( m_2^2-m_1^2-s_n^{n-2}\right) ,\\ \partial _{m_j^2}\lambda \left( s_n^{n-2},m_2^2,m_1^2\right)= & {} 2\left( s_n^{n-2}-m_1^2-m_2\right) \partial _{m_j^2}s_n^{n-2},\,\forall \, 3\le j\le n,\\ \partial _{s}\lambda \left( s_n^{n-2},m_2^2,m_1^2\right)= & {} 2\left( s_n^{n-2}-m_1^2-m_2\right) \partial _s s_n^{n-2}. \end{aligned}$$

With this, Thm. (2.2) allows to derive differential equations.

Let us rederive, for example, the differential equation for the three-edge banana. Let us define

$$\begin{aligned} F_0= & {} \Phi _R(b_3),\\ F_1= & {} \partial _{m_1^2} F_0,\\ F_2= & {} \partial _{m_2^2} F_0,\\ F_3= & {} \partial _{m_3^2} F_0,\\ F_s= & {} \partial _s F_0. \end{aligned}$$

Then, we have

$$\begin{aligned} (D-3)F_0+\sum _{j=1}^3 m_j^2 F_j=s\partial _s F_0, \end{aligned}$$

(3.13)

and similarly,

$$\begin{aligned} \left( (D-4)+\sum _{i=1}^3m_i^2\partial _{m_i^2}\right) F_j=s\partial _s F_j,\,j\in \{1,2,3\}. \end{aligned}$$

(3.14)

The integrands $I_i$ for $(D-3)F_0$,$m_1^2F_1$,$m_2^2F_2$,$m_3^2F_3$, and $sF_s$ can be written as

$$\begin{aligned} I_{i}=\frac{\textbf{num}_i(y_2)}{s^{\frac{D}{2}}}\sqrt{y_2^2-m_3^2}^{D-5} \sqrt{\lambda }^{D-5}(s_3^1,m_2^2,m_1^2) \end{aligned}$$

with suitable polynomials $\textbf{num}_i$ in $y_2$. Equation (3.13) follows immediately as the corresponding numerators ${\textbf{num}_i(y_2)}$ add to zero.

Equation (3.14) for $F_1,F_2,F_3$ can be proven in precisely the same manner, and many more differential equations follow from using the ibp identities Eqs. (3.1–3.3).

Furthermore, $F_0,F_1,F_2,F_3$ provide master integrals for the Feynman integrals $\Phi _R^D(b_3)_\nu$ [10].

Remark 3.5

Note that we can infer the independence of $F_0,F_1,F_2,F_3$ from the fact that the corresponding polynomials are different, in fact of different degree in $y_2$.

We could also use different integral representations for $F_1,F_2,F_3$ by setting

$$\begin{aligned} F_3=\partial _{m_3^2}\,{\text {rhs of Eq. (}2.1)},\\ F_2=\partial _{m_2^2}\,{\text {rhs of Eq. (}2.2)},\\ F_1=\partial _{m_1^2}\,{\text {rhs of Eq. (}2.3)}. \end{aligned}$$

and conclude from there. |

3.4 Master integrals

We want to comment on two facts:

• (i) A geometric interpretation of the known formula for the counting of master integrals for $b_n$,

• (ii) That the independence of elements x of a set $S_ {b_n}$ of master integrals does not imply the independence of elements of $\Im (x),\, x\in \left( S_ {b_n}\right)$.

3.4.1 A geometric interpretation: powercounting

Let us start with a geometric interpretation. We collect a well-known proposition [26, 27].

Proposition 3.6

The number of master integrals for the n-edge banana with different masses is $2^n-1$.

Let us pause. For $b_3$, we have four master integrals, $F_0$, and three possibilities to put a dot on an internal edge. Furthermore, we can shrink any of the three internal edges, giving us three two-petal roses as minors. This makes $7=2^3-1$ master integrals amounting to the fact that all tensor integrals $\Phi _R(b_n)\nu$ can be expressed as a linear combination of those seven, with coefficients which are rational functions in the mass squares and in s.

Similarly, for $b_4$ we have $\Phi _R^D(b_4)$ itself, four integrals $\partial _{m_i^2}\Phi _R^D(b_4)$ and six $\partial _{m_j^2}\partial _{m_i^2}\Phi _R^D(b_4)$, $i\not = j$. There are four minors as well, so that we get the desired $15=2^4-1$ master integrals.

For arbitrary n, there are indeed $\left( {\begin{array}{c} {n}\\ {j} \end{array}}\right)$ possibilities to put one dot on j edges, and

$$\begin{aligned} \sum _{j=0}^{n-2}\left( {\begin{array}{c} {n}\\ {j} \end{array}}\right) =2^{n}-n-1, \end{aligned}$$

possibilities to put a single dot on up to $n-2$ edges. Furthermore, we have n minors from shrinking one of the n edges, so we get $2^n-1$ master integrals.

Furthermore, it is obvious from the structure of the iterated integral in Eq. (2.14) that the two edges forming the innermost $b_2$ do not need a dot. Indeed, the corresponding loop integral in $k_1$ is fixed by two $\delta _+$ functions. Integration by parts then ensures that we do not need more than one dot per edge at most.

Remark 3.7

One can analyse this from the viewpoint of powercounting. Let us choose $D=4$ so that $b_2$ is log-divergent. Let us note that for $D=4$

$$\begin{aligned} 4(n-1)-2\overbrace{(2n-2)}^{\# E}=0, \end{aligned}$$

(3.15)

where $\# E$ is the number of edges of a banana graph $b_n$ which has $(n-2)$ edges with a single dot each. Equation (3.15) says that $b_n$ furnished with the maximum of $n-2$ dots gives an overall logarithmic singular integral for any n.

A lesser number of dots give a higher degree of divergence and hence higher subtractions in the dispersion integrals. Conceptually, higher degrees of divergence are probing higher coefficients in the Taylor expansion in s which provide the needed master integrals. We see below how this interferes with counting master integrals but first our geometric interpretation as given in Fig. . |

3.4.2 $b_3$ and its cell

The parametric representation of $b_3$ as given in “App. E” provides insight into the structure of its Feynman integral and the related master integrals.

Remark 3.8

Let us note that any graph $b_n$ has a spanning tree which consists of just one of its internal edges. Hence, any associated spanning tree has length one. As $b_n$ has n internal edges its associated cell $C(b_n)$ (in the sense of Outer Space [30]) is a $(n-1)$-dimensional simplex $C_n$

$$\begin{aligned} C(b_n)=C_n. \end{aligned}$$

The graph $b_n$ has internal edges $e_i$. To each such edge, we assign a length $A_i$, $0\le A_i\le \infty$ which we regard as a coordinate in the projective space $\mathbb {P}_{b_n}:=\mathbb {P}^{n-1}(\mathbb {R}_+)$.

Shrinking one edge $e_i$ to length $A_i=0$ gives the graph $b_n/e_i$ which is associated with the codimension-one boundary determined by $A_i=0$. It is a $(n-2)$-dimensional simplex $C_{n-1}$.

Note $b_n/e_i$ is a rose with $(n-1)$ petals. Each petal corresponds to a tadpole integral for a propagator with mass $m_j^2$, $j\not = i$.

Different points of $C(b_n)$ correspond to different points

$$\begin{aligned} \mathbb {P}_{b_n}\ni p:\,(A_1:A_2:\cdots :A_n). \end{aligned}$$

We can identify n! sectors ${\sigma }:\,A_{\sigma (1)}>A_{\sigma (2)}>\cdots >A_{\sigma (n)}$ for any permutation $\sigma \in S_n$ with associated sector ${\sigma }$.

$$\begin{aligned} \Phi _R^D(b_n)(s,s_0)=\int _{\mathbb {P}_{b_n}(\mathbb {R}_+)}\textrm{Int}_{b_n}(s,s_0;p)=\sum _{\sigma \in S_n}\int _{{\sigma }}T^{(\rho ^n_D)}\left[ \textrm{Int}_{b_n}(s,s_0;p)\right] , \nonumber \\ \end{aligned}$$

(3.16)

with

$$\begin{aligned} \textrm{Int}_{b_n}(s,s_0;p)=\frac{\ln \frac{\Phi (b_n)(s)(p)}{\Phi (b_n)(s_0)(p)}}{\psi _{b_n}^{\frac{D}{2}}(p)}\Omega _{b_n}. \end{aligned}$$

$T^{(\rho ^n_D)}$ is a suitable Taylor operator with subtractions at $s=s_0$ ensuring overall convergence and $\rho ^n_D$ the UV degree of divergence. Here,

$$\begin{aligned} \Phi (b_n)(s)(p)=\left( \prod _{j=1}^n A_j\right) \underbrace{\left( s-\left( \sum _{i=1}^n A_im_i^2\right) \left( \sum _{k=1}^n \frac{1}{A_k}\right) \right) }_{TP(b_n)}, \end{aligned}$$

and

$$\begin{aligned} \left( \prod _{j=1}^n A_j\right) \left( \sum _{k=1}^n \frac{1}{A_k}\right) . \end{aligned}$$

Each sector allows for a rescaling according to the order of edge variables such that the singularity is an isolated pole.

Here, $TP(b_n)$ is the toric polynomial of $b_n$ as discussed in [11, 31] and prominent in the GKZ approach used there.

Such approaches with their emphasis on hypergeometrics and the rôle of confluence have a precursor in the study of Dirichlet measures [32]. The latter have proven their relevance for Feynman diagram analysis early on [33].

The spine of $C(b_n)$ is a n-star, with the vertex in the barycentre and n rays from the barycentre bc of $C(b_n)$ to the midpoints of the n codimension-one cells $C_{n-1}$ which are $(n-2)$-simplices.

These rays provide n corresponding cubical chain complices $\textrm{cc}(i)$ each provided by single intervals [0, 1].

For the two endpoints 0 and 1 of each $\textrm{cc}(i)$, we assign:

• (i) to 1,—the barycentre bc common to all $\textrm{cc}(i)$ we assign $b_n$ with internal edges removed, hence evaluated on-shell. This corresponds to $\Im \left( \Phi _R^D(b_n)\right)$.

• (ii) To 0, we assign the graph $b_n/e_i$ (a rose with $n-1$ petals) with petals of equal size—hence a tadpole $\Phi _R^D(b_n/e_i)$ with $A_jm_j=A_km_k$, $j,k\not = i$. See Fig. 5. |

Fig. 5

The graph $b_3$ and its triangular cell $C_3$. The codimension-one boundaries (sides) are given by the condition $A_i=0$, indicated in the figure by $i=0$, $i\in \{1,2,3\}$. The graph $b_3$ with two yellow leaves as external edges is put in the barycentre. All its edges are put on-shell. The cell decomposes into six sectors $m_iA_i>m_jA_j>m_kA_k$ as indicated by $i>j>k$. The lines $m_iA_i=m_jA_j$ (indicated by $i=j$) start at the midpoint $\textrm{mid}_{i,j}:\, A_k=0,\,A_im_i=A_jm_j$ of the codimension one boundary $A_k=0$ and pass through the barycentre $\textrm{bc}:\,m_1A_1=m_2A_2=m_3A_3$ towards the corner $c_k:\,A_i=A_j=0$, labelled k. Such corners are removed. For these three lines, the three intervals $[\textrm{mid}_{i,j},\textrm{bc}]$ from the midpoints of the sides to the barycentre of the cell form the spine. It indicated in turquoise. The bold hashed line indicated by $2<3$ (so $m_2A_2<m_3A_3$) on the left and $2<1$ (so $m_2A_2<m_1A_1$) on the right is an example of a fibre over one (the vertical) part (on the $1=3$-line) of the spine (the turquoise line from $m_1A_1=m_3A_3,A_2=0$ to the barycentre). On the left, along the fibre the ratio $A_2/A_3<m_3/m_2$ is a constant, on the right similarly. Finally, to the two yellow leaves we assign incoming four-momenta $k_3,-k_3$ with $k_3^2=s$. The spine partitions the cell $C_3$ into three 2-cubes, boxes $\Box (j)$ with four corners for any $\Box (j)$: $\textrm{mid}_{i,j},\textrm{bc},\textrm{mid}_{j,k}, c_j$. For each such box $\Box (j)$ there is a diagonal $d_j$. It is a line from a corner to the barycentre: $\textrm{d}_j:\,]c_j,\textrm{bc}]$ for which we have $m_iA_i=m_kA_k$. We assign to this diagonal $\textrm{d}_j$ a graph for which edges $e_i,e_k$ are on-shell and edge $e_j$ carries a dot. Along the diagonal $\textrm{d}_j$, we have $A_jm_j>(A_im_i=A_km_k)$ (colour figure online)

Figure 5 gives the graph $b_3$ and the associated cell, a 2-simplex $C_3$. It is a triangle with corners $c_1,c_2,c_3$. Points of the cell are the interior points of $C_3$ and furthermore the points in the three codimension-one boundaries $C_2(i)$, the sides of the triangle.

The corners $c_i$ are removed and do not belong to the cell. Points of the cell parameterize the edge lengths $A_i$ of the internal edges of $b_3$ as parameters in the parametric integrand, see Eq. (E.1).

The boundaries are given by $C_2(i): A_i=0$ and correspond to tadpole integrals for tadpoles $t_2(i)=b_3/e_i$ for which edge $e_i$ has length zero.

Corners $c_k:\,A_i=A_j=0,\,i\not = j$ correspond to $b_3/e_i/e_j$ which is degenerate as it shrinks a loop.

Colours green, red, and blue indicate three different masses. It is understood that a momentum $k_3$ flows through any edge $e_i$ which is chosen to serve as a spanning tree for $b_3$.

The three edges of the graph give rise to 3! orderings of the edge lengths as indicated in the figure. We will split the parametric integral accordingly. See “App. E” for computational details.

To a $(i=j)$-diagonal of a box $\Box (k)$, we associate a $b_3$ evaluated with edges $e_i,e_j$ on-shell and edge $e_k$ dotted, so it corresponds to $\partial _{m_k^2}\Im \left( \Phi _R^D(b_3)\right)$.

In the figure, there is also an arc given which is a fibre which has the diagonal $d_j$ as the base. Integrating that fibre corresponds to integrating the $b_2$ subgraph on edges $e_i,e_j$. Points $(A_i:A_j:A_k)$ on a diagonal $d_k$ fulfil

$$\begin{aligned} A_km_k>x,\, x:=A_im_i=A_jm_j. \end{aligned}$$

To the barycentre $A_im_i=A_jm_j$, we associate $b_3$ with all three edges on-shell, a Cutkosky cut providing $\Im \left( \Phi _R^D(b_3)\right)$. To the midpoints $A_i=A_j,A_k=0$ of the edges $A_i=0$ ($e_i=0$ in the figure), we assign tadpole integrals. All in all we identified all seven master integrals in the figure. Note that the cell decomposition in Fig. 5 reflects the structure of the Newton polyhedron associated with $TP(b_3)$ [31].

Note that the requirement $A_im_i=A_jm_j$ is the locus for the Landau singularity of the associated $b_2(e_i,e_j)$ and similarly for $A_1m_1=A_2m_2=A_3m_3$ and $b_3$.

Remark 3.9

Note that the diagonals $d_j$ can be obtained by reflecting a leg of the spine at the barycentre. The three legs and the three diagonals form the six boundaries between the sectors $A_i>A_j>A_k$.

A similar analysis holds for any $b_n$. For example, for $b_4$ the cell is a tetrahedron with four corners $c_i$, $i\in \{1,2,3,4\}$. The spine is a four-star with four lines (rays) from the barycentre $bc:\,m_1A_1=m_2A_2=m_3A_3=m_4A_4$ to the midpoints of the four sides of the tetrahedraon (triangles). Reflecting these lines at the barycentre gives four diagonals $d_j:\,[bc,c_j]$ from bc to one of the four corners $c_i$.

To bc, we associate $\Im \left( \Phi _R^D(b_4)\right)$. To the diagonals $d_j$, we assign $\partial _{m_j^2}\Im \left( \Phi _R^D(b_4)\right)$ with the edges $e_i,i\not = j$, on-shell. There are six triangles with sides $d_i,d_j,]c_i,c_j[$. To those, we assign $\partial _{m_i}^2\partial _{m_j^2}\Im \left( \Phi _R^D(b_4)\right)$ with the edges $e_k,k\not = i,j$, on-shell. See Fig. .

|

Fig. 6

The cell $C(b_4)=C_4$ on the left. On the right, we see two diagonals $d_C,d_B$ and their associated graphs which have one dotted edge. Points of the triangle bc, B, C are the open convex hull of $d_C,d_B$ which we denote as the span of the diagonals $d_C,d_B$. To them, a graph with two dotted edges is assigned. On the codimension-one triangles spanned by three corners we indicate the barycentre by a coloured dot. For example, to the triangle BCD we have the yellow dot and the graph $b_4/e_y$ assigned to it where the yellow edge shrinks to length zero (colour figure online)

Continuing we get the expected tally: for $b_n$, we have $\left( {\begin{array}{c}n\\ 0\end{array}}\right) =1$ graph for the barycentre, $\left( {\begin{array}{c}n\\ 1\end{array}}\right) =n$ graphs for the diagonals, $\left( {\begin{array}{c}n\\ m\end{array}}\right) ,\ m\le (n-2)$ graphs for the span of m diagonals, and $\left( {\begin{array}{c}n\\ n-1\end{array}}\right) =n$ tadpoles. It is rather charming to see how mathematics inspired by the works of Karen Vogtmann and collaborators [30] illuminates results discussed recently in terms of intersection theory [34].

3.4.3 Real and imaginary independence and powercounting

Next, we want to compare real and imaginary parts to check that the independence of elements of $S_ {b_n}$ does not necessarily imply the independence of elements of $\Im \left( S_ {b_n}\right)$. We demonstrate this well-known fact [5] for $b_3$. Independence is indeed a question of the values of D.

For $b_3$ and $D=2$, we need no subtraction in the dispersion integral for $F_0=\Phi _R^2(b_3)$,

$$\begin{aligned} \Phi _R^2(b_3)(s)=\frac{1}{\pi }\int _{(m_1+m_2+m_3)^2}^\infty \frac{V_3^D(x,m_1^2,m_2^2,m_3^2)}{(x-s)}\textrm{d}x, \end{aligned}$$

and for $F_i=\partial _{m_i^2} F_0$ again an unsubtracted dispersion integral suffices

$$\begin{aligned} F_i(s)=\frac{1}{\pi }\int _{(m_1+m_2+m_3)^2}^\infty \frac{\partial _{m_i^2}V_3^D(x,m_1^2,m_2^2,m_3^2)}{(x-s)}\textrm{d}x. \end{aligned}$$

The four integrands $I_i$ (for the $y_2$-integration) of $\Im (F_i)$, $i\in \{0,1,2,3\}$ can be expressed over a common denominator with numerators $\textbf{num}_i(y_2)$, and for $D=2$ (the $(s_n^{n-2})^{\frac{D}{2}-1}=1$ is absent), there is indeed a relation between the four numerators.

$$\begin{aligned} \mathbf {num_3}(y_2)=c_{0}^3 \textbf{num}_0(y_2)+c_{1}^3 \textbf{num}_1(y_2)+c_{2}^3 \mathbf {num_2}(y_2), \end{aligned}$$

(3.17)

where $c_{i}^3$ are rational functions of $s,m_1^2,m_2^2,m_3^2$ independent of $y_2$.

For $D=2$, a second relation follows from the fact that the integrand involves the square root of a quartic polynomial ([5], App. D),

$$\begin{aligned} \frac{1}{\sqrt{y_2^2-m_3^2}}V_3^2(y_2)=\frac{1}{\sqrt{s}\sqrt{(y_2-m_3)(y_2+m_3)(y_2-y_+)(y_2-y_-)}}, \end{aligned}$$

where we set for the quadratic polynomial $\lambda (s_3^1(y_2),m_1^2,m_2^2)$,

$$\begin{aligned} \lambda (s_3^1(y_2),m_1^2,m_2^2)=:s(y_2-y_+)(y_2-y_-), \end{aligned}$$

which defines $y_\pm$. See Sect. 2.3.

Investigating

$$\begin{aligned} J_n=\int _{m_3}^{\textbf{up}_3^0} \frac{y_2^n}{\sqrt{s}\sqrt{(y_2-m_3)(y_2+m_3)(y_2-y_+)(y_2-y_-)}}dy_2, \end{aligned}$$

as in [5] delivers a further relation between the $F_i$, and we are hence left with only two independent master integrals for the imaginary parts of $b_3$ in $D=2$.

For $b_3$ and $D=4$, on the other hand we need a double subtraction in the dispersion integral for $F_0=\Phi _R^4(b_3)$,

$$\begin{aligned} \Phi _R^4(b_3)(s,s_0)=\frac{(s-s_0)^2}{\pi }\int _{(m_1+m_2+m_3)^2}^\infty \frac{V_3^D(x,m_1^2,m_2^2,m_3^2)}{(x-s)(x-s_0)^2}\textrm{d}x, \end{aligned}$$

whilst for $F_i=\partial _{m_i^2} F_0$ a once-subtracted dispersion integral suffices,

$$\begin{aligned} F_i(s)=\frac{(s-s_0)}{\pi }\int _{(m_1+m_2+m_3)^2}^\infty \frac{\partial _{m_i^2}V_3^D(x,m_1^2,m_2^2,m_3^2)}{(x-s)(x-s_0)}\textrm{d}x. \end{aligned}$$

The four integrands $I_i$ (for the $y_2$-integration) of $\Im (F_i)$, $i\in \{0,1,2,3\}$ have to be expressed over a different common denominator $D=4$, in particular having an extra factor $s_3^1$. There is no relation between them.

This reflects the fact that the $F_0$ dispersion

$$\begin{aligned} \Phi _R^4(b_3)(s,s_0)=\frac{(s-s_0)}{\pi }\int _{(m_1+m_2+m_3)^2}^\infty \left( \frac{V_3^D(x,m_1^2,m_2^2,m_3^2)}{(x-s)(x-s_0)} -\frac{V_3^D(x,m_1^2,m_2^2,m_3^2)}{(x-s_0)^2}\right) \textrm{d}x, \end{aligned}$$

subsumes the Taylor expansion s near $s_0$ to second order.

In contrast, the $F_i$, $i\in \{1,2,3\}$,

$$\begin{aligned} \partial _{m_i^2}\Phi _R^4(b_3)(s,s_0)=\partial _{m_i^2}\frac{1}{\pi } \int _{(m_1+m_2+m_3)^2}^\infty \left( \frac{V_3^D(x,m_1^2,m_2^2,m_3^2)}{(x-s)} -\frac{V_3^D(x,m_1^2,m_2^2,m_3^2)}{(x-s_0)}\right) \textrm{d}x, \end{aligned}$$

subsume the Taylor expansion in s near $s_0$ to first order.

This is in agreement with the powercounting in Eq. (3.15) and forces the relation between the four $F_i$ to be $\sim s\partial _s F_0$, see Eq. (3.13). The relation Eq. (3.17) is spoiled by the extra coefficient in the Taylor expansion of $\Phi _R^4(b_3)(s,s_0)$.

We are left with four, not two, master integrals. Indeed, starting with a dotted log-divergent banana integral reducing the number of dots demands more subtractions in the dispersion integral. Any relation between imaginary parts with different numbers of dots is spoiled by the difference in degree needed for the subtractions in the dispersion integral.

Appendices

Appendix A: Feynman rules for banana graphs

Having introduced the graphs $b_n$ as our subject of interest we define Feynman rules for their evaluation. We follow the momentum routing as indicated in Fig. 1.

The graph $b_n$ gives rise to an integrand $I_{b_n}$ (setting $k_0=(0,\vec {0})^T$, where the D-vector $k_0$ is set to the zero-vector $(0,\vec {0})^T\in \mathbb {M}^D$):

$$\begin{aligned} I_{b_n}=\omega ^D_{(n-1)}\prod _{j=0}^{n-1}\frac{1}{(k_{j+1}-k_j)^2-m_{j+1}^2}, \end{aligned}$$

and we set $Q_{j+1}=(k_{j+1}-k_{j})^2-m_{j+1}^2$, $0\le j\le (n-1)$ for the n quadrics $Q_{j+1}$, $j=0,\ldots ,n-1$. Here,

$$\begin{aligned} \omega ^D_{(n-1)}:=d^Dk_1\cdots d^Dk_{n-1} \end{aligned}$$

is a $D\times (n-1)$-form in a $(n-1)$-fold product $\mathbb {M}_n$ of D-dimensional Minkowski spaces

$$\begin{aligned} \mathbb {M}_n:= \left( \mathbb {M}^D\right) ^{\times (n-1)}. \end{aligned}$$

The function $\Phi _R^D(b_n)(s)$ is multi-valued as a function of $s:=k_n^2$. It has an imaginary part given by a cut which amounts to replacing for each quadric

$$\begin{aligned} \frac{1}{Q_{j+1}}\rightarrow \delta _+((k_{j+1}-k_j)^2-m_{j+1}^2), \end{aligned}$$

in the integrand $I_{b_n}$. This is Cutkosky’s theorem [36] applied to $b_n$. The distribution $\delta _+$ acts as

$$\begin{aligned} \delta _+((k_{j+1}-k_j)^2-m_{j+1}^2)=\Theta (k_{j+1;0}-k_{j;0})\delta ((k_{j+1}-k_j)^2-m_{j+1}^2), \end{aligned}$$

using the Heavyside distribution $\Theta$ and Dirac $\delta$-distribution.

The integrand for the cut banana is correspondingly

$$\begin{aligned} I_{\textrm{cut}}(b_n)= \omega ^D_{(n-1)}\prod _{j=0}^{n-1}\delta _+\left( (k_{j+1}-k_j)^2-m_{j+1}^2\right) . \end{aligned}$$

(A.1)

We take the external momentum $k_n$ to be timelike so that we can choose $k_n=(k_{n;0},\vec {0})^T$ and set $k_j=(k_{j,0},\vec {k_j})^T$. We also set $\vec {k_j}\cdot \vec {k_j}=:t_j$ and have $k_j^2=k_{j;0}^2-t_j$, and finally define $\hat{k_j}=\vec {k_j}/\sqrt{t_j}$. Hence,

$$\begin{aligned} \textrm{d}^Dk_j=\textrm{d}k_{j,0}\;\sqrt{t_j}^{D-3} \textrm{d}t_j\;\textrm{d}{\hat{k}}_j, \end{aligned}$$

with an angular measure

$$\begin{aligned} \int _{S^{D-2}} \textrm{d}{\hat{k}}_j\,1=\omega _{\frac{D}{2}}. \end{aligned}$$

Here,

$$\begin{aligned} \omega _{\frac{D}{2}}=\frac{2\pi ^{\frac{D-1}{2}}}{\Gamma (\frac{D-1}{2})},\,\Gamma \left( \frac{1}{2}\right) \equiv \sqrt{\pi }. \end{aligned}$$

(A.2)

We then have as integrations

$$\begin{aligned} \int _{\mathbb {M}^D}\textrm{d}^Dk_j f(k_j)=\int _{-\infty }^{\infty } \textrm{d}k_{j;0}\int _0^\infty \sqrt{t_j}^{D-3}\textrm{d}t_j\int _{S^{D-2}} \textrm{d}{\hat{k}}_j f(k_{j,0},t_j,\hat{k_j}). \end{aligned}$$

Appendix B: Minimal subtraction

For the reader which likes to compare with dimensional regularization and the use of minimal subtraction as renormalization, we have kept D complex in most formulae and note that in such a situation the coproduct for $b_n$ reads

$$\begin{aligned} \Delta _H(b_n)=b_n\otimes \mathbb {I}+\mathbb {I}\otimes b_n+\sum _{x,|x|\lneq n} x\otimes t_{n-|x|}. \end{aligned}$$

(B.1)

Here, the sum is over all monomials x of banana graphs $b_j$ on less than n edges. For example,

$$\begin{aligned} \Delta (b_5)=b_5\otimes \mathbb {I}+\mathbb {I}\otimes b_5+\left( {\begin{array}{c} {5}\\ {2} \end{array}}\right) b_2\otimes t_3 +\left( {\begin{array}{c} {5}\\ {3} \end{array}}\right) b_3\otimes t_2+\left( {\begin{array}{c} {5}\\ {4} \end{array}}\right) b_4\otimes t_1 +\left( {\begin{array}{c} {5}\\ {2} \end{array}}\right) \left( {\begin{array}{c} {3}\\ {2} \end{array}}\right) b_2b_2\otimes t_1. \end{aligned}$$

In Feynman graphs, this is Fig. .

Fig. 7

The Hopf algebra disentangling the five-banana $b_5$. On the right, we also get roses with n petals, or tadpoles in a physicists parlance. There are $5=\left( {\begin{array}{c} {5}\\ {4} \end{array}}\right)$ labellings for the $b_4$ banana in the first term in the second row, and $10=\left( {\begin{array}{c} {5}\\ {3} \end{array}}\right) =\left( {\begin{array}{c} {5}\\ {2} \end{array}}\right)$ for the next two tensorproducts. The final term in the third row has $30=\left( {\begin{array}{c} {5}\\ {2} \end{array}}\right) \left( {\begin{array}{c} {3}\\ {2} \end{array}}\right)$ labellings, as there are $\left( {\begin{array}{c} {5}\\ {2} \end{array}}\right)$ possibilities to label the edges of the first $b_2$ banana, and then $\left( {\begin{array}{c} {3}\\ {2} \end{array}}\right)$ to label the second one

Explicitly, $\Phi _{MS}^D(b_3)$ reads, for example,

$$\begin{aligned} \Phi _{MS}^D(b_3)= & {} -\langle \Phi ^D(b_3)\rangle +\sum _{cycl}\langle \langle \Phi ^D(b_2(e_i,e_j))\rangle \Phi ^D(t_1(e_k))\rangle +\Phi ^D(b_3)\\{} & {} -\sum _{cycl}\langle \Phi ^D(b_2(e_i,e_j))\rangle \Phi ^D(t_1(e_k)). \end{aligned}$$

Here, $\Phi ^D$ are unrenormalized Feynman rules in D dimensions which evaluate into a Laurent series in $D-2n$, n a suitable integer, $\langle \ldots \rangle$ is the projection onto the pole part and the sum is over the three cyclic permutations of i, j, k.

This MS-renormalization results $\Phi _{MS}^D(b_n)$ can be related to $\Phi _R^D(b_n)$ if so desired. See also the discussion with regards to MS and tadpoles in [28].

Appendix C: Tensor structure

1.1 Tensor integrals

We are not interested in $\Phi _R^D(b_n)$ alone. To satisfy the needs of computational practice, we should also raise the powers of quadrics by taking derivatives $\partial _{m_j^2}^k$ with respect to mass squares $m_j^2$ and we should allow scalar products $k_i\cdot k_j$ in the numerator.

For such a generalization to arbitrary powers of propagators and numerator structures, we use the notation

$$\begin{aligned} \Phi _R^D(b_n)_{\nu }(s,\{m_i^2\}), \end{aligned}$$

where $\nu$ is a $\left( \frac{n(n+1)}{2}-1\right)$-dimensional row vector with integer entries (see Sect. (2.5.1.)) in [10].

• The first n entries $\nu _i$, $1\le i\le n$ give the powers of the n edge propagators $\frac{1}{Q_e}$,

• the $(n-2)$ entries $\nu _i$, $(n+1)\le i\le (2n-2)$ are reserved for powers of $k_i\cdot k_n$ ($1\le i\le (n-2)$),

• the $(n-2)$ entries $\nu _i$, $(2n-1)\le i\le (3n-4)$ are reserved for powers of $k_2^2,\ldots , k_{n-1}^2$,

• and the remaining $(n-2)(n-3)/2$ entries are reserved for powers $\nu _{jl}$ of $k_j\cdot k_l$, $|j-l|\gneq 1$, $1\le j,l\le (n-1)$ and $3n-3\le i\le \left( \frac{n(n+1)}{2}-1\right)$.

This is all what is needed as $k_1^2=Q_1+m_1^2$ and $2k_i\cdot k_{i-1}=k_i^2+k_{i-1}^2-Q_i-m_i^2$, $n\ge i\ge 2$.

For example,

$$\begin{aligned}{} & {} \Phi _R^D(b_4)_{(\nu _1,\ldots ,\nu _{13})}(s,m_1^2,\ldots ,m_4^2) \\{} & {} \quad = \int _{\mathbb {M}_4}\omega ^D_{(3)}\prod _{j=0}^{3}\frac{(k_1\cdot k_4)^{\nu _5}(k_2\cdot k_4)^{\nu _6}(k_2^2)^{\nu _7}(k_3^2)^{\nu _8}(k_1\cdot k_3)^{\nu _{13}}}{\left( (k_{j+1}-k_j)^2-m_{j+1}^2\right) ^{\nu _{j+1}}}. \end{aligned}$$

For the imaginary part, we have correspondingly

$$\begin{aligned}{} & {} \Im \left( \Phi _R^D(b_4)_{(\nu _1,\ldots ,\nu _{13})}\right) (s,m_1^2,\ldots ,m_4^2) \\{} & {} \quad = \int _{\mathbb {M}_4}\omega ^D_{(3)} \prod _{j=0}^{3}\partial _{m_{j+1}^2}^{\nu _{j+1}} \left( \left( \prod _{l=0}^{3}\delta _+(k_{l+1}-k_l)^2-m_{l+1}^2)\right) \right. \\{} & {} \qquad \left. \times (k_1\cdot k_4)^{\nu _5}(k_2\cdot k_4)^{\nu _6}(k_2^2)^{\nu _7}(k_3^2)^{\nu _8}(k_1\cdot k_3)^{\nu _{13}}\right. \Biggr ). \end{aligned}$$

We discuss differential equations for $\Phi _R^D(b_n)_\nu$, as well as partial integration identities and the reduction to master integrals starting from our representation for $\Phi _R^D(b_n)_\nu$ in Sects. (3.3, 3.4).

1.2 Dispersion for $\Phi _R^D(b_n)_\nu$

For banana graphs $b_n$ on two vertices, dispersion for tensor integrals is rather simple:

$$\begin{aligned} \Phi _R^D(b_n)_\nu (s,s_0,\{m_j^2\})=\frac{(s-s_0)^{|[n,\nu ]|}}{\pi } \int _{(m_1+\cdots m_n)^2}^\infty \frac{V_{[n,\nu ]}^D}{(x-s)(x-s)^{|[n,\nu ]|}} \textrm{d}x, \end{aligned}$$

(C.1)

where $|[n,\nu ]|-1$ is the superficial degree of divergence of $\Phi _R^D(b_n)_\nu$ according to $\nu$:

(C.2)

This is based on

$$\begin{aligned} \Im \left( \Phi _R^D(b_n)_\nu \right) (s,s_0,\{m_j^2\})= \Theta (s-(m_1+\cdots m_n)^2)V_{[n,\nu ]}^D. \end{aligned}$$

For $V_{[n,\nu ]}^D$, see Eqs. (2.25–2.29).

Appendix D: Pseudo-thresholds

Let us remind ourselves of a parametric analysis of the second Symanzik polynomial (with masses) $\Phi$ for the banana graphs $b_b$:

$$\begin{aligned} \varphi (b_n)(s)=\left( \prod _{j=1}^n A_j\right) \left( s-\left( \sum _{j=1}^n m_j^2A_j\right) \left( \sum _{j=1}^n\frac{1}{A_j}\right) \right) . \end{aligned}$$

(D.1)

The equation

$$\begin{aligned} \varphi (b_n)(m_{\textbf{normal}}^n)=0, \end{aligned}$$

has a solution in the simplex $A_i>0$ for positive $A_i$ given by $A_im_i=A_jm_j$.

For m any pseudo-mass, the solution of $\varphi (b_n)(m)=0$ requires at least one $A_i$ to be negative and it hence gives no monodromy on the physical sheet.

Still, the variations associated with pseudo-masses and thresholds are needed for a full analysis of $\Phi _R^D(b_n)$ to find their Hodge structure.

So, let $\sigma _n$ be a sequence of the form

$$\begin{aligned} \sigma ^n:=(\pm m_1\pm m_2\pm \cdots \pm m_n), \end{aligned}$$

with a sign chosen for each entry $m_i$. Let $p(i)\in \{\pm 1\}$ be the sign of the i-entry. A global sign change leaves the pseudo-thresholds invariant ($|a-b|=|b-a|$), so we have $2^{n-1}$ choices and adopt to the convention $p(1)=+1$.

For a flag

$$\begin{aligned} (b_2\subset b_3\subset \cdots \subset b_n), \end{aligned}$$

this determines subsequences $\sigma ^2\subset \sigma ^3\subset \cdots \sigma ^n$ in an obvious manner.

Define

$$\begin{aligned} \textrm{up}_n^{j,\sigma }:=\frac{s_n^j+m_{n-j}^2 -\Bigl (\overbrace{\sum _{||,i=1}^{n-j-1}p(i)m_i}^{m_{\sigma ^{n-j-1}}}\Bigr )^2}{2\sqrt{s_n^{j}}}, \end{aligned}$$

(D.2)

which also defines the pseudo-mass $m_{\sigma ^{n-j-1}}$:

$$\begin{aligned} m_{\sigma ^{n-j-1}}= & {} \sum _{||,i=1}^{n-j-1}p(i)m_i \\= & {} \underbrace{|\cdots ||}_{(n-1)\,{\text {bars}}}m_1+p(2)m_2|+p(3)m_3|+\cdots |+p(n-j-1)m_{n-j-1}|. \end{aligned}$$

Define

$$\begin{aligned} \Theta _{n,+}=\Theta (s-(m_n+m_{\sigma ^{n-1}})^2),\, \Theta _{n,-}=\Theta ((m_n-m_{\sigma ^{n-1}})^2-s). \end{aligned}$$

Now, set for $p(n-1)=+1$:

$$\begin{aligned}{} & {} \textbf{Var}(b_n^\sigma ) = \Theta _{n,p(n))}\\{} & {} \quad \times \underbrace{\omega _{\frac{D}{2}}\int _{m_n}^{\textrm{up}_n^{0,\sigma }}V_{\sigma ^{n-1},n-1}^D(s_n^0 -2\sqrt{s_n^0}y_{n-1}+m_n^2,m_1^2,\ldots ,m_{n-1}^2) \sqrt{y_{n-1}^2-m_n^2}^{D-3}dy_{n-1}}_{V^D_{\sigma ^n,n},\,p(n-1)=+1}. \end{aligned}$$

and for $p(n-1)=-1$:

$$\begin{aligned}{} & {} \textbf{Var}(b_n^\sigma ) = \Theta _{n,p(n))}\\{} & {} \quad \times \underbrace{\omega _{\frac{D}{2}}\int _{\textrm{up}_n^{0,\sigma }}^{\infty }V_{\sigma ^{n-1},n-1}^D (s_n^0-2\sqrt{s_n^0}y_{n-1}+m_n^2,m_1^2,\ldots ,m_{n-1}^2) \sqrt{y_{n-1}^2-m_n^2}^{D-3}dy_{n-1}}_{V^D_{\sigma ^n,n},\,p(n-1)=-1}. \end{aligned}$$

Apart from the variation for the normal threshold (with $p(i)=+1$ for all $1\le i\le n$) which gives $\textbf{Var}(b_n^{(+m_1,+m_2,\ldots ,+m_n)})=\Im \left( \Phi _R^D(b_n)\right)$, we get $2^{n-1}-1$ further variations corresponding to pseudo-masses and their pseudo-thresholds. They will be discussed elsewhere.

Appendix E: $b_3$ parametrically

Let us recapitulate $b_3$ in the parametric representation. We list basic considerations. A detailed analysis in the view of [37, 38] is left to future work.

1.1 E.1. The parametric integral

Let ${\textbf{Q}}_{b_3}$ be the one-dimensional real vector space spanned by $s=k_3^2$, the square of the Minkowski four-momenta $k_3,-k_3$ assigned to the two vertices of $b_3$. Let $\mathbb {P}_{b_3}=\mathbb {P}^2(\mathbb {R}_+)$ be a projective space given by the ratios of the nonnegative side lengths of the internal edges of $\Theta$.

The parametric integrand function (we consider masses as implicit parameters)

$$\begin{aligned} F_{b_3}:{\textbf{Q}}_{b_3}\times {\textbf{Q}}_{b_3}\times \mathbb {P}_{b_3}\rightarrow \mathbb {C} \end{aligned}$$

is (see, for example, Sect. (5.2.1.) in [39])

$$\begin{aligned} F_{b_3}(s,s_0;p):= & {} (s-s_0)A_1A_2A_3\frac{\ln \left( \frac{\Phi _\Theta (s;p)}{\Phi _\Theta (s_0;p)}\right) }{\psi _\Theta ^3}\nonumber \\{} & {} \quad + (s_0A_1A_2A_3-(m_1^2A_1+m_2^2A_2+m_3^2A_3)\psi _\Theta ) \nonumber \\{} & {} \quad \times \frac{\ln \left( \frac{\Phi _\Theta (s;p)}{\Phi _\Theta (s_0;p)}\right) - (s-s_0)\left( \partial _{s}\ln \left( \frac{\Phi _\Theta (s;p)}{\Phi _\Theta (s_0;p)}\right) \right) _{s=s_0}}{\psi _\Theta ^3}. \end{aligned}$$

(E.1)

Here,

$$\begin{aligned} \Phi _{b_3}: {\textbf{Q}}_\Theta \times \mathbb {P}_\Theta \rightarrow \mathbb {C} \end{aligned}$$

is

$$\begin{aligned} \Phi _{b_3}(r;p)= & {} rA_1A_2A_3-(m_1^2A_1+m_2^2A_2+m_3^2A_3)\psi _{b_3},\\ \psi _{b_3}= & {} A_1A_2+A_2A_3+A_3A_1. \end{aligned}$$

Note $F_{b_3}(s,p)$ and $\partial _{s} F_{b_3}(s,p)$ both vanish at $s=s_0$ for all p, so these are on-shell renormalization conditions.

The parametric form is the integrand

$$\begin{aligned} \textrm{Int}_{b_3}(s,s_0;p):= & {} F_\Theta (s,s_0,p) \Omega _{b_3},\\ \Omega _{b_3}= & {} +A_1\,dA_2\wedge dA_3-A_2\,dA_1\wedge dA_3+A_3\,dA_1\wedge dA_2. \end{aligned}$$

We then have the renormalized value³

$$\begin{aligned} \Phi _R^D(b_3)(s,s_0)=\int _{\mathbb {P}^2(\mathbb {R}_+)}\textrm{Int}_\Theta (s,s_0;p), \end{aligned}$$

(E.2)

from integrating out p which is the parametric equivalent of Eqs. (2.1, 2.9).

1.2 E.2. Sectors and fibrations

To study fibrations in our integrand, we start from the fact that there are six orderings of the edge lengths for the three edge variables $A_i$.

Consider, for example, the sectors $1>3>2$ and $3>1>2$ of Fig. 5 so that edge $e_2$ has the smallest length. For the choice $1>3>2$ rescale⁴

$$\begin{aligned} A_2=a_2A_1,\,A_3=a_3A_1, \end{aligned}$$

and in that sector $1>3>2$, we have

$$\begin{aligned} \int _{\mathbb {P}^2(\mathbb {R}_+)\cap (1>3>2)}F_{b_3} \Omega _{b_3} =\int _0^\infty \left( \int _0^{a_3}F_{b_3}(1,a_2,a_3)\textrm{d}a_2\right) \textrm{d}a_3. \end{aligned}$$

A further change $a_2=a_3b_2$ leads to a sector decomposition (in the sense of physicists)

$$\begin{aligned} \int _0^\infty \left( \int _0^{1}a_3F_{b_3}(1,b_2a_3,a_3)\textrm{d}b_2\right) \textrm{d}a_3 = \int _0^{1}\underbrace{\left( \int _0^\infty a_3F_{b_3}(1,b_2a_3,a_3)\textrm{d}a_3\right) }_ {\textrm{Fib}(b_2)}\textrm{d}b_2. \end{aligned}$$

For any chosen $0<b_2<1$, $a_3F_{b_3}(1,b_2a_3,a_3)$ gives points on the corresponding chosen fibre and $\textrm{Fib}(b_2)$ is the integral along that fibre. Integrating $b_2$ integrates all fibre integrals $\textrm{Fib}(b_2)$ to the two sector integrals on both sides of the spine.

In fact, for $0<a_3<m_1/m_3$ we are on the left of the spine and for $m_1/m_3<a_3<\infty$ on the right.

Let us look at $\Phi _{b_3}$ under the rescalings.

$$\begin{aligned} \Phi _{b_3}(A_1,A_2,A_3)= & {} sA_1A_2A_3-(m_1^2A_1+m_2^2A_2+m_3^2A_3)(A_1A_2+A_2A_3+A_3A_1))\\\rightarrow & {} sa_2a_3-(m_1^2+m_2^2a_2+m_3^2a_3)(a_2+a_2a_3+a_3))\\\rightarrow & {} sb_2a_3^2-(m_1^2+m_2^2b_2a_3+m_3^2a_3)(b_2a_3+b_2a_3^2+a_3))\\= & {} a_3(sb_2a_3-(m_1^2+m_2^2b_2a_3+m_3^2a_3)(b_2+b_2a_3+1))=:\tilde{\Phi }_{b_3}(s,b_2,a_3). \end{aligned}$$

For $\psi _{b_3}$, we find

$$\begin{aligned}{} & {} (A_1A_2+A_2A_3+A_3A_1)\\{} & {} \quad \rightarrow (a_2+a_2a_3+a_3)\\{} & {} \quad \rightarrow a_3(b_2+b_2a_3+1). \end{aligned}$$

We thus find in the region where $e_2$ is the smallest edge the integrand function $\textrm{Int}_{{b_3},2}(b_2,a_3)$

$$\begin{aligned} \textrm{Int}_{{b_3},2}(b_2,a_3):= & {} a_3F_{b_3}(1,b_2a_3,a_3)=(s-s_0)b_2a_3\\{} & {} \quad \times \frac{\ln \overbrace{\left( \frac{sa_3b_2-(m_1^2+m_2^2b_2a_3+m_3^2a_3)(1+b_2(1+a_3))}{s_0a_3b_2 -(m_1^2+m_2^2b_2a_3+m_3^2a_3)(1+b_2(1+a_3))}\right) }^{\frac{\tilde{\Phi }_{b_3}(s;b_2,a_3)}{\tilde{\Phi }_{b_3}(s_0;b_2,a_3)}}}{(b_2(1+a_3)+1)^3}\\{} & {} \quad +(s_0b_2a_3-(m_1^2+m_2^2b_2a_3+m_3^2a_3)(b_2(1+a_3)+1)) \\{} & {} \quad \times \frac{\ln \left( \frac{\tilde{\Phi }_{b_3}(s;b_2,a_3)}{\tilde{\Phi }_{b_3}(s_0;b_2,a_3)}\right) - (s-s_0)\left( \partial _{s}\ln \left( \frac{\tilde{\Phi }_{b_3}(s;b_2,a_3)}{\tilde{\Phi }_{b_3}(s_0;b_2,a_3)} \right) \right) _{s=s_0}}{(b_2(1+a_3)+1)^3}. \end{aligned}$$

Note that $\textrm{Int}_{{b_3},2}(0,a_3)=0$ as it must be as petals evaluate to zero under renormalized Feynman rules in on-shell renormalization conditions.

Finally,

$$\begin{aligned} {\textrm{Fib}(b_2)}=\int _0^\infty \textrm{Int}_{{b_3},2}(b_2,a_3)\textrm{d}a_3. \end{aligned}$$

A point along the $(1=3)$-line of the spine is given by $(1,b_2,1)\in \mathbb {P}_{b_3}$, for all $0<b_2<1$.

Remark 3.10

Upon rescaling in each of the sectors in the three cubes of Fig. 5 accordingly and summing over sectors, we get a symmetric representation equivalent to averaging over the three possible ways of expressing Eq. (2.7) using any of $s_3^1(y_2,m_i^2)$ and similar to [9]. |