Abstract
We review Lie polynomials as a mathematical framework that underpins the structure of the so-called double copy relationship between gauge and gravity theories (and a network of other theories besides). We explain how Lie polynomials naturally arise in the geometry and cohomology of \(\mathcal {M}_{0,n}\), the moduli space of n points on the Riemann sphere up to Mobiüs transformation. We introduce a twistorial correspondence between the cotangent bundle \(T^*_D\mathcal {M}_{0,n}\), the bundle of forms with logarithmic singularities on the divisor D as the twistor space, and \(\mathcal {K}_n\) the space of momentum invariants of n massless particles subject to momentum conservation as the analogue of space–time. This gives a natural framework for Cachazo He and Yuan (CHY) and ambitwistor-string formulae for scattering amplitudes of gauge and gravity theories as being the corresponding Penrose transform. In particular, we show that it gives a natural correspondence between CHY half-integrands and scattering forms, certain \(n-3\)-forms on \(\mathcal {K}_n\), introduced by Arkani-Hamed, Bai, He and Yan (ABHY). We also give a generalization and more invariant description of the associahedral \(n-3\)-planes in \(\mathcal {K}_n\) introduced by ABHY.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Colour-kinematics duality and the double copy [1, 2] have had a powerful influence on recent developments in scattering amplitudes. They stem from the KLT relations in string theory [3] between gravity and Yang–Mills tree-amplitudes and have been developed as a tool for the study of multiloop gravity amplitudes and more recently for applications to perturbative classical gravity calculations in connection with gravitational waves [4]. Notwithstanding the physical applications, the underlying mathematical framework is perhaps rather surprising even at tree level. There is little hint of such a double copy structure in standard approaches to perturbation theory of the classical nonlinear theories involved. The purpose of this article is to develop some of the underpinning mathematical structures. We build on observations by Kapranov in an after dinner talk [5] concerning the relevance of Lie polynomials, both in the double copy and in the Parke–Taylor expressions that pervade the subject. We also build on the recent work by Arkani-Hamed, Bai, He and Yan [6] that introduces differential forms in the space of kinematic invariants, \(\mathcal {K}_n\). We tie them together by means of a double fibration correspondence that leads to a Penrose-like transform for the formulae of Cachazo He and Yuan (CHY) arising from the scattering equations [7, 8].
The first section provides an elementary review of the theory of Lie polynomials as relevant to this topic and expresses standard facts about the double copy in this language. In particular, the trivalent diagrams of BCJ are a representation of elements \(\Gamma \in Lie(n-1)\), the space of Lie polynomials of degree \(n-1\), and BCJ numerators \(N_\Gamma \) are homomorphisms \(N:Lie(n-1)\rightarrow V\) where V is some vector space of polynomials in the polarization data and momenta.
We next review the role played by Lie polynomials in the geometry of the moduli space \(\mathcal {M}_{0,n}\) of n points \(\sigma _i\) in \(\mathbb {CP}^1\), both in describing the compact cycles in the homology \(H_{n-3}(\mathcal {M}_{0,n}-D)\), which is isomorphic to \(Lie(n-1)\), and dually the relative cocycles in \(H^{n-3}(\mathcal {M}_{0,n},D)\), represented by the top degree holomorphic Parke–Taylor forms.
With these preliminaries in hand, we study a double fibration between the space of Mandelstam variables, \(\mathcal {K}_n\), and \(T^*_D\mathcal {M}_{0,n}\)
where p forgets the second factor and and q is defined by the incidence relations
which give the left hand side of the scattering equations. In the language of this correspondence, the CHY formulae are a Penrose transform, being simply the push down of the pullback of certain forms on \(\mathbb {T}\). We investigate other more geometrical aspects of the Penrose transform. In particular, we show that the top power of the symplectic form \(\omega ^{n-3}\) provides a correspondence between certain \((n-3)\)-forms \(w_\Gamma \) on \(\mathcal {K}_n\) that were introduced by ABHY and homology classes in \(\mathcal {M}_{0,n}\). ABHY use the \(w_\Gamma \) as numerators so that given a set of conventional numerators N one can associate a scattering \((n-3)\)-form \(\Omega _N\). These arise from our double fibration via a Penrose transform also. Dually, ABHY introduce associahedral \((n-3)\)-planes in \(\mathcal {K}_n\) that can be used to convert a scattering form into a conventional amplitude. We give an improved and extended definition of these and show how they tie into the geometry of the correspondence.
2 The double copy and Lie polynomials
Colour structures for n-point amplitudes are degree n invariant polynomials of weight one in each of the n Lie algebra ‘colours’ of the external particles. These naturally arise in Feynman rules as trivalent Feynman diagrams whose vertices are the structure constants of some unspecified Lie algebra. If we fix the nth particle, and an invariant inner product on the Lie algebra, at tree-level, such a polynomial can be realized as the inner product of the nth colour with the Lie algebra element with a Lie polynomial formed by successive commutators of the \(n-1\) other colours working through the diagram back from the nth particle. This section reviews material concerning such colour structures in the language of free Lie algebras and Lie polynomials together with their duality with words formed from permutations of the \(n-1\) labels of the first \(n-1\) external particles. A classic text on free Lie algebras is [9].
2.1 A review of words, Lie polynomials and trees
The space of words, \(W({n-1})\), is the \((n-1)!\)-dimensional linear span of words
where the letters \(x_{a(i)}\in \{x_1,\ldots ,x_{n-1}\}\) are all distinct, so that the a’s define permutations on \(n-1\) letters. There is a natural bilinear inner product on \(W(n-1)\) that is defined on monomials a and b by
i.e. (a, b) is 1 if a and b are the same word, and 0 otherwise. A ‘Lie polynomial’ in \(W(n-1)\) is any expression formed by taking \(n-2\) iterated commutators of the \(x_i\). An example is
where \([x_i,x_j]\) is the commutator, \(x_ix_j-x_jx_i\). Let \(Lie(n-1)\) be the linear subspace of \(W(n-1)\) generated by all Lie polynomials \(\Gamma \) of weight \(n-1\) in the \(n-1\) variables, \(x_1, \ldots , x_{n-1}\), with weight one in each. Every Lie monomial \(\Gamma \) defines a rooted trivalent tree decorated by an orientation. We denote this tree also by \(\Gamma \). An orientation of the tree can be presented as a planar embedding, where two planar embeddings have the same orientation if they differ from one another by an even number of flips. Thus, for example, the monomial \(\Gamma = [2,[[1,3],[5,4]]]\) is associated with the following two planar embeddings, among others.

The Jacobi identity implies the vanishing of the sum of the three four-point oriented trees corresponding to an s, t and u-channel exchange graph.

We will denote three Lie polynomials or corresponding graphs that differ only on such a four point subgraph by \(\Gamma _s, \Gamma _t\) and \(\Gamma _u\), and we will consequently have
The Lie monomial notation is useful for keeping track of the orientations of trees. Recall the inner product ( , ) defined on words. For a Lie monomial \(\Gamma \), \((\Gamma ,a)\) is the coefficient of a in the expansion of its Lie monomial \(\Gamma \). When \(\Gamma \) is not planar for the ordering a, \((\Gamma ,a) = 0\). When \(\Gamma \) is planar for the ordering a, \((\Gamma , a)\) is the orientation of that planar embedding, either \(+1\) or \(-1\). As an application of the notation, we can write
which is simply the expansion of the commutators in \(\Gamma \).
There are many characterizations of \(Lie(n-1)\) as a subspace of \(W(n-1)\) [9], and some of these have long been known in the physics literature as relations among gauge theory tree amplitudes. For instance, the U(1) decoupling identity is a consequence of Ree’s theorem.
Proposition 2.1
(Ree [10]) A polynomial \(w\in W[n-1]\) is a Lie polynomial iff  for all nontrivial shuffles
for all nontrivial shuffles  .Footnote 1
.Footnote 1
This proposition implies that \(Lie(n-1)^*\), the dual vector space of \(Lie(n-1)\), can be understood as the quotient vector space \(W(n-1)/\text {Sh}\), where \(\text {Sh}\) is the subspace generated by all nontrivial shuffles.
Lemma 2.2
(Radford [11]) The \((n-2)!\) words of the form 1a are a basis for \(Lie(n-1)^*\).
The direct expansion of \(\Gamma _{1a}\) into words is

where |u| is the length of u. It follows that
In other words, we have the following
Lemma 2.3
The Kleiss–Kuijf (KK) basis of \(Lie(n-1)^*\) given by words 1a is dual to the DDM basis of \(Lie(n-1)\) given by combs \(\Gamma _{1a}\).
An immediate consequence of this Lemma is that any \(b+\text {Sh} \in W(n-1)/\text {Sh}\) may be expanded in this basis as
Dually, given that the combs are a basis for \(Lie(n-1)\), a polynomial w is a Lie polynomial iff there is an expansion of w in the combs \(\Gamma _{1a}\). Using Lemma 2.3, we find that
By Eq. (2.3), we find that

where \(\bar{u}\) is the reversal of u. This identity implies the Kleiss–Kuijf relations, which we can restate as a theorem about Lie polynomials.
Proposition 2.4
(Kleiss–Kuijf) A polynomial \(w\in W[n-1]\) is a Lie polynomial iff the Kleiss–Kuijf relations [12] hold:

2.2 The geometry of \(\mathcal {K}_n\)
Write \(\mathcal {K}_n\simeq \mathbb {R}^{n(n-3)/2}\) for the vector space of Mandelstam variables. In coordinates \(s_{ij}\), \(i,j=1,\ldots , n\) (with \(s_{ij}=s_{ji}\), \(s_{ii}=0\)), \(\mathcal {K}_n\) is the hyperplane given by the equations
In terms of null momenta, \(k_i^\mu \), these variables are defined by \(s_{ij} = 2 k_i\cdot k_j\), and so are subject to Gram determinant conditions. We ignore these Gram conditions and treat the variables \(s_{ij}\) as independent.Footnote 2 For amplitudes, the key geometric structure in \(\mathcal {K}_n\) is the factorization hyperplanes given by \(s_I=0\), where \(I\subset \{1,2,\ldots ,n\}\) and
Let \(\bar{I}\) be the complement of I, so that \(s_{\bar{I}}=s_I\) by (2.7). Locality states that the only singularities of tree amplitudes are simple poles on these hyperplanes. A further requirement is that a double pole on the intersection of \(s_I=0\) and \(s_J=0\) occurs in an amplitude only if \(I\subset J\) or \(\bar{J}\). It follows that the allowed pole structure of a contribution to an n-point amplitude has poles along at most \(n-3\) factorization hyperplanes \(s_{I_p}=0\) for \(p=1,\ldots ,n-3\). Such choices are in one-to-one correspondence with trivalent (and unoriented) trees.
2.3 The double copy from biadjoint scalars to gauge and gravity theories
The double copy principle is that massless n-point tree amplitudes for a large web of important theories, including many gauge and gravity theories, can be expressed as a double copy in the form
Here, the denominators
are the propagator factors associated with the graph \(\Gamma \) thought of as a Feynman graph. Further, each trivalent diagram \(\Gamma \) has a pair of numerator factors \(N_\Gamma \) and \(\tilde{N}_\Gamma \) that are functions of momenta, polarization data, flavour and colour. Such factors are said to be local if they are polynomial, i.e. admit no spurious singularities.
The key additional feature required to be a BCJ numerator is that \(N_\Gamma \) and \(\tilde{N}_\Gamma \) should represent homomorphisms from Lie polynomials to some vector space V of functions,
Thus, for any three graphs \(\Gamma _s\), \(\Gamma _t\) and \(\Gamma _u\) satisfying \(\Gamma _s+\Gamma _t+\Gamma _u=0\) as Lie polynomials, we must also have that
For this reason, the numerators are not uniquely determined: given a triple \(\Gamma _s\), \(\Gamma _t\) and \(\Gamma _u\) we can perform the shift \(\delta (N_{\Gamma _s}, N_{\Gamma _t}, N_{\Gamma _u})=(s,t,u)A\) for any \(A\in V\). It also follows that BCJ numerators can be determined from their values on a comb basis \(N_{\Gamma _{1a}}\) by
In the case of Yang mills, the claim of BCJ [1] is that
for some kinematic numerators \(N_\Gamma ^{k,\epsilon }\) depending linearly on each polarization vector \(\epsilon _i\) and rationally (or even polynomially) on the momenta satisfying (2.12). The key nontrivial output of the double copy is that gravity amplitudes are obtained when \(\tilde{N}_\Gamma =N_\Gamma ^{k,\epsilon }\). The same numerators determine both the colour-ordered Yang–Mills amplitude with order a is then
and gravity amplitudes by
The most basic theory in this framework is the bi-adjoint scalar theory whose colour ordered amplitudes are given by
and we can introduce two underlying abstract amplitudes for these theories given by
Substituting (2.13) into (2.15), we obtain Yang–Mills amplitudes in terms of numerators and m(a, b) by
with a similar form for gravity
We briefly remark that the basic kinematic numerators \(N^{k,\epsilon }_\Gamma \) for Yang Mills were obtained in [13]. Related numerators for other theories can be deduced from the Yang–Mills ones. The numerators \(N^{k,\epsilon ,m}_\Gamma \) (see Table 1) can be related to \(N^{k,\epsilon }_\Gamma \) by taking some components of the polarization vectors to be in a higher dimension to the momenta, as described (at the level of the CHY integrands) in [14]. The amplitudes for the theories in Table 1 are then given by
See [4] for an up-to-date list of available numerators and their details.
We cannot simply invert (2.19) to obtain the \(N_{1b}\) as m(1a, 1b) is not invertible. Indeed, all theories that can be expressed in this double-copy format with one explicit Lie polynomial factor satisfy the fundamental BCJ relations [1]. There are many forms of the relations, one version being, for a wordFootnote 3\(a\in W(n-2)\)

Thus, (2.19) determines the \(N_{1a}\) only up to the addition of multiples of the BCJ relations. This freedom can be used to set all but \((n-3)!\) of the \(N_{1a}\) to zero, but this is at the expense of requiring numerators that are rational rather than polynomial in the momenta, so that the remaining numerators will then have spurious poles.
2.4 A note on the kinematic algebra
Given a Lie algebra, g, with an inner product, a Lie monomial \(\Gamma \in Lie(n-1)\) gives rise to a ‘colour factor’, \(c_\Gamma \), for every n-tuple of Lie algebra elements, \(T_1,\ldots ,T_n\),
This means we have a map
and it is a homomorphism, since the \(c_{\Gamma }\) clearly satisfy the Jacobi identity. The BCJ kinematic numerators for Yang–Mills, \(N^{k,\epsilon }_\Gamma \), likewise satisfy the Jacobi identity leading to a suggestion that they might arise from some kinematic algebra, an as yet unidentified Lie algebra. If that were the case, the double copy would be replacing the Yang–Mills Lie algebra numerator \(c_\Gamma \) with kinematic numerators \(N^{k,\epsilon }_\Gamma \). However, (2.12) does not imply that there is a Lie algebra, g, such that \(N_\Gamma \) is the colour factor for that Lie algebra. This is clear for example in the case of \((\Gamma ,a)\) (and the forms \(w_\Gamma \) below). Nevertheless, there has been some interesting work to identify such a Lie algebra associated with the kinematic numerators [16,17,18], (2.12).
In general, a homomorphism from \(Lie(n-1)\) to a vector space of functions can be given by choosing any \((n-2)!\) such functions, as in Eq. (2.13). These have been identified in the case of Yang–Mills by various authors by recursion and in particular for Yang Mills in [19].
3 Trees and words in \(\mathcal {M}_{0,n}\)
In this section, we consider the homology and cohomology of \(\mathcal {M}_{0,n}\), the Deligne–Mumford compactification of the space of n distinct points on the Riemann sphere \(\mathbb {CP}^1\) up to Möbius transformations. We first recall the basic properties of \(\mathcal {M}_{0,n}\). \(\mathcal {M}_{0,n}\) has a normal crossing divisor D, whose top dimensional strata are the codimension one components \(D_I\), for \(I\subset \{1,\ldots ,n\}\), where the points in I bubble off onto a new \(\mathbb {CP}^1\), attached to the first by a node.

Two such components, \(D_I\) and \(D_J\), intersect iff \(I\subset J\) or \(I\subset \bar{J}\). Then, \(D_I\cap D_J\) corresponds to nodal curves with 3 components; for example when \(I\subset J\), one containing the points I, the second \(J-I\) and the third \(\bar{J}\). It follows that the maximal intersections of these \(D_I\) are points, \(D_\Gamma \in \mathcal {M}_{0,n}\), given by the intersection of \(n-3\) compatible \(D_{I_p}\). Each such point corresponds to a nodal curve with \(n-3\) components, each with three points that are either nodes or marked points. Such a tuple of compatible sets \(I_p\) defines a trivalent tree, \(\Gamma \), with the components corresponding to the vertices and nodes to propagators. The 0-dimensional strata of D are thus in one-to-one correspondence with trivalent (and unoriented) trees.
The complement of the divisor in \(\mathcal {M}_{0,n}\) is an open top cell, \(\mathcal {M}_{0,n}^\#:= \mathcal {M}_{0,n} - D\), on which we can use simplicial coordinates \(\sigma _i\), \(i = 1, \ldots ,n\), with the gauge fixing \((\sigma _1,\sigma _{n-1},\sigma _n) = (0,1,\infty )\). However, in order to study \(\mathcal {M}_{0,n}\) in the neighbourhood of the divisor, it is useful to introduce dihedral coordinates, which are a set of cross-ratios of the points. There is one such set of coordinates for every dihedral structure [20]. Given an ordering, a, the associated dihedral coordinates are the cross-ratios
for \(1<i+1<j\) and \(\sigma _{ij} = \sigma _i - \sigma _j\). Each such cross-ratio \(u_{ij}\) is associated with the cord, \((a_i,a_{j+1})\), of the n-gon labelled by the ordering, a. We will also denote \(u_{ij}\) by \(u_I\), where \(I \subset \{1,\ldots ,n\}\) is the subset \(\{a_i,\ldots ,a_{j-1}\}\) or its complement.
If the ordering a is compatible with the set \(I\subset \{1,\ldots ,n\}\), then the divisor component \(D_I\) can be seen in these coordinates as the locus of \(u_I = 0\) [20]. The points \(D_\Gamma \) in the divisor are, in dihedral coordinates, given as follows. Choose any ordering a such that \(\Gamma \) is planar for a (i.e. \((\Gamma ,a)\ne 0\)), with propagators given by the subsets \(I_p \subset \{1,\ldots ,n-1\}\). In the dihedral coordinates associated with a, there are \(n-3\) cross-ratios \(u_{I_p}\) corresponding to the propagators of \(\Gamma \). The point \(D_\Gamma \) is then given, in these coordinates, by \(u_{I_p}= 0\) for all \(p=1,\ldots ,n-3\).
The \(u_{I_p}\) form a good set of coordinates near \(\Gamma \). Relations between such coordinate systems near different such points are obtained from the non-crossing identity
where for \(k<l\), \((k,l)\in (i,j)^c\) means that the diagonal (k, l) of the polygon with vertices \(\{1,\ldots ,n\}\) crosses the diagonal (i, j).
3.1 The cohomology of \(\mathcal {M}_{0,n}\) and Parke–Taylor forms
The dimensions of the cohomology groups of \(\mathcal {M}_{0,n}\) are given by the Poincaré polynomialFootnote 4
The cohomology ring is generated by the \(\, \mathrm {d}\log \sigma _{ij}\) in the standard gauge fixing, subject to the quadratic relations
This gives the dimension of \(\Gamma (\Omega _D^1)\) as \(\sum _{k=2}^{n-2}=n(n-3)/2\) as claimed earlier. It also follows that the top cohomology \(H^{n-3}(\mathcal {M}_{0,n},D)\simeq \Gamma (\mathcal {M}_{0,n},\Omega ^{n-3}_D)\) has dimension \((n-2)!\). A natural spanning set for \(\Gamma (\Omega ^{n-3}_D)\) is provided by the Parke–Taylor forms
In our gauge fixing
yielding now for a general choice of permutation a of \(1,\ldots ,n-1\)
The \((n-1)!\) Parke–Taylor forms defined in this way are not linearly independent, because they satisfy the shuffle relations of 2.4,

for b, c nontrivial, identicallyFootnote 5 [23]. Thus, following Proposition 2.4, we deduce that
Moreover, by Lemma 2.2, one can take a KK basis for \(H^{n-3}(\mathcal {M}_{0,n},D)\), given by the \(PT_{1a}\), for all \((n-2)!\) permutations a. It follows from Eq. (2.4) that we have the following identity.
Lemma 3.1
The forms \(PT_a\) satisfy
For future reference, observe that we can write \(PT_{1a}\) in dihedral coordinates as
since, in the standard gauge fixing,
In fact, for any tree \(\Gamma \) compatible with the ordering a we have an associated top form,
where the \(I_p\) are (some ordering of) the subsets defining the propagators of \(\Gamma \). In particular, \(PT_{\Gamma _{1a}} = PT_{1a}\). \(PT_\Gamma \) is not always equal to a standard Parke–Taylor for the given dihedral structure. For the ordering 1a, an example of a tree, \(\Gamma \), such that \(PT_{\Gamma } \ne PT_{1a}\) is the ‘snowflake’, \(\Gamma = [[[1,2],[3,4]],5]\), for which one finds
However, for a tree \(\Gamma \) in which every vertex is attached to at least one external particle, \(PT_\Gamma \) does give rise to the ordinary Parke–Taylor for that dihedral structure, as observed first in Koba and Nielsen in [24]. Such a \(\Gamma \) (with every vertex connected to an external particle) corresponds to a quiver without cycles, as discussed in [25].
Finally, note that \(\Gamma \mapsto PT_\Gamma \) is not a homomorphism from \(Lie(n-1)\) to \(H^{n-3}(\mathcal {M}_{0,n},D)\), since the \(PT_\Gamma \) do not satisfy the Jacobi identity, which in particular implies that Eq. (2.5) cannot be used to expand \(PT_\Gamma \) in a basis of \(PT_a\)’s.
3.2 Homology of \(\mathcal {M}_{0,n}\)
We saw, in Eq. (3.9), that there is an isomorphism of \(H^{n-3}(\mathcal {M}_{0,n},D)\) with \(Lie(n-1)^*\). Integration gives a perfect pairing between relative cohomology, \(H^{n-3}(\mathcal {M}_{0,n},D)\), and the homology of the complement of the divisor, \(H_{n-3}(\mathcal {M}_{0,n} - D)\) [26]. It follows that the homology \(H_{n-3}(\mathcal {M}_{0,n} - D)\) can be identified (as a vector space) with \(Lie(n-1)\).Footnote 6 In this section, we will review the description of the homology cycles of \(\mathcal {M}_{0,n}-D\).
A point \(D_\Gamma \) naturally gives rise to a class in \(H_{n-3}(\mathcal {M}_{0,n}^\#)\) represented by a real half-dimensional torus that surrounds \(D_\Gamma \). Explicitly, the cycle can be defined as the locus
for some small \(\epsilon _p\) and choice of orientation. These cycles were first described in [27], and they generate the homology, but are not independent.Footnote 7 Integrating a holomorphic top-form with \(C_\Gamma \) evaluates the residue at \(D_\Gamma \) [29]. Lemma 7.1 of [20] states that \(PT_{a}\) can only have a pole at those \(D_\Gamma \) which are compatible with the ordering a. Moreover, it is clear that we can orient the \(C_{\Gamma _a}\) so that
which leads to the following,
Lemma 3.2
The cycles \(C_{\Gamma _{1a}}\) represent a basis for \(H_{n-3}(\mathcal {M}_{0,n}^\#)\), dual to the KK basis of \(H^{n-3}(\mathcal {M}_{0,n},D)\):
where we have chosen to orient the \(C_{\Gamma _{1a}}\) using the \(PT_{1a}\) forms so that the residues are \(+1\).
The relations among the top cycles are given by Jacobi-type relations.
Lemma 3.3
(CohenFootnote 8) For three trees related by Jacobi, there exists a contraction of the sum of the corresponding cycles, \(C_{\Gamma _s}+C_{\Gamma _t}+C_{\Gamma _u}\).
An explicit homotopy contracting \(C_{\Gamma _s}+C_{\Gamma _t}+C_{\Gamma _u}\) is easy to visualize for \(n=4\), since \(\mathcal {M}^\#_{0,4}=\mathbb {CP}^1-\{0,1,\infty \}\), with boundary points \(D_{s}=0\), \(D_{t}=1\), and \(D_{u}=\infty \). Appropriately oriented, the three small circles around these points add up to zero in homology.

More generally, for \(n>4\), we can exhibit a contraction of \(C_{\Gamma _s}+C_{\Gamma _t}+C_{\Gamma _u}\) by making small all \(\epsilon \)’s in definition of the cycle, Eq. (3.12), except for the \(\epsilon \) corresponding to the propagator being exchanged. This restricts us to a \(\mathbb {CP}^1\) component of D, where the same argument made for \(n=4\) can be applied.Footnote 9
It follows from Lemma 3.3 and Eq. (2.5) that,
Combining this with Lemmas 3.1 and 3.2 implies,
Lemma 3.4
The integration pairing between \(C_\Gamma \) and \(PT_{a}\) is
4 A Penrose transform for amplitudes
Our starting point is the observation that \(\mathcal {K}_n\) can be identified with \(H^1(\mathcal {M}_{0,n},D)\). Our ‘twistor space’ for the Penrose transform will be \(\mathbb {T}=T^*_D \mathcal {M}_{0,n}\), the total space of the bundle of holomorphic 1-forms on \(\mathcal {M}_{0,n}\) with logarithmic singularities on D. The relationship with \(\mathcal {K}_n\) is given by the isomorphism
This correspondence can be expressed by considering \(d \log \) of the Koba–Nielsen factor [24], which is, in the standard gauge fixing,
This gives the general section of \(\tau \in \Gamma (T^*_D \mathcal {M}_{0,n}) \) as
The second equality shows that this is clearly invariant under translations and rescalings of the \(\sigma _i\), but full Mobius invariance (i.e. vanishing when contracted with \(\sum _i \sigma _i^2\partial _{\sigma _i}\)) requires \(\sum _i s_{ij}=0\). Our normalizations \((\sigma _1,\sigma _{n-1},\sigma _n)=(0,1,\infty )\) give the triviality of \(d\log \sigma _{in}\) and \(d\log \sigma _{1\,n-1}\) giving the correct dimensionality of the \(d\log \sigma _{ij}\) basis of \(H^1\). Note that the equations \(E_i=0\) are the scattering equations.
To more clearly demonstrate the \(d\log \) behaviour on D, given a choice of the standard ordering, we can also represent the Koba–Nielsen factor as [31]
This gives the useful representation of the general section in terms of the \(n(n-3)/2\) basis \(d\log u_{ij}\)
This representation manifests the \(d\log \) behaviour on the components of D compatible with this choice of ordering.
4.1 The double fibration and the CHY formulae
The twistor correspondence arises from the following double fibration:
where p forgets the second factor and q is defined by the incidence relations
A point in \(\mathcal {K}_n\) therefore determines a section \(\tau _i=E_i\) of \(\mathbb {T}\rightarrow \mathcal {M}_{0,n}\).
A special role is played by the zero-section \(\mathbb {T}_0\) of \(\mathbb {T}\) as it encodes the scattering equations; given generic \(s_{ij}\), the section \(\tau _i=E_i(\sigma )\) intersects \(\mathbb {T}_0\) at the \((n-3)!\) solutions to the scattering equations. We therefore introduce \(\bar{\delta }(\tau )^{n-3}\) to be the \((0,n-3)\)-form delta function supported on \(\mathbb {T}_0\). In the standard gauge fixing above, it can be defined by
More invariantly, this takes values in \((\Omega ^{n-3}_D\mathcal {M}_{0,n})^*\) so that to use it in an integrand, we will need an extra factor with values in \((\Omega ^{n-3}_D\mathcal {M}_{0,n})^2\).
A first observation is that the CHY formulae can be regarded as examples of a Penrose transform in the sense that the amplitudes are obtained as the pushdown to \(\mathcal {K}_n\) of a pullback of an object from \(\mathbb {T}\). The generic CHY formula takes the form:
Here, \(\mathcal {I}_l, \mathcal {I}_r \in \Omega ^{n-3}_D\mathcal {M}_{0,n}\) are CHY half-integrands but also often depending also on polarization data, with the most basic example being m(a, b) when \((\mathcal {I}_l,\mathcal {I}_r)=(PT_a,PT_b)\). There is an empirical direct correspondence between choices of \(I_{l/r}\) and numerators \(N_\Gamma \) with for example the CHY PfaffianFootnote 10\(\mathrm {Pf}'(M)\) corresponding to the \(N^{k,\epsilon }_\Gamma \) described earlier. See [14, 32] for details of half-integrands for other theories and their origins.
4.2 The geometry of the correspondence
A generic point \((\tau _i,\sigma _i)\) of \(\mathbb {T}\) corresponds to a codimension-\(n-3\) plane in \(\mathcal {K}_n\). This plane is the \((n-2)(n-3)/2\) dimensional space of sections that pass through the point. For a point lying in a top-stratum, \(D_I\), of the divisor, these planes lie inside the factorisation hyperplane plane \(s_I=0\). This follows from the following combination [33] of the scattering equations
and the fact that, assuming \(1\in I\) and \(n\in \bar{I}\), the second term vanishes when restricted to \(D_I\).
It follows that the point \((\tau _i,\sigma _i)=(0,D_\Gamma )\in \mathbb {T}\) corresponds to the codimension-\(n-3\) plane in \(\mathcal {K}_n\) given by the intersection of the planes \(s_{I_p}=0\), where \(I_p\) are the subsets of \(\{1, \ldots ,n-1\}\) corresponding to the momentum flowing through each propagator in \(\Gamma \). We can characterize these planes as being those planes passing through the origin with normal \(n-3\)-form
In the next section, we will see how the \(w_\Gamma \) arise from the double fibration and show how their signs are fixed to make them satisfy the same relations as the \(n-3\)-forms defined by [6].
4.3 The symplectic form and the holomorphic volume form
By studying the symplectic volume form \(\omega ^{n-3}\) on \(T^*_D\mathcal {M}_{0,n}\), we find two elementary consequences of the double fibration. In this section, we describe how the symplectic volume gives rise to a transform between \(n-3\) cycles in \(\mathcal {M}_{0,n}-D\) and the \(n-3\)-forms, Eq. (4.11), encountered above. In the next section, we will describe the associated correspondence between \((n-3)\)-planes in \(\mathcal {K}_n\) and \((n-3)\)-cycles in \(H^{n-3}(\mathcal {M}_{0,n},D)\). Distinguished classes in \(H^{n-3}\) are seen to correspond to the planes defined by [6].
The symplectic form on \(T^*_D\mathcal {M}_{0,n}\) can be written explicitly as
where \(\tau _i\) are the components of \(\tau = \sum \tau _id\sigma _i\) in these coordinates. Pulling back \(\omega ^{n-3}\) to \(\mathcal {Y}_n\), we can decompose it into a sum over a basis of \(\Gamma (\mathcal {M}_{0,n},\Omega ^{n-3}_D)\) with coefficients given by \(n-3\)-forms on \(\mathcal {K}_n\). This gives rise to a correspondence between \(n-3\)-forms on \(\mathcal {K}_n\) and \((n-3)\)-cycles in \(\mathcal {M}_{0,n}\) which we explain in this section. In the next section, we describe the associated correspondence between \((n-3)\)-planes in \(\mathcal {K}_n\) (‘ABHY planes’) and \((n-3)\)-cocycles in \(H^{n-3}(\mathcal {M}_{0,n},D)\).
Every cycle \(C_\Gamma \) in \(H_{n-3}(\mathcal {M}_{0,n}-D)\) defines an \(n-3\)-form on \(\mathcal {K}_n\),
It is clear that, for a Jacobi triple of trees,
In other words, the map \(Lie(n-1)\hookrightarrow \wedge ^{n-3}\mathcal {K}_n^*\) given by \(\Gamma \mapsto w_\Gamma \) is a homomorphism.
To find an explicit expression for \(w_\Gamma \), we use the representation (4.5) of \(q^*\tau \) in a choice of dihedral coordinates \(u_{ij}\) for which \(\Gamma \) is planar. This gives
It is then easily seen that integration of \(q^*\omega ^{n-3}\) over \(C_\Gamma \) picks out only those poles that correspond to propagators of \(\Gamma \). The residue thus gives a wedge product \(\wedge ds_{I_p}\), with the overall sign determined by the orientation of \(C_\Gamma \). Given this explicit form of \(w_\Gamma \), the Jacobi relation, Eq. (4.13), can also be understood to follow from the momentum conservation relation, \(ds+dt+du=0\) [6].
It follows from Eq. (2.5) that \(w_\Gamma \) admits the expansion
Combining this with Lemmas 3.4 and 2.3, we find that we can write the pull-back of the symplectic volume form as
Although we have used the dual comb and KK bases, this relation follows in any dual basis, because \(w_\Gamma \) and \(PT_a\) furnish representations of \(Lie(n-1)\) and \(Lie(n-1)^*\), respectively, so that(4.16) is an explicit of writing the Kronecker delta. For example, when \(n=4\), \(q^*\omega \) can be written in any one of the three KK bases,
More generally, we can rewrite \(q^*\omega ^{n-3}\) using whatever bases we choose.
Lemma 4.1
The pullback of the symplectic volume form to \(\mathcal {Y}_n\) can be written
for a basis H of \(Lie(n-1)\), and a basis K of \(Lie(n-1)^*\).
The function \(s_{ij} = X_{ij}+X_{i+1j+1} - X_{ij+1} - X_{i+1j}\) is annihilated by the derivatives \(D_I\) for each arc, I, from the point n to each one of \(2,3,...,n-2\). This can be verified for each of the five cases indicated by the dashed lines in the figure. This is used in the main text to show that the \(n-3\)-plane spanned by the derivatives \(D_I\) are also given by linear equations of the form \(s_{ij} = \text {constant}\), for \(1\le i< j-1 < n-2\)
4.4 Associahedral \((n-3)\)-planes in \(\mathcal {K}_n\) and forms on \(\mathcal {M}_{0,n}\).
An alternative way to study the correspondence is to restrict \(\omega ^{n-3}\) to different \((n-3)\)-planes in \(\mathcal {K}_n\). This correspondence is related to the construction in [34], although they discuss different planes and polytopes. Distinguished classes in \(H^{n-3}(\mathcal {M}_{0,n},D)\) correspond to the associahedral planes found in [6].
An \(n-3\)-plane in \(\mathcal {K}_n\) is defined up to translation by its tangent form \(P \in \wedge ^{n-3}\mathcal {K}_n\). For any such plane, P, the symplectic volume form gives rise to an \(n-3\)-form in \(\Gamma (\mathcal {M}_{0,n},\Omega _D^{n-3})\),

Recall the definition of \(PT_\Gamma \in \Gamma (\mathcal {M}_{0,n},\Omega _D^{n-3})\), given in Eq. (3.11), which is a top form associated with a dihedral structure, a, together with a tree \(\Gamma \) that is compatible with that ordering. \(PT_\Gamma \) corresponds to a plane \(P_\Gamma \) in \(\mathcal {K}_n\) defined as follows. Fix a dihedral structure a and let
such that we have
by the non-crossing identity, Eq. (3.2). It follows that, for a compatible set of propagators \(I_p\), defining a tree \(\Gamma \) that is compatible with a, we can define a plane
for some ordering of the propagators chosen so that

In particular, when we take \(P_{a, \Gamma }\) to be the comb, \(P_{1a}:=P_{1a,\Gamma _{1a}}\), we recover the Parke–Taylor factors in the standard KK basis,

For a general \(\Gamma \), in dihedral structure a, the equations of the plane associated with \(P_\Gamma \) can be written as
for all J compatible with the ordering a and not corresponding to a propagator of \(\Gamma \). These equations bear no obvious resemblance to those defined in [6], but we will see that our planes are the same as theirs.
First, notice that the \(P_a\) satisfy
by Lemma 3.1, and that, moreover,
using Lemma 3.4.
In [6], the ABHY planes are defined, for the ordering \(a=1\ldots n-1\) and the comb \(\Gamma _{a}\), to be defined by the \((n-2)(n-3)/2\) equations
for \(1\le i< j - 1 < n - 2\). Using the identity, \(s_{ij} = X_{ij}+X_{i+1j+1}-X_{ij+1}-X_{i+1j}\) we can verify that, for \(I_p\) in \(\Gamma _a\),
for all \(1\le i< j - 1 < n - 2\), and each p. Fixing an \(s_{ij}\), one can check this equation for each p. The chord \(I_p\) is the arc kn for \(k=2,\ldots ,n-2\). The five cases to check are (i) \(k\le i\), (ii) \(k=i+1\), (iii) \(i+1<k<j\), (iv) \(k=j\), and (v) \(k>j\). That Eq. (4.21) vanishes in these five cases is easily seen from Fig. 1. Conversely, we can define the ABHY plane for the ordering a and the comb \(\Gamma _a\) to be given by the tangent form
For each factor in \(P_a\), we can check that it annihilates the expressions in Eq. (4.20). We have the following property
For fixed i, there are five cases to check, and these are shown in Fig. 2. By these arguments, we conclude that
Lemma 4.2
The planes \(P_{a,\Gamma }\) defined by the correspondence, Eq. (4.19), are the ABHY planes when \(\Gamma _a\) is the comb for the ordering a.
The functions given by (4.20) are annihilated by the derivatives \(\partial / \partial s_{i-1i} - \partial / \partial s_{ii+1}\). This can be verified by considering the arc J in each of the five cases indicated by the dashed lines in the figure. In the text this leads to the result that the planes spanned by the vectors making up the \(P_a\) in Eq. (4.22), are also given by Eq. (4.20)
Consider moreover any triangulation \(\Gamma \) that has no internal triangles. I.e. every diagonal in the triangulation belongs to a ‘skinny’ triangle like the one illustrated in Fig. 2 (or, dually, every vertex in the tree \(\Gamma \) is connected to an external line). In this case, the same arguments that lead to Lemma 4.2 can be applied, arc by arc, to show that:
Lemma 4.3
The planes \(P_{a,\Gamma }\) defined by the correspondence, Eq. (4.19), are given by the \((n-2)(n-3)/2\) equations
for all chords (ij) compatible with the ordering that are not one of the \(n-3\) propagators of \(\Gamma \).
It is a consequence of the results in [35] that the planes in Lemma 4.3 cut out associahedra when intersected with the positive orthant \(\mathcal {K}_n^+\). The planes are called ‘generalized ABHY’ planes: when \(\Gamma \) is the comb, the planes are the same as the original ones in [6], and when \(\Gamma \) is another tree (but with every vertex connected to an external particle) the plane \(P_{a,\Gamma }\) is one of the ‘generalized ABHY’ planes whose equations are presented in [36].
4.5 Scattering forms and CHY
The scattering forms of [6] are defined by the following sum over trees,
where \(d_\Gamma =\prod _{p=1}^{n-3} s_{I_p}\) and \(I_p\) are the propagators of \(\Gamma \). The \((a,\Gamma )\)-factor reduces the sum to one over trees that are planar for the ordering a.
The symplectic form discussed above gives rise to the ABHY scattering forms on \(\mathcal {K}_n\) from the Dolbeault formula
where
To see that Eq. (4.25) is equal to Eq. (4.24), we use Lemma 4.1 to rewrite Eq. (4.25) as
We recognize that the integral is the CHY formula [7, 8] for m(a, b), defined in Eq. (2.17). It follows that Eq. (4.25) can be expanded as
which is equal to (4.24) by Eq. (4.15). We conclude that
Proposition 4.4
The ABHY scattering form \(\Omega _a\) is given by Eq. (4.25).
More generally, given any CHY half-integrand \(\mathcal {I}\), we can define an ABHY scattering form
This form admits an expansion
The coefficients of the forms \(w_{\Gamma _{1a}}\) in this sum are the BCJ numerators, \(N_{1a}\), associated with the integrand \(\mathcal {I}\). This formula is in line with earlier work on extracting BCJ numerators from CHY half integrands, especially [37]. The CHY integral as given is not changed by adding to \(\mathcal {I}\) a term that vanishes on the support of the scattering equations. Indeed, one can regard \(\mathcal {I}\) as a representative of a twisted cohomology class, as explained in [38].
All scattering forms, \(\Omega _{\mathcal {I}}\), obtained in this way are projective. Let \(\Upsilon \) be the Euler vector field on \(\mathcal {K}_n\),
We can lift \(\Upsilon \) trivially to \(\mathcal {Y}_n\) using the product structure. On objects pulled back from \(\mathbb {T}\), it then acts by
Contracting \(\Upsilon \) into \(\Omega (a)\), we find

on account of the delta functions in the integrand.
Lemma 4.5
The scattering form \(\Omega _{\mathcal {I}}\) is a projective form on \(\mathbb {P}\mathcal {K}_n\).
Finally, amplitudes are obtained by restricting the scattering forms \(\Omega _{\mathcal {I}}\) to ABHY planes, as in [6]. In fact, the restriction of \(\Omega _{\mathcal {I}}\) to \(P_a\) evaluates to give the CHY formula for the integrands \(PT_a\) and \(\mathcal {I}\), as follows from the definition of \(P_a\) (Eq. (4.19) and subsequent lines). Moreover, for a general cohomology class
we have an associated plane, \(P_N := \sum _a N_{1a} P_{1a}\). Pairing this with the general scattering form \(\Omega _{\mathcal {I}}\) gives the CHY amplitude for integrands N and \(\mathcal {I}\).
5 Discussion
We have seen that Lie polynomials underpin the colour-kinematics and double copy framework of BCJ. We have reviewed the classical fact that the top homology of \(\mathcal {M}_{0,n}-D\) is isomorphic to the Lie polynomials, \(Lie(n-1)\), and shown that there is a natural correspondence between \(T^*_D\mathcal {M}_{0,n}\) and \(\mathcal {K}_n\) under which the CHY integral formulae can be understood as a Penrose transform. This can be extended to a transform between the holomorphic Liouville form and the differential forms \(w_\Gamma \) introduced by [6], and also between CHY half-integrands and the scattering forms introduced by [6].
One underlying question in the subject is whether there is a kinematic algebra underpinning the kinematic numerators \(N_\Gamma ^{k,\epsilon }\). Although we have seen that the colour factors of Lie algebras can provide such numerators, we have also seen many examples of numerators satisfying the Jacobi identity that do not arise as colour factors for a Lie algebra: for example, \((\Gamma ,a)\) and \(w_\Gamma \) and so on. In other words, the existence of a homomorphism from \(Lie(n-1)\) to some vector space does not of itself determine a Lie algebra.
The basic results in this paper can be taken further to yield natural recursions in field theory, which lead to both Lie polynomial and ABHY-form-based proofs of the known properties of the field theory momentum kernel and of kinematic numerators. The momentum kernel can be studied also in \(T^*\mathcal {M}_{0,n}\), where it arises in the CHY treatment of KLT orthogonality [39]. It also seems likely that the framework will naturally extend to loop integrands in the context of nodal spheres following the logic of [40,41,42,43,44].
The correspondence we have described is suggestive of the naive explicit formula
for numerators in terms of CHY half-integrands. However, such formulae fail for the CHY Pfaffian that one would expect to give the basic Yang–Mills kinematic numerators; the formula is compromised by the interdependence between in particular reduced Pfaffians and scattering equations. This equation is shown to be invalid as written but a slightly different formulation in a similar spirit is shown to work when \(\mathcal {I}_l\) represents a cohomology class in the context of twisted cohomology by Mizera [45].
We remark that the twisted cycle formulation of string integrals in [46] naturally arises in the context of the holomorphic geometric quantization of \(T^*_D\mathcal {M}_{0,n}\). To carry out geometric quantization, one introduces the line bundle \(\mathcal {L}\rightarrow T^*_D\mathcal {M}_{0,n}\) with connection \(\nabla =d+ \alpha '\tau \) where \(\tau =\sum _i \tau _i d\sigma _i\) is the canonical 1-form (symplectic potential) and \(\alpha '\) plays the role of Planck’s constant. Polarized wave functions should be independent of \(\tau _i\). On pull back to the correspondence space, \(\mathcal {Y}_n\), the connection \(\nabla \) becomes the standard twisted exterior derivative associated with the Koba–Nielsen factor. Such a quantization of \(T^*\mathcal {M}_{0,n}\) perhaps most naturally arises from ambitwistor-string path-integral [47], where the Pfaffian half-integrand for kinematic numerators arises from the RNS spin field path-integral.
There are many further connections to be followed up; we briefly mention the delta algebras of [48] and the formulations of colour-kinematics duality in [49, 50].
Notes
The shuffle product of a and b,
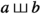 , is the sum over ordered permutations of the letters of a and b that preserve the orderings of the letters in a and b.
, is the sum over ordered permutations of the letters of a and b that preserve the orderings of the letters in a and b.One way to avoid the Gram conditions is to suppose that the \(k_i^\mu \) are n vectors in \((n-1,1)\) dimensional Minkowski space. However, the momentum conservation relation, \(\sum k_i^\mu = 0\), together with the null conditions, \(k_i^2 = 0\), imply a further determinantal condition on the \(s_{ij}\) variables, even in \(d\ge n\) dimensions.
This is eq 3.8 of [15] together with the use of the U(1)-decoupling identity in the bracketed term.
Arnol’d [21] computes the Poincaré polynomial of the cohomology of the configuration space \(M_{n-1}\) of \(n-1\) points in \(\mathbb {C}\). This can be obtained inductively via the fibration \(M_{k}\rightarrow M_{k-1}\) with fibre \(\mathbb {C}-\{\sigma _1,\ldots ,\sigma _{k-1}\}\) giving factors of \((1+(k-1)t)\). To get \(\mathcal {M}_{0,n}^\#\), one needs to take the quotient of \(M_{n-1}\) by \(\mathbb {C}^*\ltimes \mathbb {C}\), the stabilizer in \(PSL_2\) of the point at infinity. Arnol’d’s formula for the Poincaré polynomial of \(M_{n-1}\) must therefore be divided by \(1+t\) to obtain the formula here.
We thank Carlos Mafra for this reference and also refer the reader to sections 4.1. and 4.2 of [22] for further discussion.
There is a free action of the symmetric group \(S_n\) on \(H_{n-3}(\mathcal {M}_{0,n}-D)\). As a module for \(S_n\), \(H_{n-3}(\mathcal {M}_{0,n}-D)\) is not isomorphic to \(Lie(n-1)\), but \(Lie(n-1)\) twisted by the sign representation of \(S_n\).
The maximum dimension tori appearing in Lemma 3.3 can be constructed by taking the wedge products of lower dimensional tori. This leads to a natural product in the full homology \(H_*(\mathcal {M}_{0,n}-D)\), under which \(H_*\) can be identified with a graded Lie algebra, with graded Jacobi relations holding in all dimensions. [27] The (ungraded) Jacobi relation in Lemma 3.3 is a special case [27, 30].
For completeness, the CHY Pfaffian is the reduced Pfaffian of the matrix M
$$\begin{aligned} M=\begin{pmatrix}A&{}C\\ -C^t&{}B\end{pmatrix} ,\quad A_{ij}=\frac{k_i\cdot k_j}{\sigma _i-\sigma _j}, \quad B_{ij}=\frac{\epsilon _{i}\cdot \epsilon _{j}}{\sigma _i-\sigma _j} , \quad C_{ij}=\frac{k_i\cdot \epsilon _{j}}{\sigma _i-\sigma _j}, \quad \text{ for } i\ne j \end{aligned}$$constructed from polarization vectors \(\epsilon _{i}\) with \(k_i\cdot \epsilon _{i}=0 \ldots \), and \(A_{ii}=B_{ii}=0\), \(C_{ii}=\epsilon _{i}\cdot \sum k_i/\sigma _{ij}\). This matrix is degenerate, but removing two rows and columns, say ij, taking the Pfaffian and dividing by \(\sigma _{ij}\) yields a well-defined half-integrand.
References
Bern, Z., Carrasco, J., Johansson, H.: New relations for gauge-theory amplitudes. Phys. Rev. D 78, 085011 (2008). [arXiv:0805.3993]
Bern, Z., Carrasco, J.J.M., Johansson, H.: Perturbative quantum gravity as a double copy of gauge theory. Phys. Rev. Lett. 105, 061602 (2010). [arXiv:1004.0476]
Kawai, H., Lewellen, D.C., Tye, S.H.H.: A relation between tree amplitudes of closed and open strings. Nucl. Phys. B 269, 1 (1986)
Bern, Z., Carrasco, J.J., Chiodaroli, M., Johansson, H., Roiban, R.: The duality between color and kinematics and its applications. arXiv:1909.0135
Kapranov, M.: Lie operads. https://www.youtube.com/watch?v=109iC2JL-bk (2012)
Arkani-Hamed, N., Bai, Y., He, S., Yan, G.: Scattering forms and the positive geometry of kinematics, color and the worldsheet. JHEP 05, 096 (2018). [arXiv:1711.0910]
Cachazo, F., He, S., Yuan, E.Y.: Scattering of massless particles in arbitrary dimensions. Phys. Rev. Lett. 113(17), 171601 (2014) [arXiv:1307.2199]
Cachazo, F., He, S., Yuan, E.Y.: Scattering of massless particles: scalars, gluons and gravitons. JHEP 1407, 033 (2014). [arXiv:1309.0885]
Reutenauer, C.: Free Lie Algebras, vol. 7 of London Mathematical Society Monographs. New Series. The Clarendon Press, Oxford University Press, New York (1993). Oxford Science Publications
Ree, R.: Lie elements and an algebra associated with shuffles. Ann. Math. 68(2), 210–220 (1958)
Radford, D.E.: A natural ring basis for the shuffle algebra and an application to group schemes. J. Algebra 58(2), 432–454 (1979)
Kleiss, R., Kuijf, H.: Multigluon cross sections and 5-jet production at hadron colliders. Nucl. Phys. B 312(3), 616–644 (1989)
Du, Y.-J., Teng, F.: Bcj numerators from reduced pfaffian (2017)
Cachazo, F., He, S., Yuan, E.Y.: Scattering equations and matrices: from Einstein To Yang–Mills, DBI and NLSM. JHEP 07, 149 (2015). [arXiv:1412.3479]
Cachazo, F.: Fundamental BCJ Relation in N = 4 SYM. From The Connected Formulation. arXiv:1206.5970
Monteiro, R., O’Connell, D.: The kinematic algebra from the self-dual sector. JHEP 07, 007 (2011). arXiv:1105.2565
Monteiro, R., O’Connell, D.: The kinematic algebras from the scattering equations. JHEP 03, 110 (2014). arXiv:1311.1151
Chen, G., Johansson, H., Teng, F., Wang, T.: On the kinematic algebra for BCJ numerators beyond the MHV sector. arXiv:1906.10683 [hep-th] (June, 2019). arXiv: 1906.10683
Fu, C.-H., Du, Y.-J., Huang, R., Feng, B.: Expansion of Einstein–Yang–Mills amplitude. JHEP 09, 021 (2017). [arXiv:1702.0815]
Brown, F.C.S.: Multiple zeta values and periods of moduli spaces M 0, n ( R ). Annales Sci. Ecole Norm. Sup. 42, 371 (2009). ([math/0606419])
Arnol’d, V.I.: The cohomology ring of the group of dyed braids. Mat. Zametki 5, 227–231 (1969)
Mafra, C.R., Schlotterer, O.: Berends-Giele recursions and the BCJ duality in superspace and components. arXiv:1510.0884
Cresson, J.: Calcul moulien Annales de la Faculté des sciences de Toulouse. Mathématiques 18(2), 307–395 (2009)
Koba, Z., Nielsen, H.B.: Reaction amplitude for n mesons: a generalization of the Veneziano–Bardakci–Ruegg–Virasora model. Nucl. Phys. B 10, 633–655 (1969)
Arkani-Hamed, N., He, S., Lam, T., Thomas, H.: Binary geometries, generalized particles and strings, and cluster algebras (2020)
Bott, R., Tu, L.W.: Differential Forms in Algebraic Topology. Graduate Texts in Mathematics, vol. 82. Springer, New York (1982)
Cohen, F.: Homology of \(\Omega ^{(n+1)}\Sigma ^{(n+1)}X\) and \(C_{(n+1)}X,\, n>0\). Bull. Am. Math. Soc. 79(1973), 1236–1241 (1974)
Fadell, E., Neuwirth, L.: Configuration spaces. Math. Scand. 10, 111–118 (1962)
Griffiths, P., Harris, J.: Principles of Algebraic Geometry. Wiley Classics Library. Wiley, New York (1994). Reprint of the 1978 original
Cohen, F.R.: On configuration spaces, their homology, and Lie algebras. J. Pure Appl. Algebra 100(1–3), 19–42 (1995)
Koba, Z., Nielsen, H.B.: Manifestly crossing invariant parametrization of n meson amplitude. Nucl. Phys. B 12, 517–536 (1969)
Casali, E., Geyer, Y., Mason, L., Monteiro, R., Roehrig, K.A.: New ambitwistor string theories. JHEP 11, 038 (2015). [arXiv:1506.0877]
Dolan, L., Goddard, P.: Proof of the formula of Cachazo, He and Yuan for Yang–Mills tree amplitudes in arbitrary dimension. JHEP 1405, 010 (2014). [arXiv:1311.5200]
He, S., Yan, G., Zhang, C., Zhang, Y.: Scattering forms, worldsheet forms and amplitudes from subspaces. JHEP 08, 040 (2018). [arXiv:1803.1130]
Bazier-Matte, V., Douville, G., Mousavand, K., Thomas, H., Yıldırım, E.: ABHY Associahedra and Newton polytopes of \$F\$-polynomials for finite type cluster algebras. arXiv:1808.09986 [math] (2018).
Arkani-Hamed, N., He, S., Salvatori, G., Thomas, H.: Causal diamonds, cluster polytopes and scattering amplitudes (2020)
He, S., Teng, F., Zhang, Y.: String amplitudes from field-theory amplitudes and vice versa. Phys. Rev. Lett. 122 (2019)
Mizera, S.: Scattering amplitudes from intersection theory. Phys. Rev. Lett. 120(14) 141602 (2018). arXiv:1711.0046
Cachazo, F., He, S., Yuan, E.Y.: Scattering equations and Kawai–Lewellen–Tye orthogonality. Phys. Rev. D90(6), 065001 (2014). arXiv:1306.6575
Geyer, Y., Mason, L., Monteiro, R., Tourkine, P.: Loop integrands for scattering amplitudes from the Riemann sphere. Phys. Rev. Lett. 115(12), 121603 (2015). arXiv:1507.0032
Geyer, Y., Mason, L., Monteiro, R., Tourkine, P.: One-loop amplitudes on the Riemann sphere. JHEP 03, 114 (2016). [arXiv:1511.0631]
Geyer, Y., Mason, L., Monteiro, R., Tourkine, P.: Two-loop scattering amplitudes from the Riemann sphere. Phys. Rev. D94(12), 125029 (2016). arXiv:1607.0888
Geyer, Y., Monteiro, R.: Gluons and gravitons at one loop from ambitwistor strings. JHEP 03, 068 (2018). [arXiv:1711.0992]
He, S., Schlotterer, O., Zhang, Y.: New BCJ representations for one-loop amplitudes in gauge theories and gravity. Nucl. Phys. B 930, 328–383 (2018). arXiv: 1706.00640
Mizera, S.: Kinematic Jacobi identity is a residue theorem. arXiv:1912.0339
Mizera, S.: Aspects of scattering amplitudes and moduli space localization. PhD thesis, Perimeter Inst. Theor. Phys. (2019). arXiv:1906.0209
Mason, L., Skinner, D.: Ambitwistor strings and the scattering equations. JHEP 1407, 048 (2014). [arXiv:1311.2564]
Cachazo, F., Early, N., Guevara, A., Mizera, S.: \(\Delta \) -algebra and scattering amplitudes. JHEP 02, 005 (2019). [arXiv:1812.0116]
Chen, G., Johansson, H., Teng, F., Wang, T.: On the kinematic algebra for BCJ numerators beyond the MHV sector. JHEP 11, 055 (2019). [arXiv:1906.1068]
Reiterer, M.: A homotopy BV algebra for Yang–Mills and color-kinematics. arXiv:1912.0311
Acknowledgements
It is a pleasure to acknowledge informative conversations and email exchanges with Nima Arkani-Hamed, Francis Brown, Nick early, Yvonne Geyer, Carlos Mafra, Sebastian Mizera, Ricardo Monteiro, Michael Reiterer and Oliver Schlotterer and the hospitality of the CMSA at Harvard. HF would like to acknowledge support from ERC grant Galois theory of periods and applications 724638. While we were writing up this work, we became aware of the parallel work of Sebastian Mizera [45] that has some overlap with this—we are grateful to him for letting us see a preview of his work before we finished this paper.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Frost, H., Mason, L. Lie polynomials and a twistorial correspondence for amplitudes. Lett Math Phys 111, 147 (2021). https://doi.org/10.1007/s11005-021-01483-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11005-021-01483-1





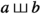 , is the sum over ordered permutations of the letters of a and b that preserve the orderings of the letters in a and b.
, is the sum over ordered permutations of the letters of a and b that preserve the orderings of the letters in a and b.