Abstract
We propose a new formula for the star product in deformation quantization of Poisson structures related in a specific way to a variational problem for a function S, interpreted as the action functional. Our approach is motivated by perturbative algebraic quantum field theory (pAQFT). We provide a direct combinatorial formula for the star product, and we show that it can be applied to a certain class of infinite-dimensional manifolds (e.g. regular observables in pAQFT). This is the first step towards understanding how pAQFT can be formulated such that the only formal parameter is \(\hbar \), while the coupling constant can be treated as a number. In the introductory part of the paper, apart from reviewing the framework, we make precise several statements present in the pAQFT literature and recast these in the language of (formal) deformation quantization. Finally, we use our formalism to streamline the proof of perturbative agreement provided by Drago, Hack, and Pinamonti and to generalize some of the results obtained in that work to the case of a nonlinear interaction.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Constructing interacting quantum field theory (QFT) models in 4 dimensions is one of the most important challenges facing modern theoretical physics. Even though there is no final consensus on how the actual axiomatic framework underlying QFT should be formulated, most attempts at construction of models try to fit into one of the established axiomatic systems: Wightman–Gårding [53], Haag–Kastler [33, 36], or Osterwalder–Schrader [46]. On the other hand, most computations in QFT are done using less rigorous methods and often rely on a perturbation theory expansion organized in terms of Feynman graphs.
A new approach that combines the advantages of a mathematically sound axiomatic framework with perturbative methods has emerged in the last 2 decades; it is called perturbative algebraic quantum field theory (pAQFT). The foundations were laid in [8, 17,18,19,20,21], and further results concerning fermionic fields and gauge theory were obtained in [28, 29, 51]. For reviews, see [16, 52].
One of the ingredients of pAQFT is formal deformation quantization—the construction of a (quantum) star product for the algebra of observables [4, 5]. The first application of deformation quantization to QFT appears in the works of Dito [13, 14].
There are two well-known general constructions of star products on finite-dimensional manifolds: The Fedosov construction [25] starts from a symplectic manifold with some torsion-free connection; the Kontsevich construction [41] starts from a Poisson structure on an affine space. The former has been generalized to the infinite-dimensional setting by Collini [12].
In this approach (commonly referred to as the “on-shell approach”), the equations of motion for the fields are imposed before quantization and the space of solutions is a sort of infinite-dimensional symplectic manifold. It is, however, not clear whether the star product constructed in [12] (following the Fedosov procedure) does satisfy Einstein causality (commutation of spacelike separated observables). In chapter 4 of [12], it is argued that the “usual” causal perturbation theory methods (see e.g. [8, 18, 20, 23]) can be combined with the ideas of Fedosov, but then it is still not entirely clear how the renormalization freedom should be taken into account and what is the interplay between the on-shell structures (e.g. the notion of on-shell smoothness used by Collini) and off-shell structures (time-ordered products in causal perturbation theory are typically defined off-shell). We also note that in causal perturbation theory, as well as in [12] when dealing with products satisfying Einstein causality, one works with formal power series in both \(\hbar \) and \(\lambda \) (the coupling constant).
Here, we choose to work in the off-shell approach, i.e. the equations of motion are imposed after quantization. The space of field configurations is a sort of infinite-dimensional Poisson manifold, which suggests that something in the spirit of Kontsevich is called for. However, the Kontsevich formula does not carry over verbatim to the infinite-dimensional case [15]. This motivates the search for an alternative formulation and a new formula for the star product that can be applied to infinite-dimensional Poisson manifolds, at least in some class of interesting examples.
A possible way forward has been suggested in [29], where an interacting star product for a sufficiently regular class of functionals has been constructed by an indirect method. There, the theory was formulated in terms of formal power series in \(\hbar \) and the coupling constant \(\lambda \). In this (perturbative) approach, the starting point is an affine configuration space with an action functional that is split into a preferred quadratic (free) part and the remainder. The free part is quantized with the help of a Hadamard distribution (this notion mimics the properties of the 2-point function of the Minkowski vacuum state). This is then translated into a star product for the full theory by using quantum Møller operators and the algebraic adiabatic limit.
As far as the relation to Kontsevich’s approach is concerned, we note that the product introduced in [29] cannot arise from Kontsevich’s construction, because the first-order (in \(\hbar \)) part of the star product is not proportional to the Poisson structure (instead, it is given in terms of the Hadamard function that differs from the Poisson structure by a symmetric bidistribution). A plausible generalization of Kontsevich’s construction would be one that constructs the star product from this first-order term and the affine structure. We will show here that such a construction cannot give the desired star product.
What then? In field theory, the Poisson structure is not a given structure, but follows from the action; hence, it is not surprising that the action is an appropriate ingredient for a construction of the star product. The affine structure is an acceptable ingredient as well. The preferred quadratic part, however, is an undesirable ingredient, because we would like to achieve a nonperturbative construction.
The purpose of the present paper is to work towards a direct construction of the star product for infinite-dimensional affine manifolds, where the Poisson structure follows from the given action. The direct formula we propose in this work agrees with the one of [29] on the perturbative level, but it goes beyond that. What we achieve here is a construction of the interacting star product that depends only on the full action, the causal structure, and the affine structure of the configuration space. This is a desirable result from the pAQFT perspective, since in many situations the split into free and interacting theory is unnatural and the physical results should not depend on this split. This is the case, for example, in quantum gravity, as indicated in [10]. Moreover, our construction is nonperturbative in the sense that it does not require a preferred quadratic action and only \(\hbar \) is treated as a formal parameter.
We start our construction by first transforming the free star product to remove the dependence on a Hadamard distribution. This means that we treat the quantization relative to the time-ordered product, rather than an (unphysical in the quantum context) pointwise product. Unfortunately, in the infinite-dimensional case, this transformation only works if the interaction and observables are sufficiently regular (for field theories in 3 or more spacetime dimensions, this implies that all their functional derivatives have to be given by smooth compactly supported functions). Nevertheless, we believe that the construction and its combinatorial structure may be relevant for a nonperturbative construction of the star product for a more realistic action. As a by-product, we also show how to nonperturbatively construct the quantum Møller operator for regular observables from the classical Møller operator. (The existence of classical Møller operators and of retarded and advanced Green functions for regular interactions is implied by the results in the paper [26], which is expected to appear soon.) Our main results are Theorems 6.29 and 6.41.
Our construction works in the finite-dimensional case without any restrictions, and it would be interesting to investigate the relation between our star product and other known constructions, for example, in geometric quantization. We will address this point in our future research. Another potential realm of applications is field theories in two spacetime dimensions, where the singularity of the Feynman propagator is logarithmic and we expect that a larger class of observables and interactions can be treated using our methods. Recently, a construction of Sine Gordon model in 2D was achieved by [1] using pAQFT methods, so it would be interesting to apply our formula for the star product to that case and to other theories, where exact results are expected to hold.
The paper is organized as follows. In Sects. 2–3, we review the construction of classical field theory in the pAQFT framework and provide a more rigorous proof of the result of [6, 19] that the retarded Møller map intertwines between the Peierls brackets of the free and interacting theories. In Sect. 4, we discuss deformation quantization. We introduce several natural quantization maps, useful in pAQFT, and prove a theorem that completely characterizes the ambiguity in constructing the time-ordering operator on regular functionals. This result mimics the Main Theorem of Renormalization proven for local functionals in [8]. In Sect. 5, we introduce the formal S-matrix and the quantum Møller operator, and in Proposition 5.11, we show how the latter can be constructed nonperturbatively on regular functionals from the classical Møller operator. Next we prove a direct formula, Eq. (6.5), for the interacting star product and show that it makes sense nonperturbatively in the coupling constant. In this section, we also discuss the relation to the formula of Kontsevich, provide some useful formulae for the quantum Møller operator, and finally, we discuss the principle of perturbative agreement.
2 Kinematical structure
In the framework of perturbative algebraic quantum field theory (pAQFT), one starts with the classical theory, which is subsequently quantized. We work in the Lagrangian framework, but there are some modifications that we need to make to deal with the infinite-dimensional character of field theory. In this section, we give an overview of mathematical structures that will be needed later on to construct models of classical and quantum field theories. Since we do not fix the dynamics yet, the content of this section describes the kinematical structure of our model.
2.1 The space of field configurations
We start with a globally hyperbolic spacetime  . Next we introduce
. Next we introduce  , the space of field configurations. The choice of
, the space of field configurations. The choice of  specifies what kind of objects our model describes (e.g. scalar fields, gauge fields, etc.).
specifies what kind of objects our model describes (e.g. scalar fields, gauge fields, etc.).
Definition 2.1
The configuration space  on the fixed spacetime
on the fixed spacetime  is realized as the space of smooth sections \(\Gamma (E\rightarrow M)\) of some vector bundle \(E\xrightarrow {\pi } M\) over M.
is realized as the space of smooth sections \(\Gamma (E\rightarrow M)\) of some vector bundle \(E\xrightarrow {\pi } M\) over M.
Definition 2.2
The space of compactly supported sections is denoted  . The space of sections of the dual bundle is denoted
. The space of sections of the dual bundle is denoted  .
.
2.2 Functionals on the configuration space
We model classical and quantum observables as smooth (in the sense of [3, 34, 43, 45]) functionals on  .
.
Consider some  and
and  . We require F to be smooth in the sense of Bastiani [3, 34, 43, 45], i.e.
. We require F to be smooth in the sense of Bastiani [3, 34, 43, 45], i.e.
Definition 2.3
Let  and
and  be topological vector spaces,
be topological vector spaces,  an open set and
an open set and  a map. The derivative of f at \(x\in U\) in the direction of
a map. The derivative of f at \(x\in U\) in the direction of  is defined as
is defined as
whenever the limit exists. The function f is called differentiable at x if \(\left<f^{(1)}(x),h\right>\) exists for all  . It is called continuously differentiable if it is differentiable at all points of U and
. It is called continuously differentiable if it is differentiable at all points of U and  is a continuous map. It is called a
is a continuous map. It is called a  -map if it is continuous and continuously differentiable. Higher derivatives are defined by
-map if it is continuous and continuously differentiable. Higher derivatives are defined by
and f is  if \(f^{(k)}\) is jointly continuous as a map
if \(f^{(k)}\) is jointly continuous as a map  . We say that f is smooth if it is
. We say that f is smooth if it is  for all \(k\in {\mathbb {N}}\).
for all \(k\in {\mathbb {N}}\).
For a detailed discussion of Bastiani smoothness in the context of classical field theory, see e.g. [7]. By definition, if \(F^{(1)}(\varphi )\) exists, then it is an element of the complexified dual space  . More generally, the nth derivative defines an element \(F^{(n)}(\varphi )\) of the continuous complex dual of the completed projective tensor product
. More generally, the nth derivative defines an element \(F^{(n)}(\varphi )\) of the continuous complex dual of the completed projective tensor product  , where \(\boxtimes \) is the exterior tensor product of vector bundles, i.e.
, where \(\boxtimes \) is the exterior tensor product of vector bundles, i.e.  (hence, it is a distribution with compact support).
(hence, it is a distribution with compact support).
Definition 2.4
The spacetime support of a function,  (where S may be any set), is defined by
(where S may be any set), is defined by

Alternatively, one can write this as:

Definition 2.5
A functional  is called local if for each
is called local if for each  there exists an open neighbourhood O in
there exists an open neighbourhood O in  and \(k\in {\mathbb {N}}\) such that for all \(\varphi \in O\) we have
and \(k\in {\mathbb {N}}\) such that for all \(\varphi \in O\) we have
where \(j^k_x(\varphi )\) is the kth jet prolongation of \(\varphi \) and \(\alpha \) is a map over M from the jet bundle to the volume-form bundle. We denote the space of local functionals by  .
.
We equip the space  of local functionals on the configuration space with the pointwise product using the prescription
of local functionals on the configuration space with the pointwise product using the prescription
where  .
.  is not closed under this product, but we can consider instead the space
is not closed under this product, but we can consider instead the space  of multilocal functionals, which is defined as the algebraic closure of
of multilocal functionals, which is defined as the algebraic closure of  under product (2.4). We can also introduce the involution operator \(*\) on
under product (2.4). We can also introduce the involution operator \(*\) on  using complex conjugation, i.e.
using complex conjugation, i.e.
In this way, we obtain a commutative \(*\)-algebra.
Functional derivatives of smooth functionals on  are compactly supported distributions. We can distinguish certain important classes of functionals by analysing the wavefront (WF) set properties of their derivatives.
are compactly supported distributions. We can distinguish certain important classes of functionals by analysing the wavefront (WF) set properties of their derivatives.
Local and multilocal functionals satisfy some important regularity properties. Firstly, for local functionals the wavefront set of \(F^{(n)}(\varphi )\) is orthogonal to the tangent bundle of the thin diagonal,
In particular, \(F^{(1)}(\varphi )\) has empty wavefront set and so is smooth for each fixed  . The latter is true also for multilocal functionals, i.e.
. The latter is true also for multilocal functionals, i.e.  . Note that using the metric volume form \(\mu _{{\mathbf {g}}}\), we can therefore identify \(F^{(1)}(\varphi )\) with an element of
. Note that using the metric volume form \(\mu _{{\mathbf {g}}}\), we can therefore identify \(F^{(1)}(\varphi )\) with an element of  .
.
Definition 2.6
A functional  is called regular (
is called regular ( ) if \(F^{(n)}(\varphi )\) has empty WF set for all \(n\in {\mathbb {N}}\),
) if \(F^{(n)}(\varphi )\) has empty WF set for all \(n\in {\mathbb {N}}\),  .
.
Remark 2.7
Some authors additionally require that a regular functional have compact support. This definition only implies that each derivative has compact support (the support of \(F^{(1)}(\varphi )\) can change with \(\varphi \), so \({{\,\mathrm{supp}\,}}F\) may not be compact).
For a regular functional, \(F^{(n)}(\varphi )\) can be identified with an element of \(\Gamma _c((E^*)^{\boxtimes n}\rightarrow M^n)^{\scriptscriptstyle {{\mathbb {C}}}}\).
3 Classical theory
3.1 Dynamics
Dynamics is introduced in the Lagrangian framework. We begin with recalling some crucial definitions after [8]. Here, \({\mathcal {D}}(M)\) denotes the space of smooth, compactly supported, real-valued functions (test functions).
Definition 3.1
A generalized Lagrangian on a fixed spacetime  is a map
is a map  such that
such that
- (i)
\(L(f+g+h)=L(f+g)-L(g)+L(g+h)\) for \(f,g,h\in {\mathcal {D}}(M)\) with \({{\,\mathrm{supp}\,}}\,f\cap {{\,\mathrm{supp}\,}}\,h=\varnothing \) (Additivity).
- (ii)
\({{\,\mathrm{supp}\,}}(L(f))\subseteq {{\,\mathrm{supp}\,}}(f)\) (Support).
- (iii)
Let
 be the oriented and time-oriented isometry group of the spacetime
be the oriented and time-oriented isometry group of the spacetime  . (For Minkowski spacetime
. (For Minkowski spacetime  is the proper orthochronous Poincaré group
is the proper orthochronous Poincaré group  .) We require that \(L(f)(u^*\varphi )=L(u_*f)(\varphi )\) for every
.) We require that \(L(f)(u^*\varphi )=L(u_*f)(\varphi )\) for every  (Covariance).
(Covariance).
Definition 3.2
An action is an equivalence class of Lagrangians under the equivalence relation [8]
The physical meaning of (3.1) is to identify Lagrangians that “differ by a total divergence”.
An action is something like a local functional with (possibly) noncompact support. It is used just as L(1) would be if it existed.
Definition 3.3
The Euler–Lagrange derivative (first variational derivative) of L is a map  defined by
defined by
where  and \(f\in {\mathcal {D}}(M)\) is chosen in such a way that \(f= 1\) on \({{\,\mathrm{supp}\,}}h\).
and \(f\in {\mathcal {D}}(M)\) is chosen in such a way that \(f= 1\) on \({{\,\mathrm{supp}\,}}h\).
Since L(f) is a local functional, \(L'\) does not depend on the choice of f. Note that two Lagrangians equivalent under relation (3.1) induce the same Euler–Lagrange derivative, so dynamics is a structure coming from actions rather than Lagrangians.
Definition 3.4
The Euler–Lagrange derivative of an action, S, is \(S'\doteq L'\) for any Lagrangian \(L\in S\).
We are now ready to introduce the equations of motion (eom’s).
Definition 3.5
The equation of motion (eom) corresponding to the action S is
understood as a condition on  .
.
Remark 3.6
The space of solutions of (3.2) may be pathological. Instead, in this algebraic setting, we should work with the quotient of  or
or  by the ideal generated by \(S'\). This plays the role of the algebra of functionals on the space of solutions.
by the ideal generated by \(S'\). This plays the role of the algebra of functionals on the space of solutions.
However, in this paper we are concerned with “off-shell” constructions, i.e. the quotient is not taken.
Definition 3.7
The second variational derivative \(S''\) of the action S is defined by
where \(L\in S\) and \(f= 1\) on \({{\,\mathrm{supp}\,}}\psi _1\cup {{\,\mathrm{supp}\,}}\psi _2\).
By definition,  is a bilinear map, due to locality it can in fact be extended to a map
is a bilinear map, due to locality it can in fact be extended to a map  , which then induces a continuous linear operator
, which then induces a continuous linear operator  . Note that if S is quadratic, then \(P_S\doteq P_S(\varphi )\) is the same for all \(\varphi \) and \(S'(\varphi )=P_S\varphi \). This is the case for the free scalar field, where \(P_S=-(\Box + m^2)\).
. Note that if S is quadratic, then \(P_S\doteq P_S(\varphi )\) is the same for all \(\varphi \) and \(S'(\varphi )=P_S\varphi \). This is the case for the free scalar field, where \(P_S=-(\Box + m^2)\).
The crucial assumption in the pAQFT approach is that \(P_S(\varphi )\) is a Green-hyperbolic operator [2], i.e. that it admits unique retarded and advanced Green’s functions (fundamental solutions)  defined by the requirements
defined by the requirements

and the support properties
where  . Note that, by the Schwartz kernel theorem, these operators can be written in terms of their integral kernels, which then satisfy appropriate support properties and
. Note that, by the Schwartz kernel theorem, these operators can be written in terms of their integral kernels, which then satisfy appropriate support properties and
The causal propagator is
Due to (3.3), the causal propagator is antisymmetric, i.e. its integral kernel satisfies
We equip the algebra of functionals with a Poisson bracket called the Peierls bracket [47].
Definition 3.8
The Peierls bracket of  is defined by
is defined by
where \(\Delta _S(\varphi )\) is used as a complex bidistribution in \(\Gamma '_c((E^*)^{\boxtimes 2}\rightarrow M^2)^{\scriptscriptstyle {{\mathbb {C}}}}\) (this can be understood as a completion of  , i.e. \(\Delta _S\) is sort of a section of the an appropriate completion of
, i.e. \(\Delta _S\) is sort of a section of the an appropriate completion of  , i.e. a bivector field).
, i.e. a bivector field).
Remark 3.9
The algebra of multilocal functionals,  , is not closed under the Peierls bracket. It works better on the algebra of microcausal functionals,
, is not closed under the Peierls bracket. It works better on the algebra of microcausal functionals,  , defined later on. For a quadratic action, the Peierls bracket gives a Poisson bracket on the algebra of regular functionals,
, defined later on. For a quadratic action, the Peierls bracket gives a Poisson bracket on the algebra of regular functionals,  .
.
In this paper, we will mainly consider an “action” of the form
where \(S_0\) is a quadratic (in \(\varphi \)) action and  is compactly supported. This is not an action in the sense of Definition 3.2, because (unless it is quadratic) V cannot be expressed as an equivalence class of Lagrangians, cannot be cut off with a test function, and is nonlocal. Nevertheless, it can be used in much the same way as an action. For example, the Euler–Lagrange derivative should be understood as \(S'=S_0'+\lambda V^{(1)}\).
is compactly supported. This is not an action in the sense of Definition 3.2, because (unless it is quadratic) V cannot be expressed as an equivalence class of Lagrangians, cannot be cut off with a test function, and is nonlocal. Nevertheless, it can be used in much the same way as an action. For example, the Euler–Lagrange derivative should be understood as \(S'=S_0'+\lambda V^{(1)}\).
Remark 3.10
The \(\lambda V\) is used as a regularized interaction term. The fact that V has compact support is a kind of infrared regularization, and the fact that it is a regular (rather than local) functional is an ultraviolet (UV) regularization. This type of IR regularization is the usual technique used in Epstein–Glaser renormalization [23]. Epstein–Glaser allows one to remove the UV cut-off and removing the IR cut-off is related to the adiabatic limit [24]. Collini [12] works with the IR cut-off, but without the UV cut-off, since he considers local functionals. Chapter 4 of [12] deals with establishing the relation of his result to the one of Epstein–Glaser, but it is unclear whether the IR cut-off can be removed in a similar manner.
With this, the definitions of the propagators must be modified slightly (this is equivalent to the definition given in Lemma 1 in [6]):
If \(\lambda \) is a formal parameter, it is easy to see that
satisfies this definition, and there is an analogous formula for \(\Delta _S^{\mathrm{R}}\).
Remark 3.11
To reduce clutter, we will often omit the \(\circ \) symbol when composing linear operators, as in Eq. (3.6).
3.2 Classical Møller maps off-shell
To avoid functional analytic difficulties, we define all the structures only for regular functionals  or local functionals
or local functionals  . We mostly work perturbatively, i.e. we use formal power series in \(\lambda \), which plays the role of a coupling constant.
. We mostly work perturbatively, i.e. we use formal power series in \(\lambda \), which plays the role of a coupling constant.
From now on, we fix a free (quadratic) action \(S_0\) and consider “actions” of the form \(S=S_0+\lambda V\) with  . For two such actions, the retarded and advanced Møller maps
. For two such actions, the retarded and advanced Møller maps  are defined on shell by the requirements that for any
are defined on shell by the requirements that for any  , \(\varphi -{\texttt {r}}_{S_1,S_2}(\varphi )\) has past-compact support and \(\varphi -{\mathtt a}_{S_1,S_2}(\varphi )\) has future-compact support. We will be using the retarded maps, but everything we say adapts easily to the advanced maps.
, \(\varphi -{\texttt {r}}_{S_1,S_2}(\varphi )\) has past-compact support and \(\varphi -{\mathtt a}_{S_1,S_2}(\varphi )\) has future-compact support. We will be using the retarded maps, but everything we say adapts easily to the advanced maps.
We will need the extension of this off-shell. Following [19], the off-shell retarded Møller map is defined by the conditions
and
These retarded Møller maps are perturbatively well defined, and restriction to solutions gives the on-shell Møller maps [19]. To simplify the notation, we abbreviate \({\texttt {r}}_{\lambda V}\doteq {\texttt {r}}_{S_0+\lambda V,S_0}\).
Møller maps act on functionals by pullback.
where  .
.
Lemma 3.12
If \(\lambda \) is a formal parameter, then the retarded Møller map satisfies the Yang–Feldman equation

Conversely, a map satisfying the Yang–Feldman equation (3.10) must be the retarded Møller map.
Proof
Apply \(P_{S_0}+\lambda V^{(2)}(\varphi )\) (where \(P_{S_0}\) is the differential operator induced by \(S_0''\)).
Apply \(\Delta _{S_0}^{\mathrm{R}}\) (which is independent of \(\varphi \)).
Rearranging gives
Since \(\mathtt r_0=\mathrm {id}\), integrating gives (3.10).
The Yang–Feldman equation is equivalent to saying that the inverse of the Møller map is
This gives \({\texttt {r}}^{-1}_{\lambda V}\) as a formal power series in \(\lambda \). The constant term is just the identity map. Therefore, this is invertible as a formal power series. Its inverse is unique, so the Møller map is that unique inverse.
More explicitly, \(\mathtt r_{\lambda V}(\varphi ) \approx \varphi \) to 0th order. Applying Eq. (3.10) iteratively improves this approximation, so that \(\mathtt r_{\lambda V}(\varphi ) \approx \varphi - \Delta ^{\mathrm{R}}_{S_0} V^{(1)}(\varphi )\) to first order and the sequence of approximations converges as a formal power series (\(\lambda \)-adically) to \(\mathtt r_{\lambda V}\). \(\square \)
Nonperturbatively, the Yang–Feldman equation may be taken as a definition of the Møller map. There is certainly no problem with defining \({\texttt {r}}^{-1}_{\lambda V}\) by Eq. (3.11), but its inverse \({\texttt {r}}_{\lambda V}\) may not actually exist. An idea how to use the Nash–Moser inverse function theorem on locally convex topological vector spaces to tackle this problem has been proposed in [11].
We will now provide an alternative proof of the result of [19] stating that \(r_{\lambda V}\) intertwines between the free and interacting Poisson brackets. The advantage of our proof is that it is explicitly performed to all orders and can be generalized to the nonperturbative setting, while the argument in [19] is essentially a proof of the infinitesimal version of the statement.
Definition 3.13
Denote the derivative of the inverse Møller map by

The transpose  is defined by reversing the arguments in the integral kernel for \(\rho \).
is defined by reversing the arguments in the integral kernel for \(\rho \).
Lemma 3.14
The derivative of the inverse Møller map is
and

Proof
Equation (3.12) follows immediately from Eq. (3.11).
The image of  is the set of
is the set of  such that \({{\,\mathrm{supp}\,}}\psi \) is past-compact and \({{\,\mathrm{supp}\,}}P_{S_0}\psi \) is compact. Because \(P_{S}(\varphi )-P_{S_0} = \lambda V^{(2)}(\varphi )\) has compact support, the image of \({\text {Im}} \Delta ^{\mathrm{R}}_S(\varphi )={\text {Im}} \Delta ^{\mathrm{R}}_{S_0}\). Also note that
such that \({{\,\mathrm{supp}\,}}\psi \) is past-compact and \({{\,\mathrm{supp}\,}}P_{S_0}\psi \) is compact. Because \(P_{S}(\varphi )-P_{S_0} = \lambda V^{(2)}(\varphi )\) has compact support, the image of \({\text {Im}} \Delta ^{\mathrm{R}}_S(\varphi )={\text {Im}} \Delta ^{\mathrm{R}}_{S_0}\). Also note that  implies \(\Delta ^{\mathrm{R}}_{S_0} \circ P_{S_0} = \mathrm {id}_{{\text {Im}} \Delta ^{\mathrm{R}}_{S_0}}\).
implies \(\Delta ^{\mathrm{R}}_{S_0} \circ P_{S_0} = \mathrm {id}_{{\text {Im}} \Delta ^{\mathrm{R}}_{S_0}}\).
With this in mind — and hiding the \(\varphi \) arguments — we have

Composing this with the transpose  gives
gives

\(\square \)
Proposition 3.15
[19, Proposition 2] Let  or
or  . The retarded Møller operator \(r_{\lambda V}\) intertwines the Peierls brackets, i.e.
. The retarded Møller operator \(r_{\lambda V}\) intertwines the Peierls brackets, i.e.
Proof
Note that the last term of Eq. (3.13) is symmetric, so subtracting the transpose of this equation gives simply
It is simpler to prove the equivalent property with \(r_{\lambda V}^{-1}\). First note that the derivative of \(r_{\lambda V}^{-1}F = F\circ {\texttt {r}}^{-1}_{\lambda V}\) is
This gives
\(\square \)
4 Deformation quantization
Suppose that  is some space of functionals that is closed under the pointwise product and some Poisson bracket. Formal deformation quantization [4] of the Poisson algebra
is some space of functionals that is closed under the pointwise product and some Poisson bracket. Formal deformation quantization [4] of the Poisson algebra  means constructing an associative algebra
means constructing an associative algebra  , where the product \(\star \) is given by a power series
, where the product \(\star \) is given by a power series
in which each \(B_n\) is a bidifferential operator (in the sense of calculus on  [3, 43, 45]) and in particular
[3, 43, 45]) and in particular
4.1 Exponential star products
The Peierls bracket of a quadratic action such as \(S_0\) is a constant bidifferential operator, in the sense that it does not depend on \(\varphi \). Some of the \(\star \)-products that we need to consider are simple in a similar way.
Definition 4.1
Given a sequence of cones \(\Lambda _n\subset T^*M\) for \(n=1.2,\dots \), we define a space of functionals by

The most important choices here are:
Regular functionals (\(*=\mathrm {reg}\)) are defined by \(\Lambda _n=\varnothing \).
Microcausal functionals (\(*={\mu \mathrm {c}}\)) are defined by
$$\begin{aligned} \Lambda _n\doteq T^*M^n{\setminus }\{(x_1,\dots ,x_n;k_1,\dots ,k_n)\mid (k_1,\dots ,k_n)\in ({\overline{V}}_+^n \cup {\overline{V}}_-^n)_{(x_1,\dots ,x_n)}\}\,. \end{aligned}$$(4.2)
This has an obvious generalization to functionals of two variables.
Definition 4.2
Let  be the set of functionals
be the set of functionals  such that for all
such that for all  , \(n_1,n_2\in {\mathbb {N}}_0\), and for \(n\doteq n_1+n_2\),
, \(n_1,n_2\in {\mathbb {N}}_0\), and for \(n\doteq n_1+n_2\),
as a distribution in \(\Gamma '(E^{\boxtimes n}\rightarrow M^n)^{\scriptscriptstyle {{\mathbb {C}}}}\), has WF set contained in \(\Lambda _n\).
Let  denote the pointwise product. In this notation, \(F\cdot G = m(F\otimes G)\). Note that
denote the pointwise product. In this notation, \(F\cdot G = m(F\otimes G)\). Note that  , and m is pullback by the diagonal. It is clear from Definition 4.2 that m extends to a map
, and m is pullback by the diagonal. It is clear from Definition 4.2 that m extends to a map  .
.
Suppose \(K\in {\Gamma _c'}({E^*}^{\boxtimes 2}\rightarrow M^2)^{\scriptscriptstyle {{\mathbb {C}}}}\) is such that the differential operator defined by
is a map  . Note that on tensor products
. Note that on tensor products
Remark 4.3
Note the nontrivial compatibility condition implicit here between the choice of  (i.e. the choice of \(\Lambda _n\)) and the singularity structure of \(K\).
(i.e. the choice of \(\Lambda _n\)) and the singularity structure of \(K\).
Definition 4.4
The exponential product given by \(K\) on  is defined by
is defined by
Proposition 4.5
Any exponential product, \(\star \), is associative.
This is proven in [40, Proposition II.4]. This is a simple generalization of the finite rank case originally proven in [32, Thm. 8]. See also [44, 54].
The involution \({}^*\) (given by complex conjugation) extends to  if we just let \(\hbar ^*=\hbar \). However, this is an antiautomorphism of \(\star \) if and only if \(K(y,x)=\overline{K(x,y)}\).
if we just let \(\hbar ^*=\hbar \). However, this is an antiautomorphism of \(\star \) if and only if \(K(y,x)=\overline{K(x,y)}\).
In terms of Eq. (4.1), if we expand (4.5) in powers of \(\hbar \), then the first term is just \(B_0=m\), and the second term is \(B_1= m\circ D\), i.e.
From this, we can see that \(\star \) gives a deformation quantization with respect to the Peierls bracket induced by \(S_0\) if and only if
So, only the antisymmetric part of \(K\) is relevant to compatibility with the Peierls bracket. The freedom in choosing the symmetric part has been exploited in the literature [9] to construct QFT models for free fields on globally hyperbolic manifolds.
Definition 4.6
Given a bidistribution, \(Y \in {\Gamma _c'}({E^*}^{\boxtimes 2}\rightarrow M^2)^{\scriptscriptstyle {{\mathbb {C}}}}\), let \({\mathcal {D}}_Y \doteq \left<Y,\frac{\delta ^2}{\delta \varphi ^2}\right>\) and \(\alpha _{Y} \doteq \mathrm{e}^{\frac{\hbar }{2}{\mathcal {D}}_Y}\).
Proposition 4.7
Consider \(K_1,K_2\in {\Gamma _c'}^{\scriptscriptstyle {{\mathbb {C}}}}({E^*}^{\boxtimes 2}\rightarrow M^2)\), whose difference, \(Y\doteq K_2-K_1\) is symmetric, and which determine products \(\star _1\) and \(\star _2\). If  is in the domain of all powers of \({\mathcal {D}}_Y\), then
is in the domain of all powers of \({\mathcal {D}}_Y\), then

is an isomorphism.
Proof
Firstly, the hypothesis that  is in the domain of all powers of \({\mathcal {D}}_Y\) means that
is in the domain of all powers of \({\mathcal {D}}_Y\) means that  is well defined.
is well defined.
Because of the symmetry of Y, applying \({\mathcal {D}}_Y\) to a product gives
More concisely,
where \(D_i\) is given by \(K_i\) in Eq. (4.3). In other words, m intertwines those two operators. This implies that it intertwines their powers and their exponentials; therefore,
since the various differential operators commute. Composing this identity on the right with \(\mathrm{e}^{\hbar D_1}\) gives
This means that

is a homomorphism. Finally, \(\alpha _{Y}\) is a formal power series with leading term the identity map; therefore, it is invertible and hence an isomorphism. \(\square \)
Remark 4.8
In the finite-dimensional setting, a proof of this result was given in [44], although it may have been known well before then. In the context of quantum field theory, it was discussed in [8].
Since only the antisymmetric part of \(K\) really matters, the simplest choice is to take \(K\) to be antisymmetric. In that case, Eq. (4.6) requires that \(K=\frac{i}{2}\Delta _{S_0}\).
Definition 4.9
The Moyal–Weyl product (denoted \(\star _{\scriptscriptstyle {0}}\)) is the exponential product defined on  by \(\frac{i}{2}\Delta _{S_0}\).
by \(\frac{i}{2}\Delta _{S_0}\).
Unfortunately, this \(\star _{\scriptscriptstyle {0}}\) does not extend to a larger space of functionals than  . This is the fault of \(\Delta _{S_0}\), whose wavefront set is
. This is the fault of \(\Delta _{S_0}\), whose wavefront set is
where \(\sim \) means that both (x, k) and \((x',k')\) belong to some null geodesic strip, i.e. a curve of the form \((\gamma ,\kappa ):I\rightarrow T^*M\), for some interval \(I \subset {\mathbb {R}}\), where \(\gamma \) is a null geodesic and \(\kappa \) is given by \(\kappa (\lambda ) = g({\dot{\gamma }}(\lambda ),.)\).
The problem is that the pullback of a tensor power of \(\Delta _{S_0}\) has a WF set that at singular points contains the whole cotangent bundle [8, 17]. This means that the second-order term of \(\star _{\scriptscriptstyle {0}}\) is only well defined on regular functionals. We can obtain a better behaved star product by a choice of \(K\) that has a smaller WF set.
With this in mind, recall that (as shown in [50]) there exists a real, symmetric, distributional bisolution to the field equation, H, such that
has WF set
where \(\partial J^+_x\subset T^*_xM\) is the set of future-pointing null vectors. Such a H is called a Hadamard distribution.
This is better, because sums of future-pointing vectors are always future-pointing, and do not give the entire cotangent space. This leaves room for \(F^{(n)}\) and \(G^{(n)}\) to have nontrivial WF sets but still gives a well-defined star product of F and G.
This is the motivation behind the definition of microcausal functionals in Definition 4.1.
Definition 4.10
Let \({{\,\mathrm{Had}\,}}\) denote the set of Hadamard distributions.
Given \(H\in {{\,\mathrm{Had}\,}}\), the Wick product (denoted \(\star _{\scriptscriptstyle {H}}\)) is the exponential product on  given by \(\Delta _{S_0}^+\).
given by \(\Delta _{S_0}^+\).
Hence,  is a deformation quantization of
is a deformation quantization of  with respect to the Peierls bracket [8] with \({}^*\) as an involution. By Proposition 4.7,
with respect to the Peierls bracket [8] with \({}^*\) as an involution. By Proposition 4.7,

is an isomorphism.
The choice of a Hadamard distribution is far from unique. It is only determined up to the addition of any smooth real symmetric bisolution. Proposition 4.7 shows that the products given by any two choices are equivalent, as

is an isomorphism. These isomorphisms are coherent in the sense that \(\alpha _{H''-H'}\circ \alpha _{H'-H}=\alpha _{H''-H}\).
This means that we can think of just one abstract algebra, \({\mathfrak {A}}\). Technically, \({\mathfrak {A}}\) is the limit of the above collection of algebras over \({{\,\mathrm{Had}\,}}\), viewed as a category with a unique morphism from any object to any other. Explicitly:
Definition 4.11

We denote the product of A and \(B\in {\mathfrak {A}}\) as \(A\bullet B\), where
The involution is defined by
Our point of view differs slightly from the one taken in [8]. In that work, \({\mathfrak {A}}\) denotes a particular realization of our abstract algebra, obtained by completion of the space  .
.
We will not need to use this definition directly very much. The point is that this algebra is isomorphic to all those constructed using Hadamard distributions, but it does not require a choice of Hadamard distribution.
The different star products come from different ways of identifying \({\mathfrak {A}}\) with  as vector spaces. In the next section, we will explain how these different identifications are related to the choice of quantization maps.
as vector spaces. In the next section, we will explain how these different identifications are related to the choice of quantization maps.
4.2 Quantization maps
In this section, we discuss quantization maps and formalize constructions known from [8, 18].
Here are some key features of \({\mathfrak {A}}\):
\({\mathfrak {A}}\) is a free module of \({\mathbb {C}}[[\hbar ]]\).
There is a surjective homomorphism
 (evaluation at the classical limit).
(evaluation at the classical limit). .
.This implies that the commutator of any \(A,B\in {\mathfrak {A}}\) satisfies
 , so \([A,B]_\bullet \in \hbar {\mathfrak {A}}\). This allows us to state the property that
, so \([A,B]_\bullet \in \hbar {\mathfrak {A}}\). This allows us to state the property that  (4.10)
(4.10)
The space of microcausal functionals  is not necessarily the only choice of classical algebra, but it will suffice here.
is not necessarily the only choice of classical algebra, but it will suffice here.
Note that a \({\mathbb {C}}\)-linear map  extends to a \({\mathbb {C}}[[\hbar ]]\)-linear map
extends to a \({\mathbb {C}}[[\hbar ]]\)-linear map  . Indeed, these are equivalent in the sense that any \({\mathbb {C}}[[\hbar ]]\)-linear map is just the linear extension of its restriction to
. Indeed, these are equivalent in the sense that any \({\mathbb {C}}[[\hbar ]]\)-linear map is just the linear extension of its restriction to  . For this reason, we will abuse notation by denoting such maps by the same symbol.
. For this reason, we will abuse notation by denoting such maps by the same symbol.
Definition 4.12
A quantization map is a linear map  such that
such that
 , and
, andthe image of the \({\mathbb {C}}[[\hbar ]]\)-linear extension of
 is closed under the noncommutative product in \({\mathfrak {A}}\).
is closed under the noncommutative product in \({\mathfrak {A}}\).
In Physics terms, a quantization map is a choice of operator ordering.
Remark 4.13
It would also be reasonable to require t\({}^*\)-linearity:

Some—but not all—of our quantization maps satisfy this condition.
Proposition 4.14
Let  be a Poisson subalgebra. A quantization map
be a Poisson subalgebra. A quantization map  induces a star product on
induces a star product on  by the condition
by the condition

Proof
First, we need to show that  is injective. Suppose that there is a nonzero element of the kernel with leading order term \(\hbar ^m F\). This means that
is injective. Suppose that there is a nonzero element of the kernel with leading order term \(\hbar ^m F\). This means that  , but
, but  , so
, so  and
and  . However,
. However,  , so this is a contradiction.
, so this is a contradiction.
So,  is a bijection to its image, and its image is an associative algebra. In this way, Eq. (4.12) defines an associative product, \(\star \), on
is a bijection to its image, and its image is an associative algebra. In this way, Eq. (4.12) defines an associative product, \(\star \), on  . For
. For  has an expansion of form (4.1) simply because this is a formal power series.
has an expansion of form (4.1) simply because this is a formal power series.
By the compatibility of  with
with  ,
,

and by Eq. (4.10),

\(\square \)
Remark 4.15
In a less formal version,  would be a map from an algebra of bounded classical observables to the algebra of sections of a continuous field of C\({}^*\)-algebras. This can still induce a star product, but Eq. (4.12) needs to become an asymptotic expansion.
would be a map from an algebra of bounded classical observables to the algebra of sections of a continuous field of C\({}^*\)-algebras. This can still induce a star product, but Eq. (4.12) needs to become an asymptotic expansion.
Let us now return to the exponential product discussed in Sect. 4.1.
Definition 4.16
Given a Hadamard distribution \(H\in {{\,\mathrm{Had}\,}}\),

is defined (in terms of Definition 4.11) by

This is a quantization map that induces the exponential product \(\star _{\scriptscriptstyle {H}}\). It is also \({}^*\)-linear.
Definition 4.17

is defined by

This is a quantization map which induces the Moyal–Weyl product, \(\star _{\scriptscriptstyle {0}}\) on  . It is also \({}^*\)-linear.
. It is also \({}^*\)-linear.
These quantization maps are related by

and

Let \({\mathfrak {A}}_\mathrm {reg}\) be the image of the extension of  to formal power series. Because the extensions of these quantization maps to formal power series are injective,
to formal power series. Because the extensions of these quantization maps to formal power series are injective,  induces a commutative “pointwise” product on \({\mathfrak {A}}_\mathrm {reg}\), and
induces a commutative “pointwise” product on \({\mathfrak {A}}_\mathrm {reg}\), and  induces one on \({\mathfrak {A}}\). If \(\Delta ^+_{S_0}\) is the 2-point function of some choice of “vacuum” state, then the commutative product induced by
induces one on \({\mathfrak {A}}\). If \(\Delta ^+_{S_0}\) is the 2-point function of some choice of “vacuum” state, then the commutative product induced by  is the normal-ordered (Wick) product, and
is the normal-ordered (Wick) product, and  can be interpreted as the corresponding normal-ordering map. Of course, this depends upon a choice of H.
can be interpreted as the corresponding normal-ordering map. Of course, this depends upon a choice of H.
4.3 Nets of algebras
Although it is not our main focus here, in AQFT, we really want to construct a net of algebras, rather than just a single algebra.
Definition 4.18
Let  be the set of open, precompact, causally convex subsets of M. Define this to be a category whose morphisms are the inclusions of subsets.
be the set of open, precompact, causally convex subsets of M. Define this to be a category whose morphisms are the inclusions of subsets.
Also, for  , we abuse notation by letting
, we abuse notation by letting

This is a functor from  to the category of subspaces of
to the category of subspaces of  .
.
In this way, the concrete construction of deformation quantization gives a net of algebras, i.e. a functor from  to a category of algebras:
to a category of algebras:

More abstractly, we have a functor (also denoted \({\mathfrak {A}}\)) from  to the category of subalgebras of \({\mathfrak {A}}\).
to the category of subalgebras of \({\mathfrak {A}}\).
For a given quantization map,  , we can define
, we can define  as the restriction of
as the restriction of  to
to  . The quantization maps that we have been considering satisfy the additional property that
. The quantization maps that we have been considering satisfy the additional property that

It follows immediately that these are the components of a natural transformation from the functor  to \({\mathfrak {A}}\) composed with the forgetful functor to vector spaces.
to \({\mathfrak {A}}\) composed with the forgetful functor to vector spaces.
4.4 Time-ordered products
In this section, we discuss the time-ordered product. One uses this structure in pAQFT to construct the S-matrix and the interacting fields (see e.g. [8]). We will come back to these in Sect. 5. Here, we want to review some basic properties of this product, emphasizing the importance of the time-ordering map  that establishes the equivalence between the time-ordered product and the pointwise product.
that establishes the equivalence between the time-ordered product and the pointwise product.
Definition 4.19
The relation \(\prec \) on  means “not later than” i.e.
means “not later than” i.e.  means that there exists a Cauchy surface to the future of
means that there exists a Cauchy surface to the future of  and to the past of
and to the past of  .
.
We want a time-ordered version of the noncommutative product \(\bullet \) to satisfy for  ,
,  and
and  ,
,

Moreover, we require that there exists a quantization map  , satisfying the support condition (4.13) and such that
, satisfying the support condition (4.13) and such that

for  .
.
There is certain freedom in how we choose  for a given \(\bullet \). We will further restrict this freedom when discussing concrete realizations of \(\bullet \) in the following section
for a given \(\bullet \). We will further restrict this freedom when discussing concrete realizations of \(\bullet \) in the following section
4.4.1 Relation to Weyl quantization
In this section, we discuss how to construct  (and hence
(and hence  ) starting from another quantization map.
) starting from another quantization map.
It is convenient to start with  and first construct
and first construct  on
on  by setting
by setting

for some  .
.
Definition 4.12 of “quantization map” implies that  . The support condition (4.13) implies that
. The support condition (4.13) implies that  is contained in the causal completion of \({{\,\mathrm{supp}\,}}F\).
is contained in the causal completion of \({{\,\mathrm{supp}\,}}F\).
We impose further conditions on  :
:
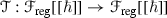 is a differential operator in the sense of calculus on
is a differential operator in the sense of calculus on  ,
, for F linear,
for F linear,
This last property is equivalent to requiring that there exists a natural endomorphism of the functor  whose component at
whose component at  is the restriction of
is the restriction of  to
to  .
.
A natural question to ask is what is the freedom in choosing  ? A similar problem arises in Epstein–Glaser renormalisation [23], where one constructs n-fold time-ordered products recursively (as multilinear maps on local functionals). There, the nonuniqueness of these maps is characterized by the Main Theorem of Renormalization (for various versions of this result, see [8, 20, 37, 48, 49]). The following theorem provides a solution to this problem for
? A similar problem arises in Epstein–Glaser renormalisation [23], where one constructs n-fold time-ordered products recursively (as multilinear maps on local functionals). There, the nonuniqueness of these maps is characterized by the Main Theorem of Renormalization (for various versions of this result, see [8, 20, 37, 48, 49]). The following theorem provides a solution to this problem for  restricted to regular functionals (and without requiring the field independence).
restricted to regular functionals (and without requiring the field independence).
Theorem 4.20
Any two operators  and
and  satisfying these conditions are related by
satisfying these conditions are related by

where
with each \(a_n(\varphi )\) a formal power series in \(\hbar \) with coefficients in symmetric distributions on \(M^n\) such that:
\(a_n(\varphi )\) is a multiple of \(\hbar \);
\(a_n(\varphi )\) is supported on the thin diagonal of \(M^n\);
\(a_n(\varphi )\) depends at most linearly on \(\varphi \);
\(a_n^{(1)}(\varphi )\) is supported on the thin diagonal of \(M^{n+1}\).
Proof
First, define  . Because
. Because  and
and  are differential, X must be differential. This means that it can be written in the form
are differential, X must be differential. This means that it can be written in the form
where \(a_n\) is valued in formal power series of symmetric distributions. If F is any linear functional, then  , so \(XF=0\), therefore \(a_0=a_1=0\).
, so \(XF=0\), therefore \(a_0=a_1=0\).
The ratio  is almost a homomorphism of the pointwise product in the sense that if F and G have causally separated support (\({{\,\mathrm{supp}\,}}G \prec {{\,\mathrm{supp}\,}}F\) or \({{\,\mathrm{supp}\,}}F\prec {{\,\mathrm{supp}\,}}G\)), then
is almost a homomorphism of the pointwise product in the sense that if F and G have causally separated support (\({{\,\mathrm{supp}\,}}G \prec {{\,\mathrm{supp}\,}}F\) or \({{\,\mathrm{supp}\,}}F\prec {{\,\mathrm{supp}\,}}G\)), then
Consequently, X is almost a derivation in the sense that if F and G have causally separated support, then
Any finite set of distinct points of M can be listed in an order consistent with the causal partial order, and there is a time slicing of  (into Cauchy surfaces) consistent with this order. Let \(x_1,\dots ,x_n\in M\) be such a list of points. There exist neighbourhoods of these points that are causally separated by Cauchy surfaces of this time slicing. Consider any
(into Cauchy surfaces) consistent with this order. Let \(x_1,\dots ,x_n\in M\) be such a list of points. There exist neighbourhoods of these points that are causally separated by Cauchy surfaces of this time slicing. Consider any  supported on these respective neighbourhoods, and any
supported on these respective neighbourhoods, and any  . Define linear functionals
. Define linear functionals
For any numbers \(m_1,\dots ,m_n\in {\mathbb {N}}\), apply X to the product \(F_1^{m_1}\dots F_n^{m_n}\) and use Eq. (4.16). Evaluating at \(\varphi _0\), this shows that
Because the section \(p_i\) can take any values around \(x_i\), this shows that \(a_{m_1+\dots +m_n}(\varphi _0)\) is not supported at
Up to symmetry, this is any point outside the thin diagonal.
Finally, consider a point \(x\in M\). If F is supported on a causally complete neighbourhood \(U\ni x\), then
must be supported on U. Take F homogeneous of degree n, so that \(F^{(n)}(\varphi )=f\in \Gamma _c(M^n,(E^*)^{\boxtimes n})^{\scriptscriptstyle {{\mathbb {C}}}}\) and \({{\,\mathrm{supp}\,}}f\subset U^n\). Now consider  such that \({{\,\mathrm{supp}\,}}\psi \cap U=\varnothing \). Since
such that \({{\,\mathrm{supp}\,}}\psi \cap U=\varnothing \). Since  has to be supported in U, we conclude that
has to be supported in U, we conclude that
We can now use this fact to conclude that the derivative \(a_n^{(1)}(\varphi )\), seen as a distribution on \(M^{n+1}\), has to be supported on the diagonal. Since X maps regular functionals to regular functionals, this implies that \(a_n(\varphi )\) can depend at most linearly on \(\varphi \). \(\square \)
In pAQFT, one also requires the stronger condition of field independence, which is usually phrased as

This just means that  should have constant coefficients. If
should have constant coefficients. If  and
and  in Theorem 4.20 satisfy this, then each \(a_n(\varphi )\) is independent of \(\varphi \).
in Theorem 4.20 satisfy this, then each \(a_n(\varphi )\) is independent of \(\varphi \).
Just as a quantization map induces a star product from \(\bullet \), it also induces a commutative product from  . For
. For  , we denote this commutative product on
, we denote this commutative product on  as
as  . This is defined analogously to Eq. (4.12) by
. This is defined analogously to Eq. (4.12) by

This is equivalent to

Because  satisfies (4.13), (4.14) implies that
satisfies (4.13), (4.14) implies that  satisfies the condition
satisfies the condition

There is a natural choice of  satisfying field independence, given in terms of the Dirac propagator, \(\Delta _{S_0}^{\mathrm {D}}\doteq \frac{1}{2} (\Delta _{S_0}^{\mathrm {R}}+\Delta _{S_0}^{\mathrm {A}})\). Set
satisfying field independence, given in terms of the Dirac propagator, \(\Delta _{S_0}^{\mathrm {D}}\doteq \frac{1}{2} (\Delta _{S_0}^{\mathrm {R}}+\Delta _{S_0}^{\mathrm {A}})\). Set

where \({\mathcal {D}}_{\mathrm {D}}=\left<\Delta _{S_0}^{\mathrm{D}},\frac{\delta ^2}{\delta \varphi ^2}\right>\).
Proposition 4.21
The time-ordered product  defined in terms of
defined in terms of  by Eq. (4.19) equals the exponential product given by Definition 4.4 with \(K=i\Delta _{S_0}^{\mathrm {D}}\).
by Eq. (4.19) equals the exponential product given by Definition 4.4 with \(K=i\Delta _{S_0}^{\mathrm {D}}\).
Proof
The Leibniz rule for differentiation implies that
which is in fact a coproduct structure. Hence,

\(\square \)
Because both \(\star _{\scriptscriptstyle {0}}\) and  are exponential products, they are related by an exponential factor. With obvious notation following Eq. (4.3), \(D_\Delta = D_{\mathrm{R}}-D_{\mathrm{A}}\) and \(D_{\mathrm{D}} = \frac{1}{2}\left( D_{\mathrm{R}}+D_{\mathrm{A}}\right) \), so \(\frac{1}{2} D_\Delta -D_{\mathrm{D}} = -D_{\mathrm{A}}\), and therefore, the relation is
are exponential products, they are related by an exponential factor. With obvious notation following Eq. (4.3), \(D_\Delta = D_{\mathrm{R}}-D_{\mathrm{A}}\) and \(D_{\mathrm{D}} = \frac{1}{2}\left( D_{\mathrm{R}}+D_{\mathrm{A}}\right) \), so \(\frac{1}{2} D_\Delta -D_{\mathrm{D}} = -D_{\mathrm{A}}\), and therefore, the relation is
From this relation, it is easy to see why  satisfies Eq. (4.18). Consider the case that \({{\,\mathrm{supp}\,}}G \prec {{\,\mathrm{supp}\,}}F\). By definition, \(\Delta _{S_0}^{\mathrm{A}}(x,y) = 0\) when \(x\nleq y\), so \(D_{\mathrm{A}}(F\otimes G)=0\) and
satisfies Eq. (4.18). Consider the case that \({{\,\mathrm{supp}\,}}G \prec {{\,\mathrm{supp}\,}}F\). By definition, \(\Delta _{S_0}^{\mathrm{A}}(x,y) = 0\) when \(x\nleq y\), so \(D_{\mathrm{A}}(F\otimes G)=0\) and

Coming back to formula (4.15), using  , we have now constructed a quantization map
, we have now constructed a quantization map  on
on  with the desired properties. We denote by \(\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}}}}\) the star product on
with the desired properties. We denote by \(\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}}}}\) the star product on  induced by
induced by  from the noncommutative product \(\bullet \) on \({\mathfrak {A}}\); this product is given by the multiplication map
from the noncommutative product \(\bullet \) on \({\mathfrak {A}}\); this product is given by the multiplication map
i.e.
The disadvantage of using  as the quantization map is that it does not extend naturally to
as the quantization map is that it does not extend naturally to  (unlike
(unlike  ). It is also not \({}^*\)-linear like
). It is also not \({}^*\)-linear like  and
and  ; instead it induces an involution on
; instead it induces an involution on  , given by the formula
, given by the formula

and compatible with \(\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}}}}\).
4.4.2 Relation to normal ordering
We can also start with  and let
and let

The relation between  and
and  implies that
implies that

where \(\Delta _{S_0}^{\mathrm{F}}\) is the Feynman propagator, defined as \(\Delta _{S_0}^{\mathrm{F}} = i\Delta _{S_0}^{\mathrm{D}} + H\).
Using  , we can introduce another exponential product on
, we can introduce another exponential product on  , denoted by \(\cdot _{{}^{{\mathcal {T}}_H}}\) and given by setting \(K=\Delta _{S_0}^{\mathrm{F}}\) in Definition 4.4. Clearly, this product is again commutative and equivalent to the pointwise product.
, denoted by \(\cdot _{{}^{{\mathcal {T}}_H}}\) and given by setting \(K=\Delta _{S_0}^{\mathrm{F}}\) in Definition 4.4. Clearly, this product is again commutative and equivalent to the pointwise product.
Since \(\Delta _{S_0}^+ - \Delta _{S_0}^{\mathrm{F}} = -i\Delta _{S_0}^{\mathrm{A}}\), the multiplication maps for \(\star _{\scriptscriptstyle {H}}\) and \(\cdot _{{}^{{\mathcal {T}}_H}}\) are related by,

which is exactly the same as the relation between \(\star _{\scriptscriptstyle {0}}\) and  ; consequently, by identical reasoning, they are also related by Eq. (4.18), and we can say that \(\cdot _{{}^{{\mathcal {T}}_H}}\) is the time-ordered product associated to \(\star _{\scriptscriptstyle {H}}\).
; consequently, by identical reasoning, they are also related by Eq. (4.18), and we can say that \(\cdot _{{}^{{\mathcal {T}}_H}}\) is the time-ordered product associated to \(\star _{\scriptscriptstyle {H}}\).
Unfortunately, although \(\star _{\scriptscriptstyle {H}}\) is defined on  , this construction only defines \(\cdot _{{}^{{\mathcal {T}}_H}}\) and
, this construction only defines \(\cdot _{{}^{{\mathcal {T}}_H}}\) and  on
on  . Renormalization in pAQFT is a matter of extending these consistently to local functionals. Again, there is some freedom in constructing such an extension [8, 37], physically interpreted as renormalization freedom. To fix this freedom, one imposes certain conditions more restrictive than those we imposed on time-ordered products of regular functionals; this is discussed extensively in [16].
. Renormalization in pAQFT is a matter of extending these consistently to local functionals. Again, there is some freedom in constructing such an extension [8, 37], physically interpreted as renormalization freedom. To fix this freedom, one imposes certain conditions more restrictive than those we imposed on time-ordered products of regular functionals; this is discussed extensively in [16].
We summarize the different exponential products used throughout this section in Table 1. Compared to the existing literature, the only new ingredient is the noncommutative product \(\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}}}}\), related to more commonly used star products by:

5 Interaction and Møller operators
5.1 The Møller operator in the abstract algebra
Consider a theory with action \(S=S_0+\lambda V\), where  is compactly supported and \(\lambda \) is the coupling constant, treated from now on as a formal parameter (similarly to \(\hbar \)).
is compactly supported and \(\lambda \) is the coupling constant, treated from now on as a formal parameter (similarly to \(\hbar \)).
We wish to construct a formal deformation quantization of  . Proposition 3.15 shows that \(r_{\lambda V}\) intertwines the Peierls brackets for S and \(S_0\). If \(\star \) is a formal deformation quantization for \(S_0\), then this gives an obvious formal deformation quantization for S. Simply define \(\star _r\) by
. Proposition 3.15 shows that \(r_{\lambda V}\) intertwines the Peierls brackets for S and \(S_0\). If \(\star \) is a formal deformation quantization for \(S_0\), then this gives an obvious formal deformation quantization for S. Simply define \(\star _r\) by
This construction was proposed by Dito [13, 14] in the case of an interacting theory on Minkowski spacetime that is equivalent to a free theory. This is simple, but it is not the best choice. We will explain the reasons for this in Sect. 5.4, after describing what we claim is a better construction.
Firstly, we need to introduce some further definitions. A central object in pAQFT for constructing interacting theories is the formal S-matrix.
Definition 5.1
The formal S-matrix is the map  given by the time-ordered exponential
given by the time-ordered exponential

Remark 5.2
Here V plays the role of an interaction term where some infrared (IR) and ultraviolet (UV) regularizations have been implemented. The former guarantees compact support and the latter regularity. An example of a regular functional is \(\varphi \mapsto \int f(x_1,\dots ,x_3)\varphi (x_1)\dots \varphi (x_3)\), where f is a compactly supported density on \(M^3\) and  . The physical interaction is recovered in the limit
. The physical interaction is recovered in the limit
Instead of taking this limit directly, in pAQFT one proceeds in two steps. First the map  is extended to a larger subset of \({\mathfrak {A}}\), to deal with the potential UV divergences (see, for example, [8, 52] for a review). Next, one takes the algebraic adiabatic limit to deal with the IR problem. For more details, see [30, 35, 52] for an alternative formulation.
is extended to a larger subset of \({\mathfrak {A}}\), to deal with the potential UV divergences (see, for example, [8, 52] for a review). Next, one takes the algebraic adiabatic limit to deal with the IR problem. For more details, see [30, 35, 52] for an alternative formulation.
The physical interpretation is that  becomes the scattering matrix of the theory, in the adiabatic limit (i.e. when the infrared regularization is removed), if it exists. One uses
becomes the scattering matrix of the theory, in the adiabatic limit (i.e. when the infrared regularization is removed), if it exists. One uses  to construct interacting fields using the quantum Møller operator given by the formula of Bogoliubov (see e.g. [8, 52] for a review):
to construct interacting fields using the quantum Møller operator given by the formula of Bogoliubov (see e.g. [8, 52] for a review):

A priori, this is defined for \(A,B\in \lambda {\mathfrak {A}}_\mathrm {reg}[[\lambda ]]\). However, the last expression makes sense for \(B\in {\mathfrak {A}}_\mathrm {reg}\) and defines a map  . Better still, we will show below that
. Better still, we will show below that  — i.e. no negative powers of \(\hbar \) survive.
— i.e. no negative powers of \(\hbar \) survive.
For the interaction  , we choose
, we choose  in this formula. The interacting product \(\bullet _{\scriptscriptstyle {\mathrm {int}}}\) on \({\mathfrak {A}}_\mathrm {reg}\) is then defined by
in this formula. The interacting product \(\bullet _{\scriptscriptstyle {\mathrm {int}}}\) on \({\mathfrak {A}}_\mathrm {reg}\) is then defined by

5.2 The Møller operator in terms of functionals
For the purpose of practical computations, it is easier to work with functionals rather than the abstract algebra \({\mathfrak {A}}_\mathrm {reg}\), so we should identify \({\mathfrak {A}}_\mathrm {reg}\) with  by using a quantization map, but there are several to choose from. This leads to abundance of products used in the literature in this context. However, the fundamental structures can be described on the level of the abstract algebra, and there one needs only two products:
by using a quantization map, but there are several to choose from. This leads to abundance of products used in the literature in this context. However, the fundamental structures can be described on the level of the abstract algebra, and there one needs only two products:  , while \(\bullet _{\scriptscriptstyle {\mathrm {int}}}\) can be constructed out of the two, as described above.
, while \(\bullet _{\scriptscriptstyle {\mathrm {int}}}\) can be constructed out of the two, as described above.
The most obvious way to work is based on the quantization map  . With this identification, the formal S-matrix becomes
. With this identification, the formal S-matrix becomes  , so one is often interested in
, so one is often interested in

The Møller operator becomes  , which is
, which is

If we instead use  , then the formula for \(R_{H,\lambda V}\) is the same, but with
, then the formula for \(R_{H,\lambda V}\) is the same, but with  , and \(\cdot _{{}^{{\mathcal {T}}_H}}\).
, and \(\cdot _{{}^{{\mathcal {T}}_H}}\).
All these formulae for the interacting star product and interacting fields are difficult to work with, because they each use two different products, neither of which is the natural pointwise product on the space of functionals.
5.3 The Møller operator in the time-ordered identification
Instead, the most convenient quantization map for computations is actually  . With this identification, the formal S-matrix becomes simply
. With this identification, the formal S-matrix becomes simply

The Møller operator becomes  , which is
, which is

The inverse of this is particularly simple:

Note that any formula for  can be converted to a formula for \(R_{H,\lambda V}\) (and vice versa) by
can be converted to a formula for \(R_{H,\lambda V}\) (and vice versa) by  .
.
Recall that the nth derivative of a functional is valued in the complex dual of the projective tensor product  .
.
Definition 5.3
Any  defines a linear map
defines a linear map

by
Note that for  , this defines a derivation. In general, this extends to linear combinations and defines differential operators. The idea is that the abelian Lie group
, this defines a derivation. In general, this extends to linear combinations and defines differential operators. The idea is that the abelian Lie group  acts on functionals by translation. This
acts on functionals by translation. This  is its own Lie algebra and in that capacity acts on functionals by derivations. The projective symmetric tensor product algebra
is its own Lie algebra and in that capacity acts on functionals by derivations. The projective symmetric tensor product algebra  is a completion of the universal enveloping algebra and acts on functionals by differential operators. The \(\triangleright \) notation is borrowed from the Hopf algebra literature.
is a completion of the universal enveloping algebra and acts on functionals by differential operators. The \(\triangleright \) notation is borrowed from the Hopf algebra literature.
A convenient way of describing elements of this algebra — and thus differential operators on functionals is as functions on  . We can define
. We can define  by giving a formula for K(w) where
by giving a formula for K(w) where  . Formally, \(K\triangleright F\) is defined by replacing \(w^{\otimes n} \) with \(F^{(n)}\). Of course, we extend all of this to formal power series, and we use functionals valued in
. Formally, \(K\triangleright F\) is defined by replacing \(w^{\otimes n} \) with \(F^{(n)}\). Of course, we extend all of this to formal power series, and we use functionals valued in  .
.
Proposition 5.4

where
for  and
and  .
.
Remark 5.5
Equation (5.4) is subtle, so it is worth expanding upon. First, J is a functional from  to formal power series with coefficients in
to formal power series with coefficients in  . In Eq. (5.4), J is evaluated at \(\varphi \) to give a formal power series with coefficients in
. In Eq. (5.4), J is evaluated at \(\varphi \) to give a formal power series with coefficients in  . This then defines a differential operator which acts on G to give a functional. Finally, this functional is evaluated at \(\varphi \).
. This then defines a differential operator which acts on G to give a functional. Finally, this functional is evaluated at \(\varphi \).
Proof
First, for some arbitrary functional F, consider \(F\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}}}}{}\) as an operator acting on G:
where
For \(F=\mathrm{e}^{i\lambda V/\hbar }\), this becomes
and so

The original proof of the next result is due to [17] and was presented for the case of local functionals. Here we are working only with regular functionals, which allows a simpler proof. (Recall that \({\mathfrak {A}}\) is an algebra over \({\mathbb {C}}[[\hbar ]]\).)
Corollary 5.6
For \(A\in \lambda {\mathfrak {A}}_\mathrm {reg}\),  , and for
, and for  . That is, the Møller operator contains no negative powers of \(\hbar \).
. That is, the Møller operator contains no negative powers of \(\hbar \).
Proof
In the expression
the numerator is of order \(\hbar \), so this cancels the \(\hbar \) in the denominator, and thus, J does not contain any negative powers of \(\hbar \). This means that  .
.
The fact that \(J\approx 1\) to 0th order in \(\lambda \) means that  is a formal power series with the identity map in leading order. As a formal power series, it can thus be inverted, and
is a formal power series with the identity map in leading order. As a formal power series, it can thus be inverted, and  exists. Finally, the other forms of the Møller operator are equivalent to this one. \(\square \)
exists. Finally, the other forms of the Møller operator are equivalent to this one. \(\square \)
Let us now discuss the classical limit. Recall that  is the evaluation at the classical limit; it corresponds to setting \(\hbar =0\).
is the evaluation at the classical limit; it corresponds to setting \(\hbar =0\).
Proposition 5.7
The classical limit of the quantum Møller operator is the classical Møller operator:

Equivalently, for  ,
,
Proof
Again, it is easiest to prove the equivalent statement for  .
.
To 0th order in \(\hbar \),
so
Also note that  is the identity operator to 0th order in \(\hbar \), so
is the identity operator to 0th order in \(\hbar \), so  .
.
Denote

This gives
This is just a Taylor series expansion, so
In other words, \({\tilde{r}}^{\scriptscriptstyle {-1}}_{\lambda V}\) is the pullback by the operator that acts on  as
as
Rearranging this gives an equation satisfied by the inverse map,
which is the Yang–Feldman equation, and so by Lemma 3.12, \(\tilde{\texttt {r}}_{\lambda V} = {\texttt {r}}_{\lambda V}\). \(\square \)
Definition 5.8
Let \(\star _{\scriptscriptstyle {H,\mathrm {int}}}\) denote the interacting product on  in the identification given by
in the identification given by  , i.e.
, i.e.

Denote the \(\star _{\scriptscriptstyle {H,\mathrm {int}}}\)-commutator by
It is now easy to see that the theory defined by \(\star _{\scriptscriptstyle {H,\mathrm {int}}}\) is indeed a quantization of the classical theory defined by the Poisson bracket \(\{\;\cdot \;,\;\cdot \;\}_{S_0+\lambda V}\) given in Definition 3.8.
Proposition 5.9
Let  , then
, then
thus  is a formal deformation quantization of
is a formal deformation quantization of  .
.
Proof
This is a straightforward consequence of Propositions 3.15 and 5.7. The quantum Møller operator intertwines \(\star _{\scriptscriptstyle {H}}\) with \(\star _{\scriptscriptstyle {H,\mathrm {int}}}\) (by definition), so it intertwines their commutators. To first order in \(\hbar \),
\(\square \)
Remark 5.10
The equivalent, more abstract, statement is [like Eq. (4.10)] that for any \(A,B\in {\mathfrak {A}}_\mathrm {reg}\),

Next we show that the quantum Møller operator can be constructed nonperturbatively, provided the classical Møller operator is known exactly. To this end, we will extract the “classical part” of the quantum Møller operator and see what remains. It will then become clear that, at a fixed order in \(\hbar \), the remaining “purely quantum part” contains only finitely many terms in its coupling constant expansion.
Proposition 5.11
Again, let \(r_{\lambda V}\) be the classical Møller operator. Define \(\triangleright _r\), \(J_1\), and \(\Upsilon _{\lambda V}\) by
and
The inverse quantum Møller operator can be computed as

Proof
The quantum correction \(J_1\) is chosen so that \(J=J_0J_1\), where \(J_0\) is defined in Eq. (5.6). Proposition 5.4 gives

This last expression contains \(\varphi \) 3 times. Note that the second \(\varphi \) is just a constant as far as \(J_0(\varphi )\triangleright \) is concerned; it is not differentiated, and indeed this is also equal to \( [J_1(\varphi )\triangleright (J_0(\varphi )\triangleright F)](\varphi )\).
Proposition 5.7 showed that \((r_{\lambda V}^{-1}G)(\varphi ) = (J_0(\varphi )\triangleright G)(\varphi )\). Setting \(G(\varphi )= (J_1(\varphi )\triangleright F)(\varphi )\) gives

\(\square \)
Remark 5.12
Rearranging (5.8) results in  , so \(\Upsilon _{\lambda V}^{-1}\) can be seen as the “purely quantum” part of the Møller operator. Such a map has been introduced in [22] for quadratic interactions (where it is called \(\beta \) and in our notation we have \(\beta \doteq r_{\lambda V}^{-1}\circ R_{0,\lambda V}\)), so our current discussion is a natural generalization of that result. The only missing step in that comparison is to transform the quantum Møller map from the
, so \(\Upsilon _{\lambda V}^{-1}\) can be seen as the “purely quantum” part of the Møller operator. Such a map has been introduced in [22] for quadratic interactions (where it is called \(\beta \) and in our notation we have \(\beta \doteq r_{\lambda V}^{-1}\circ R_{0,\lambda V}\)), so our current discussion is a natural generalization of that result. The only missing step in that comparison is to transform the quantum Møller map from the  -identification to the
-identification to the  or
or  -identification (i.e. to go from
-identification (i.e. to go from  to \(R_{0,\lambda V}\) or \(R_{H,\lambda V}\)). We will come back to this in Sect. 7.
to \(R_{0,\lambda V}\) or \(R_{H,\lambda V}\)). We will come back to this in Sect. 7.
Remark 5.13
Note that the fraction in the definition of \(J_1\) is of order at least \(\hbar \), so that every occurrence of \(\lambda \) is accompanied by a factor of \(\hbar \). If \(J_1\) is expanded in powers of \(\hbar \), then each coefficient contains only finitely many powers of \(\lambda \), so \(\lambda \) no longer needs to be treated as a formal parameter. This gives a nonperturbative definition of the quantum Møller operator, provided that the classical Møller operator exists nonperturbatively. This existence will be shown in the forthcoming paper [26].
5.4 The naive product
This shows the relationship between the interacting product and the naive product constructed from \(\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}}}}\) using the classical Møller operator. From Eq. (5.1), the naive product \(\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}},r}}\) is given by
The interacting product \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) in the identification given by  is defined by
is defined by

Equation (5.8) shows that
Note that \(\Upsilon _{\lambda V}\) is the identity map modulo \(\hbar \). This means that \(\Upsilon _{\lambda V}\), the “purely quantum” part of the inverse quantum Møller operator is the “gauge” equivalence [41] relating the naive product \(\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}},r}}\) to the preferred choice \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\).
Now we are ready to consider the relative merits of the interacting product \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) and the naive product, \(\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}},r}}\), defined by Eq. (5.1). The advantage of \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) is related to locality and the adiabatic limit. Ultimately, the interacting star product will be used to construct local nets of algebras. Consider some bounded causally convex region  and the Møller operator restricted to functionals supported in
and the Møller operator restricted to functionals supported in  . Using a local (rather than regular) interaction, it was shown in [9, 30] (in a slightly different setting) that perturbing the interaction by a compactly supported functional, supported outside
. Using a local (rather than regular) interaction, it was shown in [9, 30] (in a slightly different setting) that perturbing the interaction by a compactly supported functional, supported outside  only changes the restriction of the Møller operator by an inner automorphism. This means that for F and G supported in
only changes the restriction of the Møller operator by an inner automorphism. This means that for F and G supported in  , \(F\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}},r}}G\) (and \(F\star _{\scriptscriptstyle {H,\mathrm {int}}}G\)) only depend on the interaction in
, \(F\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}},r}}G\) (and \(F\star _{\scriptscriptstyle {H,\mathrm {int}}}G\)) only depend on the interaction in  . In other words, the net of algebras depends only locally on the interaction. We can therefore first introduce an infrared cut-off for the interaction and then remove it using the algebraic adiabatic limit construction [9, 27]. (Similarly, the retarded and advanced Møller operators are related by inner automorphisms, so they define exactly the same interacting products.)
. In other words, the net of algebras depends only locally on the interaction. We can therefore first introduce an infrared cut-off for the interaction and then remove it using the algebraic adiabatic limit construction [9, 27]. (Similarly, the retarded and advanced Møller operators are related by inner automorphisms, so they define exactly the same interacting products.)
The naive products defined from the classical Møller operator by Eq. (5.1) do not share this property. To first order in \(\lambda \),
To first order in \(\hbar \),
This gives a formula for \(\mathbin {\star _{\scriptscriptstyle {{\mathcal {T}}},r}}\) up to first order in \(\lambda \) and in \(\hbar \):
The third term is problematic, even if V is a local functional. Because of the advanced propagators, this product will change if V is changed anywhere to the past of the support of F and G. The same is true of the naive product constructed from \(\star _{\scriptscriptstyle {H}}\).
6 Graphical computations
To simplify and organize the computations, we will represent our structures in terms of graphs.
Definition 6.1
 is the set of isomorphism classes of directed graphs with n vertices labelled \(1,\dots , n\) (and possibly unlabelled vertices with valency \(\ge 1\)).
is the set of isomorphism classes of directed graphs with n vertices labelled \(1,\dots , n\) (and possibly unlabelled vertices with valency \(\ge 1\)).
Also denote

We make  a category by defining a morphism\(u:\alpha \rightarrow \beta \) to be a function that
a category by defining a morphism\(u:\alpha \rightarrow \beta \) to be a function that
Maps vertices of \(\alpha \) to vertices of \(\beta \) and edges of \(\alpha \) to edges or vertices of \(\beta \),
Respects sources and targets of edges,
Maps labelled vertices to labelled vertices,
And preserves the order of labelled vertices.
For  : \(e(\gamma )\) is the number of edges; \(v(\gamma )\) is the number of unlabelled vertices; \({{\,\mathrm{Aut}\,}}(\gamma )\) is the group of automorphisms.
: \(e(\gamma )\) is the number of edges; \(v(\gamma )\) is the number of unlabelled vertices; \({{\,\mathrm{Aut}\,}}(\gamma )\) is the group of automorphisms.
Remark 6.2
This definition of morphism differs from the standard definition of a map of graphs [42, Sec. II.7]. It is chosen to give the concept of extension that will be useful below. The meaning of isomorphism is the same.
Definition 6.3
A graph  determines an n-ary multidifferential operator, \(\vec {\gamma }\), on functionals as follows:
determines an n-ary multidifferential operator, \(\vec {\gamma }\), on functionals as follows:
An edge represents \(\Delta _{S_0}^{\mathrm{A}}(x,y)\) with the direction from y to x — i.e. such that this is only nonvanishing when the edge points from the future to the past;
If the labelled vertex j has valency r, this represents the order r derivative of the jth argument;
Likewise, an unlabelled vertex of valency r represents \(V^{(r)}\).
Definition 6.4
In diagrams, \(\Delta _{S_0}^{\mathrm{A}}\) will be denoted by a dashed line with an arrow, so all graphs in  will be drawn with dashed lines for the edges.
will be drawn with dashed lines for the edges.
6.1 Noninteracting product
Definition 6.5
 is the subset of graphs with no unlabelled vertices in which all edges go from 2 to 1.
is the subset of graphs with no unlabelled vertices in which all edges go from 2 to 1.
In terms of these, the noninteracting product can be expressed as

Example 6.6
The \(\hbar ^3\) term is given by the graph

which is the unique graph in  with 3 edges. Its automorphism group is \(S_3\), which has order 6 and gives the correct coefficient, \(\frac{1}{6}(-i\hbar )^3\).
with 3 edges. Its automorphism group is \(S_3\), which has order 6 and gives the correct coefficient, \(\frac{1}{6}(-i\hbar )^3\).
6.2 Perturbative calculations
6.2.1 Inverse Møller operator
Definition 6.7
 is the set of graphs such that every edge goes from 1 to an unlabelled vertex.
is the set of graphs such that every edge goes from 1 to an unlabelled vertex.
Example 6.8

has automorphism group \(S_3 \times ({\mathbb {Z}}_2\ltimes {\mathbb {Z}}_2^2)\).
Lemma 6.9

Proof
Taking a Taylor expansion of V about \(\varphi \) in Eq. (5.5) shows that
The term \(\left<V^{(n)}(\varphi ),(\Delta ^{\mathrm{A}}_{S_0}w)^{\otimes n}\right>\) gives the same differential operator as the graph with n edges directed from the vertex 1 to a single unlabelled vertex. We have here a sum over all possible products of such terms. This corresponds to all possible graphs in  .
.
The automorphisms of a graph  do not permute the unlabelled vertices with different valencies; thus, the automorphism group is a Cartesian product of the group of automorphisms for each of those subgraphs.
do not permute the unlabelled vertices with different valencies; thus, the automorphism group is a Cartesian product of the group of automorphisms for each of those subgraphs.
If \(\gamma \) has k unlabelled vertices of valency n, then an automorphism can permute each of those vertices, and for each such vertex, it can permute the n edges leading to it. That subgroup of automorphisms is thus a semidirect product of \(S_k\) and \((S_n)^k\). This has order \(k! (n!)^k\). \(\square \)
6.2.2 Composition of operators
The following is analogous to the concept of an extension of groups.
Definition 6.10
For  and
and  , an extension of \(\gamma \) by \(\alpha \) at \(j\in \gamma \) is a pair of an injective and a surjective morphism
, an extension of \(\gamma \) by \(\alpha \) at \(j\in \gamma \) is a pair of an injective and a surjective morphism
with  , such that \(u(\alpha )=v^{-1}(j)\), and the restriction of v to the compliment of \(u(\alpha )\) is injective.
, such that \(u(\alpha )=v^{-1}(j)\), and the restriction of v to the compliment of \(u(\alpha )\) is injective.
Two extensions are equivalent if there exists a commutative diagram between them with the identity on \(\alpha \) and \(\gamma \), and an automorphism on \(\beta \).
Example 6.11
There is an extension

which maps the first graph to the bottom edge of the second graph and then collapses that subgraph to the vertex 1 of the third graph.
Definition 6.12
The partial composition of multilinear maps is denoted by \(\circ _j\) and means the composition of one map into the jth argument of another.
Lemma 6.13
Let  and
and  and \(j=1,\dots ,m\). The partial composition at j is
and \(j=1,\dots ,m\). The partial composition at j is
where the sum is over equivalence classes of extensions of \(\gamma \) by \(\alpha \) at j.
Equivalently,
where the sum is over the set of  such that there exists such an extension of \(\gamma \) by \(\alpha \) at j and \(d_\beta \) is the number of subgraphs of \(\beta \) isomorphic to \(\alpha \) such that the quotient is isomorphic to \(\gamma \) with the subgraph mapped to j.
such that there exists such an extension of \(\gamma \) by \(\alpha \) at j and \(d_\beta \) is the number of subgraphs of \(\beta \) isomorphic to \(\alpha \) such that the quotient is isomorphic to \(\gamma \) with the subgraph mapped to j.
Proof
The composition \(\gamma \circ _j\alpha \) can be thought of as inserting \(\alpha \) in place of \(j\in \gamma \). If r is the valency of \(j\in \gamma \), then this is taking an order r derivative of \(\vec {\alpha }\). The edges represent \(\Delta _{S_0}^{\mathrm{A}}\), which is constant, so the product rule tells us that this derivative is given by a sum over all possible ways of attaching the r edges to vertices of \(\alpha \) (instead of to \(j\in \gamma \)). Any such attachment gives a graph \(\beta \) with a subgraph identified with \(\alpha \) and the quotient identified with \(\gamma \). This gives precisely the set of equivalence classes of extensions as defined above.
For the second expression, we need to write this as a sum over the graphs \(\beta \) that can appear as extensions, but one graph can appear in inequivalent extensions, so we need to understand the number of extensions with a given \(\beta \).
An extension \(\alpha \hookrightarrow \beta \twoheadrightarrow \gamma \) certainly determines a subgraph of \(\beta \) that is isomorphic to \(\alpha \). If two extensions determine the same subgraph, then it is easy to construct an automorphism of \(\beta \) that gives an equivalence between the extensions. (All of the edges of \(\beta \) are either in the subgraph or map to edges of \(\gamma \).) So, having the same subgraph is a weaker condition than equivalence of extensions.
By definition, \(d_\beta \) is the number of possible images of \(\alpha \) in extensions. Any two extensions with the same image are related by an automorphism of \(\alpha \) and an automorphism of \(\gamma \); therefore, the number of extensions is
An equivalence of extensions is always given by an automorphism of \(\beta \), so an equivalence class consists of \(|{{\,\mathrm{Aut}\,}}\beta |\) extensions; therefore, the number of equivalence classes of extensions is
\(\square \)
Example 6.14

because the last graph occurs in two inequivalent extensions.
Example 6.15

Each of these graphs has trivial automorphism group, except for the last, for which it has order 2. However, there are also 2 ways of mapping  into it to give the quotient
into it to give the quotient  . This is why the coefficient of that term is also 1.
. This is why the coefficient of that term is also 1.
6.2.3 Interacting product
Definition 6.16
 is the subset of graphs such that every edge either goes from a labelled vertex to an unlabelled vertex or from 2 to 1.
is the subset of graphs such that every edge either goes from a labelled vertex to an unlabelled vertex or from 2 to 1.
Lemma 6.17

Proof
This follows by inserting Eq. (6.1) into Eq. (6.2) and using the product rule. \(\square \)
Definition 6.18
 is the set of graphs such that:
is the set of graphs such that:
Every unlabelled vertex has at least one ingoing edge and one outgoing edge;
There are no directed cycles;
For \(1\le j<k\le n\), there does not exist any directed path from j to k.
In particular, this implies that 1 is a sink (has only ingoing edges) and n is a source (has only outgoing edges).
We are now ready to write down the graphical expansion of the interacting star product. Note that the graphs we are using are constructed from the free propagator \(\Delta ^{\mathrm{A}}_{S_0}\) and from the derivatives of the interaction term V. Later on, we will re-express things in terms of the propagator \(\Delta ^{\mathrm{A}}_{S}\) of the interacting theory and the derivatives of the full action S.
Theorem 6.19

Remark 6.20
The right-hand side is the same as in Eq. (6.3), except that  has replaced
has replaced  and \(\lambda \) has become \(-\lambda \).
and \(\lambda \) has become \(-\lambda \).
Definition 6.21
 is the set of graphs obtained by extending graphs in
is the set of graphs obtained by extending graphs in  by graphs in
by graphs in  at 1 and 2.
at 1 and 2.
Proof
For this proof, let \(F \star _{\scriptscriptstyle {?}} G\) denote the right-hand side of Eq. (6.4), so that we need to prove \(\star _{\scriptscriptstyle {?}}=\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\). That is, we need to prove that  , and Eq. (6.3) has already computed the left side.
, and Eq. (6.3) has already computed the left side.
By Lemma 6.13 and the definition of  can be computed as some sum over
can be computed as some sum over  . We will show that cancellation reduces this to the sum over
. We will show that cancellation reduces this to the sum over  in Eq. (6.3).
in Eq. (6.3).
We first need to check that  , so suppose that
, so suppose that  . By definition, all edges of \(\gamma \) either go from 1 or 2 to an unlabelled vertex or from 2 to 1. Let \(\alpha \subset \gamma \) be the subgraph of edges from 1 (to unlabelled vertices) and denote the quotient graph as \(\gamma /\alpha \). Let \(\beta \subset \gamma \) be the subgraph of edges going from 2 to (unlabelled) vertices not in \(\alpha \). All other edges of \(\gamma \) must go from 2 to vertices of \(\alpha \), therefore
. By definition, all edges of \(\gamma \) either go from 1 or 2 to an unlabelled vertex or from 2 to 1. Let \(\alpha \subset \gamma \) be the subgraph of edges from 1 (to unlabelled vertices) and denote the quotient graph as \(\gamma /\alpha \). Let \(\beta \subset \gamma \) be the subgraph of edges going from 2 to (unlabelled) vertices not in \(\alpha \). All other edges of \(\gamma \) must go from 2 to vertices of \(\alpha \), therefore

and so  .
.
Equations (6.4) and (6.2) give

where \(e=e(\alpha )+e(\beta )+e(\delta )\) and \(v=v(\alpha )+v(\beta )+v(\delta )\). Applying Lemma 6.13, this becomes

where the last sum is over \(\alpha ,\beta \subset \gamma \), such that \(1\in \alpha \), \(2\in \beta \),  , and
, and  .
.
Note that \(\alpha \subset \gamma \) is the subgraph of all edges outgoing from \(1\in \gamma \), so it is uniquely determined by \(\gamma \). On the other hand, although \(\beta \) must contain all edges from 2 to sinks that are not in \(\alpha \), it may contain any edge that goes from 2 to any other unlabelled vertex not in \(\alpha \) (see Example 6.22). The sum over \(\beta \) is over the binary choices of including or not including each of these edges, thus
if there are any such edges. This reduces the expression for  to a sum over \(\gamma \) without any such edges.
to a sum over \(\gamma \) without any such edges.
We are therefore interested in graphs  that do not contain any such ambiguous edge. This means that any edge from \(2\in \gamma \) must go to a vertex of \(\alpha \subset \gamma \) or to a sink. By the definition of
that do not contain any such ambiguous edge. This means that any edge from \(2\in \gamma \) must go to a vertex of \(\alpha \subset \gamma \) or to a sink. By the definition of  , \(1\in \gamma /\alpha \) is a sink, so any vertex of \(\alpha \subset \gamma \) other than 1 is a sink. In short, any edge from \(2\in \gamma \) must go to 1 or a sink. This implies that all unlabelled vertices are sinks, and so any edge goes from 1 or 2 to an unlabelled vertex or from 2 to 1. In other words,
, \(1\in \gamma /\alpha \) is a sink, so any vertex of \(\alpha \subset \gamma \) other than 1 is a sink. In short, any edge from \(2\in \gamma \) must go to 1 or a sink. This implies that all unlabelled vertices are sinks, and so any edge goes from 1 or 2 to an unlabelled vertex or from 2 to 1. In other words,  . In that case, all vertices of \(\gamma \) are in \(\alpha \) or \(\beta \), so \(v(\gamma )=v(\alpha )+v(\beta )\). Therefore,
. In that case, all vertices of \(\gamma \) are in \(\alpha \) or \(\beta \), so \(v(\gamma )=v(\alpha )+v(\beta )\). Therefore,

With Lemma 6.17, this shows that \(\star _{\scriptscriptstyle {?}}\) satisfies Eq. (5.10), which is the defining property of \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\). \(\square \)
Example 6.22
Consider the graph

The subgraph \(\alpha \) consists of the edges labelled (a) here (and the adjacent vertices). The edge (b) must be in the subgraph \(\beta \), but the edge (c) may or may not be in \(\beta \). The other edges cannot be in \(\beta \). The sum over the 2 possible choices of \(\beta \) with or without (c) gives 0, so that \(\gamma \) does not contribute to the formula for  .
.
6.3 Nonperturbative expression for an interacting product
In this section, we will show that the interacting star product can be written in terms of the full propagator \(\Delta ^{\mathrm{A}}_{S}\) and derivatives of S and, provided that \(\Delta ^{\mathrm{A}}_{S}\) is known exactly, the result is a formal power series in \(\hbar \), but the coupling constant \(\lambda \) can be treated as a number.
Definition 6.23
 is the set of isomorphism classes of directed graphs with labelled vertices \(1,\dots ,n\) such that:
is the set of isomorphism classes of directed graphs with labelled vertices \(1,\dots ,n\) such that:
Each unlabelled vertex has valency at least 3 and is neither a source nor a sink;
There exist no directed cycles;
For \(1\le j < k \le n\), there does not exist a directed path from j to k.
Also define

Remark 6.24
A crucial consequence of the first condition in the definition of  is that derivatives of V appearing in the graphical expansion are at least 3rd derivatives, so one can replace these with derivatives of S (\(S_0\) is quadratic).
is that derivatives of V appearing in the graphical expansion are at least 3rd derivatives, so one can replace these with derivatives of S (\(S_0\) is quadratic).
Definition 6.25
A graph  defines an n-ary multidifferential operator, \(\overset{\twoheadrightarrow }{\gamma }\), as follows:
defines an n-ary multidifferential operator, \(\overset{\twoheadrightarrow }{\gamma }\), as follows:
An edge represents \(\Delta ^{\mathrm{A}}_S\).
The labelled vertex j represents a derivative of the jth argument.
An unlabelled vertex represents a variational derivative of S.
Definition 6.26
In our diagrams, \(\Delta ^{\mathrm{A}}_S\) will be denoted by a solid line with an arrow. For this reason, graphs in  will be drawn with solid lines for the edges. (This helps to distinguish
will be drawn with solid lines for the edges. (This helps to distinguish  from
from  .)
.)
Remark 6.27
\(S''\) is the linearized equation of motion operator; thus, \(S''\Delta ^{\mathrm{A}}\) is the identity operator. This means that if there were a bivalent vertex in \(\gamma \), then \(\overset{\twoheadrightarrow }{\gamma }\) would be the same as if that vertex were removed, i.e.

For this reason,  can (and should) be thought of as a quotient of
can (and should) be thought of as a quotient of  . This leads to the appropriate definition of morphisms.
. This leads to the appropriate definition of morphisms.
Definition 6.28
For  , a morphism\(u:\alpha \rightarrow \beta \) is a function that
, a morphism\(u:\alpha \rightarrow \beta \) is a function that
Maps vertices of \(\alpha \) to vertices of \(\beta \) and edges of \(\alpha \) to directed paths in \(\beta \),
Respects sources and targets of edges,
Maps labelled vertices to labelled vertices,
And preserves the order of labelled vertices.
The concept of an extension in  follows from this definition.
follows from this definition.
The following theorem is the main result of this section. It delivers an explicit formula for the interacting star product that is nonperturbative in the coupling constant.
Theorem 6.29
For \(S=S_0+\lambda V\),

Proof
For  , the operator \(\overset{\twoheadrightarrow }{\gamma }\) can be expressed as a sum of operators given by graphs in
, the operator \(\overset{\twoheadrightarrow }{\gamma }\) can be expressed as a sum of operators given by graphs in  , with the following dictionary:
, with the following dictionary:
Because any unlabelled vertex in \(\gamma \) has valency at least 3 (say, r), \(S^{(r)} = \lambda V^{(r)}\), so this vertex corresponds to a vertex in
 and a factor of \(\lambda \).
and a factor of \(\lambda \).By Eq. (3.6), an edge in \(\gamma \) corresponds to a sum over all possible chains of edges and bivalent vertices in
 , with a factor of \(-\lambda \) for every vertex, i.e.
, with a factor of \(-\lambda \) for every vertex, i.e. 
Adding bivalent vertices along edges of graphs in  will give all graphs in
will give all graphs in  .
.
Applying this dictionary to (6.5) gives (6.4). \(\square \)
Remark 6.30
Note that after re-expressing everything in terms of full propagators, at a fixed order in \(\hbar \) there are only finitely many terms in the \(\lambda \)-expansion. Hence, the result is exact in the coupling constant, provided that \(\Delta ^{\mathrm{A}}_{S_0}\) can be constructed.
Theorem 6.19 shows that Eq. (6.5) gives the interacting product for a free action plus a regular perturbation (up to time ordering). This implies in particular that the product is associative. It is worth understanding why it is associative in greater generality.
Theorem 6.31
Suppose that S is an action and \(K(\varphi )(x,y)\) is any Green’s function for the linearized equation of motion. If \(\star \) is defined by the right-hand side of Eq. (6.5), with K in place of \(\Delta ^{\mathrm{A}}_S\), then \(\star \) is an associative product on the domain of definition of the associativity condition.
Proof
As usual, the dependence on \(\varphi \) will not be written explicitly.
The defining property of a Green’s function is  . Differentiating this gives
. Differentiating this gives
and multiplying on the left by K gives
In this equation, \(K S''\) is acting on the image of K, where it acts as the identity, so
We would first like to compute \((F_1\star F_2)\star F_3\).
To compute this, first observe that for  ,
,
where the sum is over equivalence classes of extensions at 1. These are precisely the ways of breaking up \(1\in \gamma \) and attaching the edges to \(\alpha \) (possibly by adding new vertices) to form a graph \(\beta \).
The axioms of  imply that there exists a partial order, \(\preceq \), on the vertices of
imply that there exists a partial order, \(\preceq \), on the vertices of  that is generated by the edges and \(1\succ 2\succ 3\).
that is generated by the edges and \(1\succ 2\succ 3\).
This preimage of \(1\in \gamma \) is completely determined by the structure of \(\beta \) alone. It is the complete subgraph whose vertices satisfy \(\succeq 2\). For this reason, \(d_\beta =1\) in the sense of Lemma 6.13. The number of equivalence classes of extensions is thus
This uniqueness shows that any \(\beta \) can only appear in one term of the expansion of \((F_1\star F_2)\star F_3\). Conversely, any  does occur in this expansion.
does occur in this expansion.
Together, this shows that

An essentially identical calculation (using the subgraph determined by \(\preceq 2\)) shows that \(F_1\star (F_2\star F_3)\) is given by the same formula, thus
provided that both sides are defined. \(\square \)
Example 6.32
Consider the graph

This occurs in a unique extension at 1,

corresponding to a term in \((F_1\star F_2)\star F_3\), and in a unique extension at 2

corresponding to a term in \(F_1\star (F_2\star F_3)\).
Remark 6.33
We have not proven that Eq. (6.5) gives the correct interacting product for a local action. However, Theorem 6.31 makes this a plausible conjecture.
6.3.1 Low-order terms
Explicitly, the product \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) is given up to order \(\hbar ^3\) as
where


and

6.3.2 Is there a Kontsevich-type formula?
In his famous paper on deformation quantization [41], Kontsevich presented a formula for constructing a \(\star \)-product from an arbitrary Poisson structure on a finite-dimensional vector space. Every term is a polynomial in the Poisson structure and its derivatives. In that construction, \(B_1\) is antisymmetric and proportional to the Poisson structure, so this can be thought of as constructing a \(\star \)-product from its first-order term.
The first-order term of \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) is \(\Delta ^{\mathrm{A}}_S\), which is not antisymmetric. This suggests a question. In analogy with Kontsevich’s formula, can \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) be constructed from \(\Delta ^{\mathrm{A}}_S\) and its functional derivatives?
To address this, we first need some notation. Kontsevich’s formula uses a sum over graphs in which vertices represent the Poisson structure. In his graphs, every unlabelled vertex has 2 outgoing edges. Because \(\Delta ^{\mathrm{A}}_S\) has no symmetry, in our generalization, it will be necessary to distinguish these as left and right edges.
Definition 6.34
A K-graph is a directed graph in which:
There are labelled vertices 1 and 2, and possibly unlabelled vertices;
Every edge is labelled as “left” or “right”;
Every unlabelled vertex has 2 outgoing edges, one left and one right.
As with other graphs that we have considered, a K-graph determines a bidifferential operator. The vertices 1 and 2 represent the arguments. The unlabelled vertices represent \(\Delta ^{\mathrm{A}}_S\). The edges represent derivatives.
In diagrams, these will be drawn with solid arrows on the right edges.
For example,

(Equality means equality of operators.)
To see how K-graphs can be expressed in terms of graphs in which edges represent \(\Delta ^{\mathrm{A}}_S\), consider the following examples involving parts of graphs:

Using the rules above applied to parts of graphs, one can easily treat an arbitrary K-graph.
The second-order term of \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) can indeed be constructed in this way:

In general, the operator given by a K-graph can also be given by a sum of graphs in which edges represent \(\Delta ^{\mathrm{A}}_S\) and vertices represent derivatives of S, but not vice versa. A K-graph in which each unlabelled vertex has at most one ingoing edge will give a single term; otherwise, it will give several terms.
We can come fairly close to expressing \(B^{\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}}_3\) in terms of K-graphs. The only problem is with terms in which the labelled vertices both have valency 1. We can nearly reproduce this part of \(-iB^{\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}}_3\) as

This leaves a discrepancy of

Note that these two terms each have 4 unlabelled vertices. A K-graph at order \(\hbar ^3\) has precisely 3 unlabelled vertices, and when it is translated, at least one term has 3 or fewer unlabelled vertices. In order to express (6.10) as a combination of K-graphs, we must in particular find combinations of K-graphs in which terms with 3 or fewer unlabelled vertices cancel. A tedious search shows that those combinations cannot reproduce (6.10), and thus, the third-order term of \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) cannot be constructed from \(\Delta ^{\mathrm{A}}_S\) and its derivatives. This means that \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) is not given by anything analogous to Kontsevich’s formula.
6.3.3 Interacting Wick product
These calculations have used the identification of \({\mathfrak {A}}_\mathrm {reg}\) with  defined by the quantization map
defined by the quantization map  . In order to compare results and to try to extend this to all of \({\mathfrak {A}}\), we should use the identification defined by
. In order to compare results and to try to extend this to all of \({\mathfrak {A}}\), we should use the identification defined by  . This gives a product that is related to the abstract interacting product \(\bullet _{\scriptscriptstyle {\mathrm {int}}}\) in the same way that the Wick product is related to the abstract noninteracting product \(\bullet \).
. This gives a product that is related to the abstract interacting product \(\bullet _{\scriptscriptstyle {\mathrm {int}}}\) in the same way that the Wick product is related to the abstract noninteracting product \(\bullet \).
An expression for the interacting product \(\star _{\scriptscriptstyle {H,\mathrm {int}}}\) in that identification is obtained from \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) by

for  .
.
The next step is to extend the domain of definition of \(\star _{\scriptscriptstyle {H,\mathrm {int}}}\) to local nonlinear arguments. The potential problem with this is that the expansion of the product \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) in terms of Feynman diagrams contains loops involving the advanced propagator, and lightcone divergences could be present.
Remark 6.35
Note that the advanced propagator, as a bidistributional kernel \(\Delta ^{\mathrm{A}}_S(x,y)\), has singular support given by the condition \((x-y)^2=0\) (lightcone equation). To build pointwise products of distributions, one can use Hörmander’s criterion [39], based on the concept of the wavefront set. Roughly speaking, one can multiply distributions if the sum of their wavefront sets (seen as subsets of the cotangent bundle) does not include the zero section. This condition is violated for all point on the whole past lightcone if we try to take the square of \(\Delta ^{\mathrm{A}}_S(x,y)\). For details about the wavefront sets of fundamental solutions, see, for example, [50].
Definition 6.36
 is the set of isomorphism classes of graphs with directed and undirected edges and labelled vertices \(1,\dots ,n\) such that:
is the set of isomorphism classes of graphs with directed and undirected edges and labelled vertices \(1,\dots ,n\) such that:
Each unlabelled vertex has valency at least 3, including at least one ingoing and one outgoing edge;
There exist no directed cycles;
For \(1\le j<k \le n\), there does not exist a directed path from j to k.
Definition 6.37
A graph  defines an n-ary multidifferential operator, \(\overset{\twoheadrightarrow }{\gamma }\), as follows:
defines an n-ary multidifferential operator, \(\overset{\twoheadrightarrow }{\gamma }\), as follows:
A directed edge represents \(\Delta _S^{\mathrm{A}}\);
An undirected edge represents \(\Delta _{S_0}^{\mathrm{F}}\);
The vertex j represents a derivative of the jth argument;
an unlabelled vertex represents a derivative of S.
Remark 6.38
Note that the Feynman propagator \(\Delta _{S_0}^{\mathrm{F}} = \frac{i}{2}\left( \Delta _{S_0}^{\mathrm{R}}+\Delta _{S_0}^{\mathrm{A}}\right) + H\) is defined by the free action \(S_0\) and the Hadamard distribution H. It is not a natural object from the point of view of the full action S. This suggests that there should be an alternative to  that is more adapted to S, but at the moment, we do not have a concrete proposal.
that is more adapted to S, but at the moment, we do not have a concrete proposal.
Lemma 6.39

Proof
 and
and  is the operator given by the graph
is the operator given by the graph

A graph in  has no directed edges and no unlabelled vertices; it is just a bouquet of undirected loops. Consider the unique graph with \(e(\gamma )=m\) loops. Because the functional derivative of \(\Delta _{S_0}^{\mathrm{F}}\) is 0, this graph gives the operator
has no directed edges and no unlabelled vertices; it is just a bouquet of undirected loops. Consider the unique graph with \(e(\gamma )=m\) loops. Because the functional derivative of \(\Delta _{S_0}^{\mathrm{F}}\) is 0, this graph gives the operator  . Its automorphism group is \({{\,\mathrm{Aut}\,}}\gamma = S_m\rtimes {\mathbb {Z}}_2^m\). So,
. Its automorphism group is \({{\,\mathrm{Aut}\,}}\gamma = S_m\rtimes {\mathbb {Z}}_2^m\). So,

\(\square \)
Definition 6.40
 is the subset of graphs with no loops at labelled vertices (i.e. no edge begins and ends at the same labelled vertex).
is the subset of graphs with no loops at labelled vertices (i.e. no edge begins and ends at the same labelled vertex).
 is the subset of graphs with no loops.
is the subset of graphs with no loops.
Theorem 6.41

where \(d(\gamma )\) is the number of directed edges. In particular, this is a finite sum at each order in \(\hbar \).
Proof
First, observe that

Replacing F and G with  and
and  serves to cancel out all terms with loops at 1 or 2. \(\square \)
serves to cancel out all terms with loops at 1 or 2. \(\square \)
To extend to local V, the usual procedure is to extend  to a map
to a map  that coincides with
that coincides with  on regular functionals and vanishes on local ones (see e.g. [52, Section 6.2.1]). This implies that
on regular functionals and vanishes on local ones (see e.g. [52, Section 6.2.1]). This implies that  acts as identity on local functionals.
acts as identity on local functionals.
Proposition 6.42
If  , then the sum in (6.41) can be taken over
, then the sum in (6.41) can be taken over  .
.
Proof
If  , then
, then  , so any loop at an unlabelled vertex gives 0. \(\square \)
, so any loop at an unlabelled vertex gives 0. \(\square \)
By direct inspection of the graphs, it is not clear whether the expression above can be renormalized or not. The problem is related to the presence of free Feynman propagators together with interacting advanced propagators. This is potentially an issue, since \(\Delta _{S_0}^{\mathrm{F}}-i\Delta _{S}^{\mathrm{A}}\) does not have the right WF set properties (in contrast to \(\Delta _{S_0}^{\mathrm{F}}-i\Delta _{S_0}^{\mathrm{A}}\)).
As mentioned before, this is caused by the fact that in constructing the interacting product we left the time-ordered product unchanged, since the time ordering of \(\star _{\scriptscriptstyle {H,\mathrm {int}}}\) results again in the same commutative product \(\cdot _{{}^{{\mathcal {T}}_H}}\).
Although we began with a perturbative construction using a free action \(S_0\), it is only the time-ordered product that remembers \(S_0\) and we would like this dependence to be completely removed in the interacting theory.
We hope that the results of this paper will allow us in the future to find a better version of the interacting Wick product, while keeping \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) unchanged.
6.4 Formulae for the Møller operators
In this section, we prove some combinatorial formulae for the quantum Møller operator, which can be used to streamline computations and might be the starting point for investigating renormalization in the future.
In our terms, a corolla is a graph  such that there is a single edge from 1 to each unlabelled vertex.
such that there is a single edge from 1 to each unlabelled vertex.
Corollary 6.43
Proof
This follows from Eq. (6.2) by setting \(\hbar =0\). The graphs  with \(e(\gamma )=v(\gamma )\) are precisely the corollas. \(\square \)
with \(e(\gamma )=v(\gamma )\) are precisely the corollas. \(\square \)
In our terms, a tree is a connected graph  such that 1 is a source, and each unlabelled vertex has precisely one ingoing edge.
such that 1 is a source, and each unlabelled vertex has precisely one ingoing edge.
Lemma 6.44
Proof
Any extension of a corolla by a tree is also a tree, so the composition of \(r_{\lambda V}^{-1}\) with (6.13) can be computed as a sum over trees.
Consider a tree, \(\beta \). What will the coefficient of this term be? For every subset of leaves (valency 1 vertices) of \(\beta \), there is an extension \(\alpha \hookrightarrow \beta \twoheadrightarrow \gamma \), where \(\alpha \) is \(\beta \) without those leaves, and \(\gamma \) is the corolla made from those leaves. Note how the sign of the term depends upon the number of leaves that are removed.
Lemma 6.13 shows that if \(\beta \) has m leaves, then the coefficient of this term is a multiple of
unless \(m=0\). Therefore, the only term in the composition of \(r_{\lambda V}\) with (6.13) is given by the unique tree with no leaves; the composition is the identity. \(\square \)
Definition 6.45
 is the set of trees such that no unlabelled vertex has precisely one outgoing edge.
is the set of trees such that no unlabelled vertex has precisely one outgoing edge.
Any tree can be obtained from such a graph by adding vertices along edges. As in Theorem 6.29, summing over these gives interacting advanced propagators. This gives the formula

where edges represent \(\Delta ^{\mathrm{A}}_S\) and vertices represent derivatives of \(\lambda V\).
In a similar way, inverting Eq. (6.2) gives a graphical formula for  .
.
Definition 6.46
 is the set of graphs such that:
is the set of graphs such that:
Every unlabelled vertex has at least one incoming edge;
1 is a source (has no incoming edges);
There are no directed cycles.
With this,

Next, this leads to a formula for \(R_{H,\lambda V}\). If V is local (and we set  ) then this amounts to replacing all products by time-ordered products. In terms of graphs, this is given by attaching undirected \(\Delta ^{\mathrm{F}}_{S_0}\)-edges to graphs from
) then this amounts to replacing all products by time-ordered products. In terms of graphs, this is given by attaching undirected \(\Delta ^{\mathrm{F}}_{S_0}\)-edges to graphs from  .
.
Definition 6.47
 is the set of isomorphism classes of graphs with directed and undirected edges and a labelled vertex 1, such that
is the set of isomorphism classes of graphs with directed and undirected edges and a labelled vertex 1, such that
Every unlabelled vertex has at least one incoming edge;
1 is a source;
There are no directed cycles;
There are no loops.
With this, for V local,

where undirected edges represent \(\Delta ^{\mathrm{F}}_{S_0}\), and \(d(\gamma )\) is the number of directed edges.
Definition 6.48
 is the subset of graphs such that that no unlabelled vertex has one incoming edge, one outgoing edge, and no unlabelled edge.
is the subset of graphs such that that no unlabelled vertex has one incoming edge, one outgoing edge, and no unlabelled edge.
Any graph in  can be obtained by adding vertices along directed edges of a graph in
can be obtained by adding vertices along directed edges of a graph in  . In this way, the formula can be re-expressed using the interacting advanced propagator,
. In this way, the formula can be re-expressed using the interacting advanced propagator,

where directed edges represent \(\Delta ^{\mathrm{A}}_{S}\), undirected edges represent \(\Delta ^{\mathrm{F}}_{S_0}\), and unlabelled vertices represent derivatives of \(\lambda V\).
Finally, consider the graphs in  without trees branching off of them. These are characterized by the lack of univalent vertices, i.e. leaves.
without trees branching off of them. These are characterized by the lack of univalent vertices, i.e. leaves.
Definition 6.49
 is the set of isomorphism classes of graphs with directed and undirected edges and a labelled vertex 1, such that
is the set of isomorphism classes of graphs with directed and undirected edges and a labelled vertex 1, such that
Every unlabelled vertex has at least one incoming edge and one other edge;
No unlabelled vertex has only one incoming and one outgoing edge;
1 is a source (has no incoming edges);
There are no directed cycles;
There are no loops.
We define an operator

Note that any graph giving a term of order \(\hbar ^m\) has at most 4m vertices and 5m edges. There are finitely many such graphs, so \(\lambda \) does not need to be a formal parameter in this formula.
Finally, observe that any graph in  can be obtained as an extension of a tree in
can be obtained as an extension of a tree in  by a graph in
by a graph in  . Consequently, the composition \(r_{\lambda V}\circ \Omega _{\lambda V}\) is a sum over
. Consequently, the composition \(r_{\lambda V}\circ \Omega _{\lambda V}\) is a sum over  with the same coefficients. Therefore
with the same coefficients. Therefore
which is a nonperturbative formula for \(R_{H,\lambda V}\).
Unfortunately, in order to apply the standard methods of Epstein–Glaser renormalization [20], this formula needs to be expanded in \(\lambda \) again, to show cancellation of the lightcone divergences. However, we hope that the nonperturbative formula can nevertheless lead to a well-defined object, if we use a different renormalization method (e.g. through some regularization scheme). This will be investigated in our future work.
7 Perturbative Agreement
Consider the case that V is quadratic, so that \(V^{(2)}(\varphi )\) is independent of \(\varphi \), and higher derivatives vanish. In such a situation, one can treat the interacting theory exactly and a natural question to ask is how this compares with perturbative treatment. This issue has been discussed in the literature [22, 38] under the name perturbative agreement. One way to look at it is to compare the interacting star product obtained by means of quantum Møller operators with the star product constructed directly from the advanced Green function for the quadratic action \(S_0+\lambda V\). In this case, Theorem 6.29 becomes:
Corollary 7.1
If  is quadratic, then \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) is the exponential product defined by \(-i\Delta ^{\mathrm{A}}_{S_0+\lambda V}\).
is quadratic, then \(\star _{\scriptscriptstyle {{\mathcal {T}},\mathrm {int}}}\) is the exponential product defined by \(-i\Delta ^{\mathrm{A}}_{S_0+\lambda V}\).
Proof
An unlabelled vertex of  has valency \(r\ge 3\) and represents the derivative \(S^{(r)}\), which vanishes because S is quadratic, therefore \(\overset{\twoheadrightarrow }{\gamma }=0\) unless \(\gamma \) has no unlabelled vertices. This means that Eq. (6.5) simplifies to something like Eq. (6.1):
has valency \(r\ge 3\) and represents the derivative \(S^{(r)}\), which vanishes because S is quadratic, therefore \(\overset{\twoheadrightarrow }{\gamma }=0\) unless \(\gamma \) has no unlabelled vertices. This means that Eq. (6.5) simplifies to something like Eq. (6.1):

\(\square \)
In [22, 38], the principle of perturbative agreement (PPA) is expressed as a compatibility condition for time-ordered products corresponding to \(S_0\) and \(S_0+\lambda V\). In order to prove it in our current setting, we need to pass from the  -identification to the
-identification to the  -identification.
-identification.
For the remainder of this section, we do not need V to be regular.
Lemma 7.2
If  is quadratic then
is quadratic then

and

where \(\alpha \) is defined in Proposition 4.7, \(r_{\lambda V}\) is the classical Møller operator, and

Proof
Because V is quadratic,
In this way, Eq. (5.5) simplifies to
i.e. \(J_1(\varphi ;w)=\exp \left( - \frac{\hbar \lambda }{2} \left<\delta ,w^{\otimes 2}\right>\right) \).
A consequence of these simplifications is that when any of these acts (via \(\triangleright \)) on a regular functional, then the result is still regular. Because of this, the proof of Proposition 5.4 still works.
Now, \((J_0(\varphi )\triangleright G)(\varphi ) = (r_{\lambda V}^{-1}G)(\varphi )\), and \(\mathrm{e}^{-\hbar \lambda \delta /2} \triangleright G = \alpha _{-\lambda \delta }G\). This shows that  . Inverting this gives Eq. (7.1).
. Inverting this gives Eq. (7.1).
Equation (7.2) just follows from the relationship between  and
and  . \(\square \)
. \(\square \)
Remark 7.3
Equation (7.1) is very similar to Eq. (5.8). The difference is that  is factored in a different order into classical and “purely quantum” part, since Eq. (5.8) implies
is factored in a different order into classical and “purely quantum” part, since Eq. (5.8) implies  .
.
Remark 7.4
Note that our result holds for a quadratic V that is local and compactly supported and that removing the IR regularization is a nontrivial step.
After transforming the quantum Møller map to the  -identification, (7.1) allows us to compute the map \(\beta \doteq r_{\lambda V}^{-1} R_{0,\lambda V}\) of [22]. Note the close resemblance between \(\beta \) and \(\Upsilon _{\lambda V}^{-1}\), already pointed out in Remark 5.12. We are now ready to provide a streamlined version of the proof of Theorem 5.3 of [22].
-identification, (7.1) allows us to compute the map \(\beta \doteq r_{\lambda V}^{-1} R_{0,\lambda V}\) of [22]. Note the close resemblance between \(\beta \) and \(\Upsilon _{\lambda V}^{-1}\), already pointed out in Remark 5.12. We are now ready to provide a streamlined version of the proof of Theorem 5.3 of [22].
Theorem 7.5
For V quadratic, the quantum Møller operator can be expressed in terms of the classical Møller operator as [22]
Proof
Because S is quadratic, \(\mathtt r^{-1}_{\lambda V}\) is a linear map. Its derivative is constant. Using the notation \(\rho \) for this derivative again,
Equation (3.13) simplifies to
Taking the transpose gives the same identity for the advanced propagators, and adding them shows that
The point of this is that
Remembering that  , this gives
, this gives

Equation (7.2) immediately becomes

and using the definition of  again gives Eq. (7.3) \(\square \)
again gives Eq. (7.3) \(\square \)
Relation (7.3) is in fact the condition of perturbative agreement, since \(\alpha _{i(\Delta _{S}^{\mathrm{D}}-\Delta _{S_0}^{\mathrm{D}})}\) is the map that intertwines between the time-ordered product corresponding to \(S_0\) and the one corresponding to S. Another way of expressing this relation is

where  is the time-ordering map corresponding to \(S_0\) and
is the time-ordering map corresponding to \(S_0\) and  is the analogous map corresponding to S.
is the analogous map corresponding to S.
8 Conclusions
In this paper, we have derived an explicit formula for the deformation quantization of a general class of infinite-dimensional Poisson manifolds. We have also investigated the relation between our formula and the Kontsevich formula. Although the latter has not been generalized to the infinite-dimensional setting (as for now), one can check whether our formula could in principle be derived from one that involves only the propagator (in our case, the advanced propagator) and its derivatives. By direct inspection of the graphs that appear in the third order of our expansion of the interacting star product, we have shown that our expressions cannot be derived by only using the Kontsevich-type graphs. The extra information that we need (apart from the knowledge of the propagator and its derivatives) is the action S. This is, however, always provided in the models we are working with, since they arise from classical field theory formulated in a Lagrangian setting (the Poisson structure is constructed using the action S). It would be interesting to understand whether it is even possible to construct a star product in the infinite-dimensional setting without using some additional structure; otherwise, our formula may be the best analogue of Kontsevich’s formula in this setting. We want to investigate this problem in our future work.
Our results hold for a restricted class of functions on the manifold in question, and in order to generalize these results, one needs to perform renormalization. We want to investigate this in future research. There are two possible ways forward. One is to use regularization and perform computations in concrete examples, to see how the divergences can be removed. This is expected to work for the quantum Møller operator itself (since it was constructed by perturbative methods, for example, by [20]) and could also shed some light on the singularities of the interacting product. For the latter, another strategy is to try to correct \(\star _{\scriptscriptstyle {H,\mathrm {int}}}\) by modifying the normal-ordering quantization map  .
.
We also want to see how the present results are compatible with the algebraic adiabatic limit [8, 31] and the general framework proposed in [35].
References
Bahns, D., Rejzner, K.: The quantum sine Gordon model in perturbative AQFT. Commun. Math. Phys. 357, 421–446 (2018). https://doi.org/10.1007/s00220-017-2944-4
Bär, C.: Green-hyperbolic operators on globally hyperbolic spacetimes. Commun. Math. Phys. 333(3), 1585–1615 (2015)
Bastiani, A.: Applications différentiables et variétés différentiables de dimension infinie. Journal d’Analyse mathématique 13(1), 1–114 (1964)
Bayen, F., Flato, M., Fronsdal, C., Lichnerowicz, A., Sternheimer, D.: Deformation theory and quantization. I. Deformations of symplectic structures. Ann. Phys. 111(1), 61–110 (1987)
Bayen, F., Flato, M., Fronsdal, C., Lichnerowicz, A., Sternheimer, D.: Deformation theory and quantization. I. Deformations of symplectic structures. Ann. Phys. 111(1), 111–151 (1987)
Brennecke, F., Dütsch, M.: Removal of violations of the master Ward identity in perturbative QFT. Rev. Math. Phys. 20(02), 119–51 (2008)
Brouder, C., Dang, N.V., Laurent-Gengoux, C., Rejzner, K.: Properties of field functionals and characterization of local functionals. J. Math. Phys. 59(2), 023508 (2018)
Brunetti, R., Dütsch, M., Fredenhagen, K.: Perturbative algebraic quantum field theory and the renormalization groups. Adv. Theor. Math. Phys. 13(5), 1541–1599 (2009)
Brunetti, R., Fredenhagen, K.: Microlocal analysis and interacting quantum field theories. Commun. Math. Phys. 208(3), 623–661 (2000)
Brunetti, R., Fredenhagen, K., Rejzner, K.: Quantum gravity from the point of view of locally covariant quantum field theory. Commun. Math. Phys. 345(3), 741–779 (2016)
Brunetti, R., Fredenhagen, K., Ribeiro, P.L.: Algebraic structure of classical field theory I: Kinematics and linearized dynamics for real scalar fields. Commun. Math. Phys. 368, 519–584 (2019). arXiv:1209.2148v2 math-ph
Collini, G.: Fedosov Quantization and Perturbative Quantum Field Theory, Ph.D. thesis, Leipzig (2016) arXiv:1603.09626 math-ph
Dito, J.: Star-product approach to quantum field theory: the free scalar field. Lett. Math. Phys. 20(2), 125–134 (1990)
Dito, J.: An example of cancellation of infinities in the star-quantization of fields. Lett. Math. Phys. 27, 73–80 (1993)
Dito, J.: The necessity of wheels in universal quantization formulas. Commun. Math. Phys. 338, 523–532 (2015)
Dütsch, M.: From Classical Field Theory to Perturbative Quantum Field Theory, Progress in Mathematical Physics. Birkhäuser, Basel (2019)
Dütsch, M., Fredenhagen, K.: Algebraic quantum field theory, perturbation theory, and the loop expansion. Commun. Math. Phys. 219(1), 5–30 (2001)
Dütsch, M., Fredenhagen, K.: Perturbative algebraic field theory, and deformation quantization. In: Mathematical Physics in Mathematics and Physics, Fields Inst. Commun., vol. 30, pp. 1–10 (2001)
Dütsch, M., Fredenhagen, K.: The master Ward identity and generalized Schwinger–Dyson equation in classical field theory. Commun. Math. Phys. 243(2), 275–314 (2003)
Dütsch, M., Fredenhagen, K.: Causal perturbation theory in terms of retarded products, and a proof of the Action Ward Identity. Rev. Math. Phys. 16(10), 1291–1348 (2004)
Dütsch, M., Fredenhagen, K.: Action ward identity and the Stückelberg–Petermann renormalization group. In: Rigorous Quantum Field Theory, Progress in Mathematics, vol. 251, pp. 113–123. Birkhäuser Verlag, Basel (2007)
Drago, N., Hack, T.-P., Pinamonti, N.: The generalised principle of perturbative agreement and the thermal mass. Annales Henri Poincaré 18(3), 807–868 (2016)
Epstein, H., Glaser, V.: The role of locality in perturbation theory. AHP 19(3), 211–295 (1973)
Epstein, H., Glaser, V.: Adiabatic limit in perturbation theory. In: Velo, G., Wightman, A.S. (eds.) Renormalization Theory, pp. 193–254. Springer, Berlin (1976)
Fedosov, B.V.: A simple geometrical construction of deformation quantization. J. Differ. Geom. 40(2), 213–238 (1994)
Fewster, C., Verch, R.: Nonlocal Green Hyperbolic Operators, (to appear)
Fredenhagen, K., Lindner, F.: Construction of KMS states in perturbative QFT and renormalized Hamiltonian dynamics. Commun. Math. Phys. 332(3), 895–932 (2014)
Fredenhagen, K., Rejzner, K.: Batalin–Vilkovisky formalism in the functional approach to classical field theory. Commun. Math. Phys. 314(1), 93–127 (2012)
Fredenhagen, K., Rejzner, K.: Batalin–Vilkovisky formalism in perturbative algebraic quantum field theory. Commun. Math. Phys. 317(3), 697–725 (2012)
Fredenhagen, K., Rejzner, K.: Perturbative Construction of Models of Algebraic Quantum Field Theory, pp. 31–74. Springer, Berlin (2015)
Fredenhagen, K., Rejzner, K.: Quantum field theory on curved spacetimes: axiomatic framework and examples. J. Math. Phys. 57(3), 031101 (2016)
Gerstenhaber, M.: On the deformation of rings and algebras III. Ann. Math. 88, 1–34 (1968)
Haag, R.: Local Quantum Physics. Springer, Berlin (1993)
Hamilton, R.S.: The inverse function theorem of Nash and Moser. Bull. Am. Math. Soc. 7, 65 (1982)
Hawkins, E.: A cohomological perspective on algebraic quantum field theory. Commun. Math. Phys. 360, 439–479 (2018). arXiv:1612.05161 math-ph
Haag, R., Kastler, D.: An algebraic approach to quantum field theory. J. Math. Phys. 5(7), 848–861 (1964)
Hollands, S., Wald, R.M.: On the renormalization group in curved spacetime. Commun. Math. Phys. 237, 123–160 (2002)
Hollands, S., Wald, R.M.: Conservation of the stress tensor in perturbative interacting quantum field theory in curved spacetimes. Rev. Math. Phys. 17(03), 227–311 (2005)
Hörmander, L.: The Analysis of the Linear Partial Differential Operators I: Distribution Theory and Fourier Analysis, Classics in Mathematics. Springer, Berlin (2003)
Keller, K.J.: Dimensional regularization in position space and a forest formula for regularized Epstein–Glaser renormalization, Ph.D. thesis, University of Hamburg (2010), arXiv:1006.2148 math-ph
Kontsevich, M.: Deformation quantization of Poisson manifolds, I. Lett. Math. Phys. 66, 157–216 (2003)
MacLane, S.: Categories for the Working Mathematician, Graduate Texts in Mathematics, vol. 5, 2nd edn. Springer, Berlin (1998)
Milnor, J.: Remarks on infinite-dimensional Lie groups. In: Les Houches 1983, Proceedings, Relativity, Groups and Topology, II, pp. 1007–1057 (1984)
Maeda, Y., Miyazaki, N., Omori, H., Yoshioka, A.: Star Exponential Functions as Two-valued Elements, vol. 232, pp. 483–492. Springer, Berlin (2007)
Neeb, K.H.: Monastir summer school. Infinite-dimensional Lie groups, TU Darmstadt Preprint, vol. 2433 (2006)
Osterwalder, K., Schrader, R.: Axioms for Euclidean Green’s functions. Commun. Math. Phys. 31(2), 83–112 (1973)
Peierls, R.E.: The commutation laws of relativistic field theory. In: Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, vol. 214, no. 1117, pp. 143–157 (1952)
Pinter, G.: Finite renormalizations in the Epstein Glaser framework and renormalization of the S-matrix of 4-theory. Ann. Phys. 10, 333–363 (2001)
Popineau, G., Stora, R.: A pedagogical remark on the main theorem of perturbative renormalization theory. Nucl. Phys. B 912, 70–78 (2016)
Radzikowski, M.J.: Micro-local approach to the Hadamard condition in quantum field theory on curved space-time. Commun. Math. Phys. 179, 529–553 (1996)
Rejzner, K.: Fermionic fields in the functional approach to classical field theory. Rev. Math. Phys. 23(9), 1009–1033 (2011)
Rejzner, K.: Perturbative Algebraic Quantum Field Theory. An introduction for Mathematicians, Mathematical Physics Studies. Springer, Berlin (2016)
Streater, R.F., Wightman, A.S.: PCT, Spin and Statistics, and All That. Princeton University Press, Princeton (2000)
Waldmann, S.: Poisson-Geometrie und Deformationsquantisierung: Eine Einführung. Springer, Berlin (2007)
Acknowledgements
This research was partially supported by KR’s EPSRC Grant EP/P021204/1.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hawkins, E., Rejzner, K. The star product in interacting quantum field theory. Lett Math Phys 110, 1257–1313 (2020). https://doi.org/10.1007/s11005-020-01262-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11005-020-01262-4





 be the oriented and time-oriented isometry group of the spacetime
be the oriented and time-oriented isometry group of the spacetime  . (For Minkowski spacetime
. (For Minkowski spacetime  is the proper orthochronous Poincaré group
is the proper orthochronous Poincaré group  .) We require that
.) We require that  (Covariance).
(Covariance). (evaluation at the classical limit).
(evaluation at the classical limit). .
. , so
, so 
 , and
, and is closed under the noncommutative product in
is closed under the noncommutative product in 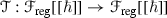 is a differential operator in the sense of calculus on
is a differential operator in the sense of calculus on  ,
, for F linear,
for F linear, and a factor of
and a factor of  , with a factor of
, with a factor of 