On the ground state for quantum graphs

Abstract

Ground-state eigenfunctions of Schrödinger operators can often be chosen positive. We analyse to which extent this is true for quantum graphs—differential operators on metric graphs. It is shown that the theorem holds in the case of generalised delta couplings at the vertices—a new class of vertex conditions introduced in the paper. It is shown that this class of vertex conditions is optimal. Relations to positivity preserving and positivity improving semigroups are clarified.

1 Introduction

Perron–Frobenius theorem [8,9,10, 17, 18, 22] states that for a symmetric matrix with positive entries the largest eigenvalue is non-degenerate and the corresponding eigenvector can be chosen having positive entries. This theorem has been generalised for differential operators, where instead of the largest eigenvalue one looks at the ground state, and is closely related to Courant nodal domain theorem stating that the nth eigenfunction has at most n nodal domains [5, 6]. This theorem has been extended for quantum graphs in [2, 11], see also [7]. Our aim is to examine to which extent a counterpart of Perron–Frobenius theorem holds for operators on metric graphs often called quantum graphs. This theorem is trivial for Laplacians with standard vertex conditions, since the ground state is a constant function. For Schrödinger operators with non-constant potential, the ground state cannot in general be calculated explicitly even for standard vertex conditions and the corresponding statement seems to become a mathematical folklore, but no rigorous proof could be traced, despite extensive literature on the subject [3, 20]. One possible explanation is that metric graphs are locally one-dimensional objects, but in one dimension the statement can be obtained as an easy corollary of Courant nodal domain theorem: if an eigenfunction has a zero, then there are two nodal domains. In fact, it is enough to use Sturm oscillation theory in that case. But for metric graphs single zeroes do not necessarily split the graphs into nodal domains and Courant theorem cannot be applied directly.

Our second source of inspiration is the intrinsic connection between positivity and non-degeneracy of the ground state and positivity preserving property of the operator or the corresponding semigroups [12, 21]. Using this connection, we shall be able to characterise a large class of differential operators on metric graphs for which it is guaranteed that the ground-state eigenfunction does not change sign. We just pick up the class of operators for which the quadratic form does not increase under taking the absolute value [see (6)]. The corresponding admissible vertex conditions have never been used before and allow to interpolate between (positive weighted) vertex delta interactions and most general vertex conditions. We call such vertex conditions generalised delta couplings. This class is a generalisation of vertex conditions already considered in [4].

The structure of the article is as follows. In Sect. 2, we prove positivity of the ground-state eigenfunction for standard vertex conditions. We believe that this form of our result will be widely used even outside the mathematical community, since standard vertex conditions are the most common conditions for quantum graphs. The case of general vertex conditions is considered in Sect. 3; an analogue of Perron–Frobenius theorem is established for the generalised delta couplings. Section 4 is devoted to positivity preserving semigroups generated by quantum graphs.

2 Positivity of the ground-state eigenfunction for standard vertex conditions

In this section, we consider Schrödinger operators on metric graphs with standard vertex conditions. To our opinion, such elementary proof is awaited by mathematical community and it will enable us to indicate important ingredients that will be used to motivate our main result (Theorem 3).

Theorem 1

Let $L_q^{\mathrm{st}} = - \frac{\hbox {d}^2}{\hbox {d}x^2} + q(x)$, $q (x) \in \mathbb R, q \in L_1 (\varGamma )$ be a standard Schrödinger operator on a finite compact connected metric graph $\varGamma$. The domain of the operator is given by all functions u from the Sobolev space $W_2^1 (\varGamma {\setminus } \mathbf V)$ (here $\mathbf V$ denotes the set of all vertices in $\varGamma$) such that

$$\begin{aligned} - u'' + qu \in L_2(\varGamma ) \end{aligned}$$

(1)

and satisfying standard vertex conditions at the vertices:

$$\begin{aligned} \left\{ \begin{array}{l} \mathrm{the\;functions \;are \;continuous}\\ \sum _{x_j \in V_i} \partial u(x_j) = 0, \end{array} \right. , \end{aligned}$$

(2)

where $\partial u (x_j)$ denotes the oriented derivative at the endpoint $x_j$ taken in the direction inside the corresponding edge. Then, the ground-state eigenfunction is unique and may be chosen strictly positive.

The original proof of Pleijel [19] of Courant nodal domain theorem can be transferred to standard quantum graphs without many modifications. That proof would imply that the ground-state eigenfunction has a single nodal domain. But this property cannot exclude the possibility that the function has zeroes—not every zero leads to nodal domains as in the case of one interval. Consider for example a non-negative function on a ring: if the function has just one zero, then there is just one nodal domain. Then, it is necessary to show that the ground-state eigenfunction cannot have zeroes without changing sign both inside the edges and at the vertices (see the second part of the proof below). Other standard methods developed for operators in infinite-dimensional spaces cannot be applied directly either [12, 14]. Moreover, the proof presented below is based on the quadratic form analysis which will play essential role in the rest of the paper.

Proof

Let u be a ground-state eigenfunction, then the function $\overline{u}$ is also a ground state, since both the differential equation

$$\begin{aligned} - u'' + q(x) u = \lambda _1 u, \; \, \lambda _1 \in \mathbb R, \end{aligned}$$

and the vertex conditions are invariant under complex conjugation. Hence, the ground state(s) can always be chosen real-valued.

The quadratic form of the operator $L_q^{\mathrm{st}}$ is given by

$$\begin{aligned} Q_{L_q^{\mathrm{st}}} = \langle u, L_q u \rangle = \int _\varGamma \vert u' (x)\vert ^2 \hbox {d}x + \int _\varGamma q(x) \vert u(x) \vert ^2 \hbox {d}x , \end{aligned}$$

(3)

and the lowest eigenvalue can be obtained by minimising the Rayleigh quotient

$$\begin{aligned} \lambda _1 = \min _{u} \frac{\int _\varGamma \vert u' (x)\vert ^2 \hbox {d}x + \int _\varGamma q(x) \vert u(x) \vert ^2 \hbox {d}x}{ \int _\varGamma \vert u(x) \vert ^2 \hbox {d}x}. \end{aligned}$$

(4)

The domain of the quadratic form is given by all functions from $W_2^1 (\varGamma {\setminus } \mathbf V)$, which are in addition continuous at the vertices. One may extend the domain of the quadratic form allowing functions which are not necessarily from $W_2^1$ on the edges, but are piece-wise $W_2^1$ and continuous. This will allow additional dummy degree two vertices on the edges, which of course can be removed if the vertex conditions are standard. We are going to call such functions admissible.

Any ground state is an admissible function minimising the Rayleigh quotient. If a function u is real-valued and admissible, then $\vert u \vert$ is also admissible with the same Rayleigh quotient. Hence, the minimiser of (4) can be chosen not only real, but even non-negative.

We shall prove now that if $\psi _1$ is a non-negative minimiser for (4), then it is never equal to zero. This would imply that $\psi _1$ may be chosen strictly positive. We need to exclude that $\psi _1$ may have zeroes on the edges or at the vertices.

If $\psi _1$ is a minimiser of the Rayleigh quotient, then it is an eigenfunction of the corresponding Schrödinger equation, i.e. it satisfies the differential equation on the edges and as well as vertex conditions (see Appendix A).

The fact that non-negative $\psi _1$ satisfies the differential equation (32) and standard vertex conditions will allow us to prove that it is never equal to zero. Assume first that $\psi _1$ is equal to zero at a certain point $x_0$ inside an edge $E_n.$ The function $\psi _1$ is a minimiser for (4) and therefore satisfies the second-order differential equation (32) on the edge. The function $\psi _1$ is continuously differentiable in particular when $x = x_0$ and its derivative there should be equal to zero, since the function is non-negative and $\psi _1(x_0) = 0$. It follows that at this particular point the function $\psi _1$ satisfies zero Cauchy data

$$\begin{aligned} \left\{ \begin{array}{ccc} \psi _1 (x_0) &{} = &{} 0 \\ \psi '_1 (x_0) &{} = &{} 0 \end{array} \right. \end{aligned}$$

and therefore is identically equal to zero on the whole edge $E_n$ as a solution to the second-order ordinary differential equation. This implies that $\psi _1$ should be equal to zero in a vertex—we come to the second possibility we need to consider.

Assume now that $\psi _1$ is equal to zero at a certain vertex $V_m.$ Since $\psi _1$ is a minimiser for (4), it satisfies the standard vertex conditions at this vertex. The function $\psi _1$ is non-negative and is equal to zero at the vertex. It follows that all normal derivatives are non-negative, but their sum is equal to zero; hence, all normal derivatives are actually equal to zero. We see that as before $\psi _1$ satisfies a second-order differential equation with zero Cauchy data on every edge incident to $V_m$. It follows that $\psi _1$ is zero not only at this particular vertex $V_m$ but at all neighbouring vertices as well. Repeating the argument, we conclude that $\psi _1$ is identically equal to zero on the whole $\varGamma$ (which is assumed to be connected) and therefore is not an eigenfunction.

It remains to prove that the lowest eigenvalue is simple. Assume that the lowest eigenvalue is not simple and there exists two orthogonal eigenfunctions $\psi _1$ and $\psi _2.$ One of these eigenfunctions can be chosen positive, say $\psi _1$, then the other one necessarily has zeroes, since it is continuous and attains both positive and negative values being orthogonal to $\psi _1.$ Every such function is identically equal to zero as we have already proven. Hence, the lowest eigenvalue is in fact simple. $\square$

In a similar way, the following corollary can be proven:

Corollary 1

Let $L_q = - \frac{\hbox {d}^2}{\hbox {d}x^2} + q(x)$, $q (x) \in \mathbb R, q \in L_1 (\varGamma )$ be a Schrödinger operator on a finite compact connected metric graph $\varGamma$. The domain of the operator is given by all functions from the Sobolev space $W_2^1 (\varGamma {\setminus } \mathbf V)$ satisfying (1) and delta-type vertex conditions at the vertices:

$$\begin{aligned} \left\{ \begin{array}{l} \mathrm{the \;functions \;are \;continuous}\\ \sum \nolimits _{x_j \in V_i} \partial u(x_j) = \alpha _i u(V_i) \end{array} \right. , \; \; \alpha _i \in \mathbb R. \end{aligned}$$

(5)

Then, the ground-state eigenfunction may be chosen strictly positive. Moreover, the corresponding eigenvalue is simple.

To prove the corollary, one needs to take into account that the domain of the quadratic form is again invariant under taking the complex conjugate and the absolute value. Moreover, if $\psi _1$ is equal to zero at a vertex, then it satisfies standard vertex conditions there.

Our proof was based on the fact that the eigenfunctions are solutions to the second-order differential equation on the edges and the following two properties of the quadratic form:

• for complex-valued functions the quadratic form is invariant under complex conjugation;

• for real-valued functions the quadratic form is invariant under taking the absolute value.

We observe that in order to carry out the proof it was enough to require that the quadratic form does not increase when taking the absolute value:

$$\begin{aligned} Q( |u |, | u | ) \le Q (u, u). \end{aligned}$$

(6)

Note that this inequality implies in particular that the domain of the quadratic form is invariant under taking the absolute value.

3 Positivity of the ground-state eigenfunction for general vertex conditions

We start by providing a counterexample showing that in order to guarantee positiveness of the ground state the set of allowed vertex conditions has to be restricted.

3.1 Counterexample

Let $\varGamma$ be the metric graph formed by two edges $E_1 = [x_1, x_2] , E_2 = [x_3, x_4]$ with two vertices $V_1 = \{ x_1, x_4 \}, \; V_2 = \{ x_2, x_3 \}$. Let $L = - \frac{\hbox {d}^2}{\hbox {d}x^2}$ be the Laplace operator defined by the following vertex conditions at the vertices:¹

$$\begin{aligned} \left\{ \begin{array}{ccc} u(x_1) &{} = &{} -u(x_4) \\ \partial u (x_1) &{} = &{} \partial u (x_4) \end{array} \right. \; \; \text{ and } \; \; \left\{ \begin{array}{ccc} u(x_2) &{} = &{} - u(x_3) \\ \partial u (x_2) &{} = &{} \partial u(x_3) \end{array} \right. . \end{aligned}$$

(7)

The lowest eigenvalue $\lambda _1 = 0$ is simple, but the corresponding eigenfunction is not sign definite

$$\begin{aligned} \psi _1(x) = \left\{ \begin{array}{cl} 1, &{} x \in E_1, \\ -1, &{} x \in E_2. \end{array} \right. \end{aligned}$$

The main reason for the ground-state eigenfunction to change sign is that the domain of the quadratic form is not invariant under taking the absolute value (only functions equal to zero at the vertices satisfy $|u(x_1) | = - | u(x_4)|, \; |u(x_2) | = - | u(x_3)|$), although the ground-state eigenfunction can be chosen real-valued. In particular, inequality (6) does not hold in this case. This counterexample supports our conjecture that one may prove positivity of the ground-state eigenfunction if we assume that the quadratic form does not increase when taking the absolute value of the function.

It is not hard to provide examples of quantum graphs with positive non-degenerate ground states. Our aim here is to characterise a wider class of vertex conditions that guarantee positivity of the ground state. Considered counterexample should not give an impression that vertex conditions leading to violation of the positivity of the ground-state eigenfunction are pathological.

3.2 A few definitions

We shall need few definitions: two are coming from [21] (positive and strongly positive functions), and one (strictly positive) is new—we need it to formulate a stronger version of the theorem.

Definition 1

A function f is called positive if it is non-negative $f(x) \ge 0.$ A function $f \in L_2 (\varGamma )$ is called strongly positive if $f(x) > 0$ holds almost everywhere on $\varGamma .$ Finally, a function f is called strictly positive if $f(x) > 0$ holds everywhere on $\varGamma$ except at those vertices, where Dirichlet conditions are assumed.

3.3 Quadratic form

In what follows, we shall need an explicit expression for the quadratic form assuming most general vertex conditions [3, 13]. Let us denote the corresponding Schrödinger operator by $L_q$. The best way is to associate with each vertex $V_m$ a certain subspace $\mathcal B_m \subset \mathbb C^{d_m}$, where $d_m$ is the degree of $V_m$, and a Hermitian matrix $A_m$: $\mathcal B_m \rightarrow \mathcal B_m.$ Then, the quadratic form of the Schrödinger operator on $\varGamma$ is given by

$$\begin{aligned} Q_{L_q} (u,u)= & {} \langle u, L_q u \rangle = \int _\varGamma \vert u' (x)\vert ^2 \hbox {d}x + \int _\varGamma q(x) \vert u(x) \vert ^2 \hbox {d}x\nonumber \\&+ \sum _{m=1}^M \langle \mathbf {u}_m, A_m \mathbf {u}_m \rangle _{\mathbb C^{d_m}}, \end{aligned}$$

(8)

where $d_m$-dimensional vectors $\mathbf {u}_m$ consist of the boundary values of the function u at the vertex $V_m$ [3]. It will be convenient to denote the coordinates of the vector $\mathbf {u}_m$ by $u(x_l)$, where $x_l \in V_m.$ Similar notation will be used for all other vectors from $\mathbb C^{d_m}.$ The domain of the quadratic form consists of all functions u from $W_2^1 (\varGamma {\setminus } \mathbf V) = \oplus _{n=1}^N W_2^1 (E_n)$ satisfying additional (Dirichlet-type) condition

$$\begin{aligned} \mathbf {u}_m \in \mathcal B_m \Leftrightarrow P_{\mathcal (B_m)^\perp } \mathbf {u}_m = 0, \end{aligned}$$

(9)

where $P_{\mathcal (B_m)^\perp }$ is the projector on the orthogonal complement to $\mathcal B_m.$ The later condition can also be written as

$$\begin{aligned} \mathbf {u} \in \mathcal B := \mathcal B_1 \oplus \mathcal B_2 \oplus \cdots \oplus \mathcal B_M. \end{aligned}$$

(10)

3.4 Generalised delta couplings

Schrödinger operators $L_q^{\mathrm{delta}}$ with classical delta couplings (5) may of course be described using the general scheme as follows. One requires that each $d_m$-dimensional vector $\mathbf {u}_m$ belongs to the subspace spanned by just one vector $\mathbf 1_{d_m} = (1,1, \ldots , 1) \in \mathbb C^{d_m}.$ The corresponding matrices $A_m$ are then $1 \times 1$ dimensional and coincide with the coupling constants $\alpha _m.$ The corresponding quadratic form is defined on continuous functions and is given by

$$\begin{aligned} Q_{L_q^{\mathrm{delta}}} ( u, u ) = \int _\varGamma \vert u' (x)\vert ^2 \hbox {d}x + \int _\varGamma q(x) \vert u(x) \vert ^2 \hbox {d}x + \sum _{m=1}^M \alpha _m \vert u(V_m) \vert ^2, \end{aligned}$$

(11)

since the value of u at a vertex $V_m$, $u(V_m)$, is well defined.

Consider a new subclass of Hermitian vertex conditions to be called generalised delta couplings. This class is a generalisation of weighted delta couplings (see for example [1] where approximations of diffusion in thin tubes of different sizes were considered) and vector-valued Robin conditions (see for example [4], where such conditions were considered in connection with positivity preserving semigroups). It appears that precisely the new class of vertex conditions guarantees that the ground-state eigenfunction is positive. As a first step, we describe generalised delta conditions for just one vertex.

With any vertex V of degree d, we associate $n \le d$ arbitrary vectors $\mathbf {a}^j$ with the following properties:

• all coordinates of $\mathbf {a}^j$ are non-negative numbers²$\mathbf {a}^j \in \mathbb R_+^{d} ;$

• the vectors have disjoint supports so that for all $\ell : x_\ell \in V$

  $$\begin{aligned} \mathbf {a}^j (x_\ell ) \cdot \mathbf {a}^i (x_\ell ) = 0, \; \text{ provided } \; j \ne i \end{aligned}$$

  holds.

Here, $\mathbf {a}^j (x_\ell )$ denotes the $\ell$th coordinate of the vector $\mathbf {a}^j .$ Without loss of generality, we assume that the vectors $\mathbf {a}^j$ are normalised:

$$\begin{aligned} \Vert \mathbf {a}^j \Vert ^2 = \sum _{x_\ell \in V} \vert a^j (x_\ell ) \vert ^2 = 1. \end{aligned}$$

The (nonzero) coordinates of the vectors $\mathbf {a}^j$ will be called weights.

The strength of the generalised delta interaction will be determined by an irreducible $n \times n$coupling matrix$\mathbf A$ which is assumed to be Hermitian. Then, the generalised delta couplings are written as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \mathbf {u} \in \mathfrak L \{ { \mathbf {a}^1, \mathbf {a}^2, \ldots , \mathbf {a}^n } \} ;\\ \displaystyle \langle \mathbf {a}^j, \partial \mathbf {u} \rangle = \sum _{i=1}^n A_{ji} \langle \mathbf {a}^i, \mathbf {u} \rangle , \end{array} \right. \end{aligned}$$

(12)

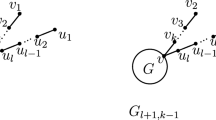
where $\mathfrak L$ denotes the linear span. The dimension n of the subspace $\mathcal B$ may be refereed to as the order of the generalised delta condition (See Fig. 1).

The first condition in (12) is a generalised continuity condition, since it can be written as follows:

$$\begin{aligned} \frac{u(x_k)}{a^j (x_k)} = \frac{u(x_l)}{a^j(x_l)} =: \mathbf{u}^j, \; \, x_k, x_l \in \mathrm{supp}\,(\mathbf {a}^j), \; \; j = 1,2, \ldots , n. \end{aligned}$$

(13)

The difference to the classical delta coupling is that the function is not necessarily continuous at the vertex. In the case of one-dimensional subspace $\mathcal B$ ($n=1$), any particular coordinate of $\mathbf {u}$ determines all other coordinates—the value of u at one endpoint determines its values at all other endpoints. But the values may be different if the weights are different. One may say that the weighted function is continuous in this case. If $n \ge 2$, then the entries of $\mathbf {u}$ are determined by n arbitrary parameters. Every coordinate in $\mathbf {u}$ belongs to the support of just one vector $\mathbf {a}^j$ for a certain j and thus determines all other coordinates in the support of $\mathbf {a}^j.$ The wave function u attains n independent weighted values associated with different groups of endpoints joined at the vertex. One should think about this condition as a weighted continuity of u at each group of endpoints.

Changing the order $n, \; 0 \le n \le d$, of the delta couplings allows one to interpolate between the classical delta couplings and the most general vertex conditions, so that $n=1$ corresponds to the usual weighted delta couplings and $n=d$—to the most general vertex conditions with $\mathcal B = \mathbb C^d.$

Note that in Eq. (13) we introduced a new reduced vector $\mathbf{u} = ( \mathbf u^1, \mathbf u^2, \ldots , \mathbf u^n)$—it contains the common weighted values of the vector $\mathbf {u}$. The dimension of the vector coincides with the dimension n of the linear subspace $\mathcal B$.

The second equation in (12) is a balance equation for the normal derivatives. The sum of normal derivatives connected with endpoints from the support of one of the vectors $\mathbf {a}^j$ is connected via the coupling matrix $\mathbf A$ to the common values of u at all other groups of endpoints, since we have

$$\begin{aligned} \langle \mathbf {a}^i, \mathbf {u} \rangle = \sum _{x_l \in \mathrm{supp}\,\mathbf {a}^i} a^i(x_l) u(x_l) = \sum \vert a^i(x_l) \vert ^2 \frac{u(x_l)}{a^i(x_l)} = (\mathbf{u})^i. \end{aligned}$$

Here we used that the vector $\mathbf {a}^i$ is normalised.

Generalised delta conditions formally include Dirichlet conditions. These conditions occur if the space $\mathcal B$ is trivial, $n= 0.$ Then, the first condition in (12) implies that the function u is equal to zero at the vertex. The second condition is void. In what follows, it will be more convenient to consider Dirichlet conditions separately, and the corresponding vertices will be called Dirichlet points.

Fig. 1

Generalised delta couplings when $d= 9$ and $n = 3$

Of course, only properly connecting vertex conditions should be considered. Vertex conditions are called properly connecting if and only if the vertex cannot be divided into several vertices so that equivalent vertex conditions connecting boundary values from each of the new vertices can be found.

For generalised delta couplings to be properly connecting two requirements should be fulfilled:

• 1. The union of supports of vectors $\mathbf {a}^j$ coincides with all endpoints in V:

  $$\begin{aligned} \cup _{j=1}^n \mathrm{supp}\; (\mathbf {a}^j) = \{ x_l \}_{x_l \in V}. \end{aligned}$$

  (14)

• 2. The matrix $\mathbf A = \{ A_{ji} \}_{j,i =1}^n$ is irreducible, i.e. it cannot be put into a block-diagonal form by permutations.

If the first condition is not satisfied, then we have classical Dirichlet conditions at the endpoints that do not belong to the support of any vector $\mathbf {a}^j.$ Such Dirichlet endpoints always form separate vertices.

If the second condition is not satisfied, then the vertex V can be chopped into two (or more) vertices preserving the vertex conditions. Such conditions correspond to the metric graph, where the vertex V is divided.

Consider now arbitrary finite metric graphs with the generalised delta couplings at the vertices. The parameters corresponding to any vertex $V_m$ will be indicated by the lower index m. The corresponding quadratic form is

$$\begin{aligned} Q_{L_q^{\mathrm{gen.delta}}} ( u, u ) = \int _\varGamma \left( \vert u' \vert ^2 + q \vert u \vert ^2 \right) \hbox {d}x + \sum _{m=1}^M \langle \mathbf{u}_m, \mathbf A_m \mathbf{u}_m \rangle _{\mathbb C^{d_m}} . \end{aligned}$$

(15)

One gets this formula as usual via integration by parts:

$$\begin{aligned} \begin{array}{ccl} \langle u, L_q^{\mathrm{gen.delta}} u \rangle &{} = &{} \displaystyle \int _\varGamma \overline{u} \left( -u'' + q u \right) \hbox {d}x \\ &{} = &{} \displaystyle \int _\varGamma \left( \vert u'\vert ^2 + q \vert u \vert ^2 \right) \hbox {d}x + \sum _{x_l} \overline{u(x_l)} \partial u(x_l)\\ &{} = &{} \displaystyle \int _\varGamma \left( \vert u'\vert ^2 + q \vert u \vert ^2 \right) \hbox {d}x + \sum _{m=1}^M \left( \sum _{x_l\in V_m} \overline{u(x_l)} \partial u(x_l) \right) . \end{array} \end{aligned}$$

The last term can be transformed as

$$\begin{aligned} \begin{array}{ccl} \displaystyle \sum _{x_l\in V_m} \overline{u(x_l)} \partial u(x_l) &{} = &{} \displaystyle \sum _{j=1}^{n_m} \frac{\overline{u(x_l)}}{a^j_m (x_l)} \vert _{\forall x_l \in \mathrm{supp}\, \mathbf {a}^j_m} \sum _{x_l \in \mathrm{supp}\,\mathbf {a}^j_m} a^j_m(x_l) \partial u(x_l) \\ &{} = &{} \displaystyle \sum _{j=1}^{n_m} \frac{\overline{u(x_l)}}{a^j_m (x_l)} \vert _{\forall x_l \in \mathrm{supp}\, \mathbf {a}^j_m} \langle \mathbf {a}^j_m, \partial \mathbf {u}_m \rangle \\ &{} = &{} \displaystyle \sum _{j=1}^{n_m} \frac{\overline{u(x_l)}}{a^j_m (x_l)} \vert _{\forall x_l \in \mathrm{supp}\, \mathbf {a}^j_m} \sum _{i=1}^{n_m} (A_m)_{ji} \langle \mathbf {a}^i_m, \mathbf {u}_m \rangle \\ &{} = &{} \displaystyle \sum _{j=1}^{n_m} \frac{\overline{u(x_l)}}{a^j_m (x_l)} \vert _{\forall x_l \in \mathrm{supp}\, \mathbf {a}^j_m} \sum _{i=1}^{n_m} (A_m)_{ji} \underbrace{ \Vert \mathbf {a}^i_m \Vert ^2}_{\displaystyle = 1 } \frac{u(x_l)}{a^j_m (x_l)} \vert _{\forall x_l \in \mathrm{supp}\, \mathbf {a}^i_m}\\ &{} = &{} \displaystyle \langle \mathbf{u}_m, \mathbf A_m \mathbf{u}_m \rangle _{\mathbb C^{n_m}} . \end{array} \end{aligned}$$

In what follows, we are going to require that the matrices $\mathbf A_m$ are not only Hermitian, but that all their non-diagonal elements are non-positive. In this case $- \mathbf A$ is a Minkowski M-matrix. With a certain abuse of rigour, we are going to call them negative Minkowski M-matrices. Such matrices possess a very important property: they are generators of positivity preserving semigroups [22].

3.5 Invariance of the quadratic form domain

It is important for the future to realise that for generalised delta interactions the domain of the quadratic form is invariant under taking the absolute value, provided that the weights are all positive. We have this property for any matrix $\mathbf A.$ One has to require that the matrix $\mathbf A$ is negative Minkowski M-matrix in order to ensure that the quadratic form does not increase under taking the absolute value. The following theorem states in particular that the quadratic form possesses these properties if and only if the vertex conditions are generalised delta couplings.

Theorem 2

Let $L_q (\varGamma )$ be a Schrödinger operator on a connected finite compact metric graph $\varGamma$ with arbitrary properly connecting vertex conditions. We assume that the potential q is summable $q \in L_1 (\varGamma )$. Furthermore, we assume that under taking the absolute value the domain of the quadratic form does not change and the value of the quadratic form does not increase

$$\begin{aligned} Q_{L_q(\varGamma )} (\vert u \vert , \vert u \vert ) \le Q_{L_q(\varGamma )} ( u, u). \end{aligned}$$

(16)

Then, the vertex conditions are either generalised delta couplings as described in (12) with all weights strictly positive and the matrices $- \mathbf A_m$ from Minkowski class or Dirichlet conditions.

Proof

We divide the proof into two steps.

Step 1The domain of the quadratic form is invariant under taking the absolute value if only if the subspace$\mathcal B$appearing in (10) is trivial or is generated by several vectors$\mathbf {e}^j$with non-negative coordinates and disjoint supports.

In other words, we claim that the boundary values of functions from the domain of the quadratic form belong to the subspace in $\mathbb C^{2N}$ (N is the number of edges in $\varGamma$) generated by the vectors $\mathbf {e}^j$ having very special properties: all coordinates are non-negative and their supports are disjoint ( i.e. no two vectors have positive coordinates with the same index).

The domain of the quadratic form is given by the requirement that the vector $\mathbf {u}$ of boundary values

$$\begin{aligned} \mathbf {u} = \left( u(x_1), u(x_2), \ldots , u (x_{2N}) \right) \equiv (u_1, u_2, \ldots , u_{2N}) \in \mathbb C^{2N} \end{aligned}$$

belongs to a certain linear subspace $\mathcal B \subset \mathbb C^{2N}.$ Consider any basis $\mathbf {e}^j, \, j= 1,2, \ldots , n,$$n \le 2N$ generating the subspace. Without loss of generality, we may assume that the vectors satisfy

$$\begin{aligned} (\mathbf {e}^j) (x_i) = \delta _{ij}, \; \; i,j = 1,2, \ldots , n. \end{aligned}$$

(17)

This can be achieved by permuting the coordinates in $\mathbb C^{2N}$ and Gaussian elimination. Note that we do not require that the basis is orthogonal.

Taking the absolute value we map any vector $\mathbf {u} \in \mathbb C^{2N}$ to a vector from $\mathbb R_+^{2N}$ in accordance with the following rule:

$$\begin{aligned} \vert \mathbf {u} \vert = \vert (u_1, u_2, \ldots , u_{2N} ) \vert = ( \vert u_1\vert , \vert u_2 \vert , \ldots , \vert u_{2N} \vert ). \end{aligned}$$

(18)

Consider the two-dimensional subspace of $\mathcal B$ generated by the vectors $\mathbf {e}^1$ and $\mathbf {e}^2.$ Every vector in this subspace is uniquely determined by its first two coordinates:

$$ \begin{aligned} \mathbf {u} = a \mathbf {e}^1 + b \mathbf {e}^2 , \, a,b \in \mathbb C \; \; \Rightarrow \; \; a = \mathbf {u} (x_1) \; \; \& \; \; b = \mathbf {u} (x_2). \end{aligned}$$

In particular, the coordinate number j is given by

$$\begin{aligned} \mathbf {u} (x_j) = a \mathbf {e}^1 (x_j) + b \mathbf {e}^2 (x_j) . \end{aligned}$$

(19)

The vector $\vert \mathbf {u} \vert$ belongs to the same subspace (it must belong to it in order to be in $\mathcal B$, since any vector in $\mathcal B$ is uniquely determined by its first n coordinates) if and only if

$$\begin{aligned} \vert \mathbf {u} \vert = \vert a \vert \, \vert \mathbf {e}^1\vert + \vert b \vert \, \vert \mathbf {e}^2 \vert \end{aligned}$$

(20)

holds. Comparing the jth coordinates calculated using (19) and (20), we obtain:

$$\begin{aligned} \vert a \mathbf {e}^1 (x_j) + b \mathbf {e}^2 (x_j) \vert = \vert a \vert \, \vert \mathbf {e}^1 (x_j) \vert + \vert b \vert \, \vert \mathbf {e}^2 (x_j) \vert . \end{aligned}$$

(21)

The later equality holds for any a and b if and only if at least one of the coordinates $\mathbf {e}^1 (x_j)$ and $\mathbf {e}^2 (x_j)$ is equal to zero, in other words only if the vectors $\mathbf {e}^1$ and $\mathbf {e}^2$ have disjoint supports.

The vector $\vert \mathbf {u} \vert$ belongs to the subspace only if it is a combination of the vectors $\mathbf {e}^1$ and $\mathbf {e}^2.$ Comparing the first two coordinates, we conclude that

$$\begin{aligned} \vert \mathbf {u} \vert = \vert a\vert \, \mathbf {e}^1 + \vert b \vert \, \mathbf {e}^2. \end{aligned}$$

The coordinates of this vector are non-negative only if the coordinates of the basis vectors $\mathbf {e}^j$ are non-negative.

The same analysis applies to any two vectors from the basis; hence, we conclude that all $\mathbf {e}^j$ not only have disjoint supports but also their entries are non-negative. It might happen that several vectors $\mathbf {e}^j$ correspond to the same vertex. Thus, we have proven that vertex conditions should be the generalised delta couplings.

Without loss of generality, we normalise vectors $\mathbf {e}^j$ and arrange them so the vectors $\mathbf {a}^j_m$ are nonzero at the endpoints belonging to the vertex $V_m$ only.

Step 2 The value of the quadratic form does not increase while taking the absolute value if and only if the Hermitian matrix $- \mathbf A = - (\mathbf A_1 \oplus \mathbf A_2 \oplus \cdots \oplus \mathbf A_M)$ is from Minkowski class (all non-diagonal entries are non-negative).

Of course, we assume here that the domain of the quadratic form does not change while taking the absolute value. We need to satisfy the inequality (16) which can be written using (15) as

$$\begin{aligned}&\displaystyle \int _\varGamma \left( \vert u\vert ' (x)\vert ^2 + q(x) \vert u(x) \vert ^2 \right) \hbox {d}x + \sum _{m=1}^M \langle \vert \mathbf{u}_m\vert , \mathbf A_m \vert \mathbf{u}_m \vert \rangle _{\mathbb C^{n_m}} \\&\quad \displaystyle \le \int _\varGamma \left( \vert u' (x)\vert ^2 + q(x) \vert u(x) \vert ^2 \right) \hbox {d}x + \sum _{m=1}^M \langle \mathbf{u}_m, \mathbf A_m \mathbf{u}_m \rangle _{\mathbb C^{n_m}}. \end{aligned}$$

The integral terms containing $\int \left( \vert u'(x) \vert ^2 + q (x) \vert u(x) \vert ^2 \right) \hbox {d}x$ can be cancelled. Hence, the following inequality should hold for each vertex

$$\begin{aligned} \langle \vert \mathbf{u}_m \vert , \mathbf A_m \vert \mathbf{u}_m \vert \rangle \le \langle \mathbf{u}_m, \mathbf A_m \mathbf{u}_m \rangle , \; \, m= 1,2, \ldots , M, \end{aligned}$$

where $\mathbf{u}_m$ are the reduced vectors of boundary values associated with the vertex $V_m$.

Our goal is to prove that the matrices $\mathbf A_m$ should have non-positive entries outside the diagonal. These matrices are Hermitian, since the quadratic form has to be real. Consider first the case where $\mathbf{u}_m$ has just two nonzero coordinates (in other words, $\mathbf {u}_m$ belongs to the linear span of say $\mathbf {a}^1_m$ and $\mathbf {a}^2_m$). Calculating the quadratic forms of $\mathbf{u}_m = (a,b, 0, \ldots )$ and $\vert \mathbf{u}_m \vert$, we get

$$\begin{aligned}&\displaystyle \langle \vert \mathbf{u}_m \vert , \mathbf A_m \vert \mathbf{u}_m \vert \rangle = \vert a\vert ^2 ( \mathbf A_m)_{11} + \vert b \vert \, \vert a \vert \left( (\mathbf A_m)_{21} + (\mathbf A_m)_{12} \right) + \vert b \vert ^2 (\mathbf A_m)_{22} \\&\quad \displaystyle \le \vert a\vert ^2 (\mathbf A_m)_{11} + \bar{b} a (\mathbf A_m)_{21} + \bar{a} b ( \mathbf A_m)_{12} + \vert b \vert ^2 (\mathbf A_m)_{22} = \langle \mathbf {u}_m , \mathbf A_m \mathbf {u}_m \rangle , \end{aligned}$$

implying that

$$\begin{aligned} \vert a \vert \, \vert b \vert \mathfrak {R}(\mathbf A_m)_{12} \le \mathfrak {R}\left( \bar{a} b (\mathbf A_m)_{12}\right) \end{aligned}$$

holds for any a and b, which is possible if and only if $( \mathbf A_m)_{12}$ is a non-positive real number. Of course, the same condition is enough even if more than two vectors are considered.

Summing up, the domain of the quadratic form is given by the requirement that at each vertex $V_m$ the vector of boundary values belongs to a subspace spanned by $n_m \le d_m$ vectors with disjoint supports and positive coordinates $\mathbf {u}_m \in \mathcal B_m = \mathfrak L \{ \mathbf {a}_m^{i} \}_{i=1}^{n_m}$ and the matrix $\mathbf A_m$ in $\mathcal B_m$ is Hermitian with non-positive non-diagonal entries. Remember that we consider only properly connecting vertex conditions implying that the supports of vectors $\mathbf {a}^j_m$ span $\mathbb C^{d_m}$ (equation (14)) and the matrix $\mathbf A_m$ is irreducible.

Thus, the vertex conditions coincide with the generalised delta couplings determined by (12). $\square$

It is straightforward to see that generalised delta couplings guarantee that (16) holds. Using Beurling–Deny criterion one may characterise possible vertex conditions with the help of Theorem 6.85 in [16], but our characterisation is much more explicit. We return to this question in Sect. 4.

3.6 Positivity of the ground state

We are ready to generalise the theorem to Schrödinger operators with generalised delta couplings.

Theorem 3

Assume that all assumptions of Theorem 2 are satisfied and the graph $\varGamma$ is connected. Then, the ground state is unique and may be chosen real, in which case it is strictly positive.

Proof

For the generalised delta couplings and Dirichlet conditions, the domain of the quadratic form is invariant under taking the absolute value and under complex conjugation. Moreover, the value of the quadratic form does not increase under these operations. Hence, as in Sect. 2 the ground state may be chosen real and non-negative. It remains to prove that such a ground-state eigenfunction is strictly positive, i.e. it is equal to zero only at the vertices, where Dirichlet conditions are assumed (Dirichlet points).

Assume the opposite: the eigenfunction $\psi _1$ is equal to zero at a certain point $x_0 \in \varGamma ,$ which is not a Dirichlet point. As before, two possibilities should be considered:

• $x_0$ is an inner point on an edge,

• $x_0$ belongs to a vertex.

If $x_0$ lies on an edge, then repeating the arguments used in the proof of Theorem 1 we conclude that $\psi _1$ is identically equal to zero on the whole edge. In particular, the function $\psi _1$ is equal to zero at the two vertices that are the endpoints of the edge.

It remains to study the case where $x_0$ belongs to one of the vertices, say $V_m$. Consider the corresponding weight vectors $\mathbf {a}^1_m, \mathbf {a}^2_m, \ldots , \mathbf {a}^{n_m}_m.$ If $x_0$ belongs to the support of $\mathbf {a}^1_m$, then the first coordinate in $\mathbf{u}_m$ is zero. We consider the second condition in (12):

$$\begin{aligned} \underbrace{\langle \mathbf {a}^1_m, \partial \mathbf {u}_m \rangle }_{\ge 0} = 0 + \sum _{i=2}^{n_m} \underbrace{ (\mathbf A_m)_{1i}}_{\le 0} \underbrace{\langle \mathbf {a}^i_m, \mathbf {u}_m \rangle }_{\ge 0}. \end{aligned}$$

The left-hand side is non-negative, since the function is non-negative inside the edges and is equal to zero at the endpoints in the support of $\mathbf {a}_1.$ The scalar products $\langle \mathbf {a}_i, \mathbf {u} \rangle$ are non-negative, since the function u is non-negative. This is possible only if

$$\begin{aligned} \langle \mathbf {a}_1, \partial \mathbf {u}_m \rangle = 0 \end{aligned}$$

and all

$$\begin{aligned} \langle \mathbf {a}_i, \mathbf {u}_m \rangle = 0, \end{aligned}$$

provided $(\mathbf A_m)_{1i} \ne 0.$ At least one of the coefficients $(\mathbf A_m)_{1i}$ is different from zero, since otherwise the matrix $\mathbf A_m$ is reducible. It follows that at least one other coordinate of $\mathbf{u}_m$ is zero. Repeating this procedure several times, we prove not only that the vector $\mathbf{u}_m$ is identically zero, but also that all scalar products of $\partial \mathbf {u}_m$ with the vectors $\mathbf {a}^1_m, \mathbf {a}^2_m, \ldots , \mathbf {a}^{n_m}_m$ are zero. It follows that all normal derivatives at $V_m$ are also zero, since $\partial \psi _1 (x_\ell ), \, x_\ell \in V_m$ are all non-negative.

It follows that on each edge incident to $V_m$ the function $\psi _1$ is a solution of the second-order differential equation satisfying trivial Cauchy data. Hence, the function is identically equal to zero on all edges incident to $V_m.$

Repeating the argument for the vertices connected to $V_m$ by an edge, we conclude that $\psi _1$ is zero on all edges incident to those vertices. Continuing this procedure, we shall prove that $\psi _1 \equiv 0$ on the whole $\varGamma$, since the graph is connected. $\square$

In fact we have proven that if the quadratic form of the Schrödinger operator on a connected finite compact metric graph does not increase under taking the absolute value, then the corresponding ground state is strictly positive, i.e. the eigenfunction is equal to zero only at the points where the Dirichlet conditions are assumed. We not only proved that $\psi _1$ is strongly positive, but characterised explicitly all points where $\psi _1$ is equal to zero. If there are no Dirichlet points, then $\psi _1$ is separated from zero $\psi _1(x) \ge \delta > 0.$

3.7 Generalised delta couplings are optimal

The goal of this subsection is to show that the assumptions of Theorem  2 are in some sense necessary to guarantee positivity of the ground-state eigenfunction: given a vertex with conditions violating these assumptions, one may construct a quantum graph with the ground-state eigenfunction either complex-valued or not sign definite.

Theorem 4

The class of generalised delta couplings and Dirichlet conditions is optimal to guarantee positivity of the ground-state eigenfunction for quantum graphs in the following sense:

Assume that Hermitian vertex conditions not from the selected class are given. Then, there exists a metric graph $\varGamma$ and a Laplace operator on it satisfying given vertex conditions at one of the vertices and generalised delta couplings and Dirichlet conditions at the other vertices such that its ground-state eigenfunction cannot be chosen non-negative.

Proof

Let $\varGamma$ be d-star graph with the edge lengths $\ell _j, j= 1,2, \ldots , d$ (to be specified later). Consider the Laplace operator on $\varGamma$ assuming Dirichlet vertex conditions at the degree one vertices and given vertex conditions at the central vertex V (not generalised delta couplings, not Dirichlet conditions).

Every Hermitian vertex condition at a degree d vertex is given by specifying a subspace $\mathcal B \subset \mathbb C^d$ and a Hermitian operator A in $\mathcal B$ such that the vertex conditions can be written in the form:

$$\begin{aligned} \mathbf {u} (V) \in \mathcal B, \quad \partial \mathbf {u} (V) = A \mathbf {u}(V), \end{aligned}$$

(22)

where $\mathbf {u}(V)$ and $\partial \mathbf {u}(V)$ are the d-dimensional vectors of function values and normal derivatives at the vertex V.

Assume that the space $\mathcal B \subset \mathbb C^d$ is spanned by K vectors $\mathbf {e}^j, \; j= 1,2, \ldots , K.$ Performing Gaußelimination and may be permutation of the edges, we may assume without loss of generality that basis vectors satisfy:

$$\begin{aligned} \big ( \mathbf {e}^j \big )_n = \delta _{jn}, \quad j,n = 1,2, \ldots , K. \end{aligned}$$

(23)

Note that at this stage we do not require that the basis is orthogonal. This basis can be extended to a basis in $\mathbf C^n$ by adding $d-K$ vectors $\mathbf {e}^{K+1}, \ldots , \mathbf {e}^d$ having all first K coordinates equal to zero:

$$\begin{aligned} \big ( \mathbf {e}^j \big )_n = 0, \quad j = K+1, \ldots , d, n = 1,2, \ldots , K. \end{aligned}$$

(24)

To determine the secular equation giving the spectrum of the Laplacian, let us assume that every edge j is parametrised as the interval $[0, \ell _j]$ with 0 corresponding to the central vertex. Every solution to the eigenfunction equation is given by

$$\begin{aligned} \mathbf {u} = \sum _{j=1}^d \Big ( \alpha _j \hbox {cos} kx + \beta _j \frac{\hbox {sin} kx}{k} \Big ) \mathbf {e}^j , \end{aligned}$$

where $\alpha _j, \beta _j \in \mathbb C$ and we used vector notations for the function u on $\varGamma ,$ which is not a restriction since any solution given by a linear combination of $\cos$ and $\sin$ functions can be extended to a whole line.

It will be convenient to decompose the space $\mathbb C^d = \mathbb C^K \oplus \mathbb C^{d-K}$ splitting the vectors $\varvec{\alpha }, \varvec{\beta }$ as follows:

$$\begin{aligned} \varvec{\alpha }^1 := \left( \begin{array}{c} \alpha _1 \\ \alpha _2 \\ \vdots \\ \alpha _K \end{array} \right) , \quad \varvec{\alpha }^2 : = \left( \begin{array}{c} \alpha _{K+1} \\ \alpha _{K+2} \\ \vdots \\ \alpha _d \end{array} \right) , \end{aligned}$$

(25)

with $\varvec{\beta }^{1,2}$ defined accordingly.

The vertex conditions at the central vertex give

$$\begin{aligned} \varvec{\beta }^1 = \mathbf A \varvec{\alpha }^1, \quad \varvec{\beta }^2 = 0, \end{aligned}$$

(26)

where the matrix $\mathbf A$ is the representation of the operator A in the introduced basis in $\mathcal B$. Note that the matrix $\mathbf A$ is not necessarily Hermitian since the basis is not assumed to be orthogonal.

Dirichlet vertex conditions at degree one vertices

$$\begin{aligned} \big ( \mathbf {u} (\ell _j) \big )_j = 0, \quad j = 1,2, \ldots , d, \end{aligned}$$

imply

$$\begin{aligned} \begin{array}{l} \Big ( \mathbf C^{11} \varvec{\alpha }^1 + \frac{1}{k} {\mathbf {A}} {\mathbf {S}}^{11} \Big ) \varvec{\alpha }^1 = 0; \\ \Big ( {\mathbf {C}}^{22} {\mathbf E}^{21} + \frac{1}{k} {\mathbf S}^{22} {\mathbf E}^{21} {\mathbf A} \Big ) \varvec{\alpha }^1 + {\mathbf C}^2 {\mathbf E}^{22} \varvec{\alpha }^2 = 0; \end{array} \end{aligned}$$

(27)

where the following notations were used:

$$\begin{aligned} \begin{array}{ccl} \mathbf C &{} = &{} \mathrm{diag}\, \{ \cos k \ell _1, \ldots , \cos k \ell _d \}; \\ \mathbf S &{} = &{} \mathrm{diag}\, \{ \sin k \ell _1, \ldots , \sin k \ell _d \}; \\ \mathbf E &{} = &{} \{ e_{ij} \}_{i,j =1}^d , \quad e_{ij} = \big (\mathbf {e}^j \big )_i .\\ \end{array} \end{aligned}$$

and $\mathbf M^{nm}, \; n,m =1,2$ denote the blocks of any matrix $\mathbf M$ in the orthogonal decomposition of $\mathbb C^d.$

The system of linear equations has a non-trivial solution only if the determinant is zero, which gives us the following secular equation:

$$\begin{aligned} \det \left( \begin{array}{cc} \displaystyle \mathbf C^{11} + \frac{1}{k} \mathbf A \mathbf S^{11} &{} \displaystyle 0 \\ \displaystyle \mathbf C^{22} \mathbf E^{21} + \frac{1}{k} \mathbf S^{22} \mathbf E^{21} \mathbf A &{} \displaystyle \mathbf C^2 \mathbf E^{22} \end{array} \right) = 0. \end{aligned}$$

(28)

To simplify calculations, we assume that the lengths of $d-K$ edges are all equal

$$\begin{aligned} \ell _{K+1} = \ell _{K+2} = \cdots \ell _d =: \ell _0. \end{aligned}$$

(29)

We are interested in the ground state of the introduced operator. We may estimate it from above by $\big ( \frac{\pi }{\ell _0} \big )^2$, since the functions

$$\begin{aligned} \sin \frac{\pi }{\ell _0}\; \mathbf {e}^j, \quad j = K+1, \ldots , d \end{aligned}$$

are clearly eigenfunctions corresponding to the eigenvalue $\big ( \frac{\pi }{\ell _0} \big )^2$. This estimate is independent of the lengths of the first K edges. In what follows, we are going to play with these lengths, but interested in the ground state we may always restrict ourselves to the region $\vert k \vert \le \frac{\pi }{\ell _0}.$

Let us examine first what happens to the secular equation in the limit $\ell _1, \ell _2, \ldots , \ell _K \rightarrow 0$ assuming of course $\vert k \vert \le \frac{\pi }{\ell _0}.$ The matrix $\mathbf S^{11}$ tends to zero implying that the limit secular equation can be written as

$$\begin{aligned} \det \left( \begin{array}{cc} \displaystyle \mathbf I &{} \displaystyle 0 \\ \displaystyle 0 &{} \displaystyle \mathbf C^2 (k) \mathbf E^{22} \end{array} \right) = 0 \Rightarrow \det \big ( \mathbf C^2 (k) \mathbf E^{22} \big ) = 0, \end{aligned}$$

since $\mathbf C^{11} (k)$ tends to the unit matrix $\mathbb C^{K}.$ The zeroes of this equation coincide with the spectrum of the Dirichlet–Dirichlet Laplacian on the interval $[0, \ell _0].$

Both determinants are given by analytic functions, convergence of analytic functions imply convergence of their zeroes in any bounded domain (Cauchy formula). Therefore, for sufficiently small $\ell _j, j= 1,2, \ldots , \ell _K$ the zeroes of the secular equation for d-star graph are close to the spectrum of the Dirichlet–Dirichlet Laplacian on $[0, \ell _0]$ with multiplicity $d-K$. Moreover, the corresponding eigenfunctions can also be obtained in the limit.

Let us assume now that only $\ell _2, \ldots , \ell _K \rightarrow 0$ but $\ell _1$ remains fixed $\ell _1 = \ell _0.$ In the matrix $\mathbf A \mathbf S^{11}$ only the first column is not small; hence, the approximate secular equation is given by

$$\begin{aligned} \Big ( \cos k \ell _0 + \frac{1}{k} a_{11} \sin k \ell _0 \Big ) \det \big ( \mathbf C^2 (k) \mathbf E^{22} \big ) = 0. \end{aligned}$$

As before, we have convergence of the zeroes as well as of the eigenfunctions.

The limit spectrum is the union of the spectrum of the Dirichlet–Dirichlet Laplacian on $[0, \ell _0 ]$ (with multiplicity $d-K$) and the spectrum of the Laplacian on the interval $[0, \ell _0 ]$ with Robin condition $u'(0) = a_{11} u(0)$ at the left endpoint and Dirichlet condition at the right. The latter spectrum is described by the equation $\cos k \ell _0 + \frac{1}{k} a_{11} \sin k \ell _0 = 0.$ The ground-state eigenfunction is given by the ground-state eigenfunction of the Robin–Dirichlet Laplacian multiplied by $\mathbf {e}^1.$ Therefore, all coordinates in $\mathbf {e}^1$ should be non-negative, otherwise the ground-state eigenfunction of the Laplacian on the d-star graph is not non-negative.

Similarly, we prove that the coordinates of all vectors $\mathbf {e}^2, \ldots , \mathbf {e}^K$ forming basis in $\mathcal B$ are non-negative.

Moreover, our proof is applicable to arbitrary basis $\mathbf {e}^j$ in $\mathcal B$; hence, these basis vectors cannot have common nonzero coordinates. Assume on the contrary that the two vectors, say $\mathbf {e}^1$ and $\mathbf {e}^2$, have non-trivial coordinate with index $j_0.$ Remember that we already know that $(\mathbf {e_1})_{j_0}$ and $(\mathbf {e}^2)_{j_0}$ are positive. Consider instead of the basis $\mathbf {e}^1, \mathbf {e}^2, \ldots , \mathbf {e}^K \in \mathcal B$ a new basis given by $\mathbf {e}_3, \ldots , \mathbf {e}^K$ and the vectors

$$\begin{aligned} \mathbf {e}^{j_0} = (\mathbf {e}^1)_{j_0}^{-1} \mathbf {e_1} \quad {\mathbf {e}^2}' = \mathbf {e}^2 - (\mathbf {e}^2)_{j_0} \, (\mathbf {e}^1)_{j_0}^{-1} \mathbf {e}^1 . \end{aligned}$$

Clearly, the new basis satisfies all requirements (after permutation of the first and $j_0$th coordinates), but the first coordinate of the vector $( {\mathbf {e}^2}')_1 = - (\mathbf {e}^2)_{j_0} \, (\mathbf {e}^1)_{j_0}^{-1}$ is clearly negative. This contradiction proves that the basis vectors in $\mathcal B$ do not have common nonzero coordinates and therefore can be chosen orthonormal. It is natural to extend this basis to an orthonormal basis in $\mathbb C^{d}.$

It remains to prove that the matrix $\mathbf A$ is not only Hermitian, but all its non-diagonal elements are non-positive. Let us assume that the lengths of the first two edges are fixed :

$$\begin{aligned} \ell _1 = \ell _2 = \ell _0 \end{aligned}$$

and consider the limit where $\ell _3, \ell _4, \ldots , \ell _K \rightarrow 0.$ The secular equation in the region $\vert k \vert < \frac{\pi }{\ell _0}$ is approximated by

$$\begin{aligned} \det \left( \cos k \ell _0 \left( \begin{array}{cc} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{array} \right) + \frac{1}{k} \left( \begin{array}{cc} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array} \right) \sin k \ell _0 \right) \; \det \big ( \mathbf C^2 (k) \mathbf E^{22} \big ) = 0. \end{aligned}$$

(30)

The zeroes coincide with the spectrum of the Dirichlet–Dirichlet Laplacian on $[0, \ell _0]$ and of the spectrum of the Laplacian defined on $\mathbf C^2$-valued functions on the interval $[0, \ell _0 ]$ satisfying Dirichlet conditions at $x = \ell _0$ and the following conditions at the origin:

$$\begin{aligned} \mathbf {u}'(0) = \left( \begin{array}{cc} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array} \right) \mathbf {u} (0). \end{aligned}$$

The lowest eigenvalue comes from the spectrum of the vector-valued problem. Here, the ground-state eigenfunction is real only if $a_{12} \in \mathbf R.$ The ground-state eigenfunction is non-negative only if $a_{12}$ is non-positive; this is proven in the same way as during Step 2 in the proof of Theorem 2.

Considering different pairs of edges, we conclude that to guarantee positivity of the ground-state eigenfunction for all graphs one should require that $\mathbf A$ is negative Minkowski M-matrix. $\square$

Our result does not imply that the ground-state eigenfunction cannot be chosen non-negative if vertex conditions at one of the vertices are not generalised delta couplings or Dirichlet. To prove necessity, we considered different graphs. Taking the d-star graph with $\ell _{K+1} = \cdots = \ell _d = \ell _0$ and $\ell _1, \ell _2, \ell _3, \ldots , \ell _K \ll \ell _0.$ As we have seen, the ground state is determined by the ground state of the Dirichlet–Dirichlet Laplacian on $[0, \ell _0]$ and therefore is independent of the matrix $\mathbf A$; hence, it is always non-negative.

4 On positivity preserving semigroups

The non-degeneracy and positivity of the ground state are often connected to the fact that the corresponding semigroup is positivity preserving. In what follows, we shall explore this direction, but first we recall a few well-known facts (see [21], some of the formulations are slightly shortened in order to fit our needs).

Proposition 1

(Theorem XIII.44 from [21]) Let H be a self-adjoint operator that is bounded from below on $L_2 (M, d \mu ) .$ Suppose that $e^{-tH}$ is positivity preserving for all $t > 0$ and that $E = \mathrm{inf}\, \sigma (H)$ is an eigenvalue. Then, the following are equivalent:

• 1. E is a simple eigenvalue with a strongly positive eigenvector.

• 2. $e^{-tH}$ is positivity improving for all $t > 0.$

Proposition 2

(Theorem XIII.50 from [21], first Beurling–Deny criterion) Let $H \ge 0$ be a self-adjoint operator on $L_2 (M, d\mu )$. Extend $\langle \psi , H \psi \rangle$ to all $L_2$ by setting it equal to infinity when $\psi$ is not in the domain of the quadratic form. Then, the following are equivalent:

• 1. $e^{-tH}$ is positivity preserving for all $t > 0.$

• 2. $\langle \vert u \vert , H \vert u \vert \rangle \le \langle u, H u \rangle$ for all $u \in L_2.$

With these propositions in mind, we can prove the following statements.

Theorem 5

Assume that all conditions of Theorem 2 are fulfilled. Then, the corresponding Schrödinger operator with $q \in L_1 (\varGamma )$ is a generator of positivity improving semigroup.

Proof

The operator is semi-bounded with discrete spectrum. The quadratic form does not increase when taking the absolute value; hence, Proposition 2 implies that the corresponding semigroup is positivity preserving.

Moreover, we have proven that the ground state is strictly positive and hence is also strongly positive. Therefore, Proposition 1 implies that the semigroup generated by the operator is positivity improving. $\square$

It is also possible to turn our reasoning to prove the opposite result:

Theorem 6

Assume that the finite compact metric graph $\varGamma$ is connected and the operator $L_q (\varGamma )$ with $q \in L_1 (\varGamma )$ is a generator of a positivity preserving semigroup in $L_2 (\varGamma ).$ Then, the ground state is strictly positive, the vertex conditions at each vertex are either Dirichlet or of generalised delta-type with all weights positive and the matrix $- \mathbf A$ is a Minkwoski M-matrix. Moreover, the semigroup is positivity improving.

Proof

The semigroup is positivity preserving if and only if the domain of the quadratic form is invariant and does not increase when taking the absolute value (see Proposition 2). We have already characterised all corresponding vertex conditions proving Theorem 2—all such vertex conditions are of generalised delta type. Then, Theorem 5 implies that the semigroup is also positivity improving. $\square$

This statement can be found in [16] (Theorem 6.85) (see also [4, 15]), but without an explicit description of the vertex conditions as we have in terms of generalised delta couplings.

Appendix A

Assume that $\psi _1$ is a non-negative minimiser for the Rayleigh quotient. Consider any function $\varphi \in C(\varGamma ) \cap C^\infty (\varGamma {\setminus } \mathbf V )$. Then, the function $\psi _1 + \alpha \varphi$ is admissible for any value of $\alpha .$ For a real-valued $\varphi$ this is possible only if

$$\begin{aligned} \left. \frac{\partial }{\partial \alpha } \left\{ \frac{\int _\varGamma \big ( \psi _1' (x) + \alpha \varphi '(x) \big )^2 \hbox {d}x + \int _\varGamma q(x) \big (\psi _1(x) + \alpha \varphi (x) \big )^2 \hbox {d}x}{ \int _\varGamma \big ( \psi _1(x) + \alpha \varphi (x)) \big )^2 \hbox {d}x} \right\} \right| _{\alpha = 0 } = 0 \end{aligned}$$

holds. This leads to the following integral equality:

$$\begin{aligned} \int _\varGamma \psi _1' (x) \varphi '(x) \hbox {d}x + \int _\varGamma q(x) \psi _1 (x) \varphi (x) \hbox {d}x - \lambda _1 \int _\varGamma \psi _1 (x) \varphi (x) \hbox {d}x = 0, \end{aligned}$$

(31)

where we used that the minimiser gives Rayleigh quotient equal to $\lambda _1.$ Taking first $\varphi \in C_0^\infty (E_n)$ for a certain edge $E_n$, we conclude that $\psi _1$ satisfies the differential equation

$$\begin{aligned} - \psi ''_1 (x) + q(x) \psi _1 (x) = \lambda _1 \psi _1 (x), \; \, x \in E_n \end{aligned}$$

(32)

in the generalised sense. Let us integrate by parts in (31)

$$\begin{aligned} - \sum _{m=1}^M \left( \sum _{x_j \in V^m} \partial \psi _1 (x_j) \right) \varphi (V^m) + \int _\varGamma \underbrace{\left( - \psi _1'' + q(x) \psi _1 (x) - \lambda _1 \psi _1 (x) \right) }_{\displaystyle \equiv 0} \varphi (x) \hbox {d}x = 0 \end{aligned}$$

where M is the number of vertices in $\varGamma$, implying that

$$\begin{aligned} \sum _{m=1}^M \left( \sum _{x_j \in V_m} \partial \psi _1 (x_j) \right) \varphi (V_m) = 0. \end{aligned}$$

Considering $\varphi$ different from zero just at any arbitrary vertex $V_m$ and equal to zero at all other vertices, we get

$$\begin{aligned} \sum _{x_j \in V_m} \partial \psi _1 (x_j) = 0 ,\end{aligned}$$

i.e. that $\psi _1$ satisfies standard conditions at each vertex (continuity follows from the fact that $\psi _1$ is admissible). Hence, every minimiser is an eigenfunction as expected.