Internally connected graphs and the Kashiwara-Vergne Lie algebra

Abstract

It is conjectured that the Kashiwara-Vergne Lie algebra $\widehat{\mathfrak {krv}}_2$ is isomorphic to the direct sum of the Grothendieck-Teichmüller Lie algebra $\mathfrak {grt}_1$ and a one-dimensional Lie algebra. In this paper, we use the graph complex of internally connected graphs to define a nested sequence of Lie subalgebras of $\widehat{\mathfrak {krv}}_2$ whose intersection is $\mathfrak {grt}_1$, thus giving a way to interpolate between these two Lie algebras.

Appendix A. The spaces \({\mathfrak {t}}{\mathfrak {r}}_n,\mathfrak {sder}_n,\mathfrak {tder}_n\)

We follow [1]. Fix $n\ge 1$. Let $\mathfrak {lie}_n$ denote the completed free Lie algebra over ${\mathbb {K}}$ on n variables $x_1,\ldots ,x_n$ and let $\text {Ass}_n=U(\mathfrak {lie}_n)$ be the completed free associative algebra in n generators. The graded vector space of cyclic words in n variables ${\mathfrak {t}}{\mathfrak {r}}_n$ is defined as

$$\begin{aligned} {\mathfrak {t}}{\mathfrak {r}}_n:=\text {Ass}^+_n/\langle (ab-ba), a,b\in \text {Ass}_n\rangle \end{aligned}$$

where $\text {Ass}_n^+$ is the augmentation ideal of $\text {Ass}_n$. The Lie algebra $\mathfrak {tder}_n$ of tangential derivations on $\mathfrak {lie}_n$ is defined as follows. A derivation u on $\mathfrak {lie}_n$ is tangential if there exist $a_1,\ldots ,a_n\in \mathfrak {lie}_n$ such that $u(x_i)=[x_i,a_i]$ for all $i=1,\ldots ,n$. The action of u on the generators completely determine the derivation. For $u=(a_1,\ldots ,a_n)$ and $v=(b_1,\ldots ,b_n)$ elements of $\mathfrak {tder}_n$, the Lie bracket is the tangential derivation $[u,v]=(c_1,\ldots ,c_n)$, where $c_k=u(b_k)-v(a_k)+[a_k,b_k]$ for all $k=1,\ldots ,n$. The Lie algebra of special derivations $\mathfrak {sder}_n$ is

$$\begin{aligned} \mathfrak {sder}_n:=\left\{ u\in \mathfrak {tder}_n| u\left( \sum \limits _{i=1}^{n}{x_i}\right) =0\right\} . \end{aligned}$$

It is a Lie subalgebra of $\mathfrak {tder}_n$. For every $a\in \text {Ass}_n$, we have a unique decomposition

$$\begin{aligned} a=a_0+\sum \limits _{k=1}^{n}(\partial _k a)x_k, \end{aligned}$$

where $a_0\in \mathbb {K}$ and $(\partial _k a)\in \text {Ass}_n$. The divergence map

$$\begin{aligned} \text {div}:\mathfrak {tder}_n&\rightarrow {\mathfrak {t}}{\mathfrak {r}}_n\\ u=(a_1,\ldots , a_n)&\mapsto \sum \limits _{k=1}^{n}tr(x_k(\partial _k a_k)) \end{aligned}$$

is a cocycle for $\mathfrak {tder}_n$ ([1], Proposition 3.6.).

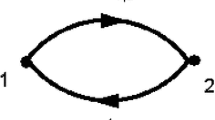
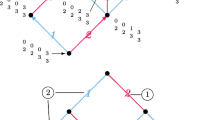
The following algorithm describes the isomorphism between $H^0(\hat{gr}\mathsf {ICG}(n)^0,d_0)$, i.e., internally trivalent trees in $\mathsf {ICG}(n)$ modulo IHX, and $\mathfrak {sder}_n$. Let $\Gamma$ be a tree representing an element of $H^0(\hat{gr}\mathsf {ICG}(n)^0,d_0)$. Pick an edge incident to the external vertex 1, cut it and make it the “root” edge. The resulting tree is a binary tree with leafs labeled by $1,\ldots , n$. Repeat this procedure for every edge incident to vertex 1, and take the sum of the trees obtained in this way. We want to interpret these binary trees as Lie words. The sign convention for this is as follows. The edges of the tree should be ordered such that its “root” edge comes first, then all edges of its left subtree, and then all edges of its right subtree. For each subtree, apply this convention recursively. The resulting linear combination of Lie words (these can be read off the trees by following the ordering of the edges) in the variables $x_1,\ldots ,x_n$ corresponds to the first component $a_1$ of a special derivation $a=(a_1,\ldots ,a_n)\in \mathfrak {sder}_n$. The ith component $a_i$ is obtained by applying the same procedure to the ith external vertex (Fig. 5).

Fig. 5

An example of the isomorphism $H^0(\hat{gr}\mathsf {ICG}(3)^0,d_0)\rightarrow \mathfrak {sder}_3$. The triple on the right corresponds to the element $([x_2,x_3],-[x_1,x_3],[x_1,x_2])$

Fig. 6

This graph will be sent to $tr(x_{m_1}x_{m_2}x_{m_3}x_{m_4}x_{m_5})-(-1)^5tr(x_{m_5}x_{m_4}x_{m_3}x_{m_2}x_{m_1})$ under the injective map $H^1(\hat{gr}\mathsf {ICG}(n)^1,d_0)\rightarrow {\mathfrak {t}}{\mathfrak {r}}_n$

We now give the map $H^1(\hat{gr}\mathsf {ICG}(n)^1,d_0)\hookrightarrow {\mathfrak {t}}{\mathfrak {r}}_n$ as described in [13]. Let $\overline{\Gamma }\in H^1(\hat{gr}\mathsf {ICG}(n)^1,d_0)$. We may assume that the representative $\Gamma$ is such that the loop passes through all internal vertices. Order the edges as in Fig. 6. In this case, we map

$$\begin{aligned} \overline{\Gamma }\mapsto tr(x_{m_1}\cdots x_{m_k})-(-1)^k tr(x_{m_k}\cdots x_{m_1}). \end{aligned}$$