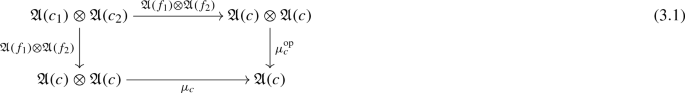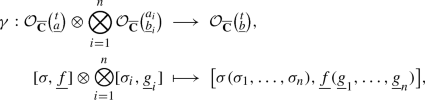Homotopy theory of algebraic quantum field theories

Abstract

Motivated by gauge theory, we develop a general framework for chain complex-valued algebraic quantum field theories. Building upon our recent operadic approach to this subject, we show that the category of such theories carries a canonical model structure and explain the important conceptual and also practical consequences of this result. As a concrete application, we provide a derived version of Fredenhagen’s universal algebra construction, which is relevant e.g. for the BRST/BV formalism. We further develop a homotopy theoretical generalization of algebraic quantum field theory with a particular focus on the homotopy-coherent Einstein causality axiom. We provide examples of such homotopy-coherent theories via (1) smooth normalized cochain algebras on $\infty$-stacks, and (2) fiber-wise groupoid cohomology of a category fibered in groupoids with coefficients in a strict quantum field theory.

1 Introduction and summary

Algebraic quantum field theory is a far developed mathematical framework to investigate quantum field theories on Lorentzian spacetimes from a model-independent perspective. Its origins lie in a seminal paper of Haag and Kastler dating back to the early 1960s [31]. More than 50 years of developments in this field have led to a broad spectrum of beautiful and deep mathematical results for quantum field theories, reaching from rigorous statements about their scattering theory, over discovering intriguing features in their representation theory, to constructing non-perturbative models in low spacetime dimensions. We refer to [10] for a recent general overview and also to [38] for a more specialized review of chiral conformal quantum field theories.

One of the major open problems in algebraic quantum field theory is that there is currently no consensus on the description of gauge theories in this framework. In particular, the important questions of what is a quantum gauge theory and how it differs from a theory without gauge symmetries are not yet sufficiently well understood. We believe that the key to address and solve these problems is to develop a generalization of algebraic quantum field theory that takes into account the crucial higher structures which are present in gauge theories. This has led us to initiate the homotopical algebraic quantum field theory program, cf. [2,3,4,5,6]. From a technical perspective, this program is about combining the conceptual/physical ideas of algebraic quantum field theory with modern techniques from homotopy theory, in the sense of model category theory (see e.g. [20, 34, 37]) or higher category theory (see e.g. [42, 43]), which are capable to describe the relevant higher structures of gauge theories. We would like to emphasize that higher structures already play a major role in other mathematical approaches to quantum field theory, most notably in topological quantum field theory (see e.g. [41]) and in the factorization algebra approach of Costello and Gwilliam [15]. Even though these frameworks provide some inspiration for our developments, they are unfortunately not directly applicable to our specific problem. This is because we are interested in quantum field theories on Lorentzian spacetimes, in contrast to theories on topological or Riemannian manifolds, and for those the causal structure on spacetime is intrinsically linked to algebraic properties of quantum field theory via the Einstein causality axiom.

Let us provide a brief non-technical explanation of what are the higher structures in gauge theory that we are talking about. Recall that in a classical gauge theory we have two different kinds of data, namely gauge fields and gauge transformations between gauge fields. Hence, when thinking of the “space of fields” in a gauge theory, one should think of a kind of higher space that consists of points, which describe the gauge fields, and also arrows between these points, which describe the gauge transformations between gauge fields. More technically, this means that the space of gauge fields is not modeled by a set, but rather by a groupoid (i.e. a category with only invertible arrows), which is the prime example of a higher structure. Let us also mention that the smooth structure on such a higher space of fields can be encoded by using the concept of a stack, which is loosely speaking a smooth groupoid. See e.g. [19, 35, 50] for the technical background on ($\infty$-)stacks and [3] for a physical example given by the stack of non-Abelian Yang–Mills fields. It is important to emphasize that the stack of gauge fields is much richer than the traditional gauge orbit space, which is the quotient space obtained by identifying all gauge equivalent gauge fields. This is because the stack does not only indicate which of the gauge fields are gauge equivalent, but it also captures higher information by counting in how many ways they are gauge equivalent. There is the following striking analogy with the homotopy theory of topological spaces: This higher information can be thought of as “loops” in the stack of gauge fields and hence should be interpreted as the 1st homotopy group of the stack, while the gauge orbit space is only its 0th homotopy group. (The precise concept is that of sheaves of homotopy groups for stacks, cf. [19, 35].) A key observation, which justifies the necessity of taking into account such higher structures, is that they are crucial for obtaining a local-to-global (i.e. descent) property of the gauge theory, see e.g. [4] for a concrete demonstration by computations and also [17, 44] for more philosophical arguments.

These higher structures play an important role also in quantum gauge theories. To get some intuition on their appearance, let us adopt for the moment the point of view of deformation quantization. In this approach the observable algebras of a quantum field theory are obtained by a deformation of the algebras of functions on the classical spaces of fields. Because in a gauge theory we have higher spaces (i.e. stacks) of gauge fields, it is natural to expect that the corresponding observable algebras will be some kind of higher algebras. Let us notice that certain shadows of such higher algebraic structures are already well known in the physics literature, where they go under the name BRST/BV formalism, see e.g. [25, 26, 36] for the corresponding developments in algebraic quantum field theory. The quantum observable algebras in this framework are described by certain differential graded algebras, which one can interpret as a quantization of a higher function algebra (Chevalley–Eilenberg algebra) on the formal neighborhood of a point of the stack of gauge fields. In this construction, the higher structures encoded in the stack of gauge fields get translated to the higher homology groups of the differential graded algebras of observables. In particular, this means that it is an important characteristic feature of quantum gauge theories that their observables are described by higher algebras instead of ordinary gauge invariant observable algebras, which would provide an incomplete picture because they describe only the 0th homologies and neglect all higher structures. Unfortunately, even though the BRST/BV formalism is able to capture some of the higher structures of a quantum gauge theory, it is intrinsically perturbative because it considers only the formal neighborhood of a point of the stack of gauge fields. We propose in Sect. 4.3 of this paper a certain non-perturbative generalization of the Chevalley–Eilenberg algebra, i.e. the classical BRST formalism, which we will obtain by developing a concept of smooth normalized cochain algebras on stacks.

The overall aim of this paper is to develop a model-independent framework for algebraic quantum field theories with values in chain complexes. As we have explained in the paragraphs above, the generalization from ordinary algebras in vector spaces to higher algebras in chain complexes is motivated by the necessity to encode and describe the crucial higher structures of quantum gauge theories within the framework of algebraic quantum field theory. Defining chain complex-valued algebraic quantum field theories is relatively straightforward, and these have already appeared in previous works related to the BRST/BV formalism [25, 26, 36]. Concretely, given a category $\mathbf{C}$ of spacetimes, a chain complex-valued algebraic quantum field theory is a functor $\mathfrak {A}: \mathbf{C}\rightarrow \mathbf{dgAlg}(k)$ to the category of differential graded algebras (over a commutative ring k) that satisfies some physically motivated properties such as the Einstein causality axiom and the time-slice axiom. There is, however, the following subtle but essential point that has been mostly ignored in previous works: A common feature of all scenarios involving higher structures is that the correct way to compare two objects is not via isomorphisms, but via weak equivalences, which can be more general than isomorphisms. For example, the weak equivalences between groupoids are equivalences of their underlying categories, the weak equivalences between topological spaces are weak homotopy equivalences, and the weak equivalences between chain complexes are quasi-isomorphisms, i.e. maps between chain complexes that induce an isomorphism in homology. We would like to stress the direct practical significance of weak equivalences: The usual technique of adding auxiliary fields and performing a gauge fixing in the BRST/BV formalism [25, 26, 36] is the prime example of a weak equivalence between chain complexes of observables that is in general not an isomorphism.

Working with categories that are endowed with a notion of weak equivalences requires special care. The main reason is that ordinary categorical concepts and constructions, such as functors, will generically fail to preserve weak equivalences, which can lead to major issues because weakly equivalent objects in such situations are regarded as “being the same.” These problems can be solved systematically by using more sophisticated concepts describing category theory with a certain homotopy theoretical flavor, such as model category theory [20, 34, 37] or higher category theory [42, 43]. These powerful frameworks provide a consistent approach to describe categories with weak equivalences together with categorical constructions that are compatible with the weak equivalences.

The main aim of this paper is to show that there exists a canonical model structure on the category of chain complex-valued algebraic quantum field theories and to explain the immense relevance of such structure both from a conceptual and from a more practical point of view. The key ingredient for these developments is our recent result in [5] that algebraic quantum field theories admit a description in terms of algebras over a suitable colored operad.

Now let us describe in more detail the content of the present paper. In Sect. 2 we recall some basic definitions and results about the model category $\mathbf{Ch}(k)$ of chain complexes of k-modules, colored operads and their homotopy theory. This will be particularly useful to fix our notations and also to make our article sufficiently self-contained for readers who have only little experience with operads and/or homotopy theory. After these purely mathematical preliminaries, we focus in Sect. 3 on $\mathbf{Ch}(k)$-valued algebraic quantum field theories. Following [5], we shall adopt a very broad and flexible definition of algebraic quantum field theory, which encompasses various related concepts such as traditional algebraic quantum field theory on a fixed spacetime [31], locally covariant quantum field theory on all spacetimes [11, 21] and chiral conformal quantum field theory on the circle [38]. In our framework each of these specific scenarios corresponds to a choice of orthogonal category$\overline{\mathbf{C}} = (\mathbf{C},\perp )$, cf. Definition 3.1. To every orthogonal category $\overline{\mathbf{C}}$ we assign the category $\mathbf{QFT}(\overline{\mathbf{C}})$ of $\mathbf{Ch}(k)$-valued quantum field theories on $\overline{\mathbf{C}}$, which is a full subcategory of the functor category $\mathbf{dgAlg}(k)^\mathbf{C}$ consisting of all functors $\mathfrak {A}: \mathbf{C}\rightarrow \mathbf{dgAlg}(k)$ that satisfy the $\perp$-commutativity axiom, cf. Definition 3.3. Making use of the crucial result of [5] that $\mathbf{QFT}(\overline{\mathbf{C}})$ is the category of algebras over a suitable colored operad $\mathcal {O}_{\overline{\mathbf{C}}}$, we can endow the category $\mathbf{QFT}(\overline{\mathbf{C}})$ with a canonical model structure. The corresponding weak equivalences admit a simple description in terms of natural transformations $\zeta : \mathfrak {A}\Rightarrow \mathfrak {B}$ between theories $\mathfrak {A},\mathfrak {B}: \mathbf{C}\rightarrow \mathbf{dgAlg}(k)$ whose components $\zeta _c : \mathfrak {A}(c)\rightarrow \mathfrak {B}(c)$ are quasi-isomorphisms of chain complexes. In particular, our rigorous concept of weak equivalences coincides with the less formal notions used in practical constructions within the BRST/BV formalism, cf. [25, 26, 36]. As a non-trivial application of this model structure, we discuss Fredenhagen’s universal algebra construction [22,23,24] for $\mathbf{Ch}(k)$-valued quantum field theories from the perspective of derived functors (cf. [20, 37, 48]). We shall present simple toy-models which show that deriving the universal algebra construction is necessary to obtain a construction that preserves weak equivalences and that produces the correct global gauge theory observables on arbitrary spacetimes. The technical details are presented in “Appendix.”

In Sect. 4 we explore a natural homotopy theoretical generalization of algebraic quantum field theory. These considerations are inspired by the concept of homotopy algebras over operads, which describe homotopy-coherent algebraic structures, such as $A_\infty$-algebras and $E_\infty$-algebras. In general, the homotopy algebras over an operad $\mathcal {O}$ are defined as algebras over a $\Sigma$-cofibrant resolution $\mathcal {O}_\infty \rightarrow \mathcal {O}$ of the operad. In Sect. 4.1 we study $\Sigma$-cofibrant resolutions ${\mathcal {O}_{\overline{\mathbf{C}}}}_\infty \rightarrow \mathcal {O}_{\overline{\mathbf{C}}}$ of our algebraic quantum field theory operads and thereby introduce homotopy quantum field theories given by algebras over the resolved colored operad ${\mathcal {O}_{\overline{\mathbf{C}}}}_\infty$. As usual, there exist many different $\Sigma$-cofibrant resolutions ${\mathcal {O}_{\overline{\mathbf{C}}}}_\infty \rightarrow \mathcal {O}_{\overline{\mathbf{C}}}$, i.e. different variants of homotopy quantum field theories. We prove that each of these variants defines a Quillen equivalent model category of homotopy quantum field theories and also that the identity $\text {id}: \mathcal {O}_{\overline{\mathbf{C}}}\rightarrow \mathcal {O}_{\overline{\mathbf{C}}}$ is an instance of a $\Sigma$-cofibrant resolution. The latter should be interpreted as a strictification result for homotopy quantum field theories to strict algebraic quantum field theories in the sense of Sect. 3. Let us stress that this strictification result does not mean that homotopy quantum field theories are useless in practice, because strictifications are extremely hard to compute and hence it can be convenient to work with non-strict homotopy quantum field theories. Inspired by our examples of non-strict homotopy quantum field theories in Sects. 4.3 and 5, we describe in Sect. 4.2 a specific $\Sigma$-cofibrant resolution $\mathcal {O}_{\overline{\mathbf{C}}}~\otimes \,\mathcal {E}_\infty \rightarrow \mathcal {O}_{\overline{\mathbf{C}}}$ that is obtained by a component-wise tensor product of our quantum field theory operad with the Barratt–Eccles $E_\infty$-operad from [7]. The resulting homotopy quantum field theories satisfy a homotopy-coherent $\perp$-commutativity axiom. In particular, every $\mathcal {E}_\infty$-algebra valued functor $\mathfrak {A}: \mathbf{C}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$ defines a homotopy quantum field theory over this resolution. In Sect. 4.3 we construct examples of such functors by taking smooth normalized cochain algebras on $\infty$-stacks, which we interpret as a non-perturbative analog of the classical BRST formalism (Chevalley–Eilenberg algebra).

In Sect. 5 we provide another class of examples of homotopy quantum field theories over our resolution $\mathcal {O}_{\overline{\mathbf{C}}} \otimes \mathcal {E}_\infty \rightarrow \mathcal {O}_{\overline{\mathbf{C}}}$. Our construction is inspired by [2], and it is based on the following idea: We start with a category fibered in groupoids $\pi : \mathbf{D}\rightarrow \mathbf{C}$ over the category of spacetimes $\mathbf{C}$. The total category $\mathbf{D}$ should be interpreted as a category of spacetimes with background gauge fields, such as spin structures, bundles and connections. Then we take a strict $\mathbf{Ch}(k)$-valued quantum field theory on the total category $\mathbf{D}$ and consider its underlying functor $\mathfrak {A}: \mathbf{D}\rightarrow \mathbf{Ch}(k)$. Over each spacetime $c\in \mathbf{C}$, there exists a groupoid $\pi ^{-1}(c)$ of background fields and we would like to take homotopy invariants of the corresponding groupoid actions on the quantum field theory $\mathfrak {A}$. We formalize this construction in terms of a homotopy right Kan extension ${\text {hoRan}}_\pi$ along the projection functor $\pi :\mathbf{D}\rightarrow \mathbf{C}$. Our main result is Theorem 5.5, which proves that after a very explicit strictification of the category fibered in groupoids according to [35], the functor ${\text {hoRan}}_\pi \mathfrak {A}: \mathbf{C}\rightarrow \mathbf{Ch}(k)$ carries canonically the structure of a homotopy quantum field theory over our resolution. This construction does not only provide toy-models of homotopy quantum field theories, but also seems to be relevant for perturbative quantum gauge theories, cf. Example 5.1. From a mathematical perspective, the homotopy quantum field theory ${\text {hoRan}}_\pi \mathfrak {A}$ admits an interpretation in terms of fiber-wise groupoid cohomology on $\pi :\mathbf{D}\rightarrow \mathbf{C}$ with coefficients in the strict quantum field theory $\mathfrak {A}$, cf. Remark 5.6.

2 Preliminaries and notations

2.1 Chain complexes

Let k be a commutative and unital ring. Throughout this paper we assume that the ring of rational numbers $\mathbb {Q}$ is a subring of k, i.e. $k\supseteq \mathbb {Q}$. This will considerably simplify our homotopy theoretical considerations, see [32, 33] and the subsections below for details. Notice that this assumption is satisfied in applications to quantum field theory, where k will be either the field of complex numbers $\mathbb {C}$ or formal power series (in Planck’s constant $\hbar$ and the coupling constants) in $\mathbb {C}$ if one is interested in perturbative theories.

We denote by $\mathbf{Ch}(k)$ the category of (possibly unbounded) chain complexes ofk-modules. Recall that a chain complex is a family of k-modules $\{V_n\,:\, n\in \mathbb {Z}\}$ together with a differential, i.e. a family of k-linear maps $\{ \text {d}: V_n\rightarrow V_{n-1}\,:\, n\in \mathbb {Z}\}$ such that $\text {d}^2=0$. We often denote chain complexes simply by symbols like $V,W,Z \in \mathbf{Ch}(k)$ and use the same letter $\text {d}$ to denote various differentials. A chain complex morphism $f : V\rightarrow W$ is a family of k-linear maps $\{f : V_n\rightarrow W_n \,:\, n\in \mathbb {Z}\}$ that is compatible with the differentials, i.e. $\text {d}\, f = f\, \text {d}$.

The category $\mathbf{Ch}(k)$ carries the following standard closed symmetric monoidal structure: The tensor product $V\otimes W$ of two chain complexes is defined as usual by

(2.1)

for all $n\in \mathbb {Z}$, together with the differential $\text {d}(v\otimes w) {:}{=}\,\text {d}v \otimes w + (-1)^{m} \, v\otimes \text {d}w$, for all $v\in V_m$ and $w\in W_{n-m}$. The monoidal unit is $k\in \mathbf{Ch}(k)$, which we regard as a chain complex concentrated in degree 0 with trivial differential $\text {d}=0$. The symmetric braiding $\tau : V\otimes W\rightarrow W\otimes V$ is defined by the usual sign rule $\tau (v\otimes w) {:}{=}\, (-1)^{ml} \, w\otimes v$, for all $v\in V_m$ and $w\in W_l$. The internal hom object [V, W] between two chain complexes is defined by

$$\begin{aligned} {[}V,W{]}_n \,{:}{=}\, \prod _{m\in \mathbb {Z}}\text {hom}_k^{}(V_m , W_{n+m}), \end{aligned}$$

(2.2)

for all $n\in \mathbb {Z}$, where $\text {hom}_k^{}$ denotes the internal hom for k-modules (that is the k-module of k-linear maps between k-modules), together with the differential $\text {d}(L) {:}{=}\,\text {d}\, L - (-1)^{n}\, L\, \text {d}$, for all $(L: V_m\rightarrow W_{n+m}) \in \text {hom}_k^{}(V_m,W_{n+m})$.

Let us further recall that a $\mathbf{Ch}(k)$-morphism $f : V\rightarrow W$ is called a quasi-isomorphism if it induces an isomorphism in homology, i.e. $H_n(f) : H_n(V) \rightarrow H_n(W)$ is an isomorphism of k-modules for each $n\in \mathbb {Z}$. The homology k-modules are defined as usual by the quotients $H_n(V) {:}{=}\, \text {Ker}(\text {d}: V_n\rightarrow V_{n-1})/\text {Im}(\text {d}: V_{n+1}\rightarrow V_n)$, for all $n\in \mathbb {Z}$. This notion of quasi-isomorphism in $\mathbf{Ch}(k)$ is part of the rich and powerful structure of a (symmetric monoidal) model category. For the definition of a model category we refer to e.g. [20, 34, 37]. For an informal approach to our paper, however, it will be sufficient to keep in mind the following core principle: A model category is a category together with three distinguished classes of morphisms—called weak equivalences, fibrations and cofibrations—that satisfy a list of axioms. These axioms are designed in such a way that weak equivalences behave (with some technical care) as good as isomorphisms, e.g. they are preserved by (derived) functors. Hence, by using techniques from model category theory, we can consistently consider two objects as being the same not only when they are isomorphic, but also when they are weakly equivalent. Such ideas and techniques are crucial for our development of a consistent framework for chain complex-valued algebraic quantum field theories in this paper. The following result is proven in [37, Sections 2.3 and 4.2].

Theorem 2.1

Define a morphism $f:V\rightarrow W$ in $\mathbf{Ch}(k)$ to be

• (i) a weak equivalence if it is a quasi-isomorphism, i.e. it induces an isomorphism in homology;

• (ii) a fibration if it is surjective in each degree $f:V_n\rightarrow W_n$;

• (iii) a cofibration if it has the left lifting property (cf. Remark 2.2) with respect to all acyclic fibrations (i.e. all morphisms in $\mathbf{Ch}(k)$ that are both a fibration and a weak equivalence).

With these choices $\mathbf{Ch}(k)$ becomes a symmetric monoidal model category. Moreover, the monoidal unit $k\in \mathbf{Ch}(k)$ is a cofibrant object, i.e. the unique morphism $0 \rightarrow k$ from the zero chain complex is a cofibration.

Remark 2.2

Let us recall that a morphism $f : V\rightarrow W$ is said to have the left lifting property with respect to a morphism $f^\prime : V^\prime \rightarrow W^\prime$ if all commutative squares of the form

admit a lift $f^{\prime \prime }$, i.e. the two triangles commute. $\vartriangle$

2.2 Homotopy theory of colored operads

Let us start with a very brief review of some relevant aspects of the theory of colored operads in a general bicomplete closed symmetric monoidal category $\mathbf{M}$. (We will later take $\mathbf{M}= \mathbf{Ch}(k)$, but the definitions below are easily stated for general $\mathbf{M}$.) We refer to [9, 55, 56] and also to our previous paper [5] for a more extensive introduction. Let $\mathfrak {C}\in \mathbf{Set}$ be a non-empty set. We refer to elements in $\mathfrak {C}$ as colors. A $\mathfrak {C}$-colored operad$\mathcal {O}$ with values in $\mathbf{M}$ is given by the following data:

• (i) for each $n\ge 0$ and $n+1$-tuple of colors $(\underline{c},t) {:}{=}\, ((c_1,\dots ,c_n),t)\in \mathfrak {C}^{n+1}$, an object

  $$\begin{aligned} \mathcal {O}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big )\in \mathbf{M}; \end{aligned}$$

  (2.4)

• (ii) for each color $c\in \mathfrak {C}$, an $\mathbf{M}$-morphism (called operadic unit) from the monoidal unit

  $$\begin{aligned} \mathbb {1}: I \longrightarrow \mathcal {O}\big (\begin{array}{c} c\\ c \end{array}\big ); \end{aligned}$$

  (2.5)

• (iii) for each $n>0$, $n+1$-tuple of colors $(\underline{a},t)\in \mathfrak {C}^{n+1}$ and $k_i+1$-tuples of colors $(\underline{b}_i,a_i)\in \mathfrak {C}^{k_i +1}$, for $i=1,\dots ,n$, an $\mathbf{M}$-morphism (called operadic composition)

  $$\begin{aligned} \gamma : \mathcal {O}\big (\begin{array}{c} t\\ \underline{a} \end{array}\big ) \otimes \bigotimes _{i=1}^n \mathcal {O}\big (\begin{array}{c} a_i\\ \underline{b}_i \end{array}\big ) \longrightarrow \mathcal {O}\big (\begin{array}{c} t\\ \underline{b} \end{array}\big ), \end{aligned}$$

  (2.6)

  where $\underline{b}\,~{:=}\, (\underline{b}_1, \dots , \underline{b}_n)$ denotes concatenation of tuples;

• (iv) for each $n\ge 0$, $n+1$-tuple of colors $(\underline{c},t) \in \mathfrak {C}^{n+1}$ and permutation $\sigma \in \Sigma _n$, an $\mathbf{M}$-morphism

  $$\begin{aligned} \mathcal {O}(\sigma ) : \mathcal {O}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big ) \longrightarrow \mathcal {O}\big (\begin{array}{c} t\\ \underline{c}\sigma \end{array}\big ), \end{aligned}$$

  (2.7)

  where $\underline{c}\sigma = (c_{\sigma (1)},\dots ,c_{\sigma (n)})$ is given by right permutation.

These four data are required to satisfy compatibility conditions: (1) The morphisms in (iv) define right $\Sigma _n$-actions, i.e. $\mathcal {O}(\sigma ^\prime ) \,\mathcal {O}(\sigma ) = \mathcal {O}(\sigma \sigma ^\prime )$. (2) The operadic compositions in (iii) are equivariant under these actions of the permutation groups. (3) The operadic compositions are associative and also unital with respect to the operadic units in (ii). (See e.g. [55, Definition 11.2.1] for the details.) The axioms for $\mathfrak {C}$-colored operads admit the following intuitive interpretation: $\mathcal {O}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big )$ in (i) is interpreted as the object of n-ary operations with input profile $\underline{c}= (c_1,\dots ,c_n)$ and target t. The morphisms in (iv) allow us to permute the input colors and the operadic compositions in (iii) allow us to compose such operations. The operadic units in (ii) should be regarded as the identity operations for each color $c\in \mathfrak {C}$.

For every non-empty set of colors $\mathfrak {C}\in \mathbf{Set}$, the $\mathfrak {C}$-colored operads with values in $\mathbf{M}$ form a category, which we denote by $\mathbf{Op}_\mathfrak {C}(\mathbf{M})$. A morphism $\phi : \mathcal {O}\rightarrow \mathcal {P}$ between two $\mathfrak {C}$-colored operads is a collection of $\mathbf{M}$-morphisms

$$\begin{aligned} \phi : \mathcal {O}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big ) \longrightarrow \mathcal {P}\big (\begin{array}{c} t \\ \underline{c} \end{array}\big ), \end{aligned}$$

(2.8)

for all $n\ge 0$ and $(\underline{c},t)\in \mathfrak {C}^{n+1}$, that is compatible with the permutation actions $\phi \, \mathcal {O}(\sigma ) = \mathcal {P}(\sigma )\,\phi$, the operadic compositions $\phi \,\gamma ^\mathcal {O}=\gamma ^\mathcal {P}\,\big (\phi \otimes \bigotimes _{i=1}^n \phi \big )$ and the operadic units $\phi \,\mathbb {1}^\mathcal {O}= \mathbb {1}^\mathcal {P}$.

Now let us focus on the case of chain complexes $\mathbf{M}= \mathbf{Ch}(k)$. Since by Theorem 2.1 we know that $\mathbf{Ch}(k)$ is a symmetric monoidal model category, it is natural to ask whether the category $\mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$ of $\mathfrak {C}$-colored operads with values in chain complexes carries an induced model structure. In the most general scenario, i.e. colored operads with values in any symmetric monoidal model category, this would not be the case. However, there has been a large amount of research on establishing criteria which ensure that the category of operads (as well as the category of algebras over an operad, see Sect. 2.3) carries a canonical model structure induced by the free-forget adjunction, cf. [8, 9, 14, 32, 33, 47, 53]. The case of interest for us, i.e. chain complexes $\mathbf{Ch}(k)$ of k-modules with $k\supseteq \mathbb {Q}$ (this technical condition is important here), has been understood by Hinich [32, 33], who has proven the following result.

Theorem 2.3

Let $\mathfrak {C}\in \mathbf{Set}$ be any non-empty set of colors. Define a morphism $\phi : \mathcal {O}\rightarrow \mathcal {P}$ in $\mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$ to be

• (i) a weak equivalence if each component $\phi : \mathcal {O}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big ) \rightarrow \mathcal {P}\big (\begin{array}{c} t \\ \underline{c} \end{array}\big )$ is a weak equivalence in $\mathbf{Ch}(k)$, i.e. a quasi-isomorphism;

• (ii) a fibration if each component $\phi : \mathcal {O}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big ) \rightarrow \mathcal {P}\big (\begin{array}{c} t \\ \underline{c} \end{array}\big )$ is a fibration in $\mathbf{Ch}(k)$, i.e. degree-wise surjective;

• (iii) a cofibration if it has the left lifting property with respect to all acyclic fibrations.

If $k\supseteq \mathbb {Q}$, these choices endow $\mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$ with the structure of a model category.

2.3 Homotopy theory of algebras over colored operads

An algebra over a colored operad $\mathcal {O}$ should be interpreted as a concrete realization/representation of the abstract operations encoded in $\mathcal {O}$. Explicitly, an algebraAover a$\mathfrak {C}$-colored operad$\mathcal {O}\in \mathbf{Op}_\mathfrak {C}(\mathbf{M})$ with values in $\mathbf{M}$ (also called an $\mathcal {O}$-algebra) is given by the following data:

• (i) for each color $c\in \mathfrak {C}$, an object

  $$\begin{aligned} A_c \in \mathbf{M}; \end{aligned}$$

  (2.9)

• (ii) for each $n\ge 0$ and $n+1$-tuple of colors $(\underline{c},t) \in \mathfrak {C}^{n+1}$, an $\mathbf{M}$-morphism (called $\mathcal {O}$-action)

  $$\begin{aligned} \alpha : \mathcal {O}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big ) \otimes A_{\underline{c}} \longrightarrow A_t, \end{aligned}$$

  (2.10)

  where $A_{\underline{c}} {:}{=}\, \bigotimes _{i=1}^n A_{c_i}$ with the usual convention that $A_{\emptyset }=I$ for the empty tuple $\emptyset \in \mathfrak {C}^0$.

These data are required to satisfy the following compatibility conditions: (1) The $\mathcal {O}$-action is equivariant under permutations, i.e. the diagrams

commute. (2) The $\mathcal {O}$-action is compatible with the operadic composition $\gamma$, i.e. the diagrams

commute. (3) The $\mathcal {O}$-action of the operadic unit $\mathbb {1}$ is trivial, i.e. the diagrams

commute. The $\mathcal {O}$-algebras form a category, which we denote by $\mathbf{Alg}(\mathcal {O})$. Concretely, a morphism $\kappa : A \rightarrow B$ between two $\mathcal {O}$-algebras is a collection of $\mathbf{M}$-morphisms

$$\begin{aligned} \kappa : A_c \longrightarrow B_c, \end{aligned}$$

(2.14)

for all colors $c\in \mathfrak {C}$, that is compatible with the $\mathcal {O}$-actions, i.e. $\kappa \, \alpha ^A = \alpha ^B\,\big (\text {id}\otimes \bigotimes _{i=1}^n\kappa \big )$.

Now let us focus on the case of chain complexes $\mathbf{M}= \mathbf{Ch}(k)$. Similarly to the scenario in Sect. 2.2, it is in general not true that the category of $\mathcal {O}$-algebras for any colored operad $\mathcal {O}$ with values in any symmetric monoidal model category carries a canonical model structure induced by the free-forget adjunction. If it does, the colored operad $\mathcal {O}$ is called admissible in the standard terminology of [8, 9, 14, 32, 33, 47, 53]. The case of interest for us, i.e. chain complexes $\mathbf{Ch}(k)$ of k-modules with $k\supseteq \mathbb {Q}$ (this technical condition is again important), has been understood by Hinich [32, 33], who has proven the following result.

Theorem 2.4

Let $\mathfrak {C}\in \mathbf{Set}$ be any non-empty set of colors and $\mathcal {O}\in \mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$ any $\mathfrak {C}$-colored operad with values in chain complexes. Define a morphism $\kappa : A \rightarrow B$ in $\mathbf{Alg}(\mathcal {O})$ to be

• (i) a weak equivalence if each component $\kappa : A_c \rightarrow B_c$ is a weak equivalence in $\mathbf{Ch}(k)$, i.e. a quasi-isomorphism;

• (ii) a fibration if each component $\kappa : A_c \rightarrow B_c$ is a fibration in $\mathbf{Ch}(k)$, i.e. degree-wise surjective;

• (iii) a cofibration if it has the left lifting property with respect to all acyclic fibrations.

If $k\supseteq \mathbb {Q}$, these choices endow $\mathbf{Alg}(\mathcal {O})$ with the structure of a model category. In other words, each $\mathfrak {C}$-colored operad $\mathcal {O}\in \mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$ is admissible when $k\supseteq \mathbb {Q}$.

Before we can conclude this section, we still have to discuss the compatibility (in a sense to be made precise below) of these model structures under a change of operad, for example, by an $\mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$-morphism. For our paper we shall need a more flexible variant of changing the operad which does not necessarily preserve the set of colors. This is captured by the following definition.

Definition 2.5

The category$\mathbf{Op}(\mathbf{Ch}(k))$of operads with varying colors is defined as follows: An object is a pair $(\mathfrak {C},\mathcal {O})$ consisting of a non-empty set $\mathfrak {C}\in \mathbf{Set}$ and a $\mathfrak {C}$-colored operad $\mathcal {O}\in \mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$. A morphism is a pair $(f,\phi ) : (\mathfrak {C},\mathcal {O})\rightarrow (\mathfrak {D},\mathcal {P})$ consisting of a map of sets $f : \mathfrak {C}\rightarrow \mathfrak {D}$ and an $\mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$-morphism $\phi : \mathcal {O}\rightarrow f^*(\mathcal {P})$ to the pullback of $\mathcal {P}$ along f. The latter is defined by the components $f^*(\mathcal {P})\big (\begin{array}{c} t\\ \underline{c} \end{array}\big ) {:}{=}\, \mathcal {P}\big (\begin{array}{c} f(t) \\ f(\underline{c}) \end{array}\big )$ and the obvious restriction of the operad structure on $\mathcal {P}$.

For every $\mathbf{Op}(\mathbf{Ch}(k))$-morphism $(f,\phi ) : (\mathfrak {C},\mathcal {O})\rightarrow (\mathfrak {D},\mathcal {P})$, we can define a pullback functor $(f,\phi )^*: \mathbf{Alg}(\mathcal {P})\rightarrow \mathbf{Alg}(\mathcal {O})$ between the categories of algebras. Concretely, given any $\mathcal {P}$-algebra A, i.e. a collection of chain complexes $A_d \in \mathbf{Ch}(k)$, for all $d\in \mathfrak {D}$, equipped with a $\mathcal {P}$-action $\alpha : \mathcal {P}\big (\begin{array}{c} s \\ \underline{d} \end{array}\big )\otimes A_{\underline{d}} \rightarrow A_s$, we define the $\mathcal {O}$-algebra $(f,\phi )^*A$ by the collection of chain complexes $((f,\phi )^*A)_c {:}{=}\, A_{f(c)}$, for all $c\in \mathfrak {C}$, equipped with the $\mathcal {O}$-action

It is well known (see e.g. [5]) that the pullback functor admits a left adjoint, i.e. we have an adjunction

for every $\mathbf{Op}(\mathbf{Ch}(k))$-morphism $(f,\phi ) : (\mathfrak {C},\mathcal {O})\rightarrow (\mathfrak {D},\mathcal {P})$. The left adjoint $(f,\phi )_!$ is often called operadic left Kan extension. It is easy to prove that these adjunctions are compatible (in the sense of Quillen adjunctions) with the model structures given in Theorem 2.4.

Proposition 2.6

For every $\mathbf{Op}(\mathbf{Ch}(k))$-morphism $(f,\phi ) : (\mathfrak {C},\mathcal {O})\rightarrow (\mathfrak {D},\mathcal {P})$, the adjunction (2.16) is a Quillen adjunction, i.e. the right adjoint functor $(f,\phi )^*$ preserves fibrations and acyclic fibrations. Furthermore, $(f,\phi )^*$ preserves also weak equivalences.

Proof

Recall that an $\mathbf{Alg}(\mathcal {P})$-morphism $\kappa : A\rightarrow B$ is a collection of $\mathbf{Ch}(k)$-morphisms $\kappa : A_d\rightarrow B_d$, for all $d\in \mathfrak {D}$, that is compatible with the $\mathcal {P}$-actions. Applying the pullback functor defines an $\mathbf{Alg}(\mathcal {O})$-morphism $(f,\phi )^*\kappa : (f,\phi )^*A\rightarrow (f,\phi )^*B$, whose underlying collection of $\mathbf{Ch}(k)$-morphisms is $\kappa : A_{f(c)}\rightarrow B_{f(c)}$, for all $c\in \mathfrak {C}$. Because fibrations and weak equivalences are defined component-wise in Theorem 2.4, and hence so are acyclic fibrations, it follows that the pullback functor preserves these classes of morphisms. $\square$

It remains to clarify under which conditions a weak equivalence between colored operads induces a Quillen equivalence between the corresponding model categories of algebras, which is the appropriate notion of equivalence between model categories [20, 37]. For this we shall consider a natural generalization of the notion of weak equivalence between $\mathfrak {C}$-colored operads established in Theorem 2.3 to the case of operads with varying colors, cf. [33, Definition 2.4.2]. In the following definition we denote by $\mathcal {O}_1$ the underlying $\mathbf{Ch}(k)$-enriched category of a $\mathfrak {C}$-colored operad $\mathcal {O}\in \mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$. Explicitly, the objects in this category are the colors $c\in \mathfrak {C}$, the chain complex of morphisms from c to t is $\mathcal {O}\big (\begin{array}{c} t \\ c \end{array}\big )\in \mathbf{Ch}(k)$, the composition of morphisms is via the operadic composition, and the identity morphisms are given by the operadic unit. We further denote by $H_0(\mathcal {O}_1)$ the (ordinary) category which is obtained by taking the 0th homology of all chain complexes of morphisms.

Definition 2.7

A morphism $(f,\phi ) : (\mathfrak {C},\mathcal {O})\rightarrow (\mathfrak {D},\mathcal {P})$ in the category of operads with varying colors $\mathbf{Op}(\mathbf{Ch}(k))$ is called a weak equivalence if

• (1) each component $\phi : \mathcal {O}\big (\begin{array}{c} t \\ \underline{c} \end{array}\big ) \rightarrow \mathcal {P}\big (\begin{array}{c} f(t) \\ f(\underline{c}) \end{array}\big )$ is a weak equivalence in $\mathbf{Ch}(k)$, i.e. a quasi-isomorphism;

• (2) the induced functor $H_0(f,\phi ) : H_0(\mathcal {O}_1)\rightarrow H_0(\mathcal {P}_1)$ is an equivalence of categories.

Remark 2.8

Notice that a morphism of $\mathfrak {C}$-colored operads $\phi : \mathcal {O}\rightarrow \mathcal {P}$ can be equivalently regarded as an $\mathbf{Op}(\mathbf{Ch}(k))$-morphism $(\text {id}_\mathfrak {C}, \phi ) : (\mathfrak {C},\mathcal {O})\rightarrow (\mathfrak {C},\mathcal {P})$. In this special case, the first condition in Definition 2.7 implies the second one. This means that the concept of weak equivalence introduced in Definition 2.7 agrees with the previous one from Theorem 2.3 for morphisms between operads with the same underlying set of colors.$\vartriangle$

An important class of operads for which such a weak equivalence induces a Quillen equivalence between their model categories of algebras is given by $\Sigma$-cofibrant colored operads, cf. [33, Definition 2.4.3]. Let us briefly recall this definition: Given any $\mathfrak {C}$-colored operad $\mathcal {O}\in \mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$, note that each of its components $\mathcal {O}\big (\begin{array}{c} t \\ \underline{c} \end{array}\big ) \in \mathbf{Ch}(k)$ carries a canonical right action of the group of automorphisms of the profile $\underline{c} = (c_1,\dots ,c_n)$. Concretely, this is given by restricting (2.7) to the subgroup $\Sigma _{\underline{c}} \subseteq \Sigma _n$ of those permutations $\sigma$ that preserve the profile, i.e. $\underline{c}\sigma = \underline{c}$. As a consequence, one may regard $\mathcal {O}\big (\begin{array}{c} t \\ \underline{c} \end{array}\big )$ as an object in the category $\mathbf{Ch}(k)^{\Sigma _{\underline{c}}}$ of chain complexes with right $\Sigma _{\underline{c}}$-action. (The morphisms in $\mathbf{Ch}(k)^{\Sigma _{\underline{c}}}$ are $\Sigma _{\underline{c}}$-equivariant chain complex morphisms.) We note that the category $\mathbf{Ch}(k)^{\Sigma _{\underline{c}}}$ carries a canonical model structure in which a morphism is a weak equivalence (respectively, a fibration) if, when forgetting the group actions, the underlying chain complex morphism is a weak equivalence (respectively, a fibration) in $\mathbf{Ch}(k)$. Cofibrations are determined by the left lifting property with respect to all acyclic fibrations.

Definition 2.9

A $\mathfrak {C}$-colored operad $\mathcal {O}\in \mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$ is called $\Sigma$-cofibrant if each component $\mathcal {O}\big (\begin{array}{c} t\\ \underline{c} \end{array} \big )$ is a cofibrant object in the model category $\mathbf{Ch}(k)^{\Sigma _{\underline{c}}}$.

The following result has been proven by Hinich [32, 33].

Theorem 2.10

Consider a weak equivalence $(f,\phi ) : (\mathfrak {C},\mathcal {O})\rightarrow (\mathfrak {D},\mathcal {P})$ in the sense of Definition 2.7. If both $\mathcal {O}$ and $\mathcal {P}$ are $\Sigma$-cofibrant, then the Quillen adjunction in (2.16) is a Quillen equivalence.

In our case of interest $k\supseteq \mathbb {Q}$, we have the following straightforward result which implies that every colored operad whose components are cofibrant chain complexes is $\Sigma$-cofibrant.

Proposition 2.11

Let $k\supseteq \mathbb {Q}$ and G be any finite group. Then every object $X\in \mathbf{Ch}(k)^G$ whose underlying chain complex is a cofibrant object in $\mathbf{Ch}(k)$ is a cofibrant object in $\mathbf{Ch}(k)^G$. As a consequence, every $\mathfrak {C}$-colored operad $\mathcal {O}\in \mathbf{Op}_\mathfrak {C}(\mathbf{Ch}(k))$ whose components $\mathcal {O}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big )$ are cofibrant objects in $\mathbf{Ch}(k)$ is $\Sigma$-cofibrant.

Proof

By definition of cofibrations in $\mathbf{Ch}(k)^G$, we have to prove that there exists a lifting

in the category $\mathbf{Ch}(k)^G$, for all acyclic fibrations $p : Y\rightarrow Z$ and all morphisms $h : X\rightarrow Z$ in $\mathbf{Ch}(k)^G$. Forgetting the right G-actions in this diagram, we obtain a lifting $\widetilde{l} : X\rightarrow Y$ in the category of chain complexes because X is by hypothesis a cofibrant object in $\mathbf{Ch}(k)$. However, such $\widetilde{l}$ is not necessarily G-equivariant. Using the crucial property that $k\supseteq \mathbb {Q}$ contains the rationals, we can always define a G-equivariant chain complex morphism by group averaging

$$\begin{aligned} l : X\longrightarrow Y~,~~x\longmapsto l(x) {:}{=}\, \frac{1}{\vert G\vert } \sum _{g\in G} \big (\widetilde{l}(x \cdot g) \big )\cdot g^{-1}, \end{aligned}$$

(2.18)

where we denote right G-actions by $\cdot$ and $\vert G\vert$ is the number of elements in G. It is easy to confirm that this defines a lifting in (2.17). $\square$

3 Strict algebraic quantum field theories in chain complexes

3.1 Orthogonal categories and quantum field theories

Given any small category $\mathbf{C}$, we denote by $\text {Mor}\,\mathbf{C}\, {}_\text {t}^{}\!\times \!{}^{}_\text {t} \,\text {Mor}\,\mathbf{C}$ the set of pairs of $\mathbf{C}$-morphisms whose targets coincide. An element in this set is of the form $(f_1 : c_1 \rightarrow c, f_2 : c_2\rightarrow c)$. The following concept of orthogonal categories has been introduced in [5].

Definition 3.1

• a) An orthogonal category is a pair $\overline{\mathbf{C}} = (\mathbf{C},\perp )$ consisting of a small category $\mathbf{C}$ and a subset ${\perp } \subseteq \text {Mor}\,\mathbf{C}\, {}_\text {t}^{}\!\times \!{}^{}_\text {t} \,\text {Mor}\,\mathbf{C}$ (called orthogonality relation) satisfying the following properties:

  • (1) Symmetry: If $(f_1,f_2)\in {\perp }$, then $(f_2,f_1)\in {\perp }$.

  • (2) Stability under post-composition: If $(f_1,f_2)\in {\perp }$, then $(g\,f_1, g\, f_2)\in {\perp }$, for all composable $\mathbf{C}$-morphisms g.

  • (3) Stability under pre-composition: If $(f_1,f_2)\in {\perp }$, then $(f_1\,h_1, f_2\,h_2)\in {\perp }$, for all composable $\mathbf{C}$-morphisms $h_1$ and $h_2$.

  Elements $(f_1,f_2)\in {\perp }$ are called orthogonal pairs, and they are also denoted by $f_1\perp f_2$.

• b) Given two orthogonal categories $\overline{\mathbf{C}}=(\mathbf{C},\perp _\mathbf{C})$ and $\overline{\mathbf{D}} = (\mathbf{D},\perp _\mathbf{D})$, an orthogonal functor$F : \overline{\mathbf{C}}\rightarrow \overline{\mathbf{D}}$ is a functor $F : \mathbf{C}\rightarrow \mathbf{D}$ that preserves the orthogonality relations, i.e. such that $f_1\perp _\mathbf{C}f_2$ implies $F(f_1) \perp _\mathbf{D}F(f_2)$.

• c) We denote by $\mathbf{OrthCat}$ the category whose objects are orthogonal categories and whose morphisms are orthogonal functors.

Now we shall present examples of orthogonal categories that are relevant for locally covariant quantum field theory [11, 21]. Further examples can be found in [5], including orthogonal categories that are relevant for ordinary algebraic quantum field theories on a fixed spacetime and chiral conformal quantum field theories.

Example 3.2

Let $\mathbf{Loc}$ be any small category that is equivalent to the usual category of oriented, time-oriented and globally hyperbolic Lorentzian manifolds of a fixed dimension $m \ge 2$, see e.g. [11, 21]. We often follow the standard terminology and use the word spacetimes for objects $M\in \mathbf{Loc}$ and spacetime embeddings for $\mathbf{Loc}$-morphisms $f : M\rightarrow M^\prime$. Let us equip $\mathbf{Loc}$ with the following orthogonality relation: $(f_1 : M_1\rightarrow M)\perp _\mathbf{Loc}(f_2 : M_2\rightarrow M)$ if and only if the images $f_1(M_1)$ and $f_2(M_2)$ are causally disjoint subsets in M. Then $\overline{\mathbf{Loc}} {:}{=}\, (\mathbf{Loc},\perp _\mathbf{Loc}) \in \mathbf{OrthCat}$ is an orthogonal category.

Let be the full subcategory of all oriented, time-oriented and globally hyperbolic Lorentzian manifolds whose underlying manifold is diffeomorphic to $\mathbb {R}^m$. With a slight abuse of notation, we shall refer to objects as diamond spacetimes. The orthogonality relation on $\overline{\mathbf{Loc}}$ restricts to an orthogonality relation on . Explicitly, if and only if $(f_1 : M_1\rightarrow M)\perp _\mathbf{Loc}(f_2 : M_2\rightarrow M)$. The embedding functor defines an orthogonal functor . $\bigtriangledown$

Let us denote by $\mathbf{dgAlg}(k)$ the category of (possibly unbounded) differential graded algebras over a commutative and unital ring $k\supseteq \mathbb {Q}$, i.e. $\mathbf{dgAlg}(k)$ is the category of associative and unital algebras in the symmetric monoidal category $\mathbf{Ch}(k)$ of chain complexes of k-modules, cf. Sect. 2.1. Given any small category $\mathbf{C}$, we consider the functor category $\mathbf{dgAlg}(k)^{\mathbf{C}}$ whose objects are covariant functors $\mathfrak {A}: \mathbf{C}\rightarrow \mathbf{dgAlg}(k)$ and whose morphisms are natural transformations $\zeta : \mathfrak {A}\Rightarrow \mathfrak {B}$ between such functors $\mathfrak {A},\mathfrak {B}: \mathbf{C}\rightarrow \mathbf{dgAlg}(k)$. Algebraic quantum field theories with values in chain complexes may be formalized by the following general definition.

Definition 3.3

Let $\overline{\mathbf{C}} = (\mathbf{C},\perp )$ be an orthogonal category.

• a) A functor $\mathfrak {A}: \mathbf{C}\rightarrow \mathbf{dgAlg}(k)$ is called $\perp$-commutative if for all $(f_1: c_1\rightarrow c)\perp (f_2:c_2\rightarrow c)$ the diagram

  

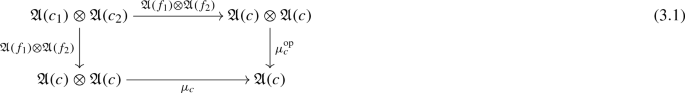
  in $\mathbf{Ch}(k)$ commutes. Here $\mu _c$ (respectively, $\mu _c^\text {op}{:}{=}\,\mu _c\,\tau$) denotes the (opposite) multiplication on the differential graded algebra $\mathfrak {A}(c)\in \mathbf{dgAlg}(k)$.

• b) The category of $\mathbf{Ch}(k)$-valued quantum field theories on$\overline{\mathbf{C}}$ is defined as the full subcategory

  $$\begin{aligned} \mathbf{QFT}(\overline{\mathbf{C}}) \,\subseteq \, \mathbf{dgAlg}(k)^\mathbf{C}\end{aligned}$$

  (3.2)

  whose objects are all $\perp$-commutative functors.

Example 3.4

For the orthogonal category $\overline{\mathbf{Loc}}$ defined in Example 3.2, a functor $\mathfrak {A}: \mathbf{Loc}\rightarrow \mathbf{dgAlg}(k)$ is $\perp$-commutative precisely when the restricted graded commutators

$$\begin{aligned} \big [\mathfrak {A}(f_1)(-), \mathfrak {A}(f_2)(-)\big ] \,:\, \mathfrak {A}(M_1)\otimes \mathfrak {A}(M_2)~\longrightarrow ~ \mathfrak {A}(M) \end{aligned}$$

(3.3)

are zero, for all pairs of spacetime embeddings $f_1 : M_1\rightarrow M$ and $f_2 : M_2\rightarrow M$ whose images are causally disjoint. Hence, the $\perp$-commutativity property of the functor $\mathfrak {A}$ is precisely the (graded) Einstein causality axiom of locally covariant quantum field theory. The category $\mathbf{QFT}(\overline{\mathbf{Loc}})$ from Definition 3.3 is thus the category of $\mathbf{Ch}(k)$-valued off-shell locally covariant quantum field theories, i.e. functors $\mathfrak {A}: \mathbf{Loc}\rightarrow \mathbf{dgAlg}(k)$ that satisfy the Einstein causality axiom, but not necessarily the time-slice axiom. If we would like to focus only on those theories which satisfy time-slice, we can localize the orthogonal category $\overline{\mathbf{Loc}}$ at the set of Cauchy morphism W, which results in another orthogonal category together with an orthogonal localization functor , see [5]. The category then describes $\mathbf{Ch}(k)$-valued on-shell locally covariant quantum field theories, i.e. functors $\mathfrak {A}: \mathbf{Loc}\rightarrow \mathbf{dgAlg}(k)$ that satisfy both the Einstein causality axiom and the time-slice axiom. $\bigtriangledown$

Example 3.5

Constructions of perturbative quantum gauge theories via the BRST/BV formalism produce $\perp$-commutative functors $\mathfrak {A}: \mathbf{Loc}\rightarrow \mathbf{dgAlg}(k)$, where $k = \mathbb {C}[[\hbar ,g]]$ is the ring of formal power series in Planck’s constant $\hbar$ and the coupling constant g, see e.g. [25, 26, 36]. Here unbounded chain complexes are crucial to support both the ghost fields (having negative degree in our homological degree convention) and the anti-fields (having positive degree).$\bigtriangledown$

3.2 The underlying operads

We have shown in [5] that the category $\mathbf{QFT}(\overline{\mathbf{C}})$ of quantum field theories on an orthogonal category $\overline{\mathbf{C}}$ (cf. Definition 3.3) admits a description in terms of the category of algebras over a suitable colored operad $\mathcal {O}_{\overline{\mathbf{C}}}$. Before we can provide a definition of this operad, we have to introduce some notation. For a small category $\mathbf{C}$, we denote by $\mathbf{C}_0$ its set of objects. Given any tuple $(\underline{c},t) = ((c_1,\dots ,c_n),t)\in \mathbf{C}_0^{n+1}$ of objects, we denote by $\mathbf{C}(\underline{c},t) {:}{=}\, \prod _{i=1}^n \mathbf{C}(c_i,t)$ the product of $\text {Hom}$-sets. Its elements will be denoted by symbols like $\underline{f} = (f_1,\dots ,f_n)\in \mathbf{C}(\underline{c},t)$. For a set $S\in \mathbf{Set}$ and a chain complex $V\in \mathbf{Ch}(k)$, we define the tensoring

$$\begin{aligned} S\otimes V \,{:}{=} \, \bigoplus _{s\in S} V\, \in \, \mathbf{Ch}(k). \end{aligned}$$

(3.4)

For example, the tensoring

$$\begin{aligned} S\otimes k = \bigoplus _{s\in S} k\, \in \, \mathbf{Ch}(k) \end{aligned}$$

(3.5)

of a set S and the monoidal unit $k\in \mathbf{Ch}(k)$ is a chain complex concentrated in degree 0 with trivial differential $\text {d}=0$. The k-module in degree 0 is the free k-module generated by S. With a slight abuse of notation, we denote for an element $s\in S$ the unit element $1\in k$ of the s-component of the direct sum (3.5) by the same symbol $s\in S\otimes k$.

Definition 3.6

Let $\overline{\mathbf{C}} = (\mathbf{C},\perp )$ be an orthogonal category. The $\mathbf{C}_0$-colored operad$\mathcal {O}_{\overline{\mathbf{C}}}\in \mathbf{Op}_{\mathbf{C}_0}(\mathbf{Ch}(k))$of$\mathbf{Ch}(k)$-valued quantum field theories on$\overline{\mathbf{C}}$ is defined by the following data:

• (i) For any $(\underline{c},t) \in \mathbf{C}_0^{n+1}$, we define the chain complex of operations by

  $$\begin{aligned} \mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} t \\ \underline{c} \end{array}\big ) \,{:}{=}\, \big (\Sigma _n \times \mathbf{C}(\underline{c},t)\big )\big /{\sim _\perp }\otimes k\,\in \,\mathbf{Ch}(k), \end{aligned}$$

  (3.6)

  where $\Sigma _n$ is the symmetric group on n letters and the equivalence relation is defined as follows: $(\sigma ,\underline{f}) \sim _\perp (\sigma ^\prime ,\underline{f}^\prime )$ if and only if $\underline{f} = \underline{f}^\prime$ and the right permutation $\sigma \sigma ^{\prime \,-1} : \underline{f}\sigma ^{-1} \rightarrow \underline{f}\sigma ^{\prime \,-1}$ is generated by transpositions of adjacent orthogonal pairs.

• (ii) For any $c\in \mathbf{C}_0$, we define the operadic unit by

  $$\begin{aligned} \mathbb {1}: k \longrightarrow \mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} c \\ c \end{array}\big )~,~~1 \longmapsto [e,\text {id}_c], \end{aligned}$$

  (3.7)

  where $e\in \Sigma _1$ is the identity permutation.

• (iii) For any $(\underline{a},t)\in \mathbf{C}_0^{n+1}$ and $(\underline{b}_i,a_i)\in \mathbf{C}_0^{k_i +1}$, we define the operadic composition by

  

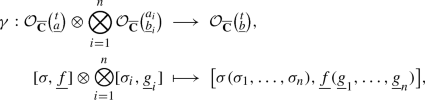  (3.8)

  where $\sigma (\sigma _1,\dots ,\sigma _n) = \sigma \langle k _{\sigma ^{-1}(1)} , \dots , k_{\sigma ^{-1}(n)}\rangle \, (\sigma _1\oplus \cdots \oplus \sigma _n)$ is the group multiplication in $\Sigma _{k_1+\cdots +k_n}$ of the corresponding block permutation and block sum permutation, and $\underline{f}(\underline{g}_1,\dots ,\underline{g}_n) = (f_1\, g_{11}, \dots , f_n\, g_{n k_n})$ is given by composition of $\mathbf{C}$-morphisms.

• (iv) For any $(\underline{c},t) \in \mathbf{C}_0^{n+1}$ and $\sigma ^\prime \in \Sigma _n$, we define the permutation action by

  $$\begin{aligned} \mathcal {O}_{\overline{\mathbf{C}}}(\sigma ^\prime ) : \mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big )\longrightarrow \mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} t\\ \underline{c}\sigma ^\prime \end{array}\big )~,~~[\sigma ,\underline{f}] \longmapsto [\sigma \sigma ^\prime , \underline{f}\sigma ^\prime ]. \end{aligned}$$

  (3.9)

The following results have been proven in [5].

Proposition 3.7

The assignment $\overline{\mathbf{C}}\mapsto \mathcal {O}_{\overline{\mathbf{C}}}$ of the colored operads from Definition 3.6 naturally extends to a functor $\mathcal {O}_{(-)} : \mathbf{OrthCat}\rightarrow \mathbf{Op}(\mathbf{Ch}(k))$.

Theorem 3.8

For any orthogonal category $\overline{\mathbf{C}}$, there exists an isomorphism

$$\begin{aligned} \mathbf{Alg}(\mathcal {O}_{\overline{\mathbf{C}}}) \,\cong \, \mathbf{QFT}(\overline{\mathbf{C}}) \end{aligned}$$

(3.10)

between the category of $\mathcal {O}_{\overline{\mathbf{C}}}$-algebras and the category of $\mathbf{Ch}(k)$-valued quantum field theories on $\overline{\mathbf{C}}$, cf. Definition 3.3. This isomorphism is natural in $\overline{\mathbf{C}}\in \mathbf{OrthCat}$.

Example 3.9

Consider the orthogonal category $\overline{\mathbf{Loc}}$ defined in Example 3.2. Then algebras over the colored operad $\mathcal {O}_{\overline{\mathbf{Loc}}}$ are precisely $\mathbf{Ch}(k)$-valued off-shell locally covariant quantum field theories, cf. Example 3.4. Furthermore, algebras over the colored operad corresponding to the orthogonal category localized at Cauchy morphisms are precisely $\mathbf{Ch}(k)$-valued on-shell locally covariant quantum field theories. $\bigtriangledown$

3.3 Homotopy theory

We are now in the position to endow the category $\mathbf{QFT}(\overline{\mathbf{C}})$ of $\mathbf{Ch}(k)$-valued quantum field theories on an orthogonal category $\overline{\mathbf{C}}$ with a model structure. Our choice of model structure is determined by the canonical model structure on the category of algebras over a colored operad in chain complexes (cf. Theorem 2.4) and our result in Theorem 3.8. Even though model categories are rather abstract concepts, we will try to explain by various examples in this section why they are crucial for many practical constructions with $\mathbf{Ch}(k)$-valued quantum field theories.

Theorem 3.10

Let us assume as before that $k\supseteq \mathbb {Q}$ contains the rationals. Let $\overline{\mathbf{C}}$ be any orthogonal category and consider the corresponding category $\mathbf{QFT}(\overline{\mathbf{C}})$ of $\mathbf{Ch}(k)$-valued quantum field theories, cf. Definition 3.3. Define a morphism $\zeta :\mathfrak {A}\Rightarrow \mathfrak {B}$ in $\mathbf{QFT}(\overline{\mathbf{C}})$ (i.e. a natural transformation between functors $\mathfrak {A},\mathfrak {B}: \mathbf{C}\rightarrow \mathbf{dgAlg}(k)$) to be

• (i) a weak equivalence if the underlying $\mathbf{Ch}(k)$-morphism of each component $\zeta _c : \mathfrak {A}(c) \rightarrow \mathfrak {B}(c)$ is a quasi-isomorphism;

• (ii) a fibration if the underlying $\mathbf{Ch}(k)$-morphism of each component $\zeta _c : \mathfrak {A}(c) \rightarrow \mathfrak {B}(c)$ is degree-wise surjective;

• (iii) a cofibration if it has the left lifting property (cf. Remark 2.2) with respect to all acyclic fibrations.

These choices endow $\mathbf{QFT}(\overline{\mathbf{C}})$ with the structure of a model category.

Proof

By Theorem 3.8, we have an isomorphism of categories $\mathbf{QFT}(\overline{\mathbf{C}})\cong \mathbf{Alg}(\mathcal {O}_{\overline{\mathbf{C}}})$. Because $k\supseteq \mathbb {Q}$, the colored operad $\mathcal {O}_{\overline{\mathbf{C}}}\in \mathbf{Op}_{\mathbf{C}_0}(\mathbf{Ch}(k))$ is admissible and hence its category of algebras $\mathbf{Alg}(\mathcal {O}_{\overline{\mathbf{C}}})$ carries the canonical model structure given in Theorem 2.4. The isomorphism $\mathbf{QFT}(\overline{\mathbf{C}})\cong \mathbf{Alg}(\mathcal {O}_{\overline{\mathbf{C}}})$ induces precisely the model structure on $\mathbf{QFT}(\overline{\mathbf{C}})$ that was claimed in the statement of this theorem. $\square$

Remark 3.11

As a side-remark, we would like to mention that the model structure of Theorem 3.10 is related to the projective model structure on functor categories: Consider the category $\mathbf{dgAlg}(k)^\mathbf{C}$ of all functors from $\mathbf{C}$ to differential graded algebras. Because $\mathbf{dgAlg}(k) = \mathbf{Alg}(\mathsf {As})$ is the category of algebras over the (1-colored, i.e. $\mathfrak {C}=1$ is a singleton) associative operad $\mathsf {As}\in \mathbf{Op}_{1}(\mathbf{Ch}(k))$, it carries a canonical model structure by Theorem 2.4. Concretely, a $\mathbf{dgAlg}(k)$-morphism $\kappa : A\rightarrow B$ is a weak equivalence (respectively, a fibration) if its underlying $\mathbf{Ch}(k)$-morphism is a quasi-isomorphism (respectively, degree-wise surjective). Then we can consider the projective model structure on the functor category $\mathbf{dgAlg}(k)^\mathbf{C}$. Concretely, this means that a natural transformation $\zeta : \mathfrak {A}\Rightarrow \mathfrak {B}$ between two functors $\mathfrak {A},\mathfrak {B}: \mathbf{C}\rightarrow \mathbf{dgAlg}(k)$ is a weak equivalence (respectively, a fibration) if the $\mathbf{Ch}(k)$-morphism underlying each component $\zeta _c : \mathfrak {A}(c)\rightarrow \mathfrak {B}(c)$ is a quasi-isomorphism (respectively, degree-wise surjective). Restricting the weak equivalences and fibrations of this model structure to the full subcategory $\mathbf{QFT}(\overline{\mathbf{C}})\subseteq \mathbf{dgAlg}(k)^\mathbf{C}$ of $\perp$-commutative functors yields the same model structure as the one in Theorem 3.10 above. It is important to emphasize that this observation does not mean that our operadic formalism is irrelevant for endowing the category of quantum field theories with a model structure. In fact, it is generically not true that restricting weak equivalences and fibrations to a full subcategory induces a model structure on it, i.e. our operadic approach to endowing $\mathbf{QFT}(\overline{\mathbf{C}})$ with a model structure is more intrinsic and fundamental.$\vartriangle$

Example 3.12

To be more explicit, let us discuss the result of Theorem 3.10 in the context of the orthogonal category $\overline{\mathbf{Loc}}$ from Example 3.2, which is relevant for locally covariant quantum field theory, see also Example 3.4. (We consider off-shell theories in this example. All statements below are of course also true for on-shell theories by replacing $\overline{\mathbf{Loc}}$ with its orthogonal localization at Cauchy morphisms.) Theorem 3.10 shows that the category $\mathbf{QFT}(\overline{\mathbf{Loc}})$ of all $\mathbf{Ch}(k)$-valued locally covariant quantum field theories carries a canonical model structure. Recalling the main intuitive principle of model category theory, this allows us to consistently regard two theories $\mathfrak {A}: \mathbf{Loc}\rightarrow \mathbf{dgAlg}(k)$ and $\mathfrak {B}: \mathbf{Loc}\rightarrow \mathbf{dgAlg}(k)$ as being the same not only when they are isomorphic, but also when they are weakly equivalent. A weak equivalence is concretely given by a natural transformation $\zeta : \mathfrak {A}\Rightarrow \mathfrak {B}$ whose components $\zeta _M : \mathfrak {A}(M)\rightarrow \mathfrak {B}(M)$ are quasi-isomorphisms between the chain complexes of observables, for all spacetimes $M\in \mathbf{Loc}$. At a more informal level, such weak equivalences are frequently used in practice for constructing perturbative quantum gauge theories via the BRST/BV formalism, see e.g. [25, 26, 36]. For example, the usual technique of adding various auxiliary fields to the differential graded algebras of observables without changing their homologies should be understood as a particular instance of our precise concept of weak equivalences developed in Theorem 3.10. The theories resulting from adding different choices of auxiliary fields are in general not isomorphic, but only weakly equivalent in the model category $\mathbf{QFT}(\overline{\mathbf{C}})$. Model category theory provides a consistent framework that allows us to treat such theories as if they would be the same. We comment more on the last point in Examples 3.14 and 3.15. $\bigtriangledown$

Now let us consider an orthogonal functor $F :\overline{\mathbf{C}}\rightarrow \overline{\mathbf{D}}$. Recalling that by Proposition 3.7 our operads are functorial on the category $\mathbf{OrthCat}$ of orthogonal categories, we obtain an $\mathbf{Op}(\mathbf{Ch}(k))$-morphism $\mathcal {O}_F : \mathcal {O}_{\overline{\mathbf{C}}} \rightarrow \mathcal {O}_{\overline{\mathbf{D}}}$. Then by Proposition 2.6 we obtain a Quillen adjunction

between the model categories of algebras. Using further the natural isomorphism of categories $\mathbf{Alg}(\mathcal {O}_{(-)})\cong \mathbf{QFT}(-)$ from Theorem 3.8, which is in fact by construction (cf. Theorem 3.10) a natural isomorphism of model categories, we immediately obtain the following result.

Proposition 3.13

Let us assume as before that $k\supseteq \mathbb {Q}$. For every orthogonal functor $F :\overline{\mathbf{C}}\rightarrow \overline{\mathbf{D}}$ there exists a Quillen adjunction

between the model categories of $\mathbf{Ch}(k)$-valued quantum field theories on $\overline{\mathbf{C}}$ and $\overline{\mathbf{D}}$, cf. Theorem 3.10. The right adjoint functor $F^*$ is explicitly given by pullback along F, i.e. for a $\perp$-commutative functor $\mathfrak {A}: \mathbf{D}\rightarrow \mathbf{dgAlg}(k)$ we have that $F^*(\mathfrak {A}) {:}{=} \mathfrak {A}\,F : \mathbf{C}\rightarrow \mathbf{dgAlg}(k)$ is given by pre-composition. Moreover, the right adjoint functor $F^*$ preserves weak equivalences.

Using standard techniques from model category theory, called derived functors [20, 37, 48], one can modify in a controlled way both the left and the right adjoint functors of the Quillen adjunction in (3.12) in order to obtain new functors that preserve weak equivalences. These derived functors provide constructions which are homotopically meaningful in the sense that they are consistent with our main principle that weakly equivalent objects should be regarded as being the same. Because by Proposition 3.13 the right adjoint functor $F^*: \mathbf{QFT}(\overline{\mathbf{D}})\rightarrow \mathbf{QFT}(\overline{\mathbf{C}})$ already preserves weak equivalences, there is no need to derive it. Hence, we may simply choose

$$\begin{aligned} \mathbb {R} F^*{:}{=}\,F^*: \mathbf{QFT}(\overline{\mathbf{D}})\longrightarrow \mathbf{QFT}(\overline{\mathbf{C}}) \end{aligned}$$

(3.13)

for the right derived functor. However, the left adjoint functor $F_! : \mathbf{QFT}(\overline{\mathbf{C}})\rightarrow \mathbf{QFT}(\overline{\mathbf{D}})$ in general does not preserve weak equivalences, and we have to derive it. The standard technique for defining a left derived functor $\mathbb {L} F_! : \mathbf{QFT}(\overline{\mathbf{C}})\rightarrow \mathbf{QFT}(\overline{\mathbf{D}})$, which does preserve weak equivalences, is via cofibrant replacements. Recall that a cofibrant replacement functor on a model category (here $\mathbf{QFT}(\overline{\mathbf{C}})$) is an endofunctor $Q : \mathbf{QFT}(\overline{\mathbf{C}}) \rightarrow \mathbf{QFT}(\overline{\mathbf{C}})$ such that $Q(\mathfrak {A})$ is a cofibrant object in $\mathbf{QFT}(\overline{\mathbf{C}})$ for every $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{C}})$, together with a natural weak equivalence $q : Q\Rightarrow \text {id}$. The model category axioms ensure that a cofibrant replacement functor always exists. Making any choice of cofibrant replacement, we define a left derived functor by pre-composition

$$\begin{aligned} \mathbb {L} F_! {:}{=}\,F_!\,Q : \mathbf{QFT}\left( \overline{\mathbf{C}}\right) \longrightarrow \mathbf{QFT}\left( \overline{\mathbf{D}}\right) . \end{aligned}$$

(3.14)

By construction, the derived functor $\mathbb {L} F_!$ preserves weak equivalences, see e.g. [37, Lemma 1.1.12]. In order to illustrate the relevance of these derived functors for quantum field theory, let us consider the following examples.

Example 3.14

Consider the orthogonal functor from Example 3.2, which describes the embedding of the category of diamond spacetimes into the category of all spacetimes. By Proposition 3.13, we obtain a Quillen adjunction

The physical interpretation of the left and right adjoint functors is as follows: The right adjoint $j^*$ is the obvious restriction functor that restricts theories defined on the category $\mathbf{Loc}$ of all spacetimes to the category of diamond spacetimes. The left adjoint $j_!$ is a universal extension functor that extends theories defined only on diamond spacetimes to all spacetimes. We have shown in [5] that the universal extension functor $j_!$ is an operadic refinement of Fredenhagen’s universal algebra construction [22,23,24].

When working with $\mathbf{Ch}(k)$-valued quantum field theories, there exists a non-trivial notion of weak equivalences (cf. Theorem 3.10) and, of course, we must ensure that both the restriction and the extension of quantum field theories along preserve these weak equivalences. This is precisely what the derived functors do for us! Concretely, we have observed in (3.13) that the right adjoint functor $j^*$ already preserves weak equivalences and hence there is no need to derive it, i.e. we may set $\mathbb {R} j^*= j^*$. In our context this means that the ordinary restriction of quantum field theories $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{Loc}})$ is a homotopically meaningful construction. On the other hand, the universal extension functor $j_!$ is not yet homotopically meaningful and it must be derived according to (3.14) by using a cofibrant replacement functor, i.e. we consider the left derived functor

(3.16)

Let us stress that the derived extension of a theory on diamond spacetimes is in general not weakly equivalent to its ordinary extension . We refer to “Appendix” for simple toy-models which explain the relevance of derived extension functors from a mathematical and physical perspective. $\bigtriangledown$

Example 3.15

In order to emphasize even more our comments in Example 3.14, let us consider the following concrete scenario: Let us take any perturbative quantum gauge theory on the full subcategory of diamond spacetimes, see e.g. [25, 26, 36] for concrete examples. (Constructing quantum gauge theories on is generically easier than constructing them on all of $\mathbf{Loc}$ because all bundles over can be trivialized.) Now suppose that we would do a second slightly different construction, e.g. by using different auxiliary fields and/or gauge fixings, and obtain another theory that is weakly equivalent to . Then, in the spirit of Fredenhagen’s universal algebra construction, we would like to extend and to the category of all spacetimes $\mathbf{Loc}$. If we would use the ordinary (i.e. underived) universal extension functor $j_!$, it is not guaranteed that and are weakly equivalent theories on $\mathbf{Loc}$. (See “Appendix” for simple toy-models which show that underived extension functors do not preserve weak equivalences.) That is of course unsatisfactory because and represent the same quantum gauge theory as they are weakly equivalent. Using instead the derived universal extension functor $\mathbb {L} j_!$, we ensure that and are weakly equivalent and hence they present the same quantum gauge theory on $\mathbf{Loc}$, as expected from the fact that and present the same quantum gauge theory on . $\bigtriangledown$

Remark 3.16

Let us recall that if $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{C}})$ is a cofibrant object, then the canonical morphism $\mathbb {L} F_! (\mathfrak {A}) = F_! \,Q(\mathfrak {A}) \xrightarrow {\ F_! q_{\mathfrak {A}}\ } F_!(\mathfrak {A})$ is a weak equivalence in $\mathbf{QFT}(\overline{\mathbf{D}})$. This means that, for any cofibrant object $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{C}})$, it is sufficient to compute the much simpler underived functor $F_!(\mathfrak {A})$ in order to obtain the correct homotopy type of $\mathbb {L} F_! (\mathfrak {A})$. It is therefore interesting to ask whether the typical examples of $\mathbf{Ch}(k)$-valued quantum field theories, e.g. those produced by the BRST/BV formalism, naturally come as cofibrant objects in $\mathbf{QFT}(\overline{\mathbf{C}})$. (We thank the anonymous referee for asking this question to us.) This is unfortunately not the case because, as we explain below, the usual canonical commutation relations in quantum (field) theory are incompatible with cofibrancy as they define non-semifree differential graded algebras.

In order to provide a simple argument, let us take $k=\mathbb {C}$ to be the field of complex numbers and consider for the moment the orthogonal category $\overline{\mathbf{C}} = (\{*\},\emptyset )$ given by a point with the empty orthogonality relation. Then $\mathbf{QFT}(\overline{\mathbf{C}}) = \mathbf{dgAlg}(\mathbb {C})$ is simply the category of (non-commutative) differential graded algebras over $\mathbb {C}$. Let $A\in \mathbf{dgAlg}(\mathbb {C})$ be generated by two generators x and p of degree 0, modulo the ideal generated by $\text {d}x =0 = \text {d}p$ and the canonical commutation relation $[x,p] = i\,1$. (Note that this is the algebra for a 1-dimensional point particle in quantum mechanics.) We now prove that $A\in \mathbf{dgAlg}(\mathbb {C})$ is not a cofibrant object by constructing an acyclic fibration $\kappa : B\rightarrow A$ that does not admit a section. Let $B\in \mathbf{dgAlg}(\mathbb {C})$ be generated by two generators x and p of degree 0 and one generator c of degree 1, modulo the ideal generated by the relations $\text {d}x =0 = \text {d}p$, $x c=0=cx$, $pc=0=cp$, $c^2=0$, $c \,\text {d}c=0$ and the modified canonical commutation relation $[x,p] = i\,(1 + \text {d}c)$. Taking the differential of these relations we further obtain that $x\,\text {d}c = 0 = \text {d}c \, x$, $p\, \text {d}c = 0 = \text {d}c\, p$, $\text {d}c\, c =0$ and $\text {d}c\, \text {d}c=0$. Hence, a generic element of B is of the form $b = a(x,p) + \alpha \,\text {d}c + \beta \,c$, where a(x, p) is a polynomial in x and p, while $\alpha ,\beta \in \mathbb {C}$ are complex numbers. We define a $\mathbf{dgAlg}(\mathbb {C})$-morphism $\kappa : B\rightarrow A$ by setting $\kappa (x)=x$, $\kappa (p)= p$ and $\kappa (c)= 0$ and observe that this is an acyclic fibration in $\mathbf{dgAlg}(\mathbb {C})$. Any section $\sigma : A\rightarrow B$ of $\kappa$ must be of the form $\sigma (x) = x + \alpha \, \text {d}c$ and $\sigma (p) = p +\alpha ^\prime \,\text {d}c$, for some $\alpha ,\alpha ^\prime \in \mathbb {C}$. It follows that this is incompatible with the commutation relations in B and A. Explicitly,

$$\begin{aligned}{}[\sigma (x),\sigma (p)]_B&= [x+\alpha \,\text {d}c, p+ \alpha ^\prime \,\text {d}c]_B= [x,p]_B = i\,(1+\text {d}c) \ne \sigma \big (i\,1\big ) \nonumber \\&= \sigma \big ([x,p]_A\big ), \end{aligned}$$

(3.17)

where the subscript indicates the algebra in which we take the commutator. Hence, $A\in \mathbf{dgAlg}(\mathbb {C})$ is not a cofibrant object.

A similar argument may be applied object-wise to any $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{C}})$ that assigns differential graded algebras involving (graded) canonical commutation relations, which in particular includes the models constructed in the BRST/BV formalism [25, 26, 36]. $\vartriangle$

4 Homotopy algebraic quantum field theories

4.1 $\Sigma$-cofibrant resolutions

Let us first recall the following standard concept of resolutions for colored operads, see e.g. [8, 9, 14, 32, 33, 47, 53].

Definition 4.1

A $\Sigma$-cofibrant resolution of a colored operad $\mathcal {O}\in \mathbf{Op}_{\mathfrak {C}}(\mathbf{Ch}(k))$ is a $\Sigma$-cofibrant operad $\mathcal {O}_\infty \in \mathbf{Op}_{\mathfrak {C}}(\mathbf{Ch}(k))$ (cf. Definition 2.9) together with an acyclic fibration

$$\begin{aligned} w : \mathcal {O}_\infty \longrightarrow \mathcal {O}\end{aligned}$$

(4.1)

in the model category $\mathbf{Op}_{\mathfrak {C}}(\mathbf{Ch}(k))$, cf. Theorem 2.3.

The role of $\Sigma$-cofibrant resolutions is that they provide a suitable framework to study homotopy-coherent algebraic structures, i.e. homotopy algebras over operads. For example, $A_\infty$-algebras (see e.g. [40, Section 9]) are algebras over a $\Sigma$-cofibrant resolution $A_{\infty }\rightarrow \mathsf {As}$ of the associative operad and $E_\infty$-algebras (see e.g. [7]) are algebras over a $\Sigma$-cofibrant resolution $E_{\infty }\rightarrow \mathsf {Com}$ of the commutative operad. As a colored example, homotopy-coherent diagrams (see e.g. [9]) are algebras over a $\Sigma$-cofibrant resolution ${\mathsf {Diag}_\mathbf{C}}_{\infty }\rightarrow \mathsf {Diag}_\mathbf{C}$ of the diagram operad over a small category $\mathbf{C}$.

It is important to emphasize the following facts about existence and “uniqueness” (see below for the precise statement) of $\Sigma$-cofibrant resolutions: (1) Recalling that $\mathbf{Op}_{\mathfrak {C}}(\mathbf{Ch}(k))$ is a model category (cf. Theorem 2.3), there exists a cofibrant replacement $q : Q(\mathcal {O})\rightarrow \mathcal {O}$ which defines a particular example of a $\Sigma$-cofibrant resolution, see e.g. [8, Proposition 4.3]. Hence, $\Sigma$-cofibrant resolutions exist for every colored operad $\mathcal {O}\in \mathbf{Op}_{\mathfrak {C}}(\mathbf{Ch}(k))$. (2) Let us assume that we have two $\Sigma$-cofibrant resolutions $w : \mathcal {O}_\infty \rightarrow \mathcal {O}$ and $w^\prime : \mathcal {O}_\infty ^\prime \rightarrow \mathcal {O}$ of a colored operad $\mathcal {O}\in \mathbf{Op}_{\mathfrak {C}}(\mathbf{Ch}(k))$. Taking also a cofibrant replacement $q : Q(\mathcal {O})\rightarrow \mathcal {O}$, we obtain a commutative diagram

in $\mathbf{Op}_{\mathfrak {C}}(\mathbf{Ch}(k))$, where the dashed arrows exist by the left lifting property (cf. Remark 2.2) because $Q(\mathcal {O})$ is a cofibrant object and w, $w^\prime$ are by definition acyclic fibrations. The 2-out-of-3 property of weak equivalences further implies that the dashed arrows are themselves weak equivalences; hence by Theorem 2.10 they induce a zigzag of Quillen equivalences

This shows that the model categories of algebras over different $\Sigma$-cofibrant resolutions are “the same” in the sense that they are related by a zigzag of Quillen equivalences. (In particular, the corresponding homotopy categories are equivalent as categories.)

Now let us focus on our case of interest, namely the quantum field theory operads from Definition 3.6. Inspired by the concept of homotopy algebras over operads, we start with the following definition.

Definition 4.2

Let $\overline{\mathbf{C}}$ be an orthogonal category and $w : {\mathcal {O}_{\overline{\mathbf{C}}}}_\infty \rightarrow \mathcal {O}_{\overline{\mathbf{C}}}$ a $\Sigma$-cofibrant resolution. The model category of homotopy quantum field theories on $\overline{\mathbf{C}}$ corresponding to this resolution is defined as $\mathbf{QFT}_w(\overline{\mathbf{C}}) {:}{=}\,\mathbf{Alg}({\mathcal {O}_{\overline{\mathbf{C}}}}_\infty )$.

Theorem 4.3

Let us assume as before that $k\supseteq \mathbb {Q}$. For every orthogonal category $\overline{\mathbf{C}}$, the $\mathbf{C}_0$-colored operad $\mathcal {O}_{\overline{\mathbf{C}}}\in \mathbf{Op}_{\mathbf{C}_0}(\mathbf{Ch}(k))$ is $\Sigma$-cofibrant. As a consequence, for every $\Sigma$-cofibrant resolution $w : {\mathcal {O}_{\overline{\mathbf{C}}}}_\infty \rightarrow \mathcal {O}_{\overline{\mathbf{C}}}$ there exists a Quillen equivalence

between the model categories of strict and homotopy quantum field theories on $\overline{\mathbf{C}}$.

Proof

Using Proposition 2.11, it is sufficient to prove that each component $\mathcal {O}_{\overline{\mathbf{C}}}(\begin{array}{c} t \\ \underline{c} \end{array}) \in \mathbf{Ch}(k)$ is a cofibrant chain complex. Using the explicit definition in (3.6), we observe that this is the case because the monoidal unit $k\in \mathbf{Ch}(k)$ is cofibrant and the $\mathbf{Set}$-tensoring [i.e. forming coproducts (3.5)] preserves cofibrant objects. This proves the first part of our claim.

Concerning the second claim, consider any $\Sigma$-cofibrant resolution $w : {\mathcal {O}_{\overline{\mathbf{C}}}}_\infty \rightarrow \mathcal {O}_{\overline{\mathbf{C}}}$. Because both the source and target of this morphism are $\Sigma$-cofibrant, it follows from Theorem 2.10 that the adjunction (4.4) is a Quillen equivalence. $\square$

Remark 4.4

Theorem 4.3 should be interpreted as a strictification result for homotopy quantum field theories. Let us explain this important point in more detail: Let $w : {\mathcal {O}_{\overline{\mathbf{C}}}}_\infty \rightarrow \mathcal {O}_{\overline{\mathbf{C}}}$ be a $\Sigma$-cofibrant resolution, e.g. the Boardman-Vogt resolution developed by Yau for our operads [56]. Algebras over ${\mathcal {O}_{\overline{\mathbf{C}}}}_\infty$ generically describe a weaker concept of quantum field theories, where functoriality, associativity and/or $\perp$-commutativity might just hold in a homotopy-coherent fashion. (The extent of this weakening depends on the choice of $\Sigma$-cofibrant resolution.) Consider any homotopy quantum field theory $\mathfrak {A}_\infty \in \mathbf{QFT}_w(\overline{\mathbf{C}})$ and replace it by a weakly equivalent cofibrant object $Q(\mathfrak {A}_\infty ) \rightarrow \mathfrak {A}_\infty$. (Notice that $Q(\mathfrak {A}_\infty )$ and $\mathfrak {A}_\infty$ describe “the same” theory from our model categorical perspective because they are weakly equivalent.) Using that (4.4) is a Quillen equivalence, we obtain from [37, Proposition 1.3.13] that the composite of

is a weak equivalence, where $\eta$ is the unit of the adjunction and we also performed a fibrant replacement R in the second step. (Because every object in $\mathbf{QFT}(\overline{\mathbf{C}})$ is fibrant, one could also drop the fibrant replacement here.) In particular, $Q (\mathfrak {A}_\infty )$, and hence also our original theory $\mathfrak {A}_\infty \in \mathbf{QFT}_w(\overline{\mathbf{C}})$, is weakly equivalent to the image under $w^*$ of the strict quantum field theory $R w_! Q (\mathfrak {A}_\infty ) \in \mathbf{QFT}(\overline{\mathbf{C}})$ (or $w_! Q (\mathfrak {A}_\infty ) \in \mathbf{QFT}(\overline{\mathbf{C}})$ if we drop the fibrant replacement). This defines a model for the strictification of our original homotopy quantum field theory $\mathfrak {A}_\infty \in \mathbf{QFT}_w(\overline{\mathbf{C}})$.$\vartriangle$

Remark 4.5

We would like to issue a warning that Theorem 4.3 and Remark 4.4 should not be misunderstood as the statement that homotopy quantum field theories are not useful. Even though it is true that each homotopy quantum field theory admits a strictification, it is highly non-trivial to compute such strictifications in practice. The reason is that in particular the cofibrant replacement in the construction of Remark 4.4 is typically extremely complicated to compute explicitly. Furthermore, as we will show in Sects. 4.3 and 5, interesting constructions naturally lead to non-strict homotopy quantum field theories, which justifies their practical relevance.$\vartriangle$

4.2 The $E_\infty$-resolution

We develop a particular functorial $\Sigma$-cofibrant resolution for our colored operads $\mathcal {O}_{\overline{\mathbf{C}}}$ that is obtained by a component-wise tensor product with the (chain version of the) Barratt–Eccles $E_\infty$-operad. This choice of resolution is motivated by the fact that it is not only relatively simple, but also sufficiently flexible to encompass the examples from Sects. 4.3 and 5 in terms of its algebras.

Let us denote by $\mathcal {E}_\infty \in \mathbf{Op}_{1}(\mathbf{Ch}(k))$ the (chain version of the) 1-colored Barratt–Eccles $E_\infty$-operad studied in [7]. This operad is defined by applying the normalized chain complex functor to the original simplicial Barratt–Eccles operad. In our work we do not need an explicit description of this operad and refer to [7, Section 1.1] for the details. Let us recall some basic properties of the operad $\mathcal {E}_\infty \in \mathbf{Op}_{1}(\mathbf{Ch}(k))$ that will be important in what follows: (1) The operad $\mathcal {E}_\infty$ provides a $\Sigma$-cofibrant resolution

$$\begin{aligned} w : \mathcal {E}_\infty \longrightarrow \mathsf {Com} \end{aligned}$$

(4.6)

of the commutative operad $\mathsf {Com}\in \mathbf{Op}_{1}(\mathbf{Ch}(k))$. (2) The degree 0 part of $\mathcal {E}_\infty$ is the associative operad $\mathsf {As} \in \mathbf{Op}_{1}(\mathbf{Ch}(k))$, i.e. there exists an $\mathbf{Op}_{1}(\mathbf{Ch}(k))$-morphism

$$\begin{aligned} i : \mathsf {As} \longrightarrow \mathcal {E}_\infty . \end{aligned}$$

(4.7)

(3) The composition of (4.7) and (4.6) is the canonical $\mathbf{Op}_{1}(\mathbf{Ch}(k))$-morphism $\mathsf {As}\rightarrow \mathsf {Com}$.

Remark 4.6

Algebras $A\in \mathbf{Alg}(\mathcal {E}_\infty )$ over the operad $\mathcal {E}_\infty \in \mathbf{Op}_{1}(\mathbf{Ch}(k))$ are differential graded algebras, together with additional higher chain homotopy data (living in positive degrees in the chain complexes underlying $\mathcal {E}_\infty$) that describe homotopy-coherent commutativity. The two operad morphisms in (4.6) and (4.7) yield a sequence of Quillen adjunctions

The right adjoint $i^*$ assigns to an $\mathcal {E}_\infty$-algebra $A\in \mathbf{Alg}(\mathcal {E}_\infty )$ its underlying differential graded algebra, i.e. it forgets the higher chain homotopy data describing homotopy-coherent commutativity. (Hence, the underlying differential graded algebra is in general non-commutative.) The right adjoint $w^*$ assigns to a commutative differential graded algebra $A\in \mathbf{Alg}(\mathsf {Com})$ the $E_\infty$-algebra whose chain homotopy data are trivial, i.e. a strictly commutative $E_\infty$-algebra.$\vartriangle$

For every orthogonal category $\overline{\mathbf{C}}$, let us define the colored operad

$$\begin{aligned} \mathcal {O}_{\overline{\mathbf{C}}}\otimes \mathcal {E}_\infty \in \mathbf{Op}_{\mathbf{C}_0}(\mathbf{Ch}(k)) \end{aligned}$$

(4.9)

by a component-wise tensor product of the quantum field theory operad from Definition 3.6 and the 1-colored operad $\mathcal {E}_\infty \in \mathbf{Op}_{1}(\mathbf{Ch}(k))$. More concretely, the chain complex of operations for $(\underline{c},t) = ((c_1,\dots ,c_n),t)\in \mathbf{C}_0^{n+1}$ reads as

$$\begin{aligned} \big (\mathcal {O}_{\overline{\mathbf{C}}}\otimes \mathcal {E}_\infty \big )\big (\begin{array}{c} t \\ \underline{c} \end{array}\big ) \,{:}{=}\, \mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} t \\ \underline{c} \end{array}\big ) \otimes \mathcal {E}_\infty (n)\,\cong \, \big (\Sigma _n \times \mathbf{C}(\underline{c},t)\big )\big /{\sim _\perp }\otimes \mathcal {E}_\infty (n)\,\in \,\mathbf{Ch}(k) \end{aligned}$$

(4.10)

and the operad structure is the tensor product of the respective operad structures. The operad morphism in (4.6) defines an $\mathbf{Op}_{\mathbf{C}_0}(\mathbf{Ch}(k))$-morphism

where the last isomorphism is due to $\mathsf {Com}(n) = k\in \mathbf{Ch}(k)$, for all $n\ge 0$. In order to simplify our notations, in the following we will denote (4.11) by

$$\begin{aligned} w_{\overline{\mathbf{C}}} : \mathcal {O}_{\overline{\mathbf{C}}}\otimes \mathcal {E}_\infty \longrightarrow \mathcal {O}_{\overline{\mathbf{C}}}. \end{aligned}$$

(4.12)

Theorem 4.7

Let us assume as before that $k\supseteq \mathbb {Q}$. For every orthogonal category $\overline{\mathbf{C}}$, the $\mathbf{Op}_{\mathbf{C}_0}(\mathbf{Ch}(k))$-morphism (4.12) defines a $\Sigma$-cofibrant resolution of the quantum field theory operad $\mathcal {O}_{\overline{\mathbf{C}}}\in \mathbf{Op}_{\mathbf{C}_0}(\mathbf{Ch}(k))$. These resolutions are functorial in the sense that $w : \mathcal {O}_{(-)}\otimes \mathcal {E}_\infty \rightarrow \mathcal {O}_{(-)}$ is a natural transformation between the functors $\mathcal {O}_{(-)} \otimes \mathcal {E}_\infty :\mathbf{OrthCat}\rightarrow \mathbf{Op}(\mathbf{Ch}(k))$ and $\mathcal {O}_{(-)}: \mathbf{OrthCat}\rightarrow \mathbf{Op}(\mathbf{Ch}(k))$.

Proof

Using the explicit definition in (4.10), we observe that each component $\big (\mathcal {O}_{\overline{\mathbf{C}}}\otimes \mathcal {E}_\infty \big )\big (\begin{array}{c} t \\ \underline{c} \end{array}\big )$ is a cofibrant chain complex because $\mathcal {E}_\infty (n)$ is cofibrant and the $\mathbf{Set}$-tensoring (i.e. forming coproducts (3.4)) preserves cofibrant objects. It follows from Proposition 2.11 that $\mathcal {O}_{\overline{\mathbf{C}}}\otimes \mathcal {E}_\infty \in \mathbf{Op}_{\mathbf{C}_0}(\mathbf{Ch}(k))$ is $\Sigma$-cofibrant.

We next have to prove that (4.12) is an acyclic fibration in $\mathbf{Op}_{\mathbf{C}_0}(\mathbf{Ch}(k))$, i.e. each component $w_{\overline{\mathbf{C}}} = \text {id}\otimes w : \mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} t \\ \underline{c} \end{array}\big )\otimes \mathcal {E}_\infty (n) \rightarrow \mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} t \\ \underline{c} \end{array}\big )\otimes k$ is an acyclic fibration in $\mathbf{Ch}(k)$, cf. Theorem 2.3 and Theorem 2.1. The fibration property is clear because each $w : \mathcal {E}_\infty (n)\rightarrow k$ is degree-wise surjective. Using further that each $w : \mathcal {E}_\infty (n)\rightarrow k$ is a weak equivalence between cofibrant objects in $\mathbf{Ch}(k)$, the left Quillen functor property of the tensor product $V\otimes (-): \mathbf{Ch}(k) \rightarrow \mathbf{Ch}(k)$ (for $V\in \mathbf{Ch}(k)$ cofibrant) implies via Ken Brown’s lemma [37, Lemma 1.1.12] that $w_{\overline{\mathbf{C}}} = \text {id}\otimes w$ is a weak equivalence too.

Functoriality of these resolutions is obvious. $\square$

Remark 4.8

In order to obtain some intuition for the algebras over $\mathcal {O}_{\overline{\mathbf{C}}}\otimes \mathcal {E}_\infty$, i.e. homotopy quantum field theories $\mathbf{QFT}_w(\overline{\mathbf{C}}) {:}{=} \mathbf{Alg}(\mathcal {O}_{\overline{\mathbf{C}}}\otimes \mathcal {E}_\infty )$, we consider some special limiting cases. Given any orthogonal category $\overline{\mathbf{C}} = (\mathbf{C},\perp )$, let us consider as an auxiliary concept the orthogonal category $\overline{\mathbf{C}}^{\max } = (\mathbf{C},\perp ^{\max })$, where $\perp ^{\max } {:}{=}\,\text {Mor}\,\mathbf{C}\, {}_\text {t}^{}\!\times \!{}^{}_\text {t} \,\text {Mor}\,\mathbf{C}$ is the maximal orthogonality relation. We have isomorphisms of categories

$$\begin{aligned} \mathbf{QFT}(\overline{\mathbf{C}}^{\max }) ~\cong ~ \mathbf{Alg}(\mathcal {O}_{\overline{\mathbf{C}}^{\max }}) ~\cong ~\mathbf{Alg}(\mathsf {Com})^{\mathbf{C}}, \end{aligned}$$

(4.13)

i.e. quantum field theories on $\overline{\mathbf{C}}^{\max }$ are functors on $\mathbf{C}$ with values in commutative differential graded algebras. For the resolution $\mathcal {O}_{\overline{\mathbf{C}}^{\max }} \otimes \mathcal {E}_\infty$, we similarly obtain isomorphisms of categories

$$\begin{aligned} \mathbf{QFT}_w(\overline{\mathbf{C}}^{\max }) ~=~ \mathbf{Alg}(\mathcal {O}_{\overline{\mathbf{C}}^{\max }}\otimes \mathcal {E}_\infty ) ~\cong ~\mathbf{Alg}(\mathcal {E}_\infty )^{\mathbf{C}}, \end{aligned}$$

(4.14)

i.e. homotopy quantum field theories on $\overline{\mathbf{C}}^{\max }$ are functors on $\mathbf{C}$ with values in $\mathcal {E}_\infty$-algebras.

The orthogonal functor $p{:}{=} \text {id}_\mathbf{C}: \overline{\mathbf{C}} \rightarrow \overline{\mathbf{C}}^{\max }$ induced by the identity $\text {id}_\mathbf{C}$ defines a colored operad morphism $\mathcal {O}_p \otimes \mathcal {E}_\infty : \mathcal {O}_{\overline{\mathbf{C}}}\otimes \mathcal {E}_\infty \rightarrow \mathcal {O}_{\overline{\mathbf{C}}^{\max }}\otimes \mathcal {E}_\infty$ and thus a Quillen adjunction

The right adjoint $p^*$ assigns to every functor $\mathfrak {B}: \mathbf{C}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$ with values in $\mathcal {E}_\infty$-algebras a homotopy quantum field theory $p^*(\mathfrak {B})\in \mathbf{QFT}_w(\overline{\mathbf{C}})$ on $\overline{\mathbf{C}}$. Because the latter theories assign homotopy-coherently commutative observable algebras to spacetimes, one should interpret them as drastically simplified toy-models that ignore all quantum theoretic and also Poisson algebraic aspects. We shall show in Sect. 4.3 that such theories naturally arise by taking suitable “function algebras” on $\infty$-stacks, which can be understood as the starting point for Poisson algebraic studies of classical gauge theories and their deformation quantization.

Now let us consider as another auxiliary concept the orthogonal category $\overline{\mathbf{C}}^{\min } = (\mathbf{C},\emptyset )$ with the trivial orthogonality relation. We have isomorphisms of categories

$$\begin{aligned} \mathbf{QFT}(\overline{\mathbf{C}}^{\min }) ~\cong ~ \mathbf{Alg}(\mathcal {O}_{\overline{\mathbf{C}}^{\min }}) ~\cong ~\mathbf{Alg}(\mathsf {As})^{\mathbf{C}} = \mathbf{dgAlg}(k)^\mathbf{C}, \end{aligned}$$

(4.16)

i.e. quantum field theories on $\overline{\mathbf{C}}^{\min }$ are functors on $\mathbf{C}$ with values in (non-commutative) differential graded algebras. We define a colored operad morphism $l : \mathcal {O}_{\overline{\mathbf{C}}^{\min }} \rightarrow \mathcal {O}_{\overline{\mathbf{C}}} \otimes \mathcal {E}_\infty$ by the components [recall (3.6) and use that the equivalence relation is trivial for $\overline{\mathbf{C}}^{\min }$]

where $\text {diag}$ denotes the diagonal map, $\pi$ is the projection to equivalence classes and i is the operad morphism from (4.7). This defines a Quillen adjunction

The right adjoint $l^*$ assigns to every homotopy quantum field theory $\mathfrak {A}\in \mathbf{QFT}_w(\overline{\mathbf{C}})$ its underlying functor with values in differential graded algebras. Because this constructions neglects the homotopies encoded in $\mathcal {E}_\infty$, such functor in general does not satisfy the strict $\perp$-commutativity axiom.

Summing up, we have seen that every homotopy quantum field theory $\mathfrak {A}\in \mathbf{QFT}_w(\overline{\mathbf{C}})$ has an underlying functor $l^*(\mathfrak {A}) : \mathbf{C}\rightarrow \mathbf{dgAlg}(k)$ that is obtained by forgetting the chain homotopy data in $\mathcal {E}_\infty$, cf. (4.18). Furthermore, every functor $\mathfrak {B}: \mathbf{C}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$ with values in $\mathcal {E}_\infty$-algebras defines a homotopy quantum field theory $p^*(\mathfrak {B})\in \mathbf{QFT}_w(\overline{\mathbf{C}})$, cf. (4.15). Examples of the latter theories are obtained in Corollary 4.11.$\vartriangle$

4.3 Toy-models via cochain algebras on stacks

We provide simple toy-models of homotopy quantum field theories on our resolved operads from Theorem 4.7 by taking suitable cochain algebras on stacks. (In this section the term “stack” always refers to “$\infty$-stacks.”) Applying this construction to diagrams of stacks will define functors $\mathbf{C}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$ with values in $\mathcal {E}_\infty$-algebras, which may be regarded as drastically simplified toy-models of homotopy quantum field theories according to Remark 4.8, see in particular (4.15). In our opinion these toy-models are interesting because they provide a convenient starting point for investigating Poisson algebraic aspects of classical gauge theories and their deformation quantization. We, however, would like to emphasize that such constructions are technically very involved, see e.g. [12, 45] for a modern homotopy theoretical approach, even in the case of linear fields [30]. We therefore postpone these problems to future works and only outline below the construction of the stacky cochain algebras, which should be interpreted physically as “function algebras” on stacks.

In this section we assume that the reader has some familiarity with simplicial sets, simplicial k-modules and the Dold–Kan correspondence, see e.g. [51] and [29]. Before we can address the more complicated case of stacks, let us discuss an analog of our construction for simplicial sets, which is given by the usual cochain algebra construction.

We denote by $\mathbf{sSet}$ the category of simplicial sets equipped with the Quillen model structure, by $\mathbf{sMod}_k$ the model category of simplicial k-modules (weak equivalences and fibrations are defined as for the underlying simplicial sets) and by $\mathbf{Ch}_{\ge 0}(k)$ the category of non-negatively graded chain complexes with the projective model structure (weak equivalences are quasi-isomorphisms and fibrations are surjective in all positive degrees). There exists a sequence of Quillen adjunctions (left adjoints point from left to right)

The first step is the free-forget adjunction between simplicial sets and simplicial k-modules, the second step is the Dold–Kan correspondence, and the last step is the inclusion-(good)truncation adjunction for chain complexes. The composite of left adjoints is the functor that assigns to a simplicial set $X\in \mathbf{sSet}$ its normalized chains $N_*(X)\in \mathbf{Ch}(k)$, where here and in the following we suppress both the free simplicial k-module functor $(-)\otimes k : \mathbf{sSet}\rightarrow \mathbf{sMod}_k$ and the inclusion functor $\iota : \mathbf{Ch}_{\ge 0}(k)\rightarrow \mathbf{Ch}(k)$.

The normalized cochains on a simplicial set are obtained by composing the normalized chains functor with the internal hom functor $[-,k]$, which is the left adjoint in the Quillen adjunction

Here the right adjoint functor is given by cotensoring, which in the present case coincides with the internal hom $k^V = [V,k]$, for all $V\in \mathbf{Ch}(k)$. The composition of the left adjoints in (4.19) and (4.20) defines a left Quillen functor

$$\begin{aligned} N^*\,:\, \mathbf{sSet}\longrightarrow \mathbf{Ch}(k)^{\text {op}}, \end{aligned}$$

(4.21)

which is the normalized cochains functor. Notice that we do not have to derive this functor because every simplicial set is cofibrant. It was shown in [7] that the normalized cochains on every simplicial set $X\in \mathbf{sSet}$ carry a canonical $\mathcal {E}_\infty$-algebra structure, i.e.

$$\begin{aligned} N^*(X) = [N_*(X),k] \in \mathbf{Alg}(\mathcal {E}_\infty ). \end{aligned}$$

(4.22)

Example 4.9

We may regard any set $S\in \mathbf{Set}$ as a constant simplicial set $S\in \mathbf{sSet}$. Forming the normalized cochains on this simplicial set, we obtain a chain complex concentrated in degree 0 with trivial differential. Concretely, it is given by $N^*(S) = \text {Map}(S,k)$, i.e. the normalized cochain algebra on a set $S\in \mathbf{Set}$ is precisely its function algebra.

More interestingly, we may regard any groupoid $\mathcal {G} \in \mathbf{Grpd}$ as a simplicial set via the nerve functor $B(\mathcal {G}) \in \mathbf{sSet}$. In this case the normalized cochain algebra $N^*(B(\mathcal {G}))$ is precisely the groupoid cohomology algebra, see e.g. [16]. $\bigtriangledown$

The construction above generalizes to the case of stacks, which loosely speaking are smooth simplicial sets. Recall from e.g. [19, 35, 50] that stacks may be described by presheaves of simplicial sets on the site of Cartesian spaces, i.e. they are objects in the category

$$\begin{aligned} \mathbf{H}\, {:}{=} \, \text {PSh}(\mathbf{Cart},\mathbf{sSet})\, =\, \mathbf{sSet}^{\mathbf{Cart}^\text {op}}. \end{aligned}$$

(4.23)

For an example, we refer to the stack of Yang–Mills fields constructed in [3].

In the following we shall endow $\mathbf{H}$ (as well as every other category of presheaves with values in a model category) with its global projective model structure. We explain in Remark 4.10 how our results can be extended to stacks, which are the fibrant objects in the local model structure on $\mathbf{H}$, cf. [19, 35]. From (4.19), we obtain the following induced sequence of Quillen adjunctions between presheaf model categories

where each functor acts object-wise on presheaves. Suppressing as before the functors $(-)\otimes k$ and $\iota$, the composition of left adjoints in (4.24) assigns to an object $X\in \mathbf{H}$ the presheaf of chain complexes $N_*(X)\in \text {PSh}(\mathbf{Cart},\mathbf{Ch}(k))$ whose value on a test space $T\in \mathbf{Cart}$ is

$$\begin{aligned} N_*(X)(T) ~=~N_*\big (X(T)\big )\in \mathbf{Ch}(k). \end{aligned}$$

(4.25)

We shall now generalize the Quillen adjunction in (4.20) to the case of presheaves. Because we are working with presheaves on Cartesian spaces, we choose $k =\mathbb {R}$ or $k=\mathbb {C}$ as the underlying base ring. (With this choice we may describe real or complex-valued cochain algebras.) We define the object $\underline{k}\in \text {PSh}(\mathbf{Cart},\mathbf{Ch}(k))$ by setting $\underline{k}(T) {:}{=} C^\infty (T,k)$ (concentrated in degree 0 with trivial differential), for all test spaces $T \in \mathbf{Cart}$. Because the category $\text {PSh}(\mathbf{Cart},\mathbf{Ch}(k))$ is enriched over $\mathbf{Ch}(k)$, we have a mapping chain complex functor $[-,-]^\infty : \text {PSh}(\mathbf{Cart},\mathbf{Ch}(k))^\text {op}\times \text {PSh}(\mathbf{Cart},\mathbf{Ch}(k))\rightarrow \mathbf{Ch}(k)$, which is explicitly given by the end formula

$$\begin{aligned}{}[V,W]^\infty = \int _{T\in \mathbf{Cart}^\text {op}} \big [V(T),W(T)\big ], \end{aligned}$$

(4.26)

for all $V,W\in \text {PSh}(\mathbf{Cart},\mathbf{Ch}(k))$, where on the right-hand side $[-,-]$ is the internal hom in $\mathbf{Ch}(k)$. There exists an adjunction

where the right adjoint is given by cotensoring $\underline{k}^V (T) = [V,\underline{k}(T)]$, for all $V\in \mathbf{Ch}(k)$ and $T\in \mathbf{Cart}$. Because $\underline{k}\in \text {PSh}(\mathbf{Cart},\mathbf{Ch}(k))$ is a fibrant object, it follows that (4.27) is a Quillen adjunction. The composition of the left adjoints in (4.24) and (4.27) defines a left Quillen functor

$$\begin{aligned} {N^{\infty }}^{*} \, : \, \mathbf{H} \longrightarrow \mathbf{Ch}(k)^\text {op}, \end{aligned}$$

(4.28)

which we call the smooth normalized cochains functor.

In contrast to the case of simplicial sets above, the smooth normalized cochains functor does not necessarily preserve weak equivalences and hence it has to be derived. In order to provide a concrete construction, we can take the very explicit cofibrant replacement functor $Q : \mathbf{H}\rightarrow \mathbf{H}$ developed by Dugger in [18] and define a derived functor by pre-composition

$$\begin{aligned} \mathbb {L} {N^{\infty }}^{*} \,{:}{=} \, {N^{\infty }}^{*} \, Q\, : \, \mathbf{H} \longrightarrow \mathbf{Ch}(k)^\text {op}. \end{aligned}$$

(4.29)

For every $X\in \mathbf{H}$, the derived smooth normalized cochains on X carry a canonical $\mathcal {E}_\infty$-algebra structure, i.e. we canonically have that

$$\begin{aligned} \mathbb {L} {N^{\infty }}^{*}(X) \, = \, \big [N_*\big (Q(X) \big ) ,\underline{k}\big ]^\infty \in \mathbf{Alg}(\mathcal {E}_\infty ). \end{aligned}$$

(4.30)

The relevant argument goes as follows: Recalling (4.26) and (4.25), we have that

$$\begin{aligned} \mathbb {L} {N^{\infty }}^{*} (X) = \int _{T\in \mathbf{Cart}^\text {op}} \big [ N_*\big (Q(X)(T) \big ),\underline{k}(T)\big ]. \end{aligned}$$

(4.31)

Using that by [7] each $N_*\big (Q(X)(T)\big )\in \mathbf{Ch}(k)$ carries a canonical $\mathcal {E}_\infty$-coalgebra structure, we obtain that each term under the end is canonically an $\mathcal {E}_\infty$-algebra and hence so is the end.

Remark 4.10

Recall that in our constructions above we have endowed the category $\mathbf{H} = \text {PSh}(\mathbf{Cart},\mathbf{sSet})$ with its global projective model structure. However, for the study of stacks the local projective model structure on $\mathbf{H}$ is more suitable, see [19, 35]. In short, the local model structure is obtained via left Bousfield localization of the global model structure at all hypercovers. This implies that local and global cofibrations are precisely the same, but there are more weak equivalences and fewer fibrations in the local model structure. We denote the local projective model structure by $\mathbf{H}_{\text {loc}}$ and recall that the category of stacks is by definition the full subcategory $\mathbf{St}\subseteq \mathbf{H}_{\text {loc}}$ of locally fibrant objects. Notice that the full subcategory $\mathbf{St}\subseteq \mathbf{H}_{\text {loc}}$ is not necessarily a model category in its own right. However, it is a so-called homotopical category in the sense of [48], i.e. a category with a notion of weak equivalences satisfying the 2-out-of-6 property. As a consequence of [34, Proposition 3.3.5], we obtain that the local weak equivalences between stacks are precisely the global weak equivalences. This implies that (4.29) restricts to a homotopical functor

$$\begin{aligned} \mathbb {L} {N^{\infty }}^{*} \,:\, \mathbf{St} \longrightarrow \mathbf{Ch}(k)^\text {op}\end{aligned}$$

(4.32)

on the homotopical category of stacks, i.e. it preserves local weak equivalences between stacks.$\vartriangle$

We conclude this subsection with an application to homotopy quantum field theory.

Corollary 4.11

Let $\overline{\mathbf{C}}$ be an orthogonal category. For every functor $X : \mathbf{C}^\text {op}\rightarrow \mathbf{St}\subseteq \mathbf{H}_{\text {loc}}$ with values in stacks (i.e. fibrant objects), we obtain a functor $\mathbb {L} {N^{\infty }}^{*}(X) : \mathbf{C}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$, i.e. via (4.15) an example of a homotopy quantum field theory $p^*\big (\mathbb {L} {N^{\infty }}^{*} (X)\big )\in \mathbf{QFT}_w(\overline{\mathbf{C}})$.

Example 4.12

Let us consider the orthogonal category $\overline{\mathbf{Loc}}$ from Example 3.2. It was shown in [3] that for each spacetime $M\in \mathbf{Loc}$ there exists a stack $\mathsf {YM}_G(M) \in \mathbf{St}$ of solutions of the Yang–Mills equation with a (possibly non-Abelian) structure group G. This assignment is contravariantly functorial, i.e. we have a functor $\mathsf {YM}_G : \mathbf{Loc}^\text {op}\rightarrow \mathbf{St}$. We interpret the derived smooth normalized cochain algebra $\mathbb {L} {N^{\infty }}^{*}(\mathsf {YM}_G(M) ) \in \mathbf{Alg}(\mathcal {E}_\infty )$ as a higher algebra of observables for classical Yang–Mills theory on the spacetime M. The corresponding functor $\mathbb {L} {N^{\infty }}^{*}(\mathsf {YM}_G) : \mathbf{Loc}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$ then defines via (4.15) a toy-model for a homotopy quantum field theory. (Let us recall from above that this construction does not yet take into account Poisson geometric aspects and/or deformation quantization of the gauge theory.)

It is important to emphasize that our higher algebras of observables $\mathbb {L} {N^{\infty }}^{*}(\mathsf {YM}_G(M) ) \in \mathbf{Alg}(\mathcal {E}_\infty )$ are valued in chain complexes. They describe more than just gauge invariant observables, which are given by the 0th homology. Our algebras should rather be interpreted as a generalization of the Chevalley–Eilenberg algebras (i.e. the BRST formalism in physics) from infinitesimal to finite gauge transformations. For (finite-dimensional) Lie groupoid cochain algebras, a precise relationship is understood via the van Est map, see e.g. [16]. We expect that a similar result holds true for stacks and will come back to this issue in a future work. $\bigtriangledown$

5 Examples via homotopy invariants

In this section we present another class of examples of non-strict homotopy quantum field theories on our resolved operads from Theorem 4.7. Our envisaged construction already appeared in a less formal and complete approach in a previous work of two of us [2], and it can be interpreted in terms of orbifoldization, i.e. it takes homotopy invariants of local groupoid actions on quantum field theories. See also [52] for a similar construction for topological field theories. The main missing point in [2] was that we could only establish the relevant homotopy data in low orders, but we had no control of its coherence. It is due to the new techniques developed in the present paper that we can now prove homotopy-coherence of the construction proposed in [2]. In Example 5.1 we explain that such constructions might also be relevant for perturbative quantum gauge theories. Let us emphasize that, in contrast to our previous examples obtained from cochain algebras on stacks (cf. Corollary 4.11), the homotopy quantum field theories obtained from orbifoldization in general do not admit a description in terms of an $\mathcal {E}_\infty$-algebra valued functor; hence, they encode quantum theoretic features.

Let $\overline{\mathbf{C}}$ be an orthogonal category and $\pi : \mathbf{D}\rightarrow \mathbf{C}$ a category fibered in groupoids. We endow $\mathbf{D}$ with the pullback orthogonality relation $\perp _\mathbf{D}{:}{=}\,\pi ^*(\perp _\mathbf{C})$, i.e. $g_1\perp _\mathbf{D}g_2$ if and only if $\pi (g_1)\perp _\mathbf{C}\pi (g_2)$. We obtain an orthogonal functor $\pi : \overline{\mathbf{D}}\rightarrow \overline{\mathbf{C}}$, which we call an orthogonal category fibered in groupoids. Given any strict $\mathbf{Ch}(k)$-valued quantum field theory $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{D}})$ on the total category $\overline{\mathbf{D}}$, we would like to define a quantum field theory on the base category $\overline{\mathbf{C}}$ by forming homotopy invariants along the groupoid fibers $\pi ^{-1}(c)\in \mathbf{Grpd}$, for all $c\in \mathbf{C}$. Since forming (homotopy) invariants corresponds to categorical (homotopy) limits, we are looking for something like a (derived) right adjoint functor of the pullback functor $\pi ^*: \mathbf{QFT}(\overline{\mathbf{C}})\rightarrow \mathbf{QFT}(\overline{\mathbf{D}})$. Unfortunately, such right adjoints (i.e. operadic right Kan extensions) generically do not exist, in contrast to the left adjoints (i.e. operadic left Kan extensions) in (2.16). We therefore propose the following alternative construction: Consider the underlying chain complex-valued functor $\mathfrak {A}: \mathbf{D}\rightarrow \mathbf{Ch}(k)$ of our quantum field theory $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{D}})$. In contrast to the situation above, the pullback functor $\pi ^*:\mathbf{Ch}(k)^\mathbf{C}\rightarrow \mathbf{Ch}(k)^\mathbf{D}$ on functor categories admits a right adjoint, which is given by the right Kan extension ${\text {Ran}}_\pi : \mathbf{Ch}(k)^\mathbf{D}\rightarrow \mathbf{Ch}(k)^\mathbf{C}$ along $\pi :\mathbf{D}\rightarrow \mathbf{C}$. The derived functor corresponding to the right Kan extension is called homotopy right Kan extension (cf. [13, 49]), and it will be denoted as usual by ${\text {hoRan}}_\pi : \mathbf{Ch}(k)^\mathbf{D}\rightarrow \mathbf{Ch}(k)^\mathbf{C}$. Forming the homotopy right Kan extension of (the underlying $\mathbf{Ch}(k)$-valued functor of) our quantum field theory $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{D}})$, however, only defines an object ${\text {hoRan}}_\pi \mathfrak {A}\in \mathbf{Ch}(k)^{\mathbf{C}}$, i.e. we do not automatically get the structure of a quantum field theory on $\overline{\mathbf{C}}$. As observed in [2] by direct computations, it is generically not true that ${\text {hoRan}}_\pi \mathfrak {A}\in \mathbf{Ch}(k)^{\mathbf{C}}$ carries the structure of a strict quantum field theory on $\overline{\mathbf{C}}$ because especially the $\perp$-commutativity property only holds true up to chain homotopies. The novel result which we shall prove in this section is as follows: Choosing a strictified model (in the sense of [35]) for the orthogonal category fibered in groupoids $\pi : \overline{\mathbf{D}}\rightarrow \overline{\mathbf{C}}$, the homotopy right Kan extension ${\text {hoRan}}_\pi \mathfrak {A}$ carries canonically the structure of a homotopy quantum field theory on $\overline{\mathbf{C}}$ corresponding to the resolution $w_{\overline{\mathbf{C}}} : \mathcal {O}_{\overline{\mathbf{C}}}\otimes \mathcal {E}_\infty \rightarrow \mathcal {O}_{\overline{\mathbf{C}}}$ from Theorem 4.7, i.e. ${\text {hoRan}}_\pi \mathfrak {A}\in \mathbf{QFT}_w(\overline{\mathbf{C}})$.

Example 5.1

Let $\overline{\mathbf{Loc}}$ be the orthogonal category of spacetimes from Example 3.2. For constructing perturbative quantum Yang–Mills theory (with non-Abelian structure group G) within the BRST/BV formalism for algebraic quantum field theory, one has to choose background principal G-bundles with connections (satisfying the classical nonlinear Yang–Mills equation) around which one can perturb. This implies that the natural assignment of observable algebras for perturbative quantum Yang–Mills theory is not to spacetimes $M\in \mathbf{Loc}$ but rather to triples (M, P, A), where $M\in \mathbf{Loc}$ is a spacetime and (P, A) is a Yang–Mills field on M, i.e. a principal G-bundle $P\rightarrow M$ with connection A satisfying the Yang–Mills equation.

Let us denote the category of such triples by $\mathbf{YM}_G\mathbf{Loc}$. A morphism $(M,P,A)\rightarrow (M^\prime ,P^\prime ,A^\prime )$ is a principal G-bundle morphism $g : P \rightarrow P^\prime$ that induces a $\mathbf{Loc}$-morphism $M\rightarrow M^\prime$ on the base spaces and that preserves the connections, i.e. $g^*A^\prime =A$. (A similar category appeared before in the work of Zahn on quantum field theories in the presence of background gauge fields [57].) Notice that there exists an obvious projection functor $\pi : \mathbf{YM}_G\mathbf{Loc}\rightarrow \mathbf{Loc}$ which assigns to a triple (M, P, A) its underlying spacetime M and to a morphism $(M,P,A)\rightarrow (M^\prime ,P^\prime ,A^\prime )$ its underlying $\mathbf{Loc}$-morphism $M\rightarrow M^\prime$. It is easy to check that $\pi : \mathbf{YM}_G\mathbf{Loc}\rightarrow \mathbf{Loc}$ is a category fibered in groupoids with fibers $\pi ^{-1}(M) \in \mathbf{Grpd}$ the groupoids of all Yang–Mills fields (P, A) over $M\in \mathbf{Loc}$, which we interpret as background fields. Pulling back the orthogonality relation from $\overline{\mathbf{Loc}}$, we obtain an orthogonal category fibered in groupoids $\pi : \overline{\mathbf{YM}_G\mathbf{Loc}} \rightarrow \overline{\mathbf{Loc}}$.

The constructions in [25, 26, 36] and in particular in [54] concretely define perturbative quantum Yang–Mills theory in terms of a functor $\mathfrak {A}: \mathbf{YM}_G\mathbf{Loc}\rightarrow \mathbf{dgAlg}(k)$ that satisfies the relevant $\perp$-commutativity axiom, i.e. $\mathfrak {A}\in \mathbf{QFT}(\overline{ \mathbf{YM}_G\mathbf{Loc}})$. This is, however, not completely satisfactory for the following reason: For a fixed spacetime $M\in \mathbf{Loc}$, we do not only obtain a single algebra of observables, but rather a whole diagram $\mathfrak {A}\vert _{\pi ^{-1}(M)}^{} : \pi ^{-1}(M)\rightarrow \mathbf{dgAlg}(k)$ of observable algebras corresponding to different choices of background fields around which we perturb. It would be desirable to construct from these data a single observable algebra $\mathfrak {A}_\pi (M)\in \mathbf{dgAlg}(k)$ that combines both the background gauge fields on M and the quantum perturbations around each background. For constructing such a single algebra one has to remove certain gauge redundancies whose origin lies in the following classical picture: Perturbations of Yang–Mills fields on a spacetime $M\in \mathbf{Loc}$ admit different presentations in terms of gauge equivalent background Yang–Mills fields. These presentations should be regarded as being equivalent and hence identified by taking a suitable (homotopy) quotient of the stack of Yang–Mills fields with perturbations. At the dual level of observable algebras, this amounts to forming the homotopy limit

$$\begin{aligned} \mathfrak {A}_\pi (M) \,{:}{=}\, \text {holim}\Big (\mathfrak {A}\vert _{\pi ^{-1}(M)}^{} : \pi ^{-1}(M)\rightarrow \mathbf{dgAlg}(k)\Big ) \in \mathbf{dgAlg}(k) \end{aligned}$$

(5.1)

of the diagram of observables on M. This means that we are taking homotopy invariants along the groupoid fibers $\pi ^{-1}(M)$. By construction, this defines a single algebra $\mathfrak {A}_\pi (M)\in \mathbf{dgAlg}(k)$ that combines the observables for the background gauge fields on M and the observables for the quantum perturbations around each background in a way that the gauge redundancies mentioned above are removed. The main aim of this section is to generalize and formalize this construction and to show that it defines, after a suitable strictification of the category fibered in groupoids, a homotopy quantum field theory, i.e. an algebra over our resolved operad from Theorem 4.7. An open problem, which is not addressed in this paper, is to compute explicitly the homotopy invariants $\mathfrak {A}_\pi (M)\in \mathbf{dgAlg}(k)$ for perturbative quantum Yang–Mills theory and to provide a physical interpretation of the homology groups of this differential graded algebra. We, however, would like to refer the reader to [2] for concrete computations in the simpler setting where the input theory $\mathfrak {A}$ consists of chain complexes concentrated in degree 0. $\bigtriangledown$

In the following we let $\overline{\mathbf{C}}$ be any orthogonal category. Because of the strictification result in [35, Theorems 1.2 and 1.4], we may work without loss of generality with presheaves of groupoids $F:\mathbf{C}^\text {op}\rightarrow \mathbf{Grpd}$ instead of categories fibered in groupoids over $\mathbf{C}$. (Example 5.2 explains how to rephrase our Example 5.1 in terms of a presheaf.) We recall that every presheaf $F \in \text {PSh}(\mathbf{C},\mathbf{Grpd})$ defines a category fibered in groupoids via the Grothendieck construction: The total category $\mathbf{C}_F$ is the category whose objects are pairs (c, x) with $c\in \mathbf{C}$ and $x\in F(c)$ and whose morphisms are pairs $(f, h) : (c,x)\rightarrow (c^\prime ,x^\prime )$ with $f : c\rightarrow c^\prime$ in $\mathbf{C}$ and $h : x \rightarrow f^*x^\prime$ in F(c). For better readability, here and in the following we use the pullback notation $f^*{:}{=} F(f) : F(c^\prime )\rightarrow F(c)$ for the functor corresponding to a $\mathbf{C}$-morphism $f : c\rightarrow c^\prime$. The composition of two $\mathbf{C}_F$-morphisms $(f, h) : (c,x)\rightarrow (c^\prime ,x^\prime )$ and $(f^\prime , h^\prime ) : (c^\prime ,x^\prime )\rightarrow (c^{\prime \prime },x^{\prime \prime })$ is given by $(f^\prime , h^\prime )\, (f, h) {:}{=} \big (f^\prime \,f, (f^*h^\prime )\, h\big ) :(c,x) \rightarrow (c^{\prime \prime },x^{\prime \prime })$. The obvious projection functor $\pi : \mathbf{C}_F \rightarrow \mathbf{C}$, given by $(c,x) \mapsto c$ and $(f,h)\mapsto f$, defines a category fibered in groupoids whose fiber $\pi ^{-1}(c)$ over $c\in \mathbf{C}$ is naturally isomorphic to the value F(c) of the presheaf $F :\mathbf{C}^\text {op}\rightarrow \mathbf{Grpd}$ on c. When endowed with the pullback orthogonality relation, we obtain an orthogonal category fibered in groupoids $\pi : \overline{\mathbf{C}}_F\rightarrow \overline{\mathbf{C}}$.

Example 5.2

Recall from Example 5.1 the category fibered in groupoids $\pi : \mathbf{YM}_G\mathbf{Loc}\rightarrow \mathbf{Loc}$ that describes Yang–Mills fields over spacetimes. The particular model we have given above is not strict because pullbacks of principal G-bundles and connections along principal bundle morphisms are only pseudo-functorial, i.e. the assignment of fibers $\mathbf{Loc}\ni M \mapsto \pi ^{-1}(M)\in \mathbf{Grpd}$ is just a contravariant pseudo-functor. A weakly equivalent strict model has been developed in [3]. More precisely, this paper constructs a functor $\mathsf {YM}_G : \mathbf{Loc}^\text {op}\rightarrow \mathbf{St}$ to the category of stacks such that $\mathsf {YM}_G(M)$ is the moduli stack of Yang–Mills fields on M. Because these Yang–Mills stacks are just 1-stacks (in contrast to $\infty$-stacks), we obtain a groupoid of Yang–Mills fields on every $M\in \mathbf{Loc}$ by taking the global points of these stacks, i.e. $F(M) {:}{=} \mathsf {YM}_G(M)(*) \in \mathbf{Grpd}$. This defines a presheaf of groupoids $F : \mathbf{Loc}^\text {op}\rightarrow \mathbf{Grpd}$ whose Grothendieck construction is weakly equivalent (in the sense of [35]) to the category fibered in groupoids $\pi : \mathbf{YM}_G\mathbf{Loc}\rightarrow \mathbf{Loc}$. Let us mention that the basic reason why the construction in [3] defines a strict presheaf is that the groupoid of Yang–Mills fields F(M) on any $M\in \mathbf{Loc}$ is described in terms of Čech data subordinate to the canonical cover given by all diamond subsets $U\subseteq M$ of M. $\bigtriangledown$

We shall now present our model for the homotopy right Kan extension ${\text {hoRan}}_\pi : \mathbf{Ch}(k)^{\mathbf{C}_F} \rightarrow \mathbf{Ch}(k)^\mathbf{C}$ along the projection functor $\pi : \mathbf{C}_F\rightarrow \mathbf{C}$.

Proposition 5.3

Let $F\in \text {PSh}(\mathbf{C},\mathbf{Grpd})$ be a presheaf of groupoids and $\mathfrak {A}:\mathbf{C}_F\rightarrow \mathbf{Ch}(k)$ a chain complex-valued functor on the corresponding Grothendieck construction. Then the following formula defines a model for the homotopy right Kan extension ${\text {hoRan}}_\pi \mathfrak {A}: \mathbf{C}\rightarrow \mathbf{Ch}(k)$ of $\mathfrak {A}$ along the projection functor $\pi : \mathbf{C}_F\rightarrow \mathbf{C}$. For all $c\in \mathbf{C}$,

$$\begin{aligned} {\text {hoRan}}_\pi \mathfrak {A}(c) \,{:}{=}\, \int _{x\in F(c)} \big [ N_*\big (B\big (F(c) \downarrow x\big )\big ) , \mathfrak {A}(c,x)\big ], \end{aligned}$$

(5.2)

where $[-,-]: \mathbf{Ch}(k)^\text {op}\times \mathbf{Ch}(k) \rightarrow \mathbf{Ch}(k)$ is the internal hom functor, $B: \mathbf{Cat}\rightarrow \mathbf{sSet}$ is the nerve functor, $N_*:\mathbf{sSet}\rightarrow \mathbf{Ch}(k)$ is the normalized chain complex functor [i.e. the composition of left adjoints in (4.19)] and $F(c) \downarrow x$ is the over category of F(c) over $x\in F(c)$.

Proof

Recall from [13, 49] that the homotopy right Kan extension can be computed point-wise as a homotopy limit: For every $c\in \mathbf{C}$, the chain complex ${\text {hoRan}}_\pi \mathfrak {A}(c)\in \mathbf{Ch}(k)$ is the homotopy limit of the diagram

where $c \downarrow \pi$ is the under category of $\pi : \mathbf{C}_F\rightarrow \mathbf{C}$ under $c\in \mathbf{C}$. In the proof of [2, Theorem 5.3] it was shown that the functor $F(c) \rightarrow c \downarrow \pi$ defined by $x\mapsto \big (\text {id}_c : c \rightarrow \pi (c,x)\big )$ is homotopy initial, i.e. there exists a weakly equivalent but simpler model where

$$\begin{aligned} {\text {hoRan}}_\pi \mathfrak {A}(c) \,= \, \text {holim}\Big (\mathfrak {A}\vert _{\pi ^{-1}(c)} : F(c)\rightarrow \mathbf{Ch}(k)\Big ) \end{aligned}$$

(5.4)

is the homotopy limit of the restriction of $\mathfrak {A}:\mathbf{C}_F\rightarrow \mathbf{Ch}(k)$ to the fiber $\pi ^{-1}(c)\cong F(c)$.

We compute (5.4) by using the standard Bousfield-Kan formula, see e.g. [34, Chapter 19] for an excellent summary. For this we endow the model category $\mathbf{Ch}(k)$ with the framing determined by the functors $\mathbf{Ch}(k)\ni V\mapsto N_*(\Delta [-])\otimes V \in \mathbf{Ch}(k)^\Delta$ and $\mathbf{Ch}(k) \ni V\mapsto [N_*(\Delta [-]),V]\in \mathbf{Ch}(k)^{\Delta ^\text {op}}$. Here $\Delta$ is the usual simplex category; hence, $\mathbf{Ch}(k)^\Delta$ is the category of cosimplicial chain complexes and $\mathbf{Ch}(k)^{\Delta ^\text {op}}$ is that of simplicial chain complexes. Moreover, $\Delta [-] : \Delta \rightarrow \mathbf{sSet}$ is the functor that assigns to $[n]\in \Delta$ the simplicial n-simplex $\Delta [n]\in \mathbf{sSet}$. The Bousfield-Kan formula in [34, Definition 19.1.5] can be written as the end

$$\begin{aligned} \text {holim}\Big (\mathfrak {A}\vert _{\pi ^{-1}(c)} : F(c)\rightarrow \mathbf{Ch}(k)\Big ) \,=\, \int _{x\in F(c)} \widehat{\mathfrak {A}}(c,x)^{B(F(c)\downarrow x)}, \end{aligned}$$

(5.5)

where $\widehat{\mathfrak {A}}(c,x) {:}{=} \big [N_*(\Delta [-]),\mathfrak {A}(c,x)\big ] \in \mathbf{Ch}(k)^{\Delta ^\text {op}}$ is the simplicial frame on $\mathfrak {A}(c,x)\in \mathbf{Ch}(k)$. The expression $\widehat{\mathfrak {A}}(c,x)^{B(F(c)\downarrow x)}$ under the end is defined in [34, Definition 16.3.1] as the limit of the diagram

Introducing for notational simplicity the category $J {:}{=} \Delta [-]\downarrow B\big ( F(c)\downarrow x\big )$, we compute

$$\begin{aligned} \widehat{\mathfrak {A}}(c,x)^{B(F(c)\downarrow x)}&\,=\, \text {lim}_{J^\text {op}}^{} \Big (\big [N_*(\Delta [-]),\mathfrak {A}(c,x)\big ]\Big ) \,\cong \, \big [N_*\big (\text {colim}_J^{} \big (\Delta [-]\big )\big ),\mathfrak {A}(c,x)\big ]\nonumber \\&\,\cong \, \big [ N_*\big (B\big (F(c) \downarrow x\big )\big ) , \mathfrak {A}(c,x)\big ]. \end{aligned}$$

(5.7)

For the first isomorphism we used that both $[-,W] : \mathbf{Ch}(k)\rightarrow \mathbf{Ch}(k)^\text {op}$, for any $W\in \mathbf{Ch}(k)$, and $N_*:\mathbf{sSet}\rightarrow \mathbf{Ch}(k)$ are left adjoint functors and hence they preserve colimits. (The colimit of a diagram $J \rightarrow \mathbf{Ch}(k)^\text {op}$ is the limit of the opposite diagram $J^\text {op}\rightarrow \mathbf{Ch}(k)$.) In the second step we used that every simplicial set $X\in \mathbf{sSet}$ is a colimit of simplicial n-simplices via

This completes our proof. $\square$

Remark 5.4

We would like to emphasize that it is because of (5.4) that the homotopy right Kan extension ${\text {hoRan}}_\pi \mathfrak {A}(c)$ describes the homotopy invariants of a functor $\mathfrak {A}: \mathbf{C}_F\rightarrow \mathbf{Ch}(k)$ along the groupoid fiber $\pi ^{-1}(c)\cong F(c)\in \mathbf{Grpd}$. Let us also stress that to obtain (5.4) one uses crucially that $\pi : \mathbf{C}_F\rightarrow \mathbf{C}$ is a category fibered in groupoids, see the proof of [2, Theorem 5.3] for the details.$\vartriangle$

Now we can state the main theorem of this section. In the proof below we use the fundamental result by Berger and Fresse [7] that the normalized chain complex of a simplicial set carries a canonical coaction of the Barratt–Eccles operad $\mathcal {E}_\infty \in \mathbf{Op}_{1}(\mathbf{Ch}(k))$.

Theorem 5.5

Let $\overline{\mathbf{C}}$ be an orthogonal category and $F \in \text {PSh}(\mathbf{C},\mathbf{Grpd})$ a presheaf of groupoids. Furthermore, let $\pi : \overline{\mathbf{C}}_F \rightarrow \overline{\mathbf{C}}$ be the orthogonal category fibered in groupoids that is obtained by the Grothendieck construction applied to F. Given any strict quantum field theory $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{C}}_F)$ on the total category $\overline{\mathbf{C}}_F$, the family of chain complexes ${\text {hoRan}}_\pi \mathfrak {A}(c)\in \mathbf{Ch}(k)$, for $c\in \mathbf{C}$, from Proposition 5.3 carries canonically the structure of an $\mathcal {O}_{\overline{\mathbf{C}}}\otimes \mathcal {E}_\infty$-algebra. In other words, ${\text {hoRan}}_\pi \mathfrak {A}\in \mathbf{QFT}_w(\overline{\mathbf{C}})$ is a homotopy quantum field theory on the base category $\overline{\mathbf{C}}$ corresponding to our resolution $w_{\overline{\mathbf{C}}} : \mathcal {O}_{\overline{\mathbf{C}}}\otimes \mathcal {E}_\infty \rightarrow \mathcal {O}_{\overline{\mathbf{C}}}$ from Theorem 4.7.

Proof

We recall from Sect. 2.3 that an $\mathcal {O}_{\overline{\mathbf{C}}} \otimes \mathcal {E}_\infty$-action on the family of chain complexes ${\text {hoRan}}_\pi \mathfrak {A}(c)\in \mathbf{Ch}(k)$, for $c\in \mathbf{C}$, is given by specifying for each $n\ge 0$ and $(\underline{c},t)\in \mathbf{C}_0^{n+1}$ a $\mathbf{Ch}(k)$-morphism

$$\begin{aligned} \alpha \,:\, \mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big ) \otimes \mathcal {E}_{\infty }(n) \otimes {\text {hoRan}}_\pi \mathfrak {A}(\underline{c}) \longrightarrow {\text {hoRan}}_\pi \mathfrak {A}(t), \end{aligned}$$

(5.9)

where ${\text {hoRan}}_\pi \mathfrak {A}(\underline{c}) = \bigotimes _{i=1}^n {\text {hoRan}}_\pi \mathfrak {A}(c_i)$, such that the compatibility conditions (2.11), (2.12) and (2.13) are satisfied. Because the chain complex $\mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big )$ is a free k-module concentrated in degree 0 with trivial differential (cf. (3.6)), we may equivalently specify $\mathbf{Ch}(k)$-morphisms

$$\begin{aligned} \alpha _{[\sigma ,\underline{f}]}^{} \,:\, \mathcal {E}_\infty (n) \otimes {\text {hoRan}}_\pi \mathfrak {A}(\underline{c}) \longrightarrow {\text {hoRan}}_\pi \mathfrak {A}(t), \end{aligned}$$

(5.10)

for all generators $[\sigma ,\underline{f}]\in \mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big )$.

Using that the homotopy right Kan extension is computed by an end (5.2), we will define (5.10) component-wise, for all $y\in F(t)$ in the groupoid associated with the target color $t\in \mathbf{C}$. To simplify our notation, we abbreviate in what follows the normalized chain complexes in (5.2) by

$$\begin{aligned} N_*(x) \,{:}{=}\, N_*\big (B\big (F(c) \downarrow x\big )\big )\in \mathbf{Ch}(k), \end{aligned}$$

(5.11)

for all $x\in F(c)$. We will define the $y\in F(t)$ component of (5.10) by a $\mathbf{Ch}(k)$-morphism

$$\begin{aligned} \alpha _{[\sigma ,\underline{f}],y}^{} \,:\, \mathcal {E}_\infty (n)\otimes \bigotimes _{i=1}^n \big [N_*( f_i^*y),\mathfrak {A}(c_i,f_i^*y)\big ] \longrightarrow \big [N_*(y),\mathfrak {A}(t,y)\big ], \end{aligned}$$

(5.12)

where in the source we projected down from the ends to the $f_i^*y\in F(c_i)$ components corresponding to the given $y\in F(t)$ and the given family of $\mathbf{C}$-morphisms $\underline{f} = (f_1 :c_1\rightarrow t ,\dots , f_n : c_n\rightarrow t)$ that can be extracted from the generator $[\sigma ,\underline{f}]\in \mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} t\\ \underline{c} \end{array}\big )$ without ambiguity. Using further the adjunction $(-)\otimes V \dashv [V,-]$, for any $V\in \mathbf{Ch}(k)$, we may equivalently consider the adjunct of the morphism (5.12). Using also the symmetric braiding on $\mathbf{Ch}(k)$ to rearrange the tensor factors, we observe that defining (5.12) is equivalent to defining a $\mathbf{Ch}(k)$-morphism

$$\begin{aligned} \widetilde{\alpha }_{[\sigma ,\underline{f}],y}^{} \,:\, \bigotimes _{i=1}^n \big [N_*(f_i^*y),\mathfrak {A}(c_i,f_i^*y)\big ]\otimes N_*(y)\otimes \mathcal {E}_\infty (n) \longrightarrow \mathfrak {A}(t,y). \end{aligned}$$

(5.13)

Using that the normalized chain complex on a simplicial set carries a canonical coaction of the $\mathcal {E}_\infty$-operad (cf. [7, Theorem 2.1.1]), we define the latter morphism by the composition of the following sequence of $\mathbf{Ch}(k)$-morphisms

Let us explain these steps in more detail: Step 1 uses the $\mathcal {E}_\infty$-coaction on normalized chains from [7, Theorem 2.1.1]. Recalling our notation in (5.11), step 2 is induced by the pullbacks $f_i^*: F(t)\downarrow y \rightarrow F(c_i)\downarrow f_i^*y$ of over categories along the given $\mathbf{C}$-morphisms $f_i : c_i\rightarrow t$. Step 3 is just a permutation of tensor factors via the symmetric braiding. In step 4 we used the standard evaluation morphism $\text {ev}: [V,W]\otimes V\rightarrow W$ for internal hom objects, which is the adjunct under $(-)\otimes V \dashv [V,-]$ of the identity $\text {id}: [V,W]\rightarrow [V,W]$. Finally, in step 5 we constructed the canonical lift $[\sigma ,(\underline{f},\text {id}_{\underline{f}^*}y)] \in \mathcal {O}_{\overline{\mathbf{C}}_F}\big (\begin{array}{c} (t,y)\\ (\underline{c},\underline{f}^*y) \end{array}\big )$ of our given element $[\sigma ,\underline{f}] \in \mathcal {O}_{\overline{\mathbf{C}}}\big (\begin{array}{c} t \\ \underline{c} \end{array}\big )$ and used the fact that $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{C}}_F)\cong \mathbf{Alg}(\mathcal {O}_{\overline{\mathbf{C}}_F})$ is by hypothesis an $\mathcal {O}_{\overline{\mathbf{C}}_F}$-algebra.

Taking the adjunct of (5.14) defines (5.12). By a direct calculation one confirms that these components are compatible with the ends, i.e. they define the morphism in (5.10) and consequently also (5.9). Confirming that the resulting morphisms satisfy the compatibility conditions (2.11), (2.12) and (2.13) is a rather lengthy but straightforward computation. $\square$

Remark 5.6

The homotopy quantum field theory ${\text {hoRan}}_\pi \mathfrak {A}\in \mathbf{QFT}_w(\overline{\mathbf{C}})$ from Theorem 5.5 admits an interpretation in terms of fiber-wise normalized cochain algebras on the category fibered in groupoids $\pi :\mathbf{C}_F\rightarrow \mathbf{C}$ with coefficients in a strict quantum field theory $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{C}}_F)$ on the total category. (In other words, this is the fiber-wise groupoid cohomology of $\pi :\mathbf{C}_F\rightarrow \mathbf{C}$ with coefficients in $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{C}}_F)$.) This can be understood by recalling that the chain complex ${\text {hoRan}}_\pi \mathfrak {A}(c)\in \mathbf{Ch}(k)$ assigned to an object $c\in \mathbf{C}$ is given by the end formula (5.2), where $F(c) \cong \pi ^{-1}(c)\in \mathbf{Grpd}$ is the corresponding groupoid fiber. (Compare this to the normalized cochains on a simplicial set with coefficients in k given by (4.22).) Similarly to ordinary groupoid cohomology [16], these chain complexes may have an interesting homology, even for the case where the input quantum field theory $\mathfrak {A}\in \mathbf{QFT}(\overline{\mathbf{C}}_F)$ is concentrated in degree 0 and has a trivial differential. Physical examples of the latter scenario have been discussed in [2], and they include e.g. Dirac fields on the groupoid of all possible spin structures over a spacetime.$\vartriangle$

Appendix

1.1 Derived local-to-global extension for toy-models

The goal of this appendix is to provide concrete evidence that derived local-to-global extension functors as in Examples 3.14 and 3.15 are crucial for gauge theory. In order to simplify our computations, we shall focus as in Remark 4.8 and Sect. 4.3 on very simple toy-models given by $\mathcal {E}_\infty$-algebra valued functors. Because our concrete examples studied below are topological field theories, in the sense that they are insensitive to the spacetime metric, we shall consider instead of the spacetime category $\mathbf{Loc}$ the category $\mathbf{Man}$ of oriented m-dimensional manifolds of finite type with orientation preserving open embeddings as morphisms. Hence, the relevant category of quantum field theories for this appendix is given by $\mathbf{QFT}_{w}(\overline{\mathbf{Man}}^{\max }) \cong \mathbf{Alg}(\mathcal {E}_\infty )^\mathbf{Man}$, where we endowed $\mathbf{Man}$ with the maximal orthogonality relation from Remark 4.8. Instead of , we consider the full orthogonal subcategory $\overline{\mathbf{Disk}}^{\max }\subseteq \overline{\mathbf{Man}}^{\max }$ of all manifolds diffeomorphic to $\mathbb {R}^m$. The corresponding orthogonal embedding functor $j : \overline{\mathbf{Disk}}^{\max } \rightarrow \overline{\mathbf{Man}}^{\max }$ then defines a Quillen adjunction

whose left adjoint is an extension functor to all manifolds for theories $\mathfrak {B}\in \mathbf{QFT}_w(\overline{\mathbf{Disk}}^{\max })\cong \mathbf{Alg}(\mathcal {E}_\infty )^\mathbf{Disk}$ that are only defined on disks.

The main technical tool that we use to compute the derived local-to-global extension of our examples below is the simplicial set tensoring for $\mathcal {E}_\infty$-algebras [27, 28]. This is a functor $\otimes :\mathbf{sSet}\times \mathbf{Alg}(\mathcal {E}_\infty )\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$ that assigns to a simplicial set $K\in \mathbf{sSet}$ and an $\mathcal {E}_\infty$-algebra $A\in \mathbf{Alg}(\mathcal {E}_\infty )$ a new $\mathcal {E}_\infty$-algebra $K\otimes A \in \mathbf{Alg}(\mathcal {E}_\infty )$. The corresponding derived tensoring is given by

$$\begin{aligned} K {\mathop {\otimes }\limits ^{\mathbb {L}}} A \,{:}{=}\, K\otimes Q(A), \end{aligned}$$

(A.2)

where Q(A) is a cofibrant replacement of A in the model category $\mathbf{Alg}(\mathcal {E}_\infty )$. The latter is also referred to as the derived higher Hochschild chains on K with coefficients in A, cf. [28].

The following technical theorem will be the key ingredient for the concrete computations of derived local-to-global extensions in the examples below.

Theorem A.1

Let $\mathfrak {A}\in \mathbf{QFT}_w(\overline{\mathbf{Disk}}^{\max })$ be naturally weakly equivalent to a constant functor $\mathbf{Disk}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$ whose value we denote by $A\in \mathbf{Alg}(\mathcal {E}_\infty )$. Then the derived local-to-global extension $\mathbb {L} j_!(\mathfrak {A}) \in \mathbf{QFT}_w(\overline{\mathbf{Man}}^{\max })$ may be computed object-wise for $M\in \mathbf{Man}$ by

$$\begin{aligned} \big (\mathbb {L}j_! (\mathfrak {A})\big )(M) \,=\, \text {Sing}(M) {\mathop {\otimes }\limits ^{\mathbb {L}}}A, \end{aligned}$$

(A.3)

where $\text {Sing}(M)\in \mathbf{sSet}$ denotes the simplicial set of singular simplices in M.

Proof

Because of $\mathbf{QFT}_w(\overline{\mathbf{Man}}^{\max }) \cong \mathbf{Alg}(\mathcal {E}_{\infty })^\mathbf{Man}$ and $\mathbf{QFT}_w(\overline{\mathbf{Disk}}^{\max }) \cong \mathbf{Alg}(\mathcal {E}_{\infty })^\mathbf{Disk}$, the left adjoint $j_!(\mathfrak {A})$ in (A.1) is given by left Kan extension of $\mathcal {E}_\infty$-algebra valued functors along the embedding functor $j: \mathbf{Disk}\rightarrow \mathbf{Man}$. The left derived functor $\mathbb {L} j_!(\mathfrak {A})$ is therefore a homotopy left Kan extension, which by [13, Proposition 1.14] can be computed object-wise for $M\in \mathbf{Man}$ as a homotopy colimit of the diagram $\mathbf{Disk}\downarrow M \rightarrow \mathbf{Disk}\xrightarrow {\mathfrak {A}} \mathbf{Alg}(\mathcal {E}_\infty )$. Using that by hypothesis $\mathfrak {A}$ is naturally weakly equivalent to a constant functor with value $A\in \mathbf{Alg}(\mathcal {E}_\infty )$, it follows from [34, Chapter 19] that this homotopy colimit is given by the derived tensoring

$$\begin{aligned} \big (\mathbb {L} j_!(\mathfrak {A})\big )(M) \,\simeq \, B(\mathbf{Disk}\downarrow M) {\mathop {\otimes }\limits ^{\mathbb {L}}} A, \end{aligned}$$

(A.4)

where $B:\mathbf{Cat}\rightarrow \mathbf{sSet}$ is the nerve functor.

To conclude the proof, it is sufficient to show that $B(\mathbf{Disk}\downarrow M) \simeq \text {Sing}(M)$ are weakly equivalent in $\mathbf{sSet}$ because the derived tensoring preserves (by construction) weak equivalences. Let us denote by $\mathbf{Open}_M$ the category of open subsets of M and introduce the functor

$$\begin{aligned} \chi \,:\, \mathbf{Disk}\downarrow M \, \longrightarrow \, \mathbf{Open}_M \end{aligned}$$

(A.5)

that sends an open embedding $(f : U \rightarrow M) \in \mathbf{Disk}\downarrow M$ of a disk U into M to its image $f(U)\in \mathbf{Open}_M$. For each point $x\in M$, consider the full subcategory $(\mathbf{Disk}\downarrow M)_x \subseteq \mathbf{Disk}\downarrow M$ of objects whose images under $\chi$ contain the point x. One easily observes that $(\mathbf{Disk}\downarrow M)_x$ is cofiltered, i.e. for any two open subsets $U_1, U_2 \subseteq M$ containing x, there exists a smaller open subset $U \subseteq U_1\cap U_2\subseteq M$ that is diffeomorphic to $\mathbb {R}^m$ and contains x. By [46, Section 1], this implies that the nerve of $(\mathbf{Disk}\downarrow M)_x$ is a contractible simplicial set. With this observation we can apply Lurie’s Seifert–van Kampen theorem [43, A.3.1] to the functor $\chi$ and conclude that there is a weak equivalence (in $\mathbf{sSet}$)

$$\begin{aligned} \text {hocolim}\big (\text {Sing}\circ \chi \big ) \,\simeq \, \text {Sing}(M), \end{aligned}$$

(A.6)

where $\chi$ is regarded here as a functor with values in topological spaces by equipping each open subset of M with the induced topology. Since $\chi (f: U \rightarrow M)$ is a contractible topological space, for each $(f: U \rightarrow M) \in \mathbf{Disk}\downarrow M$, it follows that $\text {Sing}\circ \chi : \mathbf{Disk}\downarrow M \rightarrow \mathbf{sSet}$ is naturally weakly equivalent to the constant functor $*: \mathbf{Disk}\downarrow M \rightarrow \mathbf{sSet}$ whose value is the terminal object $*\in \mathbf{sSet}$. Summing up, we obtained the following chain of weak equivalences (in $\mathbf{sSet}$)

$$\begin{aligned} \text {Sing}(M) \,\simeq \, \text {hocolim}\big (\text {Sing}\circ \chi \big ) \, \simeq \, \text {hocolim}\big (*: \mathbf{Disk}\downarrow M \rightarrow \mathbf{sSet}\big ) \,\simeq \, B(\mathbf{Disk}\downarrow M). \end{aligned}$$

(A.7)

This concludes the proof. $\square$

We shall now discuss two explicit toy-models that are inspired by topological field theory, namely simplified versions of Dijkgraaf–Witten theory and Chern–Simons theory. The aim of our first example is to show that the derived local-to-global extension $\mathbb {L} j_!$ captures the desired global gauge theory observables on topologically non-trivial manifolds, while the underived extension functor fails to do so. Hence, the following example provides a concrete argument why the derived functor is preferable also from a physical perspective.

Example A.2

Inspired by Dijkgraaf–Witten theory, we consider a field theory whose fields on a manifold M are described by the groupoid $\mathbf{PBun}_G(M)$ of principal G-bundles on M, where G is a finite nilpotent group (e.g. Abelian). Using [52, Lemma 2.8] (and its proof), we can describe (up to weak equivalence in $\mathbf{sSet}$) the nerve $B\mathbf{PBun}_G(M)$ of this groupoid by the simplicial mapping space $BG^{\text {Sing}(M)}$, where BG is the nerve of the groupoid associated with the group G. In complete analogy to Corollary 4.11, this defines a theory $\mathfrak {A}\in \mathbf{QFT}_w(\overline{\mathbf{Man}}^{\max })\cong \mathbf{Alg}(\mathcal {E}_\infty )^{\mathbf{Man}}$ that assigns to each $M\in \mathbf{Man}$ the normalized cochain algebra

$$\begin{aligned} \mathfrak {A}(M)\,{:}{=}\, N^*\big (BG^{\text {Sing}(M)}\big ) \in \mathbf{Alg}(\mathcal {E}_\infty ) \end{aligned}$$

(A.8)

on the groupoid of fields.

Our goal is to show that the derived local-to-global extension $\mathbb {L} j_!\, j^*(\mathfrak {A})$ of the restriction $j^*(\mathfrak {A})\in \mathbf{QFT}_w(\overline{\mathbf{Disk}}^{\max })\cong \mathbf{Alg}(\mathcal {E}_\infty )^{\mathbf{Disk}}$ to disks is weakly equivalent to the original theory $\mathfrak {A}$. For this we observe that $j^*(\mathfrak {A})$ is naturally weakly equivalent to the constant functor $N^*(BG) : \mathbf{Disk}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$ that assigns the normalized cochain algebra on BG. (This is because $\text {Sing}(U)\rightarrow *$ is a weak equivalence in $\mathbf{sSet}$ as the underlying topological space of every $U\in \mathbf{Disk}$ is contractible.) Hence, the hypotheses of Theorem A.1 are fulfilled, and we obtain a chain of weak equivalences (in $\mathbf{Alg}(\mathcal {E}_\infty )$)

$$\begin{aligned} \left( \mathbb {L} j_! \,j^*(\mathfrak {A})\right) (M) \,\simeq \, \text {Sing}(M) {\mathop {\otimes }\limits ^{\mathbb {L}}} N^*(BG) \,\simeq \, N^*\left( BG^{\text {Sing}(M)}\right) , \end{aligned}$$

(A.9)

where the last step was proven in [1, Proposition 5.3] and it uses the assumption that G is nilpotent. We conclude that $\mathbb {L}j_!\, j^*(\mathfrak {A}) \simeq \mathfrak {A}$.

Let us discuss these results from a more physical perspective. For a manifold $M\in \mathbf{Man}$, the $\mathcal {E}_\infty$-algebra $\mathfrak {A}(M)$ is a “higher function algebra” on the groupoid $\mathbf{PBun}_G(M)$ of principal G-bundles on M. Its 0th homology $H_0(\mathfrak {A}(M)) = \text {Map}\big (\pi _0\mathbf{PBun}_G(M) , k\big )$ is the ordinary algebra of functions on the set $\pi _0\mathbf{PBun}_G(M)$ of isomorphism classes of such bundles. This means that the $\mathcal {E}_\infty$-algebra $\mathfrak {A}(M)$ describes observables that in particular can be used to distinguish different principal G-bundles on M, which is of course what Dijkgraaf–Witten theory is about. At first sight, it seems that the restriction $j^*(\mathfrak {A})$ to disks discards such bundle observables because $\pi _0\mathbf{PBun}_G(U) \cong *$ is the point and hence the homology $H_0(\mathfrak {A}(U))\cong k$ is the trivial algebra, for all $U\in \mathbf{Disk}$. This is, however, not true: As we have proven above, the derived local-to-global extension $\mathbb {L} j_!\, j^*(\mathfrak {A})$ recovers the bundle observables from the higher algebraic structure of $j^*(\mathfrak {A})$, or equivalently of the constant functor $N^*(BG) : \mathbf{Disk}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$. In stark contrast to this, the underived local-to-global extension is not capable to recover such bundle observables because it extends our constant functor to the functor $j_!\, j^*(\mathfrak {A}) : \mathbf{Man}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$ that assigns to each $M \in \mathbf{Man}$ the coproduct $\bigsqcup _{\pi _0(M)} N^*(BG)$ of $\mathcal {E}_{\infty }$-algebras, where $\pi _0(M)$ denotes the set of connected components of M. Therefore, for M connected, the 0th homology of $j_!\, j^*(\mathfrak {A})(M)$ is the trivial algebra k. $\bigtriangledown$

In our second example we prove that the underived local-to-global extension $j_!$ is not compatible with weak equivalences. More precisely, we show that, even when it happens that $j_!$ produces the desired result for a certain choice of input, changing to a weakly equivalent input results in a non-equivalent outcome. This issue is solved (by construction) by the derived extension $\mathbb {L} j_!$.

Example A.3

Inspired by Chern–Simons theory with structure group $\mathbb {R}$, we consider a field theory whose fields on a 2-dimensional manifold M are described by the chain complex of principal $\mathbb {R}$-bundles with flat connections on M. (Throughout the whole example $\mathbf{Man}$ will be the category of 2-dimensional oriented manifolds.) The chain complex of linear observables on $M\in \mathbf{Man}$ for this theory is concretely defined by the $(-1)$-shifted compactly supported de Rham complex, i.e.

where we indicated in round brackets our homological degree conventions. We define a theory $\mathfrak {A}\in \mathbf{QFT}_w({\overline{\mathbf{Man}}}^{\max }) \cong \mathbf{Alg}(\mathcal {E}_{\infty })^\mathbf{Man}$ by assigning to each $M\in \mathbf{Man}$ the free $\mathcal {E}_{\infty }$-algebra

$$\begin{aligned} \mathfrak {A}(M) \,{:}{=} \, \mathbb {E}_{\infty }\big (\Omega _{c}^*(M)[-1]\big ) \in \mathbf{Alg}(\mathcal {E}_\infty ) \end{aligned}$$

(A.11)

over $\Omega _{c}^*(M)[-1]$. (This is a homotopy-coherent analog of the strictly commutative symmetric algebra over a chain complex.)

As in the previous example, our first goal is to show that the derived local-to-global extension $\mathbb {L} j_!\, j^*(\mathfrak {A})$ of the restriction $j^*(\mathfrak {A})\in \mathbf{QFT}_w(\overline{\mathbf{Disk}}^{\max })\cong \mathbf{Alg}(\mathcal {E}_\infty )^{\mathbf{Disk}}$ to disks is weakly equivalent to the original theory $\mathfrak {A}$. For this we observe that $j^*(\mathfrak {A})$ is naturally weakly equivalent to the constant functor $\mathbb {E}_{\infty }(\mathbb {R}[1]) : \mathbf{Disk}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$ that assigns the free $\mathcal {E}_\infty$-algebra over the 1-shifted monoidal unit $\mathbb {R}[1]$. (This is because the integration map $\int _U : \Omega _{c}^*(M)[-1]\rightarrow \mathbb {R}[1]$ is a weak equivalence between cofibrant chain complexes for every $U\in \mathbf{Disk}$.) Theorem A.1 then implies

$$\begin{aligned} \big (\mathbb {L} j_!\,j^*(\mathfrak {A})\big )(M) \,\simeq \, \text {Sing}(M) {\mathop {\otimes }\limits ^{\mathbb {L}}} \mathbb {E}_{\infty }(\mathbb {R}[1]). \end{aligned}$$

(A.12)

Because $\mathbb {E}_{\infty }(\mathbb {R}[1]) \in \mathbf{Alg}(\mathcal {E}_{\infty })$ is a free $\mathcal {E}_{\infty }$-algebra, the derived tensoring is weakly equivalent to the underived one. Using the explicit formula of [27], a direct computation then shows that

$$\begin{aligned}&\big (\mathbb {L} j_!\,j^*(\mathfrak {A})\big )(M) \simeq \text {Sing}(M) \otimes \mathbb {E}_\infty (\mathbb {R}[1]) = \mathbb {E}_{\infty }\big (N_*(\text {Sing}(M)) \otimes \mathbb {R}[1]\big ).\qquad \end{aligned}$$

(A.13)

One concludes that $\mathbb {L}j_!\, j^*(\mathfrak {A}) \simeq \mathfrak {A}$ because the 1-shifted $\mathbb {R}$-valued normalized chain complex $N_*(\text {Sing}(M)) \otimes \mathbb {R}[1]$ is naturally weakly equivalent to $\Omega _{c}^*(M)[-1]$, which is a consequence of de Rham’s theorem.

Let us now compute the underived local-to-global extension $j_!\, j^*(\mathfrak {A})$ of the restriction $j^*(\mathfrak {A})$, which is given by left Kan extension along $j : \mathbf{Disk}\rightarrow \mathbf{Man}$. Because $j_!$ can be computed object-wise as a colimit and the left adjoint functor $\mathbb {E}_\infty$ preserves colimits, one finds that

$$\begin{aligned} \big (j_!\,j^*(\mathfrak {A})\big )(M) \,&\cong \, \mathbb {E}_\infty \Big ( \text {colim}\Big ( \mathbf{Disk}\downarrow M \rightarrow \mathbf{Disk}\xrightarrow {\Omega ^*_c[-1]} \mathbf{Ch}(\mathbb {R}) \Big ) \Big ) \nonumber \\&\,\cong \, \mathbb {E}_\infty \big (\Omega ^*_c[-1](M)\big ), \end{aligned}$$

(A.14)

where in the last step one exploits a partition of unity argument on M to explicitly compute the colimit, cf. [39, Lemma 4.4.1]. Note that in this specific situation the underived extension $j_!\,j^*(\mathfrak {A})$ is naturally isomorphic to the original theory $\mathfrak {A}$, which is, however, accidental as this result is not stable under weak equivalence. In particular, if we replace the restriction $j^*(\mathfrak {A})$ by the naturally weakly equivalent constant functor $\mathbb {E}_{\infty }(\mathbb {R}[1]): \mathbf{Disk}\rightarrow \mathbf{Alg}(\mathcal {E}_\infty )$, then another direct calculation shows that

$$\begin{aligned} \big (j_!\big (\mathbb {E}_{\infty }(\mathbb {R}[1])\big )\big )(M)&\,\cong \,\mathbb {E}_\infty \Big ( \text {colim}\Big ( \mathbf{Disk}\downarrow M \rightarrow \mathbf{Disk}\xrightarrow {\mathbb {E}_\infty (\mathbb {R}[1])} \mathbf{Ch}(\mathbb {R}) \Big ) \Big ) \nonumber \\&\,\cong \, \bigsqcup _{\pi _0(M)} \mathbb {E}_\infty ( \mathbb {R}[1]), \end{aligned}$$

(A.15)

where $\pi _0(M)$ is the set of connected components of M. One easily sees that (A.14) and (A.15) are not weakly equivalent by considering for example the 2-sphere $M= \mathbb {S}^2$. The conclusion is that the underived local-to-global extension $j_!$ is inconsistent in our homotopical framework because it assigns to weakly equivalent theories $j^*(\mathfrak {A}) \simeq \mathbb {E}_\infty (\mathbb {R}[1])$ on disks genuinely different theories on all manifolds. This lack of stability under weak equivalences is of course solved (by construction) by working with the derived extension functor $\mathbb {L} j_!$. $\bigtriangledown$