Pore Pressure Uncertainty Characterization Coupling Machine Learning and Geostatistical Modelling

Abstract

Pore pressure prediction is fundamental when drilling deep and geologically complex reservoirs. Even in relatively well-characterized hydrocarbon reservoir fields, with a considerable number of drilled wells, when located in challenging geological environments, poor prediction of abnormal pore pressure might result in catastrophic events that can cause harm to human lives and infrastructures. To better quantify drilling risks, the uncertainty associated with the pore pressure prediction should be integrated within the geo-modelling workflow. Leveraging a challenging real case from the Brazilian pre-salt, the work presented herein proposes a seismic-driven gradient pore pressure modelling workflow, which combines machine learning and geostatistical co-simulation to predict high-resolution gradient pore pressure volumes. First, existing angle-dependent seismic reflection data are inverted for P- and S-wave velocity and density. Then, K-nearest neighbor is used to create a regression model between pore pressure gradient and P- and S-wave velocity, density and depth based on the well log information. The trained model is applied to predict a three-dimensional gradient pore pressure model from the models obtained from geostatistical seismic inversion. This gradient pore pressure model is a smooth representation of the highly variable subsurface and is used as secondary variable in stochastic sequential co-simulation with joint probability distributions to generate multiple high-resolution realizations of gradient pore pressure. The ensemble of co-simulated models can be used to assess the spatial uncertainty about the gradient pore pressure predictions. The results of the application example show the ability of the method to reproduce the spatial patterns observed in the seismic data and to reproduce existing gradient pore pressure well logs at two blind well locations, which were not used to condition the gradient pore pressure predictions.

1 Introduction

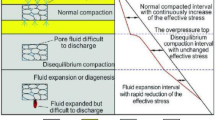
Abnormal pore pressure is one of the most relevant geohazards and an important aspect to consider when drilling deep sedimentary structures. Abnormal pore pressure is the origin of most drilling accidents in the early exploration phases of hydrocarbon reservoirs. Even in well-characterized reservoir formations, abnormal pressure is still a considerable risk factor for drilling new wells in both exploration and production phases. However, pore pressure prediction is challenging. Nevertheless, it is a crucial and fundamental tool for managing the drilling of such structures.

Pore pressure prediction has been proposed through the modelling of empirical relationships between seismic velocity, estimated during the seismic processing stage, and pore pressure. Under this framework, the most widely used approximations are the equivalent depth method (Hottmann and Johnson 1965), Eaton’s method (Eaton 1972, 1975), Bowers’ method (Bowers 1995, 2001), the Miller’s method, and the Tau method (Zhang 2011).

These empirical methods are deterministic and are based on non-linear relationships between seismic velocity, which normally results from velocity analysis performed during the seismic processing, electrical resistivity, and gradient pore pressure (GPP), whose parameters are calibrated with existing well data from the sedimentary basin under investigation or from analogue basins. However, these prediction methods do have some limitations: In the parameter calibration phase with the available data, it is difficult to obtain and assume a valid and representative model of the entire data set (i.e., these methods assume spatial stationarity), particularly when one has a deep target and a large regional data set (i.e., spatially distributed over a large area). After the calibration, when the methods are applied to a given velocity model (i.e., a low-frequency velocity model resulting from velocity analysis performed during the seismic data processing) to predict GPP, they only provide a low-frequency model of GPP with no uncertainty attached, as these velocity models are frequently retrieved from conventional seismic velocity analysis during the seismic processing (Yilmaz 1987). Nunes et al. (2015) and Soares et al. (2017) assumed the GPP predicted model from Eaton’s method as an average model to assess the GPP uncertainty with a stochastic sequential simulation with local means. For the same purpose, but with a different approach, Karmakar and Maiti (2019) implemented a Bayesian neural network optimized by scaled conjugate gradient and hybrid Monte Carlo approaches to model the pore pressure and estimate the uncertainty in predictions from well log data. However, this machine learning framework assumes that a large set of well data to train and test the prediction algorithms is available. Other authors applied alternative machine learning regression algorithms to predict pore pressure models. For example, Haris et al. (2017) employed a probabilistic neural network method to predict pore pressure by applying bulk density, V_P/V_S ratio, P-impedance (I_P), and S-impedance (I_S) as input parameters to the predictive model. Naeini et al. (2019) proposed a supervised deep learning neural network to predict pore pressure along with geomechanical and petrophysical properties for unconventional plays. Their method is implemented with many wells and seismic-derived attributes to estimate volumes. Radwan et al. (2022) compared several ML methods to predict pore pressure using geophysical well log data from a large number of wells in a case study located in New Zealand. Recently, Zhang et al. (2022) compared the performance of a set of machine learning algorithms to predict pore pressure based on petrophysical log data.

This work proposes an alternative approach to assess the uncertainty of seismic-driven gradient pore pressure models predicted at a high spatial resolution. The proposed geo-modelling workflow is based on the following three main methodological steps, which are detailed in the following sections (Fig. 1):

• (i) In a first step, elastic models of V_P, V_S and density (ρ) are predicted from geostatistical seismic amplitude-versus-angle (AVA) inversion (Azevedo et al. 2018). These models are predicted conditioned to the available partial angle stack volumes, well log data, and a variogram model that reveals the expected spatial continuity pattern.

• (ii) In a second step, machine learning (ML) regression algorithms are tested and applied to obtain the first prediction of a three-dimensional model of GPP based on the V_P, V_S, ρ models and depth.

• (iii) In the last step, once the three-dimensional volume of the GPP model is obtained by applying the ML from (ii) to the models from (i), the uncertainty of the GPP model is characterized using stochastic sequential simulation with joint probability distributions (Horta et al. 2010). We first build a joint distribution between observed values from the well log data and the corresponding predicted values of GPP with ML. A conditional distribution of GPP given the ML predicted value can be evaluated at each well log data location. Then, the uncertainty of the GPP is assessed through the stochastic sequential co-simulation with joint distributions (Horta et al. 2010; Soares et al. 2017), assessing the uncertainty of the predicted GPP models.

Fig. 1

Schematic representation of the proposed workflow

The proposed methodology is illustrated using a real three-dimensional application example from the Brazilian pre-salt. In our case study, we have a set of 12 wells with well log data located within two neighbor hydrocarbon fields, where we wish to characterize the uncertainty and risk of GPP. Figure 2 represents the spatial location of the wells and the limits of study area. Exploratory data analysis shows a great heterogeneity in the relationship between the seismic wave propagation velocity and pore pressure (i.e., there are wells with an apparently good relationship between these variables and others in which the relationship is weak or not evident).

Fig. 2

Relative location of the available well data to the seismic reflection data. The black polygons represent the location of the two existing hydrocarbon fields. The blue polygon represents the extent of the available seismic volume and the red line the location of the vertical well section used to illustrate the application example shown below

2 Characterization of V _P, V _S and Density Models with Geostatistical Seismic AVA Inversion

To predict high-resolution three-dimensional models of V_P, V_S and ρ we apply geostatistical seismic AVA inversion (Azevedo et al. 2018; Tylor-Jones and Azevedo 2022). In summary, this iterative geostatistical seismic inversion can be divided into three main steps. The first step comprises the generation of an ensemble of elastic models sequentially with stochastic sequential simulation and co-simulation (Fig. 3). The first elastic property to be generated is ρ, followed by V_P conditioned to the previously simulated model of density, and finally V_S conditioned to the previously generated V_P model. This sequential approach ensures the reproduction of the joint relationship between the elastic properties. The existing well log data are used as local conditioning data for the stochastic sequential simulation and co-simulation and to retrieve the three-dimensional variogram models for each property.

Fig. 3

Schematic representation of the iterative geostatistical seismic AVA inversion

The second step is the forward model. Within the ensemble of elastic properties, each set of V_P, V_S and ρ is forward-modelled. The angle-dependent reflection coefficients are calculated using a non-linear approximation of the Zoeppritz equations. Then, the reflectivity series are convolved with a wavelet representing each incident angle to compute synthetic partial angle stacks.

The last step is the trace-by-trace comparison between synthetic and real seismic traces and the stochastic update of the elastic models during the subsequent iteration. Synthetic and real seismic are compared on a trace-by-trace basis, considering the waveform and amplitude content of the signal. A possible equation that might be used as an objective function and that is sensitive to both parameters is shown below (Azevedo and Soares 2017)

$$ {\varvec{S}} = \frac{{2\mathop \sum \nolimits_{k = - n}^{n} \left( {d_{t + k} d_{t + k}^{*} } \right)}}{{\mathop \sum \nolimits_{k = - n}^{n} \left( {d_{t + k} } \right)^{2} + \mathop \sum \nolimits_{k = - n}^{n} \left( {d_{t + k}^{*} } \right)^{2} }}, $$

(1)

where d_t and $d_{t}^{*}$ are the observed and predicted seismic traces at sample t, and n is the size of a moving window used to compute the similarity between the two traces. As in Pearson’s correlation coefficient, S varies between −1 and 1; however, as these coefficients are used as a proxy for local correlation coefficients in the co-simulation of a new set of elastic models in the subsequent iteration, the negative values are truncated at zero. While similar to Pearson’s correlation coefficient, S allows simultaneously matching the seismic waveform and amplitude of each trace, which is critical to predict reliable subsurface earth models from seismic reflection data.

The elastic traces that produce the highest S at a given iteration are stored along with the similarity coefficient in a set of auxiliary volumes. These volumes will be used as secondary variables in the stochastic sequential co-simulation of a new set of models in the subsequent iteration. It is worth noting that S controls the degree of assimilation of the observed data in the generation of elastic models in the subsequent iteration. The iterative procedure stops when the global S between observed and predicted data is above a user-defined threshold. Once the convergence is reached, all the co-simulated models in the last iteration produce synthetic seismic highly similar to the observed one.

All the simulated and co-simulated models share some common characteristics. They exactly reproduce the well log data at the well locations, the marginal and joint distribution of the properties of interest as retrieved from the well log data and the spatial continuity patterns revealed by the variogram models. Also, depending on the variogram model used during the geostatistical simulation, and due to the integration of the well log data as conditioning data of the inversion, the inverted models show higher resolution than the recorded seismic, allowing characterization of layers at and below the seismic resolution.

A typical way to interpret the results of geostatistical inversion is by computing the pointwise average model of all the realizations that produce synthetic seismic with a S higher than a given threshold. The pointwise average model represents the most likely model and has a smoother spatial distribution than the single stochastic realizations. The pointwise average models of V_P, V_S and ρ retrieved from the last iteration of the elastic inversion are shown in Fig. 4.

Fig. 4

Vertical well section extracted from the pointwise average model of a density, b P-wave velocity, c S-wave velocity

The geostatistical seismic AVA inversion is performed in the time domain. The predicted elastic models are then converted into the depth domain using a velocity model that integrates velocity data from wells, geological information in the form of seismic horizons, and velocities estimated from the seismic velocity analysis. In the application example shown herein, no uncertainty is considered associated with the velocity model used to perform time-to-depth conversion.

3 Characterization of the GPP Model by ML Regression

The objective of this step is to predict a GPP model based on the elastic parameters (V_P, V_S and ρ), obtained by seismic inversion in the previous step, and depth. For this step, we use the pointwise average model of all the stochastic realizations of V_P, V_S and ρ generated during the last iteration of the iterative geostatistical seismic inversion.

The application example shown herein predicts GPP with K-nearest neighbor (KNN) (e.g., Hastie et al 2002). This method was selected for its best performance, in terms of train and test scores, from an ensemble of regression ML methods applied to the test data set (Table 1). However, alternative ML predictions can be used depending on the study area's complexity and the quality and number of available samples.

Table 1 ML methods tested to predict GPP from the elastic properties

In an orthonormal space A, defined by the independent variables, the regression of x₀ by KNN is calculated through the linear combination of the Z value (i.e., dependent variable) of the N closest samples x_i weighted by 1 (Fig. 5a)

$$ [Z\left( {x_{0} } \right)]^{*} = \left[ l \right]T \cdot \left[ Z \right]. $$

(2)

Fig. 5

a Representative sketch of the target sample x₀ (predicted value) with the linear combination of nearest samples in an orthonormal space. b Test accuracy curve used to select N

In the application example shown below N was set to five after applying the grid search algorithm over the parameter space. The grid search algorithm applied herein is available at Python’s scikit-learn library. During this process, all integer values of N between 5 and 10 were evaluated resulting in the test accuracy curve (Fig. 5b). N = 5 represents the minimum number of neighbors for the highest accuracy.

If we assume that the samples x_i, are spatially structured and defined by a covariance C(h) in space A, then the best least squares regression of z(x₀) is the following linear combination of z(x_i)

$$ \left[ {Z\left( {x_{0} } \right)]^{2*} = \left[ M \right]T \cdot } \right[K]^{ - 1} \cdot \left[ Z \right], $$

(3)

where [M] is the covariance matrix between sample values z(x_i) and [K] is the covariance vector of x_i and x₀.

After a random splitting of the entire data set (i.e., the well log data) into training and test data sets, the performance of the KNN regression can be evaluated by the scatter plot shown in Fig. 6 and computing the mean average error (MAE), mean squared error (MSE) and the mean absolute percentage error (MAPE) (Table 2) between predicted and observed values of the test data set.

Fig. 6

Scatter plot between observed predicted GPP values with KNN. Green circles represent training data, and blue crosses test data

Table 2 MAE, MSE and MAPE computed between observed and predicted data from the testing data set

Let us denote by ϕ the KNN regression model ${\text{GPP}} = \phi \left( {V_{{\text{P}}} , V_{{\text{S}}} , \rho , {\text{depth}}} \right)$. Based on the regression model, ϕ, the GPP model was estimated based on the independent three-dimensional volumes of V_P, V_S, ρ and depth of each sample. Figure 7 represents a sequence of depth slices extracted from the pointwise average elastic models, and Fig. 8 the corresponding depth slices of GPP obtained by this regression.

Fig. 7

Depth slices extracted from the pointwise average models of a density, b P-wave velocity, c S-wave velocity

Fig. 8

Depth slices extracted from the predicted GPP model at three different depths. Depth slices extracted at the same depths as in Fig. 7

4 Uncertainty Characterization of the GPP Model by Stochastic Sequential Simulation

Let us assume the real GPP values as variable Z and the predictions obtained by KNN regression as variable $z_{{{\text{KNN}}}}^{*}$. Although the GPP model obtained by KNN is a good regression model, there is some uncertainty attached to the regression model (i.e., the variability of the real/observed GPP values, z, for a given predicted GPP value, $z_{{{\text{KNN}}}}^{*}$). In other words, the conditional variance, ${\text{var}} (z|z_{{{\text{KNN}}}}^{*} )$, is particularly high for the lowest $z_{{{\text{KNN}}}}^{*}$ values, and low for the highest $z_{{{\text{KNN}}}}^{*}$ values (Fig. 9). The idea is to account for this variability in the spatial uncertainty assessment of GPP with stochastic sequential co-simulation.

We propose the use of stochastic sequential simulation of Z with the joint probability distribution of the predicted and real GPP values, $f\left( {z,z^{*} } \right)$. The regression model $z_{{{\text{KNN}}}}^{*}$ is used as secondary variable and, at each spatial location of the regular grid of nodes, a conditional probability distribution $f(z|z_{{{\text{KNN}}}}^{*} )$ is calculated from the bivariate distribution $f\left( {z,z_{{{\text{KNN}}}}^{*} } \right)$.

The pore pressure uncertainty of Z is obtained with the direct sequential simulation with joint probability distribution (Horta and Soares 2010). The simulated values at any location x₀ are generated from the conditional distribution functions $f_{{x_{0} }} \left( {z,z_{KNN}^{*} } \right)$, thus integrating the local uncertainty of Z.

Direct sequential simulation with joint distribution (Horta and Soares 2010) has been extensively tested in several applications related to subsurface modelling characterization (Azevedo and Soares 2017) due to the ability of the method to reproduce complex joint distributions. Direct sequential simulation with joint distribution can be summarized in the following steps:

• (i) At any spatial location x₀, selected by a random path that visits the entire regular grid of points covering the study area, the value of the regression model, $z_{{{\text{KNN}}}}^{*} \left( {x_{0} } \right)$, is retained. From the joint distribution (Fig. 6) the conditional distribution of GPP values, z(x), is calculated, conditioned to the value $z_{{{\text{KNN}}}}^{*} \left( {x_{0} } \right){:}F_{{z|z^{*} }} \left( {x_{0} } \right)$ (Fig. 9) (Horta and Soares 2010; Azevedo and Soares 2017).

• (ii) Local mean and variance of z(x₀) are calculated by simple kriging, based on the sample neighborhood values and previously simulated values (Soares 2001).

• (iii) The simulated value of GPP at x₀ is generated from the local conditional distribution function, $F_{{z|z^{*} }}^{{}} \left( {x_{0} } \right)$, calculated in (i), centered on the mean and local variances calculated in (ii).

• (iv) Return to point (i) until all values of the regular grid are simulated.

Fig. 9

Example of the joint probability distribution $F_{{z|z_{{{\text{KNN}}}}^{*} }}^{{}}$ at location x₀ = 9.35

The stochastic sequential simulation model guarantees the reproduction of the spatial continuity patterns of pore pressure (i.e., spatial covariance models), the marginal probability distribution function F_z(x₀) and the joint probability distribution function $F_{{z|z_{{{\text{KNN}}}}^{*} }}^{{}} \left( {x_{0} } \right)$.

5 Results of GPP Uncertainty Model

5.1 Pore Pressure Uncertainty Model

Fifty realizations of GPP were generated using the methodology described in Sect. 4. The pointwise average GPP model computed from this ensemble of 50 geostatistical realizations is shown in Fig. 10. The spatial continuity pattern of GPP presented in the KNN predictions is reproduced, but as expected, the pointwise average model is smoother.

Fig. 10

Depth slices extracted from the pointwise average model computed from the geostatistical realizations of the GPP model. Depth slices extracted at the same depths as in Fig. 7

Figure 11 shows the scatter plot of the simulated GPP values with direct sequential simulation with joint distributions and the values predicted by KNN for all nodes of the regular grid. There is a good reproduction of the corresponding cross-plot of experimental test data set (Fig. 6).

Fig. 11

Scatter plot between one geostatistical realization of GPP and the predicted GPP with KNN ($Z_{{{\text{KNN}}}}^{*}$)

We assess the spatial uncertainty of GPP calculating the inter-quantile distance (P25–P75) from the ensemble of GPP geostatistical realizations (illustrated with depth slices in Fig. 12). Comparing with the pointwise average models (Fig. 10), one can see these models reproduce well the uncertainty of the bivariate distribution of Fig. 6: high values of GPP tend to have low spatial uncertainty and low GPP values normally are associated with high uncertainty/variance (Fig. 13).

Fig. 12

Depth slices extracted from the inter-quantile distance model computed from the geostatistical realizations of GPP model. Horizon slices extracted at the same depths as in Fig. 7

Fig. 13

Comparison between the experimental relationship between observed and predict GPP and the spatial distribution of the predictions and spatial uncertainty

6 Discussion

Validation only at the well locations. The geo-modelling workflow proposed herein aims at characterizing a gradient pore pressure uncertainty model based on V_P, V_S and ρ models predicted from iterative geostatistical seismic AVA inversion and depth. The proposed model uses a ML regression of these independent variables to obtain a pore pressure prediction model, which is used as an auxiliary variable in a stochastic simulation with local probability distributions. The spatial uncertainty of GPP for the entire area is obtained through the ensemble of realizations of stochastic simulation.

The quality and reliability of the predicted GPP model are highly dependent on the quality of the inverted elastic models. Poor performance of the prediction of the elastic models will result in poor GPP predictions. The local, trace-by-trace, mismatch between predicted and observed seismic traces can be used to assess the local convergence of the geostatistical inversion. Also, reliable GPP predictions depend on the performance of the ML method that is being used to predict the average GPP model. If the ML model has low accuracy, then the predicted GPP will be highly uncertain. It is worth noting that the proposed methodology requires a relatively large data set to guarantee the robustness of ML regression and, consequently, the accuracy and unbiasedness of the predicted model as secondary variable.

In the application example shown herein, the final pore pressure uncertainty model was validated using two blind well locations as a tool for spatial management of risk of abnormal pore pressure incidence. Two wells were chosen to be part of a blind well test (W11 and W12) (Fig. 2). These two wells have different performance in terms of prediction quality. Each of these wells was removed one at a time, and two sets of 50 realizations were generated without one of those wells. Figure 13a shows the results for well W11: the observed values of GPP (blue line), the median, P10 and P90 of the model at the well location. Figure 13b shows the results for well W12. Note that the blue line represents a linear interpolation of the observed values. Even in the worst case (Fig. 13b), the expected error (median of the model-real) is negligible. The results obtained for both blind well locations are acceptable and validate the pore pressure model created by the proposed methodology as a consistent and reliable model (Fig. 14).

Fig. 14

Local comparison between observed and predicted GPP values for well a W11 and b W12

7 Conclusions

The prediction of local gradient pore pressure and access to the uncertainty and risk of these values based on the seismic inverse models is still an important and challenging topic in both the exploration and production phases due to the technological risks it entails.

The methodology proposed in this study for characterizing the uncertainty of a pore pressure model based on elastic models derived from seismic inversion is based on a hybrid framework with two fundamental methodological vectors: (i) The first is an ML model to predict the GPP. Once validated, in the ML test phase a bivariate probability distribution law built from predicted versus real GPP values is created. This joint distribution allows one to assess the uncertainty of the predicted 3D pore pressure model values. (ii) The second vector is a geostatistical methodology of stochastic simulation with joint probability distribution laws that is used to generate an ensemble of GPP models and to derive the spatial uncertainty of this property under study.

The results of the application to a real case study validated this framework as a very promising method for accessing local values and uncertainty of GPP models. However, the use of an ML predictor implies the availability of an amount of data that makes the predictor robust, which can limit the application of the framework to the production phase, normally with more data, or to the exploration phase but with data borrowed from similar case studies, with the consequent risk of representativeness of these data.