On the Construction of Bootstrap Confidence Intervals for Estimating the Correlation Between Two Time Series Not Sampled on Identical Time Points

Abstract

Two important issues characterize the design of bootstrap methods to construct confidence intervals for the correlation between two time series sampled (unevenly or evenly spaced) on different time points: (i) ordinary block bootstrap methods that produce bootstrap samples have been designed for time series that are coeval (i.e., sampled on identical time points) and must be adapted; (ii) the sample Pearson correlation coefficient cannot be readily applied, and the construction of the bootstrap confidence intervals must rely on alternative estimators that unfortunately do not have the same asymptotic properties. In this paper it is argued that existing proposals provide an unsatisfactory solution to issue (i) and ignore issue (ii). This results in procedures with poor coverage whose limitations and potential applications are not well understood. As a first step to address these issues, a modification of the bootstrap procedure underlying existing methods is proposed, and the asymptotic properties of the estimator of the correlation are investigated. It is established that the estimator converges to a weighted average of the cross-correlation function in a neighborhood of zero. This implies a change in perspective when interpreting the results of the confidence intervals based on this estimator. Specifically, it is argued that with the proposed modification of the bootstrap, the existing methods have the potential to provide a useful lower bound for the absolute correlation in the non-coeval case and, in some special cases, confidence intervals with approximately the correct coverage. The limitations and implications of the results presented are demonstrated with a simulation study. The extension of the proposed methodology to the problem of estimating the cross-correlation function is straightforward and is illustrated with a real data example. Related applications include the estimation of the autocorrelation function and the periodogram of a time series.

1 Introduction

Confidence intervals for the Pearson correlation coefficient are a key statistical tool to understand and quantify the uncertainty about the linear relationship between two variables observed over time. The vast amount of time-dependent data available from different fields provides a very rich set of potential applications where confidence limits for the correlation make it possible to test whether and how a certain time-dependent variable depends on another, and how this relationship might change over time. In many applied problems, the two time series that need to be compared are both unevenly spaced (the sampling is not uniform over time) and observed at unequal timescales (the set of time points for the first series is not identical to the set of time points for the second series). There may be several reasons for the irregularity of the observations. In many applications where the data collection is based on sensor networks or a distributed monitoring infrastructure (e.g., health care, environmental monitoring, geology, meteorology, network traffic studies), unevenly spaced time series observed at unequal timescales arise naturally due to the difficulty in synchronizing the different sensors, missing data, and the different sampling intervals and policies used to collect the variables (Erdogan et al. 2005). In finance, the transaction prices observed for different assets are also time series that are unevenly sampled in time and with different timescales due to the fact that transactions such as trading stock on an exchange do not occur at equally spaced time intervals. In paleoclimate studies, irregular sampling is often the result of a complex sedimentation/accumulation rate (Rehfeld et al. 2011; Mudelsee 2014). As observed by Roberts et al. (2017) for ice core records, a uniform spatial sampling produces a nonuniform sampling in time, as the spatial and temporal distribution of a sample material depends on its depth. In observational astronomy, sampling times are determined by seasonal and weather conditions and the availability of observational equipment, and are therefore inherently nonuniform (Eckner 2014). Quantifying the uncertainty of the correlation in these cases is a challenge for at least two reasons: (i) ordinary block bootstrap methods that produce bootstrap samples have been designed for time series observed at the same timescale and must be adapted; (ii) the sample Pearson correlation coefficient cannot be readily applied, and the bootstrap confidence intervals must be constructed on alternative estimators that, unfortunately, do not have the same asymptotic properties. This has important consequences for the interpretation and for the empirical coverage of the resulting methods.

A thorough search of the relevant literature yielded only one article on the construction of confidence limits for unevenly spaced time series observed at unequal timescales: the paper by Roberts et al. (2017). Their approach is an extension of the method discussed by Mudelsee (2003) and Ólafsdottir and Mudelsee (2014), which considers the simpler case where the data are unevenly spaced but coeval (i.e., observed at the same timescale), and is based on the bias-corrected and accelerated (BCa) method proposed by Efron (1987), the Gaussian kernel estimator (Rehfeld et al. 2011), and a modified version of the stationary bootstrap of Politis and Romano (1994). This paper argues that the approach of Roberts et al. (2017), hereafter called the “GK (Gaussian kernel) method”, provides a good starting point but an unsatisfactory solution to issue (i) and ignores issue (ii), giving rise to a procedure with poor statistical properties whose limitations and potential applications are not well understood.

As a first step to address these issues, a modification of the bootstrap of the GK method is proposed, and the properties of the estimator of the correlation underlying the method are investigated. It is shown that the estimator does not target the correlation between the two time series but rather a weighted average, $\rho _{0}$, of the cross-correlation function (CCF) in a neighborhood of zero where the weights depend on the features of the bivariate stationary process that generates the data and on the distributions of the inter-sampling-time intervals. Depending on the problem, $\rho _{0}$ could be very close to or very far from the true correlation. This implies that, asymptotically, the GK method has zero coverage, and introduces a change in perspective when studying the statistical properties and interpreting the confidence intervals produced by the method. In particular, it can be observed that with the proposed modification of the stationary bootstrap, the GK method has the potential to provide a useful lower bound for the absolute correlation in the non-coeval case and, in some special cases, confidence intervals with an approximately correct coverage. The limitations and implications of the results presented are demonstrated with a simulation study. The extension of the proposed methodology to the problem of estimating the CCF at a generic lag l is straightforward and is illustrated with a real data example. Related applications include the estimation of the autocorrelation function and the periodogram of a time series.

2 Stationary Bootstrap for the Non-Coeval Case

Let $\{x(i)\}_{i=1}^{n_{X}}$ and $\{y(j)\}_{j=1}^{n_{Y}}$ be two time series, of length $n_{X}$ and $n_{Y}$, respectively, sampled (evenly or unevenly) at different time points $\{t_{X}(i)\}_{i=1}^{n_{X}}$ and $\{t_{Y}(j)\}_{ij=1}^{n_{Y}}$ from a certain bivariate process $\{ X(i), Y(i) \}$. Following Ólafsdottir and Mudelsee (2014), two time series of this type may be called non-coeval. The bivariate process is assumed to be weakly stationary. The goal is to build a bootstrap-based confidence interval for the lag-0 correlation between the X and Y components of the bivariate process. Roberts et al. (2017) is the only published algorithm for this type of problem, and comprises three subroutines: ($s_1$) the stationary bootstrap; ($s_2$) the Gaussian kernel estimator; and ($s_3$) the BCa method. This section discusses the limitations of the stationary bootstrap of Roberts et al. (2017) and proposes a modified version of the bootstrap.

2.1 Stationary Bootstrap Underlying the GK Method

In Roberts et al. (2017), the stationary bootstrap (hereafter subroutine 2) is presented as a simple extension of the stationary bootstrap of Politis and Romano (1994), with block length selection as in Mudelsee (2003). However, a closer look reveals that the extension is not a trivial one. A description of subroutine 2, as can be deduced from the Matlab code provided by the authors, is presented in Online Resource 1. Let us denote the $b{\text {th}}$ bootstrap sample by

$$\begin{aligned} \{x^{*b}(i),t_{X}^{*b}(i)\}_{i=1}^{n^{b}_{X}}, \{y^{*b}(j),t_{Y}^{*b}(j)\}_{j=1}^{n_{Y}^{b}}, \,\, b=1,\ldots ,B, \end{aligned}$$

where B is the number of bootstrap samples. Two important differences between subroutine 2 and the stationary bootstrap proposed by Politis and Romano (1994) and Mudelsee (2003) for the evenly spaced and coeval case, respectively, are the notion of block (and block length) and the fact that in both Politis and Romano (1994) and Mudelsee (2003), only the X and Y values are resampled. The time points are not resampled; that is, the time points for all bootstrap samples are exactly the same as the time points for the original X and Y series. While in the coeval case a block of length l is merely a set of l consecutive (X, Y) pairs in the observed bivariate time series, it is not obvious how this definition should be generalized for time series observed at unequal timescales. In addition, concatenating blocks of X and Y values of the original series preserving the original time points (i.e., resampling only the X and Y values) would completely destroy the dependence structure of the underlying bivariate process. Roberts et al. (2017) address these problems by considering two subroutines that are labeled in Online Resource 1 as subroutine 2.1 and subroutine 2.2.

Subroutine 2.1 resamples the X and Y values using an algorithm similar to the one described in Mudelsee (2003), but also takes into account the fact that the two series are non-coeval. As described in Online Resource 1, this subroutine produces two series $\{x^{*b}(i)\}_{i=1}^{n^{b}_{X}}$, $\{y^{*b}(j)\}_{j=1}^{n^{b}_{Y}}$ with random length $n^{b}_{X}$ and $n^{b}_{Y}$ only approximately equal to the original series (but which can be different for different bootstrap samples). Although $n^{b}_{X}$ and $n^{b}_{Y}$ could by chance take the value $n_{X}$ and $n_{Y}$, in general,

$$\begin{aligned} n^{b}_{X} \simeq n_{X}, \,\, n^{b}_{Y} \simeq n_{Y}, \,\, n^{r}_{X} \ne n^{s}_{X}; \,\, n^{r}_{Y} \ne n^{s}_{Y} \, \text{ for } r \ne s. \end{aligned}$$

It should be noted that each $x^{*b}(i)$ value in the $b{\text {th}}$ bootstrap sample corresponds to a unique X value in the original time series, and similarly each $y^{*b}(j)$ value in the bootstrap sample corresponds to a unique Y value in the original time series; that is, for each $b \in \{1,\ldots ,B\}$, the resampling defines two mappings, $f_{X}^{b}(\cdot )$ and $f_{Y}^{b}(\cdot )$, such that

$$\begin{aligned} x^{*b}(i)=x(f_{X}^{b}(i)); \,\, y^{*b}(j)=y(f_{Y}^{b}(j)). \end{aligned}$$

(1)

For example, $f_{X}^{b}(3)=5$ means that the third X value in the $b{\text {th}}$ bootstrap sample corresponds to the fifth X value in the original X series, $x^{*b}(3)=x(5)$. This is also the case for the bootstrap introduced by Mudelsee (2003) for the coeval case, with the only difference being that in this case, the two mappings are the same (i.e., $f_{X}^{b}=f_{Y}^{b}$).

Subroutine 2.2 produces the time sequences $\{t^{*b}_{X}(i)\}_{i=1}^{n^{b}_{X}}$, $\{t^{*b}_{Y}(j)\}_{j=1}^{n^{b}_{Y}}$ for the $b{\text {th}}$ bootstrap sample. It should be noted that the time points of the bootstrap samples may vary from sample to sample (i.e., different bootstrap samples may have different time sequences) and are not obtained by resampling the time points of the original X and Y series. The time sequences in the bootstrap samples contain time points that do not appear in the original X and Y series. The subroutine preserves the inter-sampling-time intervals within each block of the stationary bootstrap; that is, the time difference between two X or Y values within the same block of a bootstrap sample equals the time difference between the same X or Y values in the original series. However, due to the way that consecutive blocks are concatenated in time, in the non-coeval case the subroutine does not preserve the dependence structure within each block, a basic requirement of any block bootstrap procedure. As described in Online Resource 1, for a pair ($x^{*b}(i), y^{*b}(j))$ in the $k{\text {th}}$ block of the $b{\text {th}}$ bootstrap sample, for any $k > 1$—that is, for any block except the first one—in general,

$$\begin{aligned} t_{X}^{*b}(i)-t_{Y}^{*b}(j) \ne t_{X}(f_{X}^{b}(i))-t_{Y}(f_{Y}^{b}(j)). \end{aligned}$$

This implies that pairs of (X, Y) values which are very close in time in the bootstrap sample ($t_{X}^{*b}(i)-t_{Y}^{*b}(j)$ “small”) might be very far apart in the original sample ($t_{X}(f_{X}^{b}(i))-t_{Y}(f_{Y}^{b}(j))$ “large”), and vice versa. As a result, the X-Y dependence, as measured by the CCF, is not preserved in the bootstrap sample (Mudelsee (2014), pages 95–97, already noted that for uneven spacing, the original time spacing may not be preserved by block bootstrap methods, and these should be enhanced in order to preserve the original spacing structure). To illustrate this point, $B=2000$ bootstrap samples were generated applying subroutine 2 to two unevenly spaced non-coeval time series of length $n=400$ (with dimensionless time units). The two time series were obtained by sampling a high-resolution (evenly spaced) bivariate time series generated from a first-order autoregressive (AR(1)) Gaussian process with persistence $\tau =2$ and lag-0 correlation $\rho _{XY}=0.8$. For each high-resolution time series, independently, $n=400$ (uneven) inter-sampling-time intervals were drawn from a Gamma(16, 1) distribution and rescaled to have mean 1 (a detailed explanation of the simulation scheme is provided in Sect. 3). Let $A_{0}^{*b}$ be the set of indices of (X, Y) pairs whose time distance in the $b{\text {th}}$ bootstrap sample is in a neighborhood of zero (i.e., is “small”)

$$\begin{aligned} A_{0}^{*b}=\{ (i,j) \vert -0.5<t_{X}^{*b}(i) - t_{Y}^{*b}(j) < 0.5\}. \end{aligned}$$

Denote by ${{\tilde{R}}}_{0,h_{1}}$ the set

$$\begin{aligned} {{\tilde{R}}}_{0,h_{1}}= & {} \{ (i,j) \vert -0.5<t_{X}^{*b}(i) - t_{Y}^{*b}(j)< 0.5 \text{ and } h_{1}-0.5<| t_{X}(f_{X}^{b}(i)) \\&-\, t_{Y}(f_{Y}^{b}(j))| <h_{1}+0.5 \}. \end{aligned}$$

Then the ratio between the cardinality of ${{\tilde{R}}}_{0,h_{1}}$ and the cardinality of $A_{0}^{*b}$, denoted by $R_{0,h_1}$,

$$\begin{aligned} R_{0,h_{1}}=\frac{ |{{\tilde{R}}}_{0,h_{1}}|}{|A_{0}^{*b}|}, \end{aligned}$$

represents the fraction of the (X, Y) pairs close in time in the $b{\text {th}}$ bootstrap that correspond to (X, Y) pairs whose time distance (in absolute value) in the original sample is in a neighborhood of $h_{1}$. Thus, for example, $R_{0,4}=0.3$ would imply that 30% of the (X, Y) pairs whose time distance in the $b{\text {th}}$ bootstrap sample is in a neighborhood of zero correspond to (X, Y) pairs whose time distance (in absolute value) in the original sample is in a neighborhood of 4. It should be noted that since the average time spacing for both the X and Y simulated series is 1, according to the intuition underlying the Gaussian kernel estimator (see Sect. 4), $R_{0,h_{1}}$ can also be interpreted as the fraction of the (X, Y) pairs relevant for estimating the correlation between the two time series in the $b^{th}$ bootstrap corresponding to (X, Y) pairs of observations which in the original sample would be used to estimate the cross-correlation at lag $\pm h_{1}$. Thus, a value of $R_{0,4}$ equal to 0.3 would imply that 30% of the (X, Y) pairs relevant for estimating the correlation between the two time series in the $b{\text {th}}$ bootstrap sample correspond to (X, Y) pairs of observations which in the original sample would be used to estimate the cross-correlation at lag $\pm \, 4$. The boxplot of the values $R_{0,h_{1}}$, for $h_{1} \in \{0,1,2,3,4\}$, corresponding to the 2,000 bootstrap samples obtained from subroutine 2.2 is shown in Fig. 1a, together with the boxplot of ${{\bar{R}}}_{05}=\sum _{r=5}^{\infty } R_{0,r}$. As shown in the figure, for at least 75% of the bootstrap samples, fewer than 20% of the (X, Y) pairs close in time in the bootstrap sample correspond to (X, Y) pairs that are also close in time in the original time series (the third quartile of $R_{00}$ is approximately 0.20). At the same time, for at least 75% of the bootstrap samples, over 20% of the (X, Y) pairs whose time distance is in a neighborhood of zero in the bootstrap sample correspond to (X, Y) pairs whose time distance in the original sample is 4.5 or larger (the first quartile of ${{\bar{R}}}_{05}$ is approximately 0.20). The boxplots corresponding to $R_{0,h}$, for $h_{1} \in \{0,1,2,3,4\}$ largely overlap, generally indicating that of the (X, Y) pairs relevant for estimating the correlation between the two time series in a bootstrap sample, almost the same fraction corresponds to pairs of observations which in the original sample would be used to estimate the cross-correlation at lags $0, \pm 1 , \pm 2, \pm 3$ and $\pm 4$. As a result, the dependence structure of the (X, Y) time series is not preserved in the bootstrap sample. As further evidence, for each bootstrap sample obtained using subroutine 2.2, the cross-correlation between the X and Y time series at lags 0, 1, 2, 3, and 4 was also estimated using the Gaussian kernel estimator. The boxplot of the 2,000 bootstrap-based cross-correlation estimates is shown in Fig. 2a, together with the sample cross-correlation obtained applying the Gaussian kernel estimator to the original time series. The figure shows that while the sample cross-correlation based on the original series decreases with the lag (as expected), the boxplot corresponding to the bootstrap estimates of the cross-correlation at lags 0, 1, 2, 3, and 4 almost completely overlap, suggesting an approximately constant CCF.

Fig. 1

a Boxplot of the values of $R_{0,h_{1}}$, $h_{1}=0,1,2,3,4$ and of ${{\bar{R}}}_{05}=\sum _{r=5}^{\infty } R_{0,r}$ corresponding to the 2,000 bootstrap samples obtained from subroutine 2.2; b same as in a but using the modified version of subroutine 2.2. In the boxplots, the bottom and the top of each box represent the first and third quartile, respectively. The line across the box indicates the median

Fig. 2

a Boxplot of the estimates of the cross-correlation at lags 0, 1, 2, 3, and 4 corresponding to 2, 000 bootstrap samples generated from a given time series using subroutine 2.2 b Same as in a but using the modified version of subroutine 2.2. In both cases the red circles represent the estimates of the cross-correlation based on the original time series and the Gaussian kernel estimator

2.2 Proposed Modification of the Stationary Bootstrap: The mGK Method

In order to overcome these limitations, a modified version of subroutine 2.2 is proposed, which produces the time sequences of the bootstrap sample while preserving the relative time distance between (X, Y) pairs within each block. An illustration of the intuition underlying the new subroutine is given in the toy example in Online Resource 1. A detailed description of the new subroutine can also be found in Online Resource 1. The benefits of the modified procedure are shown in Figs. 1b and 2b, which are the same as Figs. 1a and 2a but with bootstrap samples generated using the modified version of subroutine 2.2.

As shown in the figures, using the modified subroutine 2.2, in all the bootstrap samples over 94% of the (X, Y) pairs close in time in the bootstrap sample correspond to (X, Y) pairs which are also close in time in the original time series (the minimum of $R_{00}$ in Fig. 1b is approximately 0.94), while the boxplots corresponding to the bootstrap estimates of the cross-correlation at lags 0, 1, 2, 3, and 4 satisfactorily reproduce the important features of the sample CCF estimated from the original time series. Hereafter, the GK method with the modified version of subroutine 2.2 will be called the “mGK method,” and any procedure that combines the Gaussian kernel estimator with the BCa method will be termed the “GK algorithm.”

3 Monte Carlo Experiments

The performance of the GK and mGK methods was evaluated and compared via Monte Carlo experiments. $N=1000$ synthetic time series with prescribed known properties were simulated. For each of the series a 95% confidence interval was evaluated using the Matlab implementation of the GK method available from the authors at https://github.com/ jlr581/correlation. The corresponding interval for the mGK method was obtained using the Matlab code available at https://github.com/ isavig/mGK.

It should be noted that the GK method includes a fourth subroutine which consists of repeating subroutines $s_1$ to $s_3$ 25 times, producing 25 confidence intervals. The lower (upper) bound of the final confidence intervals output by the GK method is the median of the lower (upper) bounds of these 25 confidence intervals. This fourth subroutine was used in the implementation of the GK method in the Monte Carlo experiments and in the rest of the paper but has a negligible effect on the results presented. The fourth subroutine actually implies an increase in the number of bootstrap replications. In our opinion, this should be problem-dependent. In each application, the number of bootstrap replications should be set sufficiently large to guarantee that a bootstrap-based confidence interval produced by a particular method for a certain sample is reproducible with very little error when the method is applied to the same sample and should also depend on the confidence level. For these same reasons, this fourth subroutine has been eliminated in the mGK method.

In the Monte Carlo experiments, the empirical coverage was calculated as the fraction of simulations for which the confidence intervals contain the known theoretical value of the correlation. As a complementary parameter, the average length of the confidence intervals across the 1,000 simulations was also reported. The design of the Monte Carlo experiments combined the general simulation framework used by Mudelsee (2003) and Ólafsdottir and Mudelsee (2014) for the coeval case, with the sampling scheme discussed by Rehfeld et al. (2011) for time series with unequal timescales.

As in Mudelsee (2003) and Ólafsdottir and Mudelsee (2014), in each experiment, (i) the underlying process was a bivariate AR(1) process (Gaussian, in our case); (ii) the quantity of interest was the lag-0 correlation, $\rho _{XY}$, between the X and Y components of the process; and (iii) a predefined combination of the parameters that describe defining features of the process (persistence of the X and Y series, the lag-0 correlation $\rho _{XY}$), and the sampling (distribution of inter-sampling-time intervals, sample size of the X and Y series) was considered. In particular, empirical coverage was evaluated under 64 scenarios obtained by combining:

• Two values of the lag-0 correlation between the two time series: $\rho _{XY}=0.2$ and $\rho _{XY}=0.8$.

• Four values for the persistence (which is assumed to be the same for the X and Y series and is denoted by $\tau$): $\tau =0.5$, $\tau =1$, $\tau =2$, and $\tau =5$.

• Two possible choices for the distribution of the inter-sampling-time intervals of each series: gamma$(\alpha ,1)$ with $\alpha =400$ and $\alpha =16$ (see Fig. 3). The associated skewnesses ($2/\sqrt{\alpha })$ were 0.1 and 0.5, respectively. The associated coefficients of variation ($1/\sqrt{\alpha })$ were 0.05 and 0.25, respectively.

• Four sample sizes (common to the two series), $n=50, 100, 200, 400$.

Following Rehfeld et al. (2011), in each scenario the sample of a bivariate process was obtained in four steps:

Step 1::

A high-resolution (evenly spaced) bivariate time series, denoted by $\{{{\tilde{t}}_{s}}, X(s),Y(s)\}$, was generated from a bivariate Gaussian AR(1) process with common persistence $\tau$ and lag-0 correlation $\rho _{XY}$. The time spacing was set to 0.01.

Step 2::

For each series, independently, n (uneven) inter-sampling-time intervals were drawn from a $gamma(\alpha ,1)$ distribution and rescaled to have mean 1.

Step 3::

The cumulative sum of the inter-sampling-time intervals in Step 2, rounded off to two decimal places, defined the unequal timescales for the two series $\{t_{X}(i), i=1,\ldots ,n\}$, $\{t_{Y}(j), j=1,\ldots ,n\}$, respectively.

Step 4::

The observed X series was obtained by sampling the X-component of the high-resolution time series $\{{{\tilde{t}}_{s}},$ X(s),  $Y(s)\}$ in Step 1 at times $\{t_{X}(i),i=1,\ldots ,n\}$. The observed Y series was obtained sampling the Y-component of the high-resolution time series $\{{{\tilde{t}}_{s}}, X(s),Y(s)\}$ in Step 1 at times $\{t_{Y}(j), j=1, \ldots ,n\}$.

Fig. 3

Histograms of inter-sampling-time intervals generated from a gamma$(\alpha ,1)$ distribution as described in Step 2 for $\alpha =400$ (a); and $\alpha =16$ (b). In both cases $n=400$, the histograms have been rescaled to have area equal to 1, and the solid line represents the theoretical density function of the gamma$(\alpha ,1)$ distribution

The nominal standard error associated with the number of simulations ($N=1000$) is $\sigma =0.007$ ($\sigma =\sqrt{\alpha \cdot (1-\alpha )/N}$, with $\alpha =0.05$) higher than the one in Mudelsee (2003) and Ólafsdottir and Mudelsee (2014), who employ $N=47500$, but sufficiently small for the interpretation of the results of the Monte Carlo experiments.

The results of the simulation study are reported in Tables 1, 2, 3, 4, 5, 6, 7, and 8. As shown in the tables, the GK method suffers from severe undercoverage and often produces abnormally short intervals. Regardless of the scenario considered, the coverage of the GK method is well below the nominal value of 0.95, with important differences depending on the true value of the correlation ($\rho _{XY}$), the sample size (n), and the persistence of the time series ($\tau$). In particular, the coverage decreases dramatically with the true value of the correlation and tends to increase with the persistence. For 12 of the 32 scenarios corresponding to $\rho _{XY}=0.8$ (Tables 5 and 7), the coverage of the GK method is 0. In general, and counterintuitively, for a given scenario, coverage decreases as the sample size increases. A similar pattern is observed for the average length of the confidence intervals produced by the GK method, which are much shorter than for the coeval case (Ólafsdottir and Mudelsee 2014). In 6 of the 32 scenarios corresponding to $\rho _{XY}=0.8$ (Tables 6 and 8), the GK method produces degenerate confidence intervals of length 0.

Conversely, the modification of subroutine 2.2 implies a significant improvement in the coverage for the case where the true correlation between the X and Y series is $\rho _{XY}=0.2$ (Tables 1 and 3). Although the mGK method gives a coverage accuracy that might be unacceptably large for practitioners, the reported coverages are much closer to the nominal level of 0.95 and comparable to those in Ólafsdottir and Mudelsee (2014) for the non-calibrated BCa bootstrap intervals for the coeval case (and persistence of the X and Y series equal to 1 and 2, respectively). An improvement is also observed for the case when $\rho _{XY}=0.8$ (Tables 5 and 7); however, the empirical coverage for this case is still very far from the nominal value and much worse than those in Ólafsdottir and Mudelsee (2014) for the non-calibrated BCa bootstrap intervals for the coeval case. In addition, the coverage still decreases in some cases (as a function of sample size) when the sample size exceeds a certain threshold (which varies in the different scenarios considered in the simulation study). Why this is the case is explained in the next section, where a second issue of the GK algorithm is discussed.

Table 1 Empirical coverage for 95% confidence intervals for correlation: $\rho _{XY}=0.2$, sk $= 0.1$

Table 2 Average length for 95% confidence intervals for correlation: $\rho _{XY}=0.2$, sk $=0.1$

Table 3 Empirical coverage for 95% confidence intervals for correlation: $\rho _{XY}=0.2$, sk $=0.5$

Table 4 Average length for 95% confidence intervals for correlation: $\rho _{XY}=0.2$, sk $=0.5$

Table 5 Empirical coverage for 95% confidence intervals for correlation: $\rho _{XY}=0.8$, sk $=0.1$

Table 6 Average length for 95% confidence intervals for correlation: $\rho _{XY}=0.8$, sk $=0.1$

Table 7 Empirical coverage for 95% confidence intervals for correlation: $\rho _{XY}=0.8$, sk $=0.5$

Table 8 Average length for 95% confidence intervals for correlation: $\rho _{XY}=0.8$, sk $=0.5$

4 Bias of the Gaussian Kernel Estimator

The BCa, as any other method for constructing nonparametric bootstrap confidence intervals, requires the definition of an estimator of the parameter of interest, and this estimator must be consistent; that is, the distribution of the estimator should concentrate at the true value of the parameter as the sample size increases (Hall 1986, 1988; DiCiccio and Efron 1996). A consistent estimator of the correlation coefficient is the Pearson sample correlation coefficient (which is in fact the estimator used by Mudelsee (2003) and Ólafsdottir and Mudelsee (2014) for the coeval case). For time series observed at unequal timescales, however, the Pearson correlation coefficient cannot be evaluated unless some interpolation procedure is applied, although this strategy is not recommended (see Sect. 7.5 in Mudelsee (2014)). For time series with some memory properties (i.e., with non-zero persistence), the preferred approach is the Gaussian kernel estimator (underlying the GK algorithm), defined as (Rehfeld et al. 2011)

$$\begin{aligned} {{\hat{\rho }}}^{(\text {GK})}_{XY}=\frac{ \sum _{i=1}^{n_{X}} \sum _{j=1}^{n_{Y}} {{\tilde{x}}}_{i} {{\tilde{y}}}_{j} b{_{h}}( t_{X}(i)-t_{Y}(j))}{ \sum _{i=1}^{n_{X}} \sum _{j=1}^{n_{Y}} b{_{h}}( t_{X}(i)-t_{Y}(j))}, \end{aligned}$$

(2)

where

(i):

${{\tilde{x}}}_{i}=\frac{x_{i} - {{\bar{x}}}}{s_{x}}$ and ${{\tilde{y}}}_{i}=\frac{y_{i} - {{\bar{y}}}}{s_{y}}$ represent the i-th elements of the standardized (i.e., zero mean unit variance) X and Y series, respectively, obtained from the original sample by subtracting the corresponding sample means (${{\bar{x}}}$ and ${{\bar{y}}}$) from each component of the bivariate sample, and dividing by the corresponding sample standard deviations ($s_{x}$ and $s_{y}$);

(ii):

$b{_{h}}( \cdot )$ is the Gaussian kernel

$$\begin{aligned} b{_{h}}( d)= \frac{1}{\sqrt{2 \pi } h} e^{-\frac{ d^{2}}{2 h^{2}}}. \end{aligned}$$

(3)

A similar formula provides an estimate of the CCF at lag l (Rehfeld et al. 2011). To obtain the estimator of the correlation between $X_{t+l}$ and $Y_{t}$, it is sufficient in Eq. (2) to replace $b{_{h}}( t_{X}(i)-t_{Y}(j))$ with $b{_{h}^{(l)}}( t_{X}(i)-t_{Y}(j))$, where

$$\begin{aligned} b{^{(l)}_{h}}( t_{X}(i)-t_{Y}(j))=\frac{1}{\sqrt{2 \pi } h} e^{-\frac{ [(t_{X}(i)-t_{Y}(j))-l]^{2}}{2 h^{2}}}. \end{aligned}$$

The idea underlying the estimator in Eq. (2) is simple. The Pearson correlation coefficient is defined as the average of the products $({{\tilde{x}}}_{i}{{\tilde{y}}}_{j})$ of pairs whose time distance is zero. For time series observed at unequal time space, however, the set of (X, Y) pairs observed at the same time points might contain very few elements or might be empty. As an alternative, the Gaussian kernel estimator returns a weighted average of the $n_{X} n_{Y}$ products ${{\tilde{x}}_{i}} {{\tilde{y}}_{j}}$, where the weighted averaging of each pair $({{\tilde{x}}_{i}}, {{\tilde{y}}_{j}})$ is performed using a Gaussian density function that tends to zero for time differences $t_{X}(i) - t_{Y}(j)$ that are very different from zero.

The estimator requires the specification of the parameter h that represents the kernel’s bandwidth. Rehfeld et al. (2011) suggests setting $h=\varDelta /4$, where $\varDelta$ is the largest of the average spacing of the X and Y series. This ensures that practically only those pairs $( x_{i}, y_{j})$ whose time differences in absolute value are less than $\varDelta /2$ are included in the evaluation of the correlation. For example, if $\varDelta =1$, the relevant pairs for the evaluation of the correlation (or lag-0 cross-correlation) between the two times series are the pairs whose time differences $t_{X}(i) - t_{Y}(j)$ belong to the interval $(-0.5,0.5)$. Similarly, the relevant pairs for the evaluation of cross-correlation at lag 1 are those whose time differences $t_{X}(i) - t_{Y}(j)$ belong to the interval (0.5, 1.5) and so on. It should be noted that the memory of the underlying time series is a necessary property, as the estimator does not work without persistence.

Roberts et al. (2017) use a slightly different version of the estimator (see Appendix A). For comparison purposes, the version of the Gaussian kernel estimator discussed in Roberts et al. (2017) was used in the simulation study in Sect. 2.1 and in Sect. 3. This choice has a negligible effect on the results presented.

The Gaussian kernel estimator is known to be biased (Rehfeld et al. 2011; Roberts et al. 2020). In addition, it can be proved that generally, unlike the Pearson correlation coefficient for the coeval case, the estimator is not consistent (see Appendix A). In particular, as the sample size increases, the distribution of the Gaussian kernel estimator, as currently implemented, concentrates around a value, $\rho _{0}$, which is approximately a weighted average of the CCF of the underlying bivariate stationary process in a neighborhood of zero of length $\varDelta$, the largest of the average spacing of the X and Y series. The weights depend on the asymptotic distribution T of the time differences $t_{X}(i)-t_{Y}(j)$ belonging to the interval $(-0.5 \varDelta , 0.5 \varDelta )$ and on the Gaussian kernel. For example, if T is the uniform distribution over $(-0.5 \varDelta , 0.5 \varDelta )$, then the distribution of the weights follows a normal distribution centered at zero and with standard deviation $h=\varDelta /4$.

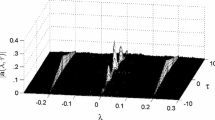
In this case $\rho _{0}$ would be a weighted average of the cross-correlations at lag h, with weights that decrease with the absolute value of h and that are approximately zero outside the interval $(-0.5 \varDelta , 0.5 \varDelta )$. The difference between $\rho _{0}$ and the true value of the correlation, $\rho _{0}-\rho _{XY}$, represents the asymptotic bias. The lack of consistency of the Gaussian kernel estimator implies that the GK algorithm—as any bootstrap procedure that combines a standard method for constructing confidence intervals with the Gaussian kernel estimator—asymptotically (i.e., for a large sample size) will have zero coverage. For a given time series, the corresponding bootstrap distribution of the Gaussian kernel estimator will also concentrate around $\rho _{0}$ asymptotically. Thus, if $|\rho _{0}-\rho _{XY}|>0$ for a sample size larger than a certain threshold (which is a function of the bias), coverage will start to decrease since the overlap between the bootstrap distribution of the estimator and a neighborhood of the true correlation will decrease. Starting from a certain value ${{\tilde{n}}}$, the bootstrap distribution of the Gaussian kernel estimator will not cover at all the true value of the correlation $\rho _{XY}$, so any confidence interval defined in terms of the percentiles of the bootstrap distribution of the estimator (such as those produced by the GK algorithm) will not contain the true value of the correlation, and the corresponding coverage will be zero. The larger the absolute value of the asymptotic bias, the sooner (i.e., for smaller ${{\tilde{n}}}$) the coverage will be zero. In general, the larger the absolute value of the asymptotic bias, the worse the coverage (although, as explained below, this is not true when a bias increase is associated with an increase in the effective sample size). As an illustration, Fig. 4 shows the true CCF (obtained through simulation) of the eight bivariate stationary processes considered in the simulation study in Sect. 3, corresponding to $\rho _{XY}=0.2, 0.8$ and $\tau =0.5, 1,2, 5$ with the Gaussian kernel superposed. Since $\varDelta =1$ in the simulation study, the bandwidth of the Gaussian kernel is $h=\varDelta /4=0.25$. One million observations of evenly spaced pairs (X, Y) have been generated for each bivariate stationary process, and the corresponding sample CCF has been taken as an approximation of the true CCF. Figure 5 shows the distribution of the time differences $t_{X}(i)-t_{Y}(j)$ belonging to the interval $(-0.5 \varDelta , 0.5 \varDelta )$ for eight sample time series corresponding to the scenarios $\rho _{XY}=0.2, 0.8$, $\tau =0.5, 1,2, 5$, sk $=0.5$, and $n=400$.

Fig. 4

CCF (obtained through simulation) of the eight bivariate stationary processes considered in the simulation study corresponding to $\rho _{XY}=0.2, 0.8$ and $\tau =0.5, 1,2, 5$ with the Gaussian kernel superposed

As shown in Fig. 5, regardless of the scenario considered, the distribution of the time differences $t_{X}(i)-t_{Y}(j)$ belonging to the interval $(-0.5 \varDelta , 0.5 \varDelta )$ is approximately uniform. Assuming that these distributions closely approximate the corresponding asymptotic counterpart, for large sample sizes the distribution of the Gaussian kernel estimator should concentrate around a value ($\rho _{0}$) which for each scenario is the weighted mean of the CCF in Fig. 4 with weights given by the Gaussian kernel (represented as a solid blue line in the same figure). This is confirmed by the sampling distribution of the Gaussian kernel estimator in the eight scenarios for sample sizes $n=50$ and $n=400$ shown in Fig. 6. Each sampling distribution is presented as a rescaled histogram (of area equal to 1) of the 1,000 values of the Gaussian kernel estimator obtained from the 1,000 time series simulated for each scenario in the simulation study. The estimated value of $\rho _{0}$ (solid red line) and the true value of the correlation (solid blue line) are superposed to the rescaled histograms.

Fig. 5

Distribution of the time differences $t_{X}(i)-t_{Y}(j)$ belonging to the interval $(-0.5 \varDelta , 0.5 \varDelta )$ for eight sample time series corresponding to the scenarios $\rho _{XY}=0.2, 0.8$, $\tau =0.5, 1,2, 5$, sk $=0.5$, and $n=400$. The value of sk and n are constant in the eight plots and are not reported in the plot title

Fig. 6

Distribution of the Gaussian kernel estimator of the correlation for 16 scenarios corresponding to different values of the true correlation, persistence and sample size of the original time series (in all cases the value of skewness is sk $=0.5$). For each scenario, 1,000 time series have been generated, and the 1,000 Gaussian kernel estimates of the correlation between the X and Y components of the series have been represented as a rescaled histogram (of area equal to 1). In all cases, the vertical blue line denotes the true correlation, and the red line the value of $\rho _{0}$. The horizontal distance between the red and blue line represents the asymptotic bias of the Gaussian kernel estimator of the correlation

As shown in Fig. 6, for each scenario the sampling distribution of the estimator concentrates around the value of $\rho _{0}$ as the sample size increases. The distance between the red and blue line in Fig. 6 represents the asymptotic bias $\rho _{0}-\rho _{XY}$. As is to be expected, in this case, the bias increases with the steepness of the CCF in a neighborhood of zero. As shown in Fig. 4, the steepness of the CCF (and thus the bias) increases with the value of the true correlation and decreases with the persistence of the time series. According to our previous discussion, generally the higher the absolute value of the asymptotic bias, the worse the coverage, and the sooner (i.e., for smaller ${{\tilde{n}}}$) the coverage will be zero. This is exactly what is observed in Tables 1, 3, 5, and 7. As shown in these four tables, coverage tends to decrease with the bias (i.e., with the value of the true correlation and the inverse of the persistence). However, it should be noted that this is not always the case. Longer persistence times reduce both the asymptotic bias and the effective sample size. A reduction in bias is good for coverage, although a reduction in the effective sample size produces a decrease in coverage (when the bias is small). When the effect of the reduction of the effective sample size overcompensates the benefits of the bias reduction, an increase in persistence decreases coverage. As illustrated in Tables 5 and 7, when $\rho _{XY}=0.8$ (and the bias is large), coverage increases as a function of persistence. However, when $\rho _{XY}=0.2$ (and the bias is small), coverage has a more erratic behavior as a function of persistence (see Tables 1 and 3). In all cases, the value of ${{\tilde{n}}}$ decreases with the bias. It is worth noting that for a same level of bias, the coverage of the GK method is much lower than that of the mGK method. This is due to the problems of subroutine 2.2 discussed in the previous section, which also explain the abnormally short intervals in Roberts et al. (2017). A more detailed explanation and an illustration are presented in Online Resource 2.

The above discussion also suggests that the current selection criterion for the bandwidth of the Gaussian kernel estimator could be improved in several ways. The default choice $h=\varDelta /4$, where $\varDelta$ is the largest of the average spacing of the X and Y series (Rehfeld et al. 2011), fails to take into account important features of the sampling and the process that are relevant for the bias of the estimator (such as the distribution of the time differences $t_{X}(i)-t_{Y}(j)$ in a neighborhood of the lag of interest and the persistence of the time series). The consideration of these features in the choice of the bandwidth parameter might reduce the bias of the Gaussian kernel estimator and improve the coverage of the mGK method.

5 A New Perspective

The lack of consistency of the Gaussian kernel estimator discussed in the previous section implies a change in perspective when studying the statistical properties and interpreting the confidence intervals produced by the GK algorithm (and any other method that combines standard bootstrap procedures to construct confidence intervals with the Gaussian kernel estimator as currently implemented). In general situations, the estimator is asymptotically biased, and as a result coverage will tend to zero as the sample size increases. This however does not imply that the GK algorithm is useless.

Depending on the features of the bivariate stationary process underlying the data generation process and the characteristics of the distribution of the inter-sampling-time intervals of each series, the absolute bias ($|\rho _{0}-\rho _{XY}|$) might be very close to zero. This is the case when, for example, (i) the persistence (which can be estimated from the observed series) is large compared to the largest of the average spacing of the X and Y series (which can also be observed); (ii) the distribution of the time differences $t_{X}(i)-t_{Y}(j)$ belonging to the interval $(-0.5 \varDelta , 0.5 \varDelta )$ is concentrated around zero; or (iii) the true correlation is expected to be small. In all these situations, the mGK method works satisfactorily.

Tables 1, 2, 3, 4, 5, 6, 7 and 8 provide an illustration of scenarios (i) and (iii). Although in all cases the coverage produced by the mGK method might be unacceptably high for practitioners (the maximum coverage attained by the mGK method is 0.910), for a persistence equal to 5 (“large”), regardless of the true value of the correlation, the mGK method produces confidence intervals that behave as expected. Coverage increases as a function of sample size, and the average length decreases. Similarly, when the true correlation is small ($\rho _{XY}=0.2$) for any value of the persistence and for a sample size greater than or equal to 200, the mGK method produces intervals with a coverage larger than 0.81 (and larger than 0.84 if the cases corresponding to the smallest persistence $\tau =0.5$ are omitted) and comparable to the coverage reported by Ólafsdottir and Mudelsee (2014) for non-calibrated BCa confidence intervals for the coeval case (note that, as shown in Fig. 6, in both cases the asymptotic bias is almost zero).

It could be argued that if the simulation scenarios discussed above are completed including the results of larger sample size ($1,000, \,5,000, \,10,000, \ldots$) in Tables 1, 3, 5, and 7, the coverage of the mGK method will tend to zero even if the bias is small. Although this is true, as shown in Tables 9 and 10, when sample size increases, even if an increasing percentage of intervals will not contain the true value of the correlation, for each of these intervals one of the extremes of the interval will come closer and closer to the true value (asymptotically the distance will equal the bias). In this respect, despite the poor coverage, these intervals still provide very useful information.

Finally, as an extreme case of distribution of the time differences $t_{X}(i)-t_{Y}(j)$ belonging to the interval $(-0.5 \varDelta , 0.5 \varDelta )$ and which concentrates around zero, Table 11 presents the output for coverage and average length by the mGK method for the case where the true correlation is high $(\rho _{XY}=0.8)$, skewness is sk $=0.1$, but the data are coeval. As shown in the table, the mGK method in this case works as expected. Coverage increases as a function of sample size, and the average length decreases. When the actual sample size is sufficiently large ($n=400$, $\tau =1$), the coverage is close to the nominal value of 0.95. Although in general the coverage produced by the mGK method might be unacceptably high for practitioners, the results are comparable to those reported by Ólafsdottir and Mudelsee (2014) for non-calibrated BCa confidence intervals for the coeval case. The same would occur with the GK method, since in the coeval case the two issues discussed in Sects. 2 and 4 disappear.

However, even in situations where the bias is large, the mGK method can be used to produce a lower bound for the absolute value of the correlation. Under quite mild conditions, it can be argued that the absolute value of $\rho _{0}$ is smaller than or equal to the absolute value of the true correlation. Thus, a confidence interval for $\rho _{0}$ provides a lower bound for the absolute value of the true correlation, as illustrated in Tables 12 and 13. The two tables report the percentage of intervals whose lower limit is smaller than 0.8 and the average value of the lower limit for each of the 1,000 simulated confidence intervals corresponding to the scenarios where $\rho _{XY}=0.8$. As can be seen, as the sample size increases, (i) the average value of the lower limit increases, approaching $\rho _{0}$, and (ii) the percentage of the intervals whose corresponding lower limit is a valid lower bound for the true correlation also increases and is greater than 97% for $n=400$. This means that in these cases with very high confidence, the true correlation can be said to be larger than the lower limit of the interval. Again, despite the poor nominal coverage, this might be very useful information. Similar reasoning would apply for negative lag-0 correlation. In this case with very high confidence, the true correlation will be smaller than the upper limit of the confidence interval (i.e., the absolute value of the true correlation will be larger than the absolute value of the upper limit of the confidence interval). For an illustration with $\rho _{XY}=-0.8$, see Online Resource 3.

Even though the above discussion is focused on correlation, and the illustrations presented refer to pairs of time series with common persistence $\tau$, the same arguments apply to the problem of estimating the CCF at a generic lag l and to time series with different persistence.

The next section presents an illustration of the application of the mGK method to estimate the CCF of a bivariate stochastic process from a sample of unevenly spaced non-coeval time series with different persistence (see Online Resource 4 for an example of the performance of the mGK method for estimating the lag-0 correlation in a Monte Carlo experiment where the two non-coeval time series have different persistence).

Table 9 Average distance of the confidence intervals that do not contain the true correlation $\rho _{XY}=0.2$ from 0.2. The distance of a confidence interval (a, b) from 0.2 is defined as $d^{\star }=min \left( \,|a-0.2| , |b-0.2| \,\right)$

Table 10 Average distance of the confidence intervals that do not contain the true correlation $\rho _{XY}=0.8$ from 0.8

Table 11 Statistical properties of 95% mGK confidence intervals: $\rho _{XY}=0.8$, sk $=0.1$—coeval case

Table 12 Percentage of 95% mGK confidence intervals whose lower limit is smaller than $\rho _{XY}=0.8$

Table 13 Average value of the lower limit of 95% mGK confidence intervals: $\rho _{XY}=0.8$

6 Application: Vostok Ice Core Records

This section presents a real data example where the persistence of the time series involved is very large compared to the largest of their average spacing, so it can be argued that the absolute bias of the Gaussian kernel estimator is very close to zero and that the mGK method works reasonably well. The time series of interest (non-coeval and unevenly spaced) are X: $\text {CO}_{2}$ and Y: deuterium (proxy for temperature variations) over the past 420,000 years (ka) from the Vostok ice core records (Petit et al. 1999). Links to the data are provided in Petit (2005) for $\text {CO}_{2}$ and in Petit and Jouzel (1999) for deuterium. The sample sizes are $n_{X}=283$ and $n_{Y}=3311$. The average time spacing for the X and Y time series is $\varDelta _{X}=1.46$ ka and $\varDelta _{Y}=0.128$ ka, respectively. Thus, the largest average spacing of the two series is $\varDelta =\text {max}\{\varDelta _{X},\varDelta _{Y}\}=1.46$ ka. The two time series are shown in Fig. 7.

Fig. 7

Ice core data: deuterium and $\text {CO}_{2}$ records from the Vostok station (Antarctica) over the past 420,000 years. The $\text {CO}_{2}$ values a are given as parts per million by volume. The total number of points is 283. The deuterium values b are given in delta notation ($\delta \text {D}$). Total number of points is 3,311. For details see Fig. 1.4 on page 10 in Mudelsee (2014)

Fig. 8

a Number of time differences $t_{X}(i)-t_{Y}(j)$ that are most relevant for estimating the CCF at lag l ($n_{{l}}$) as a function of l. b Distribution of time differences $t_{\text {CO}_{2}}(i)- t_{\delta \text {D}}(j)$ belonging to the interval $(-0.5 \varDelta , 0.5 \varDelta )$ represented as a rescaled histogram (with area equal to 1)

This data set was previously studied by Mudelsee (2014) (Sect. 7.5.4), who reported an estimated persistence of the X and Y series of $\tau _{X}=38.1$ ka and $\tau _{Y}=25.6$ ka, respectively (much larger than $\varDelta =1.46\, \text {ka} \approx 1.5$ ka), and a (lag-0) correlation between the two time series of 0.876 (estimated using the binned correlation estimator proposed by Mudelsee (2010)). For details on how the $\text {CO}_{2}$ and deuterium measurements were obtained and the modeling assumptions for the construction of the timescales, see page 10 in Mudelsee (2014). The goal is to extend Mudelsee’s analysis (2014) to evaluate 95% (pointwise) confidence limits for the CCF between the two time series using the mGK method. Although there is no requirement for the lags to be multiples of $\varDelta$, following Rehfeld et al. (2011), confidence intervals for the CCF were evaluated at lags $k \varDelta$ for integers k ($k=0,\pm \, 1, \pm \, 2, \ldots , \pm \,18$).

According to the definition of the Gaussian kernel estimator (see Sect. 4), the pairs of (X, Y) observations that are most relevant for the estimation of the CCF at lag l are those whose time differences $t_{X}(i)-t_{Y}(j)$ belong to the interval $({l} -0.5 \varDelta , { l}+0.5 \varDelta )$. Let $n_{{l}}$ be the number of such pairs for lag l. The plot of $n_{{l}}$ as a function of l is shown in Fig. 8a. The distribution of the time differences $t_{X}(i)-t_{Y}(j)$ belonging to the interval $({l} -0.5 \varDelta , {l}+0.5 \varDelta )$ is approximately uniform regardless of the value of l. As an illustration, the distribution of the time differences $t_{X}(i)-t_{Y}(j)$ belonging to the interval $(-0.5 \varDelta , 0.5 \varDelta )$ is shown in Fig. 8b.

Fig. 9

95% (pointwise) confidence limits for the CCF obtained using the mGK method (blue dot-solid lines) and the GK method (plumb dot-solid lines). The estimated CCF based on the Gaussian kernel estimator is represented as a thin black dotted line. Lag ranges corresponding to confidence intervals that do not contain zero are represented as solid lines at the bottom of the Fig. 

The 95% (pointwise) confidence limits for the CCF obtained using the mGK method are shown in Fig. 9. For comparison purposes, the corresponding confidence limits based on the GK method are also presented. The Matlab implementation available from Roberts et al. (2017) at https://github.com/jlr581/correlation was used for the GK method. This computes 25 confidence intervals each with 2,000 bootstrap iterations and outputs the median of the limits of these 25 confidence intervals as limits of the final confidence interval. The mGK method, on the other hand, was implemented using $B=10000$ bootstrap iterations to ensure a variability of the confidence limits induced by the bootstrap and a reproducibility of the results that is comparable to the GK method. Specifically, a standard deviation below 0.0025 was obtained for the confidence bounds in both cases by repeating the evaluation of the confidence interval for the lag-0 correlation with the GK method and mGK method 100 times.

As shown in Fig. 9, according to the mGK method, the maximum cross-correlation is observed at lag ${ l}=-1.5$ ka; that is, between $X_{t}$ ($\text {CO}_{2}$ at time t ka) and $Y_{t-1.5}$ (deuterium at time ($t-1.5$) ka). The corresponding 95% confidence interval is [0.786, 0.922] with length 0.136. The cross-correlation decreases almost symmetrically with the absolute value of the difference $({ l} - 1.5)$ ka. The decrease is slightly faster for positive values of the difference. The lower bound of the 95% confidence interval for the CCF is larger than 0.458 for lags between $-7.5$ ka and 3 ka. According to the mGK method, there is a positive correlation between $\text {CO}_{2}$ and deuterium for all lags between $-12$ ka and 6 ka (the lower bounds of the corresponding confidence interval is strictly positive). In line with Mudelsee’s (2014) findings, these significant high cross-correlations provide an insight into the coupling of $\text {CO}_{2}$ and temperature variations which is key to understanding the Pleistocene climate.

Qualitatively similar results are obtained using the GK method (as expected due to the low bias of the Gaussian kernel estimator and the high persistence). The 95% confidence interval at lag ${ l}=-1.5$ ka is [0.865, 0.914] with length 0.049 (much shorter than the corresponding length of the interval produced by the mGK method). Again, the cross-correlation decreases almost symmetrically with the absolute value of the difference $({ l} - 1.5)$ ka. For both methods, the width of the confidence intervals increases almost symmetrically with the absolute value of the difference ${ (l} - 1.5{)}$ ka. However, it is worth noting some important differences:

• The GK method provides shorter intervals for ${l}=0 \text { ka}, \pm \, 1.5 \text { ka}$, but for lags l smaller than $-6$ ka, the length of the confidence intervals produced by the mGK method is on average 40% of the corresponding length of the intervals produced by the GK method. For lags l smaller than $-6$ ka, the lower bound of the intervals produced by the mGK method on average also exceeds the corresponding bound of the GK method by 0.21.

• According to the GK method, there is a positive correlation between $\text {CO}_{2}$ and deuterium only for lags between $-9$ ka and 4.5 ka (Fig. 9). Thus, for example, while the confidence interval for the cross-correlation between $\text {CO}_{2}$ and deuterium at lag ${ l}=-10.5$ ka based on the GK method is $[-0.091 0.694 ]$ and shows no evidence of significant cross-correlation, according to the corresponding interval based on the mGK method ([0.194, 0.602]), the cross-correlation between $\text {CO}_{2}$ and deuterium at lag ${ l}=-10.5$ ka is at least 0.194 and therefore significant.

7 Conclusions

This paper identifies two important issues that characterize the design of bootstrap methods to construct confidence intervals for the correlation between two time series observed at unequal timescales, and explains their implications for the performance and for the interpretation of the performance of existing proposals. The first issue concerns the difficulty in adapting block bootstrap methods to time series observed at unequal timescales. The block bootstrap of Roberts et al. (2017) has been shown to be unable to preserve the dependence structure between the two time series within each block. A modification is proposed to overcome this problem. The second issue is related to the Gaussian kernel estimator, which is the recommended estimator for the correlation when the time series are observed at unequal timescales. It is demonstrated that the estimator is asymptotically biased, so any bootstrap method that relies on this estimator asymptotically has zero coverage. Within this framework, it is established that with the proposed modification of the bootstrap, the algorithm discussed in Roberts et al. (2017) has the potential to provide a useful lower bound for the absolute value of the correlation in the non-coeval case and, in some special cases, confidence intervals with approximately the correct coverage.

The results presented here are relevant in a more general context. Despite the fact that the discussion focuses on correlation, the same arguments and the proposed methodology apply to the problem of estimating the CCF at a generic lag h using an algorithm that combines a standard bootstrap method with the Gaussian kernel estimator. Section 5 contains an example of the application of the mGK method to estimate the CCF of a bivariate stochastic process from a sample of unevenly spaced non-coeval time series.

This work is only a first step toward the objective of defining suitable procedures to build confidence intervals for the CCF in this particularly difficult setting. There is much room for improvement. Specifically, five ideas that are worth exploring are as follows: (i) enhancing the proposed implementation of the stationary bootstrap, and implementing alternative definitions of “blocks” that allow the use of a moving block (and other block) bootstrap procedures (see end of Sect. 7.5.3 in Mudelsee (2014)); (ii) the use of alternative bootstrap methods to construct confidence intervals, such as the percentile-t method (Hall 1988; iii) the use of recalibration (Ólafsdottir and Mudelsee 2014; iv) the use of alternative estimators of the correlation such as SLICK (Roberts et al. 2020) and the binned correlation (Mudelsee 2010, 2014; Polanco-Martinez et al. 2019) that could reduce bias and improve coverage, possibly with little or no cost in terms of the length of the confidence intervals; and (v) the definition of a different criterion for the choice of the bandwidth parameter of the Gaussian kernel estimator. As observed in Sect. 4, the default choice $h=\varDelta /4$ does not take into account important features of the sampling and the process that are relevant for the bias of the estimator. The consideration of these features in the choice of the bandwidth parameter could reduce the bias of the Gaussian kernel estimator and improve the coverage of the mGK method, again with little or no cost in terms of the length of the confidence intervals.

At the same time, the construction of a suitable framework to address these issues requires theoretical developments. The properties of block bootstrap procedures for time-dependent data are well understood for evenly spaced time series (Lahiri 2003). However, this is not the case for unevenly spaced (coeval or non-coeval) time series (but see the autoregressive bootstrap in Mudelsee (2014)). The same is true of asymptotic theory. The discussion of the asymptotic properties of the Gaussian kernel estimator in Sect. 4 and Appendix A is primarily heuristic. However, the same notion of “sample size increase” and asymptotic behavior should be carefully defined when the time series are unevenly spaced and observed at unequal timescales. This formal treatment is beyond the scope of this paper but is undoubtedly important.

Appendix A: Lack of consistency of the Gaussian kernel estimator

Consider two unevenly spaced time series with $n_{X}$ and $n_{Y}$ observations, $\{t_{X}(i), x_{i}\}_{i=1}^{n_{X}}$, $\{t_{Y}(j), y_{j}\}_{j=1}^{n_{Y}}$ and let:

• $\varDelta$ be the largest of the average spacing of the X and Y series;

• $b_{h}( \cdot )$ the Gaussian kernel in (3);

• $\{r_{1},r_{2},\ldots , r_{m}\}$ be the set of possible values that the difference between sampling times $t_{X}(i) - t_{Y}(j)$ can take for $(i,j) \in \{1,\ldots ,n_{X}\} \times \{1,\ldots ,n_{Y}\}$;

• $D_{r}=\{ (i,j) \in \{1,\ldots ,n_{X}\} \times \{1,\ldots ,n_{Y}\} \text { s.t. } t_{X}(i) - t_{Y}(j)=r\}$, $r \in \{r_{1},r_{2},\ldots , r_{m}\}$.

Denoting by $n_{r}$ the cardinality of $D_{r}$, the Gaussian kernel estimator in (2) can be written as

$$\begin{aligned} {{\hat{\rho }}}^{(GK)}_{XY}&=\frac{ \sum _{i=1}^{n_{X}} \sum _{j=1}^{n_{Y}} {{\tilde{x}}}_{i} {{\tilde{y}}}_{j} b_{h}( t_{X}(i)-t_{Y}(j))}{ \sum _{i=1}^{n_{X}} \sum _{j=1}^{n_{Y}} b_{h}( t_{X}(i) -t_{Y}(j))}\nonumber \\&=\frac{\sum _{r \in \{r_{1},r_{2},\ldots , r_{m}\} } \sum _{(i,j) \in D_{r}} {{\tilde{x}}}_{i} {{\tilde{y}}}_{j} b_{h}(r)}{\sum _{r \in \{r_{1},r_{2},\ldots , r_{m}\}} n_{r} b_{h}(r)} \nonumber \\&=\sum _{r \in \{r_{1},r_{2},\ldots , r_{m}\}} \frac{ \sum _{(i,j)\in D_{r} }{{\tilde{x}}}_{i} {{\tilde{y}}}_{j}}{n_{r}} \cdot \frac{n_{r} b_{h}(r)}{\sum _{{{\tilde{r}}} \in \{r_{1},r_{2},\ldots , r_{m}\}} n_{{{\tilde{r}}}} b_{h}({{\tilde{r}}})} \nonumber \\&=\sum _{r \in \{r_{1},r_{2},\ldots , r_{m}\}} {{\hat{\rho }}}(r) \cdot \frac{n_{r} b_{h}(r)}{\sum _{{{\tilde{r}}} \in \{r_{1},r_{2},\ldots , r_{m}\}} n_{{{\tilde{r}}}} b_{h}({{\tilde{r}}})} \end{aligned}$$

(A1)

where ${{\hat{\rho }}}(\cdot )$ is the standard sample CCF,

$$\begin{aligned} {{\hat{\rho }}}(r)=\frac{ \sum _{(i,j)\in D_{r} }{{\tilde{x}}}_{i} {{\tilde{y}}}_{j}}{n_{r}}. \end{aligned}$$

According to (A1), the Gaussian kernel estimator is a weighted average of the values of the sample CCF at lags $r_{1}, \ldots , r_{m}$. For $i \in \{1,\ldots ,m\}$, the weight of the generic term ${{\hat{\rho }}}(r_{i})$ depends on $n_{r_{i}}$, the cardinality of the set of (X, Y) pairs whose time distance is exactly $r_{i}$, and on the value of the Gaussian kernel $b_{h}(r_{i})$. The weight increases with $n_{r_{i}}$ and decreases with the absolute value of $r_{i}$. The choice of the bandwidth parameter $h=0.25 \varDelta$ implies that, in practice, all sample correlation coefficients corresponding to lags r outside the interval $(-0.5 \varDelta , 0.5 \varDelta )$ have zero weight.

Under mild conditions, the standard sample CCF is a consistent estimator of the CCF of the underlying bivariate process. Thus, as the sample size increases, the distribution of the Gaussian kernel estimator concentrates around a value $\rho _{0}$ which is a weighted average of the CCF in a neighborhood of zero. The weights will depend on the asymptotic distribution T of the time differences $t_{X}(i)-t_{Y}(j)$ belonging to the interval $(-0.5 \varDelta , 0.5 \varDelta )$ and on the Gaussian kernel. For example, if T is the uniform distribution in $(-0.5 \varDelta , 0.5 \varDelta )$, then the distribution of the weights follows a normal distribution centered at zero and with standard deviation $h=\varDelta /4$. In this case, $\rho _{0}$ would be a weighted average of the cross-correlations at lag h, with weights that decreases with the absolute value of h and that are approximately zero outside the interval $(-0.5 \varDelta , 0.5 \varDelta )$.

Note that Roberts et al. (2017) use a modified version of the Gaussian kernel estimator, where the sample standard deviations $s_{x}$ and $s_{y}$ are replaced by the corresponding weighted versions

$$\begin{aligned} {{\tilde{s}}}_{x}= \sqrt{\frac{\sum _{i=1}^{n_{X}} (x_{i} - {{\bar{x}}})^{2} \cdot b_{i.}}{\sum _{i=1}^{n_{X}} b_{i.}}}; \,\,\,\,\,\,\, {{\tilde{s}}}_{y}= \sqrt{\frac{\sum _{j=1}^{n_{Y}} (y_{j} - {{\bar{y}}})^{2} \cdot b_{.j}}{\sum _{j=1}^{n_{Y}} b_{.j}}}, \end{aligned}$$

where

$$\begin{aligned} b_{i.}=\sum _{j=1}^{n_{Y}} b_{h}( t_{X}(i)-t_{Y}(j)); \,\,\,\,\,\,\, b_{.j}=\sum _{i=1}^{{n_{X}}} b_{h}( t_{X}(i)-t_{Y}(j)). \end{aligned}$$

In our opinion, the definition of the Gaussian kernel estimator in (2) should be preferred, since the following is not clear: (i) the intuition underlying the weighted sample standard deviations ${{\tilde{s}}}_{x}$, and ${{\tilde{s}}}_{y}$; (ii) why, if kernel weights should be applied, they should be used for computing weighted standard deviation but not weighted sample means.