1 Introduction

In petroleum reservoirs, faults are generally modeled using seismic data, well data and a knowledge of the local geology. Thore et al. (2002) list several sources of uncertainty when modeling faults based on seismic data, but conclude that the main sources are uncertainty in the seismic interpretation combined with vertical and lateral uncertainty arising from the time-depth migration of the seismic data. The interpretation uncertainty is often a consequence of the poor quality of seismic data near faults, together with the fact that faults are usually represented as surfaces, even though they are three-dimensional zones of deformation. The interpretation uncertainty encompasses both the existence of faults, and the location and local shape of the faults. The depth migration uncertainty is due to uncertainties in the velocity model and the actual seismic signal path due to non-horizontal velocity contrasts. The interpretation error is assumed to be independent for each fault, whereas the error introduced by the time-depth migration is correlated between nearby faults. Although the fault-sealing properties and the existence of additional faults are the main sources of uncertainty in reservoir performance, the fault geometry and position also have significant effects, especially for wells located near major faults (Irving et al. 2010; Rivenæs et al. 2005). An uncertainty model for fault position and geometry enables this uncertainty to be updated based on well production data (Cherpeau et al. 2012; Irving and Robert 2010; Seiler et al. 2010; Suzuki et al. 2008).

Previous implementations of uncertainty modeling for fault geometries have been based on a range of fault parameterizations; Lecour et al. (2001) describe an uncertainty model for faults modeled as triangular surfaces. Local variability is examined with a P-field simulation, which can also include a global trend such as a shift, a change in dip or a more general random function. Caumon et al. (2007) use this modeling method to update the uncertainty of a reservoir simulation grid. Hollund et al. (2002) and Holden et al. (2003) also define a stochastic model for fault geometry. They parameterize the fault as a set of fault pillars defining a series of fault segments. However, their Markov chain Monte Carlo-based algorithm has severe performance problems and does not produce geologically realistic realizations (Røe et al. 2010). The fault model can also be parameterized by defining the fault surfaces based on a three-dimensional potential field. Mallet and Tertois (2010) generate stochastic realizations of faults and horizons by perturbing the UVT transform associated with the Geochron model (Mallet 2004). This model enables the conditioning of well data. Wellmann et al. (2010) have a more data-driven approach, where the fault model is updated by perturbing the input data set. This approach is well suited for capturing the uncertainty in the input data set, but underestimates the uncertainty in areas with less data.

The algorithm presented in this paper uses a parameterization where the faults are represented as tilted, regularly gridded surfaces. This makes it possible to use standard surface modeling techniques similar to those used for modeling stratigraphic surfaces as described by Abrahamsen et al. (1991). These techniques include the application of Gaussian random fields for generating surface realizations and the use of kriging to condition the surfaces to the well data. In the uncertainty model presented in this paper, the faults are simulated independently of each other. There is no correlation between different faults, except in the lengthening or shortening effect a fault has on other faults that it might truncate. Similar to Lecour et al. (2001), the algorithm in this paper uses a p-field based simulation technique where simulations are performed in a standard normally distributed domain. The well observations are translated into this domain, and the final realizations are translated back into the real domain using quantile mapping. The transformation is defined by the fault uncertainty envelope, constrained by a pair of surfaces that restrict the location of the simulated fault surface realizations. The smoothness of the simulated fault surface is controlled by the range of the variogram used. However, where Lecour et al. (2001) use a triangulated representation of the fault surfaces, the algorithm in this paper is based on a fault representation where each surface is represented as a function on a regular grid in a rotated coordinate system. Although this representation is not as flexible with respect to modeling complex fault surfaces, it does provide a simple parameterization of the fault surface uncertainty. The use of implicit fault truncations also allows the truncation rules to be updated based on different fault surface realizations. A consistent framework for conditioning the fault surface realizations with well picks and well paths is also introduced. The fault location can optionally be given an uncertainty at the well pick locations. The well paths conditioning points represent positions known to be on a particular side of the fault surface.

This framework provides a flexible and intuitive way to represent fault uncertainty. The method allows for the inclusion of both seismic and well data, and allows both visualization of the well-conditioned fault uncertainty and simulations of realistic fault geometry to honor all the input data. The fault uncertainty model, along with the methods used for well conditioning and stochastic simulation of fault surfaces, is presented in Sect. 2, and in Sect. 3 results from the application of the methods on a simple fault model are shown. Issues that might arise when using the methods in reservoir modeling workflows are discussed in Sect. 4. The work presented in this paper is an extension of the work presented in Røe et al. (2010), and describes methods implemented in the Havana fault modeling tool (Norwegian Computing Center 2013).

2 The Fault Surface Uncertainty Model

2.1 Fault Parameterization

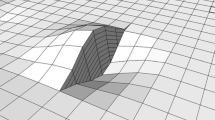
The methods presented in this paper are based on a fault representation where the faults are modeled as surfaces in a rotated coordinate system (Georgsen et al. 2012; Hoffman and Neave 2007). The rotation, given by the dip and strike angles of the general fault trend, defines a reference plane. This reference plane provides a coordinate system with the \(x\) coordinate in the strike direction, the \(y\) coordinate in the dip direction, and the \(z\) coordinate in the normal direction, with the positive \(z\) direction pointing into the footwall of the fault. The fault surface is represented as a function \(f(x,y)\) denoting the distance from the reference plane to the fault surface (Fig. 1). Truncations are specified implicitly through a list of truncation rules defining which fault will be truncated if two fault surfaces intersect. This fault parameterization is not as flexible as the general triangulated surfaces representation (Caumon et al. 2009). However, the specification of a rotated coordinate system makes it possible to use the same methods that are routinely used for modeling uncertainty in the location of stratigraphic horizons.

Fig. 1
figure 1

The fault representation used, where the fault surface is defined as a function on the reference plane

Full size image

From the seismic interpretation, a base case for the fault surface is attained, denoted by \(f_{\text {b}}(x,y)\). The uncertainty in fault location is specified by a fault uncertainty envelope around this base case, where the fault is allowed to reside within (Caers and Caumon 2011). This envelope is defined by two surfaces, \(e_{\text {hw}}(x,y)\) and \(e_{\text {fw}}(x,y)\), on either side of the base case surface, and given in the same coordinate system as the fault surface (Fig. 2).

Fig. 2
figure 2

Seismic cross-section with interpreted fault surface \(f_{\text {b}}(x,y)\) in black. The boundary surfaces \(e_{\text {hw}}(x,y)\) and \(e_{\text {fw}}(x,y)\) of the interpreted fault uncertainty envelope are shown in blue

Full size image

2.2 Prior Probability Distribution for Fault Surface Location

Within the volume defined by the fault uncertainty envelope, the location of the fault surface follows a prior probability distribution with a marginal cumulative density function \(\Pi \left( z(x,y)\right) \) defined from \(f_{\text {b}} (x,y)\), \(e_{\text {hw}}(x,y)\) and \(e_{\text {fw}}(x,y)\). A possible shape for this distribution is triangular, with the mode located at the base case and the minimum and maximum on the envelope’s boundary surfaces. This results in a model with a higher probability of the simulated fault residing near the base case, and lower probabilities for the fault being located near the edges of the envelope. Other possible distributions are uniform, or piecewise uniform, where the median coincides with the base case. In general, any bounded probability distribution can be used. To be able to use standard multi-normal theory, the stochastic simulation and well conditioning must be undertaken in a transformed domain where the uncertainty for the fault surface follows a standard normal distribution. Let \(\Phi \) be the marginal cumulative density function for the \(N(0,1)\) distribution. Then,

$$\begin{aligned} T\left( z(x,y)\right) = \Phi ^{-1}\left( \Pi \left( z(x,y)\right) \right) , \end{aligned}$$
(1)

defines a transformation from the fault surface domain into the transformed domain, and

$$\begin{aligned} T^{-1}\left( z^{*}(x,y)\right) = \Pi ^{-1}\left( \Phi \left( z^{*}(x,y)\right) \right) , \end{aligned}$$
(2)

is the inverse transformation from the transformed domain back into the fault surface domain.

2.3 Conditioning to Well Data

Two types of well data are used for conditioning: well picks, which are observations of the fault surface in the well, and well path points, which are points along a well path that do not hit the fault. Well picks may optionally be assigned an observation uncertainty. For each well data point \((x_i, y_i, z_i)\) a corresponding normal distribution \(N\left( \mu ^{*}(x_i, y_i), \sigma ^{*}(x_i, y_i)\right) \) is created in the transformed domain.

2.3.1 Well Picks with no Uncertainty

For well picks \((x_i, y_i, z_i)\) with no uncertainty, the mean and standard deviation are

$$\begin{aligned} \mu ^{*}(x_i, y_i)&= T\left( z_i(x_i, y_i)\right) , \end{aligned}$$
(3)
$$\begin{aligned} \sigma ^{*}(x_i, y_i)&= 0 . \end{aligned}$$
(4)

2.3.2 Well Picks with Uncertainty

Well picks can also be given with an uncertainty. This uncertainty is represented by an interval \([l(x_i, y_i), u(x_i, y_i)]\) within the fault envelope that restricts the distribution of the fault surface location at the well pick. The moments

$$\begin{aligned} \mu ^{*}(x_i,y_i)&= \frac{1}{2}\left( T\left( u(x_i,y_i)\right) + T\left( l(x_i,y_i)\right) \right) , \end{aligned}$$
(5)
$$\begin{aligned} \sigma ^{*}(x_i,y_i)&= \frac{1}{4}\left( T\left( u(x_i,y_i)\right) - T\left( l(x_i,y_i)\right) \right) , \end{aligned}$$
(6)

are then used to approximate a distribution within the transformed domain. With the given variance \(\sigma ^{*}\), the probability of the fault surface lying within \([l(x_i, y_i), u(x_i, y_i)]\) is about 0.95.

2.3.3 Well Path Points

Well path points are evaluated to be either in the footwall or the hanging wall of the fault. Only well path points inside the uncertainty envelope affect the distribution of the fault surface location. The updated uncertainty interval for the fault at the location of a well path point must be constructed such that it avoids the well path on the side of the fault where the point is located and coincides with the initial envelope on the other side. Let \((x_i,y_i,z_i)\) be the well path point. The interval within which the fault surface is allowed to lie is then set as

$$\begin{aligned} \left[ l(x_i,y_i), u(x_i,y_i)\right] = \left[ z_i, e_{\text {fw}}(x_i,y_i) - \delta (x_i, y_i)\right] , \end{aligned}$$
(7)

with a \(\delta \) such that \(\Pi \left( e_{\text {fw}}(x_i,y_i) - \delta (x_i, y_i)\right) = 0.995\), if the well path point is in the hanging wall, or

$$\begin{aligned} \left[ l(x_i,y_i), u(x_i,y_i)\right] = \left[ e_{\text {hw}}(x_i,y_i) + \delta (x_i, y_i), z_i\right] , \end{aligned}$$
(8)

with a \(\delta \) such that \(\Pi \left( e_{\text {hw}}(x_i,y_i) + \delta (x_i, y_i)\right) = 0.005\), if the well path point is in the footwall. \(\delta \) is added to avoid problems associated with coming too far out into the tails of the normal distribution. The distribution in the transformed domain is then approximated by the following moments:

$$\begin{aligned} \mu ^{*}(x_i,y_i)&= \frac{1}{2}\left( T\left( u(x_i,y_i)\right) + T\left( l(x_i,y_i)\right) \right) , \end{aligned}$$
(9)
$$\begin{aligned} \sigma ^{*}(x_i,y_i)&= \frac{1}{6}\left( T\left( u(x_i,y_i)\right) - T\left( l(x_i,y_i)\right) \right) . \end{aligned}$$
(10)

With this distribution, the probability of the fault surface being on the wrong side of the well path point is approximately 0.01. An alternative for conditioning the well path points is the use of inequality conditioning (Abrahamsen and Benth 2001). This would ensure that the fault surface realizations are on the correct side of the well path point, and would also ensure that the location of the fault surface inside the well path point follows the desired distribution, a truncated version of \(\Pi (z|x_i,y_i)\).

2.3.4 Well Conditioning of Fault Surfaces and Fault Uncertainty Envelopes

From the posterior mean and covariance of the Gaussian field representing the fault surface in the transformed domain, the fault surface conditioned on the well data can be predicted using kriging. Let \(\mathbf {m}\) be the vector of expected transformed well data points \((\mu _i^{*})\). The kriging vector \({\mathbf {k}}(x,y)\) is a vector of correlations between the position \((x,y)\) and each of the conditioning points \((x_i,y_i)\) as specified by a given variogram. The kriging matrix \(K\) consists of the spatial correlations between all conditioning points. The well uncertainties are given by \(\Sigma ^{*} = \mathrm{diag}\{(\sigma ^{*}(x_i, y_i))^2\}\). Standard multi-normal theory gives

$$\begin{aligned} z^{*}_{\text {post}}(x,y)&= {\mathbf {k}}(x,y) (K+\Sigma ^{*})^{-1} {\mathbf {m}}, \end{aligned}$$
(11)
$$\begin{aligned} \sigma ^{*}_{\text {post}}(x,y)&= \sqrt{1-{\mathbf {k}}(x,y) (K+\Sigma ^{*})^{-1} {\mathbf {k}}'(x,y)}, \end{aligned}$$
(12)

where \(z^{*}_{\text {post}}\) is the updated mean surface in the transformed domain, while \(\sigma ^{*}_{\text {post}}\) is the updated standard deviation. The predicted fault surface is obtained by transforming back into the fault surface domain: \(z_{\text {post}}(x,y) = T^{-1}\left( z^{*}_{\text {post}}(x,y)\right) \). To find a \(p\)-prediction band, where \(p\) is the probability of the fault surface lying within this band, let \(q\) be the quantile in the standard Gaussian distribution corresponding to the \(p\)-th percentile, \(q = \Phi ^{-1}(\frac{1-p}{2})\). An updated fault uncertainty envelope is then found by transforming the quantile surfaces to the fault surface domain

$$\begin{aligned} e^u_{hw}(x, y)&= T^{-1}\left( z^{*}_{\text {post}}(x,y) + q\,\sigma ^{*}_{\text {post}}(x,y)\right) , \end{aligned}$$
(13)
$$\begin{aligned} e^u_{fw}(x, y)&= T^{-1}\left( z^{*}_{\text {post}}(x,y) - q\,\sigma ^{*}_{\text {post}}(x,y)\right) . \end{aligned}$$
(14)

2.4 Unconditional Fault Simulation

The simulation of the fault surface is done in the transformed domain. A simulated surface, \(z^{*}_0(x,y)\), is generated with zero expectation, a variance of one and covariance defined by a variogram. The fault surface realization, \(f_s\) is then given by

$$\begin{aligned} f_s(x, y) = T^{-1}\left( z^{*}_0(x, y)\right) . \end{aligned}$$
(15)

The variogram describes how data in a surrounding area affect a given point. The variogram is described with a variogram type and correlation ranges along the fault’s strike and dip directions. Since the fault surface realizations should be smooth, a Gaussian variogram is used with a range matching the desired surface smoothness (Fig. 3).

Fig. 3
figure 3

The effect of different variogram lengths. Variogram ranges of a 100 m, b 500 m, c 1,000 m, and d 2,000 m in both dip and strike directions. The size of the box surrounding the faults is approximately 7,500 m \(\times \) 7,500 m \(\times \) 900 m

Full size image

2.5 Conditional Simulation

Kriging is used in the transformed domain to update the simulated residual surface \(z^{*}_0(x,y)\) according to well data. For each well data point, a corresponding distribution is assigned as described in Sect. 2.3. From each of these distributions, a value \(z^{*}_i\) is drawn, giving a conditioning point \((x_i, y_i, z^{*}_i)\). The residual vector \(\mathbf {r}\) is the vector of differences between \(z^{*}_0(x_i,y_i)\) and \(z^{*}_i\) in these positions. To populate the whole field, simple kriging is used as expressed by

$$\begin{aligned} z^{*}(x,y) = z^{*}_0(x,y) + {\mathbf {k}}(x,y) (K+\Sigma ^{*})^{-1}{\mathbf {r}}, \end{aligned}$$
(16)

where \({\mathbf {k}}(x,y), K\) and \(\Sigma ^{*}\) are as defined in Sect. 2.3.4. This results in a surface realization that is conditioned to the well data in the transformed domain, and the corresponding fault surface realization \(f_s\) is found by mapping \(z^{*}(x,y)\) back into the fault surface domain

$$\begin{aligned} f_s(x,y) = T^{-1}\left( z^{*}(x,y)\right) . \end{aligned}$$
(17)

3 Results

The algorithm has been tested on the Emerald Field reservoir model, one of the tutorial examples from the Roxar RMS Suite (Roxar 2012). Figure 4a, b shows the main fault in this dataset together with a fault uncertainty envelope. The interpreted fault surface is shown in orange, and has a length of approximately 7,500 m and a height of approximately 900 m. The fault uncertainty envelope is shown in purple, and has a variable width of approximately 500 m at the center of the fault, increasing to almost 700 m near the ends of the fault. The given width is several times larger than the typical fault location uncertainty, but this is done to give a clearer picture of results from the uncertainty model. In addition, two well points are shown in green.

Fig. 4
figure 4

Original and well conditioned fault data. a The fault surface (orange) together with the fault uncertainty envelope (purple) and two well picks (green). b A horizontal intersection through (a), seen from above. c, d The well-conditioned fault surface (orange) and fault uncertainty envelope (blue)

Full size image

Figure 4c, d shows the same fault conditioned to the given well points. In this case, a triangular distribution is used in combination with a Gaussian variogram with ranges of 2,000 m in both the strike and dip direction. As can be seen on the updated fault uncertainty envelope in blue, there is no uncertainty in the well data. According to the input data and the model, the probability of the fault surface being within the updated uncertainty envelope at any given point is 0.95. This results in an updated uncertainty envelope that will always be within the original uncertainty envelope, even in areas where there are no well data. Three simulated realizations from the same uncertainty model as above are shown in Fig. 5. Figure 6 shows an updated model where a well path has been added with red dots. As can be seen from the updated uncertainty model, an uncertainty of \(\pm 50\) m has been specified on the well picks. The same variogram is used as in the previous case, but the triangular distribution is exchanged for a piecewise uniform distribution with the mean equal to the interpreted base case fault surface. Since a uniform distribution is used, the updated fault uncertainty envelope, which still indicates the P95 interval, is closer to the original fault uncertainty envelope. The fault surface uncertainty distribution after well conditioning for the two cases is visualized in Fig. 7.

Fig. 5
figure 5

A set of three simulated fault surface realizations (orange lines) together with the unconditioned envelope (purple), the updated envelope (blue) and the well picks (green)

Full size image
Fig. 6
figure 6

Results for an updated fault surface uncertainty model with a well path (red dots) and with uncertainty added to the well picks. The first figure shows the predicted fault surface, whereas the other two figures show simulated fault surface realizations

Full size image
Fig. 7
figure 7

Posterior distribution for the two cases shown in Figs. 5 and 6. The blue lines are respectively the 1st, 10th, 25th, 50th, 75th and 99th percentiles of the distribution

Full size image

As can be seen from the results, the method presented gives realistic-looking fault surface realizations that honor all the input data without showing any bulls-eye effects near the well picks. As noted in Røe et al. (2010), the stochastic simulation algorithm is efficient and well suited for use in Monte Carlo methods.

4 Discussion

4.1 Handling of Fault Truncations

The extent of the faults is specified with a fault tip polygon. Depending on how this polygon is defined near truncations, the faults might be moved so that they do not touch, eliminating the truncations. Faults might also be moved in such a way that new truncations are introduced. In the authors’ opinion, this is a desirable attribute of the model since it allows examination of the uncertainty in reservoir compartmentalization, as introduced by the specified fault uncertainties. To be able to obtain the desired truncations, a set of alternative truncation rules for faults that have intersecting fault uncertainty envelopes must be specified. This specification can either be done manually by examining all possible intersections and specifying a truncation rule for each of these, or more automatically based on rules specifying the truncation hierarchy, by ordering the faults according to fault age. For workflows that rely on unchanged topology, rejection sampling can be used. If the topology of the simulated realization does not match the topology of the base case model, the realization is rejected and an alternative realization is simulated. Another approach is to establish uncertainty envelopes and fault tips in such a way that no topology-changing realizations are possible. This can be done by ensuring that the fault uncertainty envelopes only intersect near existing truncations, and that the truncated parts of the fault tips are so large that they encompass the whole uncertainty envelope of the truncating fault.

4.2 Fault Length Uncertainty

There is a significant uncertainty in fault lengths, since parts of faults will not be visible in the seismic data. Therefore, a fault tip usually is generated based on a fault displacement gradient. The length of the fault and the resulting fault tip are closely connected to the displacement field associated with the fault. A realistic stochastic model for this is important to analyze the impact of faults on reservoir performance. The fault uncertainty envelopes presented in this paper closely follow the base case seismic interpretation. However, such envelopes could be extended to also encompass the uncertainty in fault tip location.

4.3 Updating the Reservoir Simulation Grid

The algorithms listed here update the structural model. However, in most workflows the reservoir simulation grid must be updated. In general, the only way to accomplish this is to rebuild the entire grid. As shown in Seiler et al. (2010), it is possible to update the gridded fault traces based on the differences between the base case structural model used to build the reservoir simulation grid and the simulated realization. Based on these modified fault traces, the rest of the grid then can be updated. This works for grids with simple fault geometries, and for cases where there are no changes to the topology of the model.

5 Conclusions

The algorithm presented here enables the rapid stochastic simulation of realistic fault surfaces. The parameters needed are the fault uncertainty envelope and a variogram describing the smoothness of the fault surfaces. Critically, the simulated fault surfaces can be constrained by well observations and along well paths, without any significant increase in the time needed to generate a realization. Using this fast simulation of realistic fault surfaces, Monte Carlo methods can be employed to estimate probability distributions for reservoir volumes or the probability for different fault scenarios. The method can also be used in well-planning workflows where it is important to estimate and update the uncertainty of faults bounding geological targets.