Skip to main content
SpringerLink
Log in

Determination of the Period of Subcritical Growth of Small Plane High-Temperature Creep Cracks in Structural Elements

  • Published:
Materials Science Aims and scope

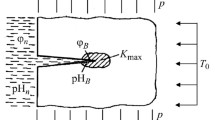
We formulate a computation model (differential equation with initial and final conditions) for the determination of the period of subcritical growth of small plane high-temperature creep cracks in structural elements. The model is based on the first law of thermodynamics, determination of the energy components of deformation of the process zone near the crack contour via the parameters of its opening, and approximate reduction of the process of creep of the material to a period of steady-state creep. The formulas for the approximate evaluation of the opening displacements of the process zone via the stress intensity factor and the mean values of loading of the structural elements are proposed. The method of equivalent areas generalized for the deformation parameters is used for the approximate solution of the problem. By using this method and the experimental data known from the literature for specific materials, we determine the period of subcritical growth of a small surface semielliptic high-temperature creep crack under the conditions of long-term static tension in a half space.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.

Similar content being viewed by others

References

  1. S. Taira, R. Ohtani, and T. Kitamura, “Application of J-integral to high-temperature crack propagation: Part I. Creep crack growth,” J. Eng. Mater. Technol., 101, 154–161 (1979).

    Article  CAS  Google Scholar 

  2. O. E. Andreikiv and N. B. Sas, “Fracture mechanics of metallic plates under the conditions of high-temperature creep,” Fiz.-Khim. Mekh. Mater., 42, No. 2, 62−68 (2006); English translation: Mater. Sci., 42, No. 2, 210−219 (2006).

  3. O. E. Andreikiv and N. B. Sas, “Subcritical growth of a plane crack in a three-dimensional body under the conditions of high-temperature creep,” Fiz.-Khim. Mekh. Mater., 44, No. 2, 19–26 (2008); English translation: Mater. Sci., 44, No. 2, 163–174 (2008).

  4. O. E. Andreikiv and N. B. Sas, “Strength of thin-walled structural elements with cracks under the conditions of creep,” Fiz.-Khim. Mekh. Mater., 43, No. 2, 33–39 (2007); English translation: Mater. Sci., 43, No. 2, 174−182 (2007).

  5. R. O. Ritchie and S. Suresh, “Mechanics and physics of the growth of small cracks,” in: Behavior of Short Cracks in Airframe Components, AGARD Conference Proceedings, No. 328, NATO Advisory Group for Aerospace Research and Development, Neuilly-sur-Seine, France (1983), pp. l-l–1-14.

  6. O. E. Andreikiv, N. S. Shtayura, and R. Ya. Yarema, “Energy-based approach to evaluation of short fatigue crack growth rate in plates,” Strength Mater., 49, No. 6, 778–787 (2017).

    Article  Google Scholar 

  7. О. E. Andreikiv, A. R. Lysyk, N. S. Shtayura, and A. V. Babii, “Evaluation of the residual service life of thin-walled structural elements with short corrosion-fatigue cracks,” Fiz.-Khim. Mekh. Mater., 53, No. 4, 84–90 (2017); English translation: Mater. Sci., 53, No. 4, 514–521 (2018).

  8. O. E Andreikiv., I. Ya. Dolins’ka, and N. V. Yavors’ka, “Estimation of the periods of initiation and propagation of creep-fatigue cracks in thin-walled structural elements,” Fiz.-Khim. Mekh. Mater., 47, No. 3, 7–15 (2011); English translation: Mater. Sci., 47, No. 3, 273–283 (2011).

  9. O. E. Andreikiv, R. M. Lesiv, and I. Ya. Dolins’ka, “Dependence of the period of subcritical growth of a creep fatigue crack on the duration of loading cycles,” Fiz.-Khim. Mekh. Mater., 45, No. 4, 31–38 (2009); English translation: Mater. Sci., 45, No. 4, 494–503 (2009).

  10. M. Shata and Z. O. Terlets’ka, Energy Approach in Mechanics of Fatigue Propagation of a Macrocrack. Fracture Mechanics and Strength of Structures [in Ukrainian], Issue 2, Kamenyar, Lviv (1999), pp. 141–148.

  11. R. М. MсMeeking, “Finite deformation analysis of crack tip opening in elastic-plastic materials and implications for fracture,” J. Mech. Phys. Solids, 25, No. 5, 357–381 (1977).

    Article  Google Scholar 

  12. M. P. Savruk, Stress Intensity Factors in Bodies with Cracks [in Russian], Naukova Dumka, Kiev (1988).

    Google Scholar 

  13. A. Fuji and М. Kitagawa, “A comparison of creep crack growth behaviour in nickel based super alloy with low alloy steel,” in: Advances in Fracture Resistance and Structural Integrity: Selected Papers from the 8th Internat. Conf. on Fracture (ICF 8) (Kyiv, June 8–14, 1993), Pergamon Press (1994), pp. 487–495.

  14. N. Yadzhak, “Generalization of the equivalent area method for the case of short fatigue cracks in a three-dimensional body,” Visn. Lviv Univ. Ser. Mech. Math., No. 89, 134–141 (2020).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. I. Franko National University of Lviv, Lviv, Ukraine

    О. Ye. Andreikiv & І. Ya. Dolinska

  2. Karpenko Physicomechanical Institute, National Academy of Sciences of Ukraine, Lviv, Ukraine

    О. Ye. Andreikiv & І. Ya. Dolinska

Authors
  1. О. Ye. Andreikiv
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. І. Ya. Dolinska
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to О. Ye. Andreikiv.

Additional information

Translated from Fizyko-Khimichna Mekhanika Materialiv, Vol. 57, No. 2, pp. 16–23, March–April, 2021.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Andreikiv, О.Y., Dolinska, І.Y. Determination of the Period of Subcritical Growth of Small Plane High-Temperature Creep Cracks in Structural Elements. Mater Sci 57, 154–162 (2021). https://doi.org/10.1007/s11003-021-00526-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11003-021-00526-1

Keywords

Search

Navigation