1 Introduction

Recently, lattice structures made of regularly repeating unit cells have proven to have many superior properties, which makes them promising solutions for various applications, such as a lightweight mechanical structure with negative thermal expansion (Wang et al. 2016), an efficient heat exchanger due to its large surface area (Imran et al. 2020), and an engineered acoustic insulator for sound absorption (Zhang et al. 2020). Elastic periodic structures, in particular, find numerous applications in wave propagation control ranging over the whole frequency spectrum of the vibration phenomenon (Dwivedi et al. 2021; Liang et al. 2022): from extremely high frequencies vibration to radiation conversion in THz frequency range (Moldosanov and Postnikov 2016), to several applications in the Micro-Electro Mechanical energy transfer (Saadon and Sidek 2015), to ultra-low few Hz in the seismic metamaterials domain (Achaoui et al. 2017).

The most important feature of the elastic/acoustic structures is the bandgap, i.e., the frequency range of prevented wave transmission: a wide and complete bandgap means robust control over the wave propagation. In many cases, complete bandgaps are presented in periodic structures with conventional building units, such as squares (Alhammadi et al. 2021; Chen et al. 2017), cylinder (Ma et al. 2016), or spherical shapes (Zhou et al. 2012). Recently, there has been an increasing interest in using the topology of the mathematically known triply periodic minimal surfaces (TPMS) to create artificial cellular materials in different applications (Abueidda et al. 2017; Al-Ketan and Abu Al-Rub 2019; Cai et al. 2022; Han and Che 2018; Simsek et al. 2020). TPMS is a locally area-minimizing surface, i.e., the surface that locally minimizes surface area for a given boundary, and thus the mean curvature at each point on the surface is zero (Siem and Carter 2023). A comprehensive review of TPMS structures can be found at Oudich et al. (2023).

The deployment of TPMS structures for vibration isolation has already been reported in the literature. Zhang et al. (2023) developed a novel metamaterial specifically to this end and optimized its dimensions to enlarge the width of the bandgap. In the experimental tests, the optimized bandgap spammed a normalized frequency from 0.3125 to 0.5150 and suppressed the propagation of elastic waves within this range, thus isolating vibrations. Sheng et al. (2023) also proposed a new metamaterial based on simple cubic and body-centered cubic lattices and obtained a broader bandgap compared with typical metamaterial for vibration suppression in the low-frequency domain. Simsek et al. (2020) carried out modal analysis of four common TPMS structures and compared different modeling methods in terms of their computational efficiency and accuracy.

However, a key challenge during the design of a lattice structure for a specific application is choosing the appropriate lattice topology. The lattice cell, used materials, and volumetric fraction play crucial roles in determining the effective elastic properties, but elastic band structures of different TPMS lattice structures are generally less studied (Castro et al. 2019; Yu et al. 2019). Most efforts to determine the appropriate topology consist of selecting a set of TPMS structures and comparing them through finite element analysis. Hur et al. (2017) compares 16 different TPMS cubic structures at different volume ratios and concluded that only six of them present complete bandgaps. In these 6 structures, the bandgap’s width increases with greater density contrast between the TPMS structure and the filling material. Therefore, larger phononic bandgaps are tailored by utilizing materials with a higher density contrast. Elmadih et al. (2019) investigates the diamond and gyroid lattices and observe the existence of complete bandgaps only in the latter. Additionally, increasing the cell size lowers the bandgap’s central frequency, at the expense of simultaneously decreasing width. Abueidda et al. (2018a, b) investigates acoustic bandgaps in the Primitive, Neovius, and IWP lattice and Michielsen and Kole (2003) carries out an extensive comparison among more than 20 TPMS structures for bandgap formation. Although the considerable effort, the number of TPMS structures is vast and only a fraction has been investigated so far.

To set forth the effort to cover more TPMS structures, this work presents a numerical elastic simulation for sub-2 kHz applications of seven TPMS lattice structures, including Primitive, Gyroid, Neovius, IWP, Diamond, Fischer–Koch S, and FRD, for volume ratios ranging from 0.1 to 0.9. The material considered for the TPMS lattice structures is polymer Nylon-12, which is immensely popular for additive manufacturing applications because of its processability. The relationship of the elastic band structure of these seven TPMS structures is investigated as a function of their relative density and cell type. By summarizing the simulation results, our work extensively assesses volume ratios' impact on bandgap properties for these TPMS structures. This quantitative exploration aids in understanding the intricate relationship between lattice type, volume ratio, and bandgap behavior – a facet not extensively addressed in the referenced study. In addition, the partial bandgap or so-called elastic wave directionality of all TPMS structures is also presented in this work, which is required for the deployment of the TPMS structures in vibration isolation applications.

1.1 Numerical method

The elastic wave propagation through the phononic crystal is studied using a three-dimensional finite element method implemented in Solid Mechanics COMSOL modules (COMSOL 2018). The governing equation is given by Eq. (1):

$$\rho \frac{{\partial^{2} u}}{{\partial t^{2} }} = \nabla .\sigma$$
(1)

where \(u\) and \(\rho\) are the displacement and density of the materials and \(\sigma\) is the stress tensor. In this work, the polymer Nylon-12 is simulated as a linear elastic material, with the following properties: \(\rho\) = 950 kg/m3, \(\nu\) = 0.4, \(E\) = 9.4 GPa. The stress–strain constitutive relation for linear materials is commonly known as Hooke's law. Equivalently, in terms of the stress \(\sigma\), Young's modulus \(E\), and strain \(\varepsilon\) (dimensionless), as given by

$$\sigma = E\varepsilon$$
(2)

A linear system having a plurality of degrees of freedom can be described by a matrix equation of the following type:

$$M\frac{{\partial^{2} u\left( {\vec{r},t} \right)}}{{\partial t^{2} }} + Ku\left( {\vec{r},t} \right) = \vec{f}\left( t \right)$$
(3)

wherewith \(M\) and \(K\) symbolizing mass and stiffness matrices, respectively, \(u\left( {\vec{r},t} \right)\) is the displacement eigenvector, and \(\vec{f}\left( t \right)\) is the applied force. Upon substituting \(u\left( {\vec{r},t} \right) = u\left( {\vec{r}} \right)exp\left( {i\omega t} \right)\) in (3), the following eigenvalue problem is obtained, as given by Eq. (4).

$$\left( {K - \omega_{i}^{2} M} \right)u = 0$$
(4)

The Floquet–Bloch periodic boundary conditions are applied to the six edges of the unit cell to have a periodically repeating nature, as indicated by Eq. (5):

$$u\left( {\vec{r}} \right) = u_{k} \left( r \right)e^{{j\overrightarrow {k \cdot } \vec{r}}}$$
(5)

where the periodicity vector is defined by its magnitude k = 2πΛ, with Λ representing the period along that specific direction, and r denotes the position vector. This analysis is undertaken with the aim of determining the eigenfrequency associated with a specified Bloch wave vector, \(k = \left( {k_{x} ,k_{y} ,k_{z} } \right)\), These displacement eigenvectors are orthogonal with respect to both \(K\) and \(M\) matrix.

$$u_{j}^{T} Mu_{i} = 0,\,\,\,\, u_{j}^{T} Ku_{i} = 0,\,\,\,i \ne j$$
(6)

The dispersion relation was calculated by determining the first 10 eigenfrequencies of the unit cell at 45 points along special points of the path in the corresponding cubic k-space. The stiffness matrix corresponds to the reciprocal of the compliance matrix.

(Ahmad et al. 2018) and can be given by:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{{{\text{xx}}}} } \\ {\sigma_{{{\text{yy}}}} } \\ {\sigma_{{{\text{zz}}}} } \\ {\sigma_{{{\text{yz}}}} } \\ {\sigma_{{{\text{zx}}}} } \\ {\sigma_{{{\text{xy}}}} } \\ \end{array} } \right\} = \frac{E}{{\left( {1 + \upsilon } \right)\left( {1 - 2\upsilon } \right)}}\left[ {\begin{array}{*{20}c} {1 - \upsilon } & \upsilon & \upsilon & 0 & 0 & 0 \\ \upsilon & {1 - \upsilon } & \upsilon & 0 & 0 & 0 \\ \upsilon & \upsilon & {1 - \upsilon } & 0 & 0 & 0 \\ 0 & 0 & 0 & {1 - 2\upsilon } & 0 & 0 \\ 0 & 0 & 0 & 0 & {1 - 2\upsilon } & 0 \\ 0 & 0 & 0 & 0 & 0 & {1 - 2\upsilon } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{{{\text{xx}}}} } \\ {\varepsilon_{{{\text{yy}}}} } \\ {\varepsilon_{{{\text{zz}}}} } \\ {\varepsilon_{{{\text{yz}}}} } \\ {\varepsilon_{{{\text{zx}}}} } \\ {\varepsilon_{{{\text{xy}}}} } \\ \end{array} } \right\}$$
(7)

where stress \(\sigma\) and strain ε are presented in a tensor form.

The employed numerical method serves as the foundation for comprehending the origin and characteristics of elastic bandgaps in the studied TPMS periodic lattice structures (Brillouin 1953; Laude 2020). Through the application of the three-dimensional finite element method, we gain insight into the behavior of elastic wave propagation within these intricate lattice frameworks. The displacement eigenvectors, describing the modes of deformation that occur when elastic waves propagate through the lattice, are calculated from the eigenvalue problem, as depicted in Eq. (4). It turns out that the interplay of material properties, geometric configurations, and wave propagation phenomena contributes to the formation of elastic bandgaps, which are key features in the numerical calculated frequency spectrum where certain frequency ranges are forbidden for propagation.

We can systematically analyze the behavior of elastic waves within TPMS lattice structures. The manipulation of factors such as the lattice geometry, unit cell properties, and material characteristics enables us to tailor the properties of bandgaps. Understanding the interaction between these factors and their impact on the frequency response of the lattice empowers us to design and engineer TPMS structures with desired bandgap characteristics, catering to specific applications in wave manipulation (Ahmed and Bottaro 2023), energy absorption (Abueidda et al. 2017; Yang et al. 2019; Zhang et al. 2018) and more.

2 Results and discussions

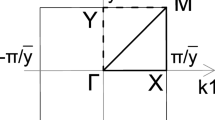
The 3D illustration of the seven different periodic lattice structures, named Primitive, Neovius, Diamond, FRD, IWP, Fischer Koch, and Gyroid, are shown in Fig. 1. Table 1 shows the cubic Bravais lattices, which are the simple cubic (SC), faced-centered cubic (FCC), and body-centered cubic (BCC) of each TPMS structure, along with the corresponding mathematical formulation. In this formulation, \({\text{a}}\) stand for the half-length of the unit cell (\({\text{a}} = 0.5{\text{ft}}\) in this work), (x, y, z) stand for the cartesian coordinates in the global coordinate system, and the parameter \({\text{c}}\) determines the relative density of the TPMS lattice. The Irreducible Brillouin Zone is shown in Table 2, along with the coordinates (in ft) of each vertex.

Fig. 1
figure 1

3D illustration of the TPMS structures

Full size image
Table 1 The structural name, cubic Bravais lattice, irreducible Brillouin zone and the level set equations for the seven co-continuous cubic network structures
Full size table
Table 2 Illustration of the Cubic Bravais lattice of the SC, BCC and FCC along with the coordinates of the irreducible Brillouin zone
Full size table

2.1 Simple cubic

The two simple cubic Primitive and Neovius structures shown in Fig. 1 are studied in this section. For both structures, the eigenfrequencies are presented as a function of wavenumber along with special points of \(R \to M \to \Gamma \to X \to M\) (Table 2) in the irreducible Brillouin zone. Each eigenfrequency corresponds to a vibration frequency where phononic waves are allowed to propagate inside the lattice structure, and thus not isolating vibrations. Figure 2 shows dispersion curves of the Primitive-based lattice structure with a relative density (volume of the solid divided by the volume of the unit cell) of 0.5. In Fig. 2, the eigenfrequencies are represented by the blue lines (dispersion curves), and the 10 first dispersion curves are considered. With this simple cubic structure, two complete bandgaps (frequency ranges with no dispersion curves over \(R \to M \to \Gamma \to X \to M\)) are formed. The first bandgap takes place between the 3rd and 4th dispersion curves from 0.99 to 1.41 kHz, while the second thinner one is observed between the 6th and 7th dispersion curves from 1.61 kHz to 1.70 kHz. The bandgaps showed in Fig. 2 stand for complete bandgaps, where no phononic wave is transmitted in any of the three directions (\(k_{1} ,k_{2}\) and \(k_{3}\)) of the irreducible Brillouin zone, (i.e., in any directions) within the bandgap frequency range. Typically, bandgaps are described according to their bandwidth (\(\Delta \omega\)) and central frequency (\(\omega_{c}\)), which are calculated as,

$$\Delta \omega = \omega_{max} - \omega_{min}$$
(8)
$$\omega_{c} = \left( {\omega_{max} + \omega_{min} } \right){/}2$$
(9)

where \(\omega_{max}\) and \(\omega_{min}\) denote the higher and lower bounds of the frequency bandgap, respectively. Therefore, the first bandgap of the Primitive lattice structure has the bandwidth and central frequency of 0.42 kHz and 1.20 kHz, respectively, while the second one has the bandwidth and central frequency of 0.092 kHz and 1.66 kHz. The results obtained for the primitive structure are like those of the Neovius-based lattice, which also belongs to the simple cubic system.

Fig. 2
figure 2

Elastic band structure of Primitive structure with a volume ratio of 0.5, along with the formation of two complete band gaps

Full size image

In Fig. 3a, b, the complete bandgaps of the Primitive and Neovius TPMS lattice structures are presented as a function of volume ratio from 0.2 to 0.9. Figure 3a represents the Primitive lattice. The first complete bandgap (the blue polygon) is found between the 3rd and 4th dispersion curves. This bandgap increases in width and central frequency monotonically as the volume ratio increases. At a volume ratio of 0.2, the width and central frequency of the first bandgap are 0.036 kHz and 0.86 kHz, respectively, and when the volume ratio is equal to 0.9, the bandgap reaches its maximum width of 0.48 kHz and maximum central frequency of 1.49 kHz. Two other bandgaps, between the 6th and 7th (red polygon) and the 7th and 8th (purple polygon) bands, are also observed at low volume ratios. The width of these two bandgaps decreases as the volume ratio increases, while their central frequency increases. The bandgap between the 7th and 8th dispersion curves is only observed at volume ratios between 0.2 and 0.5, while the bandgap between the 6th and 7th dispersion curves exists only from volume ratios of 0.4 to 0.8. Figure 3b presents the results of the Neovius structure, and three complete bandgaps are observed. The first bandgap (blue polygon) takes place between the 3rd and 4th dispersion curves and grows in width and central frequency as the volume ratio raises, similarly to the Primitive case. The second bandgap (red polygon) is considerably large, present over the entire range of volume ratios (0.1–0.9), and is comparable in width with the first bandgap. A third and narrow bandgap (purple polygon) is visible only between the volume ratios of 0.8 and 0.9. The second and third bandgaps of the Neovius case behave significantly differently from the second and third bandgap of the Primite structure, even though they are formed between the 6th and 7th and the 7th and 8th dispersion curves of both lattices.

Fig. 3
figure 3

Bandgap gaps of the a Primitive and b Neovius structure for different values of volume ratio ranging from 0.2 to 0.9

Full size image

In many applications, such as vibration isolation, seismology, medical ultrasound, and non-destructive evaluation, the presence of wave directionality (or partial bandgaps) in the lattice structure is also desirable. For the case of the Primitive lattice, wave attenuation in different directions of the irreducible Brillouin zone is presented in Fig. 4.

Fig. 4
figure 4

Partial bandgaps in each direction of the irreducible Brillouin zone for the primitive lattice structure

Full size image

In the \(R \to M\) direction (Fig. 4a), multiple bandgaps are formed between the 3rd and the 9th dispersion curves, showing that waves are strongly attenuated in these frequency regions. Below the 3rd dispersion curve (0.84 kHz), two wide bandgaps are observed (blue and purple polygon), which prevents vibrations in most of the frequency range between 0 and 0.84 kHz. For the Primitive structure, the direction \(R \to M\) is a good candidate for vibration isolation applications. In Fig. 4b (direction \(M \to \Gamma\)), considerably fewer bandgaps are formed as compared to the direction of \(R \to M\). In this case, vibrations are free to propagate at frequencies below the 3rd band at all volume ratios between 0.2 and 0.9. For the lattice structure with volume ratios above 0.6, vibrations can also propagate freely at frequency ranges above the 4th band. This means that, for the primitive structure, it is possible to isolate vibrations in the \(R \to M\) direction but allow them to propagate in the \(M \to \Gamma\) direction at frequencies below the 3rd band (at all volume ratios) or above the 4th band (above volume ratio of 0.6).

Figure 4a–d show the bandgaps formed in the \(\Gamma \to X\) and \(X \to M\) directions, respectively. The dispersion curves in the direction \(\Gamma \to X\) shows a similar behavior as that in the direction \(M \to \Gamma\), and the dispersion curves in the direction \(X \to M\) has similar bandgaps as that in the direction \(R \to M\). Note that the overlapping of all bandgaps in the elastic band structure from Fig. 4a–d results in the complete bandgap, which is presented in Fig. 3a.

2.2 Face centered cubic

The FCC structures among TPMS structures investigated in this work are the FRD and Diamond. Figure 5 depicts the dispersion curves illustrating the behavior of the Diamond lattice structure with a volume ratio of 0.5, where the wavenumber is scanned along the special points of \(X \to U \to L \to \Gamma \to X \to W \to K\) in the irreducible Brillouin zone of FCC structures. One complete bandgap is observed for the diamond structure from 1.28 to 1.40 kHz between the 3rd and 4th bands at the volume ratio of 0.5. By comparing with the Primitive and Neovius lattice structures, the Diamond structure presents a narrower bandgap and higher central frequency.

Fig. 5
figure 5

Elastic band structure of the FCC diamond structure with the volume ratio of 0.5

Full size image

Figure 6a, b show the dependency of complete bandgaps of the diamond and FRD structures on their volume ratios ranging from 0.2 to 0.9. In Fig. 6a, no bandgap is formed between volume ratios of 0.2 and 0.4, showing that waves of any frequency can be transmitted in at least one direction in the Diamond structure. At a volume ratio of 0.4, the bandgap presents a width and central frequency of 0.069 kHz and 1.240 kHz, respectively. Both width and central frequency continuously increase as the volume ratio increases, ultimately reaching 0.185 kHz and 1.809 kHz, respectively, when the volume ratio is equal to 0.9. Figure 6b presents the complete bandgaps observed in the FRD structure. However, complete bandgaps appear only at volume ratios between 0.8 and 0.9. The complete bandgaps at volume ratios between 0.8 and 0.9 have, approximately the same width as the bandgaps of the Diamond structure for the same volume ratios, and a central frequency approximately 0.1 kHz lower. Noticeably, the complete bandgap of the diamond structure is considerably narrower and with a higher central frequency than the bandgap obtained with the primitive structure, as shown in Fig. 2.

Fig. 6
figure 6

Bandgap of the FCC a Diamond and b FRD structure with different volume ratios ranging from 0.2 to 0.9

Full size image

As for the Diamond lattice structure, the partial bandgaps along different symmetric points in the FCC irreducible Brillouin zone is presented in Fig. 7a–f. Figure 7a shows several bandgaps formed in the \(X \to U\) direction, with the upper frequency of one bandgap being close to the lower frequency of the other bandgap. This shows that vibrations through the \(X \to U\) direction are attenuated at a wide range of frequencies at the entire range of volume ratios (0.2–0.9). The elastic partial bandgaps are less overlapped in the \(U \to L\) direction, as shown in Fig. 7b. Figure 7c shows only one bandgap (between the 3rd and 4th dispersion curves) in the \(L \to \Gamma\) direction and allows vibrations to propagate in all other frequencies. Figure 7d also presents one wide bandgap between the 3rd and 4th dispersion curves in the \(\Gamma \to X\) direciton. However, this bandgap is narrower than the one seen in Fig. 7c and has a slightly higher central frequency. Additionally, the bandgap of Fig. 7d exists only at volume ratios larger than 0.3. At a volume ratio of 0.2, no bandgap is observed. Between volume ratios of 0.7 and 0.8, a second bandgap is seen between the 5th and 6th dispersion curve. Figure 7e, f show similar partial bandgaps in the \(X \to W\) and \(W \to K\) directions. Then again, the overlapping of all partial bandgaps from Fig. 7a–f lead to the complete bandgap presented in Fig. 5a.

Fig. 7
figure 7

Partial bandgaps in each direction of the irreducible Brillouin zone for the Diamond lattice structure

Full size image

The discourse provided in the preceding passages regarding the Diamond lattice is equally pertinent to the FRD structure. The FRD structure presents fewer bandgaps through \(U \to L\) directions than those of the Diamond-based lattice structure hindering the performance for isolating vibrations, which causes the complete bandgap to appear only at the volume ratio above 0.8. On the \(L \to \Gamma\) and \(\Gamma \to X\) directions, one wide elastic bandgap is observed with a similar central frequency as the Diamond’s structure. The discussion on the elastic band structure of FCC FRD-based is included in Section S. III of Supporting Information.

2.3 Body centered cubic

Three BCC TPMS-based lattice structures, including IWP, Fischer Koch, and Gyroid, are investigated in this section. The dispersion curves of BCC -IWP case are presented in Fig. 8a when the volume ratio is equal to 0.4. For BCC structures, the wavenumber is scanned along special points of \(N \to P \to \Gamma \to H \to P\) in the irreducible Brillouin zone to obtain the dispersion curves. As seen, two bandgaps are formed within the region of the first ten bands.

Fig. 8
figure 8

a Elastic band structure of body-centered-cubic IWP structure with the volume ratio of 0.4. Bandgap of the b IWP, c Ficher Koch and d Gyroid structures with different values of volume ratio

Full size image

The dependency of complete bandgaps of the BCC IWP, Fischer Koch, and Gyroid lattice structures are presented in Fig. 8b–d, respectively. In Fig. 8b, IWP lattice structure shows two complete bandgaps between the volume ratios from 0.1 to 0.7. The first complete bandgap appears between the 3rd and 4th dispersion curves. At the volume ratio of 0.1, the IWP structure presents the lowest central frequency of 0.729 kHz but a small bandwidth 0.109 kHz among all the TPMS lattice structures. As the volume ratio increases, the central frequency also increases and reaches the value of 1.371 kHz at the volume ratio of 0.7. The bandgap’s width, however, does not increase significantly with the volume ratio, reaching a maximum value of 0.141 kHz. A second bandgap, between the 9th and 10th dispersion curves, also appears for volume ratios larger than 0.5. This second bandgap presents bandwidth and central frequency of the bandgap with values of 0.063 kHz and 1.804 kHz when the volume ratio is 0.5, and values of 0.188 kHz and 2.161 kHz at a volume ratio of 0.7.

In Fig. 8c, the results for the Fischer Koch structure are shown and simulations are performed for volume ratios between 0.1 and 0.6. A complete bandgap, between the 3rd and 4th dispersion curves, is formed when the volume ratio is larger than 0.2. At this volume ratio, the bandgap’s width and central frequency are 0.093 kHz and 0.967 kHz, respectively. When the volume ratio is 0.6, the width and central frequency increase to 0.232 kHz and 1.281 kHz. Noticeably, the Fischer Koch presents higher values of bandgap’s width and central frequency than the IWP structure. In Fig. 7d, the Gyroid case is presented. Here, simulations are performed for volume ratios between 0.1 and 0.9, and a complete bandgap is observed for a volume ratio above 0.2. The bandgap’s width and central frequency of the Gyroid case are very similar to the Fischer Koch structure for volume ratios between 0.2 and 0.6.

The partial bandgaps in each direction of the BCC IWP structure can be seen below in Fig. 9. As seen, results are similar to what were observed for the previous Primitive and Diamond structures: (i) there are two directions in the IWP structure \(N \to P\), shown in Fig. 9a and \(H \to P\), shown in Fig. 9d that presents several bandgaps and therefore are suitable for vibration isolation and (ii) Two directions \(P \to \Gamma\), shown in Fig. 8b and \(\Gamma \to H\), shown in Fig. 8c that present fewer bandgaps and are more susceptible to propagate waves. What differs the IWP structure from the Primitive and Diamond cases is the fact that the partial bandgap between the 3rd and 4th bands is wide in all directions of the Brillouin zone, resulting in the wide complete bandgap, as shown in Fig. 7a. Among IWP, Gyroid, Fischer Koch structures, the Gyroid presents wider bandgaps with higher central frequencies, and, for that reason, this section focuses on the results of the IWP case. Results regarding the Gyroid and Fischer Koch structures can be seen in Section S.V and S. VI of Supporting Information.

Fig. 9
figure 9

Partial bandgaps in each direction of the BCC IWP lattice structure

Full size image

2.4 Comparison among seven TPMS lattice structures

In practical applications, it is desirable to have a larger bandgap’s width and a lower central frequency to enable isolating vibration at low frequencies (Abueidda et al. 2018a, b; Elmadih et al. 2019). To this end, this section provides a quick and easy comparison among the seven lattice structures of Fig. 1 in terms of their bandgap’s width and central frequency, as shown in Fig. 10a, b, respectively. This comparison is carried out only for the complete bandgap between the 3rd and 4th bands since this bandgap appears for all the seven investigated periodic lattice structures. Although there are other complete bandgaps above the 4th band, they are narrow, appear only at short range of volume ration, and are not common to all seven TPMS structures; therefore, only the bandgap between the 3rd and 4th bands is considered in this comparison.

Fig. 10
figure 10

Comparison of the a bandwidth and b central frequency of the first bandgap among seven TPMS lattice structures investigated in this work

Full size image

Among these seven TPMS lattice structures, for low values of volume ratio (0.1 and 0.2), the IWP and Neovius present the largest bandgaps, ranging from 0.06 to 0.192 kHz. For the volume ratio larger than 0.3, the Primitive and Neovius structures present the widest bandgap width (Fig. 10a). Particularly, when the volume ratio is greater than 0.6, the bandgap’s width of the Primitive and Neovius lattice structures becomes more than 2 times larger than the width observed for the other TPMS lattice structures. The largest width of the Primitive and Neovius cases are equal to 0.482 kHz and 0.458 kHz, respectively, when the volume ratio is equal to 0.9. In Fig. 10a, it is seen that the Diamond has the narrowest bandwidth (around 0.15 kHz) among all lattice structures.

In Fig. 10b, the central frequency of the bandgap of all TPMS structures is presented tio. Overall, a nearly linear relationship between the central frequency and the relative density is observed, which results from the Bragg scattering of the lattice structures (Alonso-Redondo et al. 2015). Among these seven TPMS lattice structures, the lowest central frequencies are observed near 0.73 kHz for the Neovius, Gyroid, and IWP structures when the volume ratio is equal to 0.1. The largest central frequencies are obtained for the Diamond structure (from 1.24 to 1.81 kHz) in the volume range of 0.4 to 0.9, while the second largest central frequencies (from 1.09 to 1.44 kHz) belong to the FRD case. By summarizing the bandwidth and central frequency of the bandgap, we can find that it is possible to tailor bandgap’s width up to 0.483 kHz and tailor bandgap’s central frequency between 0.73 and 1.81 kHz by properly selecting the periodic lattice structure and volume ratio.

It is more direct to compare the dimensionless bandgap’s width \(W_{g}\) of these seven TPMS lattice structures to show which lattice structure provides a wider bandgap. The dimensionless bandgap’s width is calculated as the bandgap’s width (\(\Delta \omega\)) divided by the bandgap’s central frequency (\(\omega_{c}\)). Figure 11 shows a comparison of the dimensionless bandgap’s width of these seven periodic lattices for volume ratios varying from 0.1 to 0.9. The Primitive and Neovius-based lattice structures have the largest values of \(W_{g}\) (0.356 at the volume ratio of 0.6, and 0.357 at the volume ratio of 0.9, respectively) at almost all volume ratios, while the Diamond presents the narrowest dimensionless bandgap width (around 0.1) among all cases.

Fig. 11
figure 11

Comparison of the dimensionless bandgap’s width for the seven TPMS lattice structures investigated in this work

Full size image

3 Conclusions

The elastic band structures of seven Nylon 12-based TPMS lattice crystals, including Primitive, Gyroid, Neovius, IWP, Diamond, Fischer–Koch S, and FRD, are investigated as a function of their volume ratio. Among these seven TPMS lattice structures, the Primitive and Neovius structures present the largest (0.483 kHz) and second largest (0.485 kHz) bandwidths among all the investigated structures at volume ratios above 0.3. The Diamond and FRD present the worst performance in terms of bandgap’s width. Through the comparison of the bandwidth and central frequency of the bandgap among these seven structures, it is possible to tailor bandgap’s width up to 0.483 kHz and tailor bandgap’s central frequency between 0.73 to 1.81 kHz by properly selecting the periodic lattice structure and volume ratio. Thus, this finding provides the clues to apply TPMS-based lattice structures for acoustic or elastic applications.