Active learning algorithm through the lens of rejection arguments

Abstract

Active learning is a paradigm of machine learning which aims at reducing the amount of labeled data needed to train a classifier. Its overall principle is to sequentially select the most informative data points, which amounts to determining the uncertainty of regions of the input space. The main challenge lies in building a procedure that is computationally efficient and that offers appealing theoretical properties; most of the current methods satisfy only one or the other. In this paper, we use the classification with rejection in a novel way to estimate the uncertain regions. We provide an active learning algorithm and prove its theoretical benefits under classical assumptions. In addition to the theoretical results, numerical experiments are carried out on synthetic and non-synthetic datasets. These experiments provide empirical evidence that the use of rejection arguments in our active learning algorithm is beneficial and allows good performance in various statistical situations.

1 Introduction

The aim of machine learning consists in designing learning models that accurately maps a set of inputs from a space $\mathcal {X}$ called instance space to a set of outputs $\mathcal {Y}$ called label space. Nowadays, with the data deluge, obtaining a powerful learning model requires a lot of data from $\mathcal {X}$ to be labeled, which is time consuming in many modern applications such as speech recognition or text classification. This motivated the development of other paradigms beyond classical prediction tasks. In this paper, we focus on prediction in the binary classification setting, that is $\mathcal {Y}=\lbrace 0,1\rbrace$. In this framework, one of the most studied techniques to deal with this specificity is the iterative supervised learning procedure called active learning (Cohn et al., 1994; Castro & Nowak, 2008; Balcan et al., 2009; Hanneke, 2011; Locatelli et al., 2017, 2018) that aims at reducing the data labeling effort by carefully selecting which data need to be labeled. The goal of active learning is to achieve a high rate of correct predictions while using as few labeled data as possible. One of the key principles of active learning is to identify at each step the region of the instance space where the label requests should be made, called uncertain region in this paper, also known as disagreement region in the active learning literature (Hanneke, 2007; Balcan et al., 2009; Dasgupta, 2011). Many techniques have been developed to this aim, both in parametric (Cohn et al., 1994; Hanneke, 2007; Balcan et al., 2009; Beygelzimer et al., 2009; Hanneke et al., 2014) and nonparametric settings (Minsker, 2012; Locatelli et al., 2017, 2018).

In this paper, we are particularly interested in the nonparametric setting, where several computational difficulties have so far hampered the practical implementation of the proposed algorithms. For example, Minsker (2012) provides interesting theoretical results which partly motivated (Locatelli et al., 2017, 2018) as well as the present work, but it fails to provide a computationally efficient way to estimate the uncertain region.

To overcome these shortcomings, we present a new active learning algorithm using the paradigm called rejection. The latter typically allows the learning models to evaluate their confidence in each prediction and to possibly abstain from labeling an instance (i.e., "reject" this instance) when the confidence in the prediction of its label is too weak. This rejection will however be used in a novel way in this work to conveniently compute the uncertain region, as explained below.

Rejection and active learning typically differ on how they are interested in this uncertain region. In rejection, the interest in the uncertain region appears after the design of a learning model, that rejects a test point in order to avoid a misprediction. This is very useful in some applications such as medical diagnosis where a misprediction can be dramatic. However, in active learning, the uncertain region is used during the training process to progressively improve the model’s performance by requesting labels where the classification is difficult.

In our algorithm, we use rejection at each step k of the training process to estimate the uncertain region $A_k\subset \mathcal {X}$ based on the information gathered up to this step. Then some points are sampled from the region $A_k$ and their labels are requested. Based on these labeled examples, an estimator ${\hat{f}}_k$ is provided, that is then used to assess for each x $\in$ $A_k$ the confidence in the prediction. The points where the confidence is low are rejected and are considered to form the next uncertain region $A_{k+1}$, thereby progressively reducing the part of instance space $\mathcal {X}$ on which a model remains to be constructed. We study the rate of convergence with respect to the excess-risk of our nonparametric active learning algorithm based on histograms (or kernel methods) under classical smoothness assumptions. It turns out that combining active learning sampling together with rejection allows for optimal rates of convergence. Using numerical experiments on several datasets we also show that our active learning process can be efficiently applied to any off-the-shelf machine learning algorithm.

The paper is organized as follows: in Sect. 2 we provide the background notions of active learning and rejection separately, then review some recent works that proposed to combine these two notions, although in a way that differs from ours. Then we describe our algorithm in Sect. 3 along with the theoretical guarantees about its rate of convergence. Practical considerations to take into account when applying our algorithm are discussed in Sect. 4. Numerical experiments are presented in Sect. 5 and we conclude the paper along with some perspectives for future work in Sect. 6. The full proof of our theoretical result is relegated to the Appendix.

2 Background

In this section we review the literature related to active learning in Sect. 2.1, and the reject option framework in Sect. 2.2. Thereafter in Sect. 2.3 we provide a review on the use of the rejection in the context of active learning.

2.1 Active (and passive) learning

Given an i.i.d. sample $(X_1,Y_1), \ldots , (X_n,Y_n)$ from an unknown probability distribution P defined on $\mathcal {X}\times \mathcal {Y}$, the classification problem consists in designing a map $g: \mathcal {X}\longrightarrow \mathcal {Y}$ from the instance space to the label space. However, building such mapping might become a tricky task in particular situations where the labeling process of input instances are only available through time-consuming or expensive requests to a so-called oracle. In such applications, one might however have access to a huge amount of unlabeled data from the instance space. This motivated the use of the active learning paradigm (Cohn et al., 1994) that aims at reducing the data labeling effort by carefully selecting which data to label. In contrast, we call passive learning the setting where the model, for budget N, has access at once to N labeled observations randomly queried from the joint distribution P.

Active learning algorithms were initially designed according to somewhat heuristic principles (Settles, 1994) without theoretical guarantees on the convergence nor on the expected gain with respect to passive learning. The theory of active learning has then gradually developed (Cohn et al., 1994; Freund et al., 1997; Balcan et al., 2009; Hanneke, 2007; Dasgupta et al., 2007; Castro & Nowak, 2008; Minsker, 2012; Hanneke & Yang, 2015; Locatelli et al., 2018, 2017; Hanneke et al., 2022).

We are particularly interested in the nonparametric setting, where regularity and noise assumptions are made on the regression function. Two types of regularity assumptions are made on the regression function. The first one was introduced in the seminal work by Castro and Nowak (2008) and was also used in Locatelli et al. (2018), where it is assumed that the decision boundary $\lbrace x,\;\eta (x)=\tfrac{1}{2}\rbrace$ (where $\eta$ is the regression function) is the graph of a smooth function. The second one, which was used in Minsker (2012); Locatelli et al. (2017), assumes that the whole regression function is smooth. In this work, we will use similar regularity assumption as in Minsker (2012). Besides, the noise margin assumption corresponds to the so-called Tsybakov noise condition, and it was observed that it corresponds to the situation in which active learning can outperform passive learning (Castro & Nowak, 2008).

In this work, we design an efficient active learning algorithm, similar to that considered in Minsker (2012), but handling the uncertain region in an explicit and computationally tractable way using rejection. Our algorithm also comes with theoretical guarantees of efficiency. Indeed, in dimension $d\ge 1$, if the random variable $\max (\eta (X),1-\eta (X))$ has a bounded density (which, in turn, implies that the Tsybakov’s noise condition holds with parameter $\alpha =1)$ and the regression function belongs to the Hölder class with parameter $\beta >0$, it achieves a rate of convergence on the order $n^{-\frac{2\beta }{2\beta +d- (\beta \wedge 1) }}.$ This latter rate is optimal, as supported by the lower bound result provided in Minsker (2012), Locatelli et al. (2017). Furthermore, it outperforms the rates obtained in the passive learning counterpart, which are of the order of $n^{-\frac{2\beta }{2\beta +d}}$ (Audibert & Tsybakov, 2007).

2.2 Classification with reject option

In the present contribution, we borrow some techniques from learning with reject option. Indeed, as detailed in Sect. 3, a core component of our active strategy relies on the confidence we have on labels of the input instances. In contrast to the classical statistical learning framework where a label is provided for each observation $x\in \mathcal {X}$, learning with reject option is based on the idea that an observation for which the confidence on the label is not high enough should not be labeled. From this perspective, given a prediction function $g:\mathcal {X} \rightarrow \mathcal {Y}$, an instance $x\in \mathcal {X}$ can be either classified and the corresponding label is g(x) or rejected and no label is provided for x (according to the literature, the output for x is $\emptyset$ or any symbol as $\oplus$ meaning reject). A classifier with reject option ${\tilde{g}}$ is then a measurable mapping ${\tilde{g}}:\mathcal {X} \rightarrow \mathcal {Y}\cup \{\oplus \}$. Reject option has been first introduced in the classification setting in Chow (1957). More recently, and since the development of conformal prediction in Vovk et al. (1999, 2005), reject option has become more popular and has been brought up to date to meet the current challenges. The paper by Herbei and Wegkamp (2006) proposed the first statistical analysis of a classifier based on reject option. After these pioneer works, more papers on reject options appeared (e.g., Naadeem et al., 2010; Grandvalet et al., 2009; Yuan & Wegkamp, 2010; Lei, 2014; Cortes et al., 2016; Denis & Hebiri, 2019 and references therein). They mainly differ on the way they take into account the reject option. In particular, we can distinguish three main approaches: (1) use the reject option to ensure a predefined level of coverage; (2) use the reject option to unsure a pre-specified proportion of rejected data; (3) consider a loss that balances the coverage and the proportion of rejected data. It has been established that, while there is no best strategy, controlling the coverage requests more labeled data than controlling the rejection rate, which in turn asks more (unlabeled) data that the last strategy that does the trade-off. On the other hand this last approach does not control any of the two parameters.

Reject option has also been used in different contexts, such as in regression (Vovk et al., 2005; Denis et al., 2020) or algorithmic fairness (Schreuder & Chzhen, 2021). These papers show how reject option can be used to efficiently solve issues that are intrinsic to the problem.

2.3 Active learning with reject option

Most active learning schemes mentioned in Sect. 2.1 attempt to find the most "informative" samples in a region close the decision boundary, called uncertain region or disagreement region. Some recent works have refined this idea by adding an option to abstain from labeling (i.e., reject) the points that are considered too close to the decision boundary.

Although the intersection of rejection and active learning seems natural, their combination is fairly recent. Many active learning works (Shekhar et al., 2021; Zhu & Nowak, 2022; Puchkin & Zhivotovskiy, 2021) have provided algorithms that have rejection option, and they can be grouped depending on the studied excess error.

First, Shekhar et al. (2021) considered the nonparametric framework under some smoothness and margin noise assumptions. The authors designed an active learning algorithm with rejection option similarly to the standard reject option setting (Herbei & Wegkamp, 2006; Denis & Hebiri, 2019) by deciding not to label the instances which are located near to the decision boundary. In their framework, they derived rates of convergence for an excess-risk dedicated to the reject option (called Chow’s risk) and showed that these rates are better than those obtained by the passive learning counterpart (Denis & Hebiri, 2019). However it is not obvious in this setting how to obtain computationally tractable algorithms, among others because the hypotheses class needs to be restricted.

Second, Puchkin and Zhivotovskiy (2021) considered an empirical risk minimization approach and dealt with model misspecification. That is, given a class of classifiers $\mathcal {F}$ (which possibly does not contain the Bayes classifier), the aim is to find an estimator ${\hat{f}}$ which achieves minimum excess error of classification. By using the reject option, Puchkin and Zhivotovskiy (2021) proved that exponential savings in the number of label requests are possible in model misspecification under Massart noise assumption (Massart & Nédélec, 2006). Their algorithm outputs an improper classifier ${\hat{f}}$ (that is ${\hat{f}}$ $\notin$ $\mathcal {F}$ possibly) and mainly consists of two subroutines. The first one, named Mid-algorithm, combines the well-known disagreement-based approach (Hanneke, 2007; Balcan et al., 2009) and aggregation strategies (Mendelson, 2017) to yield a classifier with rejection option. The second subroutine focuses on converting this classifier into a classical one ${\hat{f}}$ (without rejection option), accomplished through a randomization process. The work of Puchkin and Zhivotovskiy (2021) was extended by Zhu and Nowak (2022) which provides a more efficient active learning algorithm that overcomes the difficulty of computing the uncertain region. More specifically, Zhu and Nowak (2022) considered more general noise assumptions (and therefore more general hypotheses classes) and built a classifier based on the rejection rule with exponential saving in labels for which they establish risk bounds in a general parametric setting. At each trial, the classifier does not label points for which the doubt is substantial. This decision of abstaining from classifying a point is taken by considering a set of "good" classifiers among a class of functions. In particular, a point is rejected if all "good" classifiers consider it as a difficult point, that is, the corresponding score is within the interval $[1/2 - \gamma , 1/2 + \gamma ]$, where $\gamma$ is a (small) positive real value. However, the empirical performance of the proposed algorithm is not considered in the paper. In the present paper, we focus on the classical active learning problem and derive rates of convergence for this problem, along with a practical implementation of the algorithm.

2.4 Contributions

The recent works mentioned in Sect. 2.3 (Puchkin & Zhivotovskiy, 2021; Shekhar et al., 2021; Zhu & Nowak, 2022) provide interesting theoretical contributions showing the interest of combining active learning and reject option. However the practical implementation of the related algorithms is not straightforward, notably because it is computationally difficult to estimate the uncertain region.

In this work, we use a peculiar combination of rejection and active learning to propose an active learning which is easy to compute in practice. More precisely, our contributions are threefold:

• We transform the typical classification with reject option framework (from Sects. 2.2 and 2.3) to estimate the so-called uncertain region in a novel way. Not only does this methodology provide a computationally efficient algorithm for active learning, but it also can be remarkably applied to any off-the-shelf machine learning algorithm. This is a twofold major improvement over (Minsker, 2012).

• Beyond the appealing numerical properties of our procedure, we show that it achieves optimal rates of convergence for the misclassification risk and the active sampling under classical assumptions in this setting.

• We illustrate the benefit of our method for synthetic and real datasets.

3 Active learning algorithm with rejection

In this section, after introducing some general notations and definitions, we present our algorithm in a somewhat informal way, and then provide the theoretical guarantees under some classical assumptions.

3.1 Notations and definitions

Throughout this paper $\mathcal {X}$ denotes the instance space and $\mathcal {Y} = \{0,1\}$ is the label space. Let P be the joint distribution of (X, Y). We denote by $\Pi$ the marginal probability over the instance space and by $\eta (x)=P(Y=1\vert X=x)$ the regression function. The performance of a classification rule $g: \mathcal {X} \rightarrow \{0,1\}$ is measured through the misclassification risk $R(g) = P\left( g(X) \ne Y\right)$. With this notation, the Bayes optimal rules that minimises the risk R over all measurable classification rules (Lugosi, 2002) is given by $g^*(x) = \mathbbm {1}_{\{\eta (x) \ge 1/2\}}$ and we have:

$$\begin{aligned} R(g^*)=1-\mathbb {E}_{\Pi }(f^*(X)) \hspace{5.0pt}, \end{aligned}$$

where $f^*(\cdot ) = \max (\eta (\cdot ),1-\eta (\cdot ))$ is called $\textit{score function}.$ For any classification rule g, the excess risk is given by

$$\begin{aligned} R(g) - R(g^*) = 2\mathbb {E} \left[ \left|\eta (X) - \frac{1}{2} \right|\, \mathbbm {1}_{ \{ g(X) \ne g^*(X) \} }\right] \hspace{5.0pt}. \end{aligned}$$

(3.1)

In this work, we consider the following active sampling scheme. For each $A \subset \mathcal {X}$, and $M \ge 1$, we can sample $(X_i,Y_i)_{1 \le i \le M}$ i.i.d. random variables such that

• 1. for all $i = 1, \ldots , M$, $X_i$ is distributed according to $\Pi (.|A)$;

• 2. conditionally on $X_i$, the random variable $Y_i$ is distributed according to a Bernoulli random variable with parameter $\eta (X_i)$.

[1.] As is commonly done in the active learning setting, we assume that the marginal distribution of X is known (Minsker, 2012; Locatelli et al., 2017). In the next paragraph, we describe our active algorithm for classification. As important tools that nicely merge the active sampling and the use of the rejection, we will pay a particular attention to the definition of the uncertain region and the rejection rate.

3.2 Overall description of the algorithm

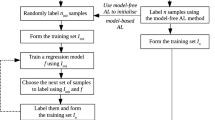
With a fixed number of label requests N (called the budget), our overall objective is to provide an active learning algorithm which outputs a classifier that performs better than its passive counterpart. The framework that we consider (Algorithm 1) is inspired from that developed in Minsker (2012), in which we incorporate rejection to estimate the uncertain region.

In the following, let $(\varepsilon _k)_{k \ge 0}$ be a sequence of positive numbers. Let $(N_k)_{k \ge 0}$ be a sequence defined such that $N_0 = \lfloor \sqrt{N} \rfloor$ and $N_{k+1} = \lfloor c_N N_k \rfloor$ with $c_N > 1$ (e.g., $c_N=1.1$ in Sect. 5). Furthermore, we consider $A_0 = \mathcal {X}=[0,1]^d$ the initial uncertain region, and thus $\varepsilon _0=1$. We construct a sequence of uncertain regions $(A_k)_{k\ge 1}$ and for $k\ge 1$, an estimator ${\hat{\eta }}_k$ of $\eta$ on $A_k$ is provided.

First, our algorithm performs an initialization phase:

• Initially, the learner requests the labels Y of $N_0$ points $X_1, \ldots , X_{N_0}$ sampled in $A_{0}$ according to $\Pi _0=\Pi$.

• Based on the initial labeled data $\mathcal {D}_{N_0}= \{(X_1,Y_1),\ldots , (X_{N_0},Y_{N_0})\}$, an estimator ${\hat{\eta }}_0$ of $\eta$ on $A_0$ is computed and an initial classifier $g_{{\hat{\eta }}_{0}} = \mathbbm {1}_{\{{\hat{\eta }}_{0} \ge 1/2\}}$ is provided.

• An estimator of the score function ${\hat{f}}_0(x)=\max ({\hat{\eta }}_0(x), 1-{\hat{\eta }}_0(x))$ associated to ${\hat{\eta }}_0$ is computed.

Afterwards, our algorithm iterates over a finite number of steps until the label budget N has been reached. Step $k\ge 1$ is described below.

• 1. Based on the previous uncertain region $A_{k-1}$, a constant $\lambda _k$ is computed such that conditionally on the data

  $$\begin{aligned} \lambda _k = \max \left\{ t, \;\; \Pi \left( {\hat{f}}_{k-1}(X) \le t |A_{k-1}\right) \le \varepsilon _k\right\} \hspace{5.0pt}, \end{aligned}$$

  (3.2)

  These $(\varepsilon _k)_{k \ge 0}$ explicitly define the sequence of the rejection rates (Denis & Hebiri, 2019).

• 2. This constant $\lambda _k$ is used to construct the current uncertain region $A_k$ which is the set where the previous classifier $g_{{\hat{\eta }}_{k-1}}(\cdot ) = \mathbbm {1}_{\{{\hat{\eta }}_{k-1}(\cdot ) \ge 1/2\}}$ might fail and thus abstains from labeling:

  $$\begin{aligned} A_k = \{x \in A_{k-1}, \;\; {\hat{f}}_{k-1}(x) \le \lambda _k\}\hspace{5.0pt}, \end{aligned}$$

  where ${\hat{f}}_{k-1}(x)=\max ({\hat{\eta }}_{k-1}(x), 1-{\hat{\eta }}_{k-1}(x))$.

• 3. According to $\pi \left( .|A_k\right)$ the learner samples i.i.d. $(X_i,Y_i), i = 1, \ldots , \lfloor N_{k} \varepsilon _k \rfloor$ used to compute an estimator ${\hat{\eta }}_k$ of $\eta$ on $A_k$.

• 4. The learner updates the classifier over the whole space $\mathcal {X}$ as follows

  $$\begin{aligned} {\hat{\eta }} = \sum _{j = 0}^{k-1} {\hat{\eta }}_j \mathbbm {1}_{\{A_{j} \backslash A_{j+1}\}} + {\hat{\eta }}_k \mathbbm {1}_{\{A_k\}}\hspace{5.0pt}. \end{aligned}$$

After the iteration process, the resulting active classifier with rejection is defined point-wise as

$$\begin{aligned} g_{{\hat{\eta }}}(x) = \mathbbm {1}_{\{{\hat{\eta }}(x) \ge 1/2\}} \hspace{5.0pt}. \end{aligned}$$

(3.3)

3.3 Theoretical guarantees

This section is devoted to the theoretical properties of the proposed procedure under common assumptions which are presented in Sect. 3.3.1. Thereafter, we state our main results in Sects. 3.3.2 and 3.3.3 that mainly show that, under classical smoothness conditions, our algorithm achieves an optimal rate of convergence for the excess-risk when the considered classifier is the histogram rule, or the kernel method, according to the regularity of the regression function $\eta$. We conclude with some general remarks in Sect. 3.3.4.

3.3.1 Assumptions

We assume that $\mathcal {X} = [0,1]^d$ and consider two assumptions that are widely considered for the study of rates convergence in the passive (Audibert & Tsybakov, 2007; Gadat et al., 2016) or active settings (Minsker, 2012; Locatelli et al., 2017).

Assumption 3.1

(Smoothness assumption) The regression function $\eta$ is $\beta$-Hölder for some $\beta \in (0,1)$, that is, there exists $s > 0$, such that for all $x,z \in [0,1]^d$:

$$\begin{aligned} \vert \eta (x)-\eta (z)\vert \le s \parallel x-z\parallel ^{\beta }_{\infty }\hspace{5.0pt}. \end{aligned}$$

Assumption 3.2

(Strong density assumption) The marginal probability admits a density $p_X$ and there exist constants $\mu _{min}, \mu _{max}>0$ such that for all $x \in [0,1]^d$ with $p_X(x)>0$, we have:

$$\begin{aligned} \mu _{min}\le p_X(x)\le \mu _{max} \hspace{5.0pt}. \end{aligned}$$

Assumption 3.1 imposes the regularity of the regression function $\eta$ while Assumption 3.2 ensures in particular that the marginal distribution of X admits a density which is bounded from below. Furthermore, we also assume that f(X) admits a bounded density.

Assumption 3.3

(Score regularity assumption) Let $f(x)=\max (\eta (x),1-\eta (x))$ be the score function. The random variable f(X) admits a bounded density (bounded by $C>0$).

Assumption 3.3 has two important consequences. The first one is that the cumulative distribution function $F_{f}$ of f(X) is Lipschitz. The second one is that the so-called Margin assumption (Tsybakov, 2004) is fulfilled with margin parameter $\alpha = 1$. This Margin assumption is also considered in Minsker (2012) for the study of optimal rates of convergence in the active learning framework.

3.3.2 Rates of convergence

In this section, we present our main theoretical result (Theorem 3.5) which highlights the performance of our algorithm. While our methodology can handle any machine learning algorithm for the estimation of the regression function $\eta$, we provide theoretical guarantees with the histogram rule (whose definition is recalled in Definition 3.4) for the estimation of the regression function at each step of the procedure described in Sect. 3.2, as in Minsker (2012). For completeness, we provide the full proof of our result in this particular case in the Appendix.

Let us denote by $\mathcal {C}_r=\lbrace R_i, \;i=1,\ldots , r^{-d}\rbrace$ a cubic partition of $[0,1]^d$ with edge length $r>0$.

Definition 3.4

(Histogram rule) Let A be a subset of $[0,1]^d$. Consider a labeled sample $\mathcal {D}_{N_A}= \left\{ (X_1^A,Y_1),\ldots ,(X_{N_A}^{A},Y_{N_A})\right\}$ of size $N_A \ge 1$, such that $X_i^A$ $(i=1,\ldots ,N_A)$ is distributed according to $\Pi (.\vert A)$. The histogram rule on A is defined as follows. Let $R_i$ $\in$ $\mathcal {C}_r$ with $R_i\cap A\ne \emptyset$. For all $x \in R_i$,

$$\begin{aligned} {\hat{\eta }}_{A,N_A,r}(x) = \frac{\Pi (A)}{\Pi (R_i \vert A)}\dfrac{1}{N_A} \sum _{j=1}^{N_{A}} Y_j \mathbbm {1}_{\{X_j \in R_i\}}\hspace{5.0pt}. \end{aligned}$$

It is known that in the passive framework, the histogram rule achieves optimal rates of convergence (Devroye et al., 1996).

Theorem 3.5

Let N be the label budget, and $\delta \in \left( 0,\frac{1}{2}\right)$. Let us assume that Assumptions 3.1, 3.2, and 3.3 are fulfilled. At each step $k \ge 0$ of the algorithm presented in Sect. 3.2, we consider

• (i) ${\hat{\eta }}_k:={\hat{\eta }}_{A_k,\lfloor N_k\epsilon _k\rfloor ,r_k}$, with $r_k=N_k^{-1/(2\beta +d)}$,

• (ii) and define $(\varepsilon _k)_{k\ge 0}$ as $\varepsilon _0=1$, and for $k\ge 1$, $\varepsilon _k=\min \left( 1,\log \left( \frac{N}{\delta }\right) \log (N) N_{k-1}^{-\beta /(2\beta +d)}\right)$.

Then with probability at least $1-\delta$, the resulting classifier defined in Equation(3.3) satisfies

$$\begin{aligned} R(g_{{\hat{\eta }}})-R(g^*)\le {\widetilde{O}}\left( N^{{ -\frac{2 \beta }{\beta +d} } }\right) , \end{aligned}$$

(3.4)

where ${\widetilde{O}}$ hides some constants and logarithmic factors.

The above result calls for several comments. First, our active classifier ${\hat{g}}$ based on the histogram rule is optimal for the active sampling w.r.t. the misclassification risk up to some logarithmic factors (see Minsker, 2012) for the minimax rates, by considering $\beta$-Hölder regression function with $\beta \le 1$ and the margin parameter equal to 1). This rate is better than the classical minimax rate in passive learning under the strong density assumption which is of order $N^{-\frac{2\beta }{2\beta +d}}$, see for instance (Audibert & Tsybakov, 2007). Second, the sequence of the rejection rates $(\varepsilon _k)_{k \ge 0}$ should be chosen in an optimal manner guided by our theoretical findings. In particular, for each k, the value of $\varepsilon _k$ is of the same order as an upper bound on the error w.r.t. the $\ell _\infty$-norm of ${\hat{\eta }}_{k-1}$, valid with high probability. This value of $\varepsilon _k$ is also linked to the probability of the uncertain region in the procedure proposed by Minsker (2012). However, the major difference with the latter reference is that our rejection rate is explicit and thus our algorithm can be efficiently computed due to the use of rejection arguments to determine the uncertain regions. Finally, our work can be extended to Hölder regression functions with parameter $\beta >1$ which is the purpose of Sect. 3.3.3.

3.3.3 Extension to higher orders of regularity ($\beta > 1)$

In the present section, we investigate the case of higher orders of Hölder regularity on the regression function $\eta$. We then assume that:

Assumption 3.6

(Smoothness assumption) The regression function $\eta$ is $\beta$-Hölder for some $\beta > 1$, that is, for all $k\le \ell$ with $\ell = \lfloor \beta \rfloor$, the k-th derivative $\eta ^{(k)}$ of $\eta$ exists and there exists $s > 0$, such that for all $x,z \in [0,1]^d$:

$$\begin{aligned} \vert \eta ^{(\ell )} (x)-\eta ^{(\ell )}(z)\vert \le s \parallel x-z\parallel ^{\beta - \ell }_{\infty }\hspace{5.0pt}. \end{aligned}$$

To extend our procedure to the case $\beta > 1$, we need to slightly modify our algorithm described in Sect. 3.2 in the following way. The changes rely on a more suitable calibration of the sequence $\varepsilon _k$, that will be expressed in Theorem 3.7 below, and in the estimation procedure that is used in the last step. In other words, the algorithm consists of two subroutines that are inspired by the work of Locatelli et al. (2017).

• Subroutine 1. The estimators ${\hat{\eta }}_1, \ldots , {\hat{\eta }}_{L-1}$ resulting from steps $k=1,\ldots ,L-1$ respectively, are obtained according to the sub-steps 1–3 in Sect. 3.2 considering histograms estimators (according to Definition 3.4). This means that for these steps nothing changes as compared to the case $\beta \le 1$. We only have to take care that we calibrate $\varepsilon _k$ according to the optimal rate of convergence of histogram rules (c.f., Theorem 3.7 for the precise calibration of $\varepsilon _k$).

• Subroutine 2. The estimator ${\hat{\eta }}_L$ resulting from step L is obtained according to the sub-steps 1–3 in Sect. 3.2 using kernel methods. The whole explicit description of the estimator used in this step as well as all technical aspects are developed in Appendix C (see Eq. C.5 for the formal definition of ${\hat{\eta }}_L$). However let us explain why we need to consider a different subroutine in the last step. In our methodology the rate of convergence is governed by the rate obtained in this last step. Moreover, histograms are not smooth enough to achieve the right optimal rate of convergence when the regularity of $\eta$ is smoother than Lipschitz. Therefore, we rely on kernel methods that are known to be optimal for the $\ell _\infty$-norm in Hölder classes (Tsybakov, 2008; Giné & Nickl, 2015) – see Appendix C for more details.

Finally, as in the case $\beta \le 1$, the resulting active classifier with rejection is given point-wise by

$$\begin{aligned} g_{{\hat{\eta }}}(x) = \mathbbm {1}_{\{{\hat{\eta }}(x) \ge 1/2\}} \hspace{5.0pt}. \end{aligned}$$

with ${\hat{\eta }}$ being the learner updated over the whole space $\mathcal {X}$ as follows

$$\begin{aligned} {\hat{\eta }} = \sum _{k = 0}^{L-1} {\hat{\eta }}_k \mathbbm {1}_{\{A_{k} \backslash A_{k+1}\}} + {\hat{\eta }}_L \mathbbm {1}_{\{A_L\}}\hspace{5.0pt}. \end{aligned}$$

(3.5)

Theorem 3.7

Let N be the label budget, and $\delta \in \left( 0,\frac{1}{2}\right)$. Let us assume that Assumptions 3.2, 3.3, and 3.6 are fulfilled. Consider the estimator ${\hat{\eta }}$ in (3.5) obtained from the above two-subroutines algorithm such that

• (i) ${\hat{\eta }}_k:={\hat{\eta }}_{A_k,\lfloor N_k\epsilon _k\rfloor ,r_k}$, with $r_k=N_k^{-1/(2\beta +d)}$,

• (ii) we define $(\varepsilon _k)_{k\ge 0}$ as $\varepsilon _0=1$, and for $k\ge 1$, $\varepsilon _k=\min \left( 1,\log \left( \frac{N}{\delta }\right) \log (N) N_{k-1}^{-1/(2\beta +d)}\right)$.

Then with probability at least $1-\delta$, the resulting classifier defined in Eq. (3.3) satisfies

$$\begin{aligned} R(g_{{\hat{\eta }}})-R(g^*)\le {\widetilde{O}}\left( N^{-\frac{2\beta }{2\beta +d-1}}\right) , \end{aligned}$$

(3.6)

where ${\widetilde{O}}$ hides some constants and logarithmic factors.

This result shows that our active learning algorithm based on rejection arguments achieves the optimal rate of convergence, when the margin parameter is equal to 1, which has already been discovered (Minsker, 2012; Locatelli et al., 2017). Notably, our methodology achieves a fast rate of convergence while allowing for efficient computation of the uncertain regions thanks to the reject option arguments.

3.3.4 Some general remarks

While our methodology is rather general and can be applied to any off-the-shelf algorithm, providing a theoretical guarantee needs to specify the estimator. In the above results, we considered histogram estimators. This type of tools is particularly convenient for our purpose since they allow, for each k, to describe the uncertain region $A_k$ as a union of cells of the partition $\mathcal {C}_r$. As a consequence, we can provide, using the strong density assumption (i.e., Assumption 3.2), an explicit lower bound of $\Pi (A_k)$ which is crucial to get Theorem 3.5. Having a theoretical lower bound for this quantity should be algorithm-specific and is often a laborious task. We believe that, as a first step, our methodology can be extended to kNN or kernel-type estimators—for which the main challenge would be to describe the $A_k$, for instance as a union of balls in the case of kNN.

Moreover, Theorems 3.5 and 3.7 are established assuming the knowledge of the marginal distribution of X. This is a classical assumption in active learning that helps for sampling. However, it is possible to extend our result to unknown distributions at the price of an additional unlabeled sample and then an additional factor $1/\sqrt{\text {size of the unlabeled sample}}$.

In view of the above remarks, we discuss the practical implementation of our proposed algorithm in Sect. 4 below.

4 Practical considerations

Some practical aspects of the procedure are discussed in Sect. 4.1 and a simple numerical illustration is provided in Sect. 4.2. The full numerical experiments are presented in Sect. 5.

4.1 Uncertain region

In this section, we discuss the effective computation of the uncertain regions. Let $k \ge 1$ represent the current step k of our algorithm. We denote by $\mathcal {D}_M = \{X_1,Y_1), \ldots ,(X_M,Y_M)\}$ the data that have been sampled until step k. The random variable ${\hat{f}}_{k-1}$ is the score function built at step $k-1$.

The construction of the uncertain region $A_{k}$ relies on $\lambda _k$ which is solution of Eq. (3.2). First of all, we randomize the score function ${\hat{f}}_{k-1}$ by introducing a variable $\zeta$ distributed according to a Uniform distribution on [0, u] independent of $\mathcal {D}_M$ and by defining the randomized score function ${\tilde{f}}_{k-1}$ as

$$\begin{aligned} {\tilde{f}}_{k-1}(X,\zeta ) = {\hat{f}}_{k-1}(X) + \zeta \hspace{5.0pt}. \end{aligned}$$

Considering the randomized score ${\tilde{f}}_{k-1}$ instead of ${\hat{f}}_{k-1}$ ensures that conditionally on $\mathcal {D}_M$, the cumulative distribution function of ${\tilde{f}}_{k-1}(X, \zeta )$, denoted by $F_{{\tilde{f}}_{k-1}}$, is continuous. Therefore, it implies that

$$\begin{aligned} {\tilde{\lambda }}_k = \max \left\{ t, \;\; \Pi \left( {\tilde{f}}_{k-1}(X) \le t |A_{k-1}\right) \le \varepsilon _k\right\} = F_{{\tilde{f}}_{k-1}}^{-1}(\varepsilon _k)\hspace{5.0pt}. \end{aligned}$$

Hence, ${\tilde{\lambda }}_k$ is expressed simply as the $\varepsilon _k$-quantile of the c.d.f. $F_{{\tilde{f}}_{k-1}}$. To preserve the statistical properties of ${\hat{f}}_{k-1}$, the parameter u is chosen sufficiently small (e.g., $u \rightarrow 0$).

Note that the computation of the c.d.f. $F_{{\tilde{f}}_{k-1}}$ requires the knowledge of the marginal distribution of X. In practice, this distribution may be unknown. In a second step, based on an unlabeled dataset $\mathcal {D}_{M_k}^{U}=\lbrace X_{i},i=1,\ldots ,M_k\rbrace$ with $X_{i}\sim \Pi (.\vert {\hat{A}}_{k-1})$, and $(\zeta _1, \ldots , \zeta _{M_k})$ i.i.d. copies of $\zeta$, we consider an estimator ${\hat{\lambda }}_k$ of ${\tilde{\lambda }}_k$ defined as follows

$$\begin{aligned} {\hat{\lambda }}_k = {\hat{F}}_{{\tilde{f}}_{k-1}}^{-1}(\varepsilon _k), \end{aligned}$$

where conditionally on the data, ${\hat{F}}_{{\tilde{f}}_{k-1}}$ is the empirical c.d.f. of the random variable ${\tilde{f}}_{k-1}(X,\zeta )$:

$$\begin{aligned} {\hat{F}}_{{\hat{f}}_k}(t) = \dfrac{1}{M_k} \sum _{i=1}^{M_k} \mathbbm {1}_{\{{\tilde{f}}_k(X_i,\zeta _i) \le t\}}\hspace{5.0pt}. \end{aligned}$$

Furthermore, the unlabeled set $\mathcal {D}_{M_k}^{U}$ is assumed to be independent of $\mathcal {D}_M$, and since it remains unlabeled, it does not contribute to the budget.

Formally, the uncertain region $A_k$ is then defined as follows

$$\begin{aligned} A_k = \left\{ (x,\zeta ) \in \mathcal {X} \times [0,u], \;\; {\tilde{f}}_{k-1}(x, \zeta ) \le {\hat{\lambda }}_k\right\} \hspace{5.0pt}. \end{aligned}$$

Therefore, $X_{M+1} \sim \Pi \left( .|A_k\right)$, is sampled from $\Pi$ such that ${\tilde{f}}_{k-1}(X_{M+1},\zeta ) \le {\hat{\lambda }}_k$ with $\zeta$ distributed according to $\mathcal {U}_{[0,u]}$.

Algorithm 1

Active learning with rejection

4.2 Illustrative example

For illustrative purposes, a two-dimensional dataset of $10^6$ data points is generated using a regression function $\eta (x_1,x_2)= \frac{1}{2}(1+\sin (\frac{\pi x_2}{2}))$. We choose the estimators $\hat{\eta _k}$ to be linear, to make the comparison with the best linear classifier ($x_2=0$) straightforward. The budget is set to $N=1000$, and the sequence of $N_k$ is chosen such that $N_k = \lfloor 1.1 \, N_{k-1}\rfloor$, starting with $N_0=\lfloor \sqrt{N}\rfloor$ and $\varepsilon _0=1$. The sequence of $\varepsilon _k$ is defined such that $\varepsilon _1=0.85$ and the subsequent $\varepsilon _k$ are adapted from Theorem 3.5. The parameter $M_k$ is set to 150. A discussion of this choice of parameters can be found in Sect. 5.2.

Figure 1 (left) represents the situation after the step $k=2$ of the algorithm, with only a subset of the $10^6$ data points represented for clarity. At step $k=1$ and $k=2$, $\lambda _{k}$ is computed using (3.2), which allows to classify the points in ${\hat{A}}_{k-1} \setminus {\hat{A}}_k$ (represented in black for $k=1$ and in brown for $k=2$). The points remaining in ${\hat{A}}_2$ are colored in red if their label has already been requested to the oracle, and in blue otherwise. At subsequent steps, points in $A_k$ are selected according to the rejection rates shown in the center part of Fig. 1, which shows the theoretical reject rates ($\varepsilon _k$, defined in Algorithm 1) in blue and the experimental ones (${\hat{\varepsilon }}_k$, counted as the number of points effectively rejected) in red. As a whole, the rejection rate is well estimated with only $M_k = 150$ unlabeled samples.

Fig. 1

Left: Illustrative dataset after the step $k=2$ of the algorithm. The points in black belong to ${\hat{A}}_0 \setminus {\hat{A}}_1$ and the brown ones to ${\hat{A}}_1 \setminus {\hat{A}}_2$. In ${\hat{A}}_2$ are the red points whose labels have been requested to the oracle and the remaining points in blue. Center: theoretical ($\varepsilon _k$, blue) and experimental (${\hat{\varepsilon }}_k$, red with error bars in grey) rejection rates. Right: average accuracy computed over 10 runs for our active learning algorithm (red), passive learning (blue), active learning with uncertainty (green), active learning with QBC (orange)

For comparison with its passive learning counterpart, a Support Vector Machine (SVM) algorithm is used, namely the SVC subroutine from scikit-learn (Pedregosa et al., 2011) with a linear kernel and a regularization parameter $C=5$). We also use two baseline active learning methods: uncertainty sampling and query by committee (QBC), adapted from Lewis and Gale (1994) and Freund et al. (1997), respectively. All numerical experiments are repeated 10 times. More details about the methods and thorough numerical experiments can be found in Sect. 5, the purpose of the current section being mostly to illustrate the algorithm. The learning curves for passive and active procedures are represented on the right of Fig. 1, up to a budget of 1000 points. The average learning curves over 10 repetitions are represented in red for active learning with reject, in green for active learning with uncertainty, in orange for active learning with QBC and in blue for passive learning with their respective error bars in lighter color. As expected with this simplistic illustrative dataset, using any active learning procedure does not provide a substantial advantage in the long run compared to passive learning, because the optimal classifier is relatively easy to find in passive learning, even with noisy data. In Sect. 5 we will compare more thoroughly the active and passive classifiers on several datasets, and show that even when the accuracy converges to the same value, active learning with reject can prove more efficient at low budget.

5 Numerical experiments

In this section, we propose a numerical comparison of our algorithm to passive learning, as well as to two popular approaches for active learning.

5.1 Classifiers and learning algorithms

To test the applicability of our algorithm to various estimators, we perform our experiments with four classifiers: linear SVM, SVM with a Gaussian kernel, random forests and k nearest neighbors from the scikit-learn library (Pedregosa et al., 2011) using the following parameters: regularization constant $C=5$ for SVM, 100 trees for random forests, $k=5$ for kNN. The other parameters from these classifiers are kept to their default value.

For each classifier, we compare our active learning algorithm with its corresponding passive learning classifier, as well as two other baseline active learning methods: uncertainty sampling and query by committee (QBC), adapted from Lewis and Gale (1994) and Freund et al. (1997), respectively. In uncertainty sampling, the unlabeled training points are ranked according to the value of $|\eta (x)-0.5|$ and the informative (i.e., least confident) points are selected by batches of $\ell$ examples with the lowest values. For QBC, a committee of 5 classifiers is created, each classifier being trained with an independent fraction of the labeled points. At each step, batches of m points are selected as informative points in the region where disagreement occurs between the members of the committee. To keep batches of points of the same order of magnitude as in our algorithm, we use $\ell =m=N_0$. The numerical experiments with each active or passive classifier are systematically repeated 10 times, to report the average and standard deviation in all tables and figures.

5.2 Parameters choice and sampling strategy

This section discusses some aspects of the practical implementation of our algorithm.

Parameters choice To perform numerical experiments, a few parameters of our model introduced in Sect. 3 have to be set. Although the objective of the paper is not to do exhaustive searches to fine-tune these parameters, we perform experiments with several values of these parameters to illustrate their effect on the results, and present an overview of the main trends in Sect. 5.4.

First, the sequence of rejection rates is defined such that $\varepsilon _0=1; \varepsilon _1=c_\varepsilon \in ]0,1[$ and the subsequent $\varepsilon _k$ are adapted from Theorem 3.5. If $c_\varepsilon$ is small, the uncertain region ${\hat{A}}_k$ will be small, which corresponds to an "aggressive" strategy where many points are considered to be correctly classified at each step. This would be suitable for simple classification problems where a reliable estimate ${\hat{\eta }}$ can be obtained with $N_0$ points. Conversely, if $c_\varepsilon$ is large, the strategy will be more "conservative" and more suitable for practical classification problems where we expect our algorithm to be most useful. We therefore use a value $c_\varepsilon =0.85$ in our simulations, tending towards the latter strategy. In Sect. 5.4 (Fig. 3), we show the effect of decreasing it to $c_\varepsilon =0.65$ and increasing it to $c_\varepsilon =0.95$.

Second, the constant $c_N$ defines the sequence $\{N_k\}_{k\ge 1}$ as $N_k=\lfloor c_N N_{k-1} \rfloor$ and thus the number of points asked to the oracle at each step k ($\lfloor N_{k} \varepsilon _k \rfloor$ on line 17 of Algorithm 1). If $c_N$ is large, the algorithm will tend to use many points at each step, thereby progressing by larger leaps and potentially consuming the budget faster. However, the effect of $c_N$ is intertwined with that of $c_\varepsilon$. Indeed, as can be seen on line 17 of Algorithm 1, the number of points asked to the oracle at each step is $\lfloor N_{k} \varepsilon _k \rfloor$, where $N_k=\lfloor c_N N_{k-1} \rfloor$. This effect is shown in Sect. 5.4, where $c_N=1.1$ is increased to $c_N=1.3$ on Fig. 3. The choice of $c_N$ mostly depends on the available budget and the desired "aggressiveness" of the strategy, in the sense discussed above for $c_\varepsilon$. We opt for a value of $c_N=1.1$ to avoid having to stop the algorithm prematurely due to an exhaustion of the budget.

Third, the number of points to build the initial classifier is theoretically set to $N_0=\lfloor \sqrt{N}\rfloor$. In practice, this number could be increased to get a better estimate of ${\hat{\eta }}_0$. Using a larger $N_0$ will however consume the budget faster. We keep the theoretical value in the simulations.

Fourth, $M_k$ unlabeled data points in $\mathcal {D}_{M_k}^{U}$ are used at each step to estimate ${\hat{\lambda }}_k$. If $M_k$ is large, the estimation of ${\hat{\lambda }}_k$ will be more accurate. As these $M_k$ points remain unlabeled, they do not contribute to the budget, and $M_k$ could in principle be large. The only restriction is that at each step k these (unlabeled) points have to be sampled independently of the (labeled) points asked to the oracle, it indirectly limits the number of points available to the oracle. Several experiments (results not shown) indicate that $M_k\ge 100$ provides a reasonable estimate of ${\hat{\lambda }}_k$, regardless of the precise value of $M_k$. We use $M_k=150$ in our experiments.

Finally, the parameter u in Sect. 4.1 is set to $10^{-5}$. Its precise value does not affect much the results, as long as it remains close to 0.

Unless otherwise stated, our numerical experiments are thus performed using a rather "conservative" approach, with the parameters discussed above set to $c_\varepsilon =0.85$, $c_N=1.1$, $N_0= \lfloor \sqrt{N}\rfloor$ and $M_k=150$.

This choice is designed to reproduce a practical situation with a limited budget and a potentially difficult classification problem.

Sampling strategy We design a sampling strategy that re-uses points whenever possible, using two recycling procedures explained below. This is not so important in our numerical experiments with synthetic data (Sect. 5.3), where $10^6$ data points are used to mimic the theoretical situation with an "infinite" pool of data. However it can become crucial in practical applications with limited labeled data, as in the non-synthetic datasets used in Sect. 5.5.

The first recycling procedure is that the unlabeled points from step $k-1$ will be re-used at step k. This does not invalidate our theory just because of the additive form of the risk over cells $A_k$. Indeed, our trained estimator has the form ${\hat{g}}(\cdot ) = \sum _{k}{\hat{g}}_k(\cdot ) \mathbbm {1}_{A_k}(\cdot )$ and then its overall risk $R({\hat{g}})$ can be decomposed on the different regions $A_k$ (by conditioning on the data used to approximate the region from the previous iteration).

The second recycling procedure is that the data already labeled by the oracle at previous iterations (up to $k-1$ included) are reused to train ${\hat{\eta }}_k$, as long as they belong to the region $A_k$. A similar procedure was used in Urner et al. (2013). This allows to improve the estimation of ${\hat{\eta }}_k$ and to limit the budget consumption. This sampling strategy is permitted because of the expression of the estimator and the decomposition of the risk as noted above. It is particularly useful in practical applications where the total amount of labeled data is limited.

5.3 Synthetic datasets

Setting Each numerical experiment is performed using a training set of $10^6$ data points with a budget of $N=1000$. The accuracy is tested on an independent test set of 5000 points, that are never used at any step in the algorithm. The parameters are set according to Sect. 5.2 and will be further discussed in Sect. 5.4. The algorithm is first challenged on three synthetic two-dimensional binary datasets (named dataset 1, 2, and 3, respectively). The three datasets are represented on the top row of Fig. 2, with the points colored in blue or cyan according to their class. Dataset 1 reproduces in two dimensions a toy example used by Dasgupta (2011), using the same distribution of points. The best linear classifier (accuracy = 0.975) is located at $x_1=-0.3$ but active learning algorithms (as well as passive to some extent) could be misled to $x_1=0$, corresponding to an accuracy of 0.95, as explained in Dasgupta (2011). Dataset 2 represents a situation where some data ($x_1<0$) are easy to classify while others ($x_1>0$) are not. Dataset 3 is a mixture of two Gaussian distributions with means of $(0, -0.5)$ and (0, 0.5), respectively, and both standard deviation are set to $\sigma =0.3$ to create some overlap, as seen on Fig. 2. All datasets are well balanced so that the precision, recall and F1-score are not reported in the paper because they do not bring much additional information.

Fig. 2

Top row: From left to right, synthetic datasets 1, 2, and 3 used in this study with the points colored in blue or cyan depending on their class. Middle: average learning curves for linear SVM classifiers, for active learning with reject (red), active learning with uncertainty (green), active learning with QBC (orange) and passive learning (blue) with their respective error bars in lighter color. Bottom: same as middle row but for SVM rbf classifiers

Our algorithm is compared with its passive counterpart and with two other classical active learning methods, as explained in Sect. 5.1. The learning curves for each dataset are presented on Fig. 2 in the case of SVM linear (middle row) and SVM rbf (bottom row) classifiers. The results are reported in Table 1.

Table 1 Average accuracy over 10 runs, on synthetic datasets 1, 2, and 3, with several classifiers: SVM_lin = linear SVM, SVM_rbf =SVM with Gaussian kernel, rf_100 = random forests (with 100 trees), and kNN_5 = k nearest neighbors (kNN, with $k=5$)

Results Dataset 1 has been used in Dasgupta (2011) to challenge active learning algorithms. Using SVM linear classifiers, Fig. 2 (left) shows that the best accuracy when reaching convergence ($N=1000$) is obtained by our active learning algorithm, which approaches the best theoretical accuracy (0.975) discussed in Dasgupta (2011). Upon convergence, our algorithm clearly surpasses its passive counterpart as well as the other two active learning algorithms. Interestingly, uncertainty sampling is better at very small budget ($N=200$) but it only reaches an accuracy within experimental error of 0.95, as predicted by Dasgupta (2011). The explanation is that uncertainty sampling is highly dependent on the $N_0$ points initially selected by random sampling. The $N_0$ points will thus not contain enough representative points from the regions of low density, which will thus be ignored by the classifier at subsequent steps, thereby introducing bias. The QBC algorithm performs poorly in the setting considered here because at any step each classifier in the committee is trained on an independent fraction of the points (a fifth in our case, since we are using 5 members in the committee), making it more prone to errors than a single classifier trained with all the available points. This effect is particularly striking for small budgets.

Dataset 2 (Fig. 2, center) represents another simple situation where classification might be difficult due to an uneven distribution of points. In this case, for SVM linear classifiers our active learning algorithm also outperforms its passive counterpart and QBC, even though it does not perform better than uncertainty sampling.

As a contrast the the first two datasets, dataset 3 (Fig. 2, right) is designed to represent an easier classification problem. In this case our active learning algorithm does not present any major advantage, but it does not deteriorate the results either, except slightly for SVM linear classifiers.

For the non-linear classifiers (e.g., SVM rbf on Fig. 2, bottom row) the difference between the algorithms after convergence is less pronounced.

5.4 Discussion about the parameters choice

The effect of the parameters in our algorithms has been discussed in Sect. 5.2 in terms of "aggressive" and "conservative" approaches and is illustrated here using numerical experiments with representative values of the parameters $c_\varepsilon$ and $c_N$, as reported on Fig. 3.

Fig. 3

Average learning curves for our algorithm with various parameters, using Dataset 1 with linear SVM classifier

This indicates that in all configurations our algorithm eventually converges to the same solution as in Fig. 3, but much faster in the case of the "aggressive" strategies ($c_\varepsilon$ = 0.65). It also shows that with $c_\varepsilon$ = 0.65 our algorithm abruptly stops before exhausting the budget of $N=1000$. This could happen in practice for two main reasons. First, the major reason is that, even though the simulations are performed with $10^6$ points, an aggressive rejection procedure may lead to a situation with not enough points in the next uncertain region $A_k$, i.e., less than the $\lfloor N_k \epsilon _k \rfloor$ needed for our algorithm to continue. This effect is thus somewhat mitigated by increasing the value of $c_N$, as can be seen on Fig. 3 when moving from $c_N$ = 1.1 to $c_N$ = 1.3. Second, all the points in the region $A_k$ could potentially belong to the same class, in which case it is impossible to build ${\hat{\eta }}_k$. This occurs less frequently in noisy datasets though.

In practical situations, with small datasets it is better to use a conservative approach. For large datasets it is possible to make it more aggressive, at the potential cost of interrupting too early (i.e., before using the limit of the budget). This shows that our algorithm can reach convergence faster than its passive counterpart, which represents a considerable improvement when the budget is limited.

5.5 Non-synthetic datasets

To illustrate the applicability of our algorithm in addition to its theoretical guarantees, numerical experiments are also performed with various datasets from the UCI machine learning repository. Three "large" (more than $10^4$ data points) datasets are used: skin (245,057 points in $\mathbb {R}^3$), fraud (20,468 points in $\mathbb {R}^{113}$) and EEG (14,980 points in $\mathbb {R}^{14}$). For those "large" datasets the budget is set to $N=1000$ in our algorithm, and the results are also presented at a low budget ($N=200$). Three "small" (less than $10^3$ data points) are also considered: breast (683 points in $\mathbb {R}^{10}$), credit (690 points in $\mathbb {R}^{14}$) and cleveland (297 points in $\mathbb {R}^{13}$). Each dataset is split into training (70%) and testing (30%). We use the same classifiers and the same parameter values as in Sect. 5.3, except for the smallest dataset (cleveland), for which we opt for values $c_\varepsilon =0.95$ and $N=1.2$, to avoid rejecting all the data points at the first iterations, as discussed in Sect. 5.4. The results for the largest dataset (skin) are presented as learning curves on Fig. 4. All results are summarized in Table 2.

Fig. 4

Skin dataset with linear SVM, rbf SVM and kNN_5 classifiers, for active learning with reject (red), active learning with uncertainty (green), active learning with QBC (orange) and passive learning (blue). Average learning curves over 10 runs are presented with their respective error bars in lighter color

These results are fairly balanced among the passive and active learning methods. The skin dataset leads to an overall advantage for active learning methods with reject or uncertainty sampling, whereas the fraud dataset gives better results for passive learning or active QBC. It could be linked to the fact that the fraud dataset is high-dimensional ($\mathbb {R}^{113}$), but the study of the dimensionality of the data is not considered in this paper. The EEG dataset remains difficult to handle for all active and passive procedures.

Our algorithm is usually expected to be more performant with simple classifiers (e.g., SVM linear) because the more elaborate classifiers from scikit-learn (Pedregosa et al., 2011) are able to reach a good accuracy. This is visible on Fig. 4 and is quite striking in Table 2 for the EEG dataset.

Table 2 Average accuracy over 10 runs, on "large" non-synthetic datasets with several classifiers: SVM_lin = linear SVM, SVM_rbf = SVM with Gaussian kernel, rf_100 = random forests (with 100 trees), and kNN_5 = k nearest neighbors (with $k=5$)

For "small" datasets, most of the time the active method improves the passive one (see Table 3). However, this improvement is rather limited, expect for cleveland dataset where the use of the active algorithm is particularly beneficial.

Table 3 Average accuracy over 10 runs, on three "small" non-synthetic datasets with several classifiers: SVM_lin = linear SVM, SVM_rbf = SVM with Gaussian kernel, rf_100 = random forests (with 100 trees), and kNN_5 = k nearest neighbors (with $k=5$)

5.6 Summary of the results and discussion

The study on synthetic datasets shows that our active learning algorithm using rejection provides a clear advantage over passive learning for the first two datasets, especially at low budget, but not for the third dataset where classification is easier. Our algorithm is only sometimes surpassed by the uncertainty sampling active algorithm, most notably for the second dataset. In non-synthetic datasets, the active learning procedures (our algorithm as well as the other active algorithms) do not appear to be very beneficial on the "small" dataset (e.g., a few hundreds points). Indeed, for such datasets the number of points $N_0$ has to be quite small, otherwise all the data are used before the active part of the procedure. In our algorithm in particular, the estimate ${\hat{\eta }}_0$ is thus likely to be inaccurate, which in turn implies an inaccurate estimation of the uncertain region in the first steps and then leads to a poorly controlled algorithm. Interestingly, even in such small datasets, our algorithm is rarely detrimental to the final accuracy reached. For the larger datasets, our algorithm could more promising, especially with proper parameter tuning allowing for more aggressive strategies. A thorough study of the parameters is however beyond the scope of this paper which focuses mostly on its sound theoretical guarantees.

6 Conclusion and perspectives

Recently several works have started to combine active learning and rejection arguments by abstaining to label some data within an active learning algorithm. This combination is very natural since active learning and rejection both focus on the most difficult data to classify. In this work, instead of completely abstaining to label some data, we use rejection principles in a novel way to estimate the uncertain region typically used in active learning algorithms. We therefore propose a computationally efficient active learning algorithm that combines active learning with rejection. We theoretically prove the merits of our algorithm and show through several numerical experiments that it can be efficiently applied to any off-the-shelf machine learning algorithm. The benefits are more pronounced when the label budget is limited, which is promising for practical applications.

Nevertheless, in the last steps of our algorithm the uncertainty about the label of some points can become very substantial, in which case it becomes natural to completely abstain from labeling. This abstention will be included in future work combined with our use of the reject option. Moreover, as pointed out in Sect. 3.3.4, the extension of our theory to other types of algorithms is an important guideline for further research.

Appendices

Appendix

The section is devoted to the proof of the main results (Theorems 3.5 and  3.7), starting with a technical result that will be used in the proofs.

Appendix A: technical result

Let us first introduce some general notations: Let A be a subset of $[0,1]^d$, and a cubic partition $\mathcal {C}_r$ as introduced in Definition 3.4. For $R\in \mathcal {C}_r$, with $R\cap A\ne \emptyset$, we introduce the regression function in R as:

$$\begin{aligned} {\bar{\eta }}(R) = \dfrac{1}{\Pi (R|A)} \int _{R \cap A} \eta (z) \Pi (dz\vert A) \end{aligned}$$

and we define ${\bar{\eta }}(x):={\bar{\eta }}(R)$ for all $x\in R$.

Here, for each $k\ge 0$, and $r_k=N_k^{-1/(2\beta +d)}$, we consider the estimator:

$$\begin{aligned} {\hat{\eta }}_k:={\hat{\eta }}_{A_k,\lfloor N_k \varepsilon _k \rfloor ,r_k}, \end{aligned}$$

(A.1)

where ${\hat{\eta }}_{A_k,\lfloor N_k \varepsilon _k \rfloor ,r_k}$ is defined according to Definition 3.4, and $A_k$ is defined in Algorithm 1. Importantly, defining ${\hat{\eta }}_k$ in this way for all $k\ge 0$ allows us to characterize the set $A_k$ in an explicit form:

$$\begin{aligned} A_k=\bigcup _{R\,\in \,\mathcal {C}_{r_k},\;R\cap A_k\ne \emptyset } R. \end{aligned}$$

Let L be defined as:

$$\begin{aligned} L=\max \lbrace j\ge 1, N> \sum _{k=0}^{j}\lfloor N_k \varepsilon _k \rfloor \rbrace . \end{aligned}$$

(A.2)

We firstly provide bounds on the maximum number of steps L (defined by (A.2)) performed by our algorithm 1.

Lemma A.1

(Bounds on the maximum number of steps L) Let us consider the variable L defined in (A.2). We have the following statements:

• 1. If the sequence of rejection rate $(\varepsilon _k)_{k\ge 0}$ used by our algorithm 1 is defined as follows: $\varepsilon _0=1$, and for $k\ge 1$, $\varepsilon _k=\min \left( 1,\log \left( \frac{N}{\delta }\right) \log (N) N_{k-1}^{-\beta /(2\beta +d)}\right) ,$ thus we have:

  $$\begin{aligned} \log _2\left( c_8\left( \frac{1}{\log \left( \frac{N}{\delta }\right) }\right) ^{\frac{d+2\beta }{\beta +d}} N^{\frac{d+3\beta }{2\beta +2d}}\right) \le L \end{aligned}$$

  and

  $$\begin{aligned} L \le \min \left( 1+\log _2\left( \left( \frac{1}{c_6\log \left( \frac{N}{\delta }\right) }\right) ^{(2\beta +d)/(\beta +d)} N^{(3\beta +d)/(2\beta +2d)}\right) , \log _2\left( \sqrt{N}\right) \right) , \end{aligned}$$

  where $c_8$, $c_6$ are constants independent of N.

• 2. If the sequence of rejection rate $(\varepsilon _k)_{k\ge 0}$ used by our algorithm 1 is defined as follows: $\varepsilon _0=1$, and for $k\ge 1$, $\varepsilon _k=\min \left( 1,\log \left( \frac{N}{\delta }\right) \log (N) N_{k-1}^{-1/(2\beta +d)}\right) ,$ thus we have:

  $$\begin{aligned} \log _2\left( c'_8\left( \frac{1}{\log \left( \frac{N}{\delta }\right) }\right) ^{\frac{2\beta +d}{2\beta +d-1}}N^{\frac{2\beta +d+1}{4\beta +2d-2}}\right) \le L \end{aligned}$$

  and

  $$\begin{aligned} L \le \min \left( 1+\log _2\left( \left( \frac{1}{c'_6\log \left( \frac{N}{\delta }\right) }\right) ^{(2\beta +d)/(2\beta +d-1)} N^{(2\beta +d+1)/(4\beta +2d-2)}\right) , \log _2\left( \sqrt{N}\right) \right) , \end{aligned}$$

  where $c'_8$, $c'_6$ are the constants independent of N.

Proof

We begin with the proof of the first item:

• 1. Notice that because of the geometric progression of $N_{j}$, and the definition of L, we have

  $$\begin{aligned} N&\le \sum _{j=0}^{L+1} N_{j}\varepsilon _{j}\\&\le N_0+c_6\log \left( \frac{N}{\delta }\right) \sum _{j=1}^{L+1} N_j N_{j-1}^{-\beta /(2\beta +d)}\\&=N_0+2c_6\log \left( \frac{N}{\delta }\right) \sum _{j=1}^{L+1} N_{j-1}^{(d+\beta )/(2\beta +d)}\\&\le N_0+ c_7\log \left( \frac{N}{\delta }\right) N_{L}^{(d+\beta )/(2\beta +d)}\quad \text {for some constant c7}. \end{aligned}$$

  Thus we get

  $$\begin{aligned} N-N_0\le c_7\log \left( \frac{N}{\delta }\right) N_{L+1}^{(d+\beta )/(2\beta +d)}&\Longrightarrow \dfrac{1}{4}N\le c_7\log \left( \frac{N}{\delta }\right) N_{L+1}^{(d+\beta )/(2\beta +d)} \quad \text {as}\; N_0=\sqrt{N}\le \dfrac{3}{4}N \nonumber \\&\Longrightarrow N_{L}\ge c_8\left( \frac{1}{\log \left( \frac{N}{\delta }\right) }\right) ^{(d+2\beta )/(\beta +d)} N^{(d+2\beta )/(\beta +d)}, \end{aligned}$$

  (A.3)

  where

  $$\begin{aligned} c_8=\dfrac{1}{2} \left( \dfrac{1}{4c_7}\right) ^{(d+2\beta )/(\beta +d)}. \end{aligned}$$

  (A.4)

  Besides, as $N_L=2^LN_0$ and $N_0=\sqrt{N}$, we obtain the first inequality

  $$\begin{aligned} L\ge \log _2\left( c_8\left( \frac{1}{\log \left( \frac{N}{\delta }\right) }\right) ^{(d+2\beta )/(\beta +d)} N^{(3\beta +d)/(2\beta +2d)}\right) . \end{aligned}$$

  (A.5)

  We can get the second inequality by starting with (C.1), that is:

  $$\begin{aligned} N_L\varepsilon _L\le N. \end{aligned}$$

  Furthermore, as $\varepsilon _L=\min \left( 1,c_6\log \left( \frac{N}{\delta }\right) N_{L-1}^{-\beta /(2\beta +d)}\right)$ (see (B.11)), we get

  $$\begin{aligned} N_L\min \left( 1,c_6\log \left( \frac{N}{\delta }\right) N_{L-1}^{-\beta /(2\beta +d)}\right) \le N. \end{aligned}$$

  If $1\le c_6\log \left( \frac{N}{\delta }\right) N_{L-1}^{-\beta /(2\beta +d)}$, we use the fact that $N_L=2^LN_0$ and $N_0=\sqrt{N}$ to deduce

  $$\begin{aligned} L\le \log _2\left( \sqrt{N}\right) . \end{aligned}$$

  (A.6)

  On the other hand, if $1> c_6\log \left( \frac{N}{\delta }\right) N_{L-1}^{-\beta /(2\beta +d)}$ then

  $$\begin{aligned} L\le 1+\log _2\left( \left( \frac{1}{c_6\log \left( \frac{N}{\delta }\right) }\right) ^{(2\beta +d)/(\beta +d)}N^{(3\beta +d)/(2\beta +2d)}\right) . \end{aligned}$$

  (A.7)

  Finally, by combining (A.6) and (A.7), we get the second inequality.

• 2. The proof of the second item is very similar to the first one. Importantly, the current choice of the sequence of rejection rate implies

  $$\begin{aligned} N_L \ge c'_8\left( \frac{1}{\log \left( \frac{N}{\delta }\right) }\right) ^{(2\beta +d)/(2\beta +d-1)}N^{(2\beta +d)/(2\beta +d-1)} \end{aligned}$$

  (A.8)

  where $c'_8$ is a constant independent of N, L.

$\square$

Appendix B: proof of theorem 3.5

We firstly provide a high probability bound on the estimation error:

Lemma B.1

(Favorable event with high probability) Let L be defined by (A.2), k $\in$ $\lbrace 0,\ldots , L\rbrace$ and E be the event defined by:

$$\begin{aligned} E=\cap _{k=0}^L E_k, \end{aligned}$$

(B.1)

where

$$\begin{aligned} E_k=\left\{ \parallel \eta -{\hat{\eta }}_k\parallel _{\infty ,A_k}\le c_5 \log \left( \frac{N{(L+1)}}{c_1\delta }\right) N_k^{-\beta /(2\beta +d)}\right\} , \end{aligned}$$

(B.2)

with $\parallel \eta -{\hat{\eta }}_k\parallel _{\infty ,A_k}:= \sup _{x\in A_{k}} |{\hat{\eta }}_k (x) -\eta (x) |$, $c_5$ is a constant independent of N and $N_k$, but dependent on L and d and $c_1$ depends on $\mu _{min}$ from Assumption (3.2). Under Assumptions 3.1 and 3.2 we have:

$$\begin{aligned} \mathbb {P}(E)\ge 1-\delta . \end{aligned}$$

Proof

Let k $\in$ $\lbrace 0,\ldots , L\rbrace$ and the corresponding estimator ${\hat{\eta }}_k$ (see (A.1)). Let $\mathcal {C}_{r_k}$ the cubic partition considered in Definition 3.4, and fix R $\in \mathcal {C}_{r_k}$. Let x $\in$ R with $R \subset A_k$.

Let $T_{j,k} = Y_j \mathbbm {1}_{\{X_j \in R\}} \frac{\Pi (A_k)}{\Pi (R)}$. We observe that $\mathbb {E}\left[ T_{j,k}\right] = {\bar{\eta }}(R)$, and

$$\begin{aligned} |T_{j,k}| \le \frac{\Pi (A_k)}{\Pi (R)}. \end{aligned}$$

(B.3)

Furthermore

$$\begin{aligned} \textrm{Var}(T_{j,k}) = \dfrac{\Pi (A_k)^2}{\Pi ^2(R)} \textrm{Var}(Y_j \mathbbm {1}_{\{X_j \in R\}}) \le \dfrac{\Pi ^2(A_k)}{\Pi ^2(R)} \int _{R} \eta (z) \Pi (dz\vert A_k) \le \frac{\Pi (A_k)}{\Pi (R)}. \end{aligned}$$

(B.4)

Hence, from Bernstein inequality, and using the fact that $\Pi (A_k) \le \varepsilon _k$, we deduce that for $t \le 1$,

$$\begin{aligned} \mathbb {P}\left( |{\hat{\eta }}_k(x)-{\bar{\eta }}(R)| \ge t \right) \le \exp \left( -\frac{\lfloor N_k\Pi (A_k)\rfloor t^2}{Var(T_{j,k})+\frac{t\Pi (A_k)}{3\Pi (R)}}\right) \le \exp \left( -\lfloor N_k\Pi (A_k)\rfloor \Pi (R)t^2/\Pi (A_k)\right) \end{aligned}$$

by using (B.4).

Note that for $t > 1$, the inequality is always satisfied. Now, applying the above inequality, we deduce that for each $t > 0$

$$\begin{aligned} \mathbb {P}\left( |{\hat{\eta }}(x)-{\bar{\eta }}(x)| \ge t\sqrt{\frac{\Pi (A_k)}{\lfloor N_k\Pi (A_k)\rfloor \Pi (R)}} \right) \le \exp (-t^2), \end{aligned}$$

Hence choosing $t = \sqrt{\log \left( \frac{N(L+1)}{c_1\delta }\right) }$, (where $c_1$ will be defined later) we deduce that for all x $\in$ R, with probability at least $1-\frac{c_1\delta }{N(L+1)}$, we have

$$\begin{aligned} |{\hat{\eta }}(x)-{\bar{\eta }}(x)| \le \sqrt{\log \left( \frac{N(L+1)}{c_1\delta }\right) \frac{2}{N_k\Pi (R)}}. \end{aligned}$$

From the strong density assumption, we then obtain that for all x $\in$ R, with probability at least $1-\frac{c_1\delta }{N(L+1)}$,

$$\begin{aligned} |{\hat{\eta }}(x)-{\bar{\eta }}(x)| \le c_2\sqrt{\log \left( \frac{N(L+1)}{c_1\delta }\right) \frac{1}{N_kr_k^d}}, \end{aligned}$$

(B.5)

where $c_2=\sqrt{\frac{2}{c_1}}$, and $c_1$ is such that $\Pi (R)\ge c_1r_k^d$ by Assumption 3.2.

To get a result in $L_{\infty }$-norm on $A_k$, it remains to consider the union bound over all R $\in$ $\mathcal {C}_{r_k}$ such that $R \cap A_k \ne \emptyset$.

$$\begin{aligned} \Vert {\hat{\eta }}-{\bar{\eta }}\Vert _{\infty ,A_k} \le \max _{R,\;R \cap A_k \ne \emptyset } \Vert {\hat{\eta }} - {\bar{\eta }}\Vert _{\infty ,R}. \end{aligned}$$

By definition, for all $k\ge 0$, the estimator ${\hat{\eta }}_k$ is constant on each cell R, in this case, we have:

$$\begin{aligned} \Pi (A_k)=\sum _{R,\;R\cap A_k=\emptyset } \Pi (R) \end{aligned}$$

Then, by using Assumption 3.2, we have:

$$\begin{aligned} \Pi (A_k)\ge \vert \lbrace R, \;R\cap A_k\ne \emptyset \rbrace \vert \ c_1 r_k^d. \end{aligned}$$

As $r_k=N_k^{-1/(2\beta +d)}$, we get for all k $\in$ $\lbrace 0, \ldots , L\rbrace$,

$$\begin{aligned} \vert \lbrace R,\; R\cap A_k\ne \emptyset \rbrace \vert \le \dfrac{1}{c_1}\Pi (A_k)N_k^{d/(2\beta +d)}\le \dfrac{1}{c_1}( \Pi (A_k)N_k)\le \frac{N}{c_1} \end{aligned}$$

(B.6)

Thus we have (conditionally on $A_k$):

$$\begin{aligned}&\mathbb {P}\left( \forall \,x\in A_k, |{\hat{\eta }}(x)-{\bar{\eta }}(x)|> c_2\sqrt{\frac{\log \left( \frac{N(L+1)}{c_1\delta }\right) }{N_kr_k^d}}\right) \\&\le \mathbb {P}\left( \max _{R,\;R \cap A_k \ne \emptyset } \Vert {\hat{\eta }} - {\bar{\eta }}\Vert _{\infty ,R}>c_2\sqrt{\frac{\log \left( \frac{N(L+1)}{c_1\delta }\right) }{N_kr_k^d}}\right) \\&\le \sum _{R,\;R\cap A_k=\emptyset } \mathbb {P}\left( \Vert {\hat{\eta }} - {\bar{\eta }}\Vert _{\infty ,R}>c_2\sqrt{\frac{\log \left( \frac{N(L+1)}{c_1\delta }\right) }{N_kr_k^d}}\right) \\&\le \vert \lbrace R,\; R\cap A_k\ne \emptyset \rbrace \vert \frac{c_1\delta }{N(L+1)}\\&\le \frac{\delta }{L+1}\quad \text {by } (B.6) \end{aligned}$$

Besides, Assumption 3.1 leads to

$$\begin{aligned} \Vert \eta -{\bar{\eta }}\Vert _{\infty , A_k}\le s r_k, \end{aligned}$$

(B.7)

thus, by combining (B.5), (B.7) and (B.6), we can obtain that with probability at least $1-\frac{\delta }{L+1}$,

$$\begin{aligned} \Vert {\hat{\eta }}_k-\eta \Vert _{\infty ,A_k} \le c_4\left( \sqrt{\log \left( \frac{N(L+1)}{c_1\delta }\right) \frac{1}{N_k r_k^d}}+r_k\right) , \end{aligned}$$

where $c_4=\max (c_2,s)$.

Finally, as $r_k = N_k^{-1/2\beta +d}$, by considering the union bound over all steps, we get with probability at least $1-\delta$,

$$\begin{aligned} \Vert {\hat{\eta }}_k-\eta \Vert _{\infty ,A_k} \le c_5 \log \left( \frac{N(L+1)}{c_1\delta }\right) N_k^{-\beta /(2\beta +d)}\quad \text {for all}\;k\in \lbrace 0,\ldots ,L\rbrace \end{aligned}$$

(B.8)

where $c_5$ depends on $c_4$, and L. $\square$

The following result proves that in the event E, the classifier $g_{{\hat{\eta }}_k}$ does not make any error of classification in the set $A_k\setminus A_{k+1}$ for all $k=0,\ldots ,L-1$, where L is defined by (A.2).

Lemma B.2

(Correct classification) Let E be the event defined by (B.1). If the sequence of rejection rate $(\varepsilon _k)_{k\ge 0}$ used by our algorithm 1 is defined as follows: $\varepsilon _0=1$, and for $k\ge 1$, $\varepsilon _k=\min \left( 1,\log \left( \frac{N}{\delta }\right) \log (N) N_{k-1}^{-\beta /(2\beta +d)}\right) .$ On the event E and under Assumption 3.3, the Bayes classifier $g^*$ agrees with $g_{{\hat{\eta }}_k}$ on the set $A_{k}\setminus A_{k+1}$ for $k\in \lbrace 0,\ldots ,L-1\rbrace$, where L is defined by (C.1), and ${\hat{\eta }}_k$ by (A.1).

Proof

Let us start by stating general facts that hold for a generic estimator ${\hat{\eta }}$ and the corresponding score function ${\hat{f}}(x) = \max ({\hat{\eta }}(x), 1-{\hat{\eta }}(x))$. We consider $F_{f}$, and $F_{{\hat{f}}}$ the cumulative distribution of f(X) and ${\hat{f}}(X)$ respectively, where $f(x) = \max (\eta (x), 1-\eta (x))$. Let $t \in (1/2,1)$, we have that conditionally on the data

$$\begin{aligned} F_{{\hat{f}}}(t) \le \left| F_{{\hat{f}}}(t)-F_{f}(t)\right| + F_{f}(t). \end{aligned}$$

Besides, the following relation holds:

$$\begin{aligned} \left| F_{{\hat{f}}}(t)-F_{f}(t)\right| \le \mathbb {E}_X\left[ \mathbbm {1}_{\{\Vert {\hat{f}}-f\Vert _{\infty } \ge |f(X)-t|\}}\right] \le 2C\Vert {\hat{f}}-f\Vert _{\infty }, \end{aligned}$$

where C is the bound on the density f provided in Assumption 3.3. Using again Assumption 3.3 we can write

$$\begin{aligned} F_{f}(t) \le C\left( t-\frac{1}{2}\right) . \end{aligned}$$

We then deduce that for all $t \in (1/2,1)$, conditionally on the data

$$\begin{aligned} F_{{\hat{f}}}(t) \le 2C\Vert {\hat{f}}-f\Vert _{\infty } + C\left( t-\frac{1}{2}\right) \le 2C\Vert {\hat{\eta }}-\eta \Vert _{\infty } + C\left( t-\frac{1}{2}\right) . \end{aligned}$$

(B.9)

Given iteration $k\in \{ 0,\ldots , L-1\}$, we set ${\hat{t}}_k = \Vert {\hat{\eta }}_k-\eta \Vert _{\infty ,A_{k}}$, and $t_k = \frac{1}{2}+ {\hat{t}}_k$. Thanks to (B.9), with ${\hat{\eta }} ={\hat{\eta }}_k$ and $t = t_k$, we deduce that (conditionally on $A_k$)

$$\begin{aligned} F_{{\hat{f}}_k}(t_k) \le 3C{\hat{t}}_k. \end{aligned}$$

Then, in the event E, we have that

$$\begin{aligned} F_{{\hat{f}}_k}(t_k)\le c_6\log \left( \frac{N}{\delta }\right) N_k^{-\beta /(2\beta +d)}, \end{aligned}$$

(B.10)

where $c_6=3c_5C$, and $c_5$ is defined in (B.8). Hence,

$$\begin{aligned} F_{{\hat{f}}_k}(t_k)\le \min \left( 1,c_6\log \left( \frac{N}{\delta }\right) N_k^{-\beta /(2\beta +d)}\right) \le \varepsilon _{k+1}. \end{aligned}$$

(B.11)

This implies that $\lambda _{k+1} \ge \frac{1}{2} + {\hat{t}}_k$ by the definition of $\lambda _{k+1}$ (given by (3.2)).

Let x $\in$ $A_k{\setminus } A_{k+1} = \{x \in A_k, \;\; {\hat{f}}_k(x) > \lambda _{k+1}\}$. Necessarily, we have

$$\begin{aligned} {\hat{f}}_k(x)-\frac{1}{2}>\Vert {\hat{\eta }}_k-\eta \Vert _{\infty ,A_{k}}\ge \vert {\hat{\eta }}_k(x)-\eta (x)\vert , \end{aligned}$$

which implies $g_{\eta }(x)=g_{{\hat{\eta }}_k}(x).$ $\square$

Lemma B.3

(Excess-error) Let E be the event defined by (B.1). Let $g_{{\hat{\eta }}}$ be the classifier provided by our algorithm. Then on the event E, we have

$$\begin{aligned} R(g_{{\hat{\eta }}})-R(g_{\eta })\le {\tilde{O}}\left( N^{-\frac{2\beta }{d+\beta }}\right) , \end{aligned}$$

where ${\tilde{O}}$ hides some constants and logarithmic factors.

Proof

Let us consider the sequence $(A_k)_{0\le k\le L}$ used in our algorithm. It is not difficult to see that $\{A_k{\setminus } A_{k+1}, k=0, \ldots , L-1\}\cup A_L$ forms a partition of $[0,1]^d$, where L is defined by (C.1).

In this case, the excess-risk of $g_{{\hat{\eta }}}$ can be rewritten as:

$$\begin{aligned} R(g_{{\hat{\eta }}})-R(g^*)=\sum _{j=0}^{L-1}\int _{\{g_{{\hat{\eta }}}\ne g^*\}\cap \{A_j\setminus A_{j+1}\}}\vert 2\eta (x)-1\vert d\Pi (x)+ \int _{A_L\cap \{g_{{\hat{\eta }}}\ne g^*\}} \vert 2\eta (x)-1\vert d\Pi (x) \end{aligned}$$

and thus

$$\begin{aligned} R(g_{{\hat{\eta }}})-R(g^*)= & {} 2 \sum _{j=1}^{L-1} \mathbb {E}_X\left[ |\eta (X)-\frac{1}{2}| \mathbbm {1}_{\{g^*(X)\ne g_{{\hat{\eta }}_j}(X)\}} \mathbbm {1}_{\{A_j \setminus A_{j+1}\}} \right] \nonumber \\{} & {} \quad +2 \mathbb {E}_X\left[ |\eta (X)-\frac{1}{2}| \mathbbm {1}_{\{g^*(X)\ne g_{{\hat{\eta }}_L}(X)\}} \mathbbm {1}_{\{A_L\}}\right] . \end{aligned}$$

(B.12)

Due to the Lemma B.2, the first term in the r.h.s of (B.12) is zero in the event E. Thus we get

$$\begin{aligned} R({{\hat{g}}})-R(g^*)&=2 \mathbb {E}_X\left[ |\eta (X)-\frac{1}{2}| \mathbbm {1}_{\{g^*(X)\ne g_{{\hat{\eta }}_L}(X)\}} \mathbbm {1}_{\{A_L\}}\right] \\&\le 2 \mathbb {E}_X\left[ |\eta (X)-\frac{1}{2}| \mathbbm {1}_{|{\eta }(X)-\frac{1}{2}|< |{\hat{\eta }}_L(X)-\eta (X)|} \mathbbm {1}_{\{A_L\}}\right] . \end{aligned}$$

We thus have

$$\begin{aligned} R({{\hat{g}}})-R(g^*)&\le 2 \Vert {\hat{\eta }}_L-\eta \Vert _{\infty ,A_L}. \mathbb {E}_X\left[ \mathbbm {1}_{|{\eta }(X)-\frac{1}{2}|< |{\hat{\eta }}_L(X)-\eta (X)|}\right] \nonumber \\&\le 4C\Vert {\hat{\eta }}_L-\eta \Vert _{\infty ,A_L}^{2}\;\text {by Assumption} 3.3. \end{aligned}$$

(B.13)

By Lemma B.1, we get with probability at least $1-\delta$

$$\begin{aligned} R({{\hat{g}}})-R(g^*) \le 4Cc_5^2 \log ^2\left( \frac{N(L+1)}{\delta }\right) N_L^{-2\beta /(2\beta +d)}. \end{aligned}$$

(B.14)

Recalling the bound (A.3) on $N_L$ provided in the proof of Lemma A.1

$$\begin{aligned} N_{L} \ge c_8\left( \frac{1}{\log \left( \frac{N}{\delta }\right) }\right) ^{(d+2\beta )/(\beta +d)}N^{(d+2\beta )/(\beta +d)} \end{aligned}$$

for some constant $c_8$, we then conclude that (B.14) becomes

$$\begin{aligned} R(g_{{\hat{\eta }}})-R(g_{\eta })\le {\tilde{O}}\left( N^{-\frac{2\beta }{\beta +d}}\right) . \end{aligned}$$

$\square$

Appendix C: proof of theorem 3.7

For the sake of simplicity, throughout the proof, we assume that the distribution $\Pi$ of the X is the uniform distribution on $[0,1]^d$. We now consider the case when $\beta > 1$. The major difference with the case $\beta \le 1$ is in the last step $k=L$. However, these modifications induce slight adaptations in earlier steps. In particular, for all $k \le L$ we set the rejection rate as:

$$\begin{aligned} \varepsilon _k =\min \left( 1,\log \left( \frac{N}{\delta }\right) \log (N) N_{k-1}^{- 1 /(2\beta +d)}\right) . \end{aligned}$$

According to this new definition, we need to consider a different event E in order to make the first term in the excess risk in (B.12) to be zero. We have the following Lemma:

Lemma C.1

Let L be defined as:

$$\begin{aligned} L=\max \lbrace j\ge 1, N> \sum _{k=0}^{j}\lfloor N_k\Pi (A_k)\rfloor \rbrace . \end{aligned}$$

(C.1)

Let k $\in$ $\lbrace 0,\ldots , L\rbrace$ and E be the event defined by:

$$\begin{aligned} {\tilde{E}}=\cap _{k=0}^{L-1} {\tilde{E}}_k, \end{aligned}$$

(C.2)

where

$$\begin{aligned} {\tilde{E}}_k=\left\{ \parallel \eta -{\hat{\eta }}_k\parallel _{\infty ,A_k}\le c_5 \log \left( \frac{N(L+1)}{c_1\delta }\right) N_k^{-{1}/(2\beta +d)}\right\} , \end{aligned}$$

(C.3)

with $\parallel \eta -{\hat{\eta }}_k\parallel _{\infty ,A_k}:= \sup _{x\in A_{k}} |{\hat{\eta }}_k (x) -\eta (x) |$, ${\hat{\eta }}_k$ is the histogram defined by (A.1), $c_1$ is a constant independent of N, but dependent on d, and $\mu _{min}$ from Assumption (3.2). The quantity $c_5$ is a constant independent of N and $N_k$, but dependent on s (from Assumption 3.6) and d. Under Assumptions 3.6 and 3.2 we have:

$$\begin{aligned} \mathbb {P}({{\tilde{E}}})\ge 1-\frac{L}{L+1}\delta . \end{aligned}$$

Proof

The proof is quite similar to that of Lemma B.1. We just have to adapt the choices of $\varepsilon _k$ as follows:

$$\begin{aligned} \varepsilon _k =\min \left( 1,\log \left( \frac{N}{\delta }\right) \log (N) N_{k-1}^{-{1}/(2\beta +d)}\right) . \end{aligned}$$

$\square$

Moreover, this modification on the calibration of $\varepsilon _k$ leads to a lower bound on $N_L$, stated by (A.8). We also have the following result which states that, in the event ${\tilde{E}}$ the classifier does not make any error in the set $A_k\setminus A_{k+1}$ for all $k=0,\ldots , L-1.$

Lemma C.2

(Correct classification) Let ${\tilde{E}}$ be the event defined by (C.2). Under Assumption 3.6, the Bayes classifier $g^*$ agrees with $g_{{\hat{\eta }}_k}$ on the set $A_{k}\setminus A_{k+1}$ for $k\in \lbrace 0,\ldots ,L-1\rbrace$, where L is defined by (C.1), and ${\hat{\eta }}_k$ by (A.1).

Proof

The proof is quite similar to that of Lemma C.2. We just have to adapt the choices of $\varepsilon _k$ as follows:

$$\begin{aligned} \varepsilon _k =\min \left( 1,\log \left( \frac{N}{\delta }\right) \log (N) N_{k-1}^{-{1}/(2\beta +d)}\right) . \end{aligned}$$

$\square$

By using the Lemma C.2, we thus obtain the following upper bound on the excess-risk of $g_{{\hat{\eta }}}$, which is valid on ${\tilde{E}}$:

$$\begin{aligned} R(g_{{\hat{\eta }}})-R(g^*)\le 4C\parallel {\hat{\eta }}_L-\eta \parallel ^2_{\infty ,A_L}. \end{aligned}$$

Therefore, in view of Lemma C.1, and the lower bound on $N_L$ provided in (A.8), to conclude the proof of Theorem 3.7, it remains to show that with probability larger than $1-\dfrac{1}{L+1}\delta$, we have

$$\begin{aligned} \parallel {\hat{\eta }}_L-\eta \parallel _{\infty ,A_L} \le C \log \left( \frac{N}{\delta }\right) N_L^{- {\beta } /2\beta +d}, \end{aligned}$$

for some positive constant C. To this end, we have to adopt the following strategy for the last iteration $k=L$: we build an estimator ${{\hat{\eta }}}_L$ at each point from the current last set $A_L$. In this set, we need to build a more refined analysis than in the previous case $\beta \le 1$. In particular, we build a kernel estimator to achieve a higher order of regularity than with histograms. Let us then consider a bounded one dimensional kernel K of order $\ell = \lfloor \beta \rfloor$ (that is, $\int u^j K(u) du = 0$ for all $j\in \left\{ 1,\ldots , \ell \right\}$, see Tsybakov (2008)) with support $[-1,1]$. Based on K, we define for all $z=(z_1,\ldots , z_d)\in [0,1]^d$, the d-dimensional kernel $K_d (z) = \prod _{j=1}^d K(z_j)$. Nevertheless, this time we do not sample $\lfloor N_L \varepsilon _L \rfloor$ points in $A_L$ but rather in a slightly bigger set $\tilde{\mathcal {A}}_{r_L}$ that we construct in the following way. Consider a first cubic partition $\mathcal {C}_{r_L}$ of $A_L$. We define the set $\tilde{\mathcal {A}}_{r_L} = \cup _{R\in \mathcal {C}_{r_L}} {\tilde{R}}$ where ${\tilde{R}}$ is a flatten version of R given by

$$\begin{aligned} {\tilde{R}} = \left\{ x\in [0,1]^d: \ \exists \, z \in R, \quad \Vert x - z \Vert _{\infty } \le r_L \right\} . \end{aligned}$$

(C.4)

Now let us consider a second cubic partition $\mathcal {C}_{r_L^{\beta }}$ of $A_L$. Importantly, each $R\in \mathcal {C}_{r_L}$ can be described by a collection of $R'$ from the second partition $\mathcal {C}_{r_L^{\beta }}$. Let then $R'\in \mathcal {C}_{r_L^{\beta }}$ and $R\in \mathcal {C}_{r_L}$ such that $R' \subset R \subset A_L$. Let $x_{R'}$ be the center of the cell $R'$. In order to construct ${{\hat{\eta }}}_L$ in the set $R'$, we consider the center $x_{R'}$ of the latter – then ${{\hat{\eta }}}_L$ will be constant on $R'$ and the constant will be equal to the value that ${{\hat{\eta }}}_L$ takes at $x_{R'}$ (below is the precise expression). An important difference with earlier steps is the definition of the variable $T_{j,L}$ that is now given by

$$\begin{aligned} T_{j,L} = Y_j \ K_d \left( \frac{X_j-x_{R'}}{r_L} \right) \mathbbm {1}_{\{X_j \in R'\}} \frac{\Pi ({\tilde{A}}_L)}{r_L^d}. \end{aligned}$$

We then consider the estimator

$$\begin{aligned} {\hat{\eta }}(x_{R'}) = \dfrac{1}{\lfloor N_L \varepsilon _L \rfloor } \sum _{X_j\in R'} T_{j,L}. \end{aligned}$$

(C.5)

We observe that $\mathbb {E}\left[ T_{j,L}\right] = \dfrac{1}{r_L^d} \int _{R'} \eta (z)K_d\left( \dfrac{z-x_{R'}}{r_L}\right) dz$. Besides, since $K_d$ is supported on $[-1,1]^d$ and by definition of $R'$, we have that

$$\begin{aligned} K_d\left( \dfrac{z-x_{R'}}{r_L}\right) = 0 \;\; \textrm{if} \;\; z \notin R', \end{aligned}$$

and then we can extend the integral in $\mathbb {E}\left[ T_{j,L}\right]$ on $\mathbb {R}$ and write

$$\begin{aligned} \mathbb {E}\left[ T_{j,L}\right] = \dfrac{1}{r_L^d} \int _{\mathbb {R}} \eta (z)K_d\left( \dfrac{z-x_{R'}}{r_L}\right) dz. \end{aligned}$$

This expression allows us to control the bias term of ${\hat{\eta }}(x_{R'})$. Indeed, using (Giné & Nickl, 2015) (see also Lemma 6 in Locatelli et al. (2017)), we can write that for any point $x_{R'}$

$$\begin{aligned} \left| \mathbb {E} \left[ {\hat{\eta }}(x_{R'})\right] - \eta (x_{R'}) \right| \le c r_L^{\beta }. \end{aligned}$$

(C.6)

Now, we provide a bound for the variance of ${\hat{\eta }}_L(x_{R'})$. First, notice that since the kernel $K_d$ is bounded, we have

$$\begin{aligned} |T_{j,L}| \le C \frac{\Pi ({\tilde{A}}_L)}{r_L^d} Y_j \mathbbm {1}_{\{X_j \in {R'}\}}, \end{aligned}$$

(C.7)

for some positive constant C – from now on, C is a positive constant that may change from one line to another. Therefore, using the fact that $Y_j^2 = Y_j$, we have

$$\begin{aligned} \textrm{Var}(T_{j,L}) \le C \dfrac{\Pi ({\tilde{A}}_L)^2}{r_L^{2d}} \mathbb {E}\left[ Y_j \mathbbm {1}_{\{X_j \in {R'}\}}\right] \le C \dfrac{\Pi ({\tilde{A}}_L)^2}{r_L^{2d}} \int _{R'} \eta (z) \Pi (dz\vert {\tilde{A}}_L) \le C \frac{\Pi ({\tilde{A}}_L) \Pi ({R'})}{r_L^{2d}}. \end{aligned}$$

Since $\Pi ({R'}) \le c r_L^d$, we deduce from the above inequality that

$$\begin{aligned} \textrm{Var}(T_{j,L}) \le C \dfrac{\Pi ({\tilde{A}}_L)}{r_L^d}. \end{aligned}$$

(C.8)

Additionally, since $\Pi (A_L) \le \varepsilon _L$ and $\Pi$ is the uniform distribution on $[0,1]^d$, we then have

$$\begin{aligned} \Pi ({\tilde{A}}_L) \le C \varepsilon _L. \end{aligned}$$

Hence from Bernstein Inequality, and using (C.8), we deduce that for all $t \le 1$,

$$\begin{aligned} \mathbb {P}\left( |{\hat{\eta }}_L(x_{R'}) - \mathbb {E}\left[ {\hat{\eta }}_L(x_{R'})\right] | \ge t \right) \le \exp \left( -\frac{\lfloor N_L\Pi ({\tilde{A}}_L)\rfloor t^2}{Var(T_{j,L})+\frac{t\Pi ({\tilde{A}}_L)}{3r_L^d}}\right) \le \exp \left( - C \lfloor N_L\Pi ({\tilde{A}}_L)\rfloor r_L^dt^2/\Pi ({\tilde{A}}_L)\right) . \end{aligned}$$

Note that for $t > 1$, the inequality is always satisfied. Now, applying the above inequality, we deduce that for all $t > 0$

$$\begin{aligned} \mathbb {P}\left( |{\hat{\eta }}_L(x_{R'}) - \mathbb {E}\left[ {\hat{\eta }}_L(x_{R'})\right] |\ge t\sqrt{\frac{\Pi ({\tilde{A}}_L)}{\lfloor N_L\Pi ({\tilde{A}}_L)\rfloor r_L^d}} \right) \le \exp (-t^2), \end{aligned}$$

Hence choosing $t = \sqrt{\log \left( \frac{\log (N)N^2(L+1)}{C\delta }\right) }$, we deduce that with probability at least $1-\frac{C\delta }{\log (N)N^2(L+1)}$, we have

$$\begin{aligned} |{\hat{\eta }}_L(x_{R'}) - \mathbb {E}\left[ {\hat{\eta }}_L(x_{R'})\right] | \le C \sqrt{\log \left( \frac{\log (N)N^2(L+1)}{C\delta }\right) \frac{1}{N_Lr_L^d}}. \end{aligned}$$

(C.9)

To get a result in $L_{\infty }$-norm on $A_L$, it remains to consider the union bound over all $x_{{R'}}$, for all $R' \subset A_L$. First, we observe that

$$\begin{aligned} \vert \lbrace R',\; R'\cap A_L\ne \emptyset \rbrace \vert \le \vert \lbrace R',\; R'\cap A_L\ne \emptyset \rbrace \vert r_L^{1-\beta }, \end{aligned}$$

which implies with Equation (B.6) that

$$\begin{aligned} \vert \lbrace R',\; R'\cap A_L\ne \emptyset \rbrace \vert \le c N r_L^{1-\beta } \le CN^2. \end{aligned}$$

(C.10)

Thus we have for N large enough conditionally on $A_L$

$$\begin{aligned}{} & {} \mathbb {P}\left( \max _{x_{R'}} |{\hat{\eta }}_L(x_{R'}) - \mathbb {E}\left[ {\hat{\eta }}_L(x_{R'})\right] |> C\sqrt{\frac{\log \left( \frac{\log (N)N^2(L+1)}{C\delta }\right) }{N_Lr_L^d}}\right) \le \\{} & {} \sum _{R',\;R'\cap A_L=\emptyset } \mathbb {P}\left( |{\hat{\eta }}_L(x_{R'}) - \mathbb {E}\left[ {\hat{\eta }}_L(x_{R'})\right] |>C\sqrt{\frac{\log \left( \frac{\log (N)N^2(L+1)}{C\delta }\right) }{N_Lr_L^d}}\right) \\{} & {} \le \vert \lbrace R',\; R'\cap A_L\ne \emptyset \rbrace \vert \frac{C\delta }{\log (N)N^2(L+1)}\\{} & {} \le \frac{\delta }{L+1}\quad \text {by}\, (C.10). \end{aligned}$$

Finally, for $x \in A_L$, we define ${\hat{\eta }}(x) = {\hat{\eta }}(x_{R'})$ if $x \in R'$. Let $x \in R'$, with $R' \subset A_L$. Since $\eta$ is Lipschitz (because it is Hölder with $\beta > 1$), using the triangle inequality together with Equation (C.6), we have

$$\begin{aligned} \Vert \eta (x)-\mathbb {E}\left[ {\hat{\eta }}_L(x_{R'})\right] \Vert _{\infty , A_L} \le \Vert \eta (x)- \eta (x_{R'})\Vert _{\infty , A_L} + \left| \mathbb {E} \left[ {\hat{\eta }}(x_{R'})\right] - \eta (x_{R'}) \right| \le C r_L^{\beta }. \end{aligned}$$

(C.11)

Thus, combined with (C.10), we obtain that with probability at least $1-\frac{\delta }{L+1}$,

$$\begin{aligned} \Vert {\hat{\eta }}_L-\eta \Vert _{\infty ,A_L} \le C\sqrt{\log \left( \frac{\log (N)N^2(L+1)}{C\delta }\right) \frac{1}{N_L r_L^d}}+Cr_L^{\beta }. \end{aligned}$$

Finally, as $r_L = N_L^{-1/2\beta +d}$, we get with probability at least $1-\frac{1}{L+1}\delta$,

$$\begin{aligned} \Vert {\hat{\eta }}_L-\eta \Vert _{\infty ,A_L} \le C \log \left( \frac{N^2}{\delta }\right) N_L^{-\beta /(2\beta +d)}, \end{aligned}$$

which, combined with the fact that $N_L$ is of order $N^{\frac{2 \beta + d}{ 2 \beta + d - 1}}$ (see in (A.8) for the formal lower bound), yields the result.