Fast parameterless prototype-based co-clustering

Abstract

Tensor co-clustering algorithms have been proven useful in many application scenarios, such as recommender systems, biological data analysis and the analysis of complex and evolving networks. However, they are significantly affected by wrong parameter configurations, since, at the very least, they require the cluster number to be set for each mode of the matrix/tensor, although they typically have other algorithm-specific hyper-parameters that need to be fine-tuned. Among the few known objective functions that can be optimized without setting these parameters, the Goodman–Kruskal $\tau$—a statistical association measure that estimates the strength of the link between two or more discrete random variables—has proven its effectiveness in complex matrix and tensor co-clustering applications. However, its optimization in a co-clustering setting is tricky and, so far, has leaded to very slow and, at least in some specific but not unfrequent cases, inaccurate algorithms, due to its normalization term. In this paper, we investigate some interesting mathematical properties of $\tau$, and propose a new simplified objective function with the ability of discovering an arbitrary and a priori unspecified number of good-quality co-clusters. Additionally, the new objective function definition allows for a novel prototype-based optimization strategy that enables the fast execution of matrix and higher-order tensor co-clustering. We show experimentally that the new algorithm preserves or even improves the quality of the discovered co-clusters by outperforming state-of-the-art competing approaches, while reducing the execution time by at least two orders of magnitude.

1 Introduction

Clustering is by far one of the most popular machine learning tasks for its ability of extracting useful summaries of the data in the preliminary phases of a knowledge discovery process. When dealing with high-dimensional matrices or tensors, also called N-way data, clustering is often superseded by co-clustering (Dhillon, 2001), which consists in processing the modes (the row and the columns for matrices, i.e., 2-way tensors) of the input tensor simultaneously. This roughly corresponds to clustering one mode while performing dimensionality reduction on the other mode, for each mode alternately, and it helps discover more meaningful clusters (called co-clusters) as each cluster on one mode benefits from the clustering on the other modes. Intrinsically, column clusters also improve the interpretability of row clusters by providing useful summary information that might help explain each row grouping in a compact way. Unfortunately, clustering and, in particular, co-clustering, is often misused, since all existing methods produce meaningless clusters if their parameters are not set properly. In fact, most objective functions optimized by state-of-the-art co-clustering algorithms are strongly affected by the number of clusters, which is, typically, an input parameter. This is because two values of the same objective function computed on two different solutions with two different numbers of clusters can not be compared directly. In other words, they belong to two different search spaces. For instance, the loss of mutual information, optimized by Dhillon et al. (2003), is minimum for the discrete partition, i.e., when each cluster contains exactly one data instance. Typically, when the modes of a tensor are N, one has to set N different cluster numbers, plus any other algorithm-specific parameter to make a co-clustering method produce accurate results. As an example, a recent co-clustering method based on deep neural networks (Xu et al., 2019) requires at least four additional user-specified parameters, without considering the number of clusters for each mode and (many) other optional hyperparameters needed to setup and fine-tune the underlying neural network architecture.

To the best of our knowledge, the only co-clustering objective function least dependent on the number of clusters is the Goodman–Kruskal’s $\tau$ association measure (Goodman and Kruskal, 1954). This measure has been originally designed to estimate the strength of the link between two discrete random variables, but it has shown its potential in several co-clustering algorithms (Robardet and Feschet, 2001; Ienco et al., 2013) as well, even for higher-order tensors (Battaglia and Pensa, 2023). Those algorithms do not require the specification of the correct number of clusters to find (sub)optimal solutions and, in general, are able to identify a meaningful number of clusters during the iterative optimization process. Despite this nice theoretical property, in some occasions, such algorithms find solutions that are deemed optimal according to $\tau$, but provide poor descriptions of the data, as they include one or two very large clusters containing the majority of the input data instances plus some small or singleton clusters. Furthermore their iterative process turns out to be very long, since, to achieve the convergence, many iterations are needed, each one being computationally very expensive. The slow convergence of $\tau$, especially in the very first iterations, counterbalances the advantages of being parameterless and limits its real applicability to small tensors with few modes.

To address these issues, we deeply investigate the mathematical properties and the convergence behavior of the Goodman–Kruskal’s $\tau$ objective function. By analyzing the behavior in a controlled experimental setting, we show that the normalization term of the original association measure may lead the co-clustering algorithm towards meaningless solutions with almost all the rows grouped together in a unique cluster. We then propose a new objective function, derived from $\tau$—thus preserving its good theoretical properties—that, contrary to the original Goodman–Kruskal’s $\tau$ definition, allows us to define a similarity measure between a single item and a cluster prototype. This choice enables us to design a new optimization schema that reduces the number of necessary iterations and execution time significantly (by two orders of magnitude, on average), leading to time performances that are similar to those of state-of-the-art matrix co-clustering methods that require the numbers of clusters as input parameters. When applied to higher-order tensors, our algorithm is the fastest among all the competitors considered in our study. Furthermore, the new definition mitigates the problem exhibited by the original $\tau$ formulation, which leads to co-clustering results that, although optimal from the point of view of the objective function, provide poor and thus useless descriptions of the data. The experiments, conducted on both synthetic and real-world matrices, also show that the improved time performances are not at the cost of the overall quality of the co-clusters. The remainder of the paper is organized as follows: a brief related literature review is reported in Sects. 2 and 3 presents some background notion on co-clustering. The fast co-clustering algorithm is introduced in Sect. 4, while its extension to tensors is presented in Sect. 5; the results of our experimental validation are discussed in Sect. 6; finally, we draw some conclusions in Sect. 7.

2 Related works

There exist several co-clustering techniques, tailored for different data types and application scenarios (Madeira and Oliveira, 2004; Govaert and Nadif, 2013; Qiu, 2004). Among the others, co-clustering has proven its effectiveness when applied to contingency tables, i.e. matrices reporting the co-occurrences between two sets of categorical values, such as documents/words, customers/products or users/movies data objects. In fact, these matrices are typically high-dimensional and extremely sparse and, thus, they cannot be handled by classical clustering methods. Furthermore, the columns of these matrices represent instances of the same categorical feature (words, products or movies, in the examples above), thus grouping them in clusters makes sense and provides additional useful information.

The main methods for contingency tables co-clustering can be roughly divided into three groups: spectral methods (Dhillon, 2001; Kluger et al., 2003), which transform the co-clustering problem into a partitioning problem on a bipartite graph; matrix factorization based methods, such as Block Value Decomposition (Long et al., 2005) and Non-Negative Matrix Tri-Factorization (Ding et al., 2006; Yoo and Choi, 2010); probabilistic approaches (Govaert and Nadif, 2010; Ailem et al., 2017), which assume the data to be generated by a probabilistic model and try to recover the underlying model parameters; methods that formulate the co-clustering problem as an optimization problem for some measure of the quality of the co-clustering solution. Example of such measures are the loss of Mutual Information (Dhillon et al., 2003), any Bregman divergence (Banerjee et al., 2007), the Goodman and Kruskal’s $\tau$ measure (Robardet and Feschet, 2001; Ienco et al., 2013), the graph modularity (Ailem et al., 2016). Instead, Xu et al. (2019) propose a deep learning model for co-clustering, that uses deep autoencoders for dimensionality reduction and Gaussian Mixture Models to infer the clustering assignments. Many extensions of the traditional co-clustering problem have been studied: as few examples, there exist algorithms to perform co-clustering in a distributed-scenario (Papadimitriou and Sun, 2008), algorithms for co-clustering heterogeneous data (Gao et al., 2005; Ienco et al., 2013), or hierarchical methods (Pensa et al., 2014; Wei et al., 2021).

In the last 3 years, the interests of scientists has significantly shifted towards multi-view approaches, with several proposal aimed at solving this type of problem (Du et al., 2021; Hussain et al., 2022). Other recent approaches have focused on improving or speeding up matrix factorization algorithms for co-clustering (Chen et al., 2023b; Wang and Ma, 2021), or to adapt the objective functions to more complex problems (Deng et al., 2021; Tang and Wan, 2021). Wang et al. (2021), instead, address the problem of multiple alternative clustering, by introducing the first algorithm that generates multiple alternative co-clusterings at the same time. Further recent contributions are aimed at improving model-based text co-clustering (Affeldt et al., 2021b, a), or enhancing bipartite graph partition-based co-clustering (Chen et al., 2023a). Finally, the problem of correctly evaluating co-clusters has also been addressed recently by Robert et al. (2021).

With the exception of the methods based on the Goodman–Kruskal’s $\tau$ or its derivations (Robardet and Feschet, 2001; Pensa et al., 2014; Ienco et al., 2013), all other approaches requires the specification of the number of desired or expected clusters in each mode. Interestingly, generalizations of some of these methods work on higher-order tensors as well (Papalexakis et al., 2013; Boutalbi et al., 2019a; Battaglia and Pensa, 2023).

In the last decades, in fact, tensors have attracted a lot of attention due to their intrinsic complexity and richness. Several ad hoc extensions of 2-way matrix methods have been proposed and, among them, also co-clustering has been naturally extended to handle tensors. The main tensor co-clustering methods are often based on tensor decomposition models (Zhou et al., 2009; Peng and Li, 2010; Papalexakis et al., 2013; Zhang et al., 2013), such as PARAFAC/CANDECOMP or Non-Negative Tucker decomposition. Instead, Wu et al. (2016) introduce a spectral co-clustering method based on a new random walk model for nonnegative square tensors; in Chi et al. (2020) the tensors are represented as weighted hypergraphs, which are cut by an algorithm based on random sampling. Other more recent approaches (Boutalbi et al., 2019a, b) rely on an extension of the latent block model. In these works, co-clustering for sparse tensor data is viewed as a multi-way clustering model where each slice of the third mode of the tensor represents a relation between two sets. Wang and Zeng (2019) present a co-clustering approach for tensors that uses a least-square estimation procedure for identifying a N-way block structure that applies to binary, continuous, and hybrid data instances. Boutalbi et al. (2022) introduce the Tensor Latent Block Model (TLBM) for the co-clustering of tensor data, that exploits the latent block model and is able to consider continuous, binary and count data. According to the authors, the derived algorithms can be also used for the clustering of multiple graphs or multi-view clustering. Finally, Battaglia and Pensa (2023) propose a tensor extension of the 2-way co-clustering algorithm based on the optimization of the Goodman and Kruskal’s $\tau$ association measure, which is, to the best of our knowledge, the only tensor co-clustering approach not requiring the number of clusters as input parameter. Unfortunately, it is also very slow and, as we will show in the next sections, sometimes leads to degenerate solutions. These are exactly the two issues that we address in this paper, by proposing a novel more effective derivation of the Goodman–Kruskal’s $\tau$ objective and a more efficient prototype-based algorithm for its fast optimization.

3 Background and problem formulation

Table 1 Symbols and notation used in the paper

Before introducing the tensor co-clustering problem, we briefly describe the notation used in this paper. As a general rule, non indexed (e.g., k) lowercase letters represent scalars, while indexed (e.g, $p_{ic})$ lowercase letters represent the single entries of a vector/matrix/tensor (with some exceptions, e.g., $k_0$). Instead, uppercase Latin or Greek symbols (e.g., A, $\Gamma$) represent some quantities computed on matrices or tensors, with the exception of X, Y and Z that denote some categorical random variables. Tensor are represented according to two different notations: script uppercase letters (for input data) or bold uppercase letters (for tensors computed during the execution of the algorithms). Matrices are represented similarly. Script uppercase letters are also used to represent sets, in our case, partitions (sets of clusters) and clusters (subsets of points). For a complete detailed distinction, we let the reader refer to Table 1. In the following, we formulate the tensor co-clustering problem as the maximization of an association measure between categorical random variables.

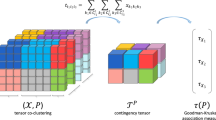
Given a tensor ${\mathcal {A}}$ with m modes, a co-clustering of ${\mathcal {A}}$ is a tuple $({\mathcal {P}}^{(1)},\dots , {\mathcal {P}}^{(m)})$ where ${\mathcal {P}}^{(i)}$ is a partition of the elements of the ith mode of ${\mathcal {A}}$, for each $i=1,\dots ,m$. As a special case, if ${\mathcal {A}}$ is a matrix (i.e. a 2-way tensor), a co-clustering of ${\mathcal {A}}$ is a pair $({\mathcal {R}},{\mathcal {C}})$, where ${\mathcal {R}}$ is a partition of the rows and ${\mathcal {C}}$ a partition of the columns of the matrix. In this paper we present a new (tensor) co-clustering algorithm based on the optimization of the Kruskal and Goodman’s $\tau$ measure, such as $\tau$CC (Ienco et al., 2013) and $\tau$TCC (Battaglia and Pensa, 2023), but using a different optimization strategy that makes the algorithm noticeably faster.

The objective function of $\tau$CC is Kruskal and Goodman’s $\tau$ (Goodman and Kruskal, 1954), an association measure that estimates the strength of the link between two discrete variables X and Y according to the proportional reduction of the error in predicting one of them knowing the other:

$$\begin{aligned} \tau _{X|Y} = \frac{e_X - {\mathbb {E}}[e_{X|Y}]}{e_X} \end{aligned}$$

(1)

where $e_X$ is the error in predicting X, i.e., the probability that two independent realizations of the random variable differ, and ${\mathbb {E}}[e_{X|Y}]$ is the expected value of the error in predicting X when Y is known. The values of $\tau _{X|Y}$ stay between 0 (when there is no association between X and Y) and 1 (when X is function of Y). Function $\tau$ can be used to evaluate a co-clustering solution: given a matrix ${\mathcal {A}}=(a_{ij})$ with non-negative values and a co-clustering $({\mathcal {R}},{\mathcal {C}})$ of ${\mathcal {A}}$, the association of the row clustering ${\mathcal {R}}$ with the column clustering ${\mathcal {C}}$ can be expressed as

$$\begin{aligned} \tau _{R|C}({\mathcal {R}},{\mathcal {C}}) = \frac{\sum _{r=1}^{|{\mathcal {R}}|}\sum _{c=1}^{|{\mathcal {C}}|} \frac{t_{rc}^2}{t_{\tiny \bullet \tiny \bullet }t_{\tiny \bullet c}} - \sum _{r=1}^{|{\mathcal {R}}|}\frac{t_{r\tiny \bullet }^2}{t_{\tiny \bullet \tiny \bullet }^2}}{1 - \sum _{r=1}^{|{\mathcal {R}}|}\frac{t_{r\tiny \bullet }^2}{t_{\tiny \bullet \tiny \bullet }^2}} \end{aligned}$$

(2)

where ${\textbf{T}}= (t_{rc})$ is the contingency table associated to the co-clustering, i.e. $t_{rc} = \sum _{i\in {\mathcal {R}}_r}\sum _{j\in {\mathcal {C}}_c}a_{ij}$, $t_{\tiny \bullet \tiny \bullet }=\sum _{r=1}^{|{\mathcal {R}}|}\sum _{c=1}^{|{\mathcal {C}}|}{t_{rc}}$, $t_{\tiny \bullet c}=\sum _{r=1}^{|{\mathcal {R}}|}{t_{rc}}$, and $t_{r\tiny \bullet }=\sum _{c=1}^{|{\mathcal {C}}|}{t_{rc}}$. Analogously, the association of the column clustering ${\mathcal {C}}$ to the row clustering ${\mathcal {R}}$ can be evaluated through the function $\tau _{C|R}({\mathcal {R}},{\mathcal {C}})$. Notice that $\tau$ is not symmetric, thus $\tau _{R|C}({\mathcal {R}},{\mathcal {C}})\ne \tau _{C|R}({\mathcal {R}},{\mathcal {C}})$ in general. The best co-clustering solutions are those that simultaneously maximize $\tau _{R|C}$ and $\tau _{C|R}$. An intuitive explanation of the meaning of $\tau _{R|C}({\mathcal {R}},{\mathcal {C}})$ and $\tau _{C|R}({\mathcal {R}},{\mathcal {C}})$ and its implication for a co-clustering solution, is given in the example below.

Example 1

Suppose that ${\mathcal {A}}$ is a sparse matrix over a set of 10 customers (the rows of ${\mathcal {A}}$) and a set of 8 products (the columns of ${\mathcal {A}}$). Assume that ${\mathcal {A}}$ is as follows

where each entry $(r_i,c_j)$ is the count of products $c_j$ purchased by customer $r_i$. A possible co-clustering over ${\mathcal {A}}$ is $({\mathcal {R}},{\mathcal {C}})$, where ${\mathcal {R}}=\{\{r_1,r_2,r_3\},\{r_4,r_5,r_6\},\{r_7,r_8\},\{r_9,r_{10}\}\}$, is the partition of customers and ${\mathcal {C}}=\{\{c_1,c_2\},\{c_3,c_4\},\{c_5,c_6\},\{c_7,c_8\}\}$ is the partition of products. We can associate, to the triple $({\mathcal {A}},{\mathcal {R}},{\mathcal {C}})$, the following contingency table ${\textbf{T}}$ obtained by summing all the rows (and columns) belonging to the same cluster together:

$${\textbf{T}} = \begin{pmatrix} 5 &{}\quad 2 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad 10 &{}\quad 0 &{}\quad 1\\ 0 &{}\quad 0 &{}\quad 10 &{}\quad 2\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 10 \end{pmatrix}.$$

The contingency matrix ${\textbf{T}}$ shows that $({\mathcal {R}},{\mathcal {C}})$ is a meaningful co-clustering solution, with well defined block co-clusters. The values of the two association measures for this co-clustering are $\tau _{R|C}({\mathcal {R}},{\mathcal {C}}) = 0.630$ and $\tau _{C|R}({\mathcal {R}},{\mathcal {C}}) = 0.625$. Now, consider a different co-clustering solution $({\mathcal {R}}',{\mathcal {C}}')$, with ${\mathcal {R}}'=\{\{r_1,r_5,r_{10}\},\{r_2,r_6,r_9\},\{r_3,r_8\},\{r_4,r_7\}\}$ and ${\mathcal {C}}'=\{\{c_1,c_8\},\{c_3,c_7\},\{c_2,c_6\},\{c_4,c_5\}\}$

$${\textbf{T}}' = \begin{pmatrix} 6 &{}\quad 0 &{}\quad 0 &{}\quad 8\\ 3 &{}\quad 7 &{}\quad 0 &{}\quad 4\\ 1 &{}\quad 1 &{}\quad 5 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 1 &{}\quad 5 \end{pmatrix}.$$

In this case, the contingency matrix ${\textbf{T}}'$ exhibits a meaningless co-clustering structure, with less crisp block co-clusters. This is confirmed by the values of the two association measures: in fact, $\tau _{R|C}({\mathcal {R}}',{\mathcal {C}}') = 0.300$ and $\tau _{C|R}({\mathcal {R}}',{\mathcal {C}}') = 0.270$.

The algorithm $\tau$CC belongs to the family of co-clustering algorithms that iteratively maximize a measure of the quality of the co-clustering (the most famous example of is the Information Theoretic Co-Clustering or ITCC (Dhillon et al., 2003). However, $\tau$CC has three peculiarities that distinguish it from the other methods.

• 1. Instead of maximizing a unique objective function, $\tau$CC’s goal is to maximize two objective functions at the same time, $\tau _{R|C}$ and $\tau _{C|R}$. Thus, co-clustering is formulated as a multi-objective optimization problem.

• 2. A stochastic local search approach is used to solve the maximization problem: at each iteration, a row is randomly selected and is moved from its original cluster to the row cluster that maximizes $\tau _{R|C}$. Then, a column is randomly selected and moved to the column cluster that maximizes $\tau _{C|R}$. Instead, the other methods use a “k-means like” optimization strategy that constructs prototypes for each cluster and, at each iteration, assigns each object to the closest prototype, using some ad hoc function to measure the closeness, opportunely designed to increase the objective function.

• 3. Unlike other objective functions, $\tau$ exhibits no monotonicity w.r.t. the number of clusters. This fact enables the algorithm $\tau$CC to compare co-clustering solutions with a different number of clusters and choose the best one: as a consequence, $\tau$CC is one of the few co-clustering algorithms able to identify the final number of clusters on its own. Instead, the magnitude of other objective functions, such as the Loss of Mutual Information adopted by ITCC, depends on the number of clusters and thus the other methods only consider co-clustering solutions with a specified number of clusters on each mode.

Despite the desirable property (3) and the proven effectiveness of the algorithm, the applicability of $\tau$CC is limited by the fact that its current optimization strategy requires an elevated number of iterations, resulting in execution times that are sensibly higher than those of the other co-clustering methods. Furthermore, in some cases, the algorithm fails in identifying a meaningful number of co-clusters, ending in a solution with a very small number of very large co-clusters unable to faithfully describe the data. In the next sections, we will present a slightly different objective function and a new optimization strategy for the algorithm $\tau$CC which, similarly to that of ITCC, is based on the assignment of the rows and columns to the most similar prototype.

In a recent work (Battaglia and Pensa, 2023), we have extended the association measure $\tau$ to handle a generic number m of categorical random variables. For instance, it is possible to measure the association among three random variables X, Y and Z as the proportional reduction of the error in predicting one of them knowing the joint distribution of the other two, obtaining three different association measures $\tau _{X|(Y,Z)}, \tau _{Y|(X,Z)}$ and $\tau _{Z|(X,Y)}$. If X, Y, Z denote the random variables representing to the co-clustering problem and $({\mathcal {X}},{\mathcal {Y}},{\mathcal {Z}})$ is a co-clustering of a 3-way tensor ${\mathcal {A}}$, the association measure can be written as

$$\begin{aligned} \tau _{X|(Y,Z)}({\mathcal {X}},{\mathcal {Y}},{\mathcal {Z}}) = \frac{\sum _{i=1}^{|{\mathcal {X}}|}\sum _{j=1}^{|{\mathcal {Y}}|}\sum _{k=1}^{|{\mathcal {Z}}|} \frac{t_{ijk}^2}{t_{\tiny \bullet \tiny \bullet \tiny \bullet }t_{\tiny \bullet jk}} - \sum _{i=1}^{|{\mathcal {X}}|}\frac{t_{i\tiny \bullet \tiny \bullet }^2}{t_{\tiny \bullet \tiny \bullet \tiny \bullet }^2}}{1 - \sum _{i=1}^{|{\mathcal {X}}|}\frac{t_{i\tiny \bullet \tiny \bullet }^2}{t_{\tiny \bullet \tiny \bullet \tiny \bullet }^2}} \end{aligned}$$

(3)

where ${\textbf{T}}=(t_{ijk})$ is the contingency tensor associated to the co-clustering. The tensor co-clustering problem is then formulated as a multi-objective optimization problem of the functions $\tau _{X|(Y,Z)}$, $\tau _{Y|(X,Z)}$ and $\tau _{Z|(X,Y)}$. Analogously to $\tau$CC, the tensor co-clustering algorithm, called $\tau$TCC, uses a stochastic local search approach to solve the maximization problem. Notice that, when $m=2$, i.e., the contingency tensor is a matrix, $\tau$TCC corresponds to $\tau$CC. The advantages and disadvantages of the 2-way version of the algorithms hold for the tensor version as well, but their effect becomes more pronounced as the number of modes of the tensors increases. The algorithm does not require the specification of any parameter, while all existing tensor co-clustering methods require at least the specification of the number of clusters on each mode of the tensor and, very often, other parameters such as the rank of the decomposition. On the other hand, the number of iterations performed by the algorithm and its computational complexity increase with the number of modes, limiting the practical application of the algorithm $\tau$TCC to relatively small tensors with few modes.

4 Fast parameterless co-clustering

In this section, we present a new objective function that leads to an arbitrary number of more meaningful co-clusters and allows for a more efficient and faster optimization strategy leveraging a prototype-based iterative algorithm whose theoretical convergence can be proved formally.

4.1 An alternative to Goodman and Kruskal’s $\tau$

Let X and Y be two categorical random variables. The function $\tau _{X|Y}$ (Eq. 1) depends on two quantities: the error in predicting X, denoted by $e_X$, and the expected error in predicting X when Y is known, denoted by ${\mathbb {E}}[e_{X|Y}]$, both laying in [0, 1]. The association between X and Y is strong if the knowledge of Y drastically reduces the error $e_X$. Notice that $e_X$ does not depend on Y and its presence in the definition of $\tau$ serves as a starting point from which to calculate the improvement in the prediction due to the knowledge of Y. Thus, intuitively, the most important component in $\tau _{X|Y}$ should be ${\mathbb {E}}[e_{X|Y}]$. However, since $\tau _{X|Y}$ measures the proportional reduction of the error, $e_X$ contributes to both the numerator and denominator of (1). Consequently, it has a great impact on the value of $\tau _{X|Y}$. As an example, imagine that X is a random variable with a very small $e_X$. Since, by definition, ${\mathbb {E}}[e_{X|Y}]<e_X$, then the expected error, when Y is known, will be very small as well, i.e., ${\mathbb {E}}[e_{X|Y}]\approx e_X$. However, although the knowledge about the distribution of Y hardly improves the prediction of X, the value of the association measure is high, due to the small denominator of $\tau _{X|Y}$. Such a situation happens also when $\tau$, formulated as in Eq. 2, is employed to measure the quality of a co-clustering $({\mathcal {R}}, {\mathcal {C}})$: in particular, $e_R$ is small when the partition ${\mathcal {R}}$ is composed by a unique cluster, or by a huge cluster and few very small extra-clusters. In fact, the function $e_R({\mathcal {R}}) = 1 - \sum _{r =1}^{|{\mathcal {R}}|}t_{r\cdot }^2$ has a maximum when $|{\mathcal {R}}|=1$. This fact may lead the algorithm $\tau$CC towards a meaningless clustering solution with (almost) all the rows grouped together into a unique cluster. A simple solution to this problem is to leave out the denominator of $\tau$ and only consider, as objective function of the co-clustering algorithm, the numerator. From now on, we will call this simplified objective function ${\hat{\tau }}_{R|C}$, defined as

$$\begin{aligned} {\hat{\tau }}_{R|C}=\sum _{r=1}^{|{\mathcal {R}}|}\sum _{c=1}^{|{\mathcal {C}}|} \frac{t_{rc}^2}{t_{\tiny \bullet \tiny \bullet }t_{\tiny \bullet c}} - \sum _{r=1}^{|{\mathcal {R}}|}\frac{t_{r\tiny \bullet }^2}{t_{\tiny \bullet \tiny \bullet }^2}. \end{aligned}$$

(4)

Fig. 1

Comparison between $\tau _{R|C}$ and ${\hat{\tau }}_{R|C}$. The two measures are considered as functions of variables $e_R$ and ${\mathbb {E}}[e_{R|C}]$

To better investigate the differences in the behavior of $\tau _{R|C}$ and ${\hat{\tau }}_{R|C}$, the two measures are plotted in Fig. 1 as functions of the two variables $e_R$ and ${\mathbb {E}}[e_{R|C}]$. For the moment, R and C are just two families of generic categorical random variables. As expected, $\tau _{R|C}$ is very high for almost all values of $e_R$, when combined to low values of ${\mathbb {E}}[e_{R|C}]$. In the lower left corner of the two heatmaps are instances of the family R with low prediction error $e_R$. Hence, when R is the family of random variables associated to each possible clustering solution, in the lower left corner there are the clustering solutions with very few clusters: according to association measure $\tau$, these clustering solutions are optimal and the algorithm $\tau$CC could end in one of these solutions. Instead, ${\hat{\tau }}_{X|Y}$ rewards more the pair of solutions (R, C) with $e_R$ much bigger than ${\mathbb {E}}[e_{R|C}]$. Since ${\mathbb {E}}[e_{R|C}] = 1 - \sum _{rc}\frac{t_{rc}^2}{t_{\cdot c}}$ is minimum when the contingency matrix of the co-clustering is diagonal, the newly proposed objective function ${\hat{\tau }}_{X|Y}$ is more suitable when we want to obtain co-clustering solutions with approximately the same number of clusters on rows and columns and block diagonal co-clusters. The following example will show the differences between the two functions when used to evaluate co-clustering.

Example 2

Let us consider the customers $\times$ products matrix ${\mathcal {A}}$, first introduced in Example 1, together with the first related co-clustering solution represented by the contingency matrix ${\textbf{T}}$. The values of the two association measures for this co-clustering are $\tau _{R|C}({\mathcal {R}},{\mathcal {C}}) = 0.630$ and ${\hat{\tau }}_{R|C}({\mathcal {R}},{\mathcal {C}}) = 0.466$. Consider now a different co-clustering solution $({\mathcal {R}}'',{\mathcal {C}})$ on ${\mathcal {A}}$, where ${\mathcal {R}}''=\{\{r_1,r_2,r_4\},\{r_3,r_5,r_6,r_7,r_8,r_9,r_{10}\}\}$ (notice that the partition on columns is the same as in the previous solution), with contingency matrix

$${\textbf{T}}'' = \begin{pmatrix} 6 &{}\quad 1 &{} \quad 0 &{}\quad 0 \\ 0 &{}\quad 12 &{}\quad 10 &{}\quad 13 \end{pmatrix}.$$

Here we have $\tau _{R|C}({\mathcal {R}}'',{\mathcal {C}}) = 0.842$ and ${\hat{\tau }}_{R|C}({\mathcal {R}}'',{\mathcal {C}}) = 0.234$. Therefore, according to measure $\tau$ the second partition is better than the first one, while ${\hat{\tau }}$ assigns an higher score to the first solution. Clearly, without any other knowledge about the dataset, it is not possible to say whether a solution is better than the other. However, it is evident that the first solution provides a more detailed summary of the data and it can also be used to interpret the column clustering more accurately. Instead, the second solution contains a large row cluster of customers that purchase many different products, described by many different column clusters.

The new association measure ${\hat{\tau }}_{R|C}$ has another advantage: the simplification of the original objective function allows us to use a more efficient optimization schema in the co-clustering algorithm, as we will show in the next section.

4.2 Prototype-based $\tau$CC

Let ${\mathcal {A}}=(a_{ij})\in {\mathbb {R}}^{n\times m}_+$ be a non-negative data matrix, with n rows and m columns, and ${\textbf{T}}$ the contingency matrix associated to the co-clustering (${\mathcal {R}}, {\mathcal {C}}$), where ${\mathcal {R}} = ({\mathcal {R}}_1, \dots , {\mathcal {R}}_k)$ and ${\mathcal {C}} = ({\mathcal {C}}_1, \dots , {\mathcal {C}}_l)$, with $1<k\le n$ and $1<l\le m$. The generic element of matrix ${\textbf{T}}$ is $t_{rc} = \sum _{i \in {\mathcal {R}}_r}\sum _{j \in {\mathcal {C}}_c} a_{ij}$, for $r=1,\dots , k$ and $c=1, \dots , l$. We will denote the sum of all the elements of ${\mathcal {A}}$ with A and the sum of all the elements of ${\textbf{T}}$ with T. It follows that $A = T$. Let us define the following quantities:

$$\begin{aligned} p_{ij}= \frac{a_{ij}}{A} \quad p_{i\cdot } = \sum _{j=1}^{m}\frac{a_{ij}}{A} \quad p_{\cdot j } = \sum _{i=1}^{n}\frac{a_{ij}}{A} \end{aligned}$$

(5)

$$\begin{aligned} q_{rc}&= \frac{t_{rc}}{T} = \frac{t_{rc}}{A} = \sum _{i \in {\mathcal {R}}_r}\sum _{j \in {\mathcal {C}}_c} \frac{a_{ij}}{A} = \sum _{i \in {\mathcal {R}}_r}\sum _{j \in {\mathcal {C}}_c} p_{ij} \end{aligned}$$

(6)

$$\begin{aligned} q_{r\cdot }&= \sum _{c=1}^{l}\frac{t_{rc}}{T} = \sum _{c=1}^{l}\frac{t_{rc}}{A} = \sum _{c=1}^{l}\sum _{i \in {\mathcal {R}}_r}\sum _{j \in {\mathcal {C}}_c} \frac{a_{ij}}{A} = \sum _{i \in {\mathcal {R}}_r} p_{i\cdot } \end{aligned}$$

(7)

$$\begin{aligned} q_{\cdot c }&= \sum _{r=1}^{k}\frac{t_{rc}}{T} = \sum _{r=1}^{k}\frac{t_{rc}}{A} = \sum _{r=1}^{k}\sum _{i \in {\mathcal {R}}_r}\sum _{j \in {\mathcal {C}}_c} \frac{a_{ij}}{A} = \sum _{j \in {\mathcal {C}}_c} p_{\cdot j} \end{aligned}$$

(8)

where $i=1,\dots ,n, j=1,\dots , m, r=1, \dots , k$ and $l=1,\dots ,l$. Intuitively, $p_{ij}$ can be interpreted as the probability of observing $a_{ij}$, while $q_{rc}$ is the probability of observing a generic co-cluster $({\mathcal {R}}_r,{\mathcal {C}}_c)$. Consequently, $p_{i\cdot }$ and $p_{\cdot j }$ are, respectively, the marginal probabilities of the object represented by the ith row and of the item represented by the jth column of ${\mathcal {A}}$. Finally, $q_{r\cdot }$ and $q_{\cdot c }$ are, respectively, the probability that a generic row is in cluster ${\mathcal {R}}_r$ and the probability that a generic column falls in cluster ${\mathcal {C}}_c$.

Hence, both $p = (p_{ij})$ and $q = (q_{rc})$ are probability distributions and $(p_{\cdot j}), (p_{i \cdot }), (q_{\cdot c}), (q_{r \cdot })$ are their marginal distributions. However, while p only depends on the original data matrix ${\mathcal {A}}$, q also depends on the partitions ${\mathcal {R}}$ and ${\mathcal {C}}$ on the rows and columns of ${\mathcal {A}}$, respectively. Let us consider the partition ${\mathcal {C}}$ fixed and suppose we want to identify the partition ${\mathcal {R}}$ that maximizes ${\hat{\tau }}_{R|C}(\cdot , {\mathcal {C}})$. We will use the following notation:

$$\begin{aligned} p_{ic} = \sum _{j \in {\mathcal {C}}_c}p_{ij} \quad p_{\cdot c} = \sum _{j \in {\mathcal {C}}_c}p_{\cdot j} = q_{\cdot c} \end{aligned}$$

(9)

for each $i=1, \dots , n$ and $c=1, \dots , l$. The objective function can be written as follows:

$$\begin{aligned} {\hat{\tau }}_{R|C}({\mathcal {R}},{\mathcal {C}})&= \sum _{r=1}^{k}\sum _{c=1}^{l} \frac{q_{rc}^2}{q_{\cdot c}} - \sum _{r=1}^{k} q^2_{r\cdot } \nonumber \\&= \sum _{r=1}^{k}\sum _{c=1}^{l}\left( \sum _{i \in {\mathcal {R}}_r} \frac{p_{ic}}{p_{\cdot c}}\right) q_{rc} - \sum _{r=1}^{k} \left( \sum _{i \in {\mathcal {R}}_r} p_{i\cdot }\right) q_{r\cdot } \nonumber \\&= \sum _{c=1}^{l}\sum _{i =1}^{n} \frac{p_{ic}}{p_{\cdot c}} q_{{\mathcal {R}}(i)c} - \sum _{i = 1}^{n} p_{i\cdot } q_{{\mathcal {R}}(i)\cdot } \end{aligned}$$

(10)

where ${\mathcal {R}}(i)$ denotes the cluster assignment of the ith row in the partition ${\mathcal {R}}$.

Here we propose an iterative strategy to find the best partition ${\mathcal {R}}$, when ${\mathcal {C}}$ is fixed. Let us suppose that, at iteration t, a partition ${\mathcal {R}}^{(t)}$ has been selected and let $q^{(t)}$ be its associated distribution. The objective function ${\hat{\tau }}_{R|C}(\cdot ,{\mathcal {C}})$ computed for this particular partition takes value

$$\begin{aligned} {\hat{\tau }}_{R|C}({\mathcal {R}}^{(t)},{\mathcal {C}}) = \sum _{i =1}^{n}\left( \sum _{c=1}^{l} \frac{p_{ic}}{p_{\cdot c}} q^{(t)}_{{\mathcal {R}}^{(t)}(i)c} - p_{i\cdot } q^{(t)}_{{\mathcal {R}}^{(t)}(i)\cdot }\right) \end{aligned}$$

(11)

We can interpret each $q^{(t)}_r$ as a prototype of the rth cluster and define a function

$$\begin{aligned} sim(p_i, q^{(t)}_r) = \sum _{c=1}^{l} \frac{p_{ic}}{p_{\cdot c}} q^{(t)}_{rc} - p_{i\cdot } q^{(t)}_{r\cdot } \end{aligned}$$

(12)

that measures the similarity between each “point” $p_i$ and each cluster prototype $q^{(t)}_r$.

The objective function can now be written as

$$\begin{aligned} {\hat{\tau }}_{R|C}({\mathcal {R}}^{(t)},{\mathcal {C}}) = \sum _{i=1}^n sim\left( p_i,q^{(t)}_{{\mathcal {R}}^{(t)}(i)} \right) \end{aligned}$$

(13)

For a fixed row i, if there is a cluster $r \ne {\mathcal {R}}^{(t)}(i)$ such that $sim(p_i, q^{(t)}_r) > sim(p_i, q^{(t)}_{{\mathcal {R}}^{(t)}(i)})$, this means that the ith object is more similar to the prototype of cluster r than to the prototype of the cluster it currently belongs to, and then it should be moved from its original cluster ${\mathcal {R}}^{(t)}(i)$ to cluster r. Thus, we can adopt the following iterative procedure, to identify the best partition ${\mathcal {R}}$: at each iteration, we compute the cluster prototypes $q^{(t)}$ related to the current partition ${\mathcal {R}}^{(t)}$ and then assign each object i to the cluster r that maximizes $sim(p_i, q^{(t)}_r)$, obtaining a new partition ${\mathcal {R}}^{(t+1)}$. In case of tie, the object is moved to the cluster r with maximum $q^{(t)}_{r\cdot }$, among those that maximize $sim(p_i, q^{(t)}_r)$. In order to decide to which cluster object i should be moved, the objective function $sim(p_i, q^{(t)}_r)$ is computed for each cluster $r \in {\mathcal {R}}^{(t)}$. At each iteration, the algorithm is able to reduce the number of clusters: if all the objects of a cluster r are assigned to other pre-existing clusters, then the number of clusters will decrease by one. Otherwise, if all the objects are moved from one cluster to another but no cluster remains empty, the number of clusters remains the same. It is obvious that the final number of clusters will be lower or equal to the number of clusters contained in the initial partition. Algorithm 1 provides a sketch of the optimization strategy just described.

Algorithm 1

$\tau \text {CC-}rows({\mathcal {A}}, {\mathcal {C}}, {\mathcal {R}}^{(0)})$

The same procedure can be applied to find the partition ${\mathcal {C}}$ of the columns when ${\mathcal {R}}$ is known, by optimizing the objective function ${\hat{\tau }}_{C|R}({\mathcal {R}},\cdot )$. We will call the analogous algorithm for column clustering $\tau$CC-columns $({\mathcal {A}},{\mathcal {R}}, {\mathcal {C}}^{(0)})$

Theorem 1

The algorithm $\tau$CC-rows (respectively, the algorithm $\tau$CC-columns) increases the objective function ${\hat{\tau }}_{R|C}(\cdot , {\mathcal {C}})$ (respectively, ${\hat{\tau }}_{C|R}({\mathcal {R}}, \cdot )$) at each iteration and terminates in a finite number of iterations.

The proof of the theorem is given in “Appendix A”. It exploits the fact that sim is a positive semi-definite bilinear form to demonstrate that ${\hat{\tau }}_{R|C}$ monotonically increases.

The following toy example illustrates how a single iteration of the algorithm $\tau$CC-rows works.

Example 3

We want to use Algorithm 1 to cluster the customers of a shop according to their purchase habits. Let

$${\mathcal {A}} = \begin{pmatrix} 2 &{}\quad 3 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 2 &{}\quad 2 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 2 &{}\quad 2 &{}\quad 3\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 5 &{}\quad 2 \end{pmatrix}$$

be the input matrix, whose rows represent the customers and whose columns are the products. Each entry $a_{ij}$ of ${\mathcal {A}}$ is the number of items of product j bought by customer i. Imagine that the column clustering ${\mathcal {C}} = \left\{ \{0,1,2\},\{3,4,5\}\right\}$ is known (for instance, the first three products are foodstuffs, while the remaining three are clothing). Suppose that the row clustering resulting from the last iteration of the algorithm is ${\mathcal {R}}^{(t)} = \left\{ \{0\}, \{1\}, \{2,3\}\right\}$. The probability distribution ${\textbf{P}}$ associated to the data matrix given the column clustering, and the probability distribution ${\textbf{Q}}^{(t)}$ of the co-clustering $({\mathcal {R}}^{(t)}, {\mathcal {C}})$ are respectively

$$\begin{aligned} {\textbf{P}}&= \begin{pmatrix} 0.23 &{}\quad 0.00\\ 0.15 &{}\quad 0.04\\ 0.00 &{}\quad 0.27\\ 0.04 &{}\quad 0.27 \end{pmatrix}&{\textbf{Q}}^{(t)}&= \begin{pmatrix} 0.23 &{}\quad 0.00\\ 0.15 &{}\quad 0.04\\ 0.04 &{}\quad 0.54 \end{pmatrix} \end{aligned}$$

Algorithm 1 assigns each row of ${\textbf{P}}$ to the cluster represented by the most similar row of ${\textbf{Q}}^{(t)}$, according to the similarity measure sim. Since the similarity between each row and each prototype is

all the rows remain in their original cluster, except $p_1$ that is moved in the first cluster. Thus, the resulting row clustering will be ${\mathcal {R}}^{(t+1)} = \left\{ \{0,1\}, \{2,3\}\right\}$, corresponding to the probability distribution

$${\textbf{Q}}^{(t+1)} = \begin{pmatrix} 0.38 &{}\quad 0.04\\ 0.04 &{}\quad 0.54 \end{pmatrix}.$$

Matrix ${\textbf{Q}}^{(t+1)}$ is useful to interpret the results of the co-clustering: the customers in the first cluster are those that mainly buy foodstuffs, while the second cluster contains customers that usually buy clothes.

So far, two different algorithms to optimize the row partition ${\mathcal {R}}$, given the column partition ${\mathcal {C}}$ and, viceversa, the column partition ${\mathcal {C}}$, given the row partition ${\mathcal {R}}$, have been presented. Theorem 1 proves that each one of the two algorithms converges to a local optimum of its respective objective function (${\hat{\tau }}_{R|C}$ or ${\hat{\tau }}_{C|R}$). A co-clustering algorithm that finds the best partitions ${\mathcal {R}}$ and ${\mathcal {C}}$ simultaneously, can be obtained by the iterative repetition of the two algorithms.

Algorithm 2

PB-$\tau$CC$({\mathcal {A}}, t_{max})$

The overall algorithm, named Prototype-Based $\tau$CC or PB-$\tau$CC, is summarized in Algorithm 2. The row and column clustering ${\mathcal {R}}^{(0)}$ and ${\mathcal {C}}^{(0)}$ can be initialized in any possible way. However, since Algorithm 2 can only decrease the number of clusters, an initial co-clustering with a number of clusters that are safely higher than the expected/desired number of clusters is preferable.

The initialization strategy we use consists in the creation of $k_0$ initial row cluster prototypes and $k_0$ column cluster prototypes. These initial synthetic prototypes are created as follows. The columns are randomly split in $k_0$ equal-width clusters. The initial row prototypes are the rows of the identity matrix $I \in {\mathbb {R}}^{k_0\times k_0}$. Then each row is assigned to the most similar prototype using the usual similarity measure (Eq. 12). If $sim(p_i, q) <0$ for any cluster prototype q, then the row $p_i$ is assigned to a new empty cluster, because the prototype of the empty cluster is 0 and $sim(p_i,0)=0>sim(p_i, q)$, for any cluster prototype q. This method, however, requires the specification of the initial number of clusters on the two modes of the matrix. Although this may seem contrary to the spirit of the algorithm, whose strong point is to be parameterless, it turns out that the choice of parameter $k_0$ does not affect the result to a great extent. This is due to the fact that the initialization method can modify the number of clusters and add a new cluster when the prototypes of the already existing clusters are not able to describe an object of the data matrix. For a more detailed analysis of this topic, the reader is referred to Sect. 6.3.

4.3 Computational complexity of PB-$\tau$CC

Here we compute the computational complexity of the new algorithm PB-$\tau$CC and compare it with that of $\tau$CC, its direct competitor.

Let $({\mathcal {R}}^{(t)},{\mathcal {C}}^{(t)})$ be the current co-clustering returned by PB-$\tau$CC at iteration t. Consider a row i of ${\mathcal {A}}$. In order to decide whether i should be moved to another cluster or not, and which cluster it should be moved to, PB-$\tau$CC computes $sim(p_i,q^{(t)}_{r})=\sum _{c=1}^{l_t} \frac{p_{ic}}{p_{\tiny \bullet c}} q^{(t)}_{rc} - p_{i\tiny \bullet }q^{(t)}_{r\tiny \bullet }$ in ${\mathcal {O}}(l_t)$, for all clusters $r\in {\mathcal {R}}$. Then the re-assignment of i is done in ${\mathcal {O}}(k_tl_t)$, where $k_t$ is the current number of clusters on the rows and $l_t$ is the current number of clusters on the columns. Similarly, the re-assignment of a column j is done in ${\mathcal {O}}(k_tl_t)$. Since the number of clusters does not increase from an iteration to the following one, $k_t \le k_0$ and $l_t \le l_0$, for each $t\ge 0$. In each iteration of the rows the re-assignment step is repeated n times (once per row), while the columns assignment step is repeated m times (once per column). Therefore, if ${\mathcal {I}}_R$ is the total number of iterations on rows and ${\mathcal {I}}_C$ is the total number of iterations on columns, the overall complexity of PB-$\tau$CC is in ${\mathcal {O}}({\mathcal {I}}_Rnk_0l_0 + {\mathcal {I}}_C mk_0l_0)={\mathcal {O}}\left( {\mathcal {I}}\max (n,m)k_0l_0\right)$, where ${\mathcal {I}}={\mathcal {I}}_R+{\mathcal {I}}_C$ is the total number of iterations. The initialization of the row clusters takes ${\mathcal {O}}(nmk_0)$ while the initialization of the column clusters takes ${\mathcal {O}}(nml_0)$. Thus the initialization phase has complexity in ${\mathcal {O}}(nm\max (k_0,l_0))$.

Instead, the direct competitor, $\tau$CC, as reported by Battaglia and Pensa (2023), has complexity in ${\mathcal {O}}({\mathcal {I}}nm)$, where ${\mathcal {I}}$ is the total number of iterations (here an iteration is the move of a single object, a row or a column). To allow for a fair comparison between the two algorithms, we should consider that the number ${\mathcal {I}}$ in PB-$\tau$CC is in general significantly lower than the number of iterations ${\mathcal {I}}$ in $\tau$CC, because in $\tau$CC ${\mathcal {I}}$ is the total number of moves of a single object (row or column) that have been done by the algorithm, while the number of moves of a single object in PB-$\tau$CC is ${\mathcal {M}} = {\mathcal {I}}_R\cdot n + {\mathcal {I}}_C \cdot m$, with ${\mathcal {I}}_R + {\mathcal {I}}_C = {\mathcal {I}}$. For instance, suppose that the two algorithms make the same number ${\mathcal {M}}$ of total moves of single objects. Then PB-$\tau$CC has complexity in ${\mathcal {O}}({\mathcal {I}}_Rnk_0l_0 + {\mathcal {I}}_C mk_0l_0) \simeq {\mathcal {O}}({\mathcal {M}}k_0l_0)$, while $\tau$CC has complexity in ${\mathcal {O}}({\mathcal {M}}nm)$.

In principle, if PB-$\tau$CC is initialized with the discrete partitions (where each object forms a singleton cluster), i.e. $k_0 = n$ and $l_0=m$, the two algorithms have the same complexity ${\mathcal {O}}({\mathcal {M}}nm)$. However, in practice, function sim (Eq. 12) is much faster to compute than the objective function $\Delta \tau$ used by $\tau$CC to decide in which a cluster $q_r$ a row $p_i$ currently belonging to cluster $q_b$ should be relocated:

$$\begin{aligned} \Delta \tau (p_i,q_b,q_r) = \frac{\Gamma \cdot \left( p_{i\tiny \bullet }(p_{i\tiny \bullet } + q_{r\tiny \bullet }-q_{b\tiny \bullet })\right) - \Omega \left( \sum _{c=1}^{l}\frac{p_{ic}}{q_{\tiny \bullet c}}(p_{ic}+q_{rc}-q_{bc})\right) }{\Omega ^2 - \Omega \cdot \left( 2p_{i\tiny \bullet }(p_{i\tiny \bullet } + q_{r\tiny \bullet }-q_{b\tiny \bullet })\right) } \end{aligned}$$

where $\Gamma = 1 - \sum _{ij}\frac{p_{ij}^2}{p_{\tiny \bullet j}}$ and $\Omega = 1 - \sum _i p_{i\tiny \bullet }^2$. This simplification in the objective function makes our algorithm remarkably more efficient than the other one (as we will show experimentally in Sect. 6).

5 Extension to tensor co-clustering

In this section, we present a higher-order version of algorithm PB-$\tau$CC. For sake of clarity, here we introduce a co-clustering algorithm for 3-way tensors, but the same procedure leads to the creation of a co-clustering for tensors with a generic number m of modes.

5.1 Prototype-based tensor co-clustering

Let ${\mathcal {A}}$ be a tensor with three modes and dimensions $(n_X,n_Y,n_Z)$. Suppose that the partition ${\mathcal {Y}}$ and ${\mathcal {Z}}$ on the second and third modes are fixed and we want to find the best partition ${\mathcal {X}}$ for the first mode. The objective function can be written as

$$ {\hat{\tau }}_{X|(Y,Z)}({\mathcal {X}},{\mathcal {Y}},{\mathcal {Z}}) = \sum _{i =1}^{n_X}\left( \sum _{u=1}^{|{\mathcal {Y}}|}\sum _{v=1}^{|{\mathcal {Z}}|} \frac{p_{iuv}}{p_{\tiny \bullet uv}} q_{{\mathcal {X}}(i)uv} - p_{i\tiny \bullet \tiny \bullet } q_{{\mathcal {X}}(i)\tiny \bullet \tiny \bullet }\right) $$

where p and q are the probability distributions associated, respectively, to the original data ${\mathcal {A}}$ and to the co-clustering $({\mathcal {X}},{\mathcal {Y}},{\mathcal {Z}})$. They can be computed using the 3-way analogous of Eqs. (5)–(9). We can consider each slice $q_w$ on the first mode of q as a cluster prototype and define a similarity measure analogous to (12) to quantify the similarity between a data point $p_i$ and a cluster prototype $q_w$:

$$\begin{aligned} sim(p_i, q_w) = \sum _{u=1}^{|{\mathcal {Y}}|}\sum _{v=1}^{|{\mathcal {Z}}|} \frac{p_{iuv}}{p_{\tiny \bullet uv}} q_{wuv} - p_{i\tiny \bullet \tiny \bullet } q_{w\tiny \bullet \tiny \bullet } \end{aligned}$$

(14)

Finally, we use this similarity measure to evaluate, at each iteration, the cluster to which each object should be moved. As for the 2-way case (Theorem 1), the iterative repetition of this assignment step monotonically increases the objective function ${\hat{\tau }}_{X|(Y,Z)}$. Once the best partition on the first mode has been selected and no further moves are possible, we can move to the next mode and repeat the entire process. The procedure just described, which we will call Prototype-Based $\tau$TCC or PB-$\tau$TCC, is the tensor generalization of Algorithm 2.

Algorithm 3

PB-$\tau$TCC$({\mathcal {A}}, t_{max})$

Algorithm 3 gives a sketch of PB-$\tau$TCC for generic m-way tensors. Here, ${\mathcal {P}}^1, \dots , {\mathcal {P}}^m$ are the m partitions (one for each node). Hence, in the 3-way case, $({\mathcal {X}},{\mathcal {Y}},{\mathcal {Z}})$ corresponds to $({\mathcal {P}}^1, {\mathcal {P}}^2, {\mathcal {P}}^3)$. Algorithm PB-$\tau$TCC only looks at the objective function related to the mode on which the re-assignment is performed: for instance, in a 3-way tensor, when moving rows only the objective function ${\hat{\tau }}_{X|(Y,Z)}$ is optimized, while ${\hat{\tau }}_{Y|(X,Z)}$ and ${\hat{\tau }}_{Z|(X,Y)}$ are not considered. As for the 2-way case, the partitions on all the modes of the tensor can be initialized in any possible way. However, since the algorithm can only decrease the number of clusters, initial co-clustering configurations with a number of clusters that are safely higher than the number of expected/desired clusters are preferable.

Although the initialization strategy proposed for matrix co-clustering can be used for tensor co-clustering too, the probability of selecting poor initial prototypes would increase with the number of modes (and with the sparsity) of the tensor. Hence, for tensor co-clustering, we adopt a strategy inspired by the classical initialization of k-means clustering and consisting in the random extraction of $k_0$, $l_0$ and $h_0$ elements from each of the three modes of ${\mathcal {A}}$ (in the case of 3-way tensors). These randomly selected elements are considered as prototypes of $k_0$, $l_0$, $h_0$ clusters in each mode, and each elements of tensor ${\mathcal {A}}$ is assigned to the most similar prototype using the usual similarity measure (12). If $sim(p_i, q) <0$ for any cluster prototype q, then the row (column) $p_i$ is assigned to a new empty cluster, since the prototype of the empty cluster is 0 and $sim(p_i,0)=0>sim(p_i, q)$, for any cluster prototype q. Notice that, in the initialization phase the case $sim(p_i,q)<0$ for all q is possible: although, the proof of Theorem 1 (see “Appendix A”) is based on the assumption that the sum of all the prototypes coincides with the sum of all the rows in the matrix, this is assumption does not hold in this case.

5.2 Computational complexity of PB-$\tau$TCC

For the tensor co-clustering algorithm PB-$\tau$TCC, the computational complexity can be derived reasoning as in the 2-way case (see Sect. 4.3). For the sake of simplicity, here we report the overall complexity for a 3-way input tensor, but the computation can be easily extended to the generic n-way case. We recall that PB-$\tau$TCC (see Algorithm 3) works similarly as PB-$\tau$CC, i.e., it moves one item in one partition while keeping the other two partitions fixed. Hence, by generalizing the reasoning done in Sect. 4.3 to the 3-way case, we can easily conclude that the overall complexity of PB-$\tau$TCC is in ${\mathcal {O}}(({\mathcal {I}}_Xn_X + {\mathcal {I}}_Yn_Y + {\mathcal {I}}_Zn_Z)\cdot k_0l_0h_0 ) \simeq {\mathcal {O}}({\mathcal {I}}\max (n_X,n_Y,n_Z)k_0l_0h_0)$, where ${\mathcal {I}} = {\mathcal {I}}_X +{\mathcal {I}}_Y + {\mathcal {I}}_Z$ is the total number of iterations of the algorithm and $k_0,l_0$ and $h_0$ are the number of clusters of the initial partition on, respectively, the first, second and third mode of the tensor. According to Battaglia and Pensa (2023), $\tau$TCC (the direct competitor of our algorithm) has complexity in ${\mathcal {O}}({\mathcal {I}}n_X n_Y n_Z)$. As for the 2-way case, it is worth noting that the number of iterations ${\mathcal {I}}$ in PB-$\tau$TCC has a different meaning than in $\tau$TCC, as in $\tau$TCC at each iteration only one object on one mode of the tensor is re-assigned, while in PB-$\tau$TCC all the objects on the same mode are re-assigned at each iteration. Thus, the total number of re-assignments of a single object is ${\mathcal {I}}$ in $\tau$TCC and is ${\mathcal {I}}_X n_X+{\mathcal {I}}_Y n_Y+{\mathcal {I}}_Z n_Z$ in PB-$\tau$TCC. Now, assuming that the two algorithms make the same number ${\mathcal {M}}$ of total moves of single objects, then PB-$\tau$TCC has complexity in ${\mathcal {O}}({\mathcal {M}}k_0l_0h_0)$, while $\tau$CC has complexity in ${\mathcal {O}}({\mathcal {M}}n_Xn_Yn_Z)$. Again, if PB-$\tau$TCC is initialized with the discrete partitions, the two algorithms have the same complexity ${\mathcal {O}}({\mathcal {M}}n_Xn_Yn_Z)$: in fact, the computational complexity of a single re-assignment step is, for both algorithms, ${\mathcal {O}}(k_t l_t h_t)$, where $k_t,l_t$ and $h_t$ are the number of clusters on the three modes at iteration t. However, in practice, the function sim (Eq. 12) is much faster to compute than the objective function $\Delta \tau$ used by $\tau$TCC to decide in which a cluster $q_r$ a row $p_i$ currently belonging to cluster $q_b$ should be relocated. In fact, Battaglia and Pensa (2023) define $\Delta \tau$ as:

$$\begin{aligned} \Delta \tau (p_i,q_b,q_r) = \frac{\Gamma \cdot \left( p_{i\tiny \bullet \tiny \bullet }(p_{i\tiny \bullet \tiny \bullet } + q_{r\tiny \bullet \tiny \bullet }-q_{b\tiny \bullet \tiny \bullet })\right) - \Omega \left( \sum _{u=1}^{|{\mathcal {Y}}|}\sum _{v=1}^{|{\mathcal {Z}}|}\frac{p_{iuv}}{q_{\tiny \bullet uv}}(p_{iuv}+q_{ruv}-q_{buv})\right) }{\Omega ^2 - \Omega \cdot \left( 2p_{i\tiny \bullet \tiny \bullet }(p_{i\tiny \bullet \tiny \bullet } + q_{r\tiny \bullet \tiny \bullet }-q_{b\tiny \bullet \tiny \bullet })\right) } \end{aligned}$$

where $\Gamma = 1 - \sum _{ijk}\frac{p_{ijk}^2}{p_{\tiny \bullet jk}}$ and $\Omega = 1 - \sum _i p_{i\tiny \bullet \tiny \bullet }^2$. In Sect. 6, we will show the practical gain, in terms of computational time, introduced by our new algorithm.

6 Experiments

In this section, we present and discuss some experimental results that show the effectiveness of the proposed method, PB-$\tau$TCC, compared to other state-of the-art algorithms for matrix and tensor co-clustering.

We choose the competitors by considering some fundamental co-clustering algorithms as well as some of the most recent and effective approaches of the state of the art in matrix and tensor co-clustering. The state-of-the-art 2-way co-clustering methods considered here are: ITCC (Dhillon et al., 2003), ModCC (Ailem et al., 2016), PLBM (Govaert and Nadif, 2010), SpectralCC (Dhillon, 2001), SpectralBiC (Kluger et al., 2003), DeepCC (Xu et al., 2019), NMTF (Non-Negative Matrix Tri-Factorization followed by k-means), TLBM (Boutalbi et al., 2022), and $\tau$CC (Ienco et al., 2013). For the first three algorithms, we use the python implementation included in package CoClust.¹ For the two spectral methods we use their Scikit-learn implementations.² For TLBM we use the python library included in package TensorClus³ using the Poisson distribution. For DeepCC and $\tau$CC, we use the code publicly provided by the authors.⁴$^{,}$⁵ Finally, for NMTF we use our own python implementation.

For tensor co-clustering, the baseline methods are: nnCP (non-negative CP decomposition), nnT (non-negative Tucker decomposition), SparseCP (Papalexakis et al., 2013), TBM (Wang and Zeng, 2019), TLBM (Boutalbi et al., 2022), and $\tau$TCC (Battaglia and Pensa, 2023). We use the TensorLy implementations for nnT and nnCP.⁶ For TLBM we use the python implementation provided in package TensorClus⁷ using the Bernoulli distribution, while for the remaining three methods we use the code provided by the authors, in Matlab,⁸ R,⁹ and Python,¹⁰ respectively.

In PB-$\tau$TCC, the number $k_0$ of initial prototypes is always set equal to 30 (a reasonable overestimation of the true number of clusters). All other methods, with the exception of $\tau$CC and $\tau$TCC, require as input the number of clusters on each mode: we set these values equal to the correct number of clusters (on the mode of the tensor for which class labels are given), and set the same number of clusters on the other modes of the tensor as well. In the matrix/tensor factorization-based methods, we tried different ranks and retain the value that gives the best clustering result. Additional parameters, when needed, are set as indicated in the original papers.¹¹

Table 2 Dataset characteristics

Table 3 Results of matrix co-clustering algorithms on real-world data, in terms of NMI computed for the labeled mode (rows)

Table 4 Results of tensor co-clustering algorithms on real-world data, in terms of NMI computed for the labeled mode (rows)

The evaluation of the performances, in terms of quality of the partitioning, is done by applying the co-clustering methods on real world datasets: we run the algorithms on 8 document-words co-occurrences matrices from the CLUTO project.¹² For tensor co-clustering, instead, the datasets are the same 3-way tensors used in (Battaglia and Pensa, 2023) to assess the quality of $\tau$TCC: DBLP,¹³ two tensors extracted from MovieLens¹⁴ and two extracted from Yelp dataset.¹⁵ Table 2 summarizes the main characteristics of these datasets. We assess the quality of the clustering solution through the Normalized Mutual Information, a measure commonly used in the clustering literature. Each algorithm is applied 30 times and the average results in terms of NMI are reported in Table 3. All experiments are executed on a server with 32 Intel Xeon Skylake cores running at 2.1 GHz, 256 GB RAM, and one Tesla T4 GPU.

6.1 Results of PB-$\tau$CC on real-world matrices and tensors

On matrices, our algorithm outperforms all the competing approaches for most datasets (see Table 3). When its NMI is not the highest one, it still ranks among the best algorithms. More in detail, PB-$\tau$CC outperforms its direct parameterless competitor $\tau$CC for all datasets but classic3 and tr41, on which the two algorithms achieve similar results. Interestingly, the number of clusters identified by PB-$\tau$CC is usually more accurate than that of $\tau$CC (see Table 5, where we report the average number of clusters founds and its variation for the main mode, as it is the only one whose we dispose of the ground truth and/or some background knowledge). As expected, the latter tends to aggregate the rows excessively. Instead, PB-$\tau$CC finds a more reasonable number of clusters, although, sometimes, the final number of detected clusters can be slightly smaller than the number of the given classes. Despite this fact, as observed in Table 3, the quality of the clustering remains high. Table 5 also reports the execution time of the two parameterless approaches and clearly shows that our method is sensibly faster than $\tau$CC, by two orders of magnitude, on average. Additionally, in Fig. 2 we report the visualization of the co-clustering (with rows and columns rearranged according to their cluster assignment) computed by PB-$\tau$CC on all datasets.

On tensors, the performances of PB-$\tau$TCC are almost always better than those of the methods requiring the number of clusters as input parameters. However, the accuracy in terms of NMI is slightly lower than that of $\tau$TCC (see Table 4). This is probably a consequence of the fact that PB-$\tau$TCC, in some cases, tends to identify an higher number of smaller clusters. However, the marked difference in the execution times between PB-$\tau$TCC and $\tau$TCC, reported in Table 5, makes the new algorithm much more suitable to handle tensors of high-dimensionality. An example of visualization of the co-clustering computed on DBLP is given in Fig. 3, where we report three representative slices whose rows and columns are rearranged according to the clustering results.

Fig. 2

Visualization of the results of PB-$\tau$CC on matrices. Rows and columns are rearranged according to their cluster membership. The dark points represent nonzeros in the original matrix

Fig. 3

Visualization of the results of PB-$\tau$TCC on DBLP for three slices. Rows and columns are rearranged according to their cluster membership. The dark points represent nonzeros in the original matrix

Table 5 Execution time (in seconds) of $\tau$CC and PB-$\tau$CC and median number of identified clusters ± IQR (interquartile range)

6.2 Execution time on synthetic data

To better investigate the difference in the execution times of the various methods, we run the different algorithms on synthetic datasets of controlled size. We construct binary matrices with three embedded block co-clusters. For matrix co-clustering, we let the shape of the matrix vary from $100\times 100$ to $1000 \times 1000$ by increasing the number of rows and columns. Figure 4a shows the performances expressed in seconds for this experiment. Instead, Fig. 4b shows the results of a similar experiment conducted on 3-way tensors: here the shape of the tensors varies from $100 \times 100 \times 10$ to $1000 \times 1000 \times 10$. In all these datasets, 20% of the matrix/tensor entries are randomly selected and their binary value is swapped (from 0 to 1, and viceversa).

The results on matrices show that, as expected, PB-$\tau$CC is significantly faster than $\tau$CC, but slower than other competitors that requires the number of clusters as input parameter (ITCC, CCMod and SpecCC). Not surprisingly, algorithm DeepCC is the slowest algorithm among the ones selected for our experiments. Instead, when 3-way tensor co-clustering is considered (Fig. 4b), PB-$\tau$TCC outperforms by far all the other competing approaches in terms of execution time.

Fig. 4

Average execution times on matrices (a) and 3-way tensors (b), varying the shape of the dataset

Fig. 5

Average execution times on n-way tensors, stating with a $100\times 100\times 10$ tensor and adding a mode of dimension 10 (a) or 100 (b) each time

Finally, we also investigate the impact of the number of modes on the execution times. We start with a 3-way tensor with shape $100 \times 100 \times 10$ and we add a new mode of dimension 10 (Fig. 5a) or of dimension 100 (Fig. 5b) at each time. In these experiments, we do not include algorithms SparseCP, TBM and TLBM, because the available implementations only handle 3-way tensors. The two plots show that PB-$\tau$TCC is the fastest algorithm, among the ones considered in this study; however, the difference in the execution times between our approach and the competing methods (nnT in particular), slightly decreases as the number of modes grows.

Fig. 6

Impact of the choice of k on algorithm PB-$\tau$CC. The figure shows the variation in the number of initial row prototypes, of the number of final row clusters, and of the number of iterations w.r.t k. The synthetic data matrix has shape $1000\times 1000$ and 5 row clusters

6.3 Choice of the initial number of prototypes

The initialization strategy we propose creates k synthetic row prototypes and l synthetic columns prototypes, where k and l can be considered as input parameters. Here we show that, in practice, they do not have any sensible impact on the results, provided that they are sufficiently high. Let K be the true number of row clusters embedded in the data. Intuitively, if $k<K$ there will be many rows that are not sufficiently similar to any extracted prototype and they will be put in singleton clusters. On the other hand, when k is very high, there will be a high number of singleton clusters as well. A good choice for parameter k is a number that is higher than the number of expected clusters embedded in the data but also significantly smaller than the number of rows of the matrix. For instance, if matrix ${\mathcal {A}}$ has 1000 rows and we would like to obtain a partition of the data in few clusters, a good choice for the initial number of clusters could be $10\le k \le 50$. Notice that, once we have decided the magnitude of the parameter, the exact value of k is not very important, as shown in Fig. 6, which provides the impact of the choice of the initial parameter k on the number of final clusters and execution times on a synthetic 1000 $\times$ 1000 matrix with 5 embedded co-clusters.

As we said at the beginning of this section, in all the experiments, the number of clusters is always set equal to 30, but, as a rule of thumb, $k=\max \{10,{n}/20\}$, where n is the number of rows. The same rule can be applied for the initial number of column clusters as well. The rationale behind this rule is that, in typical data analysis tasks, when the number of elements in one mode (e.g, the rows in matrix) is less then 200, one does not expect the final number of clusters to be much more than five. For larger datasets, instead, the rule suggests setting the number of initial prototypes in such a way that, on average, each cluster initially contains 20 elements, which we consider a rather conservative choice. In practice, all these parameters can be automatically determined from the dimensionality of the input data, with little or no impact on the final results. Of course, it could happen that, by applying the rule, the initial number of prototypes is underestimated. In this case, PB-$\tau$CC may end up with an underclustered solution. This is a limitation of our algorithm, which, by construction, can only decrease the number of clusters during the optimization process. As future work, we plan to explore the possibility of dynamically adjusting the number of clusters during the execution of the iterative steps of the algorithm, although we suspect that this could be detrimental to the good convergence properties shown by PB-$\tau$CC.

As a final remark, to be fair, we must say that, for some of the competitors, the authors also provide some criterion to identify the “best” number of clusters [this is done, for instance, by Ailem et al. (2016)]. However, the related methods always involve the repeated execution of the original algorithm, which can be unfeasible on very high-dimensional data, especially if the number of input parameters is also high.

7 Conclusion

We have introduced a prototype-based co-clustering approach optimizing a simplified version of the Goodman–Kruskal’s $\tau$ association measure, an objective function that is minimally affected by the choice of the number of clusters, a typical input parameter of any (co-)clustering algorithm. Differently from the previous attempts of using this measure to perform parameterless co-clustering on matrices and tensors, our algorithm is much faster, while at least preserving, if not improving, the quality of the extracted clusters. When compared to state-of-the-art co-clustering algorithms that require the number of clusters as input parameter, our algorithm also shows its effectiveness and feasibility. On tensor data, it is even faster than any other competitor considered in this study.

A limitation of our approach (as well as of all other algorithms optimizing the same family of objective functions) is that it is not well suited for dense numeric matrices (e.g., gene expression data), because, in this case, the association captured by the $\tau$ measure could be meaningless. As future work, we will investigate ways to exploit the good properties of the new version of $\tau$ in such more challenging contexts. Furthermore, we will investigate more in detail the suspected intrinsic ability of identifying outliers in data, which could make the overall approach even more robust.

Appendix A Proof of Theorem 1

Before proving the theorem, we need to introduce some important lemmas. The first one states that sim (Eq. 12) is a positive semi-definite symmetric bilinear form.

Lemma 1

Let $x=(x_j)_{j=1}^n \in {\mathbb {R}}^n$ be a vector such that $x_j >0$ for each j and $\sum _{j=1}^n x_j = 1$. The function

$$\begin{aligned} sim_x: (u,v) \longmapsto \sum _{j=1}^n \frac{u_j\cdot v_j}{x_j} - u_{\cdot }\cdot v_{\cdot } \end{aligned}$$

(A1)

is a positive semi-definite symmetric bilinear form.

Proof

The symmetry and the linearity of $sim_x$ in both the variables follow straightforwardly from its definition. It still remains to prove that $sim(u,u)\ge 0$ for each $u \in {\mathbb {R}}^n$. Consider vectors $a,b \in {\mathbb {R}}^n$ defined as $a_j = \frac{u_j}{\sqrt{x_j}}$ and $b_j = \sqrt{x_j}$. Then

$$\begin{aligned} 0&\le \left( \sum _{j=1}^n a_j^2\right) \left( \sum _{j=1}^n b_j^2\right) - \left( \sum _{j=1}^n a_j b_j\right) ^2 =\\&= \left( \sum _{j=1}^n \frac{u_j^2}{x_j}\right) \left( \sum _{j=1}^n x_j\right) - \left( \sum _{j=1}^n \frac{u_j}{\sqrt{x_j}} \sqrt{x_j}\right) ^2=\\&= \sum _{j=1}^n \frac{u_j^2}{x_j}-\left( \sum _{j=1}^n u_j\right) ^2=\\&=\sum _{j=1}^n \frac{u_j^2}{x_j} - u_{\cdot }^2 = sim_x(u,u) \end{aligned}$$

where the first inequality is the Cauchy-Schwarz inequality and the second equality follows from $\sum _j x_j = 1$. $\square$

The function sim through which the algorithm $\tau$CC-rows evaluates the similarity between each row of the matrix and each cluster prototype is a special case of the function family $sim_x$, with $x=(p_{\cdot c})_{c=1}^l$, because $\sum _{c=1}^l p_{\cdot c} = 1$.

Lemma 2

Let ${\mathcal {C}}$ be the fixed partition of the columns of a matrix ${\mathcal {A}}$. Let ${\mathcal {R}}^{(t)}$ be the partition found by the algorithm $\tau$CC-rows at the tth iteration and let $q^{(t)}$ be its corresponding distribution. Then, the function ${\hat{\tau }}_{R|C}$ can be written as

$${\hat{\tau }}_{R|C}({\mathcal {R}}^{(t)},{\mathcal {C}})=\sum _{r=1}^{|{\mathcal {R}}^{(t)}|}sim(q^{(t)}_r,q^{(t)}_r).$$

Lemma 3

Partition ${\mathcal {R}}^{(t+1)}$ selected by the algorithm $\tau$CC-rows at the following iteration is the partition that maximizes

$$f_{{\mathcal {C}}}({\mathcal {R}}^{(t)},{\mathcal {R}}^{(t+1)}) = \sum _{r=1}^{|{\mathcal {R}}^{(t)}|} sim(q^{(t)}_r,q^{(t+1)}_r)$$

where $q^{(t+1)}$ is the distribution associated to ${\mathcal {R}}^{(t+1)}$.

For the sake of brevity, we omit the simple proofs of the two lemmas, that exploit the linearity and symmetry of sim to rearrange the sums in the definition of ${\hat{\tau }}_{R|C}$. We can finally prove a major result of our paper.

Proof of Theorem 1

To increase readability, we use the following simplified notation: ${\hat{\tau }}(t) = {\hat{\tau }}_{R|C}({\mathcal {R}}^{(t)},{\mathcal {C}})$ and $f(t) = f_{{\mathcal {C}}}({\mathcal {R}}^{(t)},$ ${\mathcal {R}}^{(t+1)})$. We want to prove that the algorithm $\tau$CC-rows monotonically increases the function ${\hat{\tau }}(t)$ and that ${\hat{\tau }}(t)= {\hat{\tau }}(t+1)$ implies either ${\mathcal {R}}^{(t)} = {\mathcal {R}}^{(t+1)}$ or $B({\mathcal {R}}^{(t)}) < B({\mathcal {R}}^{(t+1)})$, where $B({R}^{(t)}) = \sum _{i=1}^n p_{i\cdot } q^{(t)}_{R^{(t)}(i)\cdot }$. This proves the Theorem, since ${\hat{\tau }}$ always goes through different co-clustering solutions, and the number of distinct co-clustering solutions is finite. We will show that, for each t,

$${\hat{\tau }}(t) \le f(t) \le {\hat{\tau }}(t+1)$$

The first inequality directly follows from Lemmas 2 and 3, because

$${\hat{\tau }}(t) = \sum _{r}sim\left( q^{(t)}_r,q^{(t)}_r\right) \le \sum _{r}sim\left( q^{(t)}_r,q^{(t+1)}_r\right) = f(t).$$

Furthermore, moving from partition ${\mathcal {R}}^{(t)}$ to partition ${\mathcal {R}}^{(t+1)}$, for each cluster there will be some rows that remain in the same cluster, some rows that leave the original cluster to another and some rows that enter in the cluster from another one, i.e. for each r

$$\begin{aligned} q_r^{(t+1)} = q_r^{(t)}- q^{\textbf{out}}_r + q^{\textbf{in}}_r \end{aligned}$$

(A2)

where $q^{\textbf{out}}_r$ is the sum of all the points $p_i$ such that ${\mathcal {R}}^{(t)}(i) = r\text { and } {\mathcal {R}}^{(t+1)}(i) \ne r$ and $q^{\textbf{in}}_r$ is the sum of the points $p_i$ such that ${\mathcal {R}}^{(t)}(i) \ne r\text { and } {\mathcal {R}}^{(t+1)}(i) = r$. Thus,

$$\begin{aligned} {\hat{\tau }}(t)&\le f(t) = \sum _{r}sim\left( q^{(t)}_r,q^{(t)} - q^{\textbf{out}}_r + q^{\textbf{in}}_r\right) =\\&=\sum _r sim\left( q^{(t)}_r,q^{(t)}_r\right) + \sum _r sim\left( q^{(t)}_r,q^{\textbf{in}}_r -q^{\textbf{out}}_r\right) = \\&= {\hat{\tau }}(t) + \sum _r sim\left( q^{(t)}_r,q^{\textbf{in}}_r -q^{\textbf{out}}_r\right) \end{aligned}$$

which implies

$$\begin{aligned} \sum _r sim\left( q^{(t)}_r,q^{\textbf{in}}_r -q^{\textbf{out}}_r\right) \ge 0. \end{aligned}$$

(A3)

Now, if we assume ad absurdum that ${\hat{\tau }}(t+1) < f(t)$, it would be

$$\begin{aligned} {\hat{\tau }}(t+1) < f(t)&= \sum _{r}sim\left( q_r^{(t)} +q^{\textbf{out}}_r - q^{\textbf{in}}_r,q^{(t+1)}_r\right) =\\&= {\hat{\tau }}(t+1) + \sum _r sim\left( q^{\textbf{out}}_r -q^{\textbf{in}}_r, q^{(t+1)}_r\right) \end{aligned}$$

where the first equality follows from (A2). Then

$$\begin{aligned} \sum _r sim\left( q^{\textbf{out}}_r -q^{\textbf{in}}_r,q^{(t+1)}_r\right) > 0. \end{aligned}$$

(A4)

By putting together (A3) and (A4) and exploiting the symmetry and linearity of sim, we have that

$$\begin{aligned} 0&< \sum _r sim\left( q^{(t)}_r,q^{\textbf{in}}_r -q^{\textbf{out}}_r\right) + \sum _r sim\left( q^{\textbf{out}}_r -q^{\textbf{in}}_r,q^{(t+1)}_r\right) \\&= -\sum _r sim\left( q^{\textbf{in}}_r -q^{\textbf{out}}_r,q^{\textbf{in}}_r -q^{\textbf{out}}_r\right) \end{aligned}$$

which is impossible because $sim(v,v) \ge 0$ for all $v \in {\mathbb {R}}^l$.

For the second part of the theorem, consider ${\mathcal {R}}^{(t)} \ne {\mathcal {R}}^{(t+1)}$ with ${\hat{\tau }}(t)={\hat{\tau }}(t+1)$. Then, it must be

$$\sum _{i=1}^n sim\left( p_i,q^{(t)}_{R^{(t)}(i)}\right) = {\hat{\tau }}(t)=f(t) = \sum _{i=1}^n sim\left( p_i,q^{(t)}_{R^{(t+1)}(i)}\right) $$

Moreover, $sim\left( p_i,q^{(t)}_{R^{(t)}(i)}\right) \le sim\left( p_i,q^{(t)}_{R^{(t+1)}(i)}\right)$ for all i, by definition of ${\mathcal {R}}^{(t+1)}$. It follows that $sim\left( p_i,q^{(t)}_{R^{(t)}(i)}\right) = sim\left( p_i,q^{(t)}_{R^{(t+1)}(i)}\right)$ for all i and, since the re-assignment step resolves ties in favor of the cluster with the higher $q_{r\cdot }$, it must be $q^{(t)}_{R^{(t)}(i)\cdot } \le q^{(t)}_{R^{(t+1)}(i)\cdot }$, with at least one strict inequality. Then

$$B(t) = B({\mathcal {R}}^{(t)}) = \sum _{i=1}^n p_{i\cdot } q^{(t)}_{R^{(t)}(i)\cdot } < \sum _{i=1}^n p_{i\cdot } q^{(t)}_{R^{(t+1)}(i)\cdot }=g(t)$$

To conclude the proof, it is enough to show that $g(t) \le B(t+1)$. Once noticed that B(t) can be written as $B(t) = \sum _r q^{(t)}_r \cdot q^{(t)}_r$ and that the function g(t) can be written as $g(t) = \sum _r q^{(t)}_r \cdot q^{(t+1)}_r$, the proof is analogous to the proof that $f(t) < {\hat{\tau }}(t)$, considering the function B(t) instead of the function ${\hat{\tau }}(t)$, the function g(t) instead of f(t) and the scalar product $u\cdot v = u_{\cdot }\cdot v_{\cdot }$ instead of the bilinear form sim(u, v). $\square$