1 Introduction

CNNs are increasingly being applied to imbalanced visual data in high-stakes fields such as medicine, business and law (Johnson & Khoshgoftaar, 2019). Yet, they have difficulty generalizing to classes with few examples. Imbalanced data helps focus the spotlight on generalization because it provides a contrast between majority classes, with their rich data profile, and emaciated minority classes, with few examples that typically exhibit a more narrow range of variation.

The ability of a neural network to generalize with respect to minority classes can be critical to its overall performance. For example, in medicine, physicians may be more interested in the accurate recognition of minority instances, such as cancerous lung tissue. Improving model generalization on minority classes is challenging because neural networks are opaque (Gunning & Aha, 2019). The black-box nature of CNNs makes it difficult to study the very problem that we are interested in: why does a CNN struggle to generalize on minority classes? To answer this question, we first have to unravel its decision process so that the properties of the features that cause it to misclassify minority examples can be identified. Although there are many available eXplainable Artificial Intelligence (XAI) methods that examine neural network feature relevance, there is a paucity of research that combines and analyzes data imbalance, generalization and CNN opacity in a single, unified study. XAI feature relevance methods such as LIME (Ribeiro et al., 2016) or Shapley values (Sundararajan & Najmi, 2020; Shapley, 1953) generally focus on instance, instead of class, features. Similarly, pixel attribution methods, such as saliency maps (Simonyan et al., 2013; Sundararajan et al., 2017), network deconvolution (Zeiler & Fergus, 2014), and activation maps (Selvaraju et al., 2017) focus on attributing CNN predictions on specific images to input pixels, instead of interpreting network decisions rendered on an entire class.

Fig. 1
figure 1

Illustration of feature embeddings (FE) and classification embeddings (CE), using the Resnet 32 architecture (He et al., 2016). The CNN’s embedding layers produce feature maps based on the interaction of convolutional layers and non-linear activations with input pixels. After thresholding, FE represent a low-dimensional response to the input. Based on the classification layer’s final prediction, we trace the final output (a label) to logits, classification embeddings and feature embeddings that triggered the response. By comparing the CE of the predicted class to the next largest class logit, we determine the number of relevant FE and CE (the top-K) required to make a prediction

Full size image

In this work, we strive to better understand the process by which CNNs reach their decisions on imbalanced image data. To search for an answer to this problem and to make it tractable, we examine the latent representation that CNN’s extract from input data and use when making a class prediction. After thresholding, this embedding represents a vector of low dimensional features that a linear classifier uses to predict a label. We investigate the properties of these latent features (i.e., their magnitude, identity, and frequency), their relationship to class weights, and draw general hypotheses about how CNN’s generalize with respect to majority and minority classes. To enable our research, we break a CNN into two separate networks, embedding and classification layers, so that we can concentrate on the latent features that serve as input to the recognition process. We refer to the internal representation learned by the embedding layers, after thresholding, as feature embeddings (FE) and the output of the classification layer, before summation and Softmax, as classification embeddings (CE). See Fig. 1 for an illustration.

We use CE and FE to determine the most important latent features, for an instance or a class, and call these the most relevant, or top-K, features. Feature importance is based on magnitude because the class with the largest logit determines the class prediction for models trained on cross-entropy loss, or a variant of this method. Logits, in turn, are based on a multiplication of FE and class weights, followed by summation.

1.1 Main contributions

We make the following research contributions by taking steps to explain the decision process of CNNs when operating on imbalanced data:

  • CNN minority class latent features are less diverse. We measure class feature diversity based on the number, and density, of feature and classification embeddings. We use mean as a measure of density and show that a CNN’s internal representation of minority class features is less diverse than the majority.

  • CNN minority class prediction rests on fewer, higher valued relevant features due to low diversity. A CNN’s minority class prediction rests on only a handful of features in embedding space (the top-K features), which is of lower size than the embedding dimension, but generally of higher mean magnitude than relevant majority class latent features. We hypothesize that the decision manifold is narrower for minority classes because there is less diversity of examples. The majority class distribution is more diverse, hence it requires a larger decision manifold (magnitude of relevant features) in latent space to reach a decision (represent a class).

  • Higher response, lower diversity of minority class features leads to poor generalization. Although a CNN classifier relies on a few relevant features to distinguish minority examples, it compensates by increasing the magnitude of the top-K minority features. This finding is interesting in light of previous work which found that majority classes dominate CNN model gradients (Anand et al., 1993). Because the minority class has fewer examples with less diverse features, the system’s response to top-K minority features is elevated to ensure proper classification. This may partially explain why CNN’s have difficulty generalizing to minority class examples. The system is conditioned to engineer a high response to a limited number of minority features, and when those high response features are not present in the test set (due to lower minority class FE magnitudes spread over more FE), the classifier mistakes the minority example for an adversary (majority) class with lower, and more varied, overall response to the input. In contrast, the classifier has been conditioned to expect a wider range of majority class features and hence, each individual feature has a lower magnitude and the sum of more, lower magnitude features allows the classifier to make the correct majority class prediction.

  • Generalization capacity. A CNN has difficulty generalizing from the training to test set if the range of its latent feature magnitudes differ. We demonstrate that a CNN is able to generalize from the training to the test set if there is a close match in the range of its top-K FE.

2 Background and related work

2.1 Background

We assume that CNNs perform visual recognition in a two-step process. First, low dimensional embeddings are extracted. Second, based on these low dimensional features, object classification occurs (a decision is rendered). This assumption forms the basis of our experiments, where we separate a CNN into two basic layer groups, embedding and classification, so that we can better understand the CNN decision process (classification).

There is some support for this approach. The manifold hypothesis holds that high-dimensional data can be represented on a less complicated, lower dimensional manifold (Cayton, 2005). In the computer vision field, it has similarly been hypothesized that high-dimensional image data can be expressed in a more compact form, based on latent features (Brahma et al., 2015; Bellinger et al., 2018).

Many modern CNN architectures, which use a non-linear rectified linear unit (ReLU) activation function, can be viewed as approximating high dimensional image data in a lower dimensional embedding space (with embedding layers) (Li et al., 2022; Chui & Mhaskar, 2018). If complex, high dimensional input can be reduced to a low dimensional latent space, then linear models can be more readily applied to reach a decision (in the classification layer). Stated differently, CNNs use non-linearity to find low dimensional features (with embedding layers) that can be linearly separated (by classification layers).

Although CNNs have achieved impressive results, they face key challenges, especially with regard to their ability to generalize on imbalanced data. First, classifiers tend to obtain their highest accuracy when the density of positive and negative examples along a class decision boundary are approximately the same (Kovács, 2019; Huang et al., 2019). However, when there is a wide divergence in the number and diversity of class examples, such as with majority and minority classes, the decision boundary can become blurred.

Second, the decision process of a CNN is difficult to understand, which further compounds the first problem because the decision boundary is wrapped in a black-box (Karimi et al., 2019; Mickisch et al., 2020). The machine learning (ML) sub-fields of imbalanced learning and XAI independently address these issues: improving classifier accuracy for minority classes (imbalanced learning) and model interpretability (XAI). There has been a paucity of research that combines these two approaches into a single, unified discussion.

2.2 Related work

XAI. XAI adopts a variety of approaches to explain model decisions, including: explaining more complicated models by reference to simpler ones, feature relevance, various post-hoc methods, explanation by example, and mapping predictions to inputs (Gunning & Aha, 2019; Adadi & Berrada, 2018; Linardatos et al., 2020). Many of these approaches are local in nature because they explain a model decision on a single input, and do not attempt to explain global properties of features or decision processes (Achtibat et al., 2022). For example, feature relevance techniques, which are related to our approach, such as Shapley values or Local Interpretable Model-Agnostic Explanations (LIME), show the importance of features to a single instance. Shapley values typically involve retraining a model or modifying data on a single instance to understand feature relevance (Sundararajan & Najmi, 2020). LIME requires learning another model locally around a single prediction (Ribeiro et al., 2016). All of these works focus on individual predictions, instead of class feature properties.

Other XAI techniques focus on interpreting a CNN’s internal representations. Olah et al. (2017) visualize the learned latent individual neurons, feature maps or layers of a CNN through activation maximization. This method generally requires the generation of additional images with a Generative Adversarial Network. Bau et al. (2017) propose network dissection, which evaluates the alignment of individual hidden neurons with semantic concepts; however, their method does not prioritize the most relevant features for a class and requires a pixel-wise labeled dataset. Kim et al. (2018) propose directional derivatives to quantify the degree to which a concept is important; however, their method requires the introduction of an additional, labeled dataset, and a binary classifier, such as logistic regression. Badola et al. (2021) develop the concept of instance top-K features produced by a CNN filter, although they do not apply this to imbalanced data.

CNN fragility. The general notion that neural networks, and CNNs in particular, are fragile has been explored in a number of works. Szegedy et al. (2013) were among the first to observe that the class decisions of neural networks could be changed by small perturbations of pixel inputs in the direction of the gradient. These small perturbations are imperceptible to humans and are referred to as adversarial examples. In the context of adversarial examples, Ilyas et al. (2019) demonstrate that CNNs learn highly predictive, yet brittle, patterns that are not comprehensible to humans. In the same context, Wang et al. (2020) show that CNNs learn high frequency patterns that are incomprehensible to humans and which contribute to adversarial examples (i.e., false positives).

More recently, Geirhos et al. (2020) hypothesize that deep neural networks learn short-cuts, or simple decision rules, that perform well on training data, but fail to transfer to more challenging real-world data. Pezeshki et al. (2021) theorize that gradient starvation occurs when cross-entropy loss is minimized by using only a subset of features relevant to the task, despite the presence of other predictive features. Shah et al. (2020) show that the simplicity bias of neural networks (i.e., their proclivity to exclusively use simple features) affects their robustness and ability to generalize. Our work is inspired by these studies, along with the work of Badola et al. (2021), and focuses on a subset of the features learned by a CNN (the top-K feature and classification embeddings), and how their diversity affects the ability of a CNN to generalize from the training to the test data with respect to minority classes.

Imbalanced learning. Imbalanced learning is concerned with designing methods that allow classifiers to better generalize from training to test data on minority classes (Fernández et al., 2018; He & Garcia, 2009; Buda et al., 2018). It uses a variety of approaches: re-sampling minority and majority class data, cost-sensitive methods that assign a greater loss to minority class misclassification, separating a ML system into embedding and classification phases, ensemble, and hybrid approaches (Johnson & Khoshgoftaar, 2019; Krawczyk, 2016; Bellinger et al., 2020).

Kang et al. (2019) and Zhou et al. (2020) develop a novel technique to improve CNN classification with respect to minority classes—bifurcate the model into two separate layer groups: embedding and classification. Their approach is used to improve classifier accuracy and not for explanation. Ye et al. (2020) perform an experimental assessment of feature deviation on imbalanced image data, and compare training and test set feature means, for purposes of improving classifier performance. However, they do not analyze top-K features, feature index identity or frequency. Cao et al. (2019) and Kim and Kim (2020) discuss the impact of imbalanced classes on decision boundaries, classifier weights and class rebalancing, although they do not tie this analysis into latent features.

3 Methodology

3.1 Nomenclature

The following nomenclature is used to describe our experimental setup, results and conclusions.

An image dataset, \(D=\{X,Y\}\) is comprised of instances, X, and labels, Y. An instance, \(d=\{x,y\} \in \{D\}\), consists of an image, where \(x \in \mathbb {R}^{c,h,w}\), such that c, h, and w represent a 2 dimensional image consisting of channels (RGB or red, green, blue), height and width, respectively. D can be partitioned into training and test sets (\(D=\{Train,Test\}\)).

A CNN can be described as a network of weights, W, arranged in layers, L, that operate on x to produce an output, y (a label). We partition the layers, L, into two principal parts: embedding layers and a classification layer. (See Fig. 1 for an illustration.) A CNN can then be expressed as: \(f_\theta (\cdot )= f_{W_C}[(f_{W_E})_{Th}]\), where \(f_{W_E}(\cdot )\) are the embedding layers, Th performs thresholding, \(f_{W_C}(\cdot )\) is the classification layer, \(W_E\) are embedding layer weights, and \(W_C\) are classification layer weights. Feature embeddings (FE) are the output of the embedding layers after thresholding has been applied, or \( FE = (f_{W_E})_{Th}\). Classification embeddings (CE) are the result of the Hadamard product of FE and the transpose of the classification weights, or \(CE = FE \cdot W_C.T\). Logits (LG) represent the row-wise summation of CE, or \(LG = \Sigma (CE)\). The final prediction (y) is the argmax of the Softmax of the logits, or \(y=argmax(\sigma (LG))\), where \(\sigma \) is the Softmax function. Figure 1 illustrates this nomenclature for the Resnet-32 architecture.

To distinguish classes in a dataset, D, we refer to reference and adversary classes. A reference class is the predicted label and an adversary class is any other class in C. The number of classes in C is referred to as \(N_C\), with each class \(C=\{c_1,c_2, \cdots c_n\}\). Each individual FE and CE vector can be described as \( FE =\{{fe}_1,{fe}_2, \cdots {fe}_h\}\) and \( CE =\{{ce}_1,{ce}_2, \cdots {ce}_h\}\), respectively. Each fe and ce in a single FE or CE, respectively, have a fixed index position in a vector.

3.2 Feature properties

Model FE can be extracted for all Train and Test instances, along with \(W_C\), to facilitate the analysis of class feature properties. Throughout the text, we discuss and quantify several properties of a CNN’s internal embeddings, including their identity, magnitude and frequency.

The identity of a \(fe_h\) or \(ce_h\) refers to its index position in a vector. The magnitude of a \(ce_h\) or \(fe_h\) refers to its value. The frequency of a \(fe_h\) or \(ce_h\) refers to how often it appears within a class in Train or Test.

These properties allows us to compare the number, size, range, and frequency of FE that the model uses to define a class. By contrasting majority and minority class feature properties, we can better understand the CNN’s ability to generalize to the test distribution based on its learned features and class weights.

3.3 Feature relevance and diversity: top-K FE

A CNN classifier’s prediction for a single data instance, x, is based on whether the logit of the reference class exceeds the next largest logit of an adversary class. This observation applies to CNN’s using cross-entropy loss, or a cost-sensitive variant. The label of a final class prediction represents an index in a vector of size \(N_C\). This index points in a “backward” direction to an index c in CE. For a CNN that uses cross-entropy loss, only the CE of the reference class (the prediction) and the next largest CE (largest adversary class) matter because the prediction is the argmax of the summed CE. We refer to the reference class CE as \( CE _R\) and the CE of the largest adversary class as \( CE _A\). The respective logits are \(LG_R\) and \(LG_A\).

The top-K CE of each data instance is then the number of individual CE of the reference class required to exceed the next largest logit, \(LG_A\). The ability of a given value of K to predict all instances in Train can be determined experimentally by summing the top-K CE for each instance and comparing it to each \(LG_A\) and quantifying the percentage of times that the sum exceeds \(LG_A\) in Train. We refer to this percentage as the top-K coverage ratio. The ratio is bounded by 0 and 1. For a given K, a high top-K coverage ratio means that only K number of CE are needed to predict a high percentage of instances in a training set. This same procedure can be applied on a class basis or class top-K coverage ratio.

This ratio provides an indication of feature diversity when examining classes that are imbalanced. If a minority class can be defined by a small value of K (only a handful of features are present in all class instances), then its top-K coverage ratio for the given K should be high (near 1). If a majority class has a low class coverage ratio for the same value of K, then a larger number of features are required to make accurate predictions.

Top-K FE or top-K CE are instance based measures. In other words, they determine the top features per instance; however, the specific identity of the top-K components may vary across all instances in a class. Class top-K members are the group of top-K features that occur most frequently across all instances in a class.

3.4 Class feature means

For each class, the mean value of each feature (\(\{{fe}_1,{fe}_2, \cdots {fe}_H\}\) and \(\{{ce}_1,{ce}_2, \cdots {ce}_H\}\)) is instructive because it provides insight into the model’s response to a given feature. For example, if the mean value of \({fe}_{35}\) is high for class 0, but low for class 7, then this implies that this feature is more important for purposes of distinguishing class 0. Because a CNN classifier makes it class selection linearly based on the largest logit, high valued features that compose the logit are important to its decision. The mean magnitude is also a measure of density. For example, if \(ce_1\) has a high mean magnitude for a minority class, but it has a low mean magnitude for a majority class, then it implies that \(ce_1\) frequently clusters around a high value for a minority class.

4 Experimental study set-up

4.1 Data

To conduct our experiments, we examine three popular image datasets: CIFAR-10 (Krizhevsky et al., 2009), Street View House Numbers (SVHN) (Netzer et al., 2011), and CelebA (Liu et al., 2015).

Table 1 CIFAR-10 & SVHN training class frequencies
Full size table

The datasets span three different image data types: objects (CIFAR-10), numbers (SVHN) and facial attributes (CelebA). In addition, we compare cross-entropy loss on the CIFAR-10 dataset with two cost-sensitive algorithms on the same dataset—LDAM (Cao et al., 2019) and the Focal loss (Lin et al., 2017). By comparing a single dataset (CIFAR-10) trained with different loss functions, we are better able to identify the effects of cost-sensitive algorithms on features.

In our experiments, CIFAR-10, SVHN and CelebA contain 10, 10 and 2 classes, respectively. For CelebA, the two classes are: men and women with black hair.

Table 2 Dataset training splits
Full size table

We use a single hair color because the full CelebA dataset disproportionately contains more women with blond hair then men, and we want to avoid a simple feature (hair color) that can easily distinguish classes.

The CIFAR-10 training and test sets are initially balanced. For SVHN, we randomly select training and test instances because the dataset contains an uneven number of training and test examples by class. See Table 1 for a break-out of the class frequencies for CIFAR-10 and SVHN training sets. For CelebA, we randomly select 5000 and 250 training examples for the majority and minority classes and 1000 test images for each class.

For purposes of this study, we introduce exponential imbalance into the training set (maximum imbalance ratio of 100:1), similar to Cao et al. (2019), for CIFAR-10 and SVHN. For CelebA, the imbalance ratio is 20:1.

In addition to exponential imbalance, we also consider step imbalance for CIFAR-10. We use a 20:1 imbalance level and reverse the order of imbalance (so that the classes with the larger number of instances in exponential imbalance become the minority classes with step imbalance). Reversing the order of the classes that are imbalanced allows us to determine whether imbalance affects generalization compared to the properties of specific classes.

We randomly sample 3 imbalanced training sets from the original balanced training data for all datasets. Table 2 shows the individual class and balanced accuracies (BAC) - simple means of individual class accuracies. It also shows the mean of the 3 training splits. Because there is a marginal difference in BAC, and the general trend of individual class accuracies is consistent, for the single split versus the mean of all of the splits, we select a single split for our experiments. In the case of all 4 datasets, the BAC of the selected dataset falls within the standard deviation of the 3 training runs. In the case of CIFAR-10 with exponential imbalance, several individual class accuracies of the selected dataset fall outside the standard deviation, however, by an average nominal amount of.48 points. In the case of SVHN, only a single class accuracy falls outside the standard deviation by.75 of a point and only 2 classes fall outside the standard deviation by.27 of a point on average in the case of CIFAR-10 with step imbalance.

This approach allows us to train two models with identical architectures and training regimes, but with balanced and imbalanced versions of the same datasets. We can then more precisely observe the impact of imbalance on class feature and weight selection.

The use of balanced test sets allows us to examine the effect of different training and test distributions for minority classes. More specifically, in the majority class, we would expect that the training and test feature distributions are likely more uniform, and hence, the model should be able to better generalize from the training to the test set. In contrast, for minority classes, which have a limited number of training examples, the model will likely struggle to generalize to the test set. For example, in the case of CIFAR-10, there are 5000 training and 1000 test examples for the majority class, but there are only 50 training and 1000 test examples for the smallest minority class.

4.2 Data augmentation

For the CIFAR-10 dataset, our base training regime includes limited augmentations for all classes. The basic augmentations are random crop and random horizontal flip, which are consistent with Cao et al.’s (2019) training regime for imbalanced data. For the SVHN and CelebA datasets, we did not incorporate any data augmentations into the training regime because a CNN is able to attain approx. 95% BAC on a balanced dataset without any augmentations—see Table 3. In contrast, CIFAR-10 only achieves 87.11% BAC without any augmentations on a balanced dataset, which increases to 92.65% with limited data augmentations.

4.3 Model architectures and training regime

For CIFAR-10 and SVHN, a Resnet 32 architecture is used and a Resnet 56 architecture is used for CelebA (He et al., 2016). We follow a popular training regime used in cost-sensitive learning for imbalanced data (Cao et al., 2019). More specifically, we train for 200 epochs for CIFAR-10 (including cost-sensitive methods) and SVHN with a batch size of 128, 0.1 base learning rate (LR), 0.9 momentum, 0.0002 weight decay, and LR annealing of 0.001 after 160 epochs and 0.00001 after 180 epochs. For CelebA, we train for 50 epochs and use the same hyper-parameters, except that LR annealing occurs after epochs 40 and 45.

All models are trained with PyTorch (Paszke et al., 2017) on a single RTX 3060 Nvidia GPU. We assess the performance of our trained models with BAC, which treats each class equally, regardless of the number of examples. More specifically, BAC for all classes in a dataset is calculated as the mean of the true positive rate for each class. The epoch with the best performing BAC is then selected.

4.4 Research questions

The goal of the research questions (RQ) is to better understand why CNN classifiers are less accurate when trained with imbalanced data. We approach this question by examining the latent representations (FE and CE) and the class weights that a CNN uses to arrive at its class decisions. By better understanding FE and CE properties, we expose the diversity of the class latent representations, how this diversity changes with imbalance, and how diversity may affect generalization.

As an initial matter, we first investigate the lower prediction accuracy and lower generalization capacity of CNNs trained on imbalanced data. We then count the number of latent features (feature embeddings) that a CNN classifier uses to recognize a class, and whether class imbalance affects the diversity of the learned features. We also consider the relative effect of latent representations versus classifier weights on a CNN’s decision. Finally, after establishing the importance of feature embeddings and their diversity, we consider the impact of latent features on a CNN’s ability to generalize to examples unseen during training.

Our RQs are summarized below:

  • Can classifier retraining with imbalanced data achieve balanced training accuracy?

  • What is the effect of imbalance on generalization?

  • Does a CNN rely on a handful of top-K relevant features when classifying an instance and a class?

  • Does class imbalance affect the diversity of learned latent features?

  • How significant are classifier weights versus feature embeddings to a CNN’s prediction?

  • Are majority class feature embeddings more diverse?

  • Are false positives an indicator of network memorization of training data?

5 Results

5.1 Can classifier retraining achieve balanced training accuracy?

For our initial experiment, we train two CNNs: one with balanced data and one with exponentially imbalanced data, using cross-entropy loss. We bifurcate the model trained on imbalanced data into embedding and classification layers. We re-train the imbalanced-model classifier with FE from the balanced (full) training set, but that were extracted using imbalanced embedding layers. This procedure focuses the spotlight on the benefits of classifier re-training.

For a combined CNN embedder and classifier trained on balanced CIFAR-10 data, the BAC for all classes is 92.65%. For a combined CNN extractor and classifier trained on imbalanced data, BAC is 72.56% for a model trained with cross-entropy loss. For a CNN extractor separately trained on imbalanced data and a classifier retrained with balanced data extracted by an imbalanced extractor, BAC is approx. 78–80%. This percentage is approximately the BAC achieved by several recent cost-sensitive and classifier re-balancing methods on an exponentially imbalanced CIFAR-10 dataset (Cao et al., 2019; Dablain et al., 2022). As noted in Table 3, similar results are produced by the other datasets and cost-sensitive algorithms. In other words, a classifier retrained with features extracted from an imbalanced extractor cannot recover the accuracy levels of a full CNN (embedding and classification layers) trained on balanced data. This result holds even though the classifier is retrained with features drawn from the full dataset (albeit from embedding layers trained on imbalanced data).

Table 3 Re-trained classifier BAC
Full size table

Thus, a classifier re-trained with the latent embeddings of the full, balanced training set is not able to recover the BAC of a combined CNN extractor trained on the same data. This implies that the CNN extractor trained on imbalanced data has not learned the same latent features as the CNN extractor/classifier trained on balanced data. In the following experiments, we attempt to understand why this is the case.

5.2 What is the effect of imbalance on generalization?

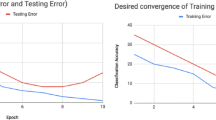
Here, we investigate a CNN’s ability to generalize on balanced and imbalanced CIFAR-10 data. Figure 2a shows that a CNN trained with a balanced CIFAR-10 training set is able to generalize from the training to the test distribution with relative ease.

Fig. 2
figure 2

a Shows that a CNN can readily generalize from training to test distributions when trained with balanced CIFAR-10 data. b When the same model architecture is trained on CIFAR-10 data with either exponential (exp) or step (c) imbalance, minority classes display much greater difficulty generalizing compared to majority classes. In the diagrams, the red dotted line indicates class imbalance levels. c Shows that, when a model is trained on an exponentially imbalanced CIFAR-10 dataset, removing simple data augmentations increases over-fitting for all classes, although the minority classes, with fewer examples, are more adversely affected. In (d), the order of the classes that are imbalanced is reversed, such that classes 0 to 4 have imbalance level 20:1 and classes 5 to 9 have no imbalance

Full size image

However, when the same dataset is imbalanced, the model displays both declining accuracy and increasing over-fitting for minority classes. In Fig. 2, the blue and green lines show training and test accuracy, respectively. The red line indicates the level of class imbalance for the CIFAR-10 dataset. For imbalanced data, the model is able to almost perfectly memorize the training data, but it has difficulty generalizing to the minority class test distribution. The same over-fitting trend for minority classes is repeated for the other datasets and cost-sensitive algorithms (see Table 4).

Figure 2 also shows the effect of basic data augmentations (c) and step imbalance (d) on over-fitting for CIFAR-10. (The models trained on SVHN and CelebA do not contain any data augmentations.)

Table 4 Effect of imbalance on generalization
Full size table

Figure 2c shows that, when a model is trained on an exponentially imbalanced CIFAR-10 dataset, removing simple data augmentations (random center crop and horizontal rotations) increases over-fitting for all classes, although the minority classes, with fewer examples, are more adversely affected. In Fig. 2d, the order of the classes that are imbalanced is reversed, such that classes 0 to 4 have imbalance level 20:1 and classes 5 to 9 have no imbalance. Even when reversing the order of class imbalance and incorporating step versus exponential imbalance, a CNN trained on CIFAR-10 exhibits greater over-fitting of minority than majority classes; although data augmentation does improve generalization capacity.

Table  4 shows BAC for the majority and minority classes, where the majority is the class with largest number of training examples and the minority is the class with the fewest. In all cases, the models have almost perfect accuracy on the training data, but have difficulty generalizing to the minority class test data, when the training sets are imbalanced. This is the case, even though the models are all trained with common deep learning regularization techniques, such as weight decay and learning rate annealing.

5.3 Does a CNN rely on top-K features?

Figure 3 shows the top-K coverage ratios for two models: one trained with balanced, and the other trained with imbalanced, CIFAR-10 data for \(K \in \{2,3,5,7\}\). For \(K=2\) or \(K=3\) (denoted with blue and green lines) in the balanced data, the top-K coverage ratio fluctuates between a low of 40% and a high of 96%. For \(K=3\), the model is better able to predict classes 6 to 9 compared to 0 to 5 on a balanced dataset. However, at \(K=5\) (red line), the ratio stabilizes between 89% and 99%; and at \(K=7\) (black line), the model is able to predict a class label over 97% of the time for all classes and training set examples on a balanced dataset.

Fig. 3
figure 3

The figure on the left displays the class top-K coverage ratio for a Resnet-32 with balanced CIFAR-10 data; and the one on the right shows imbalanced data. In both cases, \(K = 7\) accounts for over 94% of training set predictions

Full size image
Table 5 Top-K coverage ratio
Full size table

With exponentially imbalanced CIFAR-10 data, Fig. 3 shows that for \(K=2\), the model struggles to predict the majority classes (0 to 3) with only 2 features 60% of the time; however, there is a clearly sloping upward trend after that, with the model able to predict the 4 most extreme minority classes (6 to 9), with only 2 features over 90% of the time. Similar to the balanced data, at \(K=7\), the model is able to predict a class over 94% of the time with only 7 features for all classes.

In Table 5, a similar trend can be observed in other cost-sensitive algorithms and datasets. In the case of LDAM and the Focal loss, \(K=2\) and \(K=11\) constitute the number of relevant features necessary to predict 100% and over 90% of the training instances, respectively. For CelebA and SVHN, \(K=2\) and \(K=3\) are needed to predict 100% and over 94% of training instances, respectively. In all cases, K is far smaller than the dimension of the latent space (FE and CE).

Table 5 also shows the number of top-K CE required to discern instances in a step imbalanced CIFAR-10 dataset, where the order of class imbalanced is reversed (hence the minority classes in the exponential version become the majority in the step version). It shows that \(K=11\) predicts over 94.6% of the logits for a model trained with 20:1 step imbalance on CIFAR-10. Thus, even when the order of the imbalanced classes is reversed and step versus exponential imbalance is used, the number of latent features needed to discern a class is far less than the hidden dimension of model latent space (64).

These results confirm that a CNN classifier relies on a limited number of features to make its prediction, consistent with Badola et al. (2021), and this number is less than the dimension of the classification layer, such that \(K<\!\!<\!H\).

5.4 Does imbalance affect the diversity of learned features?

To gain a better understanding of why fewer latent features are required to distinguish classes, we visualize the mean magnitudes of the top-K CE for all classes.

Fig. 4
figure 4

This figure shows the 10 largest mean magnitudes of CE for CIFAR-10 classes extracted from a CNN trained on balanced data. The CE are sorted, with the CE identity varying on the x-axis by class. The shape of the histograms and the magnitude of the mean value ranges appear relatively similar for all classes

Full size image

Figure 4 shows the ten largest mean magnitudes of CE by class for a CNN trained on balanced CIFAR-10 data, with cross-entropy loss. The mean magnitudes are sorted by class so that we can clearly see the range and scale of the values for the most significant features. For balanced data, the CE for all classes reside in a narrow band between 0 and 3.4. The single largest mean CE in each class spans from 1.5 to 3.4.

In contrast, Fig. 5 reveals a wide band between the mean magnitudes of the class CE with the ten largest mean magnitudes of 0 to 9.1. For the imbalanced training set, the largest class CE mean magnitude spans from 1.8 to 9.1, which is approx. triple the balanced data range.

The CE show a clear trend of large mean magnitudes for classes with few training examples and much smaller mean magnitudes for classes with many examples.

The single largest CE for the extreme minority classes (6 to 9), with more than 20:1 imbalance, average 8.3, whereas the classes with more examples (0 to 5) average only 2.6.

The pattern of larger top-K CE mean magnitudes where \(K=1\) is present in other datasets and cost-sensitive algorithms. Table 6 shows the mean magnitude of the largest single CE for the majority class and the average for all other classes. In all cases, the majority class CE magnitude is at least 2\(\times \) smaller than the minority classes. This relationship applies to models trained on cross-entropy loss for the CelebA and SVHN datasets, as well as models trained on cost-sensitive algorithms (LDAM and Focal loss) for CIFAR-10. In order for the model to correctly predict the majority class, it must have more CE that collectively sum to a larger logit than the minority classes with fewer, but larger, relevant CE.

Fig. 5
figure 5

This figure shows the mean magnitudes of CE for CIFAR-10 classes for a CNN trained on imbalanced data. The CE are sorted, with the CE identity varying on the x-axis by class. The extreme minority classes (6–9) exhibit a more narrow band of high valued mean features with higher overall magnitude

Full size image

There is also a greater and faster drop off in the mean magnitudes of CE for minority classes, after the single largest class CE. As class imbalance increases, the mean magnitudes of the single largest CE increase and there is greater concentration of large responses in only a handful of CE. This drop off is clearly shown in Fig. 5 for CIFAR-10. As imbalance grows, fewer features with higher mean magnitudes contribute to the classifier’s prediction.

Fig. 6
figure 6

This figure shows the percentage that the top 7 CE, by class, contribute to each logit instance for a balanced and imbalanced CIFAR-10 dataset. The percentage is based on averaging all class instances. For the imbalanced data, fewer CE contribute a greater percentage to the prediction logit. For the imbalanced data, the maximum y-axis value (.8) is triple the maximum balanced value (.25)

Full size image

Figure 6 shows the percentage that the top-7 CE, by class, contribute to each logit instance for a balanced and imbalanced CIFAR-10 dataset. Each CE percentage is based on averaging all class instances. For the imbalanced data, fewer CE contribute to a greater percentage of the prediction logit. For balanced data, in the left diagram, no single CE contributes more than 26% of the predicted logit. However, in the right diagram, which depicts imbalanced data, there are 5 classes that have CE that contribute more than 35% to the predicted logit.

Table 6 Mean magnitude of class CE
Full size table

This trend is repeated for other datasets and cost-sensitive algorithms. Table 7 shows the contribution of the single largest CE to the class logit for the majority class and all other classes. In the case of the majority class, it’s largest logit contributes between 1.4 and 4 times less to the overall class logit, which indicates that the majority class relies on a wider diversity of features to arrive at its class decision. Thus, the majority class needs higher magnitudes from it’s other latent features (a more diverse set of features) to be the predicted class (the class with the largest logit).

Collectively, these results indicate that a CNN classifier forms its decisions on a small portion of the dimension of its feature inputs. In the case of minority classes, the number of relevant features is even smaller (2 or 3 in some cases).

Table 7 Top CE contribution to class logit
Full size table

We hypothesize that the number of relevant features is wider for majority classes because their examples are more diverse (i.e., there are a larger number of relevant features per class that each individually contribute smaller size magnitudes to the logit). Because the majority distribution is more diverse, the model requires a larger decision manifold (more relevant features) to distinguish the class instances, which cumulatively add up to the logit. In contrast, due to modest minority class diversity, the model generates only a few, high valued response CE to distinguish these classes.

In the next two subsections, we will consider whether the model weights \(W_C\) or the learned feature embeddings FE are responsible for the narrow, high-valued CE responses of minority classes.

5.5 How significant are classifier weights versus features to the network’s prediction?

Figure 7 shows the ten largest weight mean magnitudes, \(W_c\), by class, for imbalanced CIFAR-10 data. The majority classes have a wider cross-section of larger weights, whereas the minority class has a narrower concentration. The larger majority class weight mean magnitudes can be seen by comparing the sum of the class top-10 weight mean magnitudes for the majority and minority classes.

Table 8 shows that for all datasets and algorithms, the sum of the majority class top-10 \(W_C\) mean magnitudes are larger than the sum of the minority class top-10 \(W_C\) mean magnitudes.

The weight sums are significant because the classifier arrives at its decision by summing the element-wise multiplication of weights and FE.

Fig. 7
figure 7

This figure shows the magnitudes of the ten largest weights, \(W_c\), by class, for imbalanced CIFAR-10 data. The majority classes have a wider cross-section of larger weights, whereas the minority class large magnitudes are concentrated in fewer weights

Full size image

We hypothesize that there is a wider cross-section of larger weights in majority classes because the class top-K FE are more diverse than in the case of the majority.

The model has learned more diverse features for the majority due to more varied examples and it must weight these more frequently occurring features to distinguish majority instances.

Although the weights are clearly biased toward the majority, the magnitude of the weights does not account for the large magnitudes of the class top-10 CE members. For example, in the case of the extreme minority classes (8 and 9) for CIFAR-10, their top CE have mean magnitudes greater than 8.0, yet the corresponding weights are only approx. 1.2 (see Figs. 4, 7).

Table 8 Top 10 weight magnitudes
Full size table

A similar trend is evident in other datasets and cost-sensitive algorithms. See Table 9.

Therefore, FE must be contributing more to the class decision (CE) than the classification weights (\(W_C\)), since the magnitude of the CE is much larger than the \(W_C\) magnitudes.

Table 9 Largest weight mean versus largest CE mean
Full size table

This implies that weight (\(W_C\)) re-balancing strategies employed by some cost-sensitive, over-sampling, or classifier re-training methods may not be sufficient to redress the class imbalance problem. Although weight re-balancing may be helpful, there may be limits to the amount of class bias that it can address due to the scale difference between the weights (\(W_C\)) and CE values.

Because \(W_C\) appear to only have a minor impact on minority class CE, we next examine its other component, FE.

5.6 Are majority class features more diverse?

In this section, we take a closer look at FE, which is the other component of CE, and investigate why there is a greater concentration of high valued feature responses for minority class CE compared to majority class CE.

Fig. 8
figure 8

This figure shows the class top-K FE ratio for imbalanced CIFAR-10 data. It conveys the diversity of the most frequently occurring top-K FE in each class. The extreme majority class (0) shows no top-K class ratios greater than 67%, whereas the extreme minority classes (8 & 9) have 4 and 5 features (FE), respectively, that are present in over 90% of class instances

Full size image

Figure 8 shows the class top-K FE coverage ratios for the ten most frequently occurring features per class. The FE were extracted from a CNN trained on an exponentially imbalanced CIFAR-10 data. Low values indicate that a larger number of varied features are needed to distinguish a class. In the figure, the extreme majority class (0) shows no class top-K FE coverage ratio greater than 67%, whereas the extreme minority classes (8 & 9) have 4 and 5 FE, respectively, that are present in over 90% of class instances.

Figure 9 shows the number of top-K class FE that are required to fully describe all class instances for majority and minority classes. For cost-sensitive algorithms and all three datasets, fewer top-K are required for minority classes.

Fig. 9
figure 9

This figure shows the number of class top K FE that are necessary to describe all instances in the majority and minority classes for the CIFAR-10 dataset with the cross-entropy, focal and LDAM loss functions, and the SVHN and CelebA datasets using cross-entropy loss. In all cases, it requires significantly more class top-K FE to describe the majority class than the minority class

Full size image

Together, Figs. 8 and 9 demonstrate that it takes fewer features to describe minority than majority classes. Due to the greater diversity of majority instances, a greater number of features are needed to predict the full class.

Figure 10a shows the ten largest FE mean magnitudes, by class, for an imbalanced CIFAR-10 training set. The scale of these magnitudes more closely aligns with the ten largest mean magnitudes of imbalanced CE shown in Fig. 4 than the \(W_C\) in Fig. 7, and demonstrates that FE have a relatively larger impact on CE (i.e., the model’s decision) than \(W_C\). This observation implies that, in order to influence CE, a method must modify the FE extracted by a CNN and somehow augment the diversity of the initial, more static minority classes. However, such a task is not easy, since the test distribution or its diversity cannot be known in advance.

5.7 Are false positives an indicator of network memorization of training data?

Here, we examine how the latent features (FE) that a CNN has learned affects its ability to generalize to the minority class test distribution. We compare the model’s internal embeddings (FE) in the train, test true positive (TP) and test false positive (FP) sets so that we can identify differences in its internal embeddings when it makes correct versus incorrect predictions.

Fig. 10
figure 10

These figures show a clear divergence between the mean magnitudes of the class top-10 FE members in the training and the test false positive set; however, many of the mean magnitudes for minority class top FE are approx. half of their training set values. In contrast, there is relatively close alignment between the training and test true positives

Full size image

For a CNN trained on an exponentially imbalanced CFAR-10 dataset with cross-entropy, in the case of true positives, there is a close correlation between the mean magnitudes of the features learned in training and the features in the test set. For both CE and FE, there is 95% and 96% intersection between the top 10 most frequently occurring features in the train and test TP sets. In the case of false positives, there is still relatively high correspondence between the identity of FE or 70% alignment; however, in the case of CE, the correspondence drops to only 39%. In other words, whether the model makes correct or incorrect predictions, it basically relies on the same group of input features (FE) by class as it identified during training; however, there is a wide divergence between the final CE used to make correct and incorrect predictions when compared to training.

In order to gain insight into why this might occur, we look at the mean magnitude of the FE in the training and test sets for a model trained on CIFAR-10 and cross-entropy. Figure 10 shows a relatively close alignment between the top FE mean magnitudes of training and true positives. In contrast, the same figure shows a clear divergence between the mean magnitudes of the class top-10 FE in the training set and the test false positive set, where many of the mean magnitudes for minority class top FE are approx. half of their training set values. This visual observation is confirmed by the Frobenius norm (FB) of the mean magnitudes of fe (\( FB [\mu (Train_{FE}) - \mu (Test_{TP-FE})]\) and \( FB [\mu (Train_{FE}) - \mu (Test_{FP-FE})]\)). The Frobenius norm is 2.36 for training and test TPs and 12.42 for training and test FPs. The larger FB for training and test FPs show that the mean magnitude of the FPs are not well aligned with the training set, which affects the ability of the model to generalize.

Table 10 Frobenius norm of train, test TP & FP
Full size table

We repeated this exercise for the other datasets and cost-sensitive loss functions, with similar results. See Table 10. The table shows that the FB norms are much higher for the training and test set FPs.

The minority class true positive decision is based on a narrower group of class top-K FE that have high mean magnitudes and lower \(W_C\) (hence, the logit is based on the sum of a few high magnitude FE and weights). We hypothesize that if a model is biased to identify minority instances only when a narrow set of high valued features are present that it may harm its ability to generalize to minority class test examples that do not exhibit these characteristics.

Collectively, these results show that the model is able to generalize from the training to test distributions when there is very close correspondence between the identity of the most relevant features and the range of their values (training and test TPs). However, the model has difficulty generalizing when the range of FE differs between the training and test sets (FPs), even when there is large (70%) overlap in the identity of the class top-K FE.

6 Discussion

In this section, we discuss insights based on our experiments, future research directions, and the broader impact of our work.

6.1 General observations on CNNs

In the 1990s, Olshausen and Field (Olshausen & Field, 1997) hypothesized that mammals use a sparse coding with an over-complete basis set for object recognition purposes. In their model, the initial layer of the visual cortex (V1), uses linear basis functions to identify shape primitives (e.g., lines, edges, etc.). In their view, V1 contains an over-abundance (an over-complete set) of these linear basis functions; however, the visual stream only uses a tiny fraction of them (a sparse coding) to identify individual object classes.

Their work can be analogized to CNNs. A CNN uses linear basis functions (kernels with learnable, parameterized weights) that are rotated over an image to identify class features and spatially frequent patterns. In this work, we have shown that some CNNs, whether trained with balanced or imbalanced data, only rely on a small percentage of the output of their kernels (i.e., the feature maps or feature embeddings) to arrive at an instance or class decision. Thus, in some ways, a CNN uses an over-complete basis set (a large number of linear kernels that each generate their own feature map or feature embedding); however, it only relies on a sparse set of these basis functions (the top-K) to classify an object.

6.2 Insights on learning with imbalanced data

  • Importance of balanced training sets. CNNs trained with cross-entropy loss in a supervised manner are heavily reliant on carefully balanced training sets to achieve high accuracy. This is consistent with, and confirms, other research (Bauder et al., 2018; Weiss & Provost, 2001; Estabrooks et al., 2004).

  • Statistically frequent patterns required for recognition. Recent research by Huber et al. (2021) has shown that the human visual system’s robustness to image distortions is largely in place at an early age. In other words, whether a human is shown a limited number of versions of a truck or more examples as their experience increases with age, they can identify many varieties and transformations of an object as a truck. DiCarlo et al. (2012) hypothesize that robustness and invariance are the key computational foundation of any object recognition system. Biological visual systems appear to learn class identity preserving features irrespective of changes in location, pose, scale, illumination variability or clutter. In contrast, our experiments have shown that a CNN displays markedly different class accuracy when it is trained with a balanced dataset with many class instances versus an imbalanced dataset with only a few instances. For example, with CIFAR-10, training a CNN on a balanced dataset with 5000 truck examples versus an imbalanced dataset with only 50 examples causes classifier accuracy on this class to plummet by over 30 points (62% vs. 94%). In addition, a model trained with no data augmentations versus a model trained with only limited augmentations results in a 5 percentage point change in BAC for a balanced CIFAR-10 dataset (87.11% vs. 92.65% BAC). In other words, the ability of the model to generalize from the training to the test set can be affected by training set data imbalance and augmentation. Thus, it appears that a CNN has learned high frequency patterns that occur in a sufficiently large number of training instances. Because the model has learned statistically frequent patterns in data, it requires a diverse set of examples to find a sufficient number, and range, of latent feature magnitudes, to generalize from the training to the test set. When a minority class is characterized by a low number of latent features in a lower response range in a test set, the model struggles to generalize to more diverse latent features in the test set.

  • Role of feature magnitude in class imbalance. The magnitude or response that a CNN assigns to a feature has a large impact on CNN classification performance on imbalanced data. CNNs trained on cross-entropy loss appear to assign high magnitudes to a narrow range of minority features and lower magnitudes to a larger number (more diverse) set of majority features. This causes a disconnect during inference if the model is presented with minority class latent features (FE) that span a lower range during test than training, even if the features have the same identity. This observation confirms the brittleness of CNN latent embedding learning, which has been demonstrated in adversarial learning research (Ilyas et al., 2019; Wang et al., 2020).

  • Minority class latent feature diversity. This paper postulates that an under-appreciated issue in imbalanced image learning lies in greater diversity for minority class latent features. Imbalanced learning solutions that only target class number re-balancing, classifier retraining, increasing the cost of minority examples, or increasing the margin on class decision boundaries and that neglect the importance of FE may plateau at some point.

  • Test set false positives link to network memorization? A CNN trained on cross-entropy or a cost-sensitive variant has difficulty generalizing if the magnitude of its top-K latent features in the training set do not match the test set. Effectively, a CNN memorizes training latent features in the form of model parameters, and if the response range of the features produced by these parameters and the input differs in the test set, then the model produces false positives.

6.3 Future research

Based on our study of the role of latent features when learning with imbalanced data, there are several potential future research directions. First, we only briefly touched on the role of data augmentation in a model’s ability to generalize with respect to minority classes. In the deep learning context, Shen et al. (2022) explored the impact of data augmentation on feature learning. In the imbalanced learning context, a possible future research direction may be to investigate the impact of data augmentation techniques, such as SMOTE (Chawla et al., 2002), on latent feature diversity when learning with imbalanced data.

Second, an interesting future research direction may be to visualize the latent features learned by different datasets and CNN architectures. For example, the latent features relating to certain classes may overlap. These features can be compared, which may facilitate the discovery of methods that enable a model to better disentangle latent class representations.

Third, our experiments involved 3 image datasets, with different levels of imbalance. There is a risk of noise or variability in the results due to random sampling. We have attempted to control this risk by applying our analysis across three splits of the datasets. As discussed above, our analysis of the BAC of one split against the mean BAC of the 3 splits suggested a sufficient degree of stability in the results. However, assessing more datasets with multiple cross-validation runs in future work could further solidify these results.

7 Conclusion

CNNs are increasingly being deployed on real-world data, which is naturally skewed. Training CNNs on imbalanced image data remains an open challenge. In this paper, we take steps toward demystifying a neural network’s decision process for under-represented classes. By better understanding the role that a model’s latent features play in its decision process, we aim to further research that improves a CNN’s ability to generalize with respect to minority classes.