1 Introduction

Action recognition is a challenging task in the field of computer vision. And it is at the forefront of applications to understand the human social activity (Islam and Iqbal 2020). Action recognition based on RGB images/videos has been widely researched with deep learning methods, such as Convolution Neural Networks (CNNs). The motivation of most action recognition algorithms is to extract spatiotemporal feature representations from RGB videos. And then, a classifier is trained to distinguish different actions. Simonyan and Zisserman (2014) proposed a two-stream method to extract spatial and temporal information separately. Also, to obtain temporal features, Ji et al. (2013) extended the traditional 2D-CNN to 3D-CNN with a 3D convolution kernel.

Meanwhile, owing to the concise and compelling data source, skeleton-based action recognition is attracting more and more attention. Concretely, skeleton-based methods can effectively focus on the joint transformation of different actions by discarding redundant background information. A more robust and more efficient network based on skeleton data can be designed to recognize human actions than the RGB-based methods. And the most important thing is that skeletal data can articulate joints connection status and their dynamic changes. Rahmani and Bennamoun (2017) demonstrate skeleton-based approaches are complementary to RGB-based methods for human action recognition. The skeleton joints are constructed into a graph in the non-Euclidean space. The nodes in the graph indicate the coordinates of the body part, and the edges indicate the connection of the joints. With the feature of both nodes and the edges, a Graph Neural Networks (GNN) can be employed for graph embedding (Yang and Li 2020).

Previous work construct the joint coordinates manually into a sequence of vectors (Vemulapalli et al. 2014; Jiang et al. 2020). Then the recurrent neural network (RNNs) is utilized to process the vectors (Liu et al. 2016; Song et al. 2017; Zhang et al. 2017; Zheng et al. 2019). Alternatively, the skeleton joints are composed into a 2D pseudo-image. Then a CNN-based model is able to generate the final prediction (Liu et al. 2017; Li et al. 2017a, b; Zhang et al. 2019; Wang et al. 2021). However, both the RNN-based and CNN-based methods do not explicitly take advantage of spatial relationships and temporal dynamics. Therefore, a series of graph convolutional networks (GCNs) are proposed for skeleton-based action recognition (Yan et al. 2018; Shi et al. 2019a, b; Tang et al. 2018; Cheng et al. 2020; Song et al. 2021; Shi et al. 2020; Peng et al. 2021; Liu et al. 2021; Xie et al. 2021; Ahmad et al. 2021; Yoon et al. 2021). Inferred from CNNs, GCNs are able to process non-Euclidean data such as skeleton graphs through the regulation of the kernel size and the promotion of the convolution operation. Subsequently, a graph convolution module is widely used to construct the spatial–temporal GCN. Most of the GCN-based methods emphasize the improvement of a structure to obtain optimal spatial–temporal representations.

Shi et al. (2019a) extend the GCNs to a two-stream architecture to obtain the bones information of the skeleton data. Meanwhile, an adaptive optimal adjacency matrix is learned from the skeleton data, which means the topology of the graph is learnable. Then they built a multi-stream network describing joints, bones, and their motion information by preprocessing the skeleton data (Shi et al. 2020). Cheng et al. (2020) proposed a shift graph operation for GCNs, which provides flexible receptive fields for spatial–temporal graphs. Song et al. (2021) create a multi-stream architecture with the help of class activation maps (CAM), which increases the robustness of the model. Ahmad et al. (2021) present a sparse ST-GCN method by eliminating redundant nodes and edges of the graphs. Liu et al. (2021) propose an adaptive view transformation module for GCN to model the spatial configuration and temporal dynamics of skeleton sequence.

Previous GCN-based methods for skeleton action recognition show the ability to extract spatial–temporal information from the skeleton graphs. For a skeleton graph, the information of the nodes is aggregated layer by layer from their neighbors in the vertex domain. And the Adjacency matrix is added to the vertex-domain graph convolution to indicate the connection information. Most of the GCN network for action recognition is based on the vertex-domain graph convolution, more like template matching of graphs. In this manner, the features that focus on the local information can represent high-level semantics. However, the focus on the local information has led to their limited representation ability in some interactive actions or some actions containing overall dynamics in both spatial and temporal. For example, the average accuracy of 1s-Shift-GCN on the cross-subject of NTU-RGBD 60 dataset is 87.8%. The precision of the actions such as “A12. writing”, “A11. reading” and “A30. type on a keyboard” is only 55.9%, 59.3% and 67.3%.

To solve this problem, the spectral domain convolution based on Graph Fourier Transform (GFT) is introduced in this paper. The vertex-domain graph convolution tends to extract local information with the Adjacent matrix, while the spectral-domain graph convolution extracts global information because of the Laplacian matrix. The spectral domain convolution, which extends the convolution theorem to graphs, uses the Laplacian matrix to describe the global relationship between neighbor nodes. Spectral-domain information has been utilized for graph node classification tasks in some previous work (Estrach et al. 2014; Henaff et al. 2015; Defferrard et al. 2016). However, the structures of the network containing the spectral convolution are quite simple and crude, and this is why they perform inferior to most spatial–temporal GCNs for skeleton graphs. Therefore, this paper proposes a deep residual-connected spectral backbone to obtain the global dynamic of skeleton graphs, which is compensation for the blind spot of the regular GCN methods.

This paper is an improved version of an earlier work presented in Chen et al. (2021), named SS-GCN. Compared to our previous work, the model architecture has been greatly improved in both the vertex and spectral streams. The performance gain for each action is obtained in Fig. 7 to show that the recognition ability is improved for most action classes, primarily those with broader dynamic changes. The improved RSB includes a graph batch normalization, an activation function (the ReLU layer), and a graph pooling operation. Then the multiple spectral blocks are residual-connected, followed by a normalization layer. The new design of the spectral domain branch refers to the brilliant CNN model ResNet (He et al. 2016), to avoid gradient vanishing while the network layers increase. Finally, the spectral features are combined with the spatial–temporal features extracted from the vertex stream to recognize the action. Compared with our previous SS-GCN, the main contributions are summarized as follows:

  • To extract spatial–temporal information more effectively, the shift operation on the graph is employed to our vertex stream inspired by Shift-GCN (Cheng et al. 2020). This article further explores the effectiveness of the complementation of the vertex-domain and the spectral-domain features through a more efficient spatial–temporal stream, which proves the previous GCN is flawed in this task for some actions rely on global information.

  • A more robust spectral GCNs backbone consisting of RSBs is proposed, proving to be more effective in extracting spectral features for action recognition. Though some experiments show that spectral-based GCN performs inferior to spatial-based GCN in some computer vision tasks, our RSB shows particular improvement to the simple spectral-based GCNs adopted by our previous SS-GCN owing to the deep architecture.

  • In previous work, the motivation of the combination of the spatial–temporal information and the spectral information is not well expressed and supported. At the same time, this paper proposes using spectral-domain information to make up for the weak recognition ability of previous GCNs in some actions. An analysis of the improvement of each action category by the spectral-domain information is provided in the ablation study.

  • More extensive experiments and more comprehensive analyses are performed. Owing to the improvement on both the spectral stream and the spatial–temporal stream, DD-GCN has greatly improved our previous model SS-GCN. with an increase of 5.3%/5.5% on the NTU-RGBD 60 dataset (Shahroudy et al. 2016). The top-1 and top-5 accuracy on the Kinetics-Skeleton dataset (Kay et al. 2017) are also improved by 0.9%/2.0%. Additional experiments on NTU-RGBD 120 (Liu et al. 2020) are performed and compared with the SOTA.

The rest of the paper is organized as follows, Sect. 2 describes the related work of action recognition based on skeleton data. Section 2.1 elaborates the principle of vertex-domain graph convolution and spectral-domain graph convolution. Section 4 introduces the two-stream structure of our DD-GCN. Section 5 presents the experiment settings and results, followed by a detailed experimental analysis and comparison. Conclusion are drawn in Sect.  6.

2 Related work

Owing to the effectiveness data, there is more and more research focusing on skeleton-based action recognition. The skeleton data that indicates the coordinates dynamics shows robustness against illumination change, background variation, and body diversity. The methods are composed of the handcraft-feature methods and the deep learning methods. One typical handcraft feature is based on the theory of Lie Group (Vemulapalli et al. 2014; Jiang et al. 2020; Fernando et al. 2015). Vemulapalli et al. (2014) propose a Lie-group skeletal representation that uses rotations and translations in 3D space to model the 3D geometric relationships between different body parts specifically. Inspired by this work, Jiang et al. (2020) create a new spatial–temporal skeleton transformation descriptor (ST-STD) to obtain a comprehensive view of the skeleton in both spatial and temporal domain for each frame, followed by a denoising sparse long short term memory (DS-LSTM) network. Fernando et al. (2015) use the parameters from the ranking functions per video as a new video representation.

However, the deep learning features are more substantial than the handcraft-feature methods due to various deep models such as RNNs and CNNs. RNNs-based methods can extract the dynamic information with the ability of modeling sequences (Du et al. 2015; Liu et al. 2016, 2018; Song et al. 2017; Zhang et al. 2017; Li et al. 2018; Zheng et al. 2019). Du et al. (2015) propose an end-to-end hierarchical RNN for skeleton-based action recognition, based on the ability to model the long-term contextual knowledge of temporal sequences of the RNNs. Liu et al. (2016) further propose a tree-structure traversal method based on LSTM to deal with occlusion and noise in human skeleton data. To make better use of the multi-modal features extracted for each joint, then they (Liu et al. 2018) introduce a feature fusion method within the trust gate ST-LSTM unit. Song et al. (2017) combine the spatial attention subnetwork and the temporal attention subnetwork with the main LSTM network to pay various levels of attention to different frames. Zhang et al. (2017) propose a two-stream View Adaptive network for skeleton action recognition to eliminate the influence of the viewpoints by combining RNN features with CNN features. Li et al. (2018) introduce an independently RNN (IndRNN) architecture to ovoid the gradient vanishing while learning long-term dependencies. Zheng et al. (2019) integrate the attention mechanism into LSTM to model spatial and temporal dynamics simultaneously.

Meanwhile, by forming the skeleton into pseudo-images, CNN-based methods are also widely studied (Ke et al. 2017; Liu et al. 2017; Kim and Reiter 2017; Li et al. 2017a, b; Cao et al. 2019). Ke et al. (2017) introduce a manual clip generation method for the skeleton joints of each frame which are placed as a chain by concatenating the joints. Liu et al. (2017) present an enhanced visualization method for skeleton data according to a view-invariant transform, an image colorization, and a CNN-based model. Kim and Reiter (2017) re-design the Temporal Convolutional Neural Networks (TCN) to learn the spatial–temporal representations of the human skeleton data. Li et al. (2017a) also transform the skeleton videos to skeleton-images and utilize a multi-scale deep convolutional neural network (CNN) architecture to recognize the localized and motion features. Li et al. (2017b) construct two kinds of skeleton-image for both 3D Cartesian coordinates and skeleton motion. Then a two-stream CNN is performed for classification. Cao et al. (2019) employ CNNs to solve the sequence learning problem as an image classification problem by stacking residual blocks and skip gated links. Wang et al. (2021) combine the angle changes of the edges and the movements of the corresponding body joints to construct a skeleton edge motion network.

2.1 Graph convolutional neural networks

Nevertheless, neither CNNs nor RNNs process the non-Euclidean graphs directly. Both the sequences in RNNs and the grids in CNNs have flaws while blending spatial and temporal patterns. Therefore, several GCN-based models are proposed to capture spatiotemporal features from graphs (Yan et al. 2018; Shi et al. 2019a, b; Peng et al. 2021; Liu et al. 2021; Xie et al. 2021; Ahmad et al. 2021). Inferred by CNNs, these GCNs avoid the handcrafted part-assignment. Yan et al. (2018) propose to treat the skeleton sequences as spatiotemporal graphs and extend CNNs to the vertex domain of the graph by a spatiotemporal GCN (ST-GCN). The spatiotemporal information is shown vital for trajectory data in different domains (Knauf et al. 2016). Unlike CNNs, the convolution operation in the GCNs unit contains the input data and learnable weights and the adjacency matrix of the graph demonstrating the spatiotemporal connection. By constructing a naturally connected skeleton graph, ST-GCN eliminates the need to specify the data structure manually. Si et al. (2019) combine vertex-domain graph convolution with LSTM to capture features in both spatial configuration and temporal dynamics. Based on ST-GCN, Shi et al. (2019a) raise a two-stream adaptive GCN (2s-AGCN) to obtain the joint and the second-order information of the skeleton data. They add learnable adaptive parameters to the adjacency matrix to improve the limitations of natural connection in ST-GCN. Then 2s-AGCN is extended to MS-AAGCN (Shi et al. 2020) by a multi-stream architecture which combines the information from both joints and bones, as well as their motion trends. Another work from Shi et al. (2019b) propose a directed graph network (DGN) to model joints and bones in the natural human body, which are represented as a directed acyclic graph (DAG). Cheng et al. (2020) propose a novel shift operation for spatial GCNs based on the previous work, which greatly reduces the GFLOPs and increases the inflexibility of the receptive fields. Inspired by this work, our vertex-domain stream consists of spatiotemporal shift GCN blocks, which is more effective while extracting non-local relationships between spatial and temporal domains. Yoon et al. (2021) propose Pe-GCN with predictive encoding for latent space, which is robust to the skeleton noise. The model is trained to learn the mutual information between latent features.

The effectiveness of GCN methods for graph data comes from the aggregation of temporal and spatial patterns, which is also called vertex-domain information in this work. Nevertheless, apart from the vertex-domain methods, there are several spectral convolution methods to handle the graph data even they have not been paid attention to in skeleton-based action recognition (Estrach et al. 2014; Henaff et al. 2015; Defferrard et al. 2016). Vertex-domain methods define the convolution through the chosen center and its receptive field with the adjacency matrix. However, spectral-domain methods use the graph Laplacian matrix based on spectral graph theory (Chung and Graham 1997). In previous work, the spectral domain information is ignored when analyzing the graphs of the human skeleton.

Estrach et al. (2014) exploit a global structure of the graph with the spectrum of its graph-Laplacian matrix to generalize the convolution operator from CNNs. A vanilla GCN in the spectral domain is proposed by constructing a graph spectral convolution layer, in which the spatial filter is replaced with a spectral filter. Henaff et al. (2015) develop an improved spectral GCN by smooth the spectral filters. By smoothing the spectral filters in the spectral domain, a more localized filter in the space domain is obtained faster during the decay. Defferrard et al. (2016) learn the functions of the Laplacian directly to avoid the eigendecomposition while calculating the spectral convolution. Inspired by Cheng et al. (2020), a dual-domain graph CNN is proposed to capture both spatiotemporal and spectral information with two kinds of graph convolution operators. Inferred by ResNet, a novel residual-connected spectral backbone is proposed to avoid gradient vanishing.

3 Graph convolution operations

This section introduces two sorts of graph convolution operations according to graph signal processing (GSP) for skeleton action recognition.

3.1 Vertex-domain graph convolution

GCNs have been a widely used architecture since the work of Yan et al. (2018). By constructing the skeleton data into graph \(G=(V, E)\) with N joints and T frames, a vertex-domain graph convolution operation is defined with the thought of template matching. Because of the absence of node ordering and the structure diversity, the simplest way to design a template to calculate the convolution is to use a scalar for all neighbors. Given an input vector h of l th layer in a GNN, the vertex-domain scalar convolution is shown as follows:

$${h_i}^{l+1}=\sigma\left (\sum _{j \in \mathcal N_i} \left\langle w^l,h_{ij}^l \right\rangle \right),$$
(1)

where \(\left\langle ,\right\rangle\) is the product operation and \(\sigma\) is the activation function. \(w^{l} \in R\) is the template vector to obtain neighborhood information in layer l. And \(N_{i}\) denotes the set of all neighbor nodes of node i. For a general convolution in graph neural networks, the following formula is obtained:

$${h}^{l+1}=\sigma (Ah^{l}W^{l}),$$
(2)

where \(A\in \{0,1\}^{N \times N}\) is the Adjacency matrix of the graph, and \(W^{l}\) is the weight template learned by backpropagation. The output matrix is denoted as \(h^{l+1}\in R^{N \times d}\), where d is the dimension of the feature vectors. The intuitive meaning of vertex-domain convolution is to collect information of neighbor nodes to update its representation.

For skeleton action recognition, the formula of vertex-domain convolution operation in GCNs is shown below:

$$f_{\text{ out }}\left( v_{t i}\right) =\sum _{v_{t j} \in B\left( v_{t i}\right) } \frac{1}{Z_{t i}\left( v_{t j}\right) } f_{i n}\left( v_{t j}\right) \cdot \mathbf {w}\left( l_{t i}\left( v_{t j}\right) \right) ,$$
(3)

where \(v_{ti}\) denotes the i th vertex in the graph at time t. The feature map is denoted as f. \(\mathbf{w}\) is the refined weight function in GCNs. B is the refined sampling function. As shown in Fig. 1b, the kernel B is divided into three subsets: root \(B_{s0}\) denotes the vertex itself; centripetal \(B_{s1}\) contains the closer neighbors with gravity center; centrifugal \(B_{s2}\) contains the farther neighbors. Cardinality Z indicates the contribution of the subsets.

Fig. 1
figure 1

Illustration of the skeleton graph for vertex-domain graph convolution. The blue dots representing the body joints are connected in both spatial and temporal domain. For the vertex-domain convolution, they are divided into three handcrafted subsets: root subset \(B_{s0}\), centripetal subset \(B_{s1}\) and centrifugal subset \(B_{s2}\) (Color figure online)

Full size image

As the feature map is a \(C \times T \times N\) tensor while implementing vertex-domain graph convolution. Meanwhile Eq. 3 can be summarized as follows:

$${\mathbf {F}}_{\text{ out }}=\sum _{k}^{K_{v}} {\mathbf {W}}_{k}\left( \mathbf {F}_{i n} \mathbf {A}_{k}\right) \odot {\mathbf {M}}_{k},$$
(4)

where \(K_{v}=3\) and \({\mathbf {A}}_{k}={\mathbf {\Lambda }}_{k}^{-\frac{1}{2}} \overline{\mathbf {A}}_{k} \mathbf {\Lambda }_{k}^{-\frac{1}{2}}\). The elements \(\overline{\mathbf {A}}_{k}^{i j}\) of \(\overline{\mathbf {A}}_{k}\) denotes whether the neighbor vertex \(v_{j}\) is in the subset \(S_{ik}\) of local vertex \(v_{i}\). \(\mathbf{W}_{k}\in R^{1\times 1\times C\times C'}\) denotes the weight function. The channel of kernel and the number of kernels are denoted as C and \(C'\) respectively. Meanwhile, \({\mathbf{M}_{k}}\) is a learnable attention map to adjust the importance of each vertex.

3.2 Spectral-domain graph convolution

In skeleton action recognition, the latest methods all treat joints and bones, as well as their motion trajectories, as a spatiotemporal graph to perform vertex-domain convolution operations. However, since the skeleton data is regarded as graphs, the ignored spectral-domain information is also vital according to the Spectral Graph Theory. The analysis of the properties of a graph concerning the characteristic polynomial, eigenvalues, and eigenvectors of the Laplacian matrix, is the main part of spectral graph theory in mathematics.

The spectral convolution is performed by the following steps: Graph Laplacian matrix, Fourier functions and Fourier transform, Convolution theorem. The N th skeleton sequence in time T is converted to a spatiotemporal graph \(G=(V, E)\). According to spectral graph theory, The Adjacency matrix is represented as A. Another essential operator is the graph is Laplacian matrix L. And the simple Laplacian matrix is defined as \(L=D-A \in {R}^{n \times n}\). \(D=diag(d(v_{1}),\ldots ,d(v_{N})) \in {R}^{n \times n}\) is the diagonal degree matrix and \(d(\cdot )\) is the degree of node \(v_{i}\). Then the normalized Laplacian matrix is defined as \(L=D^{-\frac{1}{2}}(D-A)D^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\).

It is obvious that the Laplacian matrix L is a real symmetric matrix. Given a vector \(\mathbf {f}\) related to vertex \(v_{i}\), \(\mathbf {h}\) is the output vector by calculating the product of the Laplacian matrix L and \(\mathbf {v}\). And its physical implication can be clarified with the following formula:

$$\begin{aligned} \mathbf {h}&= L \mathbf {f}=(D-A) \mathbf {f}=D \mathbf {f}-A \mathbf {f}, \end{aligned}$$
(5)
$$\begin{aligned} \mathbf {h}[i]&=d(v_{i})\mathbf {f}[i]-\sum _{v_{j}\in N(v_{i})}A_{i,j}\mathbf {f}[i]\\&=\sum _{v_{j}\in N(v_{i})}1\cdot \mathbf {f}[i]-\sum _{v_{j}\in N(v_{i})}1\cdot \mathbf {f}[j]\\&=\sum _{v_{j}\in N(v_{i})}(\mathbf {f}[i]-\mathbf {f}[j]), \end{aligned}$$
(6)

where the output vector \(\mathbf {h}\) represents the difference between \(v_{i}\) and its neighbor vertex \(v_{j}\).

Laplacian matrix is also a positive semidefinite matrix and can be proved with Eq. 5 by the following formula, the quadratic form of L:

$$\begin{aligned} f^{\top }Lf&=\sum _{v_{j} \in V} \mathbf {f}[i] \sum _{v_{j} \in N\left( v_{i}\right) }(\mathbf {f}[i]-\mathbf {f}(j))\\&=\sum _{v_{i} \in V} \sum _{v_{i} \in N(v_{i})}(\mathbf {f}[i] \cdot \mathbf {f}[i]-\mathbf {f}[i] \cdot \mathbf {f}[j])\\&=\sum _{v_{i} \in V} \sum _{v_{i} \in N(v_{i})}\left( \frac{1}{2}\mathbf {f}[i] \cdot \mathbf {f}[i]-\mathbf {f}[i] \cdot \mathbf {f}[j]+\frac{1}{2}\mathbf {f}[j] \cdot \mathbf {f}[j]\right) \\&=\frac{1}{2}\sum _{v_{i} \in V} \sum _{v_{i} \in N(v_{i})}(\mathbf {f}[i]-\mathbf {f}[j])^2. \end{aligned}$$
(7)

As shown in Eq. 7, the quadratic form of the Laplacian matrix L is the sum of the squares of the difference between each vertex and its neighborhoods in a graph. From both perspectives in Eqs. 5 and 7, the physical implication of the Laplacian matrix is that it is a measure of the difference between each node and its neighbor nodes in the graph. This is quite different from the Adjacency matrix applied in vertex-domain graph convolution operation, which provides the strength of the connection of the edge between nodes.

The vital Laplacian matrix L is precisely the basic content of graph spectral convolution operation. The convolution in the vertex domain can not be expressed as a meaningful operator roughly. However, the convolution operator \(*_{\mathcal {G}}\) is easily defined in the spectral domain according to graph convolution theorem:

$$w *_{\mathcal {G}} h=U\left( \left( U^{T} w\right) \odot \left( U^{T}, h\right) \right) ,$$
(8)

where Fourier basis \(U=[u_{0}, \ldots , u_{n-1}] \in {R}^{n \times n}\). With the Fourier basis, the spectral graph convolution for signal w is defined as \(\hat{w}=U^{T}w\). Fourier transform \(U^{T}\) of the convolution of two signals (w, h) is the pointwise product of their Fourier transforms. By denoting \(\hat{w}\) and \(\hat{w}(\Lambda )\), the graph spectral convolution formula is obtained:

$$\begin{aligned} w *_{\mathcal {G}} h&=U(\hat{w}\odot U^Th)\\&=U(\hat{w(\Lambda )}\odot U^{T}h)\\&=\hat{w}(U\Lambda U^{T})h\\&=\hat{w}(\Delta )h, \end{aligned}$$
(9)

where \(\hat{w}=U^{T}w \in {R}^{n \times 1}\) and \(\Delta =U\Lambda U^{T} \in {R}^{n \times n}\). And \(\Lambda\) in \(\hat{w}(\Lambda )\) is denoted as: \(\Lambda ={\text {diag}}\left( \left[ \lambda _{0}, \ldots , \lambda _{n-1}\right] \right) \in {R}^{n \times n}\). \(\lambda _{i}\) indicates the eigenvalues of the Laplacian matrix. \(\hat{w}(\Lambda )\) is the filter to be learned in the operation of spectral graph convolution.

4 Dual-domain GCN architecture

In this section, the two-stream architecture of our dual-domain GCN (DD-GCN) to obtain both spatiotemporal and spectral information is introduced in detail. Some actions are difficult to distinguish in the time–space domain but can be effectively separated in the spectral domain. By adopting the two kinds of graph convolution operations, both spatiotemporal and spectral information are obtained with the two-stream model. The experiment results show that the characteristics of the two domains have complementary effects.

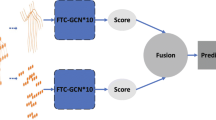
As illustrated in Fig. 2, an end-to-end GCN is proposed to extract spatiotemporal and spectral information in a skeleton graph. It consists of two streams, in which an effective GCN–TCN-Unit and a novel Spectral-Unit are applied as backbone architecture. First, The skeleton data is preprocessed for both vertex-domain and spectral-domain separately. Then, followed by a dual-domain graph neural network that adopts two graph convolution operations, the skeleton signal is represented as high-level semantic features. The complementary representation eliminates the limitations in vertex and spectral-domain to obtain better performance for skeleton action recognition.

Fig. 2
figure 2

Implementation of our dual-domain graph convolutional networks (DD-GCN). The original skeleton data is preprocessed separately for the vertex domain and the spectral domain. The vertex-domain stream consists of nine GCN–TCN-Units which can extract the spatiotemporal information effectively by Shift Operation. The spectral-domain stream consists of a residual connected spectral convolution network that contains 4 or 6 Spectral-Units. Each Spectral Unit is composed of four components in order: spectral graph convolution with Chebyshev expansion, batch normalization, ReLU function, and graph pooling layer. Both vertex-domain stream and spectral-domain stream consist of a fully connected layer. The final output of the combined architecture contains both spatiotemporal and spectral-domain information

Full size image

In the following subsection, the architecture to obtain information from both the vertex domain and the spectral domain is explained in detail.

4.1 Skeleton action graph

The N sequences of skeleton data in one sample are operated as a sequence of tensors X, representing each joint’s coordinates. The construction of the spatial–temporal graphs for the vertex-domain convolution follows the work of ST-GCN (Yan et al. 2018). As shown in Fig. 1a, the joints coordinates are represented as graph nodes, and the body connections are represented as graph edges. Meanwhile, the joints of the same body part between frames are also regarded as connected. The input tensors are denoted as \(X\in R^{N\times C\times T\times V\times M}\), and the spatial–temporal graph is denoted as \(G=(V, E)\) with N joints and T frames. All the joints in a skeleton sequence are contained in the vertex set \(V=\left\{ v_{t i} \mid t=1, \ldots , T, i=1,\ldots ,N\}\right.\). The edge set E contains the intra-skeleton edges \(E_{S}(\tau )=\left\{ v_{t i} v_{t j} \mid t=\tau ,(i, j) \in H\right\}\) and the inter-frame edges \(E_{F}=\left\{ v_{t i} v_{(t+1) i}\right\}\). The spatial–temporal graph is regarded as a tensor \(X_{spatiotemporal}\in R^{(N*M)\times C\times T\times V}\) while operating vertex-domain graph convolution. The Adjacency matrix A for spatial GCN in GCN–TCN-Unit shows the connectivity of the human body. As for spectral-domain convolution, the spectral graph is regarded as a tensor \(X_{spectral}\in R^{N\times T\times V\times (C*M)}\). Instead of the Adjacency matrix, the spectral-domain stream focuses on the Laplacian matrix L to obtain the difference between node \(V_{i}\) and neighbor nodes.

4.2 Vertex-domain graph convolutional networks

Our implementation of vertex-domain GCN is inspired by the Shift-GCN (Cheng et al. 2020). As shown by the top branch in Fig. 2 by the structured spatiotemporal graph, a multi-layer spatiotemporal GCN is applied to extract the potential semantic information in the vertex domain. Our spatiotemporal stream adopts the spatial shift operation and temporal shift operation, which is first proposed for CNNs (Wu et al. 2018). To combine spatial information with temporal information, the same backbone (vertex-domain backbone) with ST-GCN (Yan et al. 2018) is utilized, which consists of nine residual GCN–TCN-Units.

4.2.1 Spatial shift graph convolution

Graph convolution in vertex domain has been illustrated in Sect.  2.1. It is generalized from CNNs to non-Euclidean data such as graphs. The Adjacency matrix, which demonstrates the connection of graphs, is adopted in the convolution operation. For spatial convolution, the refined sampling function B is divided into three subsets (root, centripetal, centrifugal) to fix the size of convolution kernels. The process of regular spatial graph convolution is shown in Fig. 3a. During the spatial graph convolution, three kinds of the Adjacency matrix are employed (A of root, A of centripetal, and A of centrifugal), which are used to model skeleton relations. The spatial graph is constructed as a tensor \(({\mathbf {T}})_{spatial} \in R^{V\times C}\), where V is the number of nodes and C is the channel of the human skeleton coordinates, which is 3 at the beginning. However, the GFLOPs is huge when the number of nodes increases and the connection becomes complicated.

Fig. 3
figure 3

This is the illustration of spatial graph convolution without shift operation in a. Spatial graph convolution with global shift operation is shown in b. The shift operation can model various relations across different joints in different channels with much lower GFLOPs

Full size image

Therefore, a spatial graph shift operation is adopted in our Vertex-domain stream for much lesser GFLOPs, as shown in Fig. 3b while extracting spatial information of the joints. The spatial graph \({{\mathbf {T}}}_{spatial}\in R^{V\times C}\) is operated by graph shift first before calculating convolution with \(C'\) spatial kernels of size C. The dimension of the output spatial graph is \((V\times C')\). There are two kinds of spatial shift operation, the local shift and the global shift (Cheng et al. 2020). The difference between them is that the global shift operation abandons the natural connected structure of the human body and has better performance. All joints operated as connected status, which means the Adjacency matrix is an identity matrix. The shift distance is i \({\mathbf {mod}}\) N of i th channel.

By denoting a node as v and its neighbor nodes (all other nodes) as \(N_{v}=\left\{ N_{v}^{1}, N_{v}^{2}, \ldots , B_{v}^{V-1}\right\}\). As shown in Fig. 3b, the length of channel C is divided into V segments. The first segment of the feature is retained. And other \(N-1\) feature segments are shifted from all other nodes. The output tensor \(\widetilde{{\mathbf {T}}}_{spatial}\in R^{V\times C}\) after global spatial shift operation is obtained. For node v, the feature \(\widetilde{{\mathbf {T}}}_{spatial}^{v}\) is shown as follows:

$${\widetilde{\mathbf {T}}}_{spatial}^{v}={\mathbf {T}}_{spatial}^{(v,: c)}\parallel {\mathbf {T}}_{spatial}^{(N_{v}^{1}, c: 2 c)}\parallel \cdots \parallel {\mathbf {T}}_{spatial}^{(N_{v}^{V-1}, (V-1)c:)},$$
(10)

where \(c=\left\lfloor \frac{C}{V}\right\rfloor\) and \(\parallel\) denotes the concatenation of the features from different channels. Each node gains the features of its neighbor nodes after the global spatial graph shift operation. The information between channels is exchanged. And that is the reason why shift operations can model various relations across different skeletons in different channels.

Instead of dividing the neighbor nodes into three categories and calculating the spatial convolution, spatial shift operation reduces computational complexity with \(C'\) \(1\times 1\) convolution kernels.

Aiming to endow different weights because of the different importance of skeleton joints, a learnable mask M is adopted to compute the element-wise product.

$${\widetilde{\mathbf {T}}}_{M}={\widetilde{\mathbf {T}}}_{spatial} \circ \text{ Mask } ={\widetilde{\mathbf {T}}}_{spatial} \circ (\tanh (\mathbf {M})+1).$$
(11)

4.2.2 Temporal shift graph convolution

The temporal information from human skeleton graphs is extracted by the temporal shift graph convolution operation shown in the top branch of Fig. 2.

The temporal shift convolution in graph to obtain temporal information is inspired by Wu et al. (2018), in which a Shift-CNN is proposed to simplify convolution operations. To extract temporal information, the spatial tensors \({{\mathbf {T}}}_{spatial}\) from time 1 to T are stacked as a temporal tensor \({{\mathbf {T}}}_{temporal} \in R^{T\times V\times C}\), where V denotes the number of nodes and the C is the channel of the human skeleton coordinates, which is 3 at the beginning. \({{\mathbf {T}}}_{temporal}\) is divided into C partitions, \(\{{{\mathbf {T}}}_{temporal}^{1}, {\mathbf {T}}_{temporal}^{2}, \ldots , {\mathbf {T}}_{temporal}^{T}\}\). For each partition, a learnable bias parameter \(S_c,c=1,2,\ldots ,C\) is obtained for adaptive temporal shift graph convolution.

As shown in Fig. 4, the temporal tensor \({\mathbf {T}}_{temporal}\) can use the traditional Shift convolution operator naturally because of its dimension. The process of shift operation in temporal shift graph convolution is like translating the original input matrix in a certain direction. In our vertex-domain graph convolution stream, the temporal bias is defined as real numbers instead of integer constraint. So the output \(\widetilde{T}_{temporal}\in R\) of node n after temporal shift at time t in channel c can be obtained:

$$\begin{aligned} {\widetilde{T}}_{temporal}(v, t, c)&=(1-\lambda ){\mathbf {T}}_{temporal}(v,\lfloor t+S_{c}\rfloor , c)\\&\quad +\lambda {\mathbf {T}}_{temporal}(v,\lfloor t+S_{c}\rfloor +1, c), \end{aligned}$$
(12)

where \(\lambda =S_{c}-\left\lfloor S_{c}\right\rfloor\) is the margin after realization of integer for backpropagation. After the temporal shift operation, \(C'\) convolution kernels with dimension C is employed to extract temporal information.

Fig. 4
figure 4

Illustration of temporal shift convolution in vertex stream. The dimension of the temporal tensor is suitable for Shift Convolution Operators. The learnable bias is obtained for adaptive temporal shift graph convolution

Full size image

4.2.3 Vertex-domain backbone

In order to extract spatiotemporal information through human skeleton data for action recognition effectively, a similar backbone with ST-GCN (Yan et al. 2018; Cheng et al. 2020) is adopted. As shown in the top branch of Fig. 2, residual connected GCN–TCN-Units are stacked, which are composed of 2 spatial shift operations, 2 temporal shift operations, and 2 point-wise convolution layers.

The essential purpose of the vertex-domain backbone is to extract both the spatial and the temporal domain features of the topological graph. In particular, the skeleton graphs’ embedded spatiotemporal information is extracted from the skeleton graphs, which is also called vertex-domain information in this paper. Both spatial shift convolution and temporal shift convolution belong to vertex-domain convolution illustrated in Sect. 2.1. The kernels are considered as templates for matching in the spatial domain or the temporal domain.

However, this is the limitation of the previous GCNs for skeleton action recognition. Some movements of human activity are pretty similar in the vertex domain. The shift spatial–temporal convolution exploring various relations across different skeletons is challenging to learn distinguishable features for this problem. According to GSP, spectral graph convolution is promoted from another perspective.

4.3 Spectral-domain graph convolutional networks

The spectral stream aims to extract the spectral domain information, which is local, stationary, and compositional through the Laplacian matrix L of the skeleton action graph. As illustrated in Sect. 2.1, according to spectral graph theory, an RSB-based architecture is proposed based on graph spectral convolution. The spectral-domain GCN is shown to be effective to extract high-level semantic patterns with the deep residual structure. Meanwhile, the spectral convolution operation can be studied and improved with strong mathematical tools such as spectral graph theory.

4.3.1 Spectral graph convolution

The previous work in GSP defined the Fourier transform on the graph. And then, the spectral-domain convolution on the graph is proposed. The definition of spectral-domain graph convolution is illustrated by Eq. 9 in Sect. 2.1. The purpose of our spectral graph convolution is to combine the deep learning architecture with it to propose a Spectral-domain GCN backbone.

The Let l denotes the number of the layer, the spectral graph convolution is shown as follows:

$$\begin{aligned} h^{l+1}&=\sigma (w^{l} *_{\mathcal {G}} h^{l})\\&=\sigma (\hat{w}^{l}(\Delta ) h^{l}), \end{aligned}$$
(13)

where \(\sigma\) is the activation function after spectral convolution and \(h^{l}\) denotes the input signal. \(w^{l}\) is the spectral filter to obtain the output \(h^{l+1}\). We adopt \(\hat{w}(\Delta )=\sum _{k=0}^{K-1} w_{k} T_{k}(\Delta )\) which is of the form of the Chebyshev polynomial parametrization of filters in the spectral domain. The Chebyshev expansion (Hammond et al. 2009) is to approximate kernels in Graph Signal Processing (GSP). And then the Chebyshev spectral convolution operation is obtained:

$$\begin{aligned} h^{l+1}&=\sigma (\hat{w}^{l}(\Delta ) h^{l})\\&=\sigma \left( \sum _{k=0}^{K-1}{w_{k}}^{l}T_{k}(\Delta )h^{l}\right) \\&=\sigma \left( \sum _{k=0}^{K-1}{w_{k}}^{l}X_{k}\right) , \end{aligned}$$
(14)

where \(X_{k}=2 \tilde{\Delta } X_{k-1}-X_{k-2}\), \(X_{0}=h\), \(X_{1}=\tilde{\Delta } h\) and \(\tilde{\Delta }=2 \lambda _{n}^{-1} \Delta -{\text {I}}\). The parameter \(w_{k}\) which is learned by backpropagation is a vector of polynomial coefficients. With the help of Chebyshev polynomial, there is no need to do the eigen-decomposition of the Laplacian matrix. And the spectral graph convolution does not depend on the eigenvector of the Laplacian matrix.

4.3.2 Spectral graph pooling

A graph coarsening method (the Graclus multilevel clustering algorithm) (Dhillon et al. 2007) is employed during the graph coarsening before graph pooling. It produces coarser graphs corresponds to the skeleton joints coordinates based on a greedy rule. The coarsening level lev demonstrates the depth of the spectral stream. At coarsening level \(lev^{n}\), the vertex \(v_{i}\) is matched with one neighbor unmarked vertex \(v_{j}\) to maximize the local normalized cut \(W_{i j}\left( 1 / d_{vi}+1 / d_{vj}\right)\). The weights of the two matched vertices are added and marked as \(v_{i}^{n+1}\).

After coarsening phase, in which the number of nodes is divided by approximately two from one level to the next coarser level, all the nodes and their coarsened version are formed into a balanced binary tree. The rearranged signal is much easier for pooling.

4.3.3 Spectral-domain backbone

As the discussion in Sect. 2.1, the vertex-domain backbone aims to explore various relations across different skeletons. However, the spatial–temporal information extracted by Vertex-domain GCN is limited while learning different patterns because of the similarity of some actions by vertex-domain graph convolution. So a deep spectral-domain backbone is proposed in this work based on spectral-domain graph convolution, which is shown to be effective in Sect. 5.

The spectral-domain backbone consists of multiple Spectral-Units to obtain spectral information, followed by a fully connected layer for classification. The architecture of our spectral-domain backbone is shown in the bottom branch in Fig. 2. The basic Spectral-Units are residual connected aiming to learn long-term dependencies by preventing the gradient vanishing problems. The comparison between simple spectral graph convolution and our residual spectral graph (RSB) convolution is shown in Fig. 5. The BatchNorm operation also increases the robustness of the model. A Channel Pooling module is applied for the feature map addition of different coarsening layers.

Fig. 5
figure 5

This is the comparison structure between simple spectral graph convolution layers and our residual spectral block, which enables the spectral stream to go deeper and is capable of representing high-level semantics

Full size image

5 Experiments and analysis

In this section, the datasets and the implementation details of DD-GCN are illustrated, followed by an ablation study and experiment analysis. An ablation study is also performed to prove the effectiveness of the spectral-domain stream based on spectral graph convolution. In the end, there are comparisons with other state-of-the-art approaches.

5.1 Datasets description

The performance of DD-GCN is evaluated on three large-scale public skeleton-based datasets: NTU-RGBD 60 (Shahroudy et al. 2016), NTU-RGBD 120 (Liu et al. 2020) and Kinetics-Skeleton (Yan et al. 2018) for the task of action recognition. An illustration of NTU-RGBD data samples is shown in Fig. 6.

Fig. 6
figure 6

Examples for class “hand waving”. The red line and green dots represent the skeletons (Color figure online)

Full size image

5.1.1 NTU-RGBD 60 dataset

NTU-RGBD 60 dataset is a large-scale skeleton action dataset which composed of 60 action classes. And the number of all these clips is 56,880. There are 40 different persons performing all the actions. Each action is captured by three cameras at the same height but from three different angles: \(-45^{\circ} , 0^{\circ} , 45^{\circ}\). The skeleton data used in this work contains 25 human joints. (Shahroudy et al. 2016) defines two benchmarks: cross-subject (CS) set and cross-view (CV) set. Both of them are evaluated in our experiments.

5.1.2 NTU-RGBD 120 dataset

NTU RGBD 120 dataset is an extended version of the NTU-RGBD 60 dataset by adding another 60 classes and another 57,600 video/skeleton samples. It consists of 114,480 action samples divided into 120 action classes. The number of persons of different ages increases to 106. The samples are captured in three angles which is the same as NTU-RGBD 60. The skeleton data employed in this work consists of 25 human joints, as shown in Fig. 6. The two benchmarks are also defined as CS and CV. The action can be categories into Daily Actions (82), Medical Conditions (12), and Mutual Actions/Two Person Interactions (26).

5.1.3 Kinetics-Skeleton dataset

Kinetics is an activity recognition dataset for RGB-based action recognition, which consists of 300,000 videos clips in 400 classes (Kay et al. 2017). Yan et al. (2018) construct a skeleton data based on it by extracting 18 body joints for each frame with an open-source toolbox OpenPose. Then the large-scale skeleton-based dataset called Kinetics-Skeleton is obtained. The training data is set to 240,000 skeleton clips, and the test data consists of 20,000 clips. This dataset is challenging, so both the top-1 and top-5 accuracies are present as other methods do.

5.2 Implement details of DD-GCN

The DD-GCN is implemented with Pytorch deep learning framework. Some hyperparameters are needed for both the vertex-domain stream and the spectral-domain stream. For NTU-RGBD 60 dataset and NTU-RGBD 120 dataset, the optimizer is SGD (stochastic gradient descent) method. And the loss function is cross-entropy loss. Similar to Cheng et al. (2020), the weight decay and initial learning rate of the vertex-domain stream are set to 0.0001 and 0.1. The learning rate decays by 10 at epoch of 60th, 80th, 100th. For spectral-domain stream on NTU-RGBD 60 dataset and NTU-RGBD 120 dataset, the weight decay and initial learning rate of the vertex-domain stream are set to 0.003 and 0.1. The learning rate decays by 10 at epoch of 30th, 40th.

For the Kinetics-Skeleton dataset, the SGD is adopted as the optimizer. The settings of weight decay and the initial learning rate are the same with NTU-RGBD datasets in the vertex-domain stream. For spectral stream, the weight decay, Nesterov momentum for SGD, the base learning rate is set to 0.001, 0.9, 0.001. The learning rate decays by 10 at epoch of 45th, 55th.

5.3 Ablation study

In this section, multiple sorts of strategies in DD-GCN are analyzed, such as the RSB strategies, the fusion strategies, and the keyframes strategies.

5.3.1 RSB strategies

The effectiveness of the spectral-domain backbone, which adopts the residual-connected spectral block, is evaluated in Table 1. Compared with the stream adopting simple spectral graph convolution, the residual spectral stream demonstrates a better performance with an increase of 15.1% and 12.9% on NTU-RGBD 60 CS and CV. Some recent experiments show that spectral-based GCN performs inferior to spatial-based GCN in some computer vision tasks. However, our experiments based on the RSB backbone show a certain development potential of the spectral convolution. The critical problem of the previous spectral convolution network lies in relatively shallow architecture. At the same time, residual-connected architecture for the spectral-domain stream of DD-GCN is capable of capturing deep spectral information. While combined with the vertex-domain stream, which focuses on the spatiotemporal information, the residual DD-GCN has a superior performance with an increase of 1.1% and 0.7% on CS and CV. In contrast, the simple DD-GCN seems strenuous to obtain adequate spectral information for the vertex-domain stream.

Table 1 The ablation study on NTU-RGBD dataset denoting the effectiveness of the Res-Spectral Unit
Full size table

Besides the numerical results, a qualitative analysis of the situations where the RSB succeeds is performed. As shown in Fig. 7, The performance gain shows that recognition ability is improved for most action classes. For the vertex-stream 1s-AAGCN, the recognition accuracy of almost all actions has been improved. Even for the 1s-ShiftGCN, it is shown that most of the actions that are improved by spectral-domain convolution. The actions concentrate in some interactive actions (two person) or some actions with broader dynamic changes. The interactive actions contain “A52. pat on back”, “A51. kicking”, “A30. type on a keyboard”, “A50. punch/slap” and etc. The dynamically changing actions include “A6. pick up”, “A8. sit down”, “A43. falling down”, “A26. hopping” and etc. The spectral information can be seen as a kind of global information complementary to the local information extracted from the vertex-domain convolution streams. That explains why these particular actions, including broader dynamic changes, benefit from the spectral-domain stream. However, the spectral stream seems weaker while distinguishing some detailed actions, such as “A16. wear a shoe” and “A17. take off a shoe”, in which the chronological order is important.

Fig. 7
figure 7

Illustration of the performance gain (%) of the spectral-domain stream with respect to the vertex-domain stream on the NTU-RGBD 60 dataset for the CS setting. The vertical axis is calculated by subtracting the DD-GCN accuracy of each action from the vertex-domain stream. The horizontal axis denotes the class of action as provided in Shahroudy et al. (2016)

Full size image

5.3.2 Fusion strategies

As shown in Table 2, the spectral-domain stream is fused with other GCN methods, which only obtain the spatial relationships and temporal dynamics simultaneously. Three kinds of GCNs are evaluated with our spectral-domain stream. ST-GCN (Yan et al. 2018) with spectral stream improves the results by 2.2% and 2.9% on NTU-RGBD 60 CS and CV. The improvement of 1s-AAGCN (Shi et al. 2020) fused with spectral stream is 0.7% on NTU-RGBD 60 dataset. And the DD-GCN has the best fusion effect with an increase of 1.1% and 2.9% on NTU-RGBD 60 CS and CV. ST-GCN proved to have the greatest improvement even though the other two have a superior performance according to their optimized spatial–temporal unit. The experiment results of the fused Shift-GCN and the fused 1s-AAGCN strategies are quite similar. However, owing to the spatial–temporal shift operation, the GFLOPs are more than three times lighter than the one in 1s-AAGCN. As shown in Table 2, the improvement in CV (7%) is not as obvious as in CS (1.1%). As we are concerned, the CV set is a simpler set using cameras 2 and 3 (37,920 clips) for training and camera 1 (18,960 clips) for testing. For the cross-view scenario, the model only with the vertex-domain GCN has obtained a robust representation ability. However, for the cross-subject conditions, our DD-GCN will have a better improvement.

Table 2 The ablation study on NTU-RGBD dataset denoting the effectiveness of the fusion with vertex-domain stream
Full size table

The vertex-domain stream is trained with a similar configuration and steps with 1s-Shift GCN in Cheng et al. (2020). However, instead of superimposing the same backbone redundantly in parallel with different preprocessed data (joints graph, bones graph, and their motion graphs), DD-GCN achieves a comparable experiment result with the complementary information from spectral-domain convolution. The experiment results show that the spectral-domain stream can improve the spatial–temporal GCNs generally, which indicates the flaw of the previous GCNs only focusing on optimizing local representation. Concretely, DD-GCN fuses a sort of global information through spectral-domain convolution derived by the GFT. We learn a series of global filters to represent the skeleton patterns by projecting the graph signal to the spectral-domain space. Different from the aggregation of features in the vertex domain, it has better support of mathematical theory.

5.3.3 Keyframes strategies

Meanwhile, the keyframes are calculated and extracted from the skeleton sequences for DD-GCN. As shown in Table 3, there is an improvement for both accuracy and effectiveness. The keyframes are obtained by evaluating the coordinate changes with the former frame. It is considered the motion information is incorporated manually as the motion stream in other multi-stream GCN methods, which can be seen as a manual attention mechanism. By prepossessing for the rough skeleton coordinates, the two-stream architecture is much easier to train. And the performance is shown to be more robust. DD-GCN with keyframes strategies improves the results by 0.3% and 0.2% on NTU-RGBD 60 CS and CV.

Table 3 The ablation study on NTU-RGBD dataset denoting the effectiveness of the keyframes strategies
Full size table

5.4 Comparison with other state-of-the-art approaches

To demonstrate the superiority and robustness of the two-stream architecture DD-GCN is compared with the state-of-the-art methods on three large-scale skeleton datasets: NTU-RGB 60 dataset (Shahroudy et al. 2016), NTU-RGB 120 (Liu et al. 2020) and Kinetics-Skeleton dataset (Yan et al. 2018).

5.4.1 Experiments on NTU-RGBD 60 dataset

On NTU-RGBD 60 dataset, the evaluation protocols on two sets: CS and CV are applied as in Shahroudy et al. (2016). Half of the cross-subject samples are employed for training and the other half are for evaluation. As for the cross-view scenario, two-thirds are used for training, and one-third used for evaluation. The comparison results are shown in Table 4. It is shown that our DD-GCN achieves an accuracy of 88.9% on the CS set and an accuracy of 95.8% on the CV set. The results are compared with the state-of-the-art methods. There is a certain gap between the performance of the methods (Vemulapalli et al. 2014; Jiang et al. 2020) using a handcraft descriptor based on Lie Group and the deep features. In the meanwhile, our DD-GCN outperforms all RNN-based and CNN-based methods owing to the excellent graph convolution operation in both vertex domain and spectral domain. Compared with the method based on GCNs, our method also proves its superiority.

Table 4 The comparisons of experiment results on NTU-RGBD 60 dataset
Full size table

For most GCN-based networks, DD-GCN also has better results owing to complementary information from the spectral backbone. DD-GCN has dramatically improved our previous model SS-GCN (Chen et al. 2021) owing to the improvement of the structure on both the spectral stream and the spatial–temporal stream. DD-GCN outperforms ST-GCN by 7.4%/7.5% on this dataset. Compared with the three-stream RA-GCN, our two-stream model has a 1.6%/2.2% increase on CS and CV set. ST-TR-AGCN (Plizzari et al. 2021) with a two-stream architecture outperforms our work by 0.3% on CS but the same on CV because of the attention mechanism in the spatial and temporal GCN units. As shown in Fig. 7, there is a general improvement for single-stream GCNs for most kinds of actions owing to the spectral information. Although the same two-stream network Shift-GCN performs slightly better, it uses additional bones data as input to train the same network for feature fusion. The SOTA work, such as 4s Shift-GCN and MS-AAGCN, uses additional data processing methods and repeats a model to improve accuracy. Despite this, our DD-GCN with a more robust spectral stream shows the complementarity between the two ways of graph convolution by further exploring the potential of spectral-domain convolution for skeleton action recognition.

5.4.2 Experiments on NTU-RGBD 120 dataset

On NTU-RGBD 120 Dataset, two standard evaluation protocols are applied in Liu et al. (2020). The comparison results are shown in Table 5. The experiment accuracy of DD-GCN is 84.9% for the CS set, 86.0% for the CV set. Compared with 3s RA-GCN, our two-stream model has a 3.8%/3.3% increase on CS and CV set. The performance of two-stream ST-TR-AGCN (Plizzari et al. 2021) concatenating spatial–temporal module with self-attention mechanism is 2.2%/1.3% lower than DD-GCN. The DD-GCN achieves 0.7% higher accuracy on CS set and 0.5% higher on CV set than the work in Wang et al. (2021). This demonstrates the superiority of our GCN model that utilizes the residual spectral stream based on the spectral-domain graph convolution.

Table 5 The comparisons of experiment results on NTU-RGBD 120 dataset
Full size table

The results of DD-GCN on the NTU-RGBD 120 dataset are 0.4% lower than 2s Shift-GCN, which superimposes the same backbone repeatedly with additional preprocessed data, the bone graphs (the differential of spatial coordinates). Compared with the SOTA 4s Shift-GCN, our results are slightly inferior but with much lesser parameters. Nevertheless, our work has benefited by fusing two distinguishing graph convolution operators. The experiment results show that our two-stream network is reasonable and practical to obtain the local diversities and the global dynamics even without additional data.

5.4.3 Experiments on Kinetics-Skeleton dataset

On the Kinetics-Skeleton dataset, the experiment is conducted following the protocol of Yan et al. (2018). The comparison results with state-of-the-art are shown in Table 6. DD-GCN has a 36.1% top-1 accuracy and 59.5% top-5 accuracy. Our DD-GCN shows superior results while fusing spatial–temporal and spectral information. Compared with Dynamic ST-GCN (Peng et al. 2021), DD-GCN has a higher accuracy of 3.0%/4.3%. DD-GCN is comparable with two-stream network ST-TR-AGCN (Plizzari et al. 2021). The accuracy of Pe-GCN (Yoon et al. 2021) is 2.3%/3.3% lower than DD-GCN while using the data without noise. According to Fig. 7, some actions are hard to classify by traditional GCNs based on vertex-domain graph convolution, while the two-stream architecture containing a distinguish graph convolution operation is shown to enhance the robustness of the model. As shown in Table 6, a not the best but comparable result is obtained when compared to the SOTA method MS-AAGCN (Shi et al. 2020) with extra preprocessed data mentioned above. However, there is potential for further improving the spectral backbone to handle the challenging dataset with various noises.

Table 6 The comparisons of experiment results on Kinetics-Skeleton dataset
Full size table

6 Conclusion

In this paper, a dual-domain GCN (DD-GCN) for skeleton-based action recognition is proposed. We integrate spectral-domain information with spatial–temporal information through an end-to-end two-stream architecture. A spectral-GCN backbone is proposed based on the spectral-domain graph convolution. Compared with the previous GCN, which only focuses on the spatial–temporal information of the skeleton graphs, we explore the complementary spectral-GCN architecture and the necessity. With a deep residual-connected RSB backbone, the accuracy of most actions has been improved, primarily the actions with broader dynamic changes in global. The experiment results on three large-scale datasets demonstrate the effectiveness of our DD-GCN. The ablation studies explore the reasons for the superiority of DD-GCN for the task of skeleton-based action recognition. The extensive experiments on three large-scale datasets, NTU-RGBD 60, NTU-RGBD 120, and Kinetics-Skeleton, show competitive or state-of-the-art performance. In the future, we will optimize the spectral-domain backbone for skeleton-based action recognition and hope to inspire more work to focus on the dual-domain graph convolutions.