Exponentiated Weibull regression for time-to-event data

Abstract

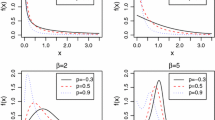
The Weibull, log-logistic and log-normal distributions are extensively used to model time-to-event data. The Weibull family accommodates only monotone hazard rates, whereas the log-logistic and log-normal are widely used to model unimodal hazard functions. The increasing availability of lifetime data with a wide range of characteristics motivate us to develop more flexible models that accommodate both monotone and nonmonotone hazard functions. One such model is the exponentiated Weibull distribution which not only accommodates monotone hazard functions but also allows for unimodal and bathtub shape hazard rates. This distribution has demonstrated considerable potential in univariate analysis of time-to-event data. However, the primary focus of many studies is rather on understanding the relationship between the time to the occurrence of an event and one or more covariates. This leads to a consideration of regression models that can be formulated in different ways in survival analysis. One such strategy involves formulating models for the accelerated failure time family of distributions. The most commonly used distributions serving this purpose are the Weibull, log-logistic and log-normal distributions. In this study, we show that the exponentiated Weibull distribution is closed under the accelerated failure time family. We then formulate a regression model based on the exponentiated Weibull distribution, and develop large sample theory for statistical inference. We also describe a Bayesian approach for inference. Two comparative studies based on real and simulated data sets reveal that the exponentiated Weibull regression can be valuable in adequately describing different types of time-to-event data.