Estimation of the cumulative incidence function under multiple dependent and independent censoring mechanisms

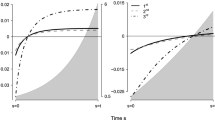
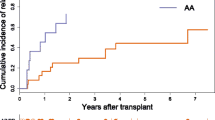
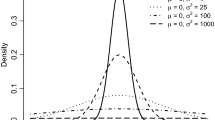
Abstract

Competing risks occur in a time-to-event analysis in which a patient can experience one of several types of events. Traditional methods for handling competing risks data presuppose one censoring process, which is assumed to be independent. In a controlled clinical trial, censoring can occur for several reasons: some independent, others dependent. We propose an estimator of the cumulative incidence function in the presence of both independent and dependent censoring mechanisms. We rely on semi-parametric theory to derive an augmented inverse probability of censoring weighted (AIPCW) estimator. We demonstrate the efficiency gained when using the AIPCW estimator compared to a non-augmented estimator via simulations. We then apply our method to evaluate the safety and efficacy of three anti-HIV regimens in a randomized trial conducted by the AIDS Clinical Trial Group, ACTG A5095.

Appendix

Equation (3) is an unbiased estimating equation for $F_{j}(t)$ since

$$\begin{aligned}&{\mathbf {E}\left( \frac{\tilde{\varDelta }}{\pi (\tilde{T}|\bar{V}_{\tilde{T}};\varLambda _{0})}\left\{ \mathbf {1}(T\le t, J=j)-{F}_{j}(t)\right\} \right) }\\&\quad = \mathbf {E} \left( \mathbf {E}\left\{ \frac{\tilde{\varDelta }}{\pi (\tilde{T}|\bar{V}_{\tilde{T}};\varLambda _{0})}\left\{ \mathbf {1}(T\le t, J=j)-{F}_{j}(t)\right\} | \bar{V}_{T},T \right\} \right) \\&\quad = \mathbf {E}\left( \frac{\mathbf {E}[\tilde{\varDelta } | \bar{V}_{T},T ]}{\pi (\tilde{T}|\bar{V}_{\tilde{T}};\varLambda _{0})} \left\{ \mathbf {1}(T\le t, J=j)-{F}_{j}(t)\right\} \right) \\&\quad = \mathbf {E}\left( 1 \cdot \left\{ \mathbf {1}(T\le t, J=j)-{F}_{j}(t)\right\} \right) \\&\quad = 0. \end{aligned}$$

The third equality follows from the fact that $\mathbf {E}\left( \tilde{\varDelta } | \bar{V}_{T},T \right) = Pr[\tilde{\varDelta } = 1 | \bar{V}_{T}, T]$ which under our coarsening at random assumption equals $\pi (\tilde{T}|\bar{V}_{\tilde{T}};\varLambda _{0})$. From this it is clear that Eq. (3) is an unbiased estimating equation for $F_{j}(t)$.

One can use the results in Robins and Rotnitzky (1992) to prove that with one type of censoring the solution to

$$\begin{aligned} \sum _{i=1}^{n}\bigg \{\frac{\tilde{\varDelta }_{i}}{\pi _{i}(\tilde{T}_{i}|\bar{V}_{\tilde{T}_{i}};\varLambda _{0})}\left\{ \mathbf {1}(T_{i}\le t, J_{i}=j)-{F}_{j}(t)\right\} - A_{i}\{F_{j}(t),\gamma ,b(\cdot )\} \bigg \}=0 \end{aligned}$$

(16)

with

$$\begin{aligned} A_{i}\{F_{j}(t),\gamma ,b(\cdot )\} \equiv \int \frac{b(u,\bar{V}_{u})}{\pi (u\text {-}|\bar{V}_{u};\varLambda _{0}(u))} dM_{C}(u) \end{aligned}$$

(17)

and $b(u,\bar{V}_{u})$ the same as in Eq. (9), is a doubly robust, locally efficient estimator for $F_{j}(t)$. Here, $dM_{C}(u) = dN_{C}(u) - d\varLambda (u)$. In our situation, with multiple types of censoring, it is easy to show that $dM_{C}(u) = \sum _{r=1}^{r*}dM_{C,r}(u)$, which leads to our augmentation term in (8). Note that with one type of failure and one type of censoring, our method reduces to that of (Rotnitzky and Robins 2005).

Now, it can be shown that for each r, since

$$\begin{aligned} \frac{b(u,\bar{V}_{u})}{\pi (u\text {-}|\bar{V}_{u};\varLambda _{0}(u))} \end{aligned}$$

is a bounded and predictable process, defined on the same filtration as $M_{C,r}(u)$,

$$\begin{aligned} \int \frac{b(u,\bar{V}_{u})}{\pi (u\text {-}|\bar{V}_{u};\varLambda _{0}(u))} dM_{C,r}(u) \end{aligned}$$

is a mean zero martingale Fleming and Harrington (1991, Thm 1.5.1). Note that the left-continuous versions of $b(u,\bar{V}_{u})$ and $\pi (u|\bar{V}_{u};\varLambda _{0}(u))$ are needed here. As a result

$$\begin{aligned} \sum _{r=1}^{r^{*}}\int \frac{b(u,\bar{V}_{u})}{\pi (u\text {-}|\bar{V}_{u};\varLambda _{0}(u))} dM_{C,r}(u) \end{aligned}$$

is also a mean zero martingale. Thus, $A_{i}\{F_{j}(t),\gamma ,b(\cdot )\}$ has mean zero. Since $A_{i}\{F_{j}(t),\gamma ,b(\cdot )\}$ has mean zero, it also follows trivially that Eq. (7) is an unbiased estimating equation for $F_{j}(t)$.