Introduction

Highly vagile bird species present a challenge for conservation because their mobility means that effective management actions must match the timing and locations of bird movements (Haig et al. 1998; Runge et al. 2016). Providing management actions at the right time and place differs from traditional conservation actions such as static reserves because it requires an understanding of the likely locations of birds, but the relative importance of the factors that determine bird movement are often unknown. This is particularly true for nomadic species, in which individuals may move irregularly over variable distances and directions, in response to resource availability, weather events, or other factors, compared to migrants which move regularly, usually over long distances in predictable directions and according to season (Mueller and Fagan 2008; Abrahms et al. 2017; Pedler et al. 2018; Watts et al. 2018).

In waterbirds, partial migration and nomadism are likely responses to variability and unpredictability in surface water availability and associated food resources at a range of scales (Chapman et al. 2011; Pedler et al. 2018; Roshier et al. 2008b; Buchan et al. 2020). Studies of Australian ducks have shown that flight initiation can be related to weather and resource conditions at the origin as well as the destination, and these studies have also posited that flight routes can be exploratory or based on individual experience (McEvoy et al. 2015; Roshier et al. 2008a). However, the influence of wind and other weather variables on the distance travelled by nomadic waterbirds, and subsequent site connectivity, are relatively poorly understood. In regular migrants, wind and weather can alter movement decisions during migration, and there is evidence of wind both facilitating or impeding migrations (Weber and Hedenström 2000; Navedo et al. 2010; Overdijk and Navedo 2012). Regular migrants adapt their routes to conserve energy in response to the environmental and weather conditions experienced during flight (La Sorte et al. 2015Horton et al. 2016) and this is likely also the case for nomadic species, with implications for connectivity and conservation management. However, until recently, opportunities to quantify such relationships and predict or forecast such variable movements have been rare.

Recent advances in tracking technology for mobile organisms are creating an explosion in data availability describing the positions of animals over time (Kranstauber et al. 2011). High resolution, high-frequency satellite tracking data can be paired with downscaled modelled and remotely-sensed environmental covariates to recreate the conditions encountered by a tracked organism in near real-time. The ability to match large datasets of position data with many predictor variables enables models to test a wide range of potential predictors to explain observed movement (Barbaree et al. 2018). These models allow inference, but to enable better decisions for species management, it would be useful to extend these models to prediction and forecasting.

Forecasting requires making testable predictions about the locations of birds. Similar to a weather forecast, the goal is to provide probabilistic estimates of likely locations of birds in advance of their movement, which can be used to help guide time- and place-based management actions, such as the provision of environmental water or predator control at predicted locations for birds (Reynolds et al. 2017; Golet et al. 2018). Relatively few studies have attempted to provide ecological forecasts, but there is a growing trend towards forecasting (Dietze et al. 2018) as the availability of ecological data streams increases with new technologies. High-profile forecasts have been published that predict bird migration along well-known migratory routes several days in advance using machine learning techniques combined with sources such as radar (Van Doren and Horton 2018) or citizen science presence data (Sullivan et al. 2014; Reynolds et al. 2017). Such approaches have great promise for regular migrants but may work less successfully for nomadic species that do not necessarily move en masse, follow regular routes or move with predictable timing.

Here, we propose a method to quantify connectivity and predict travel distances and directions using satellite tracking data for a nomadic waterbird. This is one component of a full predictive model of bird movement. Specifically, we focus on predicting how far a bird will fly, given that it undertakes a long-distance movement. Our approach predicts distance travelled given that a long-distance flight has commenced (i.e. it does not attempt to predict departure times). We use statistical modelling to infer the daily distance a bird moves and simulate bird movements along a least-cost path, drawn from distributions of predictor variables. The frequency of simulated arrivals at a location is used as a proxy of the probability of bird presence. We apply our method to predict the likelihood of arrival and probability of presence at important wetland sites to a case study of the straw-necked ibis (Threskiornis spinicollis) in Australia’s Murray–Darling basin.

Methods

Methods overview

Our method estimates two probabilities of long-distance movements, specifically (1) the probability of arrival at important wetlands; and (2) the probability of occurrence at a location. The probability of arrival measures the likelihood that the bird will be able to fly at least as far as the distance between two locations within a given time and is a useful measure of long-distance connectivity. The probability of occurrence at a location estimates the probability distribution of where birds will be located over a short time horizon (1–3 days), given that they have commenced a long-distance flight. It is useful for forecasting over comparatively short distances and timeframes.

Estimating the probability of arrival requires the following steps (Fig. 1):

Fig. 1
figure 1

Method used to determine the probability of arrival for straw-necked ibis in the Murray–Darling basin, Australia

Full size image
  1. (1)

    Statistical modelling of distance travelled, which uses a generalised additive model (GAM) to infer the expected distance that a bird will travel. The GAM uses satellite tracking data to fit distance travelled as a function of environmental predictors.

  2. (2)

    A connectivity model, which uses a resistance surface and least-cost path analysis to determine the distance between any two points in the landscape as perceived by a bird.

  3. (3)

    A simulation step, which determines the probability of arrival at a target wetland by sampling the distance travelled from the GAM model given a set of predictors. If the distance that the bird travels exceeds the least-cost distance between the origin and the target wetland, then the simulated bird arrives at the location. Conversely, if the distance travelled by the bird is less than the least-cost distance to the target wetland, the bird does not arrive. The frequency of successful arrivals is used as a measure of the probability of arrival.

Estimating the probability of occurrence uses the same first two steps as estimating the probability of arrival at important wetlands. However, the simulation step is modified. Specifically, the simulation steps are (Fig. 2):

Fig. 2
figure 2

Method used to determine the probability of occurrence for straw-necked ibis in the Murray–Darling basin, Australia

Full size image
  1. (1)

    Create a grid of fixed diameter around the origin and compute the distance to each grid cell using the least-cost path to the centroid of the grid cell.

  2. (2)

    Draw a sample of the environmental predictors to simulate a distance travelled by a bird (using the GAM) and a movement direction.

  3. (3)

    Assign the simulated bird to the nearest grid cell based on the movement direction and the distance travelled.

  4. (4)

    Repeat steps 2 and 3 many times. The probability of arrival at any grid cell is generated using the normalised frequency of arrival at the cell.

Case study: straw-necked ibis

We apply our method to 3.5 years (1327 days) of satellite tracking data (October 2016–June 2020) for 44 straw-necked ibis from the Murray–Darling basin in south–eastern Australia (Fig. 3a). The basin contains Australia’s largest river system and 16 Ramsar listed wetlands, many of which support significant colonial-nesting waterbird breeding sites (MDBA 2017), including straw-necked ibis. Significant declines in waterbird numbers across the basin (Kingsford et al. 2017) have prompted considerable effort to promote waterbird population recoveries, including management of environmental water to support mixed species breeding sites, and research tracking the movements of selected species between sites (McGinness et al. 2019). The dataset used here is a subset from the latter research, using solar GPS transmitters with location fix resolution of < 26 m, diurnal hourly fix frequencies (0700–1900 h) and a midnight fix representing the overnight roost location (McGinness et al. 2019). Straw-necked ibis spend the majority of their time foraging during the day and roosting nearby at night (McKilligan 1975), but make occasional long-distance movements which are the subject of this study. Although these long-distance movements can occur in any season, they are more frequent during spring and rare during winter (McGinness et al. 2019); Fig. 3b–c).

Fig. 3
figure 3

Summary information for our study: a Location of the Murray–Darling basin, Australia, with dark blue lines showing the main drainages. The red overlay shows the route of a straw-necked ibis that was tracked from December 2017–June 2020. The Murray–Darling basin is an important breeding and foraging stronghold for straw-necked ibis, however breeding and movements also occur outside the Basin. b Proportion of straw-necked ibis movements in different states during each season. HMM states are ordered 1–4 by increasing distance. c Indicative long-distance (HMM state 4) movements by season, scaled by relative frequency in the tracking data set

Full size image

To identify long-distance movements, we used hidden Markov modelling (HMM; using the moveHMM package in R (Michelot et al. 2016); see supporting information 2), to classify data into discrete states based on distance and direction (Patterson et al. 2009). The best-fit HMM identified 4 states, with mean hourly distances of 0.1 ± 0.09 (s.d.), 0.6 ± 0.44, 2.5 ± 2.57 and 27.5 ± 17.11 km respectively. Hourly data were aggregated to daily distances by summing the total distance moved during the day (see supporting information 2.2). HMM states were assigned to daily distances based on the most common hourly state of the bird during the day (states 1–3) or at least one fix in the state during the day (state 4). Since the first two states represent short-distance movement, we did not model them further. Data corresponding to states 3 and 4 were associated with longer-distance movement and were used for further modelling.

Each GPS fix was matched with a suite of 31 environmental covariates that were hypothesized to influence flight distance (See Table S3 in supporting information for a list of covariates). The environmental covariates fell into three main categories: landscape (e.g. aquatic ecosystem classifications (Brooks et al. 2014), water (e.g. area of water within a radius) and weather (e.g. temperature, pressure, wind, precipitation), and included several predictors derived specifically for ibis (see supporting information 2.1) and the modelled wind conditions experienced by the ibis during flight (supporting Information 2.1.1; also Fernández-López and Schliep (2019).

Identifying the drivers of flight distance

We used a generalised additive model (GAM) to infer flight distance from the environmental predictors in supporting information Table S3. GAMs are an extension of generalized linear models in which the response variable (daily distance travelled) depends linearly on unknown smooth functions of predictor variables. They provide a flexible modelling approach where the relationship between predictors and response may be nonlinear. Since the daily distance travelled is positive and nonzero, we fitted a GAM using the natural logarithm of the daily distance and a Gaussian family with an identity link.

Separate GAMs were fit for each of the longer-distance movement states (i.e. HMM states 3 and 4). To boost the number of state 4 movement days for inference, days were assigned to be in state 4 if at least one fix was recorded in state 4 during the day. This resulted in 527 days classified as state 4 movements. State 3 movements were assigned based on the most common movement state recorded during the day, resulting in 275 days classified as state 3 movements.

Several model structures were explored, including the effects of age class (adult and juveniles), different land use categories, and correlations between weather (primarily wind and temperature) and time of year (month) variables. Full details of the different model structures that were investigated are included in the ‘Formula’ fields of the Supplementary Tables in supporting information 4. The most parsimonious model structure for each movement state was selected using Akaike’s information criterion (AIC) (Akaike 1973).

Posterior prediction intervals (Francq et al. 2019) were generated from the best-fit GAMs for states 3 and 4. These intervals were subsequently used to simulate distances from covariate values. For details of the calculation of the posterior prediction interval, see supporting information 3.1.

Computing least-cost paths

To be able to simulate where birds go, it is necessary to convert the predicted distances from the GAM into flight paths for birds. Animals rarely move in straight lines, but instead interact with the landscape to follow preferred routes based on the impedance or permeability of the environment that they encounter. Resistance maps quantify the relationship between animal movement and the environment. In this study, we used a pre-existing model of habitat preference for mobile ibis to generate the resistance map (see supporting information 3.2 for details). The modelled cost of moving through a grid cell included five variables, i.e., Australian National Aquatic Ecosystem classification (Brooks et al. 2014), Multi-Resolution Valley Bottom Flatness (Gallant et al. 2012; National Vegetation Information System (NVIS Technical Working Group 2013), Catchment Scale Land Use of Australia (ABARES 2021), and Water Observations from Space (Geoscience Australia (2015). The fitted habitat model suggested that ibis preferred to move over flatter, wetter and unforested areas while in flight.

Once the resistance surface was generated, the least-cost path between any two points was computed using the gdistance package in R (van Etten 2017). The least-cost path is the minimum resistance route between locations. We assumed that organisms would attempt to follow the least-cost path through the resistance map (Nourani et al. 2018), so that the length of the least-cost path was assumed to be the distance between the two points.

Estimating the probability of arrival

We estimated the probability of arrival between known important breeding wetlands. The distance between each wetland was assumed to be the least-cost path between the centroid of the wetlands. We defined the probability of arrival at a wetland from an origin to be the frequency that a bird would exceed the distance between wetlands within a given travel time (we used d = 5 days). d daily distances were sampled from the GAM and summed to compute the total distance travelled in d days. If the total distance travelled exceeded the least-cost path between wetlands, the bird was considered to have arrived; otherwise, it did not arrive. This process was repeated for many simulated flights, and the probability of arrival was estimated by the proportion of simulations which arrived at the destination.

Estimating the probability of occurrence

The probability of occurrence estimates the likelihood that a bird will be in a location at a given time given that a long-distance flight has commenced. To calculate this, we specified a maximum radial distance from the origin and overlaid this circular area with a grid of specific cell size (we used 10 × 10 km cells for our case study). The least-cost path from the origin to each grid cell is computed and stored as an attribute of the grid. The set of grid cells represent all reachable areas, i.e. the probability sample space. The estimation of this probability is based on flight-simulations, where the probability of occurrence in a grid cell is generated by the proportion of simulated flights from the origin that are predicted to arrive in the cell.

To simulate flights for this calculation, we need to sample flight distance and direction. Both depend on environmental predictors, most notably season, wind speed and direction, and morning temperature. The inputs to our simulation are the number of days for the simulation, the wind speed and direction (one of 8 categorical directions, each representing a 45-degree compass interval), month and morning temperature. The simulation assumes that the categorical wind direction is constant (i.e. within a 45-degree compass interval) and that the bird remains in the same HMM movement state for the duration of the simulation.

To sample weather at an origin location, we used the GSODR package in R (Sparks et al. 2017) to extract 10 years (2010–2020) of daily wind speed and direction and mean temperature from the nearest weather station. We subset the data into months then sampled temperature, wind speed and wind direction values given the month. We created 8 directional states corresponding to 45-degree increments of the compass and assigned the sampled wind directions to each state.

We used an empirical Markov state-transition matrix to relate the direction of flight to the wind direction. The rows of the matrix were the 8 directional wind states and the columns of the matrix corresponded to 8 flight direction states that were equivalent to the 45-degree interval states used for the wind direction. The matrix elements represented the probabilities that a bird flew in a direction, given the wind direction corresponding to the row. These probabilities were computed from the subset of the tracking data corresponding to the modelled HMM state. Specifically, each probability was calculated from the number of observed flights in a direction given the wind direction, divided by the total number of recorded flights in which the wind blew in the direction represented by the row.

Simulation of a flight used the input season to sample temperature and wind speed uniformly from the nearest weather station data. Flight direction was then sampled from the wind direction state-transition matrix corresponding to the input wind direction state. To assign the flight to a destination grid cell within the probability sample space, we first selected the subset of gridcells that lay along the flight direction. From this subset, the destination grid cell was chosen to be the cell that had the closest least-cost path distance to the simulated flight distance.

We repeated this simulation process many times (50,000 simulated flights). The probability of arrival in a grid cell was the number of times a flight was assigned to the cell divided by the total number of simulated flights.

Results

Identifying the movement states using Hidden Markov Modelling

HMM states 1 and 2 had very short mean hourly distances travelled (0.1 km/h and 0.6 km/h) and were not modelled further. This was because it did not make sense to try to estimate the influence of environmental factors on distance travelled when movement levels were very low (i.e., by definition the influence of all variables should be low for these states).

HMM state 3, corresponding to a mid-distance movement, was driven by a strong difference in water extent. This suggested that state 3 movements are between dry and wet landscapes, so state 3 movements may represent shorter distance movements such as short return trips from a wetland to surrounding drier areas, rather than the long-distance movements of HMM state 4 that are of interest for basin-scale connectivity. The average distance travelled in HMM state 3 (3.1 km/h) was also much shorter than in HMM state 4 (28.5 km/h), supporting the hypothesis that state 3 movements are short- to mid-distance travels and not long-distance movements at the Basin scale. For this reason, we chose to consider only HMM state 4 movements in the remaining results.

Factors influencing distance travelled

When ibis were making long-distance movements, the strongest predictor of distance (HMM state 4) travelled was wind, with statistically significant but smaller effects from month. Birds tended to travel further when wind benefit was higher (Fig. 4a), and during the summer months (Fig. 4b). There was significant variation in the distance travelled between individual birds (p < 0.001; supporting information 4). Morning temperature was generally not significant however it appears to play a role in September and October.

Fig. 4
figure 4

Significant smoothed GAM partial effects of a wind benefit, and b month (date) on daily distance travelled for straw-necked ibis undertaking long-distance movement (HMM movement state 4). Only three state 4 movements were observed between June–August. Straw-necked ibis move very little in the winter months and this part of b should be interpreted with caution

Full size image

Computing the probability of arrival

On average, least cost paths between breeding sites were 182 km or 26% longer than the shortest distances, suggesting that straw-necked ibis do adjust their routes from the shortest paths to preferentially fly over or avoid particular landscape features, or to take advantage of weather conditions such as wind.

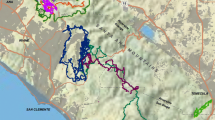
The predicted probability of arrival changed with wind and season. To illustrate this, we plotted average wind maps alongside our estimated connectivity plots. For example, for the Macquarie Marshes, predicted connectivity was strongest during the summer months (Fig. 5). Movement to wetlands to the west of the Macquarie Marshes was facilitated by south–easterly tail winds, while comparatively calm conditions in the central Basin allowed movement to more southerly wetlands. Connectivity remained strong to western wetlands in spring and autumn, supported by south–easterly winds in the northern basin, however movement to southern wetlands was impeded by southerly headwinds. During winter, wind conditions across the central Basin were comparatively calm, but headwinds and/or crosswinds (particularly easterly winds in the southern Basin) reduced connectivity to both the western and southern wetlands.

Fig. 5
figure 5

Average monthly wind maps (purple underlay) and probability of arrival of straw-necked ibis at important breeding wetlands from the Macquarie Marshes after 5 days of flight time in HMM state 4 (which represents long-distance movement). Darker pink lines show higher probabilities of arrival. Purple colours show the average wind strength for the month; wind vectors show average speed and direction. Results illustrate how connectivity changes with season by showing connectivity during months in the middle of each season. Connectivity is strongest during the summer and weakest during the winter (e.g. note the loss of connectivity between Macquarie Marshes and the Cuttaburra Channels, Paroo Overflow and Currawinya Lakes during the winter). Enlarged plots can be viewed using the Shiny app (see Data availability section), which also allows users to experiment with different origin sites

Full size image

The general pattern of connectivity observed in Fig. 5 was indicative of other major wetlands in the Basin: connectivity was strongest in the summer and weakest during the winter. The influence of wind observed for northern sites like Macquarie Marshes was also relevant for southern wetlands. For southern wetlands, relatively quiet wind conditions over summer and tail winds in spring (strong tail winds) and autumn (weaker tail winds) supported good connectivity during these months. In contrast, cross winds in winter in the southern basin reduced connectivity, particularly between northern and southern sites. Results for other wetlands can be viewed via our Shiny app (available from https://shiny.csiro.au/WaterbirdCnct).

Forecasting the probability of occurrence

Our forecasting tool predicts bird location given a minimal set of inputs (i.e., an origin location, a wind direction and the month of the year) and assuming that the bird has commenced a long-distance flight. Our forecasts provide probability density maps of likely positions for birds up to three days after departure (see example forecast in Fig. 6). In the figure, birds overwhelmingly fly in the direction of the tail wind, but the cone of likely locations becomes more diffuse as the number of days since the flight commenced increases. This means that it becomes harder to predict bird locations as more time passes. Although the effect is not very strong over short flight times, the least-cost path to each grid cell in the map creates heterogeneity within the plot, so that some cells have higher visitation probability than others (e.g. in Fig. 6, red grid cells are more frequently visited during simulations).

Fig. 6
figure 6

Three-day simulated probability of occurrence maps for straw-necked ibis departing Barmah forest in September with a southerly wind. Daily images are generated from 50,000 simulation runs. Grid cells are 10 km2

Full size image

Discussion

Our study addresses a known challenge for waterbird conservation, i.e., improving understanding of the factors affecting the distances travelled by nomadic waterbirds, the probability of birds arriving at important wetland sites, and the connectivity between these sites (Kingsford et al. 2010; McGinness 2016; Lester et al. 2020). We found that wind was an important predictor of the distance travelled by straw-necked ibis that are undertaking long-distance movements, an effect that has also been observed in other species (González-Solís et al. 2009; Liechti 2006; Nourani et al. 2018). The effect of wind speed and direction could be due to bird choices (i.e., birds deliberately wait for favourable strong winds before undertaking long distance flights (Weber and Hedenström 2000) and/or birds may simply fly further when the wind is favourable. Further study of movement cues, i.e. the factors that influence when and why birds commence, maintain and cease long-distance flights (Duriez et al. 2009; Winkler et al. 2014), would help to separate these hypotheses and would be useful for prediction (see below).

Although our study focused on a single species, our findings are likely to be relevant to other large nomadic waterbirds with similar behavioural and functional characteristics. This includes other Australian ibis, spoonbill, heron and egret species that are also known to make irregular large movements (Kingsford and Norman 2002). Our findings are also consistent with observations from regular migrants in other countries, where it is well-established that birds will adapt their migrations to coincide with favourable winds, often as a necessary condition of successful migration (Butler et al. 1997; Erni et al. 2005; Grönroos et al. 2012). Our findings thus suggest that despite the differences in the drivers of movement, Australian nomadic waterbird species may exploit wind in a similar way to obligate migrants elsewhere.

Quantifying connectivity (probability of arrival) can be used to help explain observed outcomes; for example, why did/didn’t birds arrive at breeding locations as expected? This can be done by computing the connectivity between locations and comparing the resulting insights with known outcomes. For example, if ibis did not arrive at a breeding site, was the connectivity score favourable, or was it likely that they did not arrive due to unfavourable flight conditions to the destination from other wetlands? This basin-scale connectivity approach can help to explain water management outcomes that may otherwise be difficult to explain if only the location of watering is considered. As demonstrated in Fig. 5, the probability of arrival connectivity modelling can be used to provide expected connectivity conditions at a mid-term to seasonal scale. For example, it could be used to ask whether ibis are likely to move between wetlands given an expected scenario. In the Murray–Darling basin, expected connectivity could be predicted by including seasonal weather forecasts (http://www.bom.gov.au/climate/ahead/) and the Resource Availability Scenarios (MDBA 2012) which provide seasonal outlooks for each catchment. Predicted wetland connectivity could inform water management—e.g., if a wetland was unlikely to be well-connected according to predictions, managers could discuss whether environmental water should be provided to support stopovers (and thus increase the chance of successful connectivity) or whether environmental water should instead be used elsewhere until conditions improve.

The probability of arrival modelling is useful for decision-making at the seasonal timescale, however because it does not model stopover locations, it does not provide guidance on short-term or daily actions that support movement in real time. Although our modelling demonstrates that long-distance ibis movements rely on wind, birds need water at the locations where they stopover during their long-distance flights. Providing water (or other management) at stopover sites is a way to support movement but requires a predictive model of where birds will be at a given time. We developed the probability of occurrence mapping to address this need and provided forecasts of bird position at a suitable timescale to allow management actions to be matched to bird movements. This kind of real-time management has been demonstrated to be highly successful for migrants with predictable periods of passage in North America (Golet et al. 2018). Building on the forecasting models presented here could help to ensure that environmental water is delivered to the places and times when it can be maximally effective for supporting movement (Reynolds et al. 2017).

The forecast tool has three major caveats that mean it should be viewed as a proof of concept rather than used directly for for management. Firstly, the model assumes that birds have commenced a long-distance flight. The utility of the model would be increased if we could combine it with a predictive model of when and where birds were likely to commence flight, i.e. departure cues (Duriez et al. 2009; Winkler et al. 2014; Weller et al. 2022). Studies of Australian waterbirds suggest that rainfall and water resources are key drivers in initiating movement (Kingsford et al. 2010), but the ability to detect distant resources also involves exploration and is thus not necessarily fully predictable. Grey teal (Anas gracilis), banded stilts (Cladorhynchus leucocephalus) and pacific black ducks (Anas superciliosa) respond to rainfall at destinations several hundred to thousands of kilometres away, but also undertake more opportunistic ‘ranging’ flights, including to areas without recent rain (Pedler et al. 2018; Roshier et al. 2008a). The ability to predict departure dates is also complicated by proximate weather conditions, especially rainfall and wind, which have been shown to influence departure decisions in some species, including straw-necked ibis (McKilligan 1975; Liechti 2006; McEvoy et al. 2015). Despite the challenges involved, if a predictive model of the probability of departure could be built, this component could then be linked with our existing forecasting model to predict bird locations.

Secondly, our model assumes that birds fly consistently in the HMM state 4 (i.e., long-distance flight) and do not take extended stopovers. This restricts our ability to test our predictions, since our test data is restricted to a small number of observed cases where birds fly for several days in HMM state 4 without switching states. This is further exacerbated because our model predicts the movements of an ‘average’ bird, so several test cases are necessary to validate our model. Since our model assumes a given departure point, testing our model requires capturing several multi-day long-distance movements from the same location at the same time which is difficult when relatively few birds are tagged at any one time and place. The available testing set could be vastly increased if our model could quantify the probability of switching between movement states. The probability of changing state can be parameterized using the hidden Markov Modelling approach (Patterson et al. 2009) and is a promising area for improving the model.

Thirdly, our forecasting model is currently only designed to forecast flights over a short period. This is partly because wind forecasts are only likely to be briefly accurate, and partly because our forecasting model assumes that birds fly without regard for their destination. This may be plausible early in the flight, however as the length of the flight increases and the bird gets closer to a destination wetland, they may modify their behaviour (known as ‘drift compensation’) to reach a known important wetland (Liechti 2006; Technitis et al. 2015; van Toor et al. 2018). Future research may consider this attraction to a destination, and if successful, would provide a more complete model.

Addressing the caveats of our model requires a framework for developing a full predictive model of waterbird movement. Modelling and forecasting of proximate and distal cues could be combined with our method into a predictive probabilistic model of bird movement that would be testable using high quality movement datasets. Although further research is needed to develop a full model, this is the first attempt to forecast the movements of waterbirds in the Murray–Darling basin and provides a useful first step towards facilitating a real-time management to support waterbird movement.

Conclusion

Our study identifies factors influencing long-distance movements and introduces an original approach to forecast the distance travelled by a large waterbird species and predict the probability of connectivity between important wetlands. The results suggest that straw-necked ibis respond to local water during short-distance movements associated with foraging and breeding but will make use of strong winds to support long-distance movements. Our models estimate the connectivity between important wetlands and forecast the likely location of birds given a long-distance flight has commenced and a set of environmental input conditions. Predicting where birds will be is useful for conservation management because it enables agile actions to be implemented at the times and places that are most beneficial. Although additional research is required for a fully predictive movement model, our approach demonstrates the power of long-term tracking data for understanding complex nomadic bird movements.